Summen- und Produktnotation

Als Referenz führt dieser Abschnitt die Terminologie ein, die in einigen Texten verwendet wird, um die einer Karnaugh-Map zugewiesenen Minterms und Maxterms zu beschreiben. Ansonsten gibt es hier kein neues Material.

Terminologie für Minterms

Σ (Sigma) steht für Summe und Kleinbuchstaben „m“ für Minterms. Σm gibt die Summe der Minterms an. Das folgende Beispiel wird noch einmal aufgegriffen, um unseren Standpunkt zu veranschaulichen. Anstelle einer booleschen Gleichungsbeschreibung der nicht vereinfachten Logik listen wir die Minterms auf.

f(A,B,C,D) =Σ m(1, 2, 3, 4, 5, 7, 8, 9, 11, 12, 13, 15) oder f(A,B,C,D) =Σ(m1 ,m2 ,m3 ,m4 ,m5 ,m7 ,m8 ,m9 ,m11 ,m12 ,m13 ,m15 ) 

Die Zahlen geben den Zellenstandort oder die Adresse innerhalb einer Karnaugh-Karte an, wie unten rechts gezeigt. Dies ist sicherlich ein kompaktes Mittel, um eine Liste von Minterms oder Zellen in einer K-Map zu beschreiben.

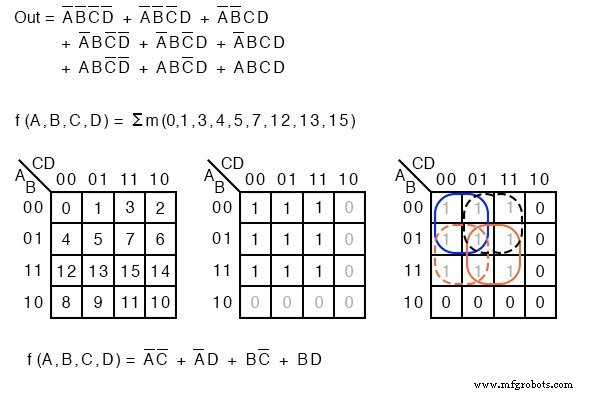
Die Sum-Of-Products-Lösung ist von der neuen Terminologie nicht betroffen. Die Minterms, 1 s, in der Map wie gewohnt gruppiert und eine Sum-OF-Products-Lösung geschrieben.

Terminologie für Maxterms

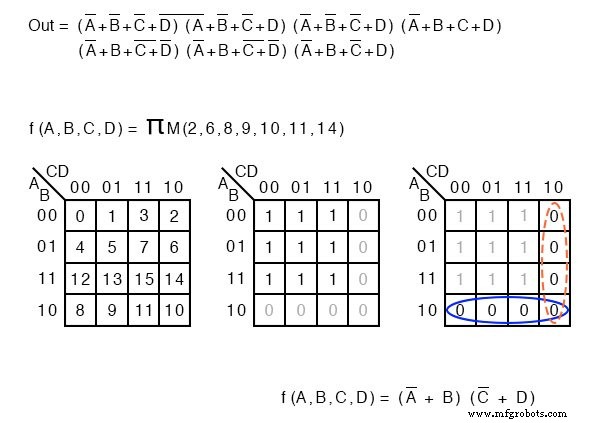
Im Folgenden zeigen wir die Terminologie zur Beschreibung einer Liste von maxterms. Das Produkt wird durch das griechische Π (pi) angezeigt, und das Großbuchstabe „M“ zeigt maxterms an. ΠM gibt das Produkt von maxterms an. Das gleiche Beispiel veranschaulicht unseren Standpunkt.

Die boolesche Gleichungsbeschreibung der nicht vereinfachten Logik wird durch eine Liste von maxterms ersetzt.

f(A,B,C,D) =Π M(2, 6, 8, 9, 10, 11, 14) oder f(A,B,C,D) =Π(M2 , M6 , M8 , M9 , M10 , M11 , M14 ) 

Wiederum geben die Zahlen K-Map-Zellenadressenstellen an. Für maxterms ist dies die Position von 0 s, wie unten gezeigt. Eine Product-OF-Sums-Lösung wird in gewohnter Weise abgeschlossen.

$$Out =(A + B + \bar{C} + D)(A + \bar{B} + \bar{C} + D) + (\bar{A} + B + C + \bar{D }) + (\bar{A} + B + \bar{C} + D)$$

$$(\bar{A} + B + \bar{C} +\bar{D})(\bar{A} + \bar{B} + \bar{C} + D)$$

VERWANDTE ARBEITSBLÄTTER:

• Arbeitsblatt für Summen von Produkten und Produkt-von-Summen-Ausdrücken
• Karnaugh-Mapping-Arbeitsblatt
• Arbeitsblatt zur Booleschen Algebra