Spannungsteilerregel (VDR) – Gelöste Beispiele für R-, L- und C-Schaltungen
Spannungsteilung „VDR“ für resistive, induktive und kapazitive Schaltungen
Was ist die Spannungsteilerregel?
Wenn in einer Schaltung mehrere Elemente in Reihe geschaltet sind, teilt sich die Eingangsspannung über die Elemente. Und in einer Schaltung, wenn mehrere Elemente parallel geschaltet sind, teilt sich der Strom über die Elemente auf.
Daher wird in einer Parallelschaltung die Stromteilerregel und in einer Reihenschaltung die Spannungsteilerregel zur Analyse und Lösung der Schaltung verwendet.
Wenn zwei oder mehr Impedanzen in Reihe geschaltet werden, wird die Eingangsspannung auf alle Impedanzen aufgeteilt. Um die Spannung über jedem Element zu berechnen, wird die Spannungsteilerregel verwendet. Die Spannungsteilerregel ist die wichtigste und einfachste Regel in der Schaltungsanalyse, um die individuelle Spannung beliebiger Elemente zu berechnen.
Die Spannungsteilerregel wird auch als Potentialteilerregel bezeichnet. Unter bestimmten Bedingungen benötigen wir eine bestimmte Ausgangsspannung. Aber wir haben diesen spezifischen Wert der Quelle nicht. In diesem Zustand stellen wir eine Reihe passiver Elemente her und reduzieren den Spannungspegel auf einen bestimmten Wert. Und hier wird die Spannungsteilerregel verwendet, um die spezifische Ausgangsspannung zu berechnen.
Je nach den in der Schaltung verwendeten Elementen kann die Spannungsteilerregel in drei Typen eingeteilt werden; Widerstandsspannungsteiler, induktiver Spannungsteiler und kapazitiver Spannungsteiler. Jetzt werden wir die Spannungsteilerregel für alle diese Arten von Schaltungen beweisen.
Verwandter Beitrag:
- Spannungsteiler „VDR“-Rechner, Beispiele und Anwendungen
- Gleichungen für Spannungs- und Stromteilerregeln (VDR und CDR)
Spannungsteilerregel für Widerstandsschaltungen
Um die resistive Spannungsteilerregel zu verstehen, nehmen wir eine Schaltung mit zwei Widerständen, die in Reihe mit der Spannungsquelle geschaltet sind.
Da die Widerstände in Reihe geschaltet sind, ist der Strom, der durch beide Widerstände fließt, gleich. Aber die Spannung ist nicht für beide Widerstände gleich. Die Eingangsspannung der Schaltung teilt sich auf beide Widerstände auf. Und der Wert der einzelnen Spannung hängt vom Widerstand ab.
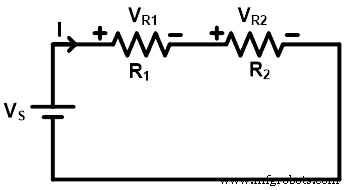
Wie in der obigen Abbildung gezeigt, zwei Widerstände R1 und R2 sind mit der Spannungsquelle Vs in Reihe geschaltet . Der von der Quelle gelieferte Gesamtstrom beträgt I Ampere. Da alle Elemente in Reihe geschaltet sind, entsteht eine einzelne Schleife und der Strom, der durch alle Elemente fließt, ist gleich (I Ampere).
Die Spannung am Widerstand R1 ist VR1 und die Spannung über dem Widerstand R2 ist VR2 . Und die gesamte zugeführte Spannung teilt sich zwischen beiden Widerständen auf. Daher ist die Gesamtspannung eine Summe von VR1 und VR2 .
VS =V R 1 + V R 2 … (1)
Nach dem Ohmschen Gesetz
VR1 =IR 1 + IR 2 … (2)
Daher aus den Gleichungen (1) und (2);
VS =IR 1 + IR 2
VS =I(R 1 + R 2 )
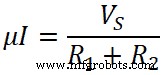
Setzen Sie nun den Wert des Stroms I in die Gleichung-(2);
VR1 =IR 1
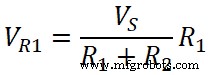
Ähnlich;
VR2 =IR 2
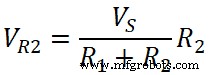
Daher ist die Spannungsteilerregel für eine Widerstandsschaltung der Stromteilerregel entgegengesetzt. Hier ist die Spannung des Widerstands ein Verhältnis der Multiplikation der Gesamtspannung und dieses Widerstands zum Gesamtwiderstand.
Verwandte Beiträge:
- Der Satz von Thevenin. Schritt-für-Schritt-Anleitung mit gelöstem Beispiel
- Theorem von Norton. Schritt-für-Schritt-Anleitung mit gelöstem Beispiel
Gelöstes Beispiel einer Widerstandsschaltung mit VDR
Beispiel-1
Finde die Spannung über jedem Widerstand mit der Spannungsteilerregel.
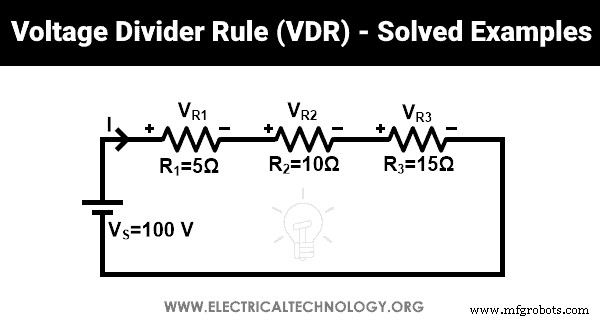
Hier drei Widerstände (R1 , R2 , und R3 ) sind in Reihe mit 100 V Quellenspannung geschaltet. Die Spannung über den Widerständen R1 , R2 , und R3 sind VR1 , VR2 , und VR3 bzw..
Die Spannung am Widerstand R1;
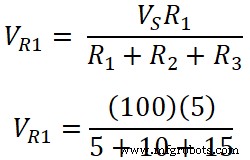
VR 3 =500 / 30
VR 3 =16,67 V
Die Spannung über dem Widerstand R2;
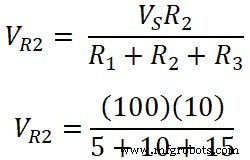
VR 3 =100 / 30
VR 3 =33,33 V
Die Spannung am Widerstand R3;
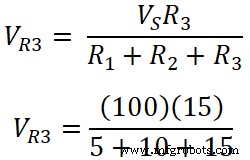
VR 3 =1500 / 30
VR 3 =50 V
Gesamtspannung VT;
VT =V R 1 + V R 2 + V R 3
VT =16,67 + 33,33 + 50
V T =100 V
VT =VS
Daher ist bewiesen, dass die Gesamtspannung =ähnlich der zugeführten Spannung ist.
Spannungsteilerregel für induktive Schaltungen
Wenn eine Schaltung mit mehr als zwei Induktoren in Reihe geschaltet wird, ist der Strom, der durch die Induktoren fließt, derselbe. Aber die Quellenspannung wird auf alle Induktivitäten aufgeteilt. In diesem Zustand kann die Spannung über dem einzelnen Induktor durch die Induktorspannungsteilerregel ermittelt werden.
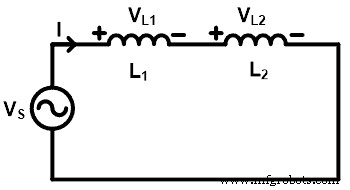
Stellen Sie sich vor, wie in der obigen Abbildung gezeigt, zwei Induktoren (L1 und L2 ) sind in Reihe geschaltet. Und der Gesamtstrom, den ich durch die Induktivität lasse. Die Spannung über der Induktivität L1 ist VL1 und die Spannung über dem Induktor L2 ist VL2 . Und die Versorgungsspannung ist VS . Jetzt müssen wir die Spannung VL1 finden und VL2 unter Verwendung der Induktivitäts-Spannungsteiler-Regel.
Wie wir die Spannungsgleichung für die Induktivität kennen;
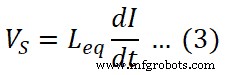
Wobei Leq ist die Gesamtinduktivität des Stromkreises. Hier sind zwei Induktivitäten in Reihe geschaltet. Daher ist die Ersatzinduktivität die Summe beider Induktivitäten.
Leq =L 1 + L 2
Von, gleichung-(3);
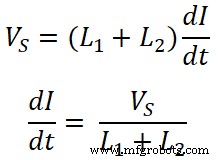
Nun die Spannung über Induktor L1 ist;
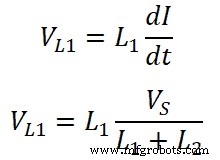
Ähnlich die Spannung über Induktor L2 ist;
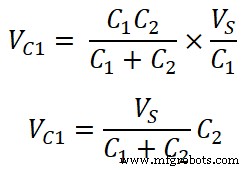
Also können wir sagen, dass die Spannungsteilerregel für eine Induktivität dieselbe ist wie für die Widerstände.
Gelöstes Beispiel einer induktiven Schaltung mit VDR
Beispiel-2
Finden Sie die Spannung über jedem Induktor für die gegebene Schaltung mithilfe der Spannungsteilerregel.
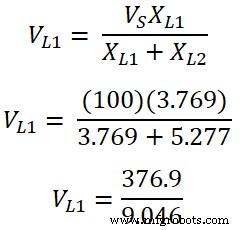
Hier sind zwei Induktoren in Reihe mit einer 100-V-60-Hz-Quelle geschaltet. Die Spannung über der Induktivität L1 ist VL1 und die Spannung über dem Induktor L2 ist VL2 .
Um die Spannung über Spulen zu finden, müssen wir die Blindimpedanz jeder Spule finden.
Die Blindimpedanz über Induktor L1 ist;
XL 1 =2 π f L1
XL 1 =2 × 3,1415 × 60 × 10 × 10 -3
XL 1 =3,769 Ω
Die Blindimpedanz über Induktor L2 ist;
XL 2 =2 π f L2
XL 2 =2 × 3,1415 × 60 × 14 × 10 -3
XL 2 =5,277 Ω
Nach der Spannungsteilerregel
Die Spannung über der Induktivität L1 ist;
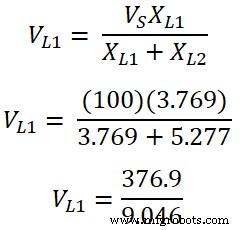
V L 1 =41,66 V
Die Spannung über Induktor L2 ist;
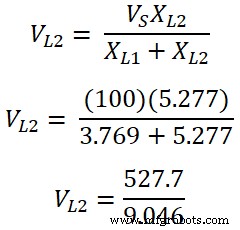
VL 2 =58,35 V
Gesamtspannung VT ist;
VT =V L 1 + V L2
VT =41,66 + 58,35
V T =100 V
VT =VS
Also ist die Gesamtspannung gleich der zugeführten Spannung.
Spannungsteilerregel für Kapazitiv Schaltungen
Bei einem Kondensator ist die Spannungsteilerregel anders als bei der Induktivität und dem Widerstand. Um die Spannungsteilerregel für Kondensatoren zu berechnen, betrachten wir eine Schaltung mit zwei oder mehr in Reihe geschalteten Kondensatoren.
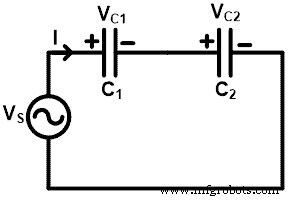
Hier sind zwei Kondensatoren in Reihe mit der Quellenspannung VS geschaltet . Die Quellenspannung teilt sich in zwei Spannungen; eine Spannung liegt über dem Kondensator C1 und eine zweite Spannung liegt über dem Kondensator C2 .
Die Spannung am Kondensator C1 ist VC1 und die Spannung über dem Kondensator C2 ist VC2 . Wie im obigen Schaltbild dargestellt, sind beide Kondensatoren in Reihe geschaltet. Daher ist die äquivalente Kapazität;
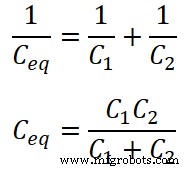
Die von der Quelle gelieferte Gesamtladung ist Q;
Q =C eq VS
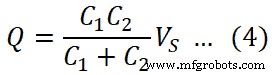
Die Spannung am Kondensator C1 ist;
VC1 =Q 1 / C 1
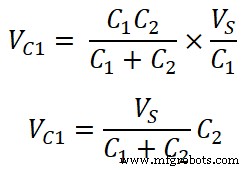
Die Spannung am Kondensator C2 ist;
VC2 =Q 1 / C 2
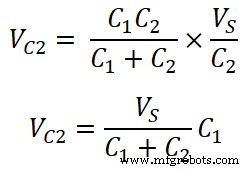
Aus der Berechnung können wir also sagen, dass die individuelle Spannung über dem Kondensator ein Verhältnis der Multiplikation der gesamten Quellenspannung und der entgegengesetzten Kapazität zur Gesamtkapazität ist.
Gelöstes Beispiel einer kapazitiven Schaltung mit VDR
Beispiel-3
Finden Sie die Spannung über jedem Kondensator für ein bestimmtes Netzwerk mithilfe der Spannungsteilerregel.
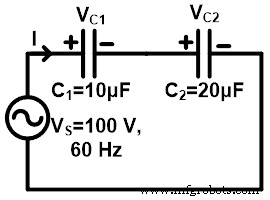
Hier sind zwei Kondensatoren in Reihe mit einer 100-V-60-Hz-Quelle geschaltet. Die Spannung am Kondensator C1 ist VC1 und die Spannung über dem Kondensator C2 ist VC2 .
Um die Spannung über jedem Kondensator zu berechnen, müssen wir die kapazitive Impedanz ermitteln.
Die kapazitive Impedanz über C1 ist;
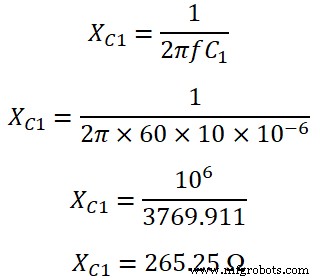
Die kapazitive Impedanz über C2 ist;
X C 2 =1 / (2 π f C2 )
X C 2 =1 / (2 π × 60 × 20 × 10 -6 )
X C 2 =10 -6 / 7539.822
X C 2 =132,63 Ω
Gemäß der Spannungsteilerregel die Spannung am Kondensator C1 ist;
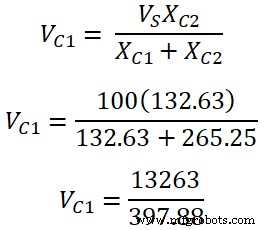
V C1 =33,33 V
die Spannung am Kondensator C2 ist;
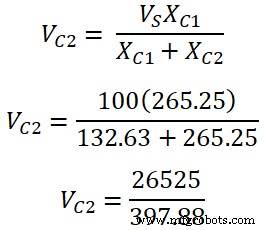
V C 2 =66,67 V
Die Gesamtspannung über dem Kondensator VT ist;
VT =V C 1 + V C2
VT =33,33 + 66,67
V T =100 V
VT =VS
Verwandte Tutorials zur Analyse elektrischer Schaltungen:
- SUPERNODE Schaltungsanalyse – Schritt für Schritt mit gelöstem Beispiel
- SUPERMESH Schaltungsanalyse – Schritt für Schritt mit gelöstem Beispiel
- Spannungsteilerregel „VDR“-Rechner – Beispiele &Anwendungen
- Current Divider Rule „CDR“-Rechner – Beispiele &Anwendungen
- Kirchhoffs Strom- und Spannungsgesetz (KCL &KVL) | Gelöstes Beispiel
- Cramers Rule Calculator – 2- und 3-Gleichungssystem für elektrische Schaltungen
- Wheatstone-Brücke – Schaltung, Funktionsweise, Ableitung und Anwendungen
- Rechner für Elektrotechnik und Elektronik
- 5000+ elektrische und elektronische Formeln und Gleichungen
Industrietechnik



