Current Divider Rule (CDR) – Gelöste Beispiele für AC- und DC-Schaltungen

Current Division „CDR“ für resistive, induktive und kapazitive Schaltungen

Was ist Current Divider Rule (CDR)?

Wenn mehrere Elemente parallel geschaltet werden, teilt sich der Strom in mehrere parallele Pfade auf. Und die Spannung ist für alle Elemente gleich, die gleich der Quellenspannung sind.

Mit anderen Worten, wenn der Strom durch mehr als einen parallelen Pfad fließt (die Spannungsteilerregel „VDR“ oder Spannungsteilung wird verwendet, um die Spannung in den Reihenschaltungen zu berechnen), die aktuelle Teilung in jedem Pfad. Der Wert des Stroms, der durch einen bestimmten Zweig fließt, hängt von der Impedanz dieses Zweigs ab.

Die Stromteilerregel oder Stromteilungsregel ist die wichtigste Formel, die häufig zum Lösen von Schaltungen verwendet wird. Wir können den Strom ermitteln, der durch jeden Zweig fließt, wenn wir die Impedanz jedes Zweigs und den Gesamtstrom kennen.

Der Strom fließt immer durch die geringste Impedanz. Der Strom hat also eine umgekehrte Beziehung zur Impedanz. Gemäß dem Ohmschen Gesetz wird der Strom, der in den Knoten eintritt, umgekehrt proportional zur Impedanz zwischen ihnen aufgeteilt.

Das bedeutet, dass die Impedanz mit dem kleineren Wert einen größeren Strom hat, da der Strom den Weg mit dem geringsten Widerstand gewählt hat. Und der Widerstand mit dem größeren Wert hat den geringsten Strom.

Je nach Schaltungselementen kann die Stromteilerregel Widerstände, Spulen und Kondensatoren beschreiben.

Stromteilerregel für Widerstandsschaltungen

Um die Widerstandsstromteilerregel zu verstehen, nehmen wir eine Schaltung, in der die Widerstände parallel geschaltet sind. Das Schaltbild ist in der Abbildung unten dargestellt.

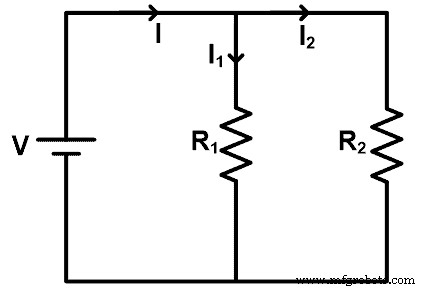
In diesem Beispiel versorgt eine Gleichstromquelle alle Widerstände. Die Spannung der Widerstände ist die gleiche wie die Quellenspannung. Aufgrund der Parallelschaltung teilt sich der Strom jedoch in verschiedene Pfade auf. Der Strom teilt sich an jedem Knoten und der Wert des Stroms hängt vom Widerstand ab.

Mit Hilfe der Stromteilerregel können wir direkt den Wert des Stroms ermitteln, der durch jeden Widerstand fließt.

In diesem Beispiel ist der von der Quelle gelieferte Hauptstrom I. Und er teilt sich in zwei Widerstände R₁ und R₂ . Der Strom fließt durch den Widerstand R₁ ist I₁ und der Strom fließt durch den Widerstand R₂ ist I₂ .

Da die Widerstände parallel geschaltet sind. Der äquivalente Widerstand ist also R_eq .

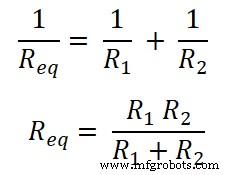
Nun, nach dem Ohmschen Gesetz;

V =I R_eq

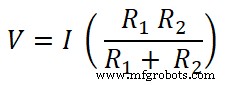
Beide Widerstände sind parallel zu einer DC-Quelle geschaltet. Daher ist die Spannung über dem Widerstand gleich der Quellenspannung. Und der Strom, der durch den Widerstand R₁ fließt ist I₁ .

Also, für Widerständler R₁;

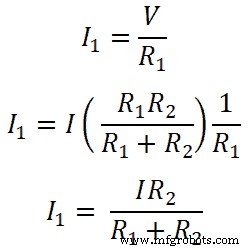
Ähnlich für Widerständler R₂;

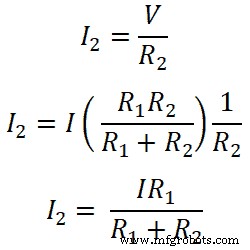
Diese Gleichung zeigt also eine Stromteilerregel für parallel geschaltete Widerstände. Aus diesen Gleichungen können wir sagen, dass der Strom, der durch den Widerstand fließt, gleich dem Verhältnis der Multiplikation des Gesamtstroms und des Gegenwiderstands mit dem Gesamtwiderstand ist.

Verwandte Beiträge:

• Der Satz von Thevenin. Schritt-für-Schritt-Anleitung mit gelöstem Beispiel
• Theorem von Norton. Schritt-für-Schritt-Anleitung mit gelöstem Beispiel

Stromteilerregel für induktive Schaltungen

Wenn Induktoren parallel geschaltet sind, können wir die Stromteilerregel anwenden, um den Strom zu ermitteln, der durch jeden Induktor fließt. Um die Stromteilerregel zu verstehen, nehmen wir eine Schaltung, in der die Induktoren parallel geschaltet sind, wie in der Abbildung unten gezeigt.

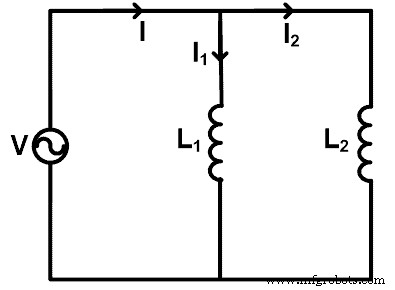
Hier zwei Induktoren (L₁ und L₂ ) sind parallel zu einer Quellenspannung V geschaltet. Der Gesamtstrom, der durch die Quelle fließt, beträgt I Ampere. Der Strom fließt durch die Induktivität L₁ ist I₁ und der Strom fließt durch die Induktivität L₂ ist I₂ .

Jetzt müssen wir die Gleichungen für den Strom I₁ finden und I₂ . Dafür finden wir die äquivalente Induktivität L_eq;

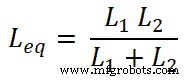
Wir wissen, dass der Gesamtstrom, der durch die Schaltung fließt, gleich I ist und entspricht:

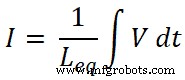
Also,

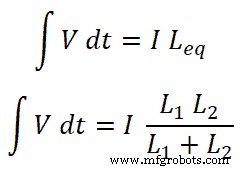
Jetzt für Induktor L₁ , Strom fließt durch diese Induktivität ist I₁;

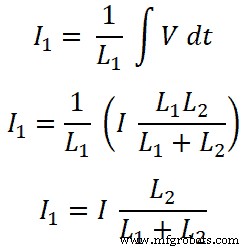
Für Induktor L₂;

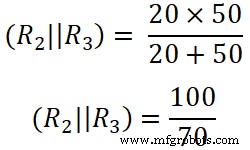
Die Stromteilerregel für den Induktor ist die gleiche wie die Stromteilerregel für die Widerstände.

Stromteilerregel für kapazitive Schaltungen

Wenn die Kondensatoren parallel geschaltet sind, können wir den Strom durch jeden Kondensator finden, indem wir die Stromteilerregel anwenden. Um die Stromteilerregel für den Kondensator zu verstehen, nehmen wir ein Beispiel, bei dem die Kondensatoren wie in der folgenden Abbildung gezeigt parallel geschaltet sind.

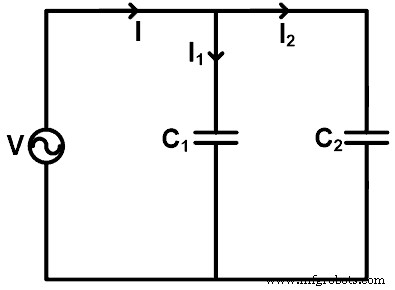
Hier zwei Kondensatoren (C₁ und C₂ ) sind parallel zu einer Spannungsquelle V geschaltet. Der Strom fließt durch den Kondensator C₁ ist I_1, und der Strom fließt durch den Kondensator C₂ ist I₂ . Der durch die Quelle gelieferte Gesamtstrom ist I.

Jetzt müssen wir die Gleichungen für den Strom I₁ finden und I₂ . Dafür finden wir die äquivalente Kapazität C_eq;

C_eq =C ₁ + C ₂

Wir kennen die Gleichung für den Strom, der durch den Kondensator fließt. Und die Gleichung für den von der Quelle gelieferten Gesamtstrom lautet:

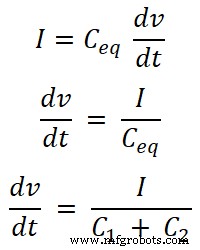
Für Kondensator C₁ ist der Strom, der durch diesen Kondensator fließt, I₁;

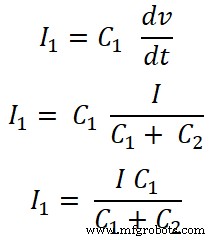
Für Kondensator C₂;

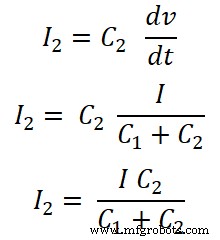
Die Stromteilerregel für den Kondensator unterscheidet sich geringfügig von der Stromteilerregel für die Induktivität und den Widerstand.

In der Kondensatorstromteilerregel ist der Strom, der durch einen Kondensator fließt, ein Verhältnis des Gesamtstroms multipliziert mit diesem Kondensator zur Gesamtkapazität.

Gelöste Beispiele für AC- und DC-Schaltungen mit CDR

Aktuelle Diver-Regel für Gleichstromkreis

Beispiel:1

Finde den Strom, der durch jeden Widerstand fließt, anhand der Stromteilerregel für das gegebene Netzwerk.

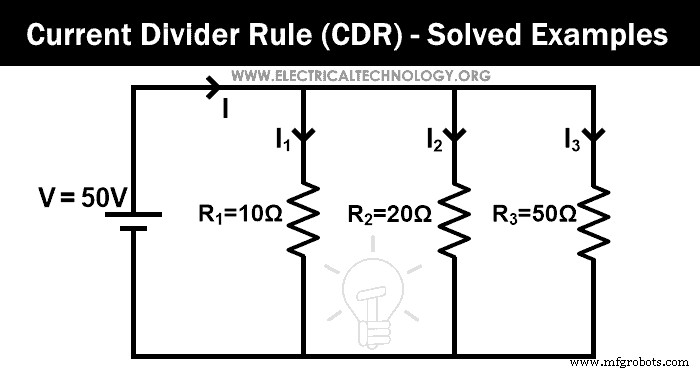
In diesem Beispiel sind drei Widerstände parallel geschaltet. Zuerst finden wir den äquivalenten Widerstand.

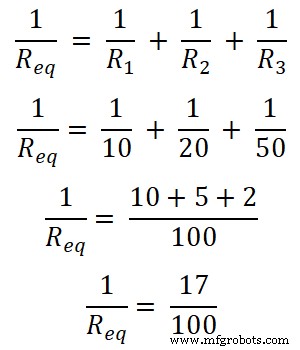
R_eq = 100/17

R_eq = 5,882 Ω

Der von der Quelle gelieferte Gesamtstrom ist I. Also gemäß dem Ohmschen Gesetz;

V =I R_eq

50V =I (5,882 Ω)

I = 50 V / 5,882 Ω

I = 8.5A

Jetzt wenden wir die Stromteilerregel auf den ersten Widerstand (10 Ω) an und der Strom, der durch diesen Widerstand fließt, ist I₁;

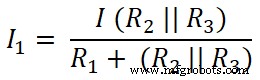
Hier R₂ und R₃ parallel geschaltet sind. Also müssen wir den äquivalenten Widerstand zwischen R₂ finden und R₃ .

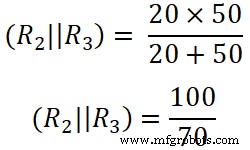
(R ₂ || R ₃ ) =14,285 Ω

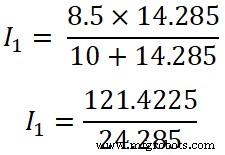
Ich ₁ =4,9999 ≈ 5 A

In ähnlicher Weise wenden wir die Stromteilerregel auf den zweiten Widerstand (20 Ω) an, und der Strom, der durch diesen Widerstand fließt, ist I₂;

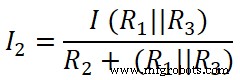
Hier

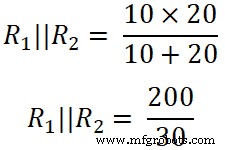
(R ₁ || R ₃ ) =8,33 Ω

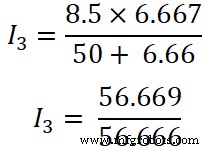
Ich ₂ =2,499 ≈ 2,5 A

Nun wenden wir die Stromteilerregel auf den dritten Widerstand (50 Ω) an und der Strom, der durch diesen Widerstand fließt, ist I₃ .

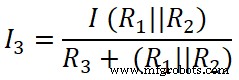
Hier

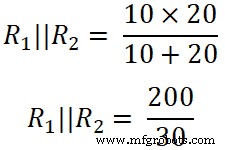
(R ₁ || R ₂ ) =6,66 Ω

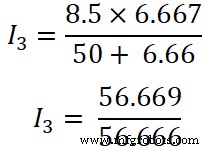
Ich ₃ =1,00 A

Die Summe aller drei Ströme lautet also:

Ich ₁ + ich ₂ + ich ₃ =5 + 2,5 + 1 =8,5 A

Und dieser Strom ist derselbe wie der von der Quelle gelieferte Gesamtstrom.

Aktuelle Diver-Regel für AC Circuit

Beispiel-2

Stellen Sie sich einen Wechselstromkreis vor, bei dem ein Widerstand und ein Kondensator parallel geschaltet sind, wie in der folgenden Abbildung gezeigt. Finden Sie den Stromfluss durch den Widerstand und den Kondensator mit der Stromteilerregel. Betrachten Sie eine Frequenz von 60 Hz.

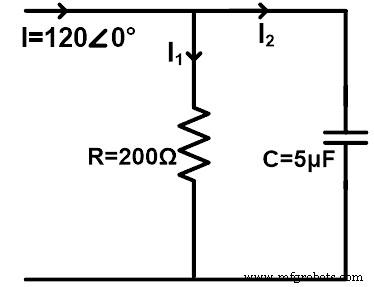
Z_R =200 Ω =200∠0°Ω

Z_C =1/(2 πf C) =1/(2 π 60(5×10 ⁶ ). ) )

Z_C =10 ⁶ / (600 π)

Z_C =530,78 ∠-90° Ω

Nun, gemäß der Stromteilerregel, ist die Gleichung des Stromflusses durch den Widerstand:

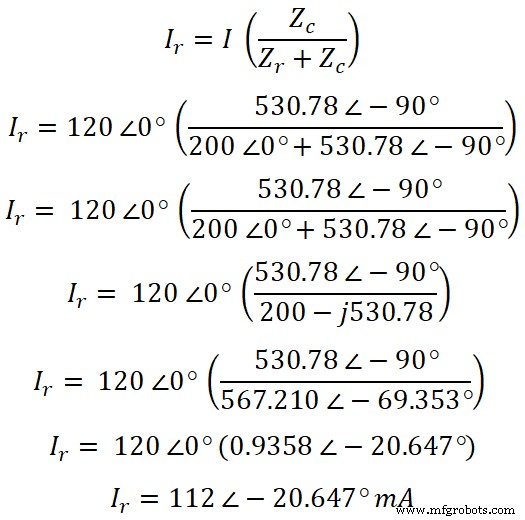
In ähnlicher Weise können wir jetzt den Strom durch den Kondensator finden. Gemäß der Stromteilerregel lautet die Stromgleichung durch den Kondensator:

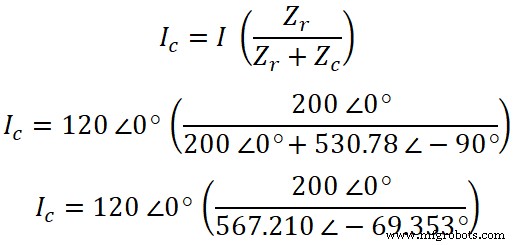
I_C =120 ∠0° (0,3526 ∠ 69,353°)

I_C =42,31 ∠ 69,353°

Wenn Sie diese Antwort beweisen wollen, können Sie beide Strömungen hinzufügen. Und der Wert dieses Stroms ist derselbe wie der Quellenstrom.

Verwandte Tutorials zur Analyse elektrischer Schaltungen:

• Kompensationssatz – Beweis, Erklärung und gelöste Beispiele
• Substitutionssatz – Schritt-für-Schritt-Anleitung mit gelöstem Beispiel
• SUPERNODE Schaltungsanalyse – Schritt für Schritt mit gelöstem Beispiel
• SUPERMESH Schaltungsanalyse – Schritt für Schritt mit gelöstem Beispiel
• Kirchhoffs Strom- und Spannungsgesetz (KCL &KVL) | Gelöstes Beispiel
• Cramers Rule Calculator – 2- und 3-Gleichungssystem für elektrische Schaltungen
• Wheatstone-Brücke – Schaltung, Funktionsweise, Ableitung und Anwendungen
• Rechner für Elektrotechnik und Elektronik
• 5000+ elektrische und elektronische Formeln und Gleichungen