Zuverlässigkeitstechnische Prinzipien für den Anlagenbauer

Manager und Ingenieure, die für die Herstellung und andere industrielle Tätigkeiten verantwortlich sind, beziehen zunehmend den Fokus auf Zuverlässigkeit in ihre strategischen und taktischen Pläne und Initiativen ein. Dieser Trend betrifft zahlreiche Funktionsbereiche, darunter Maschinen-/Anlagenkonstruktion und -beschaffung, Anlagenbetrieb und Anlagenwartung.

Mit seinen Ursprüngen in der Luftfahrtindustrie war die Disziplin Reliability Engineering in der Vergangenheit hauptsächlich auf die Gewährleistung der Produktzuverlässigkeit ausgerichtet. Diese Methoden werden immer häufiger eingesetzt, um die Produktionssicherheit von Produktionsanlagen und -ausrüstungen sicherzustellen – oft als Wegbereiter für eine schlanke Fertigung. Dieser Artikel bietet eine Einführung in die relevantesten und praktischsten dieser Methoden für die Anlagenzuverlässigkeitstechnik, einschließlich:

• Grundlegende Zuverlässigkeitsberechnungen für Ausfallrate, MTBF, Verfügbarkeit usw.
• Eine Einführung in die Exponentialverteilung – der Eckpfeiler der Zuverlässigkeitsmethoden.
• Identifizieren von Abhängigkeiten von Ausfallzeiten mit dem vielseitigen Weibull-System.
• Entwicklung eines effektiven Felddatenerfassungssystems.

Geschichte der Zuverlässigkeitstechnik

Die Anfänge des Gebiets der Zuverlässigkeitstechnik, zumindest die Nachfrage danach, lassen sich bis zu dem Zeitpunkt zurückverfolgen, als der Mensch begann, seinen Lebensunterhalt auf Maschinen zu verlassen. Die Noria zum Beispiel ist eine uralte Pumpe, die als die erste hochentwickelte Maschine der Welt gilt. Die Noria nutzte hydraulische Energie aus dem Fluss eines Flusses oder Baches und benutzte Eimer, um Wasser in Tröge, Viadukte und andere Verteilergeräte zu transportieren, um Felder zu bewässern und Gemeinden mit Wasser zu versorgen.

Wenn die Gemeinde Noria versagte, waren die Menschen, die für ihre Nahrungsversorgung von ihr abhängig waren, gefährdet. Überleben war schon immer eine große Motivationsquelle für Zuverlässigkeit und Verlässlichkeit.

Während die Ursprünge dieser Nachfrage uralt sind, blühte Zuverlässigkeitstechnik als technische Disziplin zusammen mit dem Wachstum der kommerziellen Luftfahrt nach dem Zweiten Weltkrieg wirklich auf. Den Managern von Unternehmen der Luftfahrtindustrie wurde schnell klar, dass Abstürze schlecht für das Geschäft sind. Karen Bernowski, Herausgeberin von Qualitätsfortschritt , enthüllte in einem ihrer Leitartikel Recherchen zum Medienwert des Todes mit verschiedenen Mitteln, die von MIT-Statistikprofessor Arnold Barnett durchgeführt und 1994 darüber berichtet wurden.

Barnett wertete die Anzahl der Nachrichtenartikel auf der Titelseite der New York Times pro 1.000 Todesfälle auf verschiedene Weise aus. Er fand heraus, dass krebsbedingte Todesfälle 0,02 Nachrichtenartikel auf der Titelseite pro 1.000 Todesfälle, Tötungsdelikte 1,7 pro 1.000 Todesfälle, AIDS 2,3 pro 1.000 Todesfälle und Flugunfälle 138,2 Artikel pro 1.000 Todesfälle ergaben!

Die Kosten und der hohe Bekanntheitsgrad von Unfällen im Zusammenhang mit der Luftfahrt trugen dazu bei, die Luftfahrtindustrie zu motivieren, sich stark an der Entwicklung der Disziplin Zuverlässigkeitstechnik zu beteiligen. Ebenso werden aufgrund der kritischen Natur militärischer Ausrüstung in der Verteidigung seit langem Techniken der Zuverlässigkeitstechnik eingesetzt, um die Einsatzbereitschaft sicherzustellen. Viele unserer Standards im Bereich der Zuverlässigkeitstechnik sind MIL-Standards oder haben ihren Ursprung in militärischen Aktivitäten.

Was ist Zuverlässigkeitstechnik?

Reliability Engineering beschäftigt sich mit der Langlebigkeit und Zuverlässigkeit von Teilen, Produkten und Systemen. Noch wichtiger ist, dass es um die Kontrolle des Risikos geht. Das Zuverlässigkeits-Engineering umfasst eine Vielzahl von Analysetechniken, die Ingenieuren helfen sollen, die Fehlermodi und -muster dieser Teile, Produkte und Systeme zu verstehen. Traditionell hat sich das Gebiet der Zuverlässigkeitstechnik auf die Produktzuverlässigkeit und Zuverlässigkeitssicherung konzentriert.

In den letzten Jahren haben Unternehmen, die Maschinen und andere physische Vermögenswerte in Produktionsumgebungen einsetzen, damit begonnen, verschiedene Prinzipien der Zuverlässigkeitstechnik zum Zweck der Produktionszuverlässigkeit und Zuverlässigkeitssicherung einzusetzen.

Produktionsorganisationen setzen zunehmend Zuverlässigkeits-Engineering-Techniken wie Reliability-Centered Maintenance (RCM) ein, einschließlich Analyse von Fehlermodi und Auswirkungen (und Kritikalität) (FMEA, FMECA), Ursachenanalyse (RCA), zustandsbasierte Wartung, verbesserte Arbeitsplanungsschemata, usw. Dieselben Organisationen beginnen, lebenszykluskostenbasierte Design- und Beschaffungsstrategien, Änderungsmanagement-Schemata und andere fortschrittliche Tools und Techniken einzuführen, um die Grundursachen für schlechte Zuverlässigkeit zu kontrollieren.

Die Annahme der eher quantitativen Aspekte der Zuverlässigkeitstechnik durch die Gemeinschaft zur Sicherung der Produktionszuverlässigkeit war jedoch langsam. Dies liegt zum Teil an der wahrgenommenen Komplexität der Techniken und zum Teil an der Schwierigkeit, nützliche Daten zu erhalten.

Die quantitativen Aspekte der Zuverlässigkeitstechnik mögen oberflächlich betrachtet kompliziert und entmutigend erscheinen. In der Realität kann der Anlagenzuverlässigkeitsingenieur jedoch durch ein relativ grundlegendes Verständnis der grundlegendsten und am weitesten verbreiteten Methoden ein viel klareres Verständnis davon gewinnen, wo Probleme auftreten, ihre Art und ihre Auswirkungen auf den Produktionsprozess – zumindest in quantitativer Hinsicht Sinn.

Bei richtiger Anwendung ermöglichen quantitative Werkzeuge und Methoden des Zuverlässigkeits-Engineerings dem Anlagen-Zuverlässigkeits-Engineering, die von RCM, RCA usw. bereitgestellten Frameworks effektiver anzuwenden, indem einige der ansonsten mit ihrer Anwendung verbundenen Vermutungen eliminiert werden. Allerdings müssen Ingenieure die Methoden besonders clever anwenden.

Wieso den? Der Betriebskontext und die Umgebung eines Produktionsprozesses beinhalten mehr Variablen als die etwas eindimensionale Welt der Produktzuverlässigkeitssicherung. Dies liegt an dem kombinierten Einfluss von Konstruktion, Beschaffung, Produktion/Betrieb, Wartung usw. und der Schwierigkeit, effektive Tests und Experimente zu erstellen, um die mehrdimensionalen Aspekte einer typischen Produktionsumgebung zu modellieren.

Trotz der erhöhten Schwierigkeit, quantitative Zuverlässigkeitsmethoden im Produktionsumfeld anzuwenden, lohnt es sich dennoch, sich ein fundiertes Verständnis der Werkzeuge anzueignen und gegebenenfalls anzuwenden. Quantitative Daten helfen, die Art und das Ausmaß eines Problems/einer Chance zu definieren, was eine Vorstellung von der Zuverlässigkeit bei der Anwendung anderer Zuverlässigkeits-Engineering-Tools bietet.

Dieser Artikel bietet eine Einführung in die grundlegendsten Methoden des Zuverlässigkeits-Engineerings, die auf den Anlagenbauer anwendbar sind, der an der Sicherung der Produktionszuverlässigkeit interessiert ist. Es setzt ein grundlegendes Verständnis der Algebra, der Wahrscheinlichkeitstheorie und der univariaten Statistik auf der Grundlage der Gaußschen (Normal-)Verteilung (z. B. Maß der zentralen Tendenz, Maß der Streuung und Variabilität, Konfidenzintervalle usw.) voraus.

Es sollte klargestellt werden, dass dieses Papier eine kurze Einführung in Zuverlässigkeitsmethoden ist. Es ist weder ein umfassender Überblick über die Methoden des Reliability Engineering, noch ist es in irgendeiner Weise neu oder unkonventionell. Die hier beschriebenen Methoden werden routinemäßig von Zuverlässigkeitsingenieuren verwendet und sind Kernwissenskonzepte für diejenigen, die eine professionelle Zertifizierung durch die American Society for Quality (ASQ) als Zuverlässigkeitsingenieur (CRE) anstreben.

Mehrere Bücher zum Thema Zuverlässigkeitstechnik sind in der Bibliographie dieses Artikels aufgeführt. Der Autor dieses Artikels hat Zuverlässigkeitsmethoden für Ingenieure gefunden von K. S. Krishnamoorthi und Zuverlässigkeitsstatistik von Robert Dovich als besonders nützliche und anwenderfreundliche Referenzen zum Thema Zuverlässigkeits-Engineering-Methoden. Beide werden von der ASQ Press veröffentlicht.

Bevor Sie Methoden diskutieren, sollten Sie sich mit der Nomenklatur der Zuverlässigkeitstechnik vertraut machen. Der Einfachheit halber finden Sie im Anhang dieses Artikels eine stark gekürzte Liste der wichtigsten Begriffe und Definitionen. Eine ausführlichere Definition von Zuverlässigkeitsbegriffen und -nomenklatur finden Sie in MIL-STD-721 und anderen verwandten Standards. Die im Anhang enthaltenen Definitionen stammen aus MIL-STD-721.

Grundlegende mathematische Konzepte in der Zuverlässigkeitstechnik

Für die Zuverlässigkeitstechnik gelten viele mathematische Konzepte, insbesondere aus den Bereichen Wahrscheinlichkeit und Statistik. Ebenso können viele mathematische Verteilungen für verschiedene Zwecke verwendet werden, darunter die Gaußsche (Normal-)Verteilung, die Log-Normalverteilung, die Rayleigh-Verteilung, die Exponentialverteilung, die Weibull-Verteilung und viele andere.

Für diese kurze Einführung beschränken wir unsere Diskussion auf die Exponentialverteilung und die Weibull-Verteilung, die beiden am häufigsten in der Zuverlässigkeitstechnik verwendeten. Der Kürze und Einfachheit halber wurden wichtige mathematische Konzepte wie Verteilungsgüte und Konfidenzintervalle weggelassen.

Ausfallrate und mittlere Zeit zwischen/bis zum Ausfall (MTBF/MTTF)

Der Zweck quantitativer Zuverlässigkeitsmessungen besteht darin, die Ausfallrate relativ zur Zeit zu definieren und diese Ausfallrate in einer mathematischen Verteilung zu modellieren, um die quantitativen Aspekte des Ausfalls zu verstehen. Der grundlegendste Baustein ist die Ausfallrate, die anhand der folgenden Gleichung geschätzt wird:

Wobei:
λ =Ausfallrate (manchmal auch als Gefährdungsrate bezeichnet)
T =Gesamtlaufzeit/Zyklen/Meilen/usw. während eines Untersuchungszeitraums für fehlgeschlagene und nicht fehlgeschlagene Elemente.
r =Die Gesamtzahl der während des Untersuchungszeitraums aufgetretenen Fehler.

Wenn beispielsweise fünf Elektromotoren über eine gemeinsame Gesamtzeit von 50 Jahren mit fünf Funktionsausfällen während des Zeitraums betrieben werden, beträgt die Ausfallrate 0,1 Ausfälle pro Jahr.

Ein weiteres sehr grundlegendes Konzept ist die mittlere Zeit zwischen/bis zum Ausfall (MTBF/MTTF). Der einzige Unterschied zwischen MTBF und MTTF besteht darin, dass wir MTBF verwenden, wenn wir uns auf Artikel beziehen, die repariert werden, wenn sie ausfallen. Für Artikel, die einfach weggeworfen und ersetzt werden, verwenden wir den Begriff MTTF. Die Berechnungen sind die gleichen.

Die grundlegende Berechnung zur Schätzung der Mean Time Between Failure (MTBF) und Mean Time to Failure (MTTF), beides Maße der zentralen Tendenz, ist einfach der Kehrwert der Ausfallratenfunktion. Es wird mit der folgenden Gleichung berechnet.

Wobei:
θ =Mittlere Zeit zwischen/bis zum Ausfall
T =Gesamtlaufzeit/Zyklen/Meilen/usw. während eines Untersuchungszeitraums für fehlgeschlagene und nicht fehlgeschlagene Elemente.
r =Die Gesamtzahl der während des Untersuchungszeitraums aufgetretenen Fehler.

Die MTBF für unser Beispiel für einen industriellen Elektromotor beträgt 10 Jahre, was dem Kehrwert der Ausfallrate der Motoren entspricht. Übrigens würden wir MTBF für Elektromotoren schätzen, die bei Ausfall wieder aufgebaut werden. Für kleinere Motoren, die als Wegwerfmotoren gelten, würden wir das Maß der zentralen Tendenz als MTTF angeben.

Die Ausfallrate ist ein grundlegender Bestandteil vieler komplexerer Zuverlässigkeitsberechnungen. Je nach mechanischer/elektrischer Auslegung, Betriebskontext, Umgebung und/oder Wartungseffektivität kann die Ausfallrate einer Maschine als Funktion der Zeit abnehmen, konstant bleiben, linear ansteigen oder geometrisch ansteigen (Abbildung 1). Die Bedeutung der Ausfallrate im Vergleich zur Zeit wird später ausführlicher erörtert.

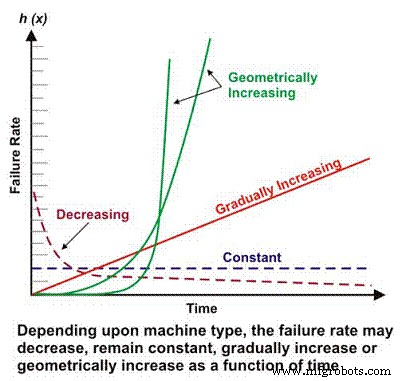
Abbildung 1. Unterschiedliche Ausfallraten im Vergleich zu Zeitszenarien

Die „Badewanne“-Kurve

Personen, die nur eine Grundausbildung in Wahrscheinlichkeit und Statistik erhalten haben, sind wahrscheinlich am besten mit der Gauß- oder Normalverteilung vertraut, die mit der vertrauten glockenförmigen Wahrscheinlichkeitsdichtekurve verbunden ist. Die Gaußsche Verteilung ist im Allgemeinen auf Datensätze anwendbar, bei denen die beiden häufigsten Maße der zentralen Tendenz, Mittelwert und Median, ungefähr gleich sind.

Überraschenderweise ist die Gaußsche Verteilung trotz ihrer Vielseitigkeit bei der Modellierung von Wahrscheinlichkeiten für Phänomene, die von standardisierten Testergebnissen bis hin zu Geburtsgewichten von Babys reichen, nicht die vorherrschende Verteilung, die in der Zuverlässigkeitstechnik verwendet wird. Die Gaußsche Verteilung hat ihren Platz bei der Bewertung der Fehlereigenschaften von Maschinen mit einem dominanten Fehlermodus, aber die primäre Verteilung, die in der Zuverlässigkeitstechnik verwendet wird, ist die Exponentialverteilung.

Bei der Bewertung der Zuverlässigkeit und der Ausfalleigenschaften einer Maschine müssen wir mit der viel geschmähten „Badewanne“-Kurve beginnen, die die Ausfallrate über der Zeit widerspiegelt (Abbildung 2). Im Konzept demonstriert die Badewannenkurve effektiv die drei grundlegenden Ausfallratenmerkmale einer Maschine:fallend, konstant oder steigend. Bedauerlicherweise wurde die Badewannenkurve in der Literatur zur Instandhaltungstechnik heftig kritisiert, da sie die charakteristische Ausfallrate für die meisten Maschinen in einer Industrieanlage nicht effektiv modellieren kann, was im Allgemeinen auf Makroebene zutrifft.

Die meisten Maschinen verbringen ihr Leben im frühen Leben oder in der Säuglingssterblichkeit und/oder in den Bereichen mit konstanter Ausfallrate der Badewannenkurve. Wir sehen selten systembedingte zeitbasierte Ausfälle in Industriemaschinen. Trotz ihrer Einschränkungen bei der Modellierung der Ausfallraten typischer Industriemaschinen ist die Badewannenkurve ein nützliches Werkzeug, um die grundlegenden Konzepte der Zuverlässigkeitstechnik zu erklären.

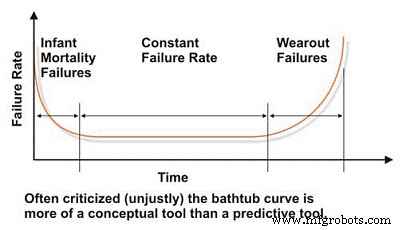
Abbildung 2. Die vielgeschmähte 'Badewanne'-Kurve

Der menschliche Körper ist ein hervorragendes Beispiel für ein System, das der Badewannenkurve folgt. Menschen und andere organische Arten neigen dazu, in ihren ersten Lebensjahren, insbesondere in den ersten Jahren, eine hohe Ausfallrate (Sterblichkeit) zu erleiden, die jedoch mit zunehmendem Alter des Kindes sinkt. Unter der Annahme, dass eine Person die Pubertät erreicht und ihre Teenagerjahre überlebt, wird ihre Sterblichkeitsrate ziemlich konstant und bleibt dort, bis alters- (zeit-)abhängige Krankheiten beginnen, die Sterblichkeitsrate zu erhöhen (Abnutzung).

Zahlreiche Einflüsse wirken sich auf die Sterblichkeitsraten aus, darunter Schwangerschaftsvorsorge und Ernährung der Mutter, Qualität und Verfügbarkeit der medizinischen Versorgung, Umwelt und Ernährung, Lebensstilentscheidungen und natürlich genetische Veranlagung. Diese Faktoren können metaphorisch mit Faktoren verglichen werden, die die Maschinenlebensdauer beeinflussen. Design und Beschaffung sind analog zur genetischen Veranlagung; Installation und Inbetriebnahme erfolgt analog zur Schwangerschaftsvorsorge und Ernährung der Mutter; und Lebensstilentscheidungen und die Verfügbarkeit medizinischer Versorgung entsprechen der Wirksamkeit der Wartung und der proaktiven Kontrolle der Betriebsbedingungen.

Die Exponentialverteilung

Die Exponentialverteilung, die einfachste und am weitesten verbreitete Formel zur Vorhersage der Zuverlässigkeit, modelliert Maschinen mit konstanter Ausfallrate oder den flachen Abschnitt der Badewannenkurve. Die meisten Industriemaschinen verbringen die meiste Zeit ihres Lebens in der konstanten Ausfallrate, daher ist sie weit verbreitet. Unten ist die Grundgleichung zum Schätzen der Zuverlässigkeit einer Maschine, die der Exponentialverteilung folgt, wobei die Ausfallrate als Funktion der Zeit konstant ist.

Wobei:
R(t) =Zuverlässigkeitsschätzung für einen Zeitraum, Zyklen, Meilen usw. (t).
e =Basis der natürlichen Logarithmen (2.718281828)
λ =Ausfallrate (1/MTBF oder 1/MTTF)

In unserem Beispiel eines Elektromotors beträgt die Wahrscheinlichkeit, dass ein Motor sechs Jahre lang ohne Ausfall läuft, bzw. die prognostizierte Zuverlässigkeit 55 Prozent, wenn Sie von einer konstanten Ausfallrate ausgehen. Dies wird wie folgt berechnet:
R(6) =2.718281828-(0.1* 6)
R(6) =0.5488 =~ 55%

Mit anderen Worten, nach sechs Jahren ist wahrscheinlich mit einem Ausfall von etwa 45 % der Bevölkerung identischer Motoren, die in einer identischen Anwendung arbeiten, zu rechnen. Es lohnt sich an dieser Stelle zu wiederholen, dass diese Berechnungen die Wahrscheinlichkeit für eine Population projizieren. Jedes einzelne Individuum aus der Population könnte am ersten Tag der Operation versagen, während ein anderes Individuum 30 Jahre dauern könnte. Das liegt in der Natur probabilistischer Zuverlässigkeitsprognosen.

Charakteristisch für die Exponentialverteilung ist, dass die MTBF an dem Punkt auftritt, an dem die berechnete Zuverlässigkeit 36,78 % beträgt, bzw. an dem 63,22 % der Maschinen bereits ausgefallen sind. In unserem Motorbeispiel ist nach 10 Jahren damit zu rechnen, dass 63,22 % der Motoren aus einer Population identischer Motoren, die in identischen Anwendungen eingesetzt werden, ausfallen. Mit anderen Worten, die Überlebensrate beträgt 36,78% der Bevölkerung.

Wir sprechen oft von der projizierten Lagerlebensdauer als L10-Lebensdauer. Dies ist der Zeitpunkt, an dem mit einem Ausfall von 10 % einer Lagerpopulation gerechnet werden sollte (90 % Überlebensrate). In Wirklichkeit überlebt nur ein Bruchteil der Lager tatsächlich den L10-Punkt. Wir haben dies als objektive Lebensdauer für ein Lager akzeptiert, wenn wir vielleicht den Punkt L63.22 ins Visier nehmen sollten, was darauf hinweist, dass unsere Lager im Durchschnitt bis zur projizierten MTBF halten – vorausgesetzt natürlich, dass die Lager folgen der Exponentialverteilung. Wir werden dieses Problem später im Abschnitt zur Weibull-Analyse des Artikels besprechen.

Die Wahrscheinlichkeitsdichtefunktion (pdf) oder Lebensdauerverteilung ist eine mathematische Gleichung, die sich der Ausfallhäufigkeitsverteilung annähert. Es ist die pdf- oder Lebenshäufigkeitsverteilung, die die bekannte glockenförmige Kurve in der Gauß- oder Normalverteilung ergibt. Unten ist das PDF für die Exponentialverteilung.

Wobei:
pdf(t) =Lebenshäufigkeitsverteilung für eine bestimmte Zeit (t)
e =Basis der natürlichen Logarithmen (2.718281828)
λ =Ausfallrate (1/MTBF oder 1/MTTF)

In unserem Beispiel eines Elektromotors berechnet sich die tatsächliche Ausfallwahrscheinlichkeit nach drei Jahren wie folgt:
pdf(3) =01. * 2.718281828-(0.1* 3)
pdf(3) =0,1 * 0,7408
pdf(3) =.07408 =~ 7,4%

Wenn wir in unserem Beispiel eine konstante Ausfallrate annehmen, die der Exponentialverteilung folgt, wird die Lebensdauerverteilung oder pdf für die industriellen Elektromotoren in Abbildung 3 ausgedrückt. Lassen Sie sich nicht durch die abnehmende Natur der pdf-Funktion verwirren. Ja, die Ausfallrate ist konstant, aber das PDF geht mathematisch von einem Ausfall ohne Ersatz aus, sodass die Population, aus der Ausfälle auftreten können, kontinuierlich reduziert wird – asymptotisch gegen Null geht.

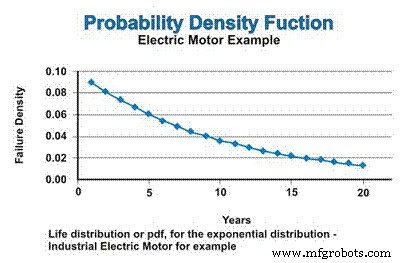
Abbildung 3. Die Wahrscheinlichkeitsdichtefunktion (pdf)

Die kumulative Verteilungsfunktion (cdf) ist einfach die kumulative Anzahl von Ausfällen, die man über einen bestimmten Zeitraum erwarten kann. Bei der Exponentialverteilung ist die Ausfallrate konstant, sodass die relative Rate, mit der ausgefallene Komponenten zum cdf hinzugefügt werden, konstant bleibt. Wenn jedoch die Population aufgrund von Fehlern abnimmt, nimmt die tatsächliche Anzahl der mathematisch geschätzten Fehler als Funktion der abnehmenden Population ab. Ähnlich wie sich pdf asymptotisch Null nähert, nähert sich cdf asymptotisch eins (Abbildung 4).

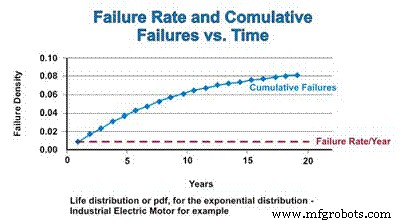
Abbildung 4. Fehlerrate und die kumulative Verteilungsfunktion

Der Abschnitt der abnehmenden Ausfallrate der Badewannenkurve, der oft als Säuglingssterblichkeitsbereich bezeichnet wird, und der Verschleißbereich werden im folgenden Abschnitt erörtert, der sich mit der vielseitigen Weibull-Verteilung befasst.

Weibull-Verteilung

Die Weibull-Analyse wurde ursprünglich von Wallodi Weibull, einem schwedischen Mathematiker, entwickelt und ist mit Abstand die vielseitigste Verteilung, die von Zuverlässigkeitsingenieuren verwendet wird. Obwohl es als Verteilung bezeichnet wird, ist es eigentlich ein Werkzeug, das es dem Zuverlässigkeitsingenieur ermöglicht, zuerst die Wahrscheinlichkeitsdichtefunktion (Fehlerhäufigkeitsverteilung) eines Satzes von Fehlerdaten zu charakterisieren, um die Fehler als frühe Lebensdauer, konstant (exponentiell) oder Verschleiß zu charakterisieren (Gaussian oder Log normal) durch Auftragen der Zeit bis zum Ausfall auf einem speziellen Plotterpapier mit dem Log der Zeiten/Zyklen/Meilen bis zum Ausfall eine logarithmisch skalierte X-Achse gegen den kumulativen Prozentsatz der Bevölkerung, der durch jeden Ausfall auf einem Log dargestellt wird -log skalierte Y-Achse (Abbildung 5).

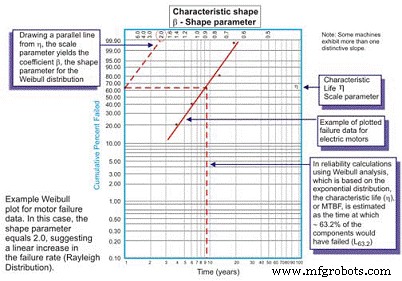
Abbildung 5. Der einfache Weibull-Plot – kommentiert

Nach der Darstellung ist die lineare Steigung der resultierenden Kurve eine wichtige Variable, die als Formparameter bezeichnet wird, dargestellt durch â, die verwendet wird, um die Exponentialverteilung an eine große Anzahl von Fehlerverteilungen anzupassen. Wenn der â-Koeffizient oder der Formparameter kleiner als 1,0 ist, weist die Verteilung im Allgemeinen auf ein frühes Leben oder ein Versagen der Säuglingssterblichkeit hin. Wenn der Formparameter etwa 3,5 überschreitet, sind die Daten zeitabhängig und weisen auf Verschleißfehler hin.

Dieser Datensatz nimmt typischerweise die Gauß- oder Normalverteilung an. Wenn der â-Koeffizient über ~3,5 ansteigt, wird die glockenförmige Verteilung enger und zeigt eine zunehmende Kurtosis (Spitze am oberen Ende der Kurve) und eine kleinere Standardabweichung. Viele Datensätze weisen zwei oder sogar drei unterschiedliche Regionen auf.

Für Zuverlässigkeitsingenieure ist es beispielsweise üblich, eine Kurve zu zeichnen, die den Formparameter während des Einfahrens darstellt, und eine andere Kurve, die die konstante oder allmählich ansteigende Ausfallrate darstellt. In einigen Fällen entsteht eine dritte deutliche lineare Steigung, um eine dritte Form zu identifizieren, den Verschleißbereich.

In diesen Fällen nimmt die PDF der Fehlerdaten tatsächlich die bekannte Badewannenkurvenform an (Abbildung 6). Die meisten in Anlagen verwendeten mechanischen Geräte weisen jedoch einen Bereich der Säuglingssterblichkeit und einen Bereich konstanter oder allmählich ansteigender Ausfallraten auf. Es ist selten, dass eine Kurve entsteht, die Verschleiß darstellt. Das charakteristische Leben oder η (griechisch „Eta“ in Kleinbuchstaben) ist die Weibull-Näherung des MTBF. Es ist immer die Funktion von Zeit, Meilen oder Zyklen, bei der 63,21% der untersuchten Einheiten versagt haben, was die MTBF/MTTF für die Exponentialverteilung ist.

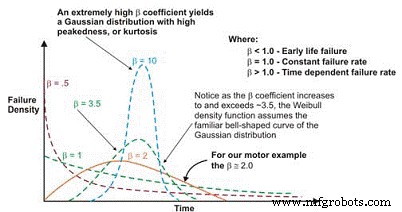
Abbildung 6. Abhängig vom Formparameter ist die Weibull-Fehlerdichte Kurve kann mehrere Verteilungen annehmen, was sie für die Zuverlässigkeitstechnik so vielseitig macht.

Als Vorbehalt, dieses Werkzeug an die Exzellenz in der Wartung und im Betrieb zu binden, wenn wir die Zwangsfunktionen, die zu mechanischen Versagen in Lagern, Getrieben usw. führen, wie Schmierung, Verschmutzungskontrolle, Ausrichtung, Auswuchtung, bei entsprechendem Betrieb usw. würden tatsächlich mehr Maschinen ihre Lebensdauer erreichen. Maschinen, die ihre Ermüdungslebensdauer erreichen, weisen die bekannte Verschleißcharakteristik auf.

Die Verwendung des β-Koeffizienten zum Anpassen der Ausfallratengleichung als Funktion der Zeit ergibt die folgende allgemeine Gleichung:

Wo:
h(t) =Ausfallrate (oder Gefahrenrate) für eine gegebene Zeit (t)
e =Basis der natürlichen Logarithmen (2.718281828)
θ =Geschätzte MTBF/MTTF
β =Weibull-Formparameter aus dem Diagramm.

Und die folgende Zuverlässigkeitsfunktion:

Wo:
R(t) =Zuverlässigkeitsschätzung für einen Zeitraum, Zyklen, Meilen usw. (t)
e =Basis der natürlichen Logarithmen (2.718281828)
θ =Geschätzte MTBF/MTTF
β =Weibull-Formparameter aus dem Diagramm.

Und die folgende Wahrscheinlichkeitsdichtefunktion (pdf):

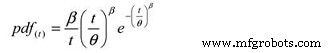
Wo:
pdf(t) =Schätzung der Wahrscheinlichkeitsdichtefunktion für einen Zeitraum,
Zyklen, Meilen usw. (t)
e =Basis der natürlichen Logarithmen (2.718281828)
θ =Geschätzte MTBF/MTTF
β =Weibull-Formparameter aus dem Diagramm.

Es sollte beachtet werden, dass, wenn β gleich 1,0 ist, die Weibull-Verteilung die Form der Exponentialverteilung annimmt, auf der sie basiert.

Für Uneingeweihte kann die Mathematik, die zur Durchführung der Weibull-Analyse erforderlich ist, entmutigend erscheinen. Aber sobald Sie die Mechanik der Formeln verstanden haben, ist die Mathematik wirklich ganz einfach. Darüber hinaus wird die Software heute die meiste Arbeit für uns erledigen, aber es ist wichtig, die zugrunde liegende Theorie zu verstehen, damit der Anlagenzuverlässigkeitsingenieur die leistungsstarke Weibull-Analysetechnik effektiv einsetzen kann.

In unserem zuvor besprochenen Beispiel von Elektromotoren haben wir zuvor die Exponentialverteilung angenommen. Wenn die Weibull-Analyse jedoch Frühausfälle durch einen β-Formparameter von 0,5 aufdecken würde, würde die Schätzung der Zuverlässigkeit nach sechs Jahren ~46% betragen, nicht die geschätzten ~55% unter Annahme der exponentiellen Verteilung. Um Verschleißausfälle zu reduzieren, müssen wir uns auf unsere Lieferanten verlassen, um eine besser gebaute und gelieferte Qualität und Zuverlässigkeit zu bieten, die Motoren besser zu lagern, um Rost, Korrosion, Reibverschleiß und andere statische Verschleißmechanismen zu vermeiden, und die Installation besser zu machen und Inbetriebnahme neuer oder umgebauter Maschinen.

Umgekehrt, wenn die Weibull-Analyse ergeben würde, dass die Motoren überwiegend verschleißbedingte Ausfälle aufweisen, was einen β-Formparameter von 5,0 ergibt, würde die Zuverlässigkeitsschätzung nach sechs Jahren ~ 93 % betragen, anstatt der geschätzten ~ 55 % unter Annahme einer exponentiellen Verteilung. Bei zeitabhängigen Verschleißausfällen können wir eine planmäßige Überholung oder einen geplanten Austausch durchführen, vorausgesetzt, wir haben eine gute Schätzung der MTBF/MTTF, nachdem wir den Verschleißbereich erreicht haben, und eine ausreichend kleine Standardabweichung, um Entscheidungen zum Wiederaufbau/Ersetzen mit hoher Zuverlässigkeit zu treffen, die sind nicht übermäßig teuer.

In unserem Motorbeispiel beginnt die Ausfallrate unter der Annahme eines β-Formparameters von 5,0 nach etwa fünf oder sechs Jahren schnell anzusteigen Zeit. Alternativ können wir das Design verbessern, indem wir auf die dominante(n) Fehlerart(en) abzielen, mit dem Ziel, die „Spannungsfestigkeit“-Interferenzen zu verringern. Mit anderen Worten, wir können versuchen, die Schwächen der Maschine durch Konstruktionsänderungen zu beseitigen, mit dem Ziel, die Ursachen der zeitabhängigen Ausfälle zu beseitigen.

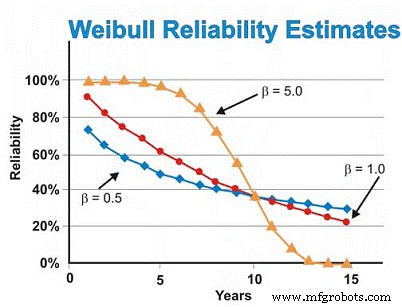
Unter der Annahme, dass alles mit Ausnahme des β-Formparameters konstant ist, zeigt Abbildung 7 den Unterschied, den der β-Formparameter in der Zuverlässigkeitsschätzung unter Annahme von β-Formwerten von 0,5 (frühe Lebensdauer), 1,0 (konstant oder exponentiell) und 5,0 (Verschleiß) hat für eine Reihe von Zeitschätzungen. Diese Grafik veranschaulicht visuell das Konzept des steigenden Risikos gegenüber der Zeit (β =0,5), des konstanten Risikos gegenüber der Zeit (β =1,0) und des zunehmenden Risikos gegenüber der Zeit (β =5).

Abbildung 7. Verschiedene Zuverlässigkeitsprojektionen als Funktion der Zeit für Unterschiedliche Weibull-Formparameter

Der Weibull-Plot mit mehreren Neigungen

Beim Zeichnen einer am besten passenden Regressionslinie durch die Datenpunkte in einem Weibull-Plot ist der Korrelationskoeffizient häufig schlecht, was bedeutet, dass die tatsächlichen Datenpunkte weit von der Regressionslinie abweichen. Dies wird durch Untersuchung des Korrelationskoeffizienten R oder konservativer R2 bewertet, der die Datenvariabilität bezeichnet. Wenn die Korrelation schlecht ist, sollte der Zuverlässigkeitsingenieur die Daten untersuchen, um zu bewerten, ob zwei oder mehr Muster vorhanden sind, die auf große Unterschiede in Fehlermodi, Betriebskontext usw. hinweisen können. Dies führt häufig zu zwei oder mehr Beta-Schätzungen (Abbildung 8).

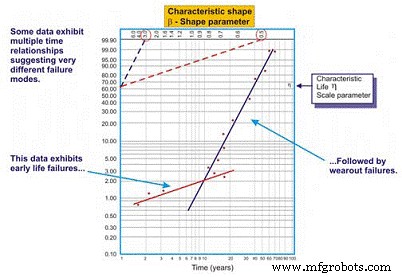
Abbildung 8. Ein Beispiel für einen Multi-Beta-Weibull-Plot

Wie wir in unserem Beispiel in Abbildung 8 sehen, funktioniert der Datensatz besser, wenn zwei unterschiedliche Regressionslinien gezeichnet werden. Die erste Zeile weist einen Beta-Formparameter von 0,5 auf, was auf ein frühes Versagen der Lebensdauer hindeutet. Die zweite Linie weist eine Betaform von 3,0 auf, was darauf hindeutet, dass das Ausfallrisiko mit der Zeit zunimmt. Bei komplexen Geräten, insbesondere bei mechanischen Geräten, kommt es häufig zu Einlauffehlern, wenn sie neu oder kürzlich umgebaut wurden. Daher ist das Ausfallrisiko direkt nach der Erstinbetriebnahme am höchsten.

Sobald das System seine Einlaufphase durchlaufen hat, die je nach Systemtyp Minuten, Stunden, Tage, Wochen, Monate oder Jahre dauern kann, tritt das System in ein anderes Risikomuster ein. In diesem Beispiel tritt das System in einen Zeitraum ein, in dem das Ausfallrisiko als Funktion der Zeit zunimmt, sobald das System seine Einlaufzeit verlässt.

Die Multi-Beta bietet dem Zuverlässigkeitsingenieur eine genauere Risikoeinschätzung als Funktion der Zeit. Mit diesem Wissen ist er oder sie besser in der Lage, mildernde Maßnahmen zu ergreifen. In der frühen Lebensphase sind wir beispielsweise geneigt, die Präzision zu verbessern, mit der wir produzieren/umbauen, installieren und in Betrieb nehmen. Darüber hinaus können wir Überwachungstechniken hinzufügen und/oder unsere Überwachungshäufigkeit während der Hochrisikophase erhöhen. Nach der Einlaufzeit können wir Überwachungstechniken einführen, die auf zeitabhängige Verschleißausfälle abzielen, von denen angenommen wird, dass sie das System beeinträchtigen, die Überwachungshäufigkeit entsprechend erhöhen oder in einigen Fällen präventive Wartungsmaßnahmen für harte Zeiten planen.

Systemzuverlässigkeit schätzen

Sobald die Zuverlässigkeit von Komponenten oder Maschinen in Bezug auf den Betriebskontext und die erforderliche Einsatzzeit festgestellt wurde, müssen Anlageningenieure die Zuverlässigkeit eines Systems oder Prozesses beurteilen. Auch hier werden der Kürze und Einfachheit halber die Schätzungen der Systemzuverlässigkeit für serielle, parallele und redundante Systeme mit geteilter Last (R/n-Systeme) erörtert.

Seriensysteme
Bevor wir Seriensysteme besprechen, sollten wir Zuverlässigkeits-Blockdiagramme besprechen. Zuverlässigkeits-Blockdiagramme sind kein kompliziertes Werkzeug, sondern bilden einen Prozess von Anfang bis Ende ab. Bei einem Reihensystem folgt auf Subsystem A Subsystem B und so weiter. Im Seriensystem hängt die Fähigkeit zum Einsatz von Subsystem B vom Betriebszustand von Subsystem A ab. Wenn Subsystem A nicht in Betrieb ist, ist das System unabhängig vom Zustand von Subsystem B ausgefallen (Abbildung 9).

To calculate the system reliability for a serial process, you only need to multiply the estimated reliability of Subsystem A at time (t) by the estimated reliability of Subsystem B at time (t). The basic equation for calculating the system reliability of a simple series system is:

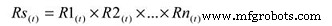
Where:
Rs(t) – System reliability for given time (t)
R1-n(t) – Subsystem or sub-function reliability for given time (t)

So, for a simple system with three subsystems, or sub-functions, each having an estimated reliability of 0.90 (90%) at time (t), the system reliability is calculated as 0.90 X 0.90 X 0.90 =0.729, or about 73%.

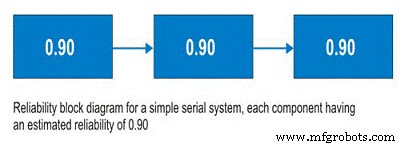
Figure 9. Simple Serial System

Parallel Systems
Often, design engineers will incorporate redundancy into critical machines. Reliability engineers call these parallel systems. These systems may be designed as active parallel systems or standby parallel systems. The block diagram for a simple two component parallel system is shown in Figure 10.

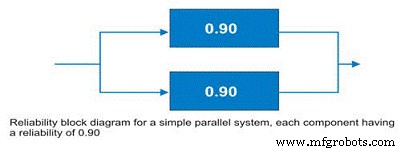
Figure 10. Simple parallel system – the system reliability is increased to 99% due to the redundancy.

To calculate the reliability of an active parallel system, where both machines are running, use the following simple equation:

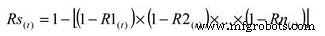
Where:
Rs(t) – System reliability for given time (t)
R1-n(t) – Subsystem or sub-function reliability for given time (t)

The simple parallel system in our example with two components in parallel, each having a reliability of 0.90, has a total system reliability of 1 – (0.1 X 0.1) =0.99. So, the system reliability was significantly improved.

There are some shortcut methods for calculating parallel system reliability when all subsystems have the same estimated reliability. More often, systems contain parallel and serial subcomponents as depicted in Figure 11. The calculation of standby systems requires knowledge about the reliability of the switching mechanism. In the interest of simplicity and brevity, this topic will be reserved for a future article.

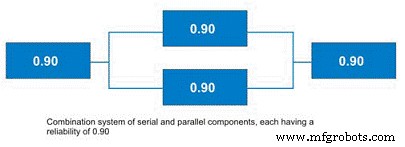
Figure 11. Combination System with Parallel and Serial Elements

r out of n Systems (r/n Systems)
An important concept to plant reliability engineers is the concept of r/n systems. These systems require that r units from a total population in n be available for use. A great industrial example is coal pulverizers in an electric power generating plant. Often, the engineers design this function in the plant using an r/n approach. For instance, a unit has four pulverizers and the unit requires that three of the four be operable to run at the unit’s full load (see Figure 12).

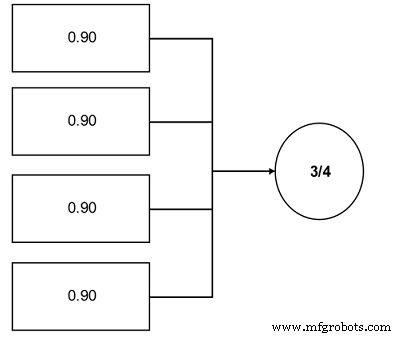
Figure 12. Simple r/n system example – Three of the four components are required.

The reliability calculation for an r/n system can be reduced to a simple cumulative binomial distribution calculation, the formula for which is:

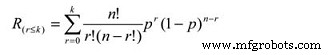
Where:
Rs =System reliability given the actual number of failures (r) is less than or equal the maximum allowable (k)
r =The actual number of failures
k =The maximum allowable number of failures
n =The total number of units in the system
p =The probability of survival, or the subcomponent reliability for a given time (t).

This equation is somewhat more complicated. In our pulverizer example, assuming a subcomponent reliability of 0.90, the equation works out as a summation of the following:
P(0) =0.6561
P(1) =0.2916

So, the likelihood of completing the mission time (t) is 0.9477 (0.6561 + 0.2916), or approximately 95%.

Field Data Collection
To employ the reliability analysis methods described herein, the engineer requires data. It is imperative to establish field data collection systems to support your reliability management initiatives. Likewise, as much as possible, you’ll want to employ common nomenclature and units so that your data can be parsed effectively for more detailed analysis. Collect the following information:

• Basic System Information
• Operating Context
• Environmental Context
• Failure Data

A good general system for data collection is described in the IEC standard 300-3-2. In addition to providing instructions for collecting field data, it provides a standard taxonomy of failure modes. Other taxonomies have been established, but the IEC standard represents a good starting point for your organization to define its own. Likewise, DOE standard NE-1004-92 offers a very nice standard nomenclature of failure causes.

An important benefit derived from your efforts to collect good field data is that it enables you to break the “random trap.” As I mentioned earlier, the bathtub curve has been much maligned – particularly in the Reliability-Centered Maintenance literature. While it’s true that Weibull analysis reveals that few complex mechanical systems exhibit time-dependent wearout failures, the reason, at least in part, is due to the fact that the reliability of complex systems is affected by a wide variety of failure modes and mechanisms.

When these are lumped together, there is a “randomizing” effect, which makes the failures appear to lack any time dependency. However, if the failure modes were analyzed individually, the story would likely be very different (Figure 13). For certain, some failure modes would still be mathematically random, but many, and arguably most, would exhibit a time dependency. This kind of information would arm reliability engineers and managers with a powerful set of options for mitigating failure risk with a high degree of precision. Naturally, this ability depends upon the effective collection and subsequent analysis of field data.

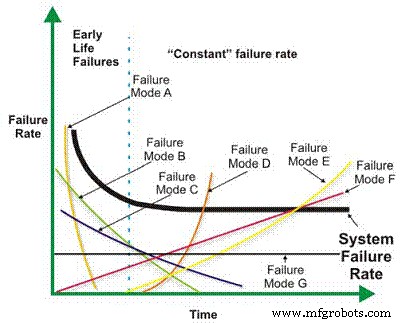
Figure 13. Good field data collection enables you to break the random trap.

This brief introduction to reliability engineering methods is intended to expose the otherwise uninitiated plant engineer to the world of quantitative reliability engineering. The subject is quite broad, however, and I’ve only touched on the major reliability methods that I believe are most applicable to the plant engineer. I encourage you to further investigate the field of reliability engineering methods, concentrating on the following topics, among others:

• More detailed understanding of the Weibull distribution and its applications

• More detailed understanding of the exponential distribution and its applications

• The Gaussian distribution and its applications

• The log-normal distribution and its applications

• Confidence intervals (binomial, chi-square/Poisson, etc.)

• Beta distribution and its applications

• Bayesian applications of reliability engineering methods

• Stress-strength interference analysis

• Testing options and their applicability to plant reliability engineering

• Reliability growth strategies and management

• More detailed understanding of field data collection.

Most important, spend time learning how to apply reliability engineering methods to plant reliability problems. If your interest in reliability engineering methods is high, I encourage you to pursue professional certification by the American Society for Quality as a reliability engineer (CRE).

References
Troyer, D. (2006) Strategic Plant Reliability Management Course Book, Noria Publishing, Tulsa, Oklahoma.

Bernowski, K (1997) “Safety in the Skies,” Quality Progress , January.

Dovich, R. (1990) Reliability Statistics, ASQ Quality Press, Milwaukee, WI.

Krishnamoorthi, K.S. (1992) Reliability Methods for Engineers, ASQ Quality Press , Milwaukee, WI.

MIL Standard 721

IEC Standard 300-3-3

DOE Standard NE-1004-92

Appendix:Select reliability engineering terms from MIL STD 721
Availability – A measure of the degree to which an item is in the operable and committable state at the start of the mission, when the mission is called for at an unknown state.

Capability – A measure of the ability of an item to achieve mission objectives given the conditions during the mission.

Dependability – A measure of the degree to which an item is operable and capable of performing its required function at any (random) time during a specified mission profile, given the availability at the start of the mission.

Failure – The event, or inoperable state, in which an item, or part of an item, does not, or would not, perform as previously specified.

Failure, dependent – Failure which is caused by the failure of an associated item(s). Not independent.

Failure, independent – Failure which occurs without being caused by the failure of any other item. Not dependent.

Failure mechanism – The physical, chemical, electrical, thermal or other process which results in failure.

Failure mode – The consequence of the mechanism through which the failure occurs, i.e. short, open, fracture, excessive wear.

Failure, random – Failure whose occurrence is predictable only in the probabilistic or statistical sense. This applies to all distributions.

Failure rate – The total number of failures within an item population, divided by the total number of life units expended by that population, during a particular measurement interval under stated conditions.

Maintainability – The measure of the ability of an item to be retained or restored to specified condition when maintenance is performed by personnel having specified skill levels, using prescribed procedures and resources, at each prescribed level of maintenance and repair.

Maintenance, corrective – All actions performed, as a result of failure, to restore an item to a specified condition. Corrective maintenance can include any or all of the following steps:localization, isolation, disassembly, interchange, reassembly, alignment and checkout.

Maintenance, preventive – All actions performed in an attempt to retain an item in a specified condition by providing systematic inspection, detection and prevention of incipient failures.

Mean time between failure (MTBF) – A basic measure of reliability for repairable items:the mean number of life units during which all parts of the item perform within their specified limits, during a particular measurement interval under stated conditions.

Mean time to failure (MTTF) – A basic measure of reliability for non-repairable items:The mean number of life units during which all parts of the item perform within their specified limits, during a particular measurement interval under stated conditions.

Mean time to repair (MTTR) – A basic measure of maintainability:the sum of corrective maintenance times at any specified level of repair, divided by the total number of failures within an item repaired at that level, during a particular interval under stated conditions.

Mission reliability – The ability of an item to perform its required functions for the duration of specified mission profile.

Reliability – (1) The duration or probability of failure-free performance under stated conditions. (2) The probability that an item can perform its intended function for a specified interval under stated conditions. For non-redundant items this is the equivalent to definition (1). For redundant items, this is the definition of mission reliability.