Experimentelle Forschung zur Stabilität und natürlichen Konvektion von TiO2-Wasser-Nanofluid in Gehäusen mit unterschiedlichen Rotationswinkeln

Hintergrund

Da Nanofluid hergestellt wird, wird es aufgrund seiner hervorragenden Wärmeleiteigenschaften [1,2,3] weit verbreitet im Bereich der Wärmeübertragung eingesetzt [4,5,6], insbesondere im Bereich der natürlichen Konvektion [7,8,9].

Die Wärmeübertragungseigenschaften von Nanoflüssigkeiten durch natürliche Konvektion werden von vielen Forschern numerisch untersucht. Er et al. [10, 11] wandten eine einphasige und eine zweiphasige Gitter-Boltzmann-Methode an, um die natürliche Konvektionswärmeübertragung von Al₂ . numerisch zu untersuchen O₃ -Wasser-Nanofluid in einer quadratischen Kavität. Sheikholeslami et al. [12] untersuchten die magnetohydrodynamischen Wärmeübertragungseigenschaften durch natürliche Konvektion eines horizontalen zylindrischen Gehäuses mit einem inneren dreieckigen Zylinder, der mit Al₂ . gefüllt war O₃ -Wasser-Nanofluid durch eine Gitter-Boltzmann-Simulationsmethode. Uddinet al. [13] untersuchten die natürliche Konvektionswärmeübertragung verschiedener Nanofluide entlang einer vertikalen Platte, die in ein poröses Medium eingebettet war, basierend auf dem Darcy-Forchheimer-Modell. Meng et al. [14] untersuchte numerisch die natürliche Konvektion eines mit Al₂ . gefüllten horizontalen Zylinders O₃ -Wasser-Nanoflüssigkeit. Ahmed et al. [15] verwendeten eine Zweiphasengitter-Boltzmann-Methode, um die natürliche Konvektion von CuO-Wasser-Nanofluid in einem geneigten Gehäuse zu untersuchen. Qiet al. [16] simulierte numerisch die natürliche Konvektion von Cu-Ga-Nanofluid in einem Gehäuse.

Zusätzlich zu den oben genannten numerischen Simulationen zur natürlichen Konvektion von Nanoflüssigkeiten werden die experimentellen Studien zur natürlichen Konvektion von Nanoflüssigkeiten von immer mehr Forschern durchgeführt. Liet al. [17] untersuchten experimentell die natürliche Konvektionswärmeübertragung von ZnO-EG/Wasser-Nanofluid. Huet al. [18, 19] untersuchten experimentell die Verbesserung der natürlichen Konvektionswärmeübertragung eines quadratischen Gehäuses, das mit TiO₂ . gefüllt war -Wasser und Al₂ O₃ -Wasser-Nanofluids bzw. Hoet al. [20] untersuchten experimentell die natürliche Konvektionswärmeübertragung von vertikalen quadratischen Gehäusen unterschiedlicher Größe, die mit Al₂ . gefüllt waren O₃ -Wasser-Nanoflüssigkeit. Heris et al. [21,22,23] untersuchten experimentell die konvektiven Wärmeübertragungseigenschaften verschiedener Arten von Nanoflüssigkeiten (Cu/Wasser, Al₂ O₃ -Wasser bzw. CuO-Wasser) in runden Röhrchen. Mansouret al. [24] untersuchten experimentell die Mischkonvektion eines mit Al₂ . gefüllten geneigten Rohres O₃ -Wasser-Nanoflüssigkeit. Changet al. [25] untersuchten experimentell die natürliche Konvektion von Al₂ O₃ -Wasser-Nanofluid in dünnen Gehäusen. Wen et al. [26, 27] untersuchten experimentell die konvektiven Wärmeübertragungseigenschaften von Al₂ O₃ -Wasser-Nanofluide und TiO₂ -Wasser-Nanofluide unter Laminar-Flow-Bedingungen. Xuanet al. [28] untersuchten experimentell die Konvektionswärmeübertragung von Cu-Wasser-Nanofluid in einem geraden Messingrohr.

Die oben genannten Literaturstellen haben einen großen Beitrag zu den natürlichen Konvektionswärmeübertragungseigenschaften von Nanofluiden geleistet. Die Verbesserung der natürlichen Konvektionswärmeübertragung von Gehäusen mit unterschiedlichen Drehwinkeln, die mit Nanofluid gefüllt sind, muss jedoch weiter untersucht werden. Daher sind die Stabilität und die natürlichen Konvektionswärmeübertragungseigenschaften von TiO₂ -Wasser-Nanofluid in Gehäusen mit unterschiedlichen Drehwinkeln (α = −45°, α = 0°, α = 45° und α = 90°) werden in dieser Arbeit experimentell untersucht.

Methode

Herstellung von Nanofluid und seine Stabilität

TiO₂ als Nanopartikel gewählt. Abbildung 1 zeigt die REM-, TEM- und XRD-Bilder von TiO₂ Nanopartikel bei unterschiedlichen Vergrößerungszeiten. Aus REM-Bildern ist ersichtlich, dass sich die Nanopartikel leicht ansammeln, und es sind einige Maßnahmen erforderlich, um die stabilen Nanofluide herzustellen. Aus TEM-Bildern kann auch festgestellt werden, dass die Partikelgröße etwa 10 nm beträgt und die Formen der Nanopartikel flach sind. Flache Nanopartikel haben bei gleichem Massenanteil eine größere Wärmeübertragungsfläche als kugelförmige Nanopartikel, was für die Verbesserung der Wärmeübertragung von Vorteil ist. Abbildung 1g zeigt die XRD-Muster des TTP-A10 TiO₂ Nanopartikel. Wie beobachtet, deuten die starken und scharfen Peaks darauf hin, dass das TTP-A10 TiO₂ Nanopartikelprobe ist hochkristallin. Die durchschnittliche Partikelgröße der Probe kann mit der Scherrer-Gleichung berechnet werden, die in Gl. (1). Das TiO₂ Nanopartikelgrößen sind 6, 9, 14, 20 und 35 nm, berechnet aus diesen Beugungspeakwerten (111, 200, 021, 202 und 311), und die kleinsten Nanopartikelgrößen betragen etwa 6 und 9 nm basierend auf den Beugungspeakwerten (111 und 200). Die großen Nanopartikelgrößen können durch die Aggregation von Nanopartikeln verursacht werden. Die kleinsten Werte (6 und 9 nm) können die tatsächlichen Größen von Nanopartikeln sein, die Größe einiger Nanopartikel kann 6 nm betragen und die meisten Nanopartikelgrößen können etwa 9 nm betragen, die näher an der Beschreibung des Herstellers liegen ( 10 nm) und die TEM-Bilder (10 nm).

wo k ist der Wert für den Formfaktor und k = 0,9; λ die Röntgenwellenlänge ist; und β ist die Linie, die die volle Breite beim halben Maximum (FWHM) der Spitzenhöhe im Bogenmaß erweitert, und θ ist der Bragg-Beugungswinkel.

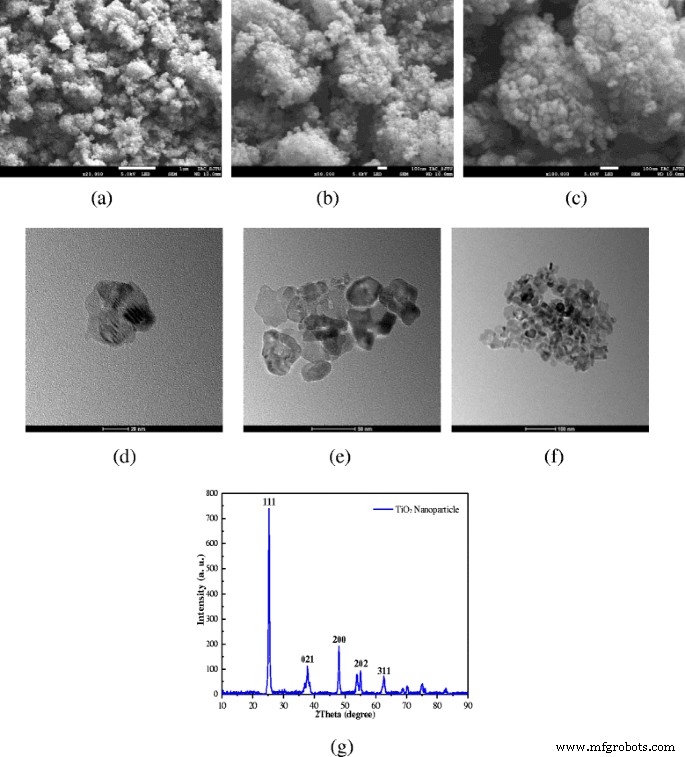
Morphologie von Nanopartikeln. REM-, TEM- und XRD-Bilder von TiO₂ Nanopartikel bei unterschiedlichen Vergrößerungszeiten. a SEM × 20000. b SEM × 50000. c SEM × 100000. d TEM 20 nm. e TEM 50 nm. f TEM 100 nm. g XRD

TiO₂ -Wasser-Nanofluid mit unterschiedlichen Nanopartikel-Massenanteilen (wt% = 0.1%, wt% = 0.3% und wt% = 0.5%) wird nach dem zweistufigen Verfahren hergestellt, das in Abb. 2 dargestellt ist. Die mechanische Rührzeit beträgt die Hälfte eine Stunde für jeden der Teilschritte und die Beschallungszeit beträgt 40 Minuten. Tabelle 1 zeigt die Informationen einiger Materialien und Ausrüstungen bei der Herstellung von Nanoflüssigkeiten. Abbildung 3 zeigt das TiO₂ -Wasser-Nanofluid vor dem Verlegen und nach 72 Stunden. Es ist zu erkennen, dass sich im Reagenzglas nur wenige Nanopartikel ablagern und das in dieser Veröffentlichung hergestellte Nanofluid eine gute Stabilität aufweist.

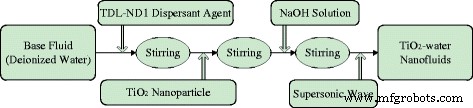
Herstellung von Nanofluiden. Herstellungsverfahren von TiO₂ -Wasser-Nanofluide nach einem zweistufigen Verfahren

Stabilitätsbeobachtung von TiO₂ -Wasser-Nanoflüssigkeit. TiO₂ -Wasser-Nanofluid zu verschiedenen Zeiten. a Vor dem Verlegen. b Nach 72 Stunden

Neben der Untersuchung, ob sich Nanopartikel im Reagenzglas ablagern, werden die Auswirkungen der Transmission (τ ) von Nanofluid auf seine Stabilität werden ebenfalls diskutiert. Abbildung 4 zeigt die Transmission (τ ) Veränderungen von TiO₂ -Wasser-Nanofluid (wt% = 0.5%) mit unterschiedlichen pH-Werten und Dosierungen (m ) des Dispergiermittels. Die Durchlässigkeit wird mit einem Ultraviolett-Spektrophotometer für sichtbares Licht (UV-1800(PC)) gemessen. Wie wir wissen, reflektieren die Nanopartikel das meiste Licht und haben ein hohes Reflexionsvermögen (eine niedrige Durchlässigkeit), wenn sich die Nanopartikel gleichmäßig im Wasser verteilen. Daher ist die Stabilität des Nanofluids umgekehrt proportional zum Transmissionsgrad, und das stabile Nanofluid weist einen geringen Transmissionsgrad auf. Aus Abb. 4 ist zu entnehmen, dass das Nanofluid mit m = 6 Gew.% und pH = 8 hat die geringste Durchlässigkeit und die beste Stabilität. Die Nanofluide mit unterschiedlichen Nanopartikel-Massenanteilen in diesem Experiment werden bei m . hergestellt = 6 Gew.% und pH = 8, was die Stabilität von Nanoflüssigkeiten gewährleisten kann.

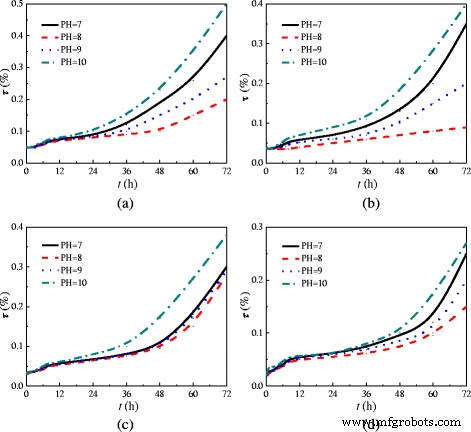
Transmission von TiO₂ -Wasser-Nanoflüssigkeit. Transmission (τ ) Veränderungen von TiO₂ -Wasser-Nanofluid (wt% = 0.5%) unter verschiedenen pH-Werten mit Zeiten (h ) in unterschiedlichen Dosen (m ) des Dispergiermittels. a m =5 Gew.-%. b m =6 Gew.-%. c m =7 Gew.-%. d m = 8 Gew.-%

Experimentelles System

Abbildung 5 zeigt die schematische Darstellung der drei Versuchssätze. Die Abmessungen der drei rechteckigen Gehäuse sind 10 cm (Breite) × 20 cm (Höhe), 5 cm (Breite) × 20 cm (Höhe) und 20 cm (Breite) × 20 cm (Höhe). Die Breite und Höhe sind definiert als W und H , bzw. das Seitenverhältnis (A ) des Gehäuses ist definiert als A = W /H . Die linke Wand (Kupferplatte) des Gehäuses wird durch eine an Gleichstrom angeschlossene Silikonheizplatte beheizt. Die rechte Wand (Kupferplatte) des Gehäuses wird durch das Kühlwasser in einem kleinen Hohlraum (das Material ist ebenfalls Kupfer) gekühlt, der an ein Wasserbad mit konstanter Temperatur angeschlossen ist. Die Temperaturen von zwei Seiten des Gehäuses werden von sechs Thermoelementen gemessen, die an ein Datenerfassungsgerät (Agilent 34972A) angeschlossen sind. Die äußere Isolierschicht wird verwendet, um den Wärmeverlust zu verhindern.

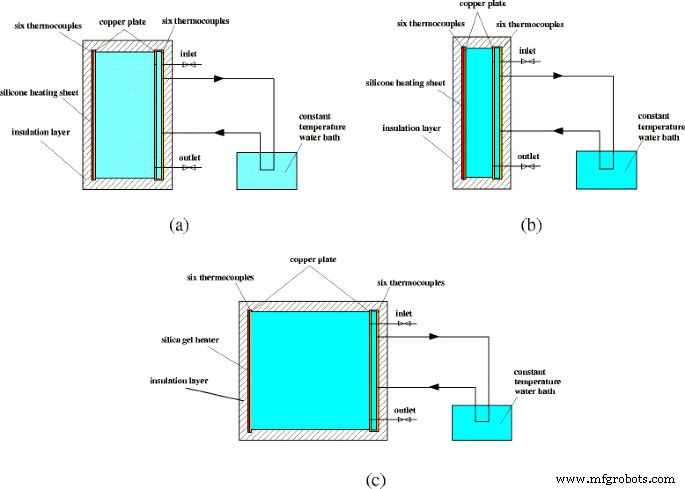
Schematische Darstellungen von Experimentiersätzen. Schematische Diagramme von drei verschiedenen Experimentiersätzen mit Seitenverhältnis. a A = 1:2. b A = 1:4. c A = 1:1

Die natürlichen Konvektionswärmeübertragungseigenschaften der beiden Gehäuse mit unterschiedlichen Drehwinkeln (α = −45°, α = 0°, α = 45° und α = 90°) gefüllt mit TiO₂ -Wasser-Nanofluid werden in dieser Arbeit untersucht. Für das Gehäuse mit α = −90°, die obere Wand ist die heiße Wand und die untere Wand ist die kalte Wand, und die Wärmeübertragung im Gehäuse ist hauptsächlich Wärmeleitung. Das Manuskript untersucht jedoch hauptsächlich die natürliche Konvektionswärmeübertragung von Nanoflüssigkeit in der Umhüllung, daher die Umhüllung mit α = −90° wird in diesem Manuskript nicht berücksichtigt. Abbildung 6 zeigt die schematische Darstellung von Gehäusen mit unterschiedlichen Drehwinkeln.

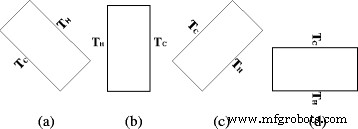
Schematische Darstellung der Drehwinkel. Schematische Darstellung der Gehäuse mit vier verschiedenen Drehwinkeln. a α = −45°. b α = 0°. c α = 45°. d α = 90°

Datenverarbeitung

Die Macht Q von der Silikon-Heizfolie bereitgestellt wird, ist wie folgt:

wo U und ich sind die Spannung bzw. Elektrizität des Gleichstroms.

Die Wirkleistung Q _Netz ist wie folgt:

wo Q _Verlust ist der Wärmeverlust, der von einem Wärmestrommesser gemessen wird.

Die Temperatur der Kupferplattenseite neben der Silikonheizplatte \({T}_{\mathrm{H}}^{*}\) ist wie folgt:

wo T ₁ , T ₂ , …, T ₆ sind die Temperaturen von Thermoelementen.

Die Temperatur der Kupferplattenseite (linke Seite des Gehäuses) neben dem Nanofluid T _H ist wie folgt:

wo δ = 0,005m ist die Dicke der Kupferplatte, A ist die Fläche der Kupferplatte, λ _w ist die Wärmeleitfähigkeit der Kupferplatte.

Die Temperatur der Kupferplattenseite (rechte Seite des Gehäuses) neben der Isolationsschicht T _C ^∗ ist wie folgt:

wo T ₇ , T ₈ , …, T ₁₂ sind die Temperaturen der Thermoelemente in der rechten Gehäuseseite.

Wenn der thermische Gleichgewichtszustand erreicht ist, ist die Temperatur des Kühlwassers gleich der Temperatur der Kupferplattenseite neben dem Kühlwasser. Die Temperatur der Kupferplattenseite (rechte Seite des Gehäuses) neben dem Nanofluid T _C kann wie folgt berechnet werden:

Die qualitative Temperatur T _m ist wie folgt definiert:

Der konvektive Wärmeübergangskoeffizient h ist wie folgt:

Die Nusselt-Nummer ist wie folgt definiert:

wo λ _f ist die Wärmeleitfähigkeit der Flüssigkeit im Gehäuse.

Unsicherheitsanalyse

Die Fehlerübertragungsformel des konvektiven Wärmeübertragungskoeffizienten lautet wie folgt [19]:

Die Fehlerübertragungsformel der Nusselt-Zahl lautet wie folgt [19]:

Basierend auf den Gl. (10) und (11) betragen die Fehler des konvektiven Wärmeübertragungskoeffizienten und der Nusselt-Zahl in diesem Experiment 5,65 bzw. 6,34 %. Es zeigt sich, dass die Fehler der Versuchsreihen gering sind, was die Zuverlässigkeit und Genauigkeit der Versuchsergebnisse gewährleisten kann.

Ergebnisse und Diskussionen

Testvalidierung

Vor der Studie zu Nanofluid ist die Experimentvalidierung notwendig. Abbildung 7 zeigt den Vergleich der Nusselt-Zahlen zwischen den experimentellen Ergebnissen von Wasser und den Ergebnissen der veröffentlichten Literatur für Gehege mit A = 1:2, A = 1:4 und A = 1:1. Die maximalen Fehler für Gehäuse mit A = 1:2, A = 1:4 und A = 1:1 sind 8,4, 9,5 bzw. 8,1 %. Es kann festgestellt werden, dass die experimentellen Ergebnisse eine gute Übereinstimmung mit den Ergebnissen der veröffentlichten Literatur [20, 29] aufweisen, was die Genauigkeit und Zuverlässigkeit des experimentellen Systems bestätigt.

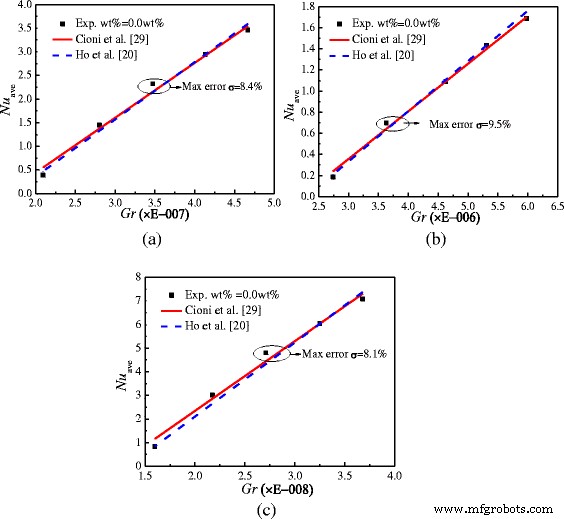
Validierung des Experimentiersatzes. Vergleich der Nusselt-Zahlen zwischen den experimentellen Ergebnissen und der veröffentlichten Literatur in Beilagen mit zwei unterschiedlichen Seitenverhältnissen. a A = 1:2. b A = 1:4. c A = 1:1

Anlage mit A = 1:2

Die Auswirkungen von Drehwinkeln auf die Wärmeübertragungseigenschaften durch natürliche Konvektion von TiO₂ -Wasser-Nanofluid werden in diesem Papier diskutiert. Abbildung 8 zeigt die Veränderungen der durchschnittlichen Nusselt-Zahlen mit den Drehwinkeln des Gehäuses mit A = 1:2. Aus Abb. 8 ist zu entnehmen, dass die Nusselt-Zahlen mit den Drehwinkeln zunächst zu- und dann abfallen. Das Gehäuse mit Drehwinkel α = 0° hat die höchste Nusselt-Zahl gefolgt von der Einfassung mit den Drehwinkeln α = 45° und α = 90°, das Gehäuse mit Drehwinkel α = −45° hat die niedrigste Nusselt-Zahl. Wärmeleitung spielt eine immer größere Rolle, wenn der Drehwinkel kleiner wird (α ≤ −90°), und die Wärmeübertragung ist fast eine Wärmeleitung, wenn der Drehwinkel auf α . sinkt = −90°. Wenn sich die heiße Wand oben und die kalte Wand unten im Gehäuse befindet (α = −90°), die Auftriebsrichtung ist nach oben gerichtet, aber die obere Wand verhindert, dass sich die Flüssigkeit nach oben bewegt. Die Bewegung des Nanofluids im Gehäuse ist gering, und die Hauptwärmeübertragung ist die Wärmeleitung, die eine kleine Nusselt-Zahl verursacht. Das Gehäuse mit α = −45° ist näher am Gehäuse mit α = −90° und zeigt die kleinste Nusselt-Zahl im Vergleich zu anderen Drehwinkeln. Für die Gehäuse mit Drehwinkel α = 45° und α = 90°, die Flüssigkeit in der Nähe der unteren heißen Wand wird erwärmt und bewegt sich nach oben und die Flüssigkeit in der Nähe der oberen kalten Wand wird abgekühlt und bewegt sich nach unten. Die Richtungen von heißem Fluid und kaltem Fluid sind entgegengesetzt und verhindern die natürliche Konvektionswärmeübertragung, die eine niedrigere Nusselt-Zahl im Vergleich zum Gehäuse mit α . bewirkt = 0° aber eine höhere Nusselt-Zahl im Vergleich zum Gehäuse mit α = −45°. Es ist auch zu erkennen, dass die Unterschiede zwischen verschiedenen Drehwinkeln mit der Heizleistung zunehmen. Dies liegt daran, dass die Auswirkungen von Drehwinkeln die Hauptrolle auf die Wärmeübertragung bei geringer Heizleistung spielen und die Auswirkungen der Konvektion auf die Wärmeübertragung gering sind. Die konvektive Wärmeübertragungsintensität nimmt jedoch mit der Heizleistung zu und spielt die Hauptrolle bei der Wärmeübertragung bei hoher Heizleistung, was die größeren Unterschiede zwischen den verschiedenen Drehwinkeln bei hoher Heizleistung im Vergleich zu niedriger Heizleistung verursacht.

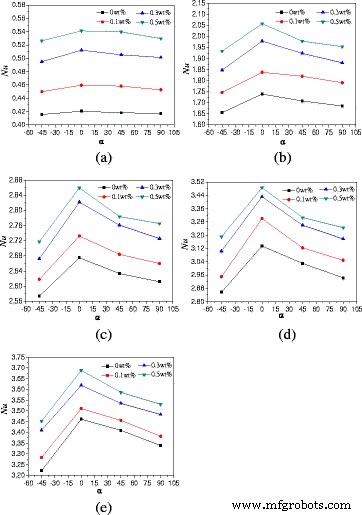
Änderungen der Nusselt-Zahlen mit Drehwinkeln (A = 1:2). Durchschnittliche Nusselt-Zahlen ändern sich des Nanofluids mit den Rotationswinkeln des Gehäuses (A = 1:2) bei unterschiedlichen Heizleistungen. a Q = 1 W. b Q = 5 W. c Q = 10 W. d Q = 15 W. e Q = 20 W

Neben den Drehwinkeln werden auch die Auswirkungen des Nanopartikel-Massenanteils auf den natürlichen Konvektionswärmeübergang diskutiert. Abbildung 9 zeigt die Veränderungen der mittleren Nusselt-Zahlen mit Nanopartikel-Massenanteilen. Es zeigt sich, dass die Nusselt-Zahlen mit den Nanopartikel-Massenanteilen ansteigen. Für Heizleistung Q = 1 W und α = 0°, TiO₂ -Wasser-Nanofluid mit Gew.% = 0,1%, Gew.% = 0,3% und Gew.% = 0,5% kann die Wärmeübertragung um 9,3, 21,8 bzw. 28,7% im Vergleich zu Wasser verbessern. Das Verstärkungsverhältnis nimmt mit der Heizleistung ab. Für Heizleistung Q = 20 W und α = 0°, TiO₂ -Wasser-Nanofluid mit Gew.% = 0,1%, Gew.% = 0,3% und Gew.% = 0,5% kann die Wärmeübertragung um 1,4, 4,6 bzw. 6,6% im Vergleich zu Wasser verbessern. Die Turbulenzintensität spielt bei hoher Heizleistung eine große Rolle und die Auswirkungen des Nanopartikel-Massenanteils auf die Wärmeübertragung werden gering.

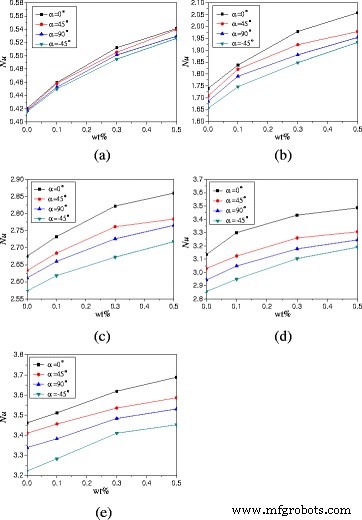
Änderungen der Nusselt-Zahlen mit Nanopartikel-Massenanteilen (A = 1:2). Durchschnittliche Nusselt-Zahlen Änderungen der Nanoflüssigkeit im Gehäuse (A = 1:2) mit Nanopartikel-Massenanteilen bei unterschiedlichen Heizleistungen. a Q = 1 W. b Q = 5 W. c Q = 10 W. d Q = 15 W. e Q = 20 W

Die Auswirkungen von Heizleistungen auf den natürlichen Konvektionswärmeübergang werden in dieser Arbeit untersucht. Abbildung 10 zeigt die Veränderungen der mittleren Nusselt-Zahlen mit der Heizleistung. Für α = 0°, TiO₂ -Wasser-Nanofluid bei Q = 5 W, Q = 10 W, Q = 15 W und Q = 20 W kann die Wärmeübertragung um 280,2, 428,4, 544,1 und 581,5 % im Vergleich zu Q . verbessern = 1 W. Hohe Heizleistung erhöht die Turbulenzintensität und verbessert die Wärmeübertragung.

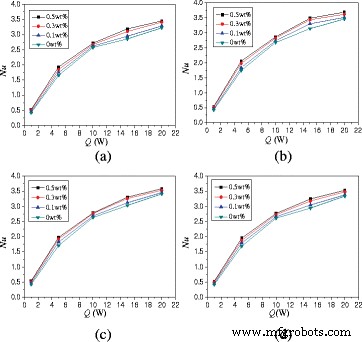
Änderungen der Nusselt-Zahlen mit Heizleistung (A = 1:2). Durchschnittliche Nusselt-Zahlen Änderungen der Nanoflüssigkeit im Gehäuse (A = 1:2) mit Heizleistung bei unterschiedlichen Drehwinkeln. a α = −45°. b α = 0°. c α = 45°. d α = 90°

Anlage mit A = 1:4

Um die Auswirkungen von Aspektverhältnissen von Gehäusen auf die Wärmeübertragung zu untersuchen, wurden die natürlichen Konvektionswärmeübertragungseigenschaften von Gehäusen mit A = 1:4 gefüllt mit TiO₂ -Wasser-Nanofluid untersucht. Abbildung 11 zeigt die Veränderungen der durchschnittlichen Nusselt-Zahlen mit den Drehwinkeln des Gehäuses. Es kann erhalten werden, dass eine ähnliche Schlussfolgerung wie A = 1:2, dass Nusselt-Zahlen mit den Drehwinkeln zuerst zu- und dann abfallen. Für Nanofluid mit wt% = 0.5% Beispiel sind die Unterschiede zwischen A = 1:4 und A = 1:2 sind, dass die Verstärkungsverhältnisse (von 6,5 auf 20,7%) der Nusselt-Zahl im Gehege (A = 1:4, α = 0°) verglichen mit dem im Gehäuse (A = 1:4, α = −45°) sind höher als die Verstärkungsverhältnisse (von 2,85 bis 9,3%) der Nusselt-Zahl im Gehäuse (A = 1:2, α = 0°) verglichen mit dem im Gehäuse (A = 1:2, α = −45°).

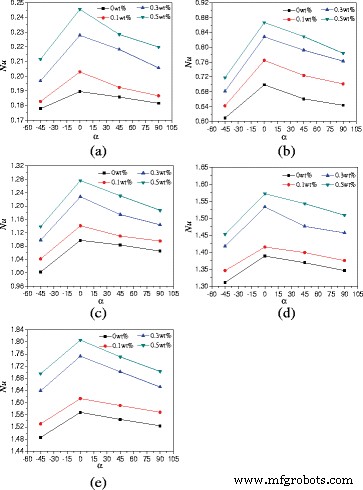
Änderungen der Nusselt-Zahlen mit Drehwinkeln (A = 1:4). Durchschnittliche Nusselt-Zahlenänderungen des Nanofluids mit den Rotationswinkeln des Gehäuses (A = 1:4) bei unterschiedlichen Heizleistungen. a Q = 1 W. b Q = 5 W. c Q = 10 W. d Q = 15 W. e Q = 20 W

Abbildung 12 zeigt die Veränderungen der mittleren Nusselt-Zahlen mit Nanopartikel-Massenanteilen. Für Heizleistung Q = 1 W und α = 0°, TiO₂ -Wasser-Nanofluid mit Gew.% = 0,1%, Gew.% = 0,3% und Gew.% = 0,5% kann die Wärmeübertragung um 7,1, 20,2 bzw. 29,5 % im Vergleich zu Wasser verbessern. Das Verstärkungsverhältnis nimmt mit der Heizleistung ab. Für Heizleistung Q = 20 W und α = 0°, TiO₂ -Wasser-Nanofluid mit Gew.% = 0,1%, Gew.% = 0,3% und Gew.% = 0,5% kann die Wärmeübertragung um 2,9, 11,8 bzw. 15,1% im Vergleich zu Wasser verbessern.

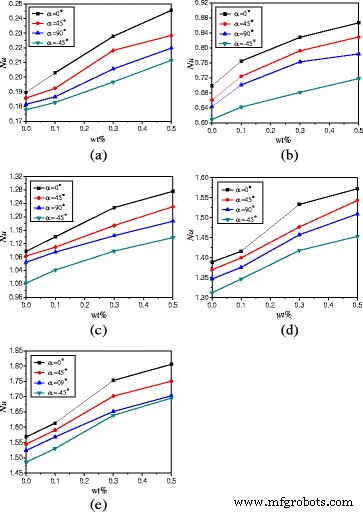
Änderungen der Nusselt-Zahlen mit Nanopartikel-Massenanteilen (A = 1:4). Durchschnittliche Nusselt-Zahlen Änderungen der Nanoflüssigkeit im Gehäuse (A = 1:4) mit Nanopartikel-Massenanteilen bei unterschiedlichen Heizleistungen. a Q = 1 W. b Q = 5 W. c Q = 10 W. d Q = 15 W. e Q = 20 W

Abbildung 13 zeigt die Veränderungen der mittleren Nusselt-Zahlen mit der Heizleistung. Die durchschnittliche Nusselt-Zahl von Nanofluid kann um 242,4% ~ 701,5% im Vergleich zu Wasser bei der Heizleistung Q = 1 W erhöht werden. Für α = 0°, TiO₂ -Wasser-Nanofluid mit Gew.-% = 0,5% bei Q = 5 W, Q = 10 W, Q = 15 W und Q = 20 W kann die Wärmeübertragung um 253,0, 419,9, 540,3 und 635,6 % im Vergleich zu Q . verbessern = 1 W bzw..

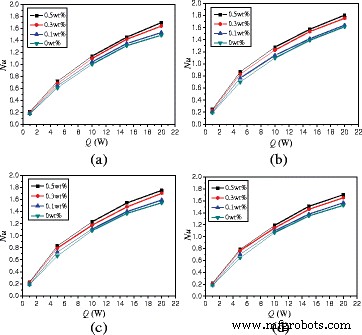
Änderungen der Nusselt-Zahlen mit Heizleistung (A = 1:4). Durchschnittliche Nusselt-Zahlen Änderungen der Nanoflüssigkeit im Gehäuse (A = 1:4) mit Heizleistung bei unterschiedlichen Drehwinkeln. a α = −45°. b α = 0°. c α = 45°. d α = 90°

Vergleich zwischen A = 1:2, A = 1:4 und A = 1:1

Aufgrund der Längenbeschränkung dieses Beitrags sind die Ergebnisse der Anlage mit A = 1:1 sind nur in Abb. 14 angegeben, und die Auswirkungen unterschiedlicher Drehwinkel, Nanopartikel-Massenanteile und Heizleistungen auf die Wärmeübertragung können alle in Abb. 14 gezeigt werden. Um die Wärmeübertragungseigenschaften von Gehäusen mit zu vergleichen A = 1:2, A = 1:4 und A = 1:1, Abb. 14 zeigt den Vergleich der durchschnittlichen Nusselt-Zahlen zwischen A = 1:2, A = 1:4 und A = 1:1 bei verschiedenen Drehwinkeln. Es zeigt sich, dass die Nusselt-Zahlen mit dem Seitenverhältnis des Gehäuses zunehmen. Die Nusselt-Nummern der Anlage (A = 1:1 und A = 1:2) um 190,6% ~ 224,4% und 103,6% ~ 172,0% gegenüber den Nusselt-Beilagenzahlen (A = 1:4) jeweils unter den gleichen Bedingungen. Für Q = 1 W und α = 0° Beispiel, Nanofluid mit wt% = 0.5%, wt% = 0.3%, wt% = 0.1% und wt% = 0.0% im Gehäuse mit A = 1:2 kann die Wärmeübertragung um 120,4, 124,9, 126,5 und 121,9 % im Vergleich zum Gehäuse mit A . verbessern = 1:4. Das Verstärkungsverhältnis nimmt mit der Heizleistung ab. vFür Q = 20 W und α = 0°, Nanofluid mit wt% = 0.5%, wt% = 0.3%, wt% = 0.1% und wt% = 0.0% im Gehäuse mit A = 1:2 kann den Wärmeübergang um 104,2, 106,5, 117,6, 120,7 % gegenüber dem im Gehäuse mit A = 1:4 verbessern. Es wurde auch festgestellt, dass die Nusselt-Zahl-Anstiege von Gew.-% =  0,1 % auf Gew.-% =  0,3 % größer sind als die von Gew.-% =  0,3 % auf Gew.-% =  0,5 %. Dies liegt daran, dass die Erhöhung der Wärmeleitfähigkeit die Hauptrolle bei der Wärmeübertragung von Gew.-% =  0,1 % auf Gew.-% =  0,3 % spielt, was eine große Verbesserung bewirkt. Die Viskositätserhöhung beginnt jedoch die Hauptrolle bei der Wärmeübertragung von Gew.-% =  0,3 % auf Gew.-% =  0,5 % zu spielen, was eine kleine Verbesserung bewirkt. Da Abb. 14 alle experimentellen Ergebnisse abdecken kann, sind die detaillierten Ergebnisse von Abb. 14 in den Tabellen 2, 3 und 4 gezeigt.

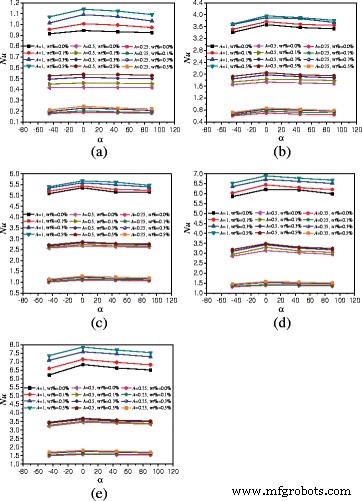
Nusselt numbers comparison between different aspect ratios. Comparison of average Nusselt numbers of nanofluid in different aspect ratios (A  = 1:1, A  = 1:2, and A = 1:4) and rotation angle enclosures at different heating powers. a Q  = 1 W. b Q  = 5 W. c Q  = 10 W. d Q  = 15 W. e Q  = 20 W

Conclusions

The stability and natural convection heat transfer characteristics of the two enclosures with different rotation angles (α  = −45°, α  = 0°, α  = 45°, and α  = 90°) filled with TiO₂ -water nanofluid are experimentally investigated. Some conclusions are obtained as follows:

1. (1)

   TiO₂ -water nanofluid with m  = 6 wt% and pH = 8 has the lowest transmittance and has the best stability.

2. (2)

   The enclosure with rotation angle α  = 0° has the highest Nusselt number followed by the enclosure with rotation angles α  = 45° and α  = 90°; the enclosure with rotation angle α  = −45° has the lowest Nusselt number.

3. (3)

   There is a higher heat transfer performance in a bigger aspect ratio enclosure. The Nusselt numbers of enclosure (A  = 1:1 and A  = 1:2) can be enhanced by 190.6% ~ 224.4% and 103.6% ~ 172.0% compared with the Nusselt numbers of enclosure (A  = 1:4) at the same conditions.

4. (4)

   Nusselt numbers increase with nanoparticle mass fractions, but the enhancement ratio decreases with the heating power.

5. (5)

   Average Nusselt numbers increase with the heating power. Average Nusselt numbers of nanofluid can be enhanced by 701.5% compared with water at the best.