Untersuchungen von Leerstandsstrukturen im Zusammenhang mit ihrem Wachstum im h-BN-Blatt

Hintergrund

Hexagonales Bornitrid (h -BN)-Blatt ist ein einschichtiges Material ähnlich dem Graphen, das aus einer gleichen Anzahl von Bor- und Stickstoffatomen besteht und attraktive physikalische Eigenschaften in Bezug auf die Anwendung von Nanogeräten aufweist. Während seiner Synthese wird einschichtiges h -BN-Blech weist verschiedene Defekte wie Leerstellen und Korngrenzen auf [1, 2]. Diese Defekte können die atomare und elektronische Struktur von einlagigen h verändern -BN-Blatt und beeinflussen somit die Leistung von h -BN-basierte Geräte.

Weil h -BN-Faltblatt besteht aus zwei Arten von Atomen, im Gegensatz zum Graphenblatt teilen sich die Kantenstrukturen seiner Cluster, Nanobänder oder Nanolöcher in zwei Arten:N-terminiert und B-terminiert. Die stabilste Struktur der Clusterkante hat eine N-terminierte Kante mit Zickzackstruktur [3, 4]. In früheren theoretischen Studien wurden die atomaren und elektronischen Strukturen von Leerstellenstrukturen in einschichtigen h -BN-Faltblatt hängen von der Art der Terminationsatome und ihrer Leerstellengröße ab [3,4,5,6,7,8,9,10,11]. Das heißt, die berechnete Stabilität von Dreiecksleerstellenstrukturen und die magnetischen Eigenschaften hängen von der Art der terminierten Atome und der Leerstellengröße der Dreiecksleerstelle aufgrund einzelner Elektronen an den Randatomen ab. Die dreieckigen Leerstellenstrukturen wurden in Experimenten zur Verwendung eines freistehenden h . gefunden -BN-Blatt [12,13,14,15]. Die Bestrahlung mit Elektronenstrahlen führt zu einer zunehmenden Größe von Leerstellenstrukturen, die unabhängig von der Leerstellengröße die Dreiecksform beibehalten [12, 13].

Vor kurzem haben wir über die Studie zum Wachstum der dreieckigen Leerstelle von einschichtigen h . berichtet -BN-Blatt [15]. Im Experiment wurde beobachtet, dass Atome in h -BN-Blatt werden in Form der Bündel, nicht jedes Atoms, am Rand von Leerstellenstrukturen ausgestoßen. Darüber hinaus haben wir kurz theoretische Ergebnisse erwähnt, um das Leerstandswachstum in h . zu erklären -BN-Blatt mit dreieckiger Form.

In diesem Artikel befassen wir uns mit der detaillierten Untersuchung der atomaren Strukturen der dreieckigen Leerstelle von einschichtigen h -BN-Blatt. Die lokal stabilen Strukturen dreieckiger Leerstellen hängen von der Leerstellengröße mit N-terminierter Zickzackkante ab. Dann untersuchen wir durch Erhöhung der Leerstellengröße die Stabilität der optimierten Strukturen mit einem fehlenden BN-Paar und ihre magnetischen Eigenschaften.

Rechenmethoden

Wir haben die dichtefunktionaltheoretischen Berechnungen mit dem Vienna Ab-initio-Simulationspaket (VASP) durchgeführt [16, 17]. Der Plane-Wave-Basissatz mit der Energiegrenze von 400 eV wird verwendet, um elektronische Wellenfunktionen zu beschreiben. Die Ionen werden durch projektorerweiterte Wellenpotentiale repräsentiert [18, 19] und die verallgemeinerte Gradientennäherung wird verwendet, um das Austauschkorrelationsfunktional zu beschreiben [20, 21]. Um die schwachen Van-der-Waals-(vdW)-Wechselwirkungen zu nehmen, verwenden wir Grimmes DFT-D2-vdW-Korrektur [22] basierend auf einer semi-empirischen GGA-Typ-Theorie.

Die atomaren Positionen aller Strukturen werden mit Restkräften kleiner als 0,01 eV/Å entspannt. Für die Brillouin-Zonen-Integration verwenden wir nur den Gammapunkt im speziellen K-Punkte-Schema des Monkhorst-Pack. Die Gitterkonstante unseres Modells wird mit 2,56 Å berechnet, was mit dem experimentellen Wert übereinstimmt [23]. Um den Unterschied in den rekonstruierten Strukturen nach fehlendem BN-Paar zu untersuchen, betrachten wir (9 × 9) und (15 × 15) Superzellen in unseren Berechnungen.

Ergebnisse und Diskussion

Dreieckige Stellenausschreibung in h -BN-Tabelle

Zuerst haben wir verschiedene Stellengrößen von einzelnen h . betrachtet -BN-Blatt zur Untersuchung des Größeneffekts von Leerstandsstrukturen. Da N-terminierte Leerstellenstruktur von h -BN-Faltblatt ist eine stabilere Struktur als ein B-terminiertes [3, 4], wir konzentrieren uns hauptsächlich auf N-terminierte dreieckige Leerstellenstrukturen. Um die Leerstandsgröße von h . zu kontrollieren -BN-Blatt, wir erhöhen die Anzahl der ausgestoßenen Atome in h -BN-Blatt behält die dreieckige Form bei. Die B-terminierten Leerstellenstrukturen führen nach der Relaxation zu einer kleinen Verzerrung in ihrem Scheitelbereich mit schwacher Bindung zwischen B-Atomen (hier nicht gezeigt), während die N-terminierten Strukturen eine deutliche Änderung an den Ecken ihrer dreieckigen Leerstelle zeigen. Unter den unterschiedlichen Leerstellengrößen der N-terminierten Dreiecksform finden wir zwei Arten von optimierten (d. h. lokal stabilen) Strukturen. Eine davon ist eine symmetrische Struktur (bezeichnet als N-symm), bei der im Vergleich zum ursprünglichen h . keine merkliche Strukturänderung am Scheitelpunkt der Dreiecksleerstelle gefunden wird -BN-Faltblatt, während die andere eine Verzerrungsstruktur (bezeichnet als NN-Bindung) ist, die N-N-Bindungen an allen Ecken der Dreiecksloch-Leerstelle in h . zeigt -BN-Blatt.

Bei Monovakanzen B (V_1B ) in h -BN-Blatt zeigt die optimierte Struktur nur eine Konfiguration, nämlich die N-symm-Struktur. Aufgrund der starken Abstoßungskraft zwischen N-Atomen, die sich am Scheitel der dreieckigen Leerstelle befinden, vergrößert sich der Abstand zwischen den N-Atomen (2,66 Å) im Vergleich zu dem von unberührtem h -BN-Faltblatt (2,48 Å) und B-N-Bindungslängen am Rand der dreieckigen Leerstelle nehmen ab.

Wenn die Größe der dreieckigen Leerstelle von h -BN-Blatt wird erhöht, um V_3B+1N . zu erhalten und V_6B+3N Strukturen, wobei V _{m B+n N} stellt eine dreieckige Vakanz mit m . dar fehlende B-Atome und n fehlenden N-Atomen können die optimierten Strukturen sowohl N-symm- als auch NN-Bindungsstrukturen aufweisen, wie in Abb. 1 gezeigt. Diese Ergebnisse stimmen mit der vorherigen theoretischen Studie für die Leerstellenstrukturen [6] überein.

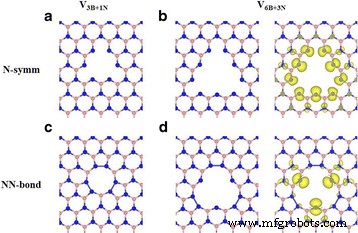
Optimierte Leerstandsstrukturen von a V_3B+1N und b V_6B+3N mit N-symmetrischer Struktur und c V_3B+1N und d V_6B+3N mit NN-Bindungsstruktur. Blau und rosa Kugeln B- bzw. N-Atome darstellen. Neben Grundstücken b und d sind die Unterschiede in der Spindichte projiziert auf die Ebene des V_6B+3N Strukturen

Die optimierte Struktur größerer Leerstände als die von V_6B+3N Struktur repräsentiert nur eine Konfiguration, d. h. eine NN-Bindungsstruktur. Diese große Leerstellenstruktur hat die längere Kantenlänge der Dreiecksform als die der kleinen Leerstellenstruktur, was bedeutet, dass die BN-Bindungen um das Leerstellenloch herum weniger von der Bildung von NN-Bindungen am Scheitel des Leerstellenlochs in großen Leerstellenstrukturen beeinflusst werden (und somit die Bindungslängen zwischen B- und N-Atomen bleiben am Rand der Leerstellenstruktur nahezu gleich). Berechnete Bindungslängen zwischen N-Atomen an den Ecken von dreieckigen Leerstellen und relative Energien von zwei Arten von Leerstellenstrukturen sind in Tabelle 1 aufgeführt. Wir stellen fest, dass die N-N-Bindungslängen und die relativen Energien von der Größe der Leerstellen abhängen. Der Unterschied der relativen Energien zwischen N-symm- und NN-Bindungsstrukturen nimmt mit zunehmender Größe der dreieckigen Leerstellenstruktur ab. Im Gegensatz dazu erweisen sich die B-terminierten Leerstellenstrukturen unabhängig von ihrer Größe als nur eine Struktur mit einer schwachen B-B-Bindung am Scheitelpunkt (siehe Tabelle 1).

Die berechneten magnetischen Gesamtmomente von Leerstellenstrukturen variieren je nach Leerstellengröße, abgeschlossenen Atomen und optimierten Strukturen (siehe Tabelle 1). In den N-symm-Strukturen ist der Wert des magnetischen Moments in Einheiten von μ _B ist gleich der Anzahl der Stickstoffatome, die sich am Rand von dreieckigen Leerstellenstrukturen befinden, da diese N-Atome nach dem Fehlen von Atomen und dem Aufbrechen von B-N-Bindungen im h . baumelnde Bindungen haben -BN-Blatt. Es wird jedoch berechnet, dass sich die gesamten magnetischen Momente von N-N-Bindungsstrukturen mit verschiedenen Leerstellengrößen aufgrund der Bildung der N-N-Bindungen (homopolare Sigma-Bindung) an den Ecken der dreieckigen Leerstellenstrukturen von denen der N-Symmetriestrukturen unterscheiden. Die gesamten magnetischen Momente für V_3B+1N , V_6B+3N , und V_10B+6N Strukturen mit N-N-Bindungen am Scheitelpunkt der Leerstelle sind 0, 3 und 6 μ _{B ,} bzw. Abbildung 1b, d zeigt den Unterschied der Spindichten für V_6B+3N Strukturen mit N-symm (M = 9 μ _B ) und N-N-Bindung (M = 3μ _B ) Strukturen.

BN-Paar fehlt am Randbereich des Leerstellenlochs

Als nächstes haben wir die Situation des Fehlens von BN-Paaren in N-terminierten Leerstellenstrukturen im Detail untersucht, da beobachtet wurde, dass die Größe der Leerstellenlochstrukturen durch das Fehlen von B- und N-Atomen am Rand von dreieckigen Leerstellenstrukturen im Experiment vergrößert wird [14 ]. Es wurde auch berichtet, dass, wenn die Stellenausschreibungen wachsen, die dreieckige Form in h . beibehält -BN-Faltblatt, B- und N-Atome werden bevorzugt paarweise oder gebündelt von der Randfläche von Leerstellenstrukturen ausgestoßen [15].

Um die Stabilität von Leerstellenstrukturen in Abhängigkeit von der fehlenden Position zu untersuchen, erhöhen wir die Superzellengröße von h -BN-Blatt bis zu 15 × 15 Elementarzelle und erhalten die größere Leerstellengröße wie V_15B+10N und V_21B+15N . Es wurde gefunden, dass die optimierten Relaxationen für diese Leerstellen nur zu einer stabilen Atomkonfiguration führen, d. h. der NN-Bindungskonfiguration. Die N-N-Bindungslängen an den Scheitelpunkten und die gesamten magnetischen Momente sind in Tabelle 1 aufgeführt. Wir wählen ein großes N-terminiertes V_21B+15N dreieckige Leerstellenstruktur, eingebettet in die Superzelle, um weitere fehlende Positionen zu berücksichtigen (Abb. 2a). Wie in Abb. 2a gezeigt, fehlt die Anzahl möglicher Positionen des BN-Paares am Rand von V_21B+15N Die Leerstandsstruktur beträgt sechs. Nach Relaxation der Leerstellenstruktur mit fehlendem BN-Paar an verschiedenen Positionen finden wir den Unterschied in den optimierten Strukturen in Abhängigkeit von den fehlenden Positionen, wie in den Abb. 2b–g gezeigt. Die optimierten Strukturen werden in Abhängigkeit von den fehlenden Positionen in drei Typen unterteilt; Ecke fehlt (1 und 6), in der Nähe der Ecke fehlt (2 und 5) und in der Mitte fehlen (3 und 4) Positionen.

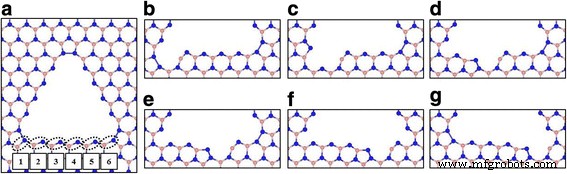
Optimierte Strukturen von a V_21B+15N Stellenstruktur mit möglichen fehlenden Positionen von BN-Paar und b –g V_22B+16N Leerstandsstrukturen nach fehlendem BN-Paar an bestimmten Positionen. Die gepunkteten Kreise mit Nummerierung in a repräsentieren mögliche Positionen des fehlenden BN-Paares. Die Positionen mit Nummerierung 1 bis 6 werden als b bezeichnet Ecke-1, c Gesicht-1, d Gesicht-2, e Gesicht-3, f Gesicht-4 und g Ecke-2 fehlende Strukturen bzw.

Nachdem ein BN-Paar am Rand der dreieckigen Leerstellenstruktur fehlt, zeigt die optimierte Struktur einen rekonstruierten hexagonalen offenen BN-Ring nahe der fehlenden Position, in der die B-N-Bindungslängen am verzerrten BN-Ring etwas kürzer sind; dies bedeutet, dass die Wechselwirkungen zwischen B- und N-Atomen stärker werden und die Anordnung der Elektronenladungsverteilung in den B-N-Bindungen verändern. Die fehlende Ecke-1-Struktur (fehlende Nummerierung 1) ist fast unverändert, mit Ausnahme des Bereichs des verzerrten offenen BN-Rings, wie in Abb. 2b gezeigt.

Es wurde festgestellt, dass andere Strukturen (fehlende Nummerierung 2–6) ein N-Dimer mit fünfeckiger Form am Rand aufweisen, wie in Abb. 2d–g gezeigt, außer Abb. 2c mit N-Dimer am Scheitelpunkt. Das heißt, die N-Atome in der Nähe der fehlenden Position haben die baumelnde Bindung aufgrund der fehlenden und bilden das N-Dimer (siehe Abb. 2d–g). Die Anwesenheit des N-Dimers in jeder Struktur beeinflusst ihre Stabilität und magnetischen Eigenschaften. Wir berechnen die relativen Energien und gesamten magnetischen Momente von BN-Paar-Missing-Strukturen aus V_21B+15N Stellenangebotsstruktur, die in Tabelle 2 aufgeführt sind.

Basierend auf den relativen Energien stellen wir fest, dass die Stabilität der fehlenden Strukturen des BN-Paares zunimmt, wenn sich die fehlende Position dem Zentrum der Dreieckskante nähert (siehe Tabelle 2). Die berechneten magnetischen Gesamtmomente, die durch terminierte N-Atome am Rand optimierter Leerstellenstrukturen verursacht werden, hängen von der fehlenden Position ab. Die magnetischen Momente von zwei Ecken fehlenden Strukturen sind gleich (M = 12μ _B ). Nach dem Fehlen beträgt die Anzahl der terminierten N-Atome 13 in den fehlenden Eckenstrukturen, was das magnetische Moment M . ergeben könnte = 13μ _B . Das magnetische Moment eines N-Atoms in den verzerrten offenen BN-Ringen verschwindet jedoch aufgrund der oben erwähnten Umlagerung der Ladungsverteilung. Die magnetischen Momente anderer Strukturen variieren in Abhängigkeit von den fehlenden Positionen aufgrund des rekonstruierten offenen BN-Rings und/oder N-Dimers, die sich in der Nähe des fehlenden Punktes befinden. Abbildung 3 zeigt die Spindichten optimierter Strukturen, die nach fehlendem BN-Paar erhalten wurden. Aus diesen Spindichten wissen wir, woher die in Tabelle 2 aufgeführten magnetischen Momente kommen.

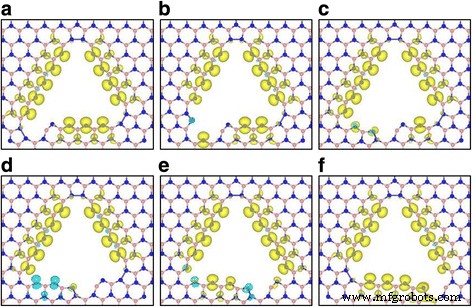
Die Spindichte (ρ_Spin-Up -ρ_Spin-down ) Verteilungen für die optimierten Strukturen von BN-Paar fehlt. Gelb und hellblau Isoflächen zeigen die positiven bzw. negativen Werte der Spindichten an

Für eine genaue Analyse der Unterschiede zwischen optimierten Strukturen in Abhängigkeit von den fehlenden Positionen wählen wir drei Konfigurationen (Ecke-1, Fläche-2 und Fläche-3) aus sechs fehlenden BN-Paar-Strukturen aus und berechnen ihre elektronische Zustandsdichte (DOS). In den DOS-Plots befinden sich die Defektzustände innerhalb der Bandlücke des unberührten h -BN-Blatt, wie in Abb. 4 gezeigt, wobei das Valenzbandmaximum und das Leitungsbandminimum des ursprünglichen h -BN-Blatt werden durch VBM bzw. CBM angezeigt. Im lokalen DOS (LDOS)-Plot zeigen die grau schattierten Bereiche und die roten durchgezogenen Linien die LDOS von N-Atomen der Leerstellenstrukturen vor bzw. nach fehlendem BN-Paar an. Insbesondere die Zustände von N-Kantenatomen sind im LDOS-Plot um das Fermi-Niveau konzentriert. Wie in den DOS- und LDOS-Plots gezeigt, zeigen die Spinzustände von N-Kantenatomen die asymmetrischen Merkmale. Die Corner-1-Missing-Struktur in Abb. 4a zeigt baumelnde Bindungszustände von N-Atomen im Bereich von −0.5 bis 1.0 eV der DOS- und LDOS-Diagramme:Auffallenderweise stammen die baumelnden Bindungszustände, die nur in der Randflächenregion lokalisiert sind, hauptsächlich von Spin -Down-Zustände von LDOS (siehe Spindichte-Diagramme, die sich auf die Peakpositionen mit den Nummern 3 bis 6 im LDOS-Diagramm beziehen). In den LDOS-Plots zweier flächenfehlender Strukturen (Abb. 4b, c) erscheinen nicht nur die Spin-down-Zustände, sondern auch die Spin-up-Zustände der N-Kantenatome als baumelnde Bindungszustände, die nur in der Kantenflächenregion in der Nähe von lokalisiert sind das Fermi-Niveau (−0.5~1.0 eV). Das heißt, diese Spin-Up- und Spin-Down-Diagramme beziehen sich auf die mit 3 bis 6 nummerierten Peakpositionen im LDOS-Diagramm von Fig. 4b und die mit 2 bis 5 nummerierten im LDOS-Diagramm von Fig. 4c. Andererseits haben alle fehlenden Strukturen des BN-Paares die Energiebandlücke. Die Bandlücken betragen ungefähr 0,35, 0,24 bzw. 0,36 eV für die fehlenden Strukturen von Ecke-1, Fläche-2 bzw. Fläche-3.

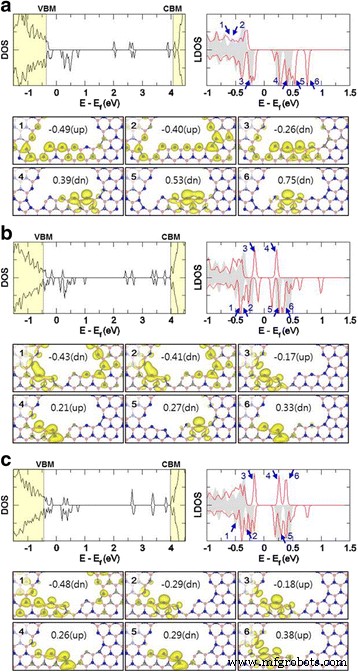
Gesamt-DOS, LDOS der N-Kantenatome und die Spindichte-Plots nahe dem Fermi-Niveau für die optimierten Strukturen von V_21B+15N Stellenstruktur mit fehlendem BN-Paar:a Ecke-1 fehlt, b Gesicht-2 fehlt und c Gesicht-3 fehlende Strukturen. Das Licht gelb schattierte Regionen in der Gesamt-DOS repräsentieren die Regionen der Valenzbänder und Leitungsbänder des unberührten h -BN-Blatt bzw. Das Graue schattierte und rote durchgezogene Linien sind LDOS von N Atomen vor und nach fehlendem BN-Paar am Rand von dreieckigem Leerstandsstruktur

Schlussfolgerungen

Wir haben die strukturellen und elektronischen Eigenschaften der dreieckigen Leerstellenstrukturen von h . untersucht -BN-Blatt mit First-Principles-Berechnungen. Es zeigte sich, dass die optimierten dreieckigen Leerstandsstrukturen von ihrer Leerstandsgröße abhängen. Die stabilste Konfiguration großer Leerstellenstrukturen hat die N-N-Bindung an jedem Eckpunkt der Dreiecksleerstelle, die ihre magnetischen Momente bestimmt. Wenn das Fehlen eines BN-Paares am Rand einer dreieckigen Leerstellenstruktur mit einer großen Lochgröße im h auftritt -BN-Faltblatt, wie im Experiment beobachtet, ist die stabilste Struktur eine flächenlose Struktur mit Bildung von N-N-Bindungen. Die magnetischen Momente und LDOS der optimierten Strukturen hängen von den fehlenden Positionen des BN-Paares am Rand der Dreiecksleerstelle ab.