Eigenschaften von elektromagnetischen Längsschwingungen in Metallen und deren Anregung an ebenen und sphärischen Oberflächen

Hintergrund

Die Bestrahlung einer ebenen Metalloberfläche mit Femtosekunden-Laserpulsen führt häufig zur Bildung von laserinduzierten periodischen Oberflächenstrukturen (LIPSSs) [1]. Neben dem LIPSS wurden hyperfeine Welligkeiten, sogenannte High-Spatial-Frequency-LIPSS (HSFL) beobachtet [1, 2]. Die räumlichen Perioden der HSFL sind deutlich kleiner als die Bestrahlungswellenlänge λ ₀ . Für Aluminium beispielsweise wurde dieser Zeitraum auf 20 bis 200 nm bei λ . geschätzt ₀ =0,8 μ m [2, 3]. Während die Orientierung der Welligkeiten bei gewöhnlichem LIPSS senkrecht zur Laserlichtpolarisation war, war die Orientierung von HSFL oft senkrecht und manchmal parallel zur Polarisation. Ähnliche HSFL wurden auf den Oberflächen von transparenten Dielektrika, Halbleitern und Metallen gebildet. Der Ursprung der HSFL wurde durch verschiedene Mechanismen wie die Erzeugung der zweiten Harmonischen, die Beteiligung spezifischer Arten von Plasmonenmoden, Selbstorganisation und lokale Feldverstärkungen während des inhomogenen Durchbruchs in dielektrischen Materialien erklärt [2, 3].

Das Ziel dieser Studie ist es, einen Wellenprozess zu suchen, der ein Muster mit einer kurzen Periode erzeugen könnte Λ λ ₀ . Wir untersuchen die Eigenschaften von longitudinalen (L) elektromagnetischen Wellen in Metallen, auch bekannt als Plasmawellen. Unsere Studie besteht aus den folgenden neuartigen Schritten. Zuerst begannen wir unsere Forschung mit der Definition der räumlichen Streuung der Permittivität. Wie unten gezeigt, ist die allgemeine Definition nutzlos, wenn ein zu untersuchendes Medium nicht einheitlich und unendlich ist. Daher schlagen wir ein neues Konzept der räumlich dispersiven dielektrischen Funktion ε . vor . Diese Funktion stellt die direkte Proportionalität zwischen zwei Vektorfeldern her, E (r ,ω ) und D (r ,ω ), aber nicht die Amplituden E (k ,ω ) und D (k ,ω ) von ebenen Wellen. Folglich ist die Menge ε hängt vom Quadrat der Wellenzahl ab, k ² , der Parameter der Vektor-Helmholtz-Gleichung für das elektrische Feld E (r ,ω ), aber nicht der Wellenvektor k der ebenen Wellen. Um eine solche neuartige Funktion abzuleiten, haben wir dann die Reaktion der Leitungselektronen auf eine elektromagnetische Mode bestimmt, indem wir die Boltzmann-Transportgleichung in der Relaxationszeit-Approximation gelöst haben. Es wurden die sogenannten transversalen und longitudinalen Lindhard-Dielektrikumsfunktionen erhalten. Darüber hinaus haben wir festgestellt, dass der Längs-Lindhard und die viel einfachere hydrodynamische Funktion in einem weiten Parameterbereich nahe beieinander liegen. Zur Veranschaulichung der Theorie wurde die Lichtauslöschung durch Silber- und Gold-Nanokügelchen betrachtet. Wir zeigen zum ersten Mal, dass die nichtlokale Mie-Theorie die Blauverschiebung, die Verbreiterung und das eventuelle Verschwinden der Plasmonenresonanzen erklärt, die mit einer Abnahme der Größe der Edelmetall-Nanokugeln beobachtet werden. Schließlich wurde das neu entwickelte theoretische Modell angewendet, um die Möglichkeit einer Beteiligung der Longitudinalmoden an der Bildung der laserinduzierten Oberflächenstrukturen zu untersuchen. Zu diesem Zweck haben wir die Fresnel-Theorie unter Berücksichtigung übertragener Longitudinalwellen modifiziert.

Methoden

Zur Bestimmung der elektromagnetischen Felder in stückweise homogenen Medien wurde die klassische elektromagnetische Theorie angewendet. Das elektrische Feld E in jeder einheitlichen Domäne des heterogenen Mediums wurde angenommen, dass es sich um eine Lösung der Vektor-Helmholtz-Gleichung (VHE) handelt:

wo Δ ist der Laplace-Operator.

Wie üblich sind die Tangentialkomponenten des elektrischen E und magnetisch H Felder sind über die Grenzen der Medien hinweg kontinuierlich. Außerdem haben wir berücksichtigt, dass Elektronen in Metall eingeschlossen sind; daher folgende zusätzliche Randbedingung (ABC) für die Normalkomponente der Stromdichte j an der Metalloberfläche S wurde verwendet:(j n )| _{r ∈S} =0.

Um den Leitungsstrom in Metall zu bestimmen, haben wir die Boltzmann-Transportgleichung (BTE) in der Relaxationszeit-Approximation gelöst:

wo f ist die Einteilchen-Verteilungsfunktion im Phasenraum (r , v ), v ist die mikroskopische Elektronengeschwindigkeit, e und m sind die Elektronenladung bzw. -masse, B ist die magnetische Induktion, f ₀ eine Gleichgewichtsverteilungsfunktion ist und τ ist die Entspannungszeit.

Im Folgenden leiten wir Formeln für die räumlich dispersiven dielektrischen Funktionen her. Dann verwenden wir sie, um die Lichtreflexion von einer ebenen Metalloberfläche und die Lichtstreuung an einer Edelmetall-Nanokugel zu untersuchen.

Ergebnisse und Diskussion

Räumliche Ausbreitung von ε in einem heterogenen Medium

In der Literatur wird eine räumlich dispersive dielektrische Funktion ε wird über die folgende Beziehung [4–6] definiert:

wo ε ₀ ist die elektrische Konstante, D (ω , r ) ist die Amplitude der Verschiebungsvektorschwingung mit der Kreisfrequenz ω in Punkt r , und E (ω , r ^′ ) die Amplitude der elektrischen Feldschwingung im Punkt r ^′ . Fourier-Transformationen von Gl. (3) gib die Gleichung an

wobei ein räumlich dispersives ε (ω , k ) hängt vom Wellenvektor k . ab einer ebenen elektromagnetischen Welle. Unserer Meinung nach ist Gl. (3) ist nicht nur in einem unendlich homogenen Volumen mehrdeutig, sondern wir haben es mit stückweise heterogenen Systemen zu tun, bei denen Grenzen berücksichtigt werden sollten und k sind in verschiedenen Medien nicht gleich.

Unser Ansatz verwendet keine Ausdehnung der elektromagnetischen Wellen über ebene Wellen. Die räumlich dispersive Permittivität bestimmt die Beziehung zwischen D (ω , r ) und eine besondere Lösung des Vektors Helmholtz-Gl. (1):

Hier E (ω , r ) bezeichnet die Verteilung des elektrischen Feldes, aber nicht nur den Vektor E in Punkt r .

Längs- und Querdielektrische Funktionen

Die Permittivität von Metallen wird üblicherweise durch die Leitfähigkeit σ . ausgedrückt [4]:

wo ε _g ist ein Teil der dielektrischen Funktion, die die Polarisation des Festkörpers ermöglicht; ε _g =1 für ein einfaches Metall. Um σ . zu bestimmen , haben wir die Stromdichte berechnet

wobei \(\textrm{d}\mathbf{v}=\frac{v}{m}\,\textrm{d}\epsilon\,\textrm{d}\,\Omega,\) d ​​Ω =sinθ dθ dϕ , v , θ , ϕ sind die Kugelkoordinaten der Geschwindigkeit. Im Gegensatz zu früheren Untersuchungen haben wir den Wellenvektor k . nicht eingeführt fand aber eine HdO-Lösung in Form einer unendlichen Reihe mit den Operatoren v ∇ handeln auf v E :

wo Γ =1/τ . Dann, f ₀ wurde durch eine Nulltemperatur-Fermi-Dirac-Verteilung angenähert und nach Integration über ε in Gl. (7), wir haben

wobei \(\omega_{\mathrm{p}}^{2}=\frac{e^{2}\,n_{e}}{m\,\varepsilon_{0}},\) _p ist die Plasmafrequenz, \(\mathbf{u}=\frac{\mathbf{v}}{v}\) ist der Einheitsvektor in Richtung von v ,\(l=\frac{v_{\mathrm{F}}}{-i \omega +\Gamma},\) v _F ist die Fermi-Geschwindigkeit. Außerdem haben wir die Integrale berechnet

wo n ist eine natürliche Zahl. Die folgende Abhängigkeit von j auf willkürlich elektrisches Feld E wurde endlich erhalten

Es gibt zwei Arten von Lösungen für Gl. (1), divergenzfrei, die Gleichung ∇ . erfüllen ·E =0 und rotationslos, die Gleichung

Für eine ebene Welle mit E ∝ exp[i (k r −ω t )], Gl. (14) verwandelt sich in die Beziehung k ×E =0, was zeigt, dass die Welle longitudinal ist (L). Um Prozesse in kugelförmigen Körpern zu simulieren, verwendet man am besten die vektoriellen Kugelharmonischen L , M , und N als vollständiger Satz orthogonaler Funktionen. In diesem Fall gilt Gl. (14) spezifiziert Oberwellen L . Die Wellenzahl der L-Wellen und L Moden wird durch das folgende Dispersionsgesetz bestimmt

Aus Gl. (6) und (13) finden wir, dass Lösungen zu Gl. (1) Erfüllen der Bedingung von Gl. (14) geben die folgende Längspermittivität

wo Φ ist die Phi-Funktion von Lerch,

\(a=\frac{kv_{\mathrm{F}}}{\omega +i\Gamma}\).

Die erhaltene Permittivität unterscheidet sich von der von Kliewer und Fuchs [7] definierten nur in der Schreibweise:

Die Identität

erlaubt es, Gl. (18) wie folgt

Im Fall von Γ =0, diese Formel hat die Form einer Gleichung, die von Klimontovich und Silin [8] abgeleitet wurde, die Landau-Dumping in entarteten Plasma untersuchten (siehe [9], [10, Gl. (40.17)] und [11]). Die Permittivität der äquivalenten Gl. (16), (18) und (20) wird allgemein als die dielektrische Lindhard-Funktion bezeichnet (mit Bezug auf [12]), obwohl diese Funktion zuerst von Klimontovich und Silin [8] erhalten wurde.

Die transversale Lindhard-Permittivität [7] kann mit Gl. (13) wenn ∇ ·E =0. Im tatsächlichen Fall von v _F k ω , reduziert sie sich auf die dielektrische Drude-Funktion

Diese Funktion stimmt mit experimentellen Daten für viele Metalle überein [13]. Wenn |a |<1, die longitudinale Permittivität (16) vereinfacht die hydrodynamische dielektrische Funktion:

Reflexion einer ebenen elektromagnetischen Welle von einer flachen Metalloberfläche

Randbedingungen

In diesem Abschnitt bestimmen wir die Richtung des Wellenvektors k ^L und Amplitude der L-Welle, die in Metall während der Reflexion einer ebenen elektromagnetischen Welle von einer flachen Metalloberfläche angeregt wird.

Betrachten Sie eine ebene Welle, die auf die Dielektrikum-Metall-Grenzfläche einfällt z =0, wobei der Wellenvektor im xz liegt Flugzeug. Das elektrische Feld im dielektrischen Medium 1 besteht aus dem einfallenden E _ich und reflektiertes E _r Wellen, das Feld in Metall 2 hat das transversale E _t und in einigen Fällen längs E ^L Komponenten. Gemäß den Maxwell-Randbedingungen sind die transversalen Komponenten der elektrischen und magnetischen Feldvektoren in der Ebene z . stetig =0. Außerdem werden die Elektronen nicht aus Metall herausgeschleudert; daher ist die Normalkomponente der elektrischen Stromdichte bei z . null =0,

wären \(\hat{\mathbf{z}}\) der Einheitsvektor in Richtung von z Achse.

Alle Terme in den Maxwell-Randbedingungen müssen die gleiche Abhängigkeit von x . haben und y . Diese Anforderung hat mehrere Konsequenzen. Zunächst kann festgestellt werden, dass L-Wellen nur bei p-Polarisation angeregt werden können, wenn der elektrische Vektor der einfallenden Welle E ^{(ich )} ist parallel zur Einfallsebene. Mit anderen Worten, Plasmonenpolaritonen können durch eine transversale magnetische (TM) Welle erzeugt werden. Der Effekt ist ähnlich wie bei einer Metallkugel [14]. Zweitens lassen sich aus den Bedingungen

wobei Indizes 1x und 2x bezeichne das x -Projektionen der Vektoren in Medien 1 bzw. 2, θ ₁ ist der Einfallswinkel.

Reflexions- und Transmissionskoeffizienten

Lassen Sie uns das Feld bestimmen, das von einer ebenen p-polarisierten elektromagnetischen Welle gebildet wird, die auf eine ebene Metalloberfläche einfällt. Es ist praktisch, die Komponenten der elektrischen und magnetischen Felder durch das x . auszudrücken Bestandteil von E ^{(ich )} , nämlich E x (r)=− r E x (i) für die reflektierte Welle, E x (t)=t E x (i) für die übertragene Transversalwelle und

für die gesendete Longitudinalwelle, hier r ist ein Reflexionskoeffizient, t und t _L sind Transmissionskoeffizienten.

Aus den Maxwell-Randbedingungen und dem ABC von Gl. (23) geschrieben in der folgenden Form

wir haben

Bei δ =0, der Koeffizient r wird zum Fresnel-Reflexionskoeffizienten der p-polarisierten Welle (siehe zB Gl. (2.49) von [4]). Unter der gleichen Bedingung t ist nicht der Fresnel-Transmissionskoeffizient, da unsere Definitionen von t und r unterscheiden sich von denen von Fresnel.

Auslöschung des Lichts durch Metall-Nanosphäre

In einem vorhergehenden Artikel verallgemeinerte einer der Autoren die Lorentz-Mie-Theorie unter Berücksichtigung des ABC von Gl. (23). Ein Analogon des Fresnel-Koeffizienten r , der Mie-Koeffizient b _l für den reflektierten TM-Modus des l th Auftrag wurde gefunden

wo

ψ _l und ζ _l sind die Riccati-Bessel- und Riccati-Hankel-Funktionen der Ordnung l , bzw; j _l die sphärische Bessel-Funktion ist, bezeichnet die Primzahl die Ableitung einer Funktion nach ihrem Argument.

Vergleichen wir Vorhersagen der klassischen und verallgemeinerten Lorentz-Mie-Theorie mit experimentellen Daten. In [15] untersuchten Hilger, Tenfelde und Kreibig Extinktionsspektren von Silbernanopartikeln, die auf dielektrischen Oberflächen abgeschieden wurden. In der ersten Phase der Studie erzeugten die Forscher Strahlen aus Silberpartikeln mit mittleren Durchmessern von 2, 3,5 und 4 nm, bestimmten die Partikelgrößenverteilung für einen der Strahlen, zeichneten Extinktionsspektren auf und schätzten den Parameter A =0,25 der phänomenologischen Formel Γ =Γ _b +A v _F /R , wobei Γ _b ist die Volumenmetall-Relaxationsrate für Silberkugeln im Vakuum. Zuerst berechneten wir die Extinktionsspektren für einen Strahl aus Silberkugeln mit dem mittleren Durchmesser 〈D 〉=2 nm und experimentelle Größenverteilung, die den Bereich von D . überspannt =1 bis D =4 nm. Unsere Theorie enthält keine einstellbaren Parameter. Um die dielektrischen Funktionen zu definieren, haben wir die von Lynch und Hunter [16] vorgeschlagene tabellarische Darstellung des Brechungsindex von Bulk-Silber verwendet (siehe Abb. 1). Wir haben auch die Gl. (16), (21) und (22) mit ω _p =9.17 eV, Γ _b =0,021 eV, v _F =1,39×10 ⁶ m/s und A =0,25. Die Ergebnisse der Berechnungen und das experimentelle Spektrum sind in Abb. 2 dargestellt.

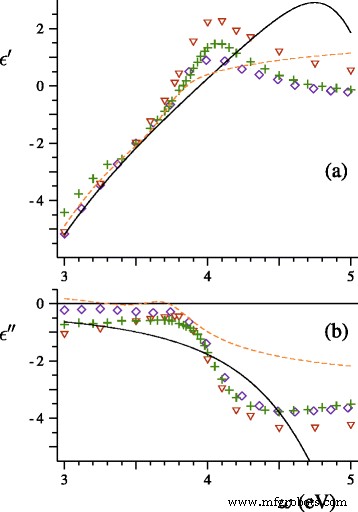
Echt (a ) und imaginär (b ) Teile der dielektrischen Funktion von Silber nach Johnson und Christy (◇) [20], Lynch und Hunter (+) [16], Weber (△) [21], Hao und Nordlander (gestrichelte Linie ) [22] und Drachev et al. (durchgezogene Linie ) [23]

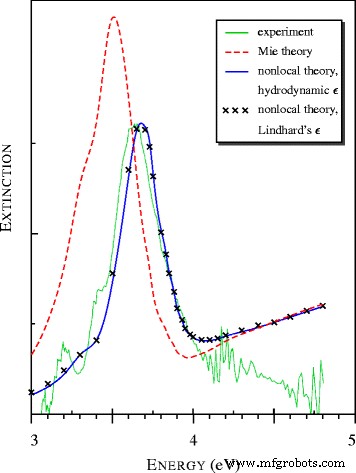
Spektren der Lichtextinktion durch Silberpartikel im Nanometerbereich, beobachtet in [15] und berechnet mit lokalen und nichtlokalen Modellen. Alle theoretischen Spektren werden in gemeinsamen relativen Einheiten dargestellt

Die theoretischen Spektren in Abb. 2 wurden unter Verwendung der Klimontovich-Silin-Lindhard- und viel einfacheren hydrodynamischen dielektrischen Funktionen berechnet. Es ist überraschend, dass beide Berechnungen ähnliche Ergebnisse lieferten, obwohl |a |>1 im Bereich der Plasmonenresonanz.

Für die nanometergroßen Silberkugeln ist bekannt, dass sich das Maximum im Extinktionsspektrum, die sogenannte Fröhlich [17], Plasmonen- und Oberflächenplasmonenpolariton (SPP) [15] Resonanz, von 3,5 auf 3,65 eV verschiebt [18]. Das nichtlokale Modell stimmt hervorragend mit den experimentellen Daten überein, während die lokale (Mie)-Theorie das Maximum bei ω . angibt ≃3.5 eV (siehe Abb. 2 und Tabelle 1).

Die Berechnung der Blauverschiebung der Plasmonenresonanz kann durch folgende Überlegung unterstützt werden. In der elektrostatischen Näherung sind nur b ₁ trägt zum Extinktionsquerschnitt Q bei _ext und Gl. (30) kann mit den folgenden Näherungen vereinfacht werden

Also, Q _ext hat ein Maximum bei

Die erhaltene Bedingung (33) berücksichtigt die Anregung des L Modi (mit dem Begriff δ ₁ ) und unterscheidet sich daher von der Fröhlich-Resonanzbedingung [17]:.

In Experiment [15] sind die Spitzenfrequenzen ω _m und Resonanzbreiten Δ ω der Extinktionsspektren waren fast unabhängig von 〈D . Diese Funktion von Δ ω scheint mit der klassischen Mie-Theorie nicht einverstanden zu sein. Tatsächlich sagt die lokale Theorie eine Verbreiterung der Plasmonenresonanzen mit der Abnahme von D . voraus (bei A =0,25), wie in Tabelle 1 gezeigt. Gleichzeitig liefert die nichtlokale Theorie ungefähr gleiche Resonanzbreiten, aber unterschiedliche Peakpositionen. Die Überlagerung der Beiträge aller Teilchen ergibt den Wert von Δ ω die in bemerkenswerter Übereinstimmung mit den experimentellen Daten sind. Es ist interessant, dass die nichtlokale Theorie eine Verbreiterung der Plasmonenresonanz eines Strahls sogar bei A . vorhersagt =0.

Bei ω>4 eV liegen die glatten theoretischen Kurven in Abb. 2 höher als die Maische der engen, eng beieinander liegenden experimentellen Peaks. Die Interband-Absorption dominiert in diesem Spektralbereich, wie in Abb. 1 bestätigt wird. Die beobachteten Besonderheiten des Spektrums sind wahrscheinlich eine Folge eines Übergangs von den Kontinuumsbändern zu einer diskreten Niveaustruktur. Ein solcher Quantengrößeneffekt wurde bereits früher in einer Studie über die optischen Eigenschaften von Goldnanokügelchen entdeckt [19]. Als die Silberkugelgröße auf 〈D . erhöht wurde 〉=3.5 nm, die Absorption nahm zunächst relativ zum Maximum zu und bildete ein Plateau mit einer Reihe kleiner äquidistanter Einbrüche. Dann nahm die Absorption bei 〈D . leicht ab =4 nm.

Um die Bildung des blauen Flügels der Plasmonenresonanz zu studieren, haben wir die Extinktionsspektren von Ultra-Zinn-Silber-Partikeln berechnet und in Abb. 3 dargestellt. Bemerkenswert in Abb. 3 ist das vollständige Verschwinden der Plasmonenresonanz bei D =1 nm. Zuvor wurde dieser Effekt in der experimentellen Untersuchung von Gold-Nanosphären beobachtet [19]. Insbesondere wurden in Abb. 9 von [19] die experimentellen Spektren von Partikeln mit Durchmessern von 1.7, 1.9, 2.0, 2.1, 2.3 und 2.5 Nanometer mit den Spektren verglichen, die mit der lokalen Mie-Theorie berechnet wurden. Die Übereinstimmung war schlecht, da die Verbreiterung der Plasmonenresonanz und ihre Position nicht beschrieben wurden [19]. Die Versuche, die Passgenauigkeit durch Variation der Partikelgröße und Modifikation der dielektrischen Funktionen zu verbessern, waren nicht sukzessive. Laut den Autoren von [19] widersetzt sich das beobachtete ungewöhnlich breite oder abgesenkte kollektive Oszillationsband einer Anpassung an die vorgeschlagenen Korrekturen der lokalen Mie-Theorie. Wie aus Abb. 4 ersichtlich, ändert sich die Situation dramatisch, wenn die nichtlokale Mie-Theorie angewendet wird. Beachten Sie, dass wir keine einstellbaren Parameter verwendet haben. Die tabellarische Darstellung des komplexen Brechungsindex von Johnson und Christy [20] wurde verwendet, um die dielektrische Funktion von Gold zu bestimmen. Andere Parameter, einschließlich A =1 und der Brechungsindex von Toluol (1.37) wurden aus [19] entnommen.

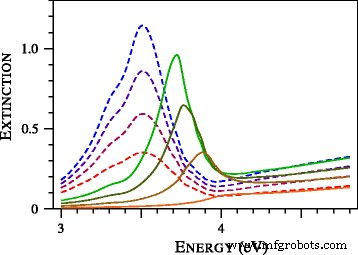
Normalisierter Extinktionsquerschnitt von Silberpartikeln mit Durchmessern von 2,2, 1,8, 1,4 und 1,0 nm, berechnet mit lokalen (gestrichelten Linien ) und nichtlokal (durchgezogene Kurven ) Mie-Theorien. Je kleiner das Partikel, desto niedriger die Kurve. Alle theoretischen Querschnitte werden in gemeinsamen relativen Einheiten dargestellt

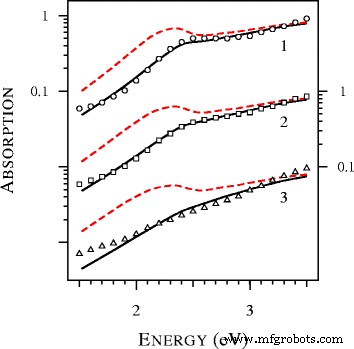
Absorptionsspektren berechnet mit den lokalen (gestrichelten Linien ) und nichtlokal (durchgezogene Linien ) Mie-Theorie und experimentelle Daten (Punkte ) aus Abb. 9 von [19] für Goldkugeln mit D =2.5, 2.1 und 1.7 nm in Toluol (Kurven 1 und Kreise , Kurven 2 und Quadrate , und Kurven 3 und Dreiecke , bzw). Alle theoretischen Spektren sind bei 4,12 eV auf Eins normiert und vertikal verschoben

Wellenzahlen der Längswellen

Die longitudinalen Moden unterscheiden sich von den transversalen durch viel höhere Werte der Wellenzahlen. Für die in Abb. 2 dargestellten Berechnungen entspricht beispielsweise der Realteil von \(k_{2}^{\mathrm{L}}\) der räumlichen Periode \(\Lambda =2 \pi /\Re k_{ 2}^{\mathrm {L}}\) abnehmend von 9 auf 2 nm bei ω von 3 auf 4 eV ansteigend. In diesem ω Intervall wurde der Absolutwert des Verhältnisses \(k_{2}^{\mathrm {L}}/k_{2}\) von 130 auf 100 verringert und der Parameter δ von Gl. (27) von 0,01 auf 0,005 bei θ . verringert ₁ =π /4. Daraus schließen wir, dass die Anregung der L-Wellen an einer ebenen Silberoberfläche vernachlässigt werden kann. Die L Es wurde festgestellt, dass Moden in nanometergroßen Silberclustern von Bedeutung sind.

Eine Ersetzung des Termes \(-\,\omega^{2}_{\mathrm{p}}/(\omega^{2}+i\Gamma\omega)\) in Gl. (16) von ε ^T −ε _g nach Gl. (21) erlaubt uns, die Dispersionsgleichung umzuschreiben. (15) in der folgenden Form

Im einfachsten Fall von ε _g =1 und Γ =0, Gl. (35) sagt voraus, dass Metall sowohl für transversale als auch für L-Wellen bei ω . transparent ist>ω _p aber beide k ^L und k ^T sind komplex bei ω <ω _p .

Wenn ein Festkörper transparent ist, kann eine Longitudinalwelle durch schrägen Einfall einer p-polarisierten Welle auf eine ebene Oberfläche angeregt werden. Es gibt mehrere unterschiedliche Merkmale dieses Effekts. Erstens können die Longitudinalwellen an einer ebenen Oberfläche erzeugt werden, während besondere Anstrengungen unternommen werden sollten, um die Oberflächenplasmonenpolaritonen anzuregen [4, 5]. Zweitens wird im Interferenzmuster die elektromagnetische Feldstärke nicht entlang, sondern senkrecht zur Grenzfläche moduliert. Daher können aufgrund von Spallation des Festkörpers Hohlräume in Ebenen parallel zur Oberfläche auftreten. Nach der Definition von ω _p , Bedingung ω>ω _p in Festkörpern (zB Halbleitern) mit einer geringen Dichte der Stromträger erfüllt werden. Wir untersuchen diesen Fall hier nicht, weil die Formel von ε ^L wurde für entartetes Elektronengas abgeleitet.

Schlussfolgerungen

Um eine ortsabhängige dielektrische Funktion zu definieren, haben alle bisherigen Forscher die Wechselwirkung von Materie mit einer ebenen elektromagnetischen Welle in Betracht gezogen. Dieser Ansatz ist in der Nanooptik nicht konstruktiv und rigoros, wenn das Feld in einer Kavität lokalisiert ist und die Randbedingungen irgendwie berücksichtigt werden müssen. Wir haben dieses Problem gelöst, indem wir die Reaktion des Mediums auf ein elektrisches Feld berechnet haben, das der Vektor-Helmholtz-Gleichung genügt. Die abgeleitete räumlich dispersive dielektrische Funktion hängt vom Quadrat der Wellenzahl ab, einem Parameter der Helmholtz-Gleichung, aber nicht vom Wellenvektor einer ebenen Welle.

Wir berichten über die durch Anregung der Longitudinalwellen in Metallen veränderten Fresnel-Reflexionskoeffizienten. Eine ähnliche Verallgemeinerung wurde früher für die Mie-Koeffizienten gemacht. Hier wurde die Theorie durch Simulation der Lichtauslöschung durch nanometergroße Silber- und Goldcluster bestätigt. Die berechnete Verschiebung von 3.5 auf 3.65 eV und die Breite der Oberflächenplasmonenresonanz des Silberpartikelstrahls stimmen hervorragend mit den experimentellen Daten überein. Außerdem erklärt das nichtlokale Modell das Verschwinden der Plasmonenresonanz von goldenen Kugeln mit Durchmessern von etwa 2 nm. Es ist wichtig, dass die L-Welle auf einer ebenen Oberfläche durch eine ebene einfallende Welle angeregt werden kann. Dies ist der Hauptunterschied der Plasmonenpolaritonen von den Oberflächenplasmonenpolaritonen.

The properties of the electromagnetic oscillations in metals have been examined. It has been found that the absolute values of the wavenumbers of the longitudinal waves are much larger than those of the transverse waves. For example, in silver at a photon energy of 3.5 eV, the ratio of the absolute values of the wavenumbers is equal to 130. There, the real part of the wavenumber of the longitudinal wave corresponds to a wavelength of 7 nm. The large difference in the wavenumbers prevents excitation of the L waves at a planar surface. However, the L modes have been shown to be excited in silver and gold nanometer-sized particles.