ZURÜCKGEZOGENE ARTIKEL:Können bidirektionale Direktkommunikationsprotokolle als sicher angesehen werden?

Hintergrund

Die Quantenkryptographie, insbesondere Quantenschlüsselverteilungs-(QKD)-Protokolle, bietet uns im Gegensatz zur klassischen eine wahrscheinlich unzerbrechliche Kommunikation basierend auf den quantenphysikalischen Eigenschaften der Informationsträger [8, 23, 25]. Bisher basierten die Implementierungen hauptsächlich auf dem BB84-Protokoll [2], das bedingungslos sicher ist, sofern die Quantenbitfehlerrate (QBER) niedrig genug ist. Die QBER in BB84-ähnlichen Protokollen kann jedoch hoch sein, und da wir die Bit-Flips von Lauschern (Eve) nicht von Bit-Flips unterscheiden können, die durch Verluste und Unvollkommenheiten verursacht werden, ist die Anforderung, die QBER niedrig genug für die Verarbeitung der Bits zu haben, oft schwer zu erfüllen, z , 4-State-BB84 mit mehr als 11 % [26] und 6-State-BB84 [5] mit mehr als 12,6 % [26] Störung (D ) müssen abgebrochen werden (D ist definiert als der Prozentsatz der Polarisations-Flips, die von Eve verursacht werden, maximal 0,5). Seit D nicht von der inhärenten QBER der Leitung unterschieden werden kann, sind diese Ebenen der Gesamt-QBER unsicher (gegenseitige Informationen zwischen dem Absender (Alice) und Eva (I _AE ) übertrifft die zwischen Alice und dem Empfänger (Bob) (I _AB ):Ich _AE>Ich _AB für D>0.11,0.126) und kann daher nicht durchgeführt werden, nur weil Eve könnte in der Warteschlange sein.

Auf der Suche nach effizienteren Protokollen wurden Zweiwegeprotokolle vorgeschlagen und implementiert. Insbesondere verschränkte Photonen-Zwei-Wege-Protokolle basierend auf zwei [4] (auch als Ping-Pong bezeichnet) (pp) Protokoll) und vier (Ψ ^∓ ,Φ ^∓ ) [6] Bell-Statements einerseits und ein Single-Photon-deterministisches Lucamarini-Mancini (LM05)-Protokoll andererseits [1, 19]. Mehrere Varianten, Modifikationen und Verallgemeinerungen des letzteren Protokolls sind in [11, 12, 24, 27] angegeben. Zwei Varianten wurden in [7] und [14] implementiert. Das frühere pp-Protokoll wurde 2008 von Ostermeyer und Walenta implementiert [22], während das Protokoll mit vier Bell-Zuständen nicht mit linearen Optikelementen implementiert werden kann [20, 29]. In den oben genannten Referenzen wurden verschiedene Sicherheitseinschätzungen eingeholt.

In [17] liefern Lu, Fung, Ma und Cai einen Sicherheitsbeweis für eine deterministische LM05-QKD für die in [1, 19] vorgeschlagene Angriffsart. Trotzdem behaupten sie, es sei ein Beweis für die unbedingte Sicherheit von LM05. In [10] liefern Han, Yin, Li, Chen, Wang, Guo und Han einen Sicherheitsbeweis für ein modifiziertes pp-Protokoll und beweisen seine Sicherheit gegen kollektive Angriffe in verrauschten und verlustbehafteten Kanälen.

Alle Überlegungen zur Sicherheit von Zwei-Wege-Protokollen gehen davon aus, dass Eve jedes Signal zweimal angreift, einmal auf dem Weg von Bob zu Alice und später auf dem Rückweg von Alice zu Bob, und dabei das Signal in stört den Nachrichtenmodus. Wie wir weiter unten zeigen, gibt es jedoch andere Angriffe, bei denen eine nicht nachweisbare Eve Bobs Signale entsprechend Alices Codierung eines an sie gesendeten und später von Eve gelesenen Ködersignals kodiert.

In diesem Papier zeigen wir, dass in den deterministischen Zwei-Wege-QKD-Protokollen unter einem bestimmten Abfang- und Neusendeangriff eine nicht nachweisbare Eve alle Nachrichten im Nachrichtenmodus (MM) erfassen kann und dass die gegenseitigen Informationen zwischen Alice und Bob konstant und gleich sind zu einem. Das bedeutet, dass die Sicherheit der Protokolle nicht über Standardverfahren zur Auswertung des geheimen Anteils von Schlüssellängen hergestellt werden kann.

Methoden

Wir analysieren die Angriffe auf zwei verschiedene Zwei-Wege-QKD-Protokolle:verschränkte Photonen- und Einzelphotonen-Protokolle. Insbesondere gehen wir auf das Verfahren ein, das es Eve ermöglicht, alle Nachrichten im Nachrichtenmodus vorzulesen und dabei unauffindbar zu bleiben. Anschließend führen wir eine Sicherheitsanalyse durch, um gegenseitige Informationen zwischen Alice und Eva sowie zwischen Alice und Bob in Abhängigkeit von der Störung zu berechnen, die Eve beim Abhören verursachen könnte. Schließlich wenden wir die erhaltenen Ergebnisse auf das Verfahren an, das darauf abzielt, die unbedingte Sicherheit von Zwei-Wege-Protokollen zu beweisen.

Ergebnisse und Diskussion

Zwei-Wege-Protokolle für verschränkte Photonen

Wir betrachten ein Zwei-Wege-Protokoll mit verschränkten Photonen basierend auf zwei Bell-Zuständen (pp-Protokoll) [4]. Bob bereitet verschränkte Photonen in einem der Bell-Zustände vor und sendet eines der Photonen an Alice und hält das andere in einem Quantenspeicher. Alice gibt das Photon entweder so zurück, wie es ist, oder reagiert darauf, um beide Photonen in einen anderen Bell-Zustand zu versetzen. Die Bell-Statements, die sie auf diese Weise sendet, sind ihre Nachrichten an Bob. Bob kombiniert das Photon, das er von Alice erhält, mit dem, das er behalten hat, und entschlüsselt an einem Strahlteiler (BS) Alices Nachrichten. Solche Nachrichten werden in einem Nachrichtenmodus gesendet (MM). Es gibt auch einen Kontrollmodus (CM), in dem Alice Bobs Photon misst. Sie gibt das Umschalten zwischen den Modi über einen öffentlichen Kanal sowie die Ergebnisse ihrer Messungen in CM bekannt.

Wir definieren die Bell-Basis als eine Basis bestehend aus zwei Bell-Zuständen

wobei |H 〉 _i (|V 〉 _i ), ich =1,2, repräsentieren horizontal (vertikal) polarisierte Photonenzustände.

Photonenpaare im Zustand |Ψ ⁻ 〉 werden von einer abwärtskonvertierten verschränkten Photonenquelle erzeugt. Um |Ψ . zu senden ⁻ 〉 Zustand Alice gibt ihr Photon gerade an Bob zurück. Um |Ψ . zu senden ⁺ 〉, legt sie eine Halbwellenplatte (HWP(0°)) in den Weg ihres Photons, wie in Abb. 1b gezeigt. Der HWP ändert das Vorzeichen der vertikalen Polarisation.

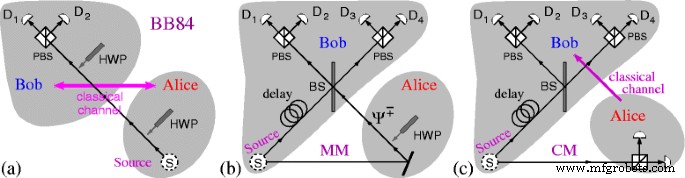
Schemata der Protokolle BB84 und Ping-Pong (pp). a BB84 – klassische und Quantenkanäle werden verschmolzen. b MM des pp-Protokolls – Quantenkanal. c CM des pp-Protokolls – klassischer Kanal

Bei Bobs BS sind die Photonen im Zustand |Ψ ⁻ 〉 wird geteilt und diejenigen im Zustand |Ψ ⁺ 〉 wird sich zusammenschließen.

Eve führt ihren von Nguyen [21] entworfenen Angriff wie folgt aus:Sie legt Bobs Photon zuerst in einen Quantenspeicher und verwendet eine Kopie von Bobs Gerät, um Alice ein Photon von einem herunterkonvertierten Paar im Zustand |Ψ ⁻ 〉 wie in Abb. 2 gezeigt. Wenn Eve das Photon von Alice erhält, kombiniert sie es mit dem anderen Photon des Paares und bestimmt den Bell-Zustand auf dieselbe Weise wie Bob. Sie verwendet dieses Ergebnis, um den gleichen Bell-Zustand für Bob zu erzeugen, indem sie die entsprechenden HWPs in den Pfad von Bobs Photon legt.

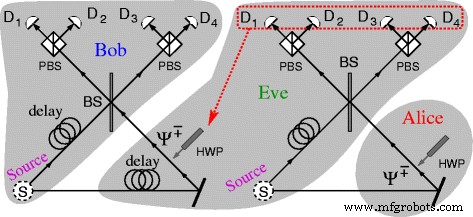
Nguyens Angriff [21] auf das pp-Protokoll. Eve ist in der Lage, jede der Bell-State-Nachrichten im Nachrichtenmodus des pp-Protokolls deterministisch zu kopieren

Somit kann Eve jede einzelne Nachricht in MM kopieren und daher ist das Senden von Nachrichten in MM gleichbedeutend mit dem Senden von Klartext „gesichert“ durch CM. Wir werden später auf diesen Punkt zurückkommen.

Hier betonen wir, dass Photonen die vierfache Entfernung zurücklegen, die sie in BB84 zurücklegen. Wenn also die Wahrscheinlichkeit, dass ein Photon nur über die Bob-Alice-Distanz detektiert wird, p . ist , die Wahrscheinlichkeit, über die Bob-Alice-Bob-Distanz erkannt zu werden, beträgt p ⁴ was mit den exponentiell ansteigenden Verlusten über die Distanz auch die Wahrscheinlichkeit der Erkennung der Störung, die Eve in CM einführt, exponentiell verringert.

Einzelphotonen-Zwei-Wege-Protokolle

Wir beginnen mit einer kurzen Vorstellung des LM05-Protokolls [18, 19]. Wie in Abb. 3 gezeigt, bereitet Bob ein Qubit in einem der vier Zustände |0〉, |1〉 vor (die Pauli Z Eigenzustände), |+〉 oder |−〉 (Pauli X eigenstates) und schickt es an sein Gegenüber Alice. Im MM modifiziert sie den Qubit-Zustand, indem sie entweder I . anwendet , was das Qubit unverändert lässt und die logische 0 . codiert , oder durch Anwenden von i J =Z X , das den Qubit-Zustand umkehrt und die logische 1 kodiert . (ich J |0〉=−|1〉,i J |1〉=|0〉,i J |+〉=|−〉,i J |−〉=−|+〉.) Alice schickt nun das Qubit zurück an Bob, der es in derselben Basis misst, in der er es vorbereitet hat, und Alices Operationen, d. h. ihre Nachrichten, ohne Basisabgleichsverfahren deterministisch herleitet.

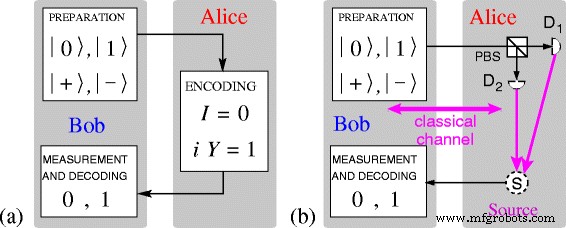
LM05-Protokoll. a Nachrichtenmodus (MM) nach [19, Abb. 1]. b Steuermodus

Der von uns betrachtete Angriff auf das LM05-Protokoll wird von Lucamarini in [18, S. 61, Abb. 5.5]. Es ist in Abb. 4 gezeigt. Eve verzögert Bobs Photon (Qubit) in einer Faserspule (einem Quantenspeicher) und sendet ihr eigenes Täuschungsphoton in einen der vier Zustände |0〉, |1〉, |+〉 oder | −〉 stattdessen zu Alice. Alice verschlüsselt ihre Nachricht über I oder i J und sendet das Photon zurück. Eve misst es in derselben Basis, in der sie es vorbereitet hat, liest die Nachricht vor, codiert Bobs verzögertes Photon über I , wenn sie 0 gelesen hat , oder über i J , wenn sie 1 gelesen hat , und sendet es an Bob zurück.

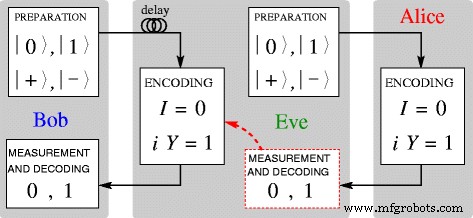
Lucamarinis Angriff auf das LM05-Protokoll. Schemata werden nach [18, S. 61,Abb. 5.5]

Eve erfährt nie die Zustände, in denen Bob seine Photonen gesendet hat, aber das ist im MM irrelevant, da nur Polarisations-Flipping oder Nicht-Flipping-Nachrichten kodieren. Alice muss auch Bobs Zustände nicht kennen [19]. Dies bedeutet, dass Eve nur in CM enthüllt werden konnte, in der Alice eine projektive Messung des Qubits entlang einer zufällig gewählten Basis zwischen Z . durchführt und X , bereitet ein neues Qubit im gleichen Zustand wie das Ergebnis der Messung vor, sendet es an Bob zurück und gibt dies über einen klassischen öffentlichen Kanal [19] preis, wie in Abb. 4 gezeigt.

An dieser Stelle sollte betont werden, dass Photonen in LM05 die doppelte Distanz zurücklegen, die sie in BB84 zurücklegen. Wenn also die Wahrscheinlichkeit, dass ein Photon nur über die Bob-Alice-Distanz detektiert wird, p . ist , die Wahrscheinlichkeit, über die Bob-Alice-Bob-Distanz erkannt zu werden, beträgt p ² und Eve könnte sich in CM exponentiell besser verstecken als in BB84.

Sicherheit von Zwei-Wege-Protokollen

In einem BB84-Protokoll mit mehr als 11% Störung ist die gegenseitige Information zwischen Alice und Eva ich _AE ist höher als die gegenseitige Information zwischen Alice und Bob I _AB und man muss es abbrechen.

Für unsere Angriffe gibt es keine Störung (D ), die Eve in MM induziert, und die gegenseitige Information zwischen Alice und Bob ist gleich eins.

Daher, anders als in BB84, I _AB und ich _AE sind keine Funktionen von D und das hindert uns daran, die Sicherheit mit dem Standardansatz nachzuweisen.

Außerdem gibt es in einer realistischen Implementierung kein signifikantes D auch in MM. Wenn Bob zum Beispiel ein Photon in |H . sendet 〉 Zustand und Alice ändert ihn nicht, dann erkennt Bob |H 〉 mit einer Wahrscheinlichkeit nahe 1, mit oder ohne Eva und unabhängig von der Entfernung. Die einzige QBER, die von der Faserlänge abhängt, ist diejenige, die aus den Dunkelzahlen der Detektoren stammt [28]. In einer kürzlich durchgeführten Implementierung einer Einweg-QKD lag die Gesamt-QBER über eine Distanz von 250 km unter 2% [13]. Wir können die Dunkelzählungen und damit alle unkontrollierten Polarisationskippungen praktisch vollständig eliminieren, indem wir supraleitende Übergangskantensensor (TES)-Photonendetektoren verwenden. Die höchste Effizienz solcher Detektoren liegt derzeit bei über 98 % [9, 15, 16] und ihre Dunkelzählwahrscheinlichkeit ist praktisch null.

Für BB84 und praktisch alle Einweg-Einphotonen-Protokolle, die kürzlich implementiert wurden oder für die Implementierung in Betracht gezogen wurden, wird die Sicherheit der Protokolle über die kritische QBER durch Berechnung des geheimen Anteils bewertet [26]

wo l ist die Länge der Liste, die den letzten Schlüssel bildet und n ist die Länge der Liste, die den Rohschlüssel bildet, I _AB =1+D log2D +(1−D ) log2(1−D ) und ich _AE =−D log2D −(1−D ) log2(1−D ) und ihre Schnittmenge ergibt D =0,11. Äquivalent, r =1+2D log2D +2(1−D ) log2(1−D ) geht auf 0 zurück, wenn D erreicht 0,11.

Wir haben eine solche Option für unsere Angriffe auf Zwei-Wege-Protokolle nicht, da sie aus Gl. (2) und (3) dass r ist nie negativ. Eigentlich geht es nur gegen 0, wenn Eve die ganze Zeit in der Schlange ist.

Seit D hat nichts mit dem MM-Modus zu tun, es liegt an Alice und Bob, zu entscheiden, nach welchem ​​D sie würden ihre Übertragung abbrechen. Was auch immer 0≤D . ist ≤0.5 sie wählen, ich _AB −Ich _AE sollen immer nicht negativ sein und sie haben kein kritisches D wie in BB84, wo die Kurven I _AB (D ) und ich _AE (D ) Schnittpunkt für D =0,11 in MM wie in Fig. 5a gezeigt. Für bidirektionale deterministische Protokolle ist das Niveau von D , die in CM (und nicht in MM) definiert ist, hat keine Auswirkung auf I _AB , d.h. es gibt keinen Unterschied, ob D =0 oder D =0,5, wie in Fig. 5b gezeigt; 0≤D <0.5 würde nur bedeuten, dass Eve nicht die ganze Zeit in der Warteschlange ist, aber Bob bekommt von Alice immer die vollständigen Informationen:wenn Eve nicht in der Warteschlange ist, weil sie nicht in der Warteschlange ist, und wenn Eve in der Warteschlange ist, weil sie leitet treu alle Nachrichten von Alice an Bob weiter.

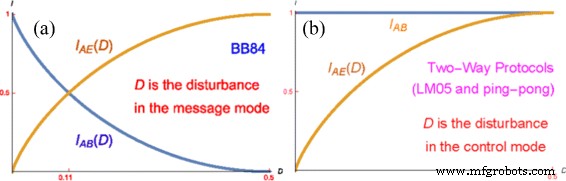
Mutual-Information-Plots für BB84 vs. deterministische Zwei-Wege-Protokolle. a Einweg-probabilistisches Protokoll BB84. b Zwei-Wege-deterministische Protokolle mit entweder verschränkten Bell-Zuständen oder mit LM05-ähnlichen Einzelphotonen-Zuständen. Der wesentliche Unterschied zwischen ihnen besteht darin, dass in a Eve verursacht Polarisationswechsel im Nachrichtenmodus, während in b Eve verursacht im Nachrichtenmodus idealerweise keinen Flip

Wir können davon ausgehen, dass Eve nur einen Teil der Nachrichten schnappt, um die QBER in CM auf einem niedrigen Niveau zu halten (und haben I _AE ≤1) was für Alice und Bob akzeptabel wäre. Vor diesem Hintergrund können wir versuchen, die Sicherheitsbewertung für unseren Angriff durchzuführen und zu überprüfen, ob die für andere Angriffsarten auf LM05 in [1, 17] durchgeführten Beweise der unbedingten Sicherheit auch für ihn gelten.

In dem oben erwähnten Sicherheitsnachweis [17], der als bedingungslos gilt , die Autoren zuerst, in Abschn. III.A, behaupten, dass Eve die Qubits sowohl im Bob-Alice- als auch im Alice-Bob-Kanal angreifen muss, um Alices Schlüsselbits zu erhalten, und in Sec. III.B, Gl. (1,3), gehen sie davon aus, dass Eve Bobs Qubit ausliest und eine Störung des Nachrichtenmodus sowohl im Bob-Alice- als auch im Alice-Bob-Kanal induziert (Fehlerrate e; letzter Absatz von Sek. III.B und erster Absatz von Sek. III.F).

Bei den betrachteten Angriffen misst Eve jedoch nicht Bobs Qubits. Sie speichert sie einfach in einem Quantenspeicher. Sie schickt Alice ihre eigenen Qubits und liest ab, ob sie diese verändert hat (Y ) oder nicht (ich ). Dann bewirbt sie sich Y oder ich Bobs Qubits gespeichert und an ihn zurückgesendet. Folglich verursacht sie auch keine Störung im Alice-Bob-Kanal. Auch verwendet sie keine Ancillas wie in [17]. Daher ist die Analyse, die in [17] durchgeführt wurde, um die Schlüsselbits zu erhalten, auf unseren Angriff nicht anwendbar.

Da der in [17] vorgelegte Sicherheitsnachweis nur für den darin betrachteten Angriff gilt und nicht für den oben genannten Angriff von Lucamarini, ist er nicht universell, d. h. er kann nicht als unbedingt betrachtet werden .

Lassen Sie uns nun überlegen, ob ein bekanntes Standardverfahren verwendet werden kann, um die Sicherheit des LM05-Protokolls herzustellen. Im Protokoll haben wir weder Sichtung noch Fehlerrate im Nachrichtenmodus. Daher kann auch der Standardfehlerabgleich nicht angewendet werden.

Das einzige Verfahren, das uns bleibt, um die Sicherheit herzustellen, ist die Verstärkung der Privatsphäre. Wenn Eve nur einen Bruchteil der Daten besitzt, verliert sie die Spur ihrer Bits und die von Alice und Bob werden schrumpfen. Eve kann möglicherweise Daten wiederherstellen, indem sie die fehlenden Bits errät und alle Bits wieder in die Hash-Funktion einfügt. Wenn dies nicht gelingt, werden ihre Informationen teilweise gelöscht. Alice und Bob stoßen jedoch bei der Gestaltung ihres Sicherheitsverfahrens (z. B. Hash-Funktion) auf ein entscheidendes Problem, das garantieren würde, dass Eve keine Informationen über den endgültigen Schlüssel hat. Sie haben keine kritische Anzahl von Eves Bits wie in BB84 (11%), die explizit in die Gleichungen des Privacy-Amplification-Verfahrens aufgenommen werden [3].

Mit einem Wort, die Privatsphäre, die verstärkt sein sollte ist nicht gut definiert. Das Entwerfen eines Protokolls für eine solche „blinde“ Privatsphärenverstärkung ist ein komplexes Unterfangen [3], und es stellt sich die Frage, ob uns das Senden von – tatsächlich – Klartext über MM, das durch gelegentliche Überprüfung von Photonenzuständen in CM gesichert ist, einen Vorteil gegenüber bietet oder eine bessere Sicherheit als das BB84-Protokoll.

In Tabelle 1 listen wir die Eigenschaften eines BB84-ähnlichen Protokolls bei einem willkürlichen Angriff im Vergleich zu Zwei-Wege-Protokollen bei den oben genannten Angriffen auf, was darauf hindeutet, dass es schwierig wäre, die oben genannte Frage positiv zu beantworten.

Schlussfolgerungen

Zusammenfassend betrachteten wir deterministische Angriffe auf zwei Arten von Zwei-Wege-QKD-Protokollen (pp mit verschränkten Photonen und LM05 mit einzelnen Photonen), bei denen eine nicht nachweisbare Eve alle Nachrichten im Nachrichtenmodus (MM) entschlüsseln kann und zeigten, dass die gegenseitige Information zwischen Alice und Bob ist keine Störungsfunktion, sondern gleich der Einheit, egal ob Eve in der Reihe ist oder nicht. Eve verursacht eine Störung (D ) nur im Kontrollmodus (CM) und daher sind der Standardansatz und die Protokolle zur Schätzung und Berechnung der Sicherheit nicht verfügbar, da sie alle das Vorhandensein von D . annehmen im MM. Als Ergebnis ein kritisches D kann nicht bestimmt werden, das Standardfehlerkorrekturverfahren kann nicht zur Eliminierung von Eves Informationen angewendet werden, die Effizienz der Datenschutzverstärkung ist eingeschränkt und die unbedingte Sicherheit kann nicht als nachgewiesen angesehen werden. In gewisser Weise ist das Senden des Schlüssels durch Alice gleichbedeutend mit dem Senden eines unverschlüsselten Klartextes, der durch einen unzuverlässigen Indikator für die Anwesenheit von Eve „gesichert“ ist, und solche Protokolle können für die Implementierung nicht in Betracht gezogen werden, zumindest nicht bevor man beweist oder widerlegt, dass eine neue Art von Sicherheitsverfahren für solche deterministischen Angriffe entwickelt werden können.

Wir betonen, dass es für die Entscheidung, ob ein Protokoll bedingungslos sicher ist oder nicht, unerheblich ist, ob Eve Angriffe ausführen kann, die effizienter sind als die oben betrachteten Angriffe für ein ausgewähltes D in CM . Ein Nachweis bedingungsloser Sicherheit sollte sie alle abdecken.

Änderungsverlauf