Stabiler Single-Mode-Betrieb eines Quantenkaskadenlasers mit verteilter Rückkopplung durch Facettenbeschichtungen mit optimiertem Reflexionsvermögen

Hintergrund

Quantenkaskadenlaser (QCLs) im mittleren Infrarotbereich [1] sind eine der vielversprechendsten Lichtquellen für viele kommerzielle Anwendungen. Diese praktischen Anwendungen wie Gassensorik, Freiraumkommunikation und hochauflösende Spektroskopie [2,3,4,5] würden eine QCL mit hoher Leistung, verbesserter Singlemode-Zuverlässigkeit und geringen Kosten erfordern. Infolgedessen hat sich die Leistung dieser Geräte seit der Demonstration des ersten Distributed Feedback (DFB)-QCL im Jahr 1997 [6] stark verbessert, indem der Dauerstrichbetrieb (CW) bei Raumtemperatur mit hoher Leistung über die gesamte Länge demonstriert wurde mittlerer Infrarotbereich [7,8,9,10]. Die meisten DFB-QCLs, die auf einer vergrabenen Gitterstruktur basieren, haben jedoch das Problem zufällig gespaltener Facetten, die den Laserfrequenzmodus bestimmen. Aufgrund der gleichen Verluste in zwei Bandkantenmoden kann ein stabiler Singlemode-Betrieb nicht garantiert werden [11]. Insbesondere bei hohen Temperaturen oder großen Injektionsströmen kommt es immer zu Modensprüngen, die für die Anwendungen in diesen Single-Mode-Geräten nachteilig sind.

Um einen stabilen Single-Mode-Betrieb zu erhalten, wurde eine Viertelwellen-Phasenverschiebung (λ/4 PS) in die Gitterperiode eingeführt, damit der Laser im Defektmodus arbeiten kann; somit kann eine Konkurrenz zwischen den beiden Bandkantenmoden vermieden werden. Für die Herstellung von λ/4 PS-Gitter muss jedoch Elektronenstrahllithographie verwendet werden, was zeitaufwendig und teuer ist [12]. Ein verstärkungsgekoppelter DFB-Laser ist eine gute Wahl, um einen stabilen Single-Mode-Betrieb für konventionelle Halbleiterlaser zu erreichen [13]. Es ist jedoch für QCL unrealistisch, die verstärkungsgekoppelten DFB-Laser wegen des großen Verlustes, der durch den geätzten aktiven Bereich verursacht wird, herzustellen. Ein weiteres kunstvolles Verfahren besteht darin, den Hohlraumverlustkopplungsmechanismus zu verwenden, um den Differenzverlust zwischen zwei DFB-Modi zu erhöhen. Es wird angenommen, dass eine geeignete Facettenbeschichtung mit Reflexionsvermögen einen stabilen Einmodenbetrieb sogar bei hohen Temperaturen und großen Strömen erreichen kann. Obwohl einige Forschungen der Facettenbeschichtung gewidmet sind, konzentrieren sie sich immer auf die Bildung einer optimalen äquivalenten Kavitätenlänge L _wählen um die Wall-Plug-Effizienz (WPE) für Laser zu erhalten, anstatt die Single-Mode-Zuverlässigkeit [14, 15]. Auch die optimierte Reflektivitätsbeschichtung sollte ein vielversprechender Weg sein, um die Konkurrenz zwischen zwei DFB-Modi aufzulösen und interessant, systematisch untersucht zu werden.

In diesem Beitrag wird der stabile Singlemode-Betrieb von DFB-QCLs bei λ ~ 4,76 μm wird nach Antireflexbeschichtung (AR)/Hochreflexionsbeschichtung (HR) angezeigt. Die AR-Beschichtung besteht aus einem Doppelschichtdielektrikum aus Al₂ O₃ (380 nm) und Ge (33 nm). Diese Geräte weisen eine sehr niedrige Schwellenstromdichte von 0,65 kA/cm ² . auf bei 20 °C. Bis zu einer Temperatur von 90 °C wird im CW-Betrieb ohne Modensprung eine Single-Mode-Emission mit einem Side-Mode-Suppression Ratio (SMSR) über 26 dB erreicht. Es wird angenommen, dass eine Antireflexionsbeschichtung auf der vorderen Facette sehr wertvoll ist, um eine zufällige Phase der Kavitätsfacette zu unterdrücken.

Methoden

Theorie und Simulation

Der Kern der Simulation des Antireflexionsbeschichtungseffekts in einem endlichen DFB-Resonator ist die Berechnung des Modenverlusts für zwei Bandkantenmoden. Die Transfermatrixmethode wäre ein geeigneter Weg, um die gesamte Laserstruktur zu analysieren [16, 17]. Wir betrachten die Anwendung dieses Verfahrens auf Vorrichtungen, die ein longitudinales Brechungsindexprofil ähnlich dem in Abb. 1 gezeigten aufweisen _eff,1 , n _eff,2 ) und beschichtete Folien (n ₃ , n ₄ ) im geführten Modus. Die komplexen Brechungsindizes der in der Berechnung verwendeten Hauptmaterialien sind wie folgt aufgelistet:InP (3.088 + i*2e−4), InGaAs (3.4 + i*2.9e−5), aktiver Bereich (3.298 + i*4e−5), hochdotiertes InP (2.81 + i*1.4e−2), SiO₂ (1.3603 + i*6.3e−4), Au (1.341 + i*32.582), Al₂ O₃ (1.5348 + i*3.2967e−3) und Ge (4.0165 + i*4e−2). Dann die verschiedenen effektiven Indizes n _eff,1 = 3.1599 + i*5.17e−5 und n _eff,2 = 3.1662 + i*5.6756e−5 wurden mit COMSOL durch die partielle Differentialgleichungsfunktion (PDE) berechnet. Es wird angenommen, dass der Laser in einem einzigen transversalen Modus betrieben wird, sodass die Ausbreitungseigenschaften des Lichts an jedem Punkt entlang der Laserkavität durch eine einzelne skalare komplexe Größe beschrieben werden, k , das ist der Wellenvektor des Mediums. Es wird weiterhin angenommen, dass der Laser linear polarisiert ist und sein zugehöriges elektrisches Feld eine sinusförmige Zeitabhängigkeit hat e ^{ich ωt} . Nach diesen oben gegebenen Annahmen ergibt sich ein eindimensionaler ebener elektromagnetischer Wellenfaktor E _z , die den Teil der speziellen Variation der Wellenfunktion beschreibt, erfüllt die Helmholtz-Gleichung

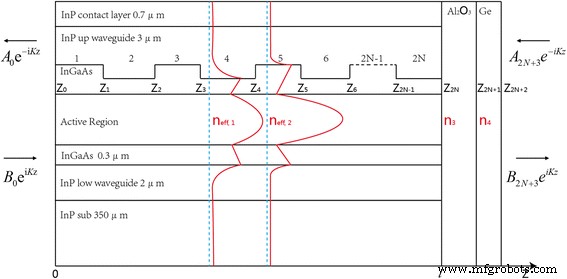
Schematische Darstellung des Modells einer endlichen DFB-Kavität mit Antireflexbeschichtung auf dem longitudinalen optischen Modenprofil

K (z) ist gegeben durch

wo ω und c sind jeweils die Kreisfrequenz und Lichtgeschwindigkeit und n (z) ist der komplexe Brechungsindex an jedem Punkt entlang der Laserkavität. Der Wellenvektor k was gelöst werden muss, lässt sich in zwei Teile gliedern:k _r und k _ich . Der echte Teil k _r bestimmt die Wellenlänge des Lichts in der Laserkavität, während der Imaginärteil k _ich stammt aus dem Modenverlust der endlichen Kavität, der für die Dämpfung verantwortlich ist. Aus Abb. 1 ist ersichtlich, dass der Laser als Mehrsektionsgerät mit 2N . betrachtet werden kann + 2 Abschnitte mit N ist die Gitterperiode. In jedem dieser Abschnitte ist das elektrische Feld E _n (z) ist eine Linearkombination von zwei sich gegenläufig ausbreitenden exponentiell ebenen Wellen, wobei eine mit der komplexen Amplitude A . abnimmt _n und der andere steigt mit B _n . Die Gleichung wird wie folgt beschrieben:

Insgesamt gibt es 2N + 3 Schnittstellen. An jeder dieser Grenzflächen müssen sowohl das elektrische Feld als auch seine Ableitung bezüglich der Ausbreitungsrichtung auf beiden Seiten der Grenzfläche gleich sein. Die Gleichung erhält man wie folgt:

Die Transfermatrix M (d _n ) ist gegeben durch

Da der elektrisch gepumpte Laser ein selbstschwingendes Gerät ist, gibt es keine einfallenden Wellen von außerhalb des Geräts. Daraus ergibt sich die Randbedingung B ₀ = A _{2N + 3} = 0, und die Gleichung wird zu

Jeder Wert des Wellenvektors k kann mit Hilfe von Matlab durch Gl. (6). Die Imaginärteile k _ich entsprechend den Verlusten der Hohlraummoden würde helfen, die AR-Beschichtungseffekte zu analysieren.

Abbildung 2a zeigt die berechneten Ergebnisse basierend auf einer Transfermatrix-Simulation. Wie die beiden roten Kurven gezeigt haben, ändert sich der Verlust der Hochfrequenzmode mit abnehmender Reflektivität sehr langsam, während die Niederfrequenzmode stark ansteigt. Der Einschub zeigt das für die Nieder- und Hochfrequenzmode berechnete Modenprofil für eine einzelne Periode des Gitters. Wie dargestellt, weist der Niederfrequenzmodus eine höhere elektrische Feldstärke in den Gitterpeaks auf, die der Teil des Gitters mit höherem Index sind, und außerdem ist der Hochfrequenzmodus stärker im Teil des Gitters mit niedrigerem Index konzentriert. Beim Modell mit unendlichem Resonator ohne Facettenreflektivität weist der Hochfrequenzmodus immer einen geringeren Modenverlust auf als der Niederfrequenzmodus. Könnte man die Wirkung von Endfacettenspiegeln vernachlässigen, dann wird immer die Hochfrequenzmode mit den kleineren Wellenleiterverlusten lasern. Das Vorhandensein von Endfacettenspiegeln führt jedoch zu Reflexionen, die die DFB-Moden in der Laserkavität konstruktiv oder destruktiv stören. Diese Interferenz beeinflusst den endlichen Gitterhohlraumverlust jeder Mode und kann bestimmen, welche Modenlaser. Wir bemerken, dass die Wirkung der Spiegel am größten ist, wenn die Position beider Spiegel mit einer Spitze der elektrischen Feldamplitude eines DFB-Modus zusammenfällt, was auch der Fall ist, wenn sich die Spiegel an einem Knoten für den anderen DFB-Modus befinden. Hier fallen die Spiegel für die unbeschichtete Facette mit der Spitze der Niederfrequenzmode zusammen, und dann stören die Reflexionen von den Endspiegeln maximal konstruktiv die in der Laserkavität vorhandene Mode. Dies führt aufgrund des konstruktiven Beitrags des Spiegels zu einem verringerten Gesamtmodenverlust. Mit abnehmender Reflektivität und zusätzlichen Phasenverschiebungseinflüssen durch die Verwendung der Doppelschicht-AR-Beschichtung nahm der Verlust des Niederfrequenzmodus mit der Abnahme der Reflektivität aufgrund des abgeschwächten Interferenzeffekts und des erhöhten Spiegelverlusts allmählich zu. In der Zwischenzeit änderte sich der Verlust des Hochfrequenzmodus aufgrund des verstärkten Interferenzeffekts ein wenig. Dies führt dazu, dass der Δ-Modenverlust eine ähnliche Funktion wie eine Exponentialfunktion hat, insbesondere wenn das Reflexionsvermögen der vorderen Facette <0,15 ist. Gemäß der Simulation tritt nur ein minimaler Punkt innerhalb des gesamten Spektrums aus, wenn das Reflexionsvermögen der vorderen Facette < 0,11 ist, was bedeutet, dass Modensprung theoretisch nicht auftreten kann, weil ein weiterer Bandkantenmodenverlust zu hoch zum Lasern ist.

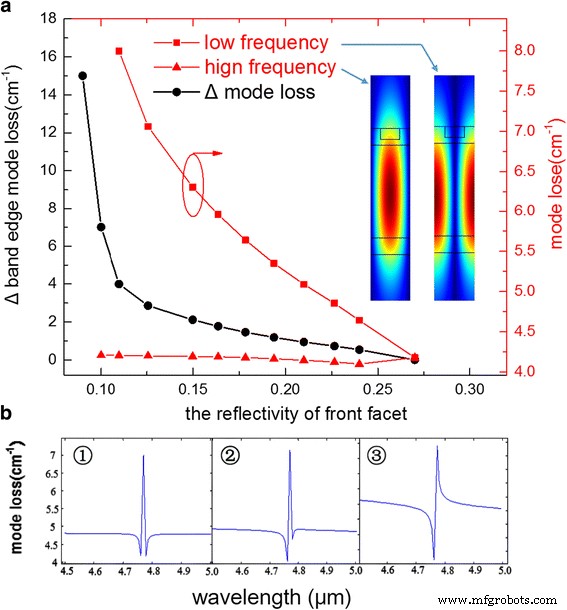
a Die beiden roten Kurven sind der Modenverlust des Hoch- bzw. Niederfrequenzmodus. Die schwarze Kurve ist der Differenzmodusverlust zwischen den beiden mit bezeichneten Bandkantenmodi. Der Einschub zeigt das für die Nieder- und Hochfrequenzmode berechnete Modenprofil für eine einzelne Periode des Gitters. b Das berechnete Modenverlustspektrum basierend auf einer Transfermatrix-Simulation mit verschiedenen AR-Beschichtungen

Abbildung 2b zeigt die drei typischen Modenverlustspektren während der Simulation, wobei die Hoch- und Niederfrequenzmoden 4,762 bzw. 4,779 µm betragen. Der erste ist der DFB-QCL ohne AR-Beschichtung. Wir können deutlich sehen, dass der Sperrbereich von der Gitterrückkopplung herrührt, und die beiden Bandkantenmoden sind fast gleich. Die zweite ist eine spezifische AR-Beschichtung mit 200 nm Al₂ O₃ und 5 nm Ge mit einem Reflexionsvermögen von 0,22. Der Unterschied zwischen zwei Bandkantenmoden wird offensichtlich. Die letzte zeigt, dass bei einer Beschichtung mit niedrigerem Reflexionsvermögen der Δ-Modenverlust so groß ist, dass der Niederfrequenzmode unter den Verlust des Sperrbandes versinkt. Obwohl die niedrigere Reflektivität theoretisch der größere Δ-Modenverlust ist, sollten wir auch berücksichtigen, dass die extrem niedrige Reflektivität in Geräten enorme Spiegelverluste verursacht, die den WPE stark absinken lassen würden. Dies ist ein Kompromiss, um die Filmdicke basierend auf dem Experiment zu wählen.

Geräteherstellung

Der QCL-Wafer wurde auf einem n-dotierten (Si, 3 × 10 ¹⁷ cm ⁻³ ) InP-Substrat durch Festkörperquellen-Molekularstrahlepitaxie (MBE) basierend auf einem Zwei-Phonon-Resonanz-Design. Der aktive Kern enthält 40 Stufen von dehnungskompensiertem In_0,669 Ga_0.331 As/In_0.362 Al_0,638 B. Quantentöpfen und Barrieren, die Ref. ähnlich sind. [18]. Die Schichtenfolge war wie folgt:2 µm untere InP-Mantelschicht (Si, 2,5 × 10 ¹⁶ cm ⁻³ ), 0,3 μm dickes passendes In_0,47 Ga_0,53 Als Schicht (Si, 4 × 10 ¹⁶ cm ⁻³ ), 40 Aktiv-/Injektorstufen, 0,3 µm dickes In_0,47 Ga_0,53 Als Schicht (Si, 4 × 10 ¹⁶ cm ⁻³ ), 3 μm obere InP-Mantelschicht (Si, 2,5 × 10 ¹⁶ cm ⁻³ ) und 0,7 μm hochdotierte InP-Mantelschicht (Si, 5 × 10 ¹⁸ cm ⁻³ ). Das durchschnittliche Dotierungsniveau der aktiven Region wurde empirisch auf 2,4 × 10 ¹⁶ . eingestellt cm ⁻³ . Um das vergrabene Gitter herzustellen, wurde der obere Mantel bis auf die obere InGaAs-Schicht entfernt. Das DFB-Gitter erster Ordnung mit einer Periode von Λ = 0,755 μm (Tastverhältnis σ = 20%) wurde auf der 300 nm dicken oberen InGaAs-Schicht mittels holographischer Lithographietechnik definiert und anschließend durch nasschemisches Ätzen bis zu einer Tiefe von ca. 90 nm geätzt. Dann wird ein 3 µm dickes niedrig dotiertes (Si, 2,5 × 10 ¹⁶ cm ⁻³ ) InP-Schicht gefolgt von einer 0,2-μm-Dotierung (verändernd von 1 × 10 ¹⁷ cm ⁻³ bis 3 × 10 ¹⁷ cm ⁻³ ) InP-Schicht und ein 0,5-μm-InP (5 × 10 ¹⁸ cm ⁻³ ) Kontaktschicht wurden nacheinander als oberer Mantel durch metallorganische Gasphasenepitaxie (MOVPE) hergestellt.

Nach der Implementierung des Gittermusters und des Nachwachsens wurde der Epi-Wafer in 10 &mgr;m breite Rippen geätzt, und dann wurden die Wellenleiter wieder in das MOVPE-System eingeführt und in halbisolierendem InP (Fe) vergraben. Ein 450 nm dickes SiO₂ Die Schicht wurde durch plasmaunterstützte chemische Gasphasenabscheidung (PECVD) zur Isolierung um den Steg herum abgeschieden, und der elektrische Kontakt wurde durch eine Ti/Au-Schicht bereitgestellt. Anschließend wurde eine zusätzliche 5 µm dicke Goldschicht galvanisiert, um die Wärmeableitung weiter zu verbessern. Die Wellenleiter wurden in 2 mm lange Stäbe gespalten, und die Tests wurden an Geräten mit optimierten Facettenbeschichtungen für das Reflexionsvermögen durchgeführt. Beide Rückseiten-Facetten-HR-Beschichtung bestehend aus Al₂ O₃ /Ti/Au/Ti/Al₂ O₃ (400/5/100/10/200 nm) und die Frontfacette AR-Beschichtung bestehend aus Al₂ O₃ /Ge (380/33 nm) werden durch Elektronenstrahlverdampfung abgeschieden. Die berechnete Reflektivität der Frontfacette beträgt 3,4% für eine Wellenlänge von 4,76 µm, und die detaillierte Beziehung zwischen der Schwankung der Beschichtungsdicke und der Reflektivität wurde in unserem zuvor veröffentlichten Artikel [19] diskutiert. Die Laser wurden mit der Epischicht nach unten auf SiC-Kühlkörpern mit Indiumlot montiert und dann mit einem externen Kontaktpad drahtgebondet. Zur spektralen und elektrischen Charakterisierung werden die Laser auf einem Peltier-Element montiert und die Temperatur am Kühlkörper mit einem Thermistor überwacht.

Ergebnisse und Diskussion

Abbildung 3 zeigt die Emissionsspektren unterhalb der Schwelle, die sich dynamisch von Elektrolumineszenz zu Laser mit zunehmendem Strom ändern, der mit dem Bruker Vertex 70 FTIR und einem stickstoffgekühlten HgCdTe-Detektor gemessen wird. Das Laserspektrum knapp über dem Schwellenwert zeigt an, dass das Gerät im Grundmodus arbeitet und wir bei einem Strom von 285 mA deutlich den Sperrbereich des Grundmodus erhalten. Ab der Sperrbandbreite Δν = 3.076 cm ⁻¹ und der effektive Index n _eff = 1/(2νΛ) = 3.153, berechnen wir einen Kopplungskoeffizienten κ = Δν ·π ·n _eff = 30,4 cm ⁻¹ , was für unsere HR-beschichtete 2 mm lange Kavität zu einem Kupplungsprodukt κL . führt von 12.1, was gut mit unserer Gerätefertigung übereinstimmt. Das Produkt von κL weit größer als die vorherige theoretische Untersuchung κL ≈ 1 [20] zeigt an, dass ein überkoppeltes Schema erhalten wird, das vorteilhaft ist, um den Singlemode innerhalb des gesamten Strom- und untersuchten Temperaturbereichs zu sichern.

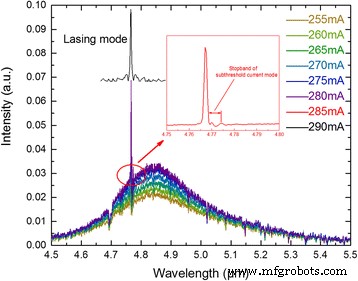
Unterschwelliges DC-Spektrum des Geräts gemessen bei 30 °C

Abbildung 4a zeigt die typische CW-Leistungs-Strom-Spannung (P -ich -V ) Kurve des DFB-Lasers bei verschiedenen Kühlkörpertemperaturen zwischen 20 und 90 °C. Die Ausgangsleistung erreicht 200 mW für das 2 mm lange Gerät mit einer niedrigen Schwellenstromdichte von 0,65 kA/cm ² bei 20 °C. Die Schwellenspannung (V _te ) von 13,2–14,2 V wurde über den Temperaturbereich von 20–90 °C gemessen. Es ist erwähnenswert, dass Mode-Hop nur bei niedrigeren Kühlkörpertemperaturen unter 60 °C existiert, was leicht aus dem P . abgeleitet werden kann -ich Kurve. Eine hohe Wärmesenkentemperatur würde zu einer stärkeren Wärmeansammlung im Laserkern beitragen, so dass ein thermischer Effekt einen anderen Modenlasen hemmte und Modensprünge nicht auftreten würden. Abbildung 4b zeigt das P -ich -V Kurve des DFB-Lasers, dass auf seiner Vorderseite eine Antireflexbeschichtung (AR) aufgebracht wurde, und wir wählen eine Reflektivität der AR-Beschichtung von 3,4%. Jedes glatte P -ich Kurven zeigen an, dass bei der von uns gemessenen Temperatur kein Modensprung existiert. Abbildung 4c, d zeigt das Laserspektrum bei verschiedenen Strömen von 150 bis 250 mA mit einem Schritt von 25 mA. Aus Fig. 4d ist ersichtlich, dass wir mit optimierter AR-Facettenbeschichtung anstelle von Modensprung in Fig. 4c einen stabilen Singlemode um verschiedene Ströme herum erreichen. Die Frequenz steht immer in einem linearen Zusammenhang mit dem Injektionsstrom und dem aktuellen Abstimmungskoeffizienten Δν /Δich = − 0,024 cm ⁻¹ mA ⁻¹ beweist, dass die AR-Beschichtung eine einfache und effiziente Methode ist, um das Problem des Modensprungs in DFB-QCLs zu lösen.

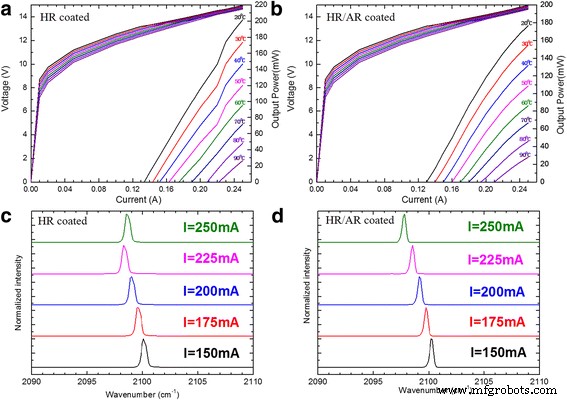
a , b Ausgangsleistung gegen Strom des im CW-Modus betriebenen DFB-Lasers bei verschiedenen Kühlkörpertemperaturen zwischen 20 und 90 °C zusammen mit V -ich Kurven. c , d CW-Laserspektren bei verschiedenen Strömen von 150 bis 250 mA mit einem Schritt von 25 mA bei 20 °C

Abbildung 5 zeigt die Emissionsspektren des beschichteten DFB-Lasers bei unterschiedlichen Kühlkörpertemperaturen von 20 bis 90 °C. Die Messungen wurden mit einem NICOLET 8700 FTIR-Spektrometer mit 0,25 cm ⁻¹ . durchgeführt Auflösung im Schnellscanmodus. Im gesamten untersuchten Temperaturbereich wird eine Single Longitudinal Mode Emission mit einem Side-Mode Suppression Ratio (SMSR) von 26 dB bei einer hohen Temperatur von 90 °C beobachtet. Wie im Einschub von Fig. 5 gezeigt, wurde eine Verschiebung des Peak-Emissionsspektrums von 2100,4 cm ^–1 . beobachtet bei 20 °C bis 2088,6 cm ⁻¹ bei 90 °C, entsprechend einem Temperatur-Tuning-Koeffizienten Δν /ΔT = − 0,168 cm ⁻¹ K ⁻¹ . Die gute lineare Abstimmung zeigte, dass während der Änderung der Kühlkörpertemperatur kein Modenspringen auftrat. Darüber hinaus zeigen alle genannten Geräte aufgrund der genauen Steuerung der Stegbreite im CW-Betrieb im Fundamentalmodus ein dominantes einzelnes laterales Fernfeld.

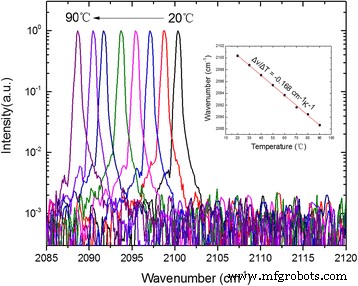
Singlemode-Emissionsspektren des DFB-Lasers bei einem treibenden Schwellenstrom von 1,1 für verschiedene Kühlkörpertemperaturen von 20–90 °C. Die Einlage zeigt die linear angepasste Abstimmcharakteristik der Laserfrequenz mit der Temperatur

Der CW-WPE wurde berechnet und als Funktion der elektrischen Eingangsleistungsaufnahme in Abb. 6 aufgetragen. Bei 20 °C wurde ein maximaler WPE von 4,7% um 240 mA bei einer Ausgangsleistung von 170 mW erhalten. Die maximalen WPE betrugen bei 50 bzw. 90 °C immer noch 2,9 bzw. 0,8%. Bisher waren diese Werte für die niederschwelligen DFB-QCLs aufgrund unserer hohen Materialqualität und optimierten Reflektivitätsfacettenbeschichtung noch sehr hoch. Es wird angenommen, dass das WPE durch die optimierte Auswahl der Laserhohlraumlängen unter Berücksichtigung des Beschichtungseffekts weiter verbessert werden kann.

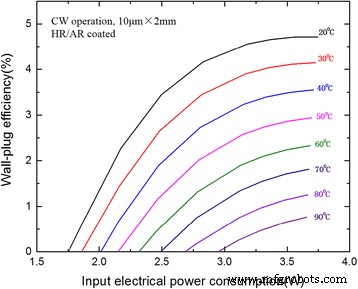
Steckdoseneffizienz in Abhängigkeit von der elektrischen Verlustleistung des 2 mm langen HR- und AR-beschichteten DFB-QCL

Schlussfolgerungen

Wir haben den CW-Betrieb von Singlemode-DFB-QCLs bei Raumtemperatur bei λ . demonstriert ~ 4,76 μm. Durch Abscheidung einer AR-Beschichtung bestehend aus einem Doppelschichtdielektrikum Al₂ O₃ und Ge auf der Frontfacette wurde ein stabiler Singlemode ohne Modensprung unter allen Strom- und Temperaturbedingungen erfolgreich realisiert. Bei 20 °C wurde eine CW-Ausgangsleistung von bis zu 170 mW mit einer sehr niedrigen Schwellenstromdichte von 0,65 kA/cm ² . beobachtet . Solche Geräte stellen einen wichtigen Schritt dar, um einen stabilen Singlemode-Betrieb von DFB-QCLs im mittleren Infrarot-Spektralbereich für praktische Anwendungen zu nutzen.

Abkürzungen

AR:

Antireflexion

BH:

Vergrabene Heterostruktur

CW:

Dauerwelle

DFB:

Verteiltes Feedback

Personal:

Hohe Reflexion

MBE:

Molekularstrahlepitaxie

MOVPE:

Metallorganische Gasphasenepitaxie

PDE:

Partielle Differentialgleichung

PECVD:

Plasmaunterstützte chemische Gasphasenabscheidung

P -ich -V :

Leistung-Strom-Spannung

QCL:

Quantenkaskadenlaser

SMSR:

Seitenmodus-Unterdrückungsverhältnis

V _te :

Schwellenspannung

WPE:

Effizienz der Steckdosenleiste

λ /4 PS:

Eine Viertelwellen-Phasenverschiebung