High-Q-Fano-Resonanz in Terahertz-Frequenz basierend auf einem asymmetrischen Metamaterial-Resonator

Hintergrund

Metamaterial ist eine Art künstliches Material mit exotischen Eigenschaften wie negativem Brechungsindex [1] und ultrahohem Brechungsindex [2], die von natürlichen Materialien in den meisten Situationen nicht realisiert werden können. Ein solches künstliches Material besteht aus einer großen Menge periodischer metallischer Einheiten, und seine Eigenschaften (z. B. Permittivität und Permeabilität) können leicht durch Ändern der geometrischen Parameter der Einheiten gesteuert werden [3]. Infolgedessen hat die Erforschung von Metamaterialien in den letzten Jahren große Aufmerksamkeit auf sich gezogen. In diesem Bereich sind viele neue Anwendungen entstanden, darunter perfekte Absorption [4, 5], Metamaterialsensoren [6,7,8,9], Cloaking [10], Fano-Effekte [11] usw.

Die Linienform der Fano-Resonanz unterscheidet sich stark vom symmetrischen Lorentz-Profil. Es ist asymmetrisch und scharf mit einem relativ hohen Q -Faktor. Seit Fano den Quantenmechanismus der Fano-Resonanz theoretisch aufgedeckt hat [12], ist er zu einem heißen Thema geworden. Um den Ursprung der Fano-Resonanz zu veranschaulichen, wurden mehrere Theorien aufgestellt, darunter die quantenmechanische Analyse von Fano [12], das klassische Oszillatormodell [13], die Theorie der gekoppelten Mode [14] und die elektromagnetische Theorie der Fano-Resonanz [15, 16]. . Gemäß der von Gallinet und Martin [16] vorgeschlagenen elektromagnetischen Theorie der Fano-Resonanz wird das charakteristische Fano-Profil der Kopplung zwischen einer nichtstrahlenden Mode und einer strahlenden Mode zugeschrieben, die auch als Kontinuum betrachtet werden kann.

Im Terahertz-Bereich kann die scharfe Fano-Resonanz durch Einführung einer schwachen Asymmetrie in Metamaterialien erreicht werden [17,18,19,20], die zum Auftreten einer zugrunde liegenden Dunkelschwingung führen kann [21]. Außerdem können Graphenmaterialien auch verwendet werden, um die Fano-Resonanz zu erzeugen und sogar zu modulieren [22, 23]. Verglichen mit den meisten EIT (elektromagnetisch induzierte Transparenz) [24, 25] und PIT (plasmoneninduzierte Transparenz) [26, 27] ist die Fano-Linienform viel schärfer und schmaler. Das Q -Faktor des Fano-Profils [17, 28] ist in vielen Situationen ungefähr zehnmal größer als der der Lorentzschen Linienform [29,30,31]. Diese Eigenschaft macht die Fano-Resonanz zu einer vielversprechenden Wahl, um eine empfindliche Detektion zu realisieren [8]. Das Q -Faktor vieler Metamaterialien ist nicht hoch genug [17, 32, 33], was ihre Anwendungen in Bezug auf die Sensorik einschränkt. Um die Fano-Resonanz weit verbreitet und effizient auf die Sensorik anzuwenden, ist es eine notwendige Aufgabe, den Q . stark zu verbessern -Faktor einer Metaoberfläche.

Kürzlich wurden einige Metamaterialstrukturen entwickelt, um ein hohes Q . zu realisieren Fano-Resonanz. Ding et al. schlugen ein zweischichtiges Metamaterial vor, das aus zwei Sätzen asymmetrischer Spaltringe mit unterschiedlichen geometrischen Parametern besteht. Es kann drei Fano-Resonanzen unterstützen, deren Q -Faktoren sind 33, 42 bzw. 25 [19]. Eine symmetrische Dimerstruktur bestehend aus identischen Spit-Ring-Resonatoren auf jeder Schicht wurde ebenfalls vorgestellt, um ihren Q . zu verbessern -Faktor [34]. Diese gestapelten Strukturen leiden jedoch unter technischen Herausforderungen bei der Herstellung. Hohes Q Resonanz mit einfachem Strukturdesign bleibt immer noch ein heißes Thema.

In diesem Beitrag demonstrieren wir eine koplanare Metamaterialstruktur, die aus vier Metallstreifen besteht. In jeder Elementarzelle sind drei parallele Streifen senkrecht zum vierten angeordnet. Diese Struktur kann ein hohes Q . unterstützen Fan-Resonanz (Q -Wert ca. 58) bei 0,81 THz mit 25% Transmission. Diese scharfe Linienform stammt aus der Wechselwirkung zwischen dem hellen (strahlenden) Modus und dem dunklen (nicht strahlenden) Modus. Zur weiteren Diskussion wird die elektromagnetische Theorie der Fano-Resonanz herangezogen [15, 16]. Die Eigenschaften der Fano-Resonanz können über die Steuerung geometrischer Parameter verändert werden. Die Erfassungsleistung des Geräts wird diskutiert. Darüber hinaus können durch Hinzufügen weiterer Streifen in die ursprünglich entworfene Struktur mehrere Fano-Resonanzen realisiert werden.

Methoden/Experimental

Zahlreiche Untersuchungen weisen darauf hin, dass eine Verletzung der Symmetrie einer Struktur eine asymmetrische Fano-Linienform induzieren kann [17, 18, 35, 36, 37]. Basierend auf diesem Konzept entwerfen wir dieses in Abb. 1 gezeigte Vierstreifen-Metamaterial, wobei Streifen 2 so eingestellt ist, dass er eine Symmetriebrechung realisiert. Abbildung 1a zeigt das dreidimensionale Diagramm des vorgeschlagenen Metamaterials. 1b, c zeigt jeweils die Seitenansicht und die Draufsicht der Struktureinheit. Die metallischen Vierstreifen-Resonatoren sind oben auf einem idealen dielektrischen Substrat angeordnet, dessen Realteil des Brechungsindex 1,5 und Imaginärteil 0 beträgt. In Wirklichkeit entspricht dieses dielektrische Material Siliziumdioxid. Das heißt, das Substrat ist im Terahertz-Bereich verlustfrei. Wir wählen Au mit Leitfähigkeit σ = 4,09 × 10 ⁷ S/m, um den metallischen planaren Resonator zu bilden, dessen Dicke 0,2 µm beträgt. Der Wiederholungszeitraum beträgt P _x = P _y = 180 µm. Drei parallele Streifen (1, 2 und 3) haben die gleiche Größe. Ihre Länge beträgt l _x = 120 μm und Breite ist w = 20 μm. Streifen 4 ist senkrecht zu den anderen Streifen (1, 2 und 3). Seine Länge beträgt l _y = 150 μm und Breite ist w = 20 μm. Der Abstand zwischen der Achse des Streifens 2 und dem Mittelpunkt der Struktur beträgt d = 30 μm. Zur Simulation dieses planaren Metamaterials wird die Finite-Differenzen-Zeitbereichsmethode verwendet. Um Simulationszeit und Rechenspeicher zu sparen, wählen wir die Maschenweiten von Δx = Δy = 1 μm und Δz = 0,02 μm. Wir finden, dass die Simulationsergebnisse in diesem Fall ziemlich genau sind. Auch bei kleineren Maschenweiten bleiben die Simulationsergebnisse nahezu unverändert. Die simulierten Randbedingungen entlang x -Achse und y -axis werden als periodisch gesetzt und die Bedingung entlang z -axis wird als perfekt aufeinander abgestimmte Ebenen festgelegt. 1a zeigt, dass die gesamte Struktur von einem Strahl einer normal einfallenden THz-Welle beleuchtet wird. Wie in Abb. 1b, c zu sehen, ist der elektrische Vektor E und magnetischer Vektor H des einfallenden THz-Strahls sind y -Achse polarisiert und x -Achse jeweils polarisiert.

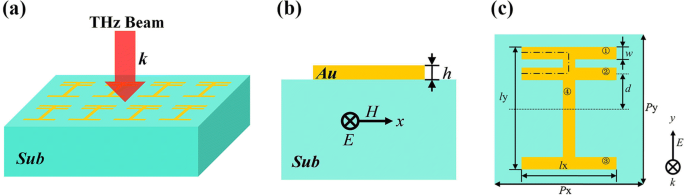
Dreidimensionales Diagramm des vorgeschlagenen Metamaterials (a ). Seitenansicht (b ) und Draufsicht (c ) des asymmetrischen Metamaterial-Resonators; die äquivalente Länge l ist durch eine strichpunktierte Linie gekennzeichnet

Ergebnisse und Diskussion

Das Transmissionsspektrum der vorgeschlagenen Metaoberfläche ist in Abb. 2a dargestellt. Es gibt zwei Übertragungseinbrüche bei den Frequenzen von 0,430 THz und 0,809 THz mit den Übertragungsraten von 0,10 % bzw. 26,45 %. Um die folgende Erklärung prägnanter zu gestalten, verwenden wir R _s R_s und R _d um diese beiden Resonanzmodi zu markieren, R _s für den Modus resonant bei 0,430 THz und R _d für den Resonanzmodus bei einer höheren Frequenz. Die optische Übertragungsrate von R _s zeigt ein symmetrisches Lorentz-Profil mit einer relativ großen Bandbreite von 0,256 THz. Im Vergleich dazu R _d weist eine asymmetrische Fano-Linienform auf, die mit einer Bandbreite von 0,014 THz viel schärfer ist. Q -Faktor ist ein wichtiges Kriterium zur Beurteilung der Linienform. Sie kann erhalten werden, indem die Mittenfrequenz durch die Bandbreite geteilt wird. Tatsächlich ist das Q -Faktor von R _d kann 58 erreichen, 30-mal mehr als das Q -Wert von R _s , das zu den zugrunde liegenden Anwendungen in vielen Bereichen beiträgt. Die Existenz des asymmetrischen Fano-Profils wurzelt in der Wechselwirkung zwischen einem dunklen Modus und einem hellen Modus, d. h. der Wechselwirkung zwischen einem nicht strahlenden Zustand und einem Kontinuum, die aus einem strahlenden Zustand erzeugt wird [16, 38, 39]. Im Rest des Beitrags werden der detaillierte Mechanismus der Fano-Linienform diskutiert und theoretische Transmissionsspektren analysiert. Obwohl die Transmission bei 0,809 THz in der vorgeschlagenen Metaoberfläche 26,45% beträgt, kann sie weiter reduziert werden. Nach [40, 41] kann die Verwendung von verlustbehafteten dielektrischen Materialien die Transmission reduzieren. In unseren Simulationen wählen wir als Substratmaterial ein ideales Material mit einem realen Brechungsindex von 1,5, das keinen Verlust im Terahertz-Bereich aufweist. Eine praktikable Methode zur Reduzierung der Transmission ist die Verwendung eines verlustbehafteten Materials mit einem komplexen Brechungsindex, um das Substrat anstelle dieses idealen verlustfreien Materials zu bilden.

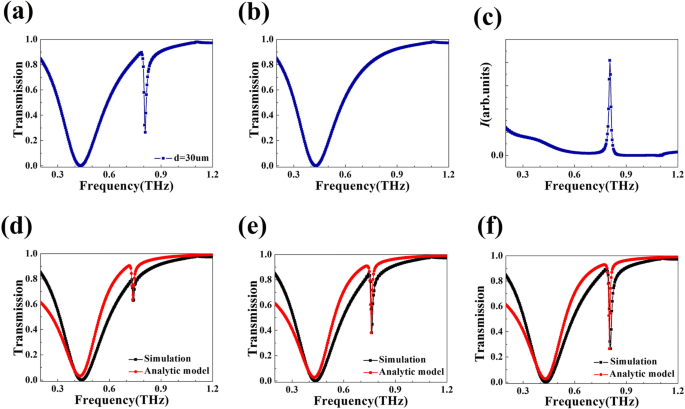
a Transmissionskurve der entworfenen Metaoberfläche durch numerische Simulation. b Transmissionsspektrum des hellen Modus. c Feldstärke der vorgeschlagenen Vierstreifen-Nanostruktur, beleuchtet von einer Dipolquelle. d , e , f Simuliertes (rote Kurve) und theoretisches (schwarze Kurve) Transmissionsspektrum der entworfenen Struktur mit d = 10 μm, d = 20 μm und d = 30 μm bzw.

Um den Ursprung der Transmissionskurve herauszufinden, muss die Verteilung des elektrischen Felds ∣E ∣ und das z Komponente des Magnetfelds (H _Z ) bei der Mittenfrequenz zweier Resonanzeinbrüche sind in Abb. 3 dargestellt. Wir finden große Unterschiede zwischen den Feldverteilungen von R _s und R _d . Abbildung 3a zeigt, dass das elektrische Feld des Resonanzmodus R _s konzentriert sich hauptsächlich auf Streifen 1 und Streifen 3, insbesondere die Enden dieser beiden Streifen. Es gibt jedoch eine sehr geringe Verteilung des elektrischen Felds an anderen Teilen der Struktur, einschließlich Streifen 2 und Streifen 4. Eine solche Verteilung des elektrischen Felds ist auf das elektromagnetische Feld des normal einfallenden Lichts zurückzuführen, dessen elektrischer Vektor E ist zusammen y -Achse. Daher R _s kann als fundamentale Resonanz (d. h. lokalisierte elektromagnetische EM (elektromagnetische) Reaktion) angesehen werden [42]. Außerdem ist die Verteilung der z Komponente des Magnetfelds (H _Z ) für Modus R _s ist in Abb. 3b gezeigt, aus der wir die Oberflächenstromverteilung erhalten können. Es wurde gezeigt, dass die Analyse des Oberflächenstroms eine wichtige Methode sein kann, um aufzudecken, wie die Kopplung von Moden eine Fano-Resonanz erzeugt [28]. Wie in Abb. 3b gezeigt, fließt Oberflächenstrom vom unteren zum oberen Teil der Struktur und trägt zur Ansammlung entgegengesetzter Ladungen auf beiden Seiten von Streifen 1 und Streifen 3 bei. Im Gegensatz dazu ist die Feldverteilung bei der Mittenfrequenz von R _d ist eher anders. Um Streifen 1 und Streifen 2 wird ein intensives elektrisches Feld gefunden (Abb. 3c), das ungefähr viermal größer ist als das der Mode R _s . Nach der Verteilung von H _Z Feld, das in Fig. 3d gezeigt ist, ist klar, dass der Oberflächenstrom zwischen Streifen 1 und Streifen 2 nach oben fließt, während der Strom zwischen Streifen 2 und Streifen 3 entgegengesetzt fließt. Auf Makroebene kann eine solche Feldverteilung als eine Art Ladungsinduktion zwischen den horizontalen Streifen angesehen werden. Aus der Sicht der Modenkopplung ist dieses Phänomen auf die Wechselwirkung zwischen dem Hellmodus und dem Dunkelmodus zurückzuführen.

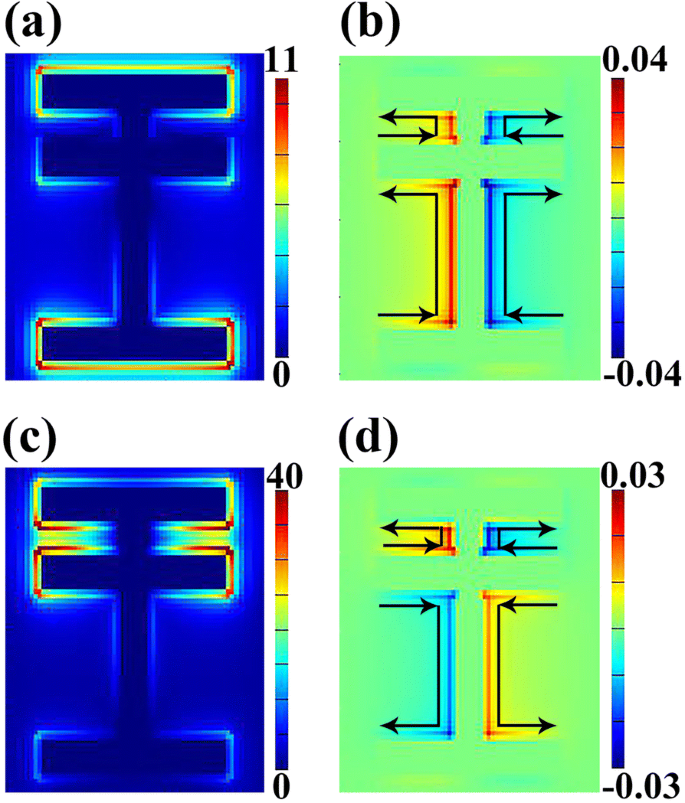
Verteilungen des elektrischen Feldes ∣E∣ (a ) und z Komponente des Magnetfelds (H_Z ) (b ) bei 0,430 THz (R _s ); Verteilungen von ∣E∣ (c ) und H_Z (d ) bei 0,809 THz (R _d ); schwarze Pfeile in b und d repräsentieren die Richtung des Oberflächenstroms

Um unsere Erklärung zu vertiefen und zu quantifizieren, werden die Spektren des Hell- und Dunkelmodus simuliert und die elektromagnetische Theorie der Fano-Resonanz [15, 16] in der vorgeschlagenen Struktur verwendet. 2b zeigt das Transmissionsspektrum einer Struktur, deren periodische Einheit aus den Streifen 1, 3 und 4 besteht. Die von einer solchen Struktur unterstützte Resonanzmode kann direkt durch eine ebene Welle angeregt werden; daher handelt es sich um den „hellen Modus“. Im Gegensatz dazu kann eine Dunkelmode nicht durch einen Strahl einer ebenen Welle angeregt werden; es kann durch ein sich schnell änderndes Feld angeregt werden, beispielsweise das Nahfeld eines Dipols [15, 43]. Abbildung 2c zeigt die Feldstärke des von einer Dipolquelle beleuchteten Vierstreifen-Metamaterials [44]. Die Maxwell-Gleichungen bilden eine solide Grundlage der elektromagnetischen Theorie der Fano-Resonanz in Nanostrukturen. Nach den Maxwell-Gleichungen ist der elektrische Vektor E gehorcht der folgenden Wellengleichung:

$$ {\in}^{-1}\left(\mathbf{r},\upomega\right)\nabla\times\nabla\times\mathbf{E}\left(\mathbf{r},\upomega\ rechts)-\frac{\upomega^2}{{\textrm{c}}^2}\mathbf{E}\left(\mathbf{r},\upomega\right)=0 $$ (1)

wobei ω die Frequenz des einfallenden Strahls ist und ∈(r , ω) ist die komplexe Dielektrizitätskonstante des verlustbehafteten Materials. Das elektrische Feld E und die Permittivität ∈ beziehen sich sowohl auf die Frequenz ω als auch auf den Ortsvektor r . Zwei orthogonale Projektionsoperatoren P und Q können verwendet werden, um die Wellenfunktion ∣E . zu trennen> in einen hellen Modus P ∣ E> und ein dunkler Modus Q ∣ E>, d. h. ein strahlender und ein nicht strahlender Modus [15, 38]. Durch komplizierte Herleitung kann das Verhältnis der Gesamtfeldstärke zur Intensität des hellen Modus angegeben werden als

$$ {I}_{\mathrm{a}}\left(\upomega \right)=\frac{{\left(\frac{\upomega^2-{\upomega_{\mathrm{a}}}^2 }{2{W}_{\mathrm{a}}{\upomega}_{\mathrm{a}}}+q\right)}^2+b}{{\left(\frac{\upomega^2 -{\upomega_{\mathrm{a}}}^2}{2{W}_{\mathrm{a}}{\upomega}_{\mathrm{a}}}\right)}^2+1} $$ (2)

wo W _a und ω_a sind die Bandbreite bzw. die Mittenfrequenz der asymmetrischen Resonanz. Der asymmetrische Parameter q und der Modulationsdämpfungsparameter b sind beide unentbehrlich um I zu beschreiben _a (ω) [15, 16]. Die Gl. (2) legt nahe, dass ich _a (ω) weist ein asymmetrisches Profil auf, was schließlich zu der asymmetrischen Fano-Linienform in der Transmissionskurve führt.

Die Intensität des hellen Modus R _s folgt einem glatten Lorentzschen Profil. Sie hängt von der Frequenz ω ab und gehorcht der folgenden Gleichung:

$$ {I}_{\mathrm{s}}\left(\upomega \right)=\frac{a^2}{{\left(\frac{\omega^2-{\omega_{\mathrm{s .) }}}^2}{2{W}_{\mathrm{s}}{\omega}_{\mathrm{s}}}\right)}^2+1} $$ (3)

davon W _s und ω _s sind die Bandbreite bzw. die Mittenfrequenz des in Abb. 2b angezeigten Spektrums und a ist der Maximalwert der Resonanzamplitude. Die Gesamtstärke Ich (ω ) der Resonanz kann durch das Produkt von I . berechnet werden _a und ich _s , aus dem wir endlich die Transmission T erhalten können (ω).

$$ I\left(\omega \right)={I}_{\mathrm{a}}\left(\omega \right)\times {I}_{\mathrm{s}}\left(\omega\ rechts) $$ (4) $$ T\left(\omega \right)=1-I\left(\omega \right) $$ (5)

Um die Forderung der Energieeinsparung zu erfüllen, a sollte nicht größer als 1 sein. W _a und ω _a lässt sich aus Mittenfrequenz und Bandbreite berechnen [15, 16]. Der asymmetrische Parameter q sowie der Modulationsdämpfungsparameter b kann durch die Methode von [16] erhalten werden. Auf diese Weise erhalten wir das theoretische Transmissionsspektrum dieser asymmetrischen Struktur. In Abb. 2f stellt die schwarze Kurve das Transmissionsspektrum dar, das durch das FDTD-Verfahren gegeben wurde, und die rote Kurve gibt die Ergebnisse unserer Berechnung an, die auf der elektromagnetischen Theorie der Fano-Resonanz basiert. Der durchgängige Trend der schwarzen und roten Kurve weist darauf hin, dass es sinnvoll ist, die Übertragungseigenschaften des Resonators auf die Kopplung von Hell- und Dunkelmode zurückzuführen. Diese Schlussfolgerung stimmt auch mit der Feldverteilung in Abb. 3 überein.

Der geometrische Parameter d beschreibt den Abstand zwischen der Achse des Streifens 2 und dem Mittelpunkt der gesamten Struktur (Abb. 1c). Sie kann die Mittenfrequenz von Transmissionseinbrüchen sowie deren Transmissionskoeffizienten stark beeinflussen. Entsprechende Transmissionsspektren mit unterschiedlichen d sind in Fig. 2d gezeigt, z. Die schwarze Kurve und die rote Kurve repräsentieren das Transmissionsspektrum basierend auf Simulation bzw. theoretischer Berechnung. Mit d ändert sich von 10 auf 30 µm, wird deutlich, dass sich ein scharfer Fano-Einbruch vertieft, der aus der zunehmenden Kopplungsstärke zwischen dem hellen Modus und dem dunklen Modus resultiert. Außerdem ist die Mittenfrequenz des Modus R _d existiert eine deutliche Blauverschiebung, wenn Streifen 2 näher an Streifen 1 platziert wird. Basierend auf dem LC-Schaltungsmodell ist die Resonanzfrequenz von R _d ist gegeben durch [45].

$$ {\omega}_{\mathrm{d}}=\frac{1}{2\uppi\sqrt{\mathrm{LC}/2}}\propto\frac{1}{\mathrm{l}} $$ (6)

wo l ist die äquivalente Länge des entsprechenden Resonators. Gleichung (6) zeigt an, dass die Mittenfrequenz ω _d ist umgekehrt proportional zu l . In unserer Struktur äquivalente Länge l wird durch die Länge der strichpunktierten Linie in Fig. 1c angezeigt. Dies liegt daran, dass die Feldverteilungen von R _d beschränken sich hauptsächlich auf die Streifen 1 und 2. Die Länge von Streifen 1 (und 2) und der Abstand zwischen den beiden Streifen zusammen entscheiden l. Wenn d nimmt der Abstand zwischen den beiden Streifen ab. Daher nimmt, wie in Abb. 1c gezeigt, die äquivalente Länge ab, wenn d ändert sich von 10 auf 30 µm. Dies führt zu einem Anstieg von R _d s Resonanzfrequenz.

Nach der von Fano 1961 vorgeschlagenen Theorie der Fano-Resonanz [12] wird der Prozess der Autoionisation untersucht und die asymmetrische Linienform der Resonanz auf die Interferenz zwischen einem Kontinuum und einem diskreten Zustand zurückgeführt. Dies ist auch der Ursprung dieser asymmetrischen Eigenschaften des Metamaterial-Resonators, die in diesem Artikel vorgestellt werden. Wie in Fig. 4 gezeigt, kann ein Drei-Niveau-System verwendet werden, um den Übergangsmechanismus der Struktur zu verdeutlichen. R ₀ dient als Grundzustand des Gesamtsystems. Heller Modus R ₁ ist eine Strahlungsmode, die direkt durch den normal einfallenden Strahl angeregt werden kann. In diesem System ist der strahlungslose Zustand R ₂ kann, wie bereits diskutiert, als „Dark Mode“ [21] angesehen werden. R ₂ kann durch die Symmetriebrechung angeregt werden. Die Einführung einer Asymmetrie bietet einen Kanal, der es dem hellen Modus ermöglicht, mit dem dunklen Modus zu koppeln, und führt daher zur Fano-Resonanz [46].

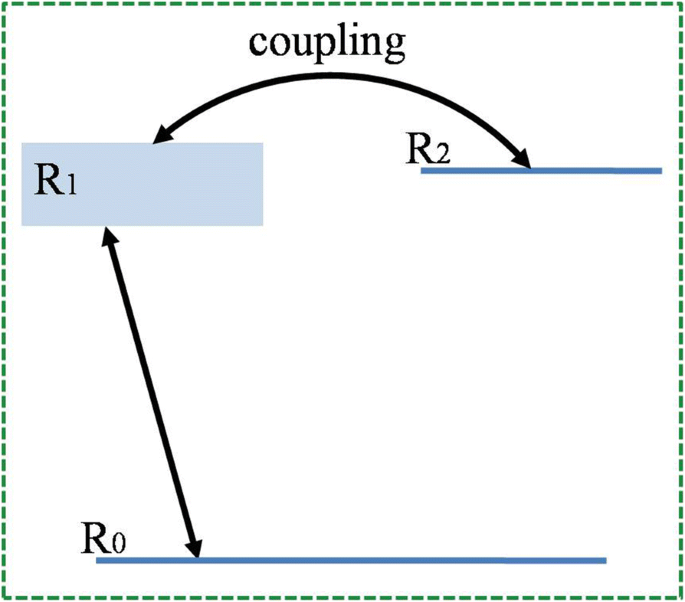
Schematische Darstellung des Drei-Ebenen-Systems

Die starke Wechselwirkung zwischen einfallender elektromagnetischer Welle und der Analytschicht macht ein hohes Q Fano-Resonanz, eine vielversprechende Methode zur ultraempfindlichen Erkennung des Brechungsindex n [8]. Die in Abb. 5a vorgeschlagene Vorrichtung kann als effektiver Sensor zum Erfassen des Brechungsindex n . fungieren der Analytschicht auf der Oberseite, deren Dicke 4 µm beträgt. Die Mittenfrequenz des Fano-Dip ändert sich mit der Änderung von n . Daher können wir den Brechungsindex erhalten, indem wir die Resonanzfrequenz von R . analysieren _d . Abbildung 5b zeigt die Verschiebung der Resonanzfrequenz von Fano dip im Gerät. Eine deutliche Rotverschiebung erscheint, wenn n wird von 1 auf 1,6 erhöht. Die Wahrnehmungsempfindlichkeit S gleich \( \frac{\varDelta f}{\varDelta n}\). Hier, S des Sensors wird mit 0,105 THz/RIU (Brechungsindexeinheit) berechnet. FOM (Figure of Merit) ist bekanntlich ein entscheidendes Kriterium für die Leistungsfähigkeit eines Sensors [47]. Sie kann berechnet werden durch FOM = \(\frac{S}{\mathrm{linewidth}}\). In dieser vorgestellten Struktur kann der FOM-Wert 7.501 erreichen, was auf einem idealen Niveau liegt [47, 48]. Die Erfassungsfähigkeit wird üblicherweise auch durch FOM* = \(\frac{S^{\ast}}{I}\) und S* = \(\frac{\varDelta I}{\varDelta n}\) diskutiert, was bezieht sich auf die erfasste Intensität. Das Berechnungsergebnis von S* in dieser Struktur ist 2,6/RIU. Und das FOM* in unserer Struktur wird mit 10 berechnet. Wir haben auch einige Arbeit geleistet, um die Variation der Reaktion mit der Dicke der Analytschicht herauszufinden. Bitte beachten Sie die Zusatzdatei 1.

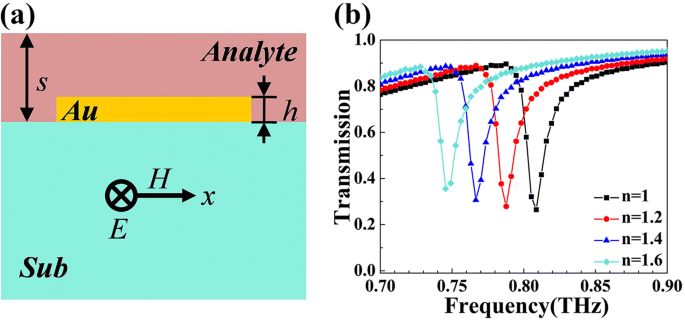
a Querschnitt des Sensors. b Abhängigkeit der Transmissionsspektren von den Änderungen des Brechungsindex n

Mehrere Fano-Resonanzen können in vielen Situationen Anwendung finden. Die meisten plasmonischen Fano-Metamaterialien sind jedoch darauf ausgelegt, eine einzelne Fano-Resonanz zu unterstützen [11, 17]. Daher ist es für sie nicht einfach, mehrere Fano-Resonanzen durch die Anpassung der Struktur zu realisieren. In diesem Papier realisieren wir mehrere Fano-Resonanzen, indem wir dem ursprünglichen Design des Metamaterials weitere horizontale Streifen hinzufügen. Als repräsentatives Beispiel stellen wir eine Fünf-Streifen-Struktur vor. Das schematische Diagramm des Fünfstreifen-Resonators ist in Fig. 6a gezeigt. Streifen 1, 2, 3 und 4 haben die gleiche Größe und sind parallel zueinander. Ihre Länge beträgt l _x = 120 μm und Breite ist w = 20 μm. Streifen 3 befindet sich in der Mitte und der Abstand d zwischen den Achsen von Band 2 und Band 3 beträgt 32 µm. Streifen 5 ist senkrecht zu den anderen vier Streifen. Seine Länge beträgt l _y = 150 μm und Breite ist w = 20 μm. Die Randbedingungen und die Maschenweite werden wie bei der Simulation des Vierstreifen-Resonators beibehalten. Das Simulationsergebnis ist in Abb. 6b dargestellt, in der wir deutlich zwei scharfe Fano-Einbrüche bei 0,75 THz und 0,91 THz finden. Das Q Werte dieser beiden Vertiefungen sind 61 bzw. 65. Es sollten mehr Fano-Einbrüche erzeugt werden, wenn mehr horizontale Streifen in die Struktur eingefügt werden.

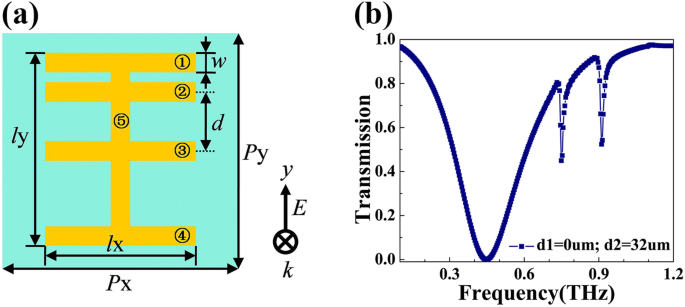
a Draufsicht auf die vorgeschlagene Fünf-Streifen-Struktur. b Simulierte Transmissionskurve des Fünfstreifen-Resonators