Erzeugen und Manipulieren hochwertiger Faktoren der Fano-Resonanz in einem Nanoring-Resonator durch Stapeln eines halben Nanorings

Hintergrund

Oberflächenplasmonenpolaritonen (SPPs) haben in den letzten Jahren aufgrund ihrer Fähigkeit, die Licht-Materie-Wechselwirkung in nanoskaligen Dimensionen zu manipulieren, großes Interesse auf sich gezogen [1,2,3,4,5,6]. Aufgrund der Fortschritte in der Nanofabrikation, der nanooptischen Charakterisierung und der Verbesserungen in der computergestützten Elektromagnetik im Vollfeld, die zur Entstehung des Gebiets der Nanoplasmonik geführt haben, wurden mehr Einblick und Kontrolle über lokalisierte Plasmonenresonanzen in metallischen Nanostrukturen gewonnen . Im Allgemeinen werden natürlich Plasmonenresonanzen isolierter Nanostrukturen wie Scheiben [7], Dreiecke [8, 9], Stäbchen [10, 11] und Ringe [12, 13] analysiert. Als fundamentaler Resonanzeffekt werden Fano-Resonanzen, die aus der Interferenz breiter und schmaler Anregungsmoden resultieren, typischerweise in Ringstab-Nanostrukturen [14], plasmonischen Oligomerclustern [15], nichtsphärischen Anordnungen [16], graphenbasierten Strukturen [17] erzeugt. , Quantenpunkte [18] usw. Trotz vieler Forschungsanstrengungen ist die Bildung von Fano-Resonanzen bei bestimmten Wellenlängen in plasmonischen Nanostrukturen aufgrund ihrer komplexen Natur, die der Hybridisierung der verfügbaren Moden entspricht, eine herausfordernde Aufgabe [ 19,20,21]. Darüber hinaus können Verzögerungseffekte [22, 23] durch den Einfallswinkel variiert werden, was die Existenz dunkler multipolarer Moden ermöglicht [24,25,26,27], die kürzlich im Kontext von Metamaterialien ausgenutzt wurden [28,29,30 ]. Dies ist jedoch in Systemen schwierig, in denen Moden höherer Ordnung im interessierenden Spektralbereich angeregt werden [31] oder wenn die Moden sehr komplex sind und sich räumlich über einen großen Teil der Nanostruktur erstrecken [32]. Und die plasmonischen Nanostrukturen sind kaum räumlich gedreht auf einer Subwellenlängenskala untersucht worden. Informationen über die räumliche Verteilung plasmonischer Nanostrukturen sind entscheidend, um den Mechanismus aufzuklären, der zur Modenerzeugung aus plasmonischen Strukturen führt. Darüber hinaus können wir ein Rezept dafür liefern, wie ein plasmonisches Element effizient an das andere plasmonische Element gekoppelt werden kann.

In diesem Artikel demonstrieren wir verschiedene Fano-Resonanzen in einer gestapelten Nanostruktur, die aus einem einzelnen Nanoring und einem halben Nanoring besteht. Numerische Ergebnisse aus Finite-Difference-Time-Domain-(FDTD)-Simulationen zeigen, dass die Mode geradzahliger Fano-Resonanz durch die Stapelmethode bei senkrechtem Einfall und nicht durch eine allgemeine Methode bei schrägem Einfall besonders angeregt und kontrolliert wird. Unser Ansatz bietet neue Einblicke in die spektralen Eigenschaften der Fano-Resonanz. Die verschiedenen spektralen Merkmale, die mit mehreren Fano-Resonanzen verbunden sind, entsprechen jeweils unterschiedlichen plasmonischen Moden. Bemerkenswerterweise werden die mehrfachen Fano-Resonanzen mit den Rotationsmoden erreicht, die auf den unterschiedlichen Orientierungswinkeln des halben Nanorings basieren. Im Spektrum werden gleichzeitig zwei hohe Qualitätsfaktoren von Fano-Resonanzen mit effektiver Dephasierungszeit erreicht. Diese Ergebnisse können potenzielle Anwendungen für Nanosensoren in hochintegrierten Schaltungen haben. Darüber hinaus zeigen wir, wie die Geometrie der Struktur die Fano-Resonanz bestimmt und wie sich die vorhandenen Anfangsmoden in die verschiedenen Moden umwandeln, um sie zu steuern. Diese Kontrolle, die mit den Eigenschaften der Nanostruktur verbunden ist, ist für praktische Anwendungen sehr wichtig, da sie eine hohe Designflexibilität, bemerkenswerte und robuste Abstimmbarkeit und hervorragende Leistung bietet.

Methoden

Das vorgeschlagene konzentrische System, bestehend aus einem Silber-Nanoring (Johnson und Christy), gestapelt mit einem halben Silber-Nanoring, wie schematisch in Abb. 1 gezeigt, wird auf verschiedene Strahlungsmoden untersucht. Hier ist der Radius des Nanorings/halber Nanoring-Innenradius (Rin ) und Außenradius des Rings (Rout ) sind 310 bzw. 400 nm. Für unsere Plattform wird die Höhe der strukturellen Handhelix [33] durch den Winkel θ . bestimmt , das ist der Orientierungswinkel des halben Nanorings, der sich vom Achsdraht verschiebt (entlang der y -Richtung) des konzentrischen Systems. Für die Struktur werden der Nanoring und der halbe Nanoring mit der Dicke (t ) werden auf ein Substrat gelegt, dessen Periode p . ist und der Brechungsindex wird auf 1 gesetzt. Die entsprechenden geometrischen Parameter sind wie folgt angegeben:t =40 nm und p =1000 nm. Um unsere numerischen Berechnungen von Lumerical FDTD Solutions durchzuführen, müssen die Gittergrößen im x und y und z Richtungen werden als Δx . gewählt =Δy =Δz =1 nm [16] und Δt =Δx /2c; hier, c ist die Lichtgeschwindigkeit im Vakuum. Es wird angenommen, dass die einfallende ebene Wellenbeleuchtung entlang der rückwärtigen z . verläuft -Richtung mit der Polarisation entlang des y -Richtung in den Simulationen. Darüber hinaus wird der Berechnungsbereich durch perfekt angepasste Schichten (PMLs) im z . abgeschnitten -Richtung und die periodische Grenze im x - und y -Wegbeschreibung.

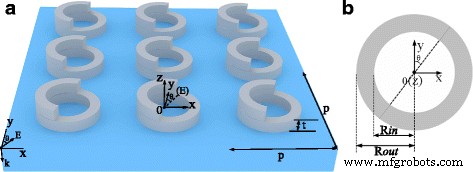
a Schematische Darstellung des Silber-Nanorings/Halb-Nanorings, die geometrischen Parameter sind Rin =310 nm, Rout =400 nm, t =40 nm und p =1000 nm. b Die der Einzelzelle der Nanostruktur entsprechende Draufsicht ist rechts angeordnet. Der Orientierungswinkel des halben Nanorings, der sich vom Achsdraht verschiebt (entlang der y -Richtung) des konzentrischen Systems ist θ

Ergebnisse und Diskussion

Abbildung 2a, c zeigt die optischen Eigenschaften der plasmonischen Nanostrukturen, die einzeln betrachtet werden. Da die Nanostrukturen bei senkrechtem Einfall nur ungerade Moden plasmonischer Resonanzen aufwiesen [25], ist die Mode dritter Ordnung des Nanorings bei 1027 nm A kann unter normaler Beleuchtung mit Polarisation entlang des y . angeregt werden -Achse, was impliziert, dass der Resonanzmodus dritter Ordnung des Nanorings superstrahlend ist. In dieser Geometrie entsteht die Fano-Linienform aus der hybridisierten Kopplung zwischen einer Plasmonenresonanz der Scheibe und einer Plasmonenresonanz, die durch die Scheibe des Anti-Punkts unterstützt wird [34, 35], die qualitativ als die dipolare Plasmonenscheibe beschrieben werden kann, die mit ein scheibenförmiges Loch in einem metallischen Film (Lochstruktur) [36], wie in Abb. 2b explizit dargestellt. Aus Abb. 2b können wir das Konzept der Plasmonenhybridisierung deutlich nutzen, um den Ursprung der Fano-Resonanz dritter Ordnung zu erklären, bei der die Plasmonenmoden als Bindung verstanden werden können (D _B ) oder Antibanding (D _AB ) Moduskombination der Nanodisk (D _D ) und dem Gegenpunkt (D _H ) Plasmonenmodi. Darüber hinaus ist der Dipol des Einzelhalb-Nanoring-Modus erster Ordnung bei 1297 nm B wird deutlich beobachtet, wie explizit in Abb. 2c gezeigt.

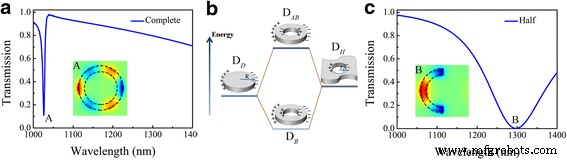
a Transmissionseigenschaften von Spektren des vollständigen Nanorings allein. Die Verteilung von z -Komponente des elektrischen Feldes bei der Wellenlänge von 1027 nm, gekennzeichnet durch den Einschub A. b Mechanismus der plasmonischen Hybridisierung zwischen den dipolaren Moden der Scheibe (D _D ) und Gegenpunkt (Loch) (D _H ) Strukturen und das Energiediagramm der degenerierten Plasmonenbindung (D _B ) und antibindend (D _AB ) Modi. Die Vorzeichen „+“ und „–“ stehen für die positiven bzw. negativen Ladungen. c Transmissionsspektren des einzelnen halben Nanorings. Die Verteilung von z -Komponente des elektrischen Feldes bei der Wellenlänge von 1297 nm, gekennzeichnet durch den Einschub B

Um die Transmissionseigenschaften der gestapelten Nanostruktur weiter aufzuklären, haben wir auch berechnet, dass die spektrale Reaktion des gestapelten Systems eine Kombination der einzelnen Schichtmoden ist, wie in Abb. 3a gezeigt. Um das positive und das negative Dipolmoment vollständig zu kompensieren, kann eine Fano-Resonanz im Modus zweiter Ordnung außer dem Weg eines schrägen Einfalls nicht direkt angeregt werden [22]. Abbildung 3b zeigt den Modus dritter Ordnung (m =3) Die Fano-Resonanz ähnelt dem zuvor analysierten Fall in Abb. 2b. Als der auf dem Nanoring stehende halbe Nanoring untersucht wurde, wurde der Modus dritter Ordnung (m =3) Die Fano-Resonanz bleibt fast invariant. Darüber hinaus ist der Modus zweiter Ordnung (m =2) Die Fano-Resonanzeffizienz wurde bei einer Wellenlänge von 1160 nm erreicht, wie explizit in Abb. 3c gezeigt. Wenn wir die superstrahlenden Plasmonenresonanzmoden vergleichen, können wir schließen, dass die Fano-Resonanz vom Stapeleinfluss herrührt. Und eine Modifikation der Umstände in oder um die Nanoringe wirkt sich auf den Resonanzmodus aus [10]:Seine Resonanzwellenlänge ändert sich im Vergleich zu der des einzelnen Nanorings oder des halben Nanorings. Der Stapelkontakt verursacht eine starke Blauverschiebung der fundamentalen Mode erster Ordnung, während die geometrische Form des Stapelnanorings/halben Nanorings immer noch eine effiziente Anregung von Moden höherer Ordnung ermöglicht. Diese beiden plasmonenresonanten Moden erster Ordnung des gestapelten Nanorings/halben Nanorings sind auf 1160 nm blauverschoben, was zur Existenz einer Mode zweiter Ordnung (m =2) Fano-Resonanzen, bei denen sich die Mode erster Ordnung des Nanorings bei einer relativ langen Wellenlänge mehr als die des halben Nanorings verschiebt. Wir zeigen, dass neue Resonanzmoden vom Fano-Typ aufgrund der Hybridisierung zwischen der Mode erster Ordnung des Nanorings und des halben Nanorings angeregt werden. Da sich diese beiden Moden gegenseitig beeinflussen können, ist dies auf die Kompensation des Retardationseffekts bei Fano-Interferenz zurückzuführen. Es ist offensichtlich, dass dieser Modus zweiter Ordnung (m =2) Die Fano-Resonanz wird aufgrund der unterschiedlichen Transmissionsverteilungen und Ausbreitungseigenschaften der Nanostruktur durch den Stapel des halben Nanorings bestimmt. Wie zu erkennen ist, hat einerseits die Existenz des halben Nanorings wenig Einfluss auf die Mode dritter Ordnung (m =3) Fano-Resonanz, die die tollen Eigenschaften beibehält. Andererseits zeigt es, dass der halbe Nanoring einen positiven Einfluss auf die Mode zweiter Ordnung hat (m =2) Fan-Resonanz. Bemerkenswerterweise beträgt die Halbwertsbreite (FWHM) der Resonanz zweiter Ordnung 14 nm, was einen Qualitätsfaktor (Q -Faktor) bis zu 82,8. Und wir berechneten die FWHM der Resonanz dritter Ordnung in der gestapelten Nanostruktur zu 9 nm, die sich effektiv bei 1027 nm mit einem hohen Qualitätsfaktor von 114 befindet Elemente, die größer als 20 [37], 50 [38] und 62 [10] ist. Darüber hinaus kann die Dephasierungszeit der induzierten Resonanzmode deren Eigenschaften der Resonanzen entscheidend beeinflussen. Wir haben die Dephasierungszeit des induzierten Resonanzmodus über T . berechnet _r =2 ℏ /Γ _L (r =2, 3) [39,40,41], wobei ℏ ist die reduzierte Planck-Konstante und Γ _L ist die homogene Linienbreite der Fano-Resonanz. Die Dephasierungszeit des Resonanzmodus zweiter Ordnung (m =2) T ₂ wird auf 0,10 ps geschätzt, und der Resonanzmodus dritter Ordnung (m =3) T ₃ wird auf 0,12 ps geschätzt. Seit den Fano-Resonanzen, Dephasierungszeiten T ₀ liegen vermutlich in der Größenordnung von 10 fs [41] und sind daher zu kurz, um mit verfügbaren Laserpulsen zuverlässig aufgelöst zu werden. Beide T ₂ und T ₃ sind größer als die allgemeinen Fano-Resonanzen. Dephasierungszeiten T _0, was leicht zu realisieren ist.

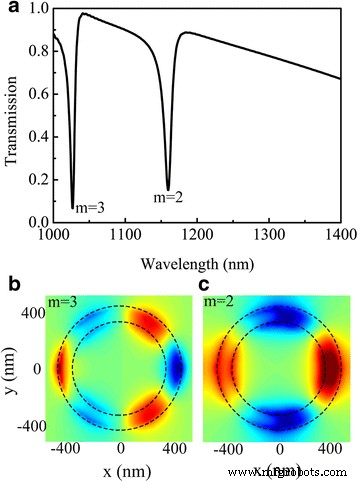
a Transmissionsspektren des gekoppelten Systems in Abb. 1 (gekennzeichnet durch eine schwarze Linie) durch den halben Silbernanoring gekoppelt mit dem vollständigen Silbernanoring. b , c Verteilungen von z -Komponente des elektrischen Feldes bei Wellenlängen von 1027 (m =3) und 1160 nm (m =2) bzw.

Als nächstes wird auch die Abhängigkeit der Fano-Resonanz von Parametern des Systems untersucht. Tatsächlich kann man, wie es beim plasmonischen Resonator der Fall ist, die spektralen Eigenschaften der Resonanzen durch Ändern des Drehwinkels der Handhelix des halben Nanorings auswählen. Betrachten wir senkrechten Einfall mit linear polarisiertem Licht entlang des y -Achse (θ =0°), sieht man, dass für θ =0°, werden nur die Resonanzmoden zweiter und dritter Ordnung angeregt, wie in Abb. 3a gezeigt. Abb. 4a zeigt jedoch Spektren einer geringfügigen Variation des Drehwinkels der Handhelix, die einen viel größeren Einfluss auf die Nanostrukturen hat, wobei beobachtet wird, dass die 5°-Drehung des halben Nanorings zu einer neuen Modenresonanz führt (bezeichnet als Rotationsmode m =r ). Wenn der halbe Nanoring zusammen mit θ . platziert wird =5° Drehung, drei asymmetrische Einbrüche existieren im Spektrum. Um die hybridisierten Moden zu identifizieren, tragen wir die Oberflächenladungsverteilungen entsprechend den drei Einbrüchen im hybridisierten Spektrum auf, wie in Abb. 4b–d gezeigt. Das elektrische Felddiagramm beschreibt die Hybridisierung der Plasmonenmoden, die von diesem gestapelten System unterstützt werden. Außerdem sollte man beachten, dass der Modus dritter Ordnung (m =3) als superstrahlende Mode unter einer solchen Anregung fast keine Änderung entlang des y -Achse der Nanostruktur, während die Fano-Resonanz zweiter Ordnung (m =2) stimmt mit dem obigen Mechanismus überein, identifiziert als Hybridisierungsmodus erster Ordnung des halben Nanorings und des Nanorings. Insbesondere der Rotationsresonanzmodus (m =r ) des Nanorings kann wegen des Retardationseffekts nicht in einer einzigen Konfiguration angeregt werden. Der Einbruch in den Wellenlängen-Rotationsmodi (m =r ) wird auch zwischen Resonanzmoden erster Ordnung des halben Nanorings und des Nanorings hybridisiert. In der Rotationssituation zeigt die Fano-Resonanz die gleiche Ladungsverteilung mit der Mode zweiter Ordnung (m =2), jedoch mit einem strukturellen Drehwinkel der Handhelix, wie in der Ladungsverteilung in Abb. 4d gezeigt. Basierend auf der Mode zweiter Ordnung wird die Rotationsmode durch Rotationsverfahren unterstützt und zeigt eine asymmetrische Rotverschiebung (Verschiebung zu langen Wellenlängen). Der sich drehende halbe Nanoring hat eine Doppelfunktion, dass einer als halber Nanoring verwendet wird, um den Modus zweiter Ordnung zu erzeugen, und der andere als drehender halber Nanoring dient, um den Rotationsmodus anzuregen. Beachten Sie, dass die Resonanz des Einbruchs im Spektrum verstärkt oder verschwinden kann, was zu einer flexiblen Modulation in integrierten Schaltkreisen führt.

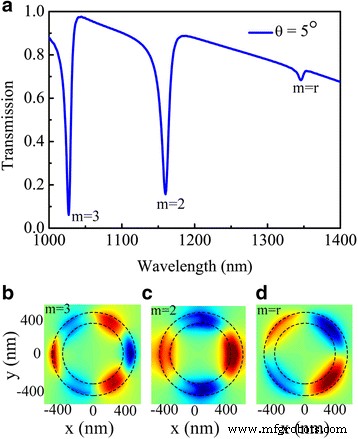
a Die spektrale Empfindlichkeit einer Silber-Nanostruktur mit einem sich ändernden Winkel θ =5° des halben Nanorings. Verteilungen von z -Komponente des elektrischen Feldes bei Wellenlängen von 1027 (b ), 1160 (c ) und 1346 nm (d ) bzw.

Abbildung 5 zeigt Spektren einer Nanostruktur mit gleichen Durchmessern, aber mit einem sich ändernden Helixwinkel des halben Nanorings abweichend von der Richtung der Polarisation des elektrischen Felds. Die Winkeldifferenz führt zur Variation des Rotationsresonanzmodus (m =r ), was mit der obigen Analyse der Modi übereinstimmt. Wenn die Winkeldifferenz sehr groß wird, wie im Fall von θ =0° bis θ =30°, wird die Linienform des hybridisierten Spektrums ausgeprägter. Es ist zu erkennen, dass der Modus (m =r ) ist nicht dominant genug, da der halbe Nanoring aufgrund seiner geringen Winkelgröße ein geringes Rotationsmoment hat. Und der rotierende Resonanzmodus wird mit zunehmendem Winkel sichtbar. Somit weist die gesamte Struktur drei Modi auf. Außerdem ist der Modus zweiter Ordnung (m =2) wird kleiner, da das Nettomoment entlang des y -Achse ist klein, was zu einer schwachen Interferenz führt, die für ein ausgeprägtes Fano-Profil im Modus zweiter Ordnung (m =2). Wenn der Winkel des halben Nanorings größer wird, wird der Resonanzunterschied offensichtlich, sodass die Überlappung der beiden Moden deutlich wird, wodurch das asymmetrische Fano-Profil (m =r ) unverwechselbarer.

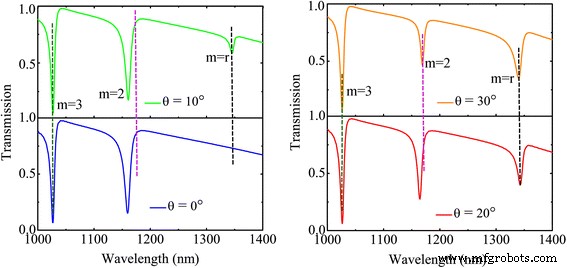
Die blaue, grüne, rote und Ursprungslinie zeigen die Transmissionsspektren der Simulation für verschiedene Rechtsdrehwinkel θ =0°, 10°, 20° bzw. 30°, mit den anderen Parametern dieselben wie in Abb. 1

Es ist interessant zu sehen, dass für eine Nanostruktur, die aus einem Nanoring gleicher Länge, aber einem halben Nanoring besteht, auch eine ausgeprägte (eigentlich viel schärfere) Fano-Resonanz zweiter Ordnung angeregt werden kann, die zwei hochwertige Fano gleichzeitig stimulieren kann Zeit und trägt zur Entwicklung integrierter Schaltkreise bei. Dies zeigt weiter, dass sich die spezielle Form des Nanorings von denen in anderen Nanopartikelsystemen unterscheidet. Der Grund für das besondere Verhalten der Plasmonenhybridisierung liegt darin, dass für den halben Nanoring, wo ihre Enden relativ andockende Nanoringe sind, der starke Einfluss den geraden Modus der Nanostruktur induziert. Da jedoch der Winkel des halben Nanorings variiert wird, ist der Rotationsmodus (m =r ) angeregt, was anschließend drei Fano-Resonanzprofile erzeugt. Wenn sich der halbe Nanoring von y . in eine andere Richtung verschiebt, -Richtung des konzentrischen Systems (im Fall von θ =0°, − 10°, − 20°, − 30°), ist das Phänomen der Nanostruktur das gleiche wie in Abb. 5. Wir können die gleichen Schlussfolgerungen ziehen, dass eine geringfügige Variation des Drehwinkels viel mehr Einfluss auf die Nanoring-Resonanzmoden. Es gibt die neue Modenresonanz (Rotationsmode m =r ) im Einklang mit den Beschreibungen zuvor.

Schlussfolgerungen

Zusammenfassend wurde eine neuartige plasmonische Silber-Nanostruktur analysiert und untersucht, die Modenresonanzen zu einem Hybridsystem kombiniert, das aus einem Nanoring besteht, der durch einen halben Nanoring gestapelt ist und eine Fano-Resonanz im nahen Infrarotbereich des Spektrums unterstützt. Die Nanostruktur weist eine hohe Abstimmbarkeit und robuste Kontrolle ihrer spektralen Eigenschaften mit nur wenigen strukturellen Drehparametern der Handhelix auf. Die Analyse der elektrischen Feldverteilung ergab, dass die verschiedenen Moden für bestimmte Frequenzen angeregt werden können. Andernfalls werden mehrere Fano-Resonanzen durch Drehen des Winkels des halben Nanorings erreicht und dann werden die Mechanismen erheblich gestört. Der Stapel eines halben Nanorings schafft einen Weg zum Realisieren verschiedener Fano-Resonanzmoden im plasmonischen Resonanzsystem. Darüber hinaus haben die Fano-Linienformen einen hohen Qualitätsfaktor, der leicht für Nanosensoren in hochintegrierten Schaltkreisen angewendet werden kann.

Abkürzungen

FDTD:

Zeitbereich mit endlicher Differenz

FWHM:

Volle Breite bei halbem Maximum

PMLs:

Perfekt aufeinander abgestimmte Schichten

Q -Faktor:

Qualitätsfaktor

SPPs:

Oberflächenplasmonenpolaritonen