Abstimmung der elektronischen Eigenschaften von blauem Phosphor/Graphen-ähnlichen GaN-van-der-Waals-Heterostrukturen durch vertikales externes elektrisches Feld

Einführung

Zweidimensionale (2D) Materialien wie Graphen [1], Übergangsmetalldichalkogenide (TMDs) [2], schwarzes Phosphoren (BP) [3] und graphenähnliches GaN (g-GaN) [4] wurden in der aufgrund ihrer faszinierenden physikalischen Eigenschaften und Anwendungsmöglichkeiten in Geräten ins Rampenlicht gerückt. Als sich schnell entwickelndes Forschungsgebiet bleibt der Aufbau der Heterostrukturen aus den isolierten Atomen ein spannendes Forschungsfeld. Es gilt als neuartiger Weg zum Bau von Bauelementen, der die Eigenschaften jeder isolierten Komponente mit idealen Eigenschaften aus der Nanoelektronik integriert [5, 6]. Aufgrund der Wechselwirkung der Atomschichten [7] besitzen diese Heterostrukturen im Vergleich zu den reinen 2D-Materialien hervorragende Eigenschaften, und ihre Eigenschaften bleiben ohne Degradation erhalten, wenn sie schichtweise miteinander verbunden werden. Bis heute wurden viele Anstrengungen unternommen, um Van-der-Waals-(vdW)-Heterostrukturen zu erhalten. Es ist erwähnenswert, dass die auf blauem Phosphoren (blue-P) basierenden vdW-Heterostrukturen wie blue-P/TMDs [8,9,10] und blue-P/graphene [11] aufgrund ihrer hervorragenden elektronischen und optische Eigenschaften.

Unter den oben genannten 2D-Halbleitermaterialien wurde 2016 zum ersten Mal eine Blue-P-Monoschicht durch epitaktisches Wachstum auf Au (111)-Substraten hergestellt [7]. Z. Zhanget. al. sagten das epitaktische Wachstum von Blau-P-Monoschichten auf GaN(001)-Substraten voraus und schlugen einen unkonventionellen „Halbschicht“-Wachstumsmechanismus vor. Es wird auch darauf hingewiesen, dass Blue-P aufgrund der chemischen Affinität zwischen Phosphor und Gallium und der guten Gitteranpassung auf der Oberfläche von GaN (001) stabiler ist [12]. Blue-P, bestehend aus einer vertikal gewellten, aber einzelnen Schicht von Phosphoratomen, zieht aufgrund seiner hervorragenden Eigenschaften wie der großen Bandlücke und der hohen Mobilität ein intensives Forschungsinteresse auf sich [13, 14]. Darüber hinaus kann g-GaN als neuartiges 2D-Material experimentell mittels einer migrationsverstärkten verkapselten Wachstumstechnik (MEEG) synthetisiert werden [15]. Theoretische Simulationen haben gezeigt, dass g-GaN ein Halbleiter mit einer indirekten Bandlücke ist, der durch ein externes elektrisches Feld effizient manipuliert werden kann [16]. Wie andere 2D-Materialien kann auch g-GaN bequem hydriert und halogeniert werden. All diese Studien haben gezeigt, dass g-GaN ein alternativer 2D-Halbleiter für Anwendungen in vielen wichtigen Bereichen der Zukunft ist. Der Gitterparameter von g-GaN könnte gut mit Blau-P übereinstimmen, was darauf hindeutet, dass Blau-P/g-GaN ein ideales Materialsystem für den Aufbau von Heterostrukturen sowie eine ausgezeichnete Einfügeschicht zum Abstimmen ihrer elektronischen Eigenschaften ist durch die Wechselwirkung zwischen den Schichten. In diesem Zusammenhang ist es wichtig, die elektronischen und optischen Eigenschaften der blauen-P/g-GaN vdW-Heterostrukturen zu untersuchen. Es wurden jedoch nur wenige Untersuchungen untersucht, um die Eigenschaften von Blue-P/g-GaN-vdW-Heterostrukturen zu untersuchen [17, 18].

In dieser Arbeit werden die elektronischen Struktureigenschaften und die Variationstendenz der Bandlückenenergie (E _g ) mit dem vertikalen äußeren elektrischen Feld (E _ext ) in den blauen-P/g-GaN-vdW-Heterostrukturen werden bewertet und unter Verwendung der First-Principles-Rechnungen mit vdW-korrigiertem Austauschkorrelationsfunktional durchgeführt.

Rechenmethoden

Die Bandstrukturen und elektrischen Eigenschaften der Monolayer- und Bilayer-Blue-P/g-GaN-vdW-Heterostrukturen wurden mit dem Cambridge Serial Total Energy Package (CASTEP) [19] untersucht, das auf der Dichtefunktionaltheorie (DFT) basiert [20 , 21] in einem Plane-Wave-Basissatz mit dem Potential des Projektors Augmented Wave (PAW) [22, 23]. Zur Beschreibung der Elektronenaustausch-Korrelationsenergie wird die generalisierte Gradienten-Approximation (GGA) mit der Perdew-Burke-Ernzerhof (PBE) [24]-Funktion verwendet. Da die GGA-PAW-Näherung normalerweise das E . unterschätzt _g von Halbleitern wird zu deren Korrektur das Hybridisierungsfunktional HSE06 durchgeführt. Die Wirkung der vdW-Wechselwirkung [25] wird durch die DFT-D2-Methode von Grimme beschrieben. Hier wurde eine Grenzenergie von 500 eV für die ebene Wellenbasis eingestellt, um die Konvergenz der Gesamtenergie sicherzustellen. Eine Vakuumdicke von 20 Å entlang der Z Richtung der Blau-P/g-GaN-Heterostrukturen hinzugefügt, um die Wechselwirkung mit den falschen Nachbildungsbildern zu eliminieren. Die Atompositionen werden optimiert, bis die Konvergenztoleranz der Kraft auf jedes Atom kleiner als 0,001 eV/Å ist. Die erste Brillouin-Zonen-Integration wird von einem feinen Raster von 7 × 7 × 1 für die Strukturoptimierung und 21 × 21 × 1 für die elektronische Zustandsberechnung verwendet.

Ergebnisse und Diskussion

Mehrere in unserer vorherigen Arbeit gezeigte Strukturen wurden als Benchmark untersucht, um die stabilste Struktur der Doppelschichtheterostrukturen zu erhalten [18]. Die optimierten Gitterkonstanten betragen 3,25 und 3,20 für Bilayer-Blue-P bzw. g-GaN, deren Werte mit den berichteten Studien übereinstimmen [9, 26]. Die Gitterfehlanpassung beträgt nur etwa 2% [18]. Um die minimale Energiekonfiguration zu erhalten und die thermische Stabilität der Strukturen zu bewerten, wird die Blau-P-Schicht relativ zur g-GaN-Schicht verschoben und die niedrigste Energiekonfiguration um endliche Beträge gefunden δ_{x /y} . Die Entwicklung der Gesamtenergiedifferenz als Funktion von δ_x und δ_y wird in unseren früheren Studien gezeigt [18]. Abbildung 1a zeigt die atomaren Strukturen der Seiten- und Draufsicht von Doppelschicht-Blau-P auf g-GaN. Der optimale Stapelmodus von Blue-P-Doppelschichten stimmt mit dem vorherigen Papier überein [27]. Abbildung 1b zeigt den Zusammenhang zwischen der Bindungsenergie (E _b ) an der Grenzfläche und der Schichtabstand von blue-P und g-GaN (d _blau-P/g-GaN ). Seine Definition wurde in unseren früheren Studien ausführlich beschrieben [18]. Das E _b beträgt etwa 49 meV für das einlagige Blau-P mit einem Gleichgewichtsabstand von 3,57 . Für die Doppelschicht ist die Bindungsenergie fast dieselbe wie die der Einzelschicht, während der Gleichgewichtsabstand 3.52 beträgt. Diese Bindungsenergien haben dieselbe Größenordnung wie andere vdW-Kristalle, wie BP/Graphen [E _b =60 meV] [11], Blau-P/Graphen [E _b =70 meV] [6] und zweischichtiges Blau-P [E _b =25 meV] [27].

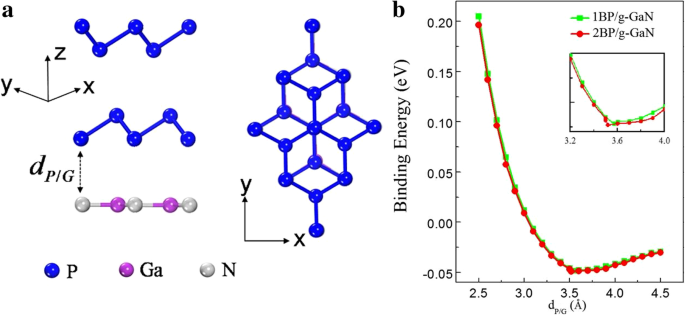
a Seitenansicht und Draufsicht der Doppelschicht Blue-P auf g-GaN. b Bindungsenergie als Funktion des Abstands d _blau-P/g-GaN für das Monolayer- und Bilayer-System. Der Einschub zeigt den Zoom nahe dem Minimum der Bindungsenergie

Abbildung 2a-b zeigt die Bandstrukturen der Monoschicht-Blau-P/g-GaN-Heterostruktur und der Doppelschicht-Blau-P/g-GaN-Heterostruktur mit E _g von 1,26 eV bzw. 1,075 eV, berechnet unter Verwendung von GGA. Für die HSE06-Methode ist das E _g beträgt 2,2 eV bzw. 1,91 eV. Bei beiden Heterostrukturen liegen die Zustände minimaler Energie im Leitungsband nahe dem Punkt M und die Zustände maximaler Energie im Valenzband am Punkt K, die beiden Punkte haben nicht den gleichen Kristallimpuls in der Brillouin-Zone. Somit ist die Bandlücke eine indirekte Bandlücke für beide Halbleiterheterostrukturen. Das E _g der Monolayer-Blau-P/g-GaN-Heterostruktur um 0,63 eV im Vergleich zu Monolayer-Blau-P (1,89 eV) verringert, während das E _g von Doppelschicht-Blau-P (1.118 eV) schrumpft 0,043 eV im Gegensatz zur Doppelschicht-Blau-P/g-GaN-Heterostruktur. Die Bandverbiegung kann aus der Differenz zwischen den Fermi-Niveaus des Blau-P mit dem g-GaN-System und dem freistehenden Blau-P erreicht werden [28]:ΔE _F =W − W _P , wobei W ist die Austrittsarbeit des zusammengesetzten Systems (blau-P/g-GaN) und W _P ist die Austrittsarbeit des unberührten Blau-P. Das ΔE _F von − 1.17 eV und − 0.81 eV für die Monoschicht-Blau-P/g-GaN-Heteroübergänge bzw. die Doppelschicht-Blau-P/g-GaN-Heteroübergänge erhalten, wie in Abb. 2c, d gezeigt. Wie man sehen kann, ist der Typ der Energiebandausrichtung die gestaffelte Lücke (Typ II) an den Grenzflächen für alle Monolayer-Blau-P/g-GaN-Heterostrukturen und die Bilayer-Blau-P/g-GaN-Heterostrukturen.

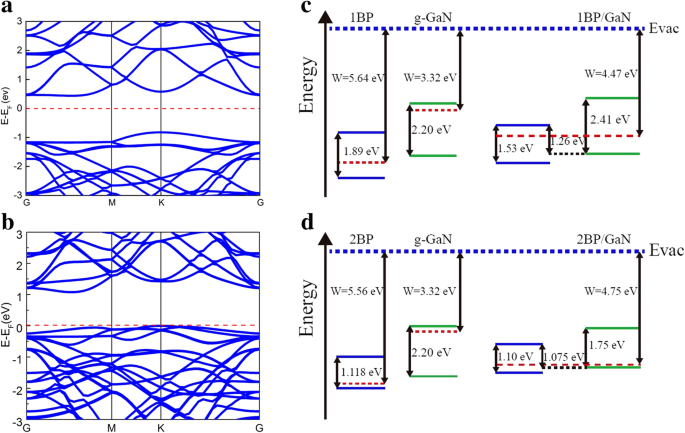
Bandstrukturen von a Monolayer-Blue-P/g-GaN-Heterostruktur und b Doppelschicht-Blau-P/g-GaN-Heterostruktur; Bandausrichtungen und Arbeitsfunktionen in Bezug auf c Monolayer-Blue-P/g-GaN-Heterostruktur und d Doppelschicht-Blau-P/g-GaN-Heterostruktur

Die Heterostruktur wird häufig einem externen elektrischen Feld ausgesetzt, um ihre elektronischen Eigenschaften abzustimmen, während sie auf nanoelektronische Bauelemente angewendet wird. Um den Einfluss des E . zu untersuchen _ext auf der elektronischen Struktur werden die Bandstrukturen mit unterschiedlichen E . berechnet _ext für die Blau-P/g-GaN-Heterostrukturen. Wie in früheren Arbeiten berichtet, kann die geometrische Struktur der Heterostruktur vernachlässigt werden, aber die Bandstruktur ändert sich stark unter verschiedenen E _ext [29]. Abbildung 3a zeigt die Entwicklung des E _g als Funktion des E _ext von − 1,0 eV/Å bis 1,0 eV/Å. Die Richtung von E _ext von oben (g-GaN-Schicht) nach unten (blau-P-Schicht) wird als Vorwärtsrichtung genommen. Es wird deutlich gezeigt, dass Monolayer-Blue-P/g-GaN- und Bilayer-Blue-P/g-GaN-Heterostrukturen eine Bandlückenmodulation mit dem E . aufweisen _ext . Für Monolayer-Blau-P/g-GaN, im Fall des Vorwärts E _ext , das E _g steigt linear mit steigendem E _ext ≤ 0,4 eV/Å (L-Anstiegsbereich). Die Monoschicht-blau-P/g-GaN erreicht ihr maximales E _g wenn E _ext =0,5 eV/Å und zeigt geringe Änderung bei E _ext liegt im Bereich 0,4 <E _ext <0,6 eV/Å (Sättigungsbereich), was die Bandverschiebungen verstärkt, um die Trennung von Elektron-Loch-Paaren zu fördern. Die anfängliche Vergrößerung in E _g wird auf das Gegengewicht von E . zurückgeführt _ext teilweise durch das eingebaute elektrische Feld (E _int ). Das E _g kommt mit zunehmendem E zu einem linear abnehmenden Bereich _ext> 0,6 eV/Å (L-Abnahmebereich). Somit zeigt die Heterostruktur ein Metallverhalten, wenn sie einem stärkeren elektrischen Feld ausgesetzt wird. Dies ist sowohl auf den dielektrischen Durchbruch als auch auf das Ladungstunneln zurückzuführen. Im Gegensatz dazu ist das E _g nimmt linear mit zunehmendem E ab _ext (L-Abnahmebereich) unter einem umgekehrten E _ext , verursacht durch die Verschiebung der Bandkante des Leitungsbandminimums (CBM) zum Valenzbandmaximum (VBM). Wenn jedoch E _ext =− 0,7 eV/Å, beginnt die Bandlücke stark abzunehmen, was möglicherweise auf den Zusammenbruch zurückzuführen ist. Wenn E _ext <− 0.8 eV/Å erfährt der Blau-P/g-GaN-Heteroübergang einen Übergang vom Halbleiter zum Metall (Metallbereich). Diese Ergebnisse zeigen, dass sowohl E _g und der Übergang von Halbleiter zu Metall der Blau-P/g-GaN-Heterostruktur hängt von der elektrostatischen Ansteuerung ab, die in elektronischen und optoelektronischen Hochleistungsgeräten verwendet werden könnte. Darüber hinaus ist die Wirkung von E _ext auf dem E _g zwischen den Doppelschichten aus Blau-P- und g-GaN-Heterostruktur ist dieselbe wie bei der Einzelschicht, jedoch mit einem kleineren elektronischen Feld für den Übergang von Halbleiter zu Metall.

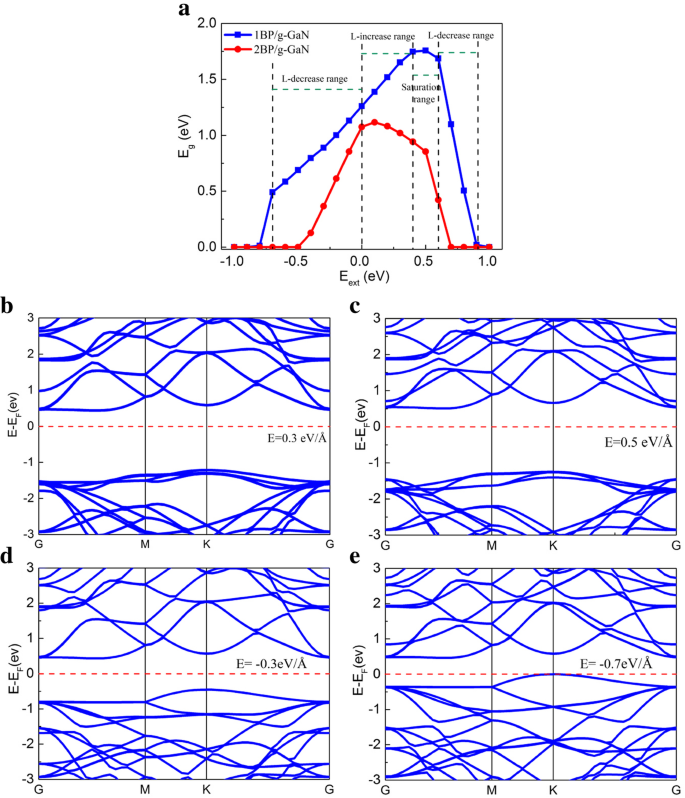
a E _g gegen E _ext von Monolayer-Blau-P/g-GaN- und Bilayer-Blau-P/g-GaN-Heterostrukturen. b –e Die Bandstrukturen der Monolayer-Blue-P/g-GaN-Heterostruktur mit E _ext von 0,3 eV/Å, 0,5 eV/Å, – 0,3 eV/Å und 0,7 eV/Å. Das E _F ist auf 0 gesetzt und wird durch die rote gestrichelte Linie angezeigt

Um die Wirkung des elektrischen Felds auf die Bandstruktur zu untersuchen, wird die Beziehung zwischen den Energiebandstrukturen und dem externen elektrischen Feld berechnet. Die Bandstrukturen der Monolayer-Blue-P/g-GaN-Heterostrukturen mit E _ext von 0.3 eV/Å, 0.5 eV/Å, − 0.3 eV/Å und 0.7 eV/Å sind in Abb. 3b–e dargestellt. In Abb. 3b-c unter den 0,3 eV/Å und 0,5 eV/Å von E _ext , das E _g steigt auf 1,651 eV und 1,757 eV an. Dies zeigt an, dass das Quasi-Fermi-Niveau der g-GaN-Monoschicht nach unten verschoben ist und das Quasi-Fermi-Niveau der Blau-P-Monoschicht nach oben angehoben wird. In Abb. 3d-e jedoch für − 0.3 eV/Å und − 0.7 eV/Å von E _ext , das E _g auf 0,888 eV und 0,49 eV verringern. Das Quasi-Fermi-Niveau von g-GaN bewegt sich nach oben und das Quasi-Fermi-Niveau von Blau-P bewegt sich nach unten. Die Ergebnisse zeigen, dass die Bandlücke linear mit der angewendeten vertikalen E variiert _ext , was auf einen riesigen Stark-Effekt hinweist [30]. Beim Anwenden eines vertikalen E _ext , würden sich die Teilbandzustände der Valenz- und Leitungsvalenz vermischen, was zu einer feldinduzierten Aufspaltung der elektronischen Niveaus führen würde. Die durch das äußere Feld induzierte elektrostatische Potentialdifferenz veränderte die elektronischen Strukturen in der Nähe des Fermi-Niveaus erheblich [31].

Abbildung 4a–d zeigt die Isofläche der Ladungsakkumulation (mit orangefarbener Farbe) und Verarmung (hellgrün), die die Änderung der Ladungsdichte des blauen P/g-GaN-Heteroübergangs mit dem E . zeigt _ext Wert von 0,3 eV/Å, 0,5 eV/Å, – 0,3 eV/Å bzw. – 0,7 eV/Å. Beim Anwenden eines Vorwärts E _ext , wie in Fig. 4a-b gezeigt, neigen positive Ladungen (Löcher) dazu, von der Blau-P-Schicht auf die g-GaN-Schicht zu übertragen, und negative Ladungen (Elektronen) werden von der g-GaN- auf die Blau-P-Schicht übertragen. Gleichzeitig ist zu erkennen, dass die Ladungsübertragungsmenge mehr als 0,3 eV/Å beträgt, wenn das elektrische Feld 0,5 eV/Å beträgt. Im Wesentlichen orientiert ein positives externes elektrisches Feld die Ladung entlang der Richtung des Spannungsfelds, wodurch die Ladung auf die Atomebene beschränkt wird, die Ladung jedoch in diesen Ebenen belassen wird, wodurch die Ladungsübertragung von Blau-P auf g-GaN erleichtert wird. Im Gegensatz dazu ist das negative E _ext induziert die Ansammlung/Verarmung von Elektronen auf der gegenüberliegenden Seite, wie in Abb. 4c-d dargestellt. Vor allem negative externe elektrische Felder positionieren die Ladung zurück zum Spannungsfeld und übertragen so die Ladung von g-GaN auf blau-P. Dementsprechend ist das Quasi-Fermi-Niveau der g-GaN-Monoschicht und E _VBM steigen, während das Quasi-Fermi-Niveau der Blau-P-Monoschicht und E _CBM abnehmen, was zu einer linearen Verringerung der Bandlücke führt. Gleichzeitig werden Elektronen von Blau-P auf g-GaN unter einem umgekehrten E . übertragen _ext . Es wurde festgestellt, dass die Menge der übertragenen Ladung mit der Zunahme der elektrischen Feldstärke zunimmt.

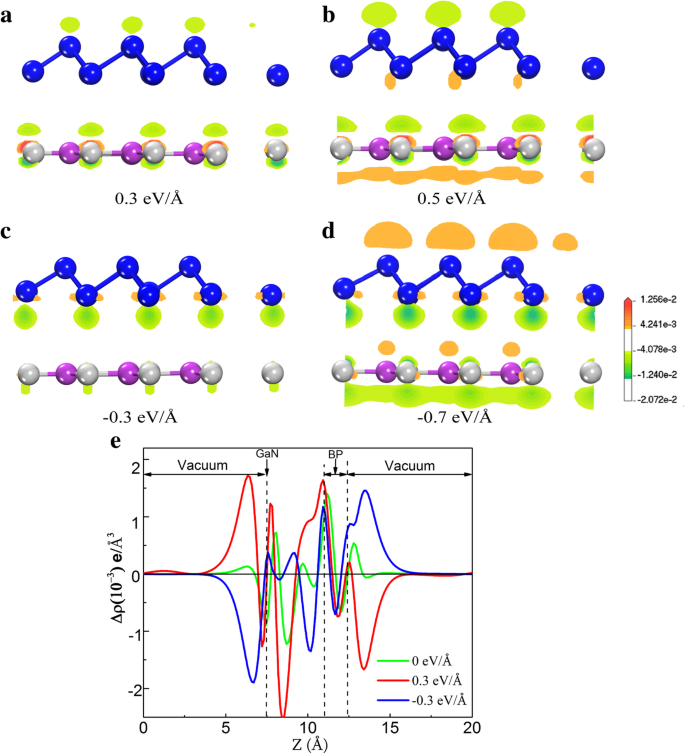
a –d Isofläche der Ladungsakkumulation und -verarmung der Monolayer-BlueP/g-GaN-Heterostruktur unter E _ext von 0,3 eV/Å, 0,5 eV/Å, – 0,3 eV/Å bzw. – 0,7 eV/Å. Orange und hellgrüne Isoflächen repräsentieren positive Ladungsakkumulation bzw. Ladungsverarmung. e Planar-gemittelte Elektronendichte Δρ(z ) bei unterschiedlichem elektrischem Feld für Monolayer-Blue-P/g-GaN

Um deutlich zu machen, wie E _ext die elektronische Eigenschaft moduliert, wird die integrierte Ladungsdichtedifferenz der Monoschicht-Blau-P/g-GaN-Heterostruktur als Funktion des senkrechten Abstands berechnet, dargestellt in Fig. 4e. Die positiven Werte in Fig. 4e zeigen eine Ladungsakkumulation an und die negativen Werte repräsentieren eine Ladungsverarmung. Für E _ext =0, die Ladungsdichtedifferenz der Heterostruktur ergibt sich aus ∆ρ =ρ_{Heterostruktur} −ρ_g-GaN −ρ_blau-P . Die Änderung der ebenen durchschnittlichen Ladungsdichtedifferenz an Grenzflächen zeigt an, dass die Elektronen von der g-GaN-Schicht zur blauen-P-Schicht über die Grenzfläche hinweg übertragen wurden, während die Löcher auf der g-GaN-Seite verblieben. Die oberflächengemittelte Differenzladung bei einem elektrischen Feld wird für 0,3 eV/Å und – 0,3 eV/Å berechnet. Das E _ext können Einfluss auf die Ladungsübertragung in der Heterostruktur nehmen. Es kann beschrieben werden als [29]

wobei \( \int {\rho}_{E_{\mathrm{ext}}}\left(x,y,z\right) dxdy\ \mathrm{and}\int {\rho}_{E_0}\left (x,y,z\right) dxdy \) sind die Ladungsdichte bei (x , y , z ) Punkt in der Superzelle der Monolayer-BP/g-GaN-Heterostruktur mit und ohne E _ext , bzw. Die Richtung der Ladungsübertragung durch das negative (blaue Linie) E _ext ist entgegengesetzt zu dem des positiven (rote Linie) E _ext . Die integrierte Ladungsdichte veranschaulicht quantitativ, dass die Menge der übertragenen Ladungen mit der Stärke des E . zunimmt _ext . Der Wert der Ladungstransfers für die blaue-P/g-GaN-Heterostruktur mit 0,3 eV/Å von E _ext größer als 0 eV/Å und – 0,3 eV/Å ist, da das positive externe elektrische Feld die Ladungen entlang der Richtung des angelegten Felds lokalisiert und die Ladungen auf g-GaN-Ebenen beschränkt.

Um die Beiträge von Blue-P und g-GaN in der Bandstruktur zu unterscheiden, wird die projizierte Zustandsdichte der Heterostrukturen berechnet und in Abb. 5a dargestellt. Es ist ersichtlich, dass der Beitrag von VBM hauptsächlich von g-GaN und der Beitrag zum Mitreißen hauptsächlich von blauem P stammt. Abbildung 5b zeigt die Isofläche der Ladungsakkumulation und -verarmung der Monoschicht-Blau-P/g-GaN und Doppelschicht-Blau-P/g-GaN unter einem externen Feld von 0.5 eV/Å bzw. 0.7 eV/Å. Aufgrund des dielektrischen Durchbruchs des Doppelschicht-Blau-P/g-GaN bei einem externen Feld von 0,7 eV/Å wäre der Strom in Bezug auf die Ladungsübertragung unter dem zunehmenden externen Feld gesättigt, was dem in Fig. 3a entspricht.

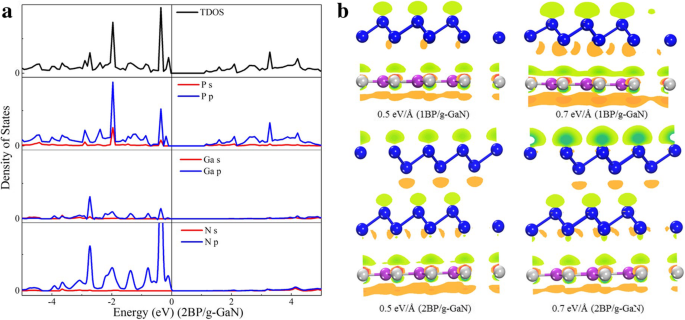
a TDOS der Bilayer-Blue-P/g-GaN-Heterostruktur. PDOS von P, Ga und N in Heterostruktur. b Isofläche der Ladungsakkumulation und -verarmung der Monoschicht-Blau-P/g-GaN-Heterostruktur unter E _ext von 0,3 eV/Å, 0,5 eV/Å, – 0,3 eV/Å bzw. – 0,7 eV/Å

Schlussfolgerung

Zusammenfassend werden die strukturellen und elektronischen Eigenschaften der vdW-Heterostrukturen Monolayer-Blue-P/g-GaN und Bilayer-Blue-P/g-GaN mithilfe von First-Principle-Rechnungen untersucht. Die Ergebnisse zeigen, dass die Monolayer-Blue-P/g-GaN-Heterostruktur ein Halbleiter mit indirekter Bandlücke mit intrinsischer Bandausrichtung vom Typ II ist. Der Bandversatz und E _g von Monolayer-Blue-P/g-GaN und Bilayer-Blue-P/g-GaN können kontinuierlich durch E . abgestimmt werden _ext , und die Beziehung zwischen E _g und E _ext weist auf einen Stark-Effekt hin. Das E _g wird Null bei − 0.8 und 0.9 eV/Å für Monolayer-Blue-P/g-GaN und − 0.5 und 0.7 eV/Å für Bilayer-Blue-P/g-GaN, was einen Übergang von Halbleiter zu Metall anzeigt.

Abkürzungen

2D:

Zweidimensional

Blau-P:

Blaues Phosphoren

BP:

Schwarzes Phosphoren

CASTEP:

Cambridge Serial Total Energy Package

CBM:

Leitungsband-Minimum

DFT:

Dichtefunktionaltheorie

GGA:

Verallgemeinerte Gradientennäherung

G-GaN:

Graphen-ähnliches GaN

MEEG:

Durch Migration verstärktes gekapseltes Wachstum

PAW:

Projektor-verstärkte Welle

PBE:

Perdew-Burke-Ernzerhof

TMDs:

Übergangsmetalldichalkogenide

VBM:

Valenzband-Maximum

vdW:

van der Waals