Plasmoninduzierte Transparenz in einer asymmetrischen Bowtie-Struktur

Hintergrund

Der elektromagnetisch induzierte Transparenzeffekt (EIT), der aus der quantenzerstörenden Interferenz zwischen zwei Pfaden in dreistufigen Atomsystemen resultiert [1, 2], zeigt enorme potenzielle Anwendungen bei langsamer Lichtausbreitung [3, 4], nichtlinearer Optik [5] und optischer Speicher [6]. In einem EIT-System reduziert der Quanteninterferenzeffekt die Lichtabsorption über einen schmalen Spektralbereich, wodurch eine scharfe Resonanz mit nahezu perfekter Transmission innerhalb eines breiten Absorptionsprofils entsteht [7]. Der EIT-Effekt reagiert jedoch sehr empfindlich auf eine Verbreiterung aufgrund von atomarer Bewegung. Die Realisierung des EIT-Effekts erfordert stabile Gaslaser und rigorose Umgebungen, was seine praktischen Anwendungen behindert. Kürzlich wurden Arten von Konfigurationen vorgeschlagen, um eine EIT-ähnliche Übertragung ohne strenge experimentelle Bedingungen nachzuahmen, einschließlich gekoppelter Mikroresonatoren [8,9,10,11,12], Split-Ring und Metamaterialien [13,14, 15,16] bestehend aus dielektrischen und metallischen Materialien. Unter diesen erfordert die auf Metamaterial basierende EIT mit periodischen Einheitsmustern ein angeregtes Signallicht, das in einer Richtung nicht parallel zur Chipoberfläche einfällt. Mit dem angeregten Signallicht, das parallel zur Chipoberfläche einfällt, sind gekoppelte Mikroresonatoren bemerkenswert, um die Anforderungen von On-Chip-Integrationsanwendungen der EIT-ähnlichen Übertragung zu erfüllen. Um den Platzbedarf von EIT-Geräten weiter zu reduzieren, wurde plasmoneninduzierte Transparenz (PIT) als Analogon zum klassischen EIT mit starker optischer Begrenzung jenseits der Beugungsgrenze für elektromagnetische Wellen vorgeschlagen [17,18,19]. Oberflächenplasmonen sind optisch induzierte Schwingungen der freien Elektronen an der Grenzfläche Metall/Dielektrikum, die einen starken optischen Einschluss und miniaturisierte photonische Komponenten aufweisen [20, 21]. In letzter Zeit sind plasmonische Wellenleiter aus Metall/Isolator/Metall (MIM) mit extrem hoher optischer Begrenzung und engerem Abstand zu benachbarten Wellenleitern ein sehr vielversprechender nanoskaliger Wellenleiter, der in der Lage ist, die Beugungsgrenze zu überwinden und vielfältige Anwendungen für plasmonische Sensoren [22], Koppler [ 23] und Filter [24]. Somit hat die MIM-basierte PIT-Übertragung ein enormes Potenzial in On-Chip-Anwendungen der optischen Kommunikation, der optischen Informationsverarbeitung und der nichtlinearen Optik.

Hier schlagen wir eine neuartige verstimmte Resonatorstruktur vor, um eine PIT-Übertragung in MIM-Wellenleitern zu erreichen. Das Bauelement mit planarer Struktur besteht aus zwei verstimmten dreieckigen Resonatoren und einem Buswellenleiter, die eine asymmetrische Bowtie-Struktur bilden, um den PIT-Effekt zu ermöglichen. Aufgrund der empfindlichen und linearen Reaktion der transparenten Spitzenwellenlänge auf strukturelle Parameter und das Medium innerhalb des Wellenleiters ermöglicht die vorgeschlagene Vorrichtung eine PIT-basierte Brechungsindexmessung. Mit seiner kompakten und einfach herzustellenden Struktur könnte das Gerät bei der photonischen Integration auf dem Chip von großer Bedeutung sein.

Methoden

Das Schema der asymmetrischen Bowtie-Struktur ist in Abb. 1 dargestellt, wobei das Hintergrundmaterial in Blau Silber ist, dessen Permittivität durch das Drude-Modell von \({\varepsilon}_r={\varepsilon}_{\infty}- beschrieben wird. {\omega}_p^2/\left({\omega}^2+ j\gamma\omega \right)\), mit ε _∞ =3,7, ω _p =9,1 eV und γ =0,018 eV. Die hier in der obigen Gleichung übernommenen Parameter passen zu den experimentellen Daten bei den optischen Kommunikationsfrequenzen [25]. Alle MIM-Wellenleiter sind mit Luft gefüllt. Der lange Streifen in der Mitte der Struktur ist der Buswellenleiter zur Lichtübertragung. Auf beiden Seiten des Busses sind Waveguides die Bowtie-Resonatoren. Die Bowtie-Resonatoren sind asymmetrisch, wobei verstimmte Strukturparameter wie Höhe und Winkel mit H . bezeichnet werden _du , H _d , θ ₁ , und θ ₂ . Die Wirbel der Dreiecke in der Bowtie liegen in der Mitte des Bushohlleiters. Somit haben die Bowtie-Resonatoren kleine Verbindungen zum Buswellenleiter, die eine effiziente Kopplung zwischen ihnen ermöglichen. Die Breite der Buswellenleiter ist auf 100 nm festgelegt und die Länge des Buswellenleiters hat außer dem Übertragungsverlust keine Auswirkung auf das PIT-Übertragungsspektrum. Daher ist seine Länge unter Berücksichtigung der Kompaktheit und Integration auf 1 μm festgelegt. Zwei Gitter an beiden Enden des Bus-Wellenleiters sollen eine Breitband- oder Wellenlängen-Sweep-Lichtquelle injizieren und das Transmissionsspektrum sammeln. Das Transmissionsspektrum wurde numerisch mit der Finite-Elemente-Methode mit Streurandbedingungen berechnet. In der numerischen Simulation wurde eine ebene Welle vom linken Gitter des Buswellenleiters durch einen Port injiziert, um grundlegende TM-Moden von SPs anzuregen. Das übertragene Licht wurde vom rechten Gitter des Bus-Wellenleiters gesammelt, der als T . definiert ist = P _aus /P _in , wobei P _in =  ∫ P oavzdS ₁ und P_out =  ∫ PoavzdS ₂; Poavz ist das z Bestandteil des zeitlich gemittelten Leistungsflusses. Die Transmissionsspektren der Struktur werden durch parametrisches Abtasten der Eingangswellenlänge erhalten. Diese asymmetrische Bowtie-Struktur könnte durch die folgenden Schritte hergestellt werden:zuerst Abscheiden eines Ag-Films mit einer Dicke von 500  nm auf einem Siliziumdioxid/Silizium-Substrat; dann Abscheiden eines Siliziumdioxidfilms mit einer Dicke von 500  nm; schließlich das erforderliche Muster einschließlich der Gitter durch EBL und Ätzen herstellen. Das vorgeschlagene Apertur-gekoppelte Schema hat möglicherweise weniger strenge Herstellungsanforderungen als Geräte, die auf evaneszenter Kopplung basieren und kann verwendet werden, um eine effiziente Kopplung in anderen wichtigen plasmonischen MIM-Strukturen zu erreichen.

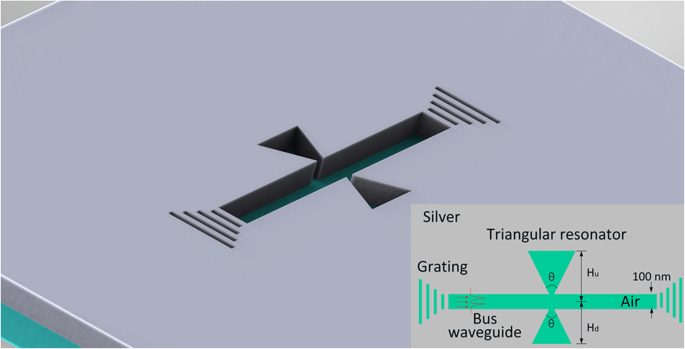
Schematische Darstellung der asymmetrischen Bowtie-Struktur

Ergebnisse und Diskussion

Im Gegensatz zu den normalen rechteckigen Resonatoren werden die dreieckigen Resonatoren in der Bowtie nicht nur durch die Seitenlänge, sondern auch durch die Winkel bestimmt. Daher untersuchen wir zunächst den Einfluss des Winkels, der mit dem Buswellenleiter verbunden ist, auf die Übertragungs- und Resonanzeigenschaften der vorgeschlagenen Struktur mit einem einzigen dreieckigen Resonator. Die Transmissionsspektren eines einzelnen dreieckigen Resonators sind in Abb. 2 dargestellt. Alle Höhen des Resonators sind auf 0,8 μm festgelegt. Der obere Winkel des dreieckigen Resonators ist mit dem Bus-Wellenleiter verbunden, wodurch elektromagnetische Energie seitlich vom Bus-Wellenleiter in den dreieckigen Resonator eingekoppelt werden kann. Somit erscheinen in den Spektren in Fig. 2 tiefe Transmissionstäler. Diese Menge, Bandbreite und Talwellenlängen werden durch die strukturellen Parameter des Resonators bestimmt. Für den Winkel von 20° gibt es zwei tiefe Transmissionstäler im Spektrum. Das Resonanztal bei der längeren Wellenlänge ist 0. Ordnung bzw. 0. Ordnung in Längs- bzw. Horizontalrichtung. Mit abnehmender Wellenlänge erlaubt die Resonatorhöhe einen weiteren Stehwellenknoten, der in Längsrichtung 1. Ordnung ist. Die Situation für den Winkel von 40° ist ähnlich der von 20°. Mit zunehmendem Winkel entsteht ein weiteres Resonanztal im Spektrum. Der größere Winkel bewirkt, dass die Modalverteilung in horizontaler Richtung aufgespalten wird, wodurch in horizontaler Richtung ein Modus höherer Ordnung erster Ordnung gebildet wird. Für einen größeren Winkel von 80° teilt sich die Mode von L:0. Ordnung in einer horizontalen Richtung auf und bildet L:1.; H:1. Modus. Somit führt der zunehmende Winkel sowohl zur Verschiebung der Wellenlänge als auch zur Aufspaltung der Modalverteilung in horizontaler Richtung, wodurch Moden höherer Ordnung gebildet werden. Die Verschiebungswellenlänge hat keinen direkten Bezug zum Winkel, da die Variation des Winkels auch die Seitenlänge verändert. Um die stetigen Resonanzeigenschaften beizubehalten, werden kleine Winkel bevorzugt.

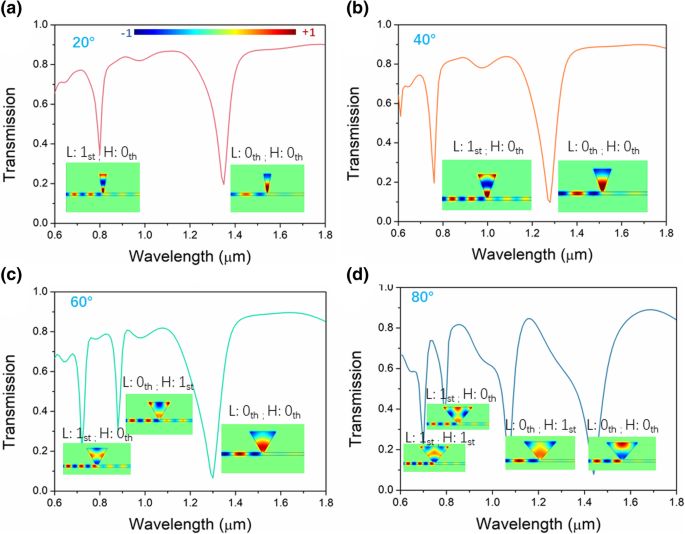
Transmissionsspektren des einzelnen Dreiecksresonators für Winkel von 20° (a ), 40° (b ), 60° (c ) und 80° (d ). Einschübe sind Magnetfeld H _z entsprechend den Resonanzwellenlängen

Die Höhe des Resonators ist der Schlüsselparameter für die Resonanzeigenschaften. Die Transmissionsspektren des Geräts mit einem einzelnen dreieckigen Resonator für eine Resonatorhöhe von 0,8 bis 1,1 µm sind in Abb. 3a dargestellt. Bei der Simulation wurde ein Hohlraumwinkel von 40° gewählt. Im Wellenlängenbereich von 1,2 bis 1,8 µm weist jedes der Spektren einen einzigen Einbruch auf, das heißt das Resonanztal. Alle Taldurchlässigkeiten liegen bei etwa 0,1. Da die elektromagnetische Verteilung von H _z bei den resonanten und nicht resonanten Wellenlängen zeigt in den Einfügungen von Fig. 3a, der Großteil der elektromagnetischen Energie wird bei der resonanten Wellenlänge in den dreieckigen Resonator eingekoppelt, während die meisten anderen Wellenlängen des eingespeisten Breitbandlichts durch den Buswellenleiter übertragen werden. Mit der inkrementellen Höhe zeigt die Talwellenlänge ein Rotverschiebungsverhalten. Wie in Fig. 3b gezeigt, ist die Verschiebungswellenlänge mit ausgezeichneter Linearität proportional zur Höhe. Die Verschiebung der Resonanzwellenlänge kann über die Stehwellenbedingung Nλ . erklärt werden _N = 2n _g L , N = (1, 2, 3…). Für ein bestimmtes N , verursacht die größere Höhe des dreieckigen Resonators die Rotverschiebung der Resonanzwellenlänge, während die kürzere Höhe die Blauverschiebung der Resonanzwellenlänge verursacht. Bei verschiedenen Winkeln bleibt das Verhältnis zwischen Resonanzwellenlänge und -höhe ähnlich, was eine Herstellung ohne strenge Anforderungen ermöglicht.

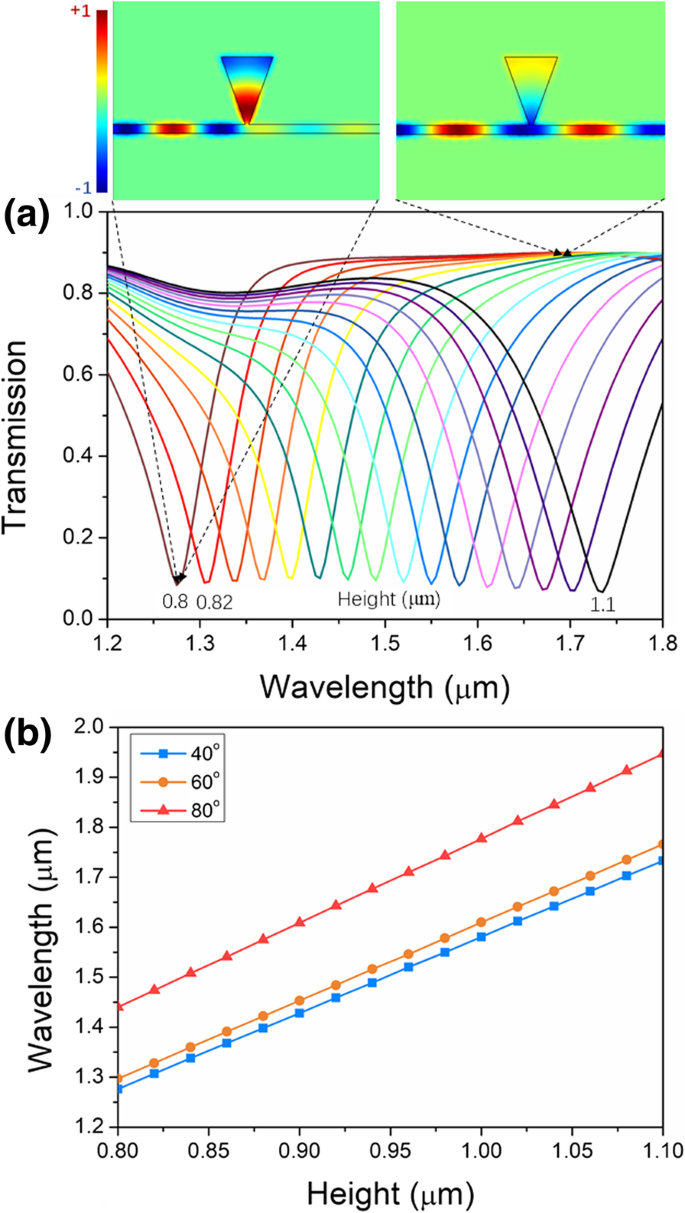
Übertragungseigenschaften des einzelnen dreieckigen Resonators. ein Transmissionsspektren des einzelnen Dreiecksresonators für verschiedene Höhen. b Höhenabhängigkeit der Resonanzwellenlänge für Winkel von 40°, 60° und 80°. Einschübe sind Magnetfeld H _z entsprechend den resonanten und nicht-resonanten Wellenlängen

Um eine PIT-Übertragung zu realisieren, ist eine starke Kopplung zwischen Doppelresonatoren mit leicht verstimmter Resonatorlänge erforderlich. Die vorgeschlagene asymmetrische Bowtie-Struktur aus dreieckigen Resonatoren mit leicht verstimmten Höhen ermöglicht eine starke Kopplung zwischen den Resonatoren. Durch Feinabstimmung der Höhen der doppelten Dreiecksresonatoren erscheint eine transparente Transmissionsspitze im verbotenen Band des einzelnen Resonators. Wie in Abb. 4a gezeigt, wurde der Winkel von 20° ausgewählt, um nur ein Tal innerhalb des Wellenlängenbereichs beizubehalten, und die Höhen wurden fein ausgewählt, um das PIT-Übertragungsband für Anwendungen in der optischen Kommunikation bei etwa 1,55 μm zu platzieren. Das Transmissionsspektrum des einzelnen Resonators mit einer Höhe von 0,93 µm ist als gestrichelte rote Linie dargestellt. Sein Tal liegt bei 1,47 μm. Um einen strukturellen Unterschied zusammen mit einem Talunterschied einzuführen, wird der einzelne Resonator mit einer Höhe von 1,02 µm verwendet, um den vorherigen Resonator zu paaren. Das Spektrum ist als blaue gestrichelte Linie dargestellt und sein Tal liegt bei 1,61 µm. Dann koppelt sich die elektromagnetische Energie innerhalb der gepaarten Resonatoren stark und bildet ein Transmissionsspektrum mit zwei tiefen Tälern und einem transparenten Peak, der als schwarze durchgezogene Linie dargestellt ist. Der transparente Peak befindet sich in der Mitte zwischen den beiden tiefen Tälern, die für einzelne Resonatoren ein verbotenes Band waren. Wie die Einschübe zeigen, koppelt im ersten Tal eine größere elektromagnetische Energie in den Resonator unter dem Buswellenleiter statt in den oberen Resonator ein. Im zweiten Tal wird stattdessen größere elektromagnetische Energie in den oberen Resonator eingekoppelt. Diese sind denen von Einzelresonatoren sehr ähnlich. An der transparenten Spitze werden etwa 75 % elektromagnetische Energie durch den Bus-Wellenleiter übertragen, und nur ein kleiner Teil der Energie wird in die asymmetrischen Bowtie-Resonatoren eingekoppelt, wodurch ein transparentes Band für die sich ausbreitende elektromagnetische Energie gebildet wird. Es ist anzumerken, dass PIT auch in asymmetrischer Bowtie-Struktur mit unterschiedlichen Winkeln erhalten werden kann. Jedoch variiert die Talwellenlänge zusammen mit der Peakwellenlänge nicht monoton mit dem Winkel, was zu einer sehr schwierigen Steuerung des transparenten Peaks führt. Darüber hinaus führt der Resonator mit größeren Winkeln, wie im obigen Abschnitt erwähnt, zu einer Mehrmodenresonanz, die für die Steuerung des PIT-Effekts nachteilig ist. Daher wird in dieser Arbeit nur die höhenunterschiedsinduzierte PIT erläutert. Der PIT-Effekt in der vorgeschlagenen asymmetrischen Bowtie-Struktur ist höhensensitiv. Um den transparenten Peak bei der optischen Kommunikationswellenlänge zu halten, werden mehrere Sätze von Höhenwerten mit Höhenunterschieden von 30 bis 190 nm ausgewählt, um den Einfluss des Höhenunterschieds auf den PIT-Effekt zu untersuchen. Wie in Fig. 4b gezeigt, kann durch feines Auswählen von Sätzen von Resonatorhöhenwerten der transparente Peak bei 1,55 μm gehalten werden. Das maximale Verhältnis von transparentem Peak zu Absorptionstal kann mehr als 10 dB betragen. Die Breite und das Transmissionsvermögen haben beide eine positive Beziehung zum Höhenunterschied. In Abb. 4c ist die Halbwertsbreite (FWHM) des transparenten Bands proportional zum Höhenunterschied mit einem ungefähr linearen Verhalten, das mit dem Verhalten in Abb. 3b übereinstimmt. Aufgrund der vorhandenen metallischen Ableitung ist die völlig transparente Übertragung des PIT-Effekts unpraktisch. Die Spitzentransmission nimmt mit zunehmender Höhendifferenz zunächst schnell zu und ist dann tendenziell über 0,8 stabil.

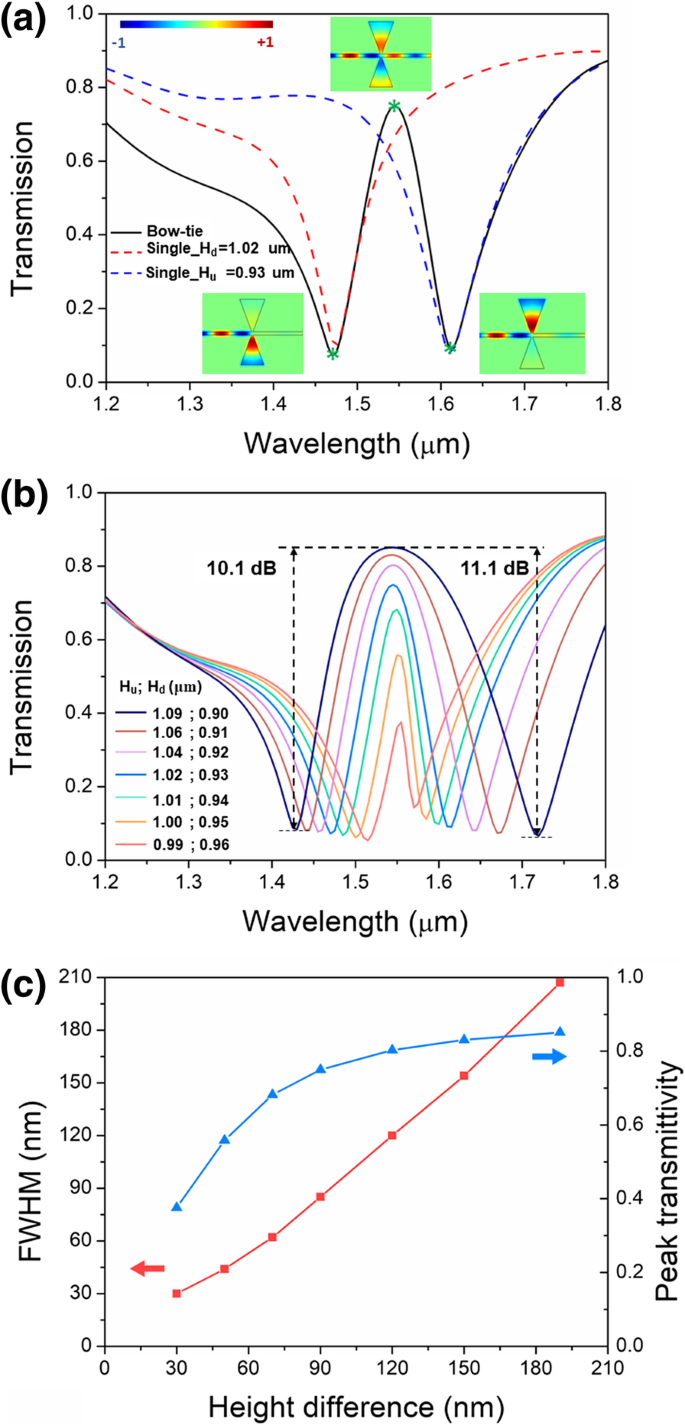
PIT-Übertragung der asymmetrischen Bowtie-Struktur. a PIT Transmissionsspektrum. b PIT-Transmissionsspektren für unterschiedliche Höhenunterschiede. c FWHM und maximale Transmission als Funktionen des Höhenunterschieds

Wie in den obigen Abschnitten ausgeführt, werden das Tal und die transparente Spitze durch die strukturellen Parameter und das Mediummaterial innerhalb des Resonators und des Buswellenleiters bestimmt. Somit ist die PIT-basierte Erfassung in der vorgeschlagenen asymmetrischen Bowtie-Struktur möglich. Bisher sind Bushohlleiter und Resonatoren mit Luft gefüllt, also leer und können als Flüssigkeitsbehälter verwendet werden. In der Simulation sind Bushohlleiter und Resonatoren mit Flüssigkeit gefüllt. Sein Brechungsindex variiert von 1,30 bis 1,40 und deckt verschiedene gängige Flüssigkeiten wie Wasser, Aceton, Methylalkohol, Ethylalkohol, Propylalkohol, Glucoselösung usw. ab [26]. Wie in Abb. 5a gezeigt, verhält sich der transparente Peak mit zunehmendem Brechungsindex der Flüssigkeit rotverschoben. Jeder Peak kann offensichtlich unterschieden werden und die Peaktransmission bleibt nahezu stabil. In Fig. 5b sind die Funktionen der Spitzenwellenlänge als Brechungsindex für Höhenunterschiede von 50 nm, 70 nm, 90 nm, 120  nm und 150  nm direkt proportional. Die Wellenlängenverschiebung weist eine ausgezeichnete Linearität auf. Die berechneten Empfindlichkeiten für die Höhenunterschiede sind alle ungefähr gleich 1140 nm/RIU, und die entsprechende Erfassungsauflösung beträgt 8,8 × 10 ⁻⁵ RIU. Der asymmetrische Bowtie-PIT-basierte Sensor hat also eine sehr hohe Empfindlichkeit und eine ausgezeichnete Immunität gegenüber Fertigungsabweichungen.

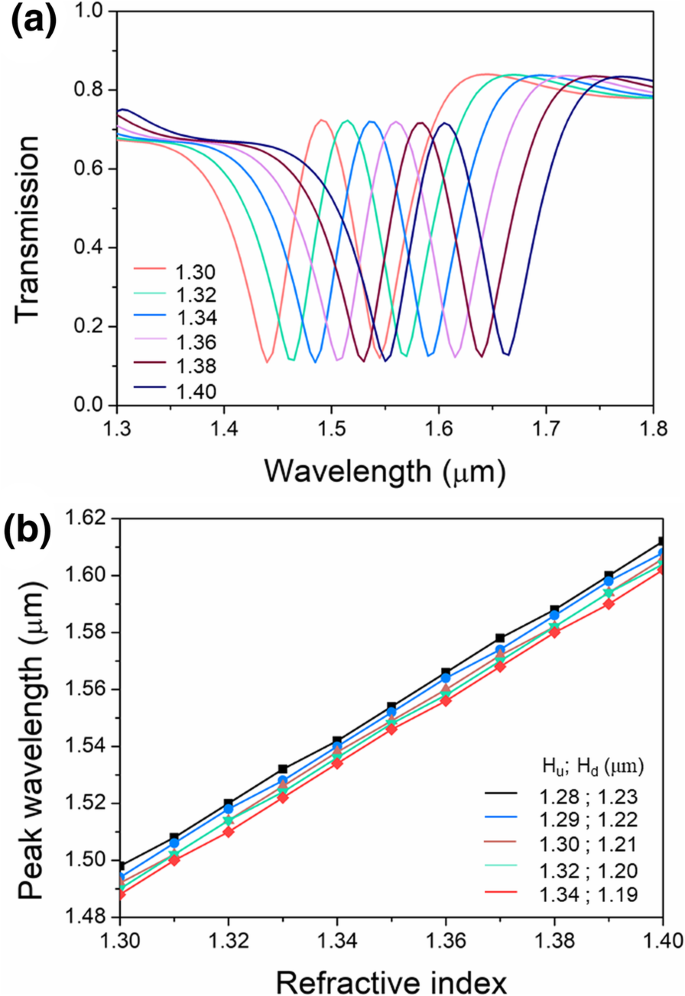
PIT-basierte Sensoreigenschaften. a Transmissionsspektren von 90 nm Höhenunterschied für Brechungsindex variierend von 80 bis 120 nm. b Abhängigkeit der Peakwellenlänge vom Brechungsindex für verschiedene Höhenunterschiede

Schlussfolgerungen

Wir haben eine asymmetrische Bowtie-Struktur vorgeschlagen, um den PIT-Effekt zu realisieren. Die Transmissionseigenschaften von Resonatoren mit unterschiedlichen Strukturparametern wurden numerisch mit der Finite-Elemente-Methode berechnet. Durch die starke Kopplung zwischen den verstimmten Dreiecksresonatoren kann im verbotenen Band einzelner Resonatoren ein transparentes Übertragungsband erhalten werden. Da alle drei Dimensionen kleiner als die Freiraumwellenlänge sind, hat das Gerät eine einfache und ultrakompakte Struktur. Das Gerät verfügt außerdem über eine ausgezeichnete Immunität gegenüber Fertigungsabweichungen, wodurch es leicht ohne strenge Anforderungen hergestellt werden kann. Darüber hinaus wurde die PIT-basierte Sensoreigenschaft unter Verwendung der vorgeschlagenen asymmetrischen Bowtie-Struktur demonstriert. Das Gerät kann eine maximale Empfindlichkeit von 1140 nm/RIU erreichen; die entsprechende Erfassungsauflösung beträgt 8,8 × 10 ⁻⁵ RIU. Die Empfindlichkeit weist eine ausgezeichnete Linearität und Konsistenz für unterschiedliche Höhenunterschiede auf. Somit bietet unsere vorgeschlagene asymmetrische Bowtie-Struktur eine neue Plattform für On-Chip-EIT-ähnliche Geräte und Brechungsindexsensoren.

Verfügbarkeit von Daten und Materialien

Der Datensatz ist uneingeschränkt verfügbar.

Abkürzungen

EIT:

Elektromagnetisch induzierte Transparenz

FWHM:

Volle Breite auf halbem Maximum

MIM:

Metall-Isolator-Metall

PIT:

Plasmoneninduzierte Transparenz