Ein entwickelter Ausdruck des chemischen Potenzials für eine schnelle Verformung in Nanopartikelelektroden von Lithium-Ionen-Batterien

Einführung

Für die Entwicklung tragbarer elektronischer Geräte, Elektrofahrzeuge und großmaßstäblicher Energiespeicher werden eine Reihe von Hochleistungselektrodenmaterialien wie Silizium vorgeschlagen, die während der Lithiierung extreme Volumenänderungen erfahren, in Lithiumbatterien eingesetzt [1,2 ,3]. Die durch homogene volumetrische Verformung induzierte Spannung wird als diffusionsinduzierte Spannung bezeichnet, die beim zyklischen Laden und Entladen zu Sprödbruch führen kann und dieser negative Effekt die Kapazität der Batterie weiter verschlechtert [4]. Verbundmaterialien von Lithium-Ionen-Batterieelektroden sind im Allgemeinen komplex und ihre Morphologien sind unterschiedlich, was es schwieriger macht, das Batterieverhalten durch Theorie oder Gleichung zu erklären. In theoretischen Modellen werden die Eigenschaften von Verbundwerkstoffen normalerweise durch Berücksichtigung der Änderungen der Elektrodenmaterialparameter in Raumkoordinaten simuliert, während der Grenzflächeneffekt von Verbundwerkstoffen vernachlässigt wird. Derzeit werden im theoretischen Modell hauptsächlich drei typische Elektrodenformen, nämlich kugelförmig, zylindrisch und plattenförmig, berücksichtigt. Darunter sind sphärische und zylindrische Formen normalerweise eindimensionale Modelle, und es sind sowohl eindimensionale als auch zweidimensionale Modelle für Plattenelektroden verfügbar. In letzter Zeit haben sich eine Reihe von Studien auf den diffusionsinduzierten Stress in Silizium-Nanopartikel-Elektroden von Lithium-Ionen-Batterien konzentriert. Yang et al. [5] präsentierten ein chemomechanisches Modell zur Untersuchung der durch Lithiierung induzierten Phasenumwandlung, morphologischen Entwicklung, Spannungserzeugung und Bruch in kristallinen Silizium-Nanodrähten. Liet al. [6] untersuchten den Einfluss der lokalen Geschwindigkeit auf diffusionsinduzierten Stress in Silizium-Nanopartikel-Elektroden. Zhao et al. [7] analysierten die diffusionsinduzierte Spannung unter Berücksichtigung der inelastischen Verformung des Wirtsmaterials. In all diesen oben genannten Arbeiten ist die grundlegende Physik die atomare oder ionische Diffusion in Festkörpern unter mehreren treibenden Kräften. Die atomare Diffusion in einem Festkörper kann die Festkörperzusammensetzung von ihrem stöchiometrischen Zustand ändern und durch die diffusionsinduzierte Spannung beeinflusst werden. Diese Wechselwirkung zwischen Spannung und Diffusion wird durch das thermodynamische Gleichgewicht der Festkörper bestimmt.

Larche und Cahn [8] entwickelten ein thermodynamisches Gerüst für Mehrkomponenten-Feststoffe, die unter nicht-hydrostatischer Belastung ein Gleichgewicht erreichen. Das Gerüst basierte auf der Annahme, dass die durch die Änderung der Zusammensetzung verursachte Verformung klein und isotrop ist. Als Ergebnis wurde ein spannungsabhängiges chemisches Potenzial eingeführt, um die Wechselwirkung zwischen Stress und Diffusion zu berücksichtigen. Wu [9] leitete ein anderes spannungsabhängiges chemisches Potential ab, an dem der Eshelby-Impulstensor anstelle der hydrostatischen Cauchy-Spannung beteiligt ist. Auf dieser Grundlage haben Cui et al.[10] haben ein neues chemisches Potenzial für die endliche Deformation von Festkörpern vorgeschlagen. Allerdings soll in diesen Arbeiten die Ableitung nur dann rigoros sein, wenn die Verformung klein oder die Verformungsgeschwindigkeit im Vergleich zur Diffusion gering genug ist. Es ist wahrscheinlich, dass es bei einer Siliziumelektrode aufgrund ihrer großen Volumenausdehnung in der Zusammensetzung (∼  400 %) einen erheblichen Fehler macht, wenn sie schnell lithiiert wird.

In dieser Arbeit präsentieren wir einen entwickelten Ausdruck des chemischen Potenzials ohne Annahme einer geringen Deformationsrate, der sich vom traditionellen Ausdruck von Cui unterscheidet [10]. Dieses Modell ist für die schnelle Deformation der Elektroden während des Ladens oder Entladens etabliert und ist unabhängig von den Morphologien, da das chemische Potential eher eine intensive Größe als eine extensive Größe ist. Der Unterschied zwischen diesen beiden Ausdrücken des chemischen Potentials in Bezug auf die Spannungsverteilung und die Li-Konzentration wird sowohl unter potentiostatischen als auch galvanostatischen Operationen in Si-Nanopartikel-Elektroden analysiert. Das Ergebnis zeigt, dass die Differenz mit zunehmender Verformungsrate zunimmt. Gleichzeitig wird ein kritischer Radius gefunden, bei dem es keinen Unterschied zwischen dem durch diese beiden Ausdrücke des chemischen Potentials verursachten Li-Fluss und der hydrostatischen Cauchy-Spannung während des größten Teils des lithiierten Prozesses gibt.

Methoden

Mechanische Gleichungen

Das Einbringen von Lithium in Elektroden kann eine Volumenänderung verursachen. Der Einfachheit halber verwenden wir zwei Möglichkeiten, die Deformation und Bewegung der Festkörper zu beschreiben, nämlich die Lagrange-Beschreibung und die Euler-Beschreibung. Die Bewegung materieller Partikel in einem Kontinuumsmedium kann beschrieben werden durch

wobei x sind die Euler-Koordinaten, X sind die Lagrange-Koordinaten und U ist das Verschiebungsfeld. Die Formänderung des Kontinuumskörpers kann durch den Deformationsgradientensor charakterisiert werden, der gegeben ist durch

wobei Grad den Gradientenoperator in der Lagrange-Beschreibung darstellt und I ist der Einheitstensor zweiter Ordnung.

Für ein kugelförmiges Teilchen sind die Lagrange-Koordinaten und die Euler-Koordinaten eines materiellen Punktes (R, , ) bzw. (r, θ, ) im Kugelsystem. Dann ist der Deformationsgradientensor F wird gefunden als

Beim Laden oder Entladen kann die Formänderung der Elektrode in zwei Prozesse eingeteilt werden:(a) eine Formänderung durch die Einlagerung von Lithium und (b) eine reversible elastische Verformung. Diese beiden Deformationsprozesse können durch zwei getrennte Gradienten-Tensoren beschrieben werden und der gesamte Deformations-Gradienten-Tensor kann geschrieben werden als

wo F ^e stellt die elastische Verformung dar, F ^c stellt die Formänderung aufgrund der Einlagerung von Lithium dar. Gleichung (4) repräsentiert den Prozess des Elektrodenmaterials vom anfänglichen (unverformten) Zustand zum aktuellen (verformten) Zustand. Unter der Annahme, dass die Formänderung aufgrund der Einlagerung von Lithium isotrop ist, F ^c kann gegeben werden durch

wobei Ω das partielle Molvolumen darstellt.

Aus Gl. (3–5), der elastische Deformationsgradientensor F ^e ist

Der gesamte Green-Lagrange-Spannungstensor E kann geschrieben werden als

wobei der elastische Dehnungstensor E ^e und diffusionsinduzierter Dehnungstensor E ^c sind

bzw.

Ersetzen von Gl. (6) in Gl. (8) sind die radialen und tangentialen Komponenten des Green-Lagrange-Dehnungstensors

Der konstitutive Zusammenhang für die Verformung kann aus der Dehnungsenergiedichte bestimmt werden als

wo W die elastische Dehnungsenergiedichte in der Lagrange-Beschreibung ist und P ist der erste Piola-Kirchhoff-Stress. Wenn das Material außerdem linear elastisch ist, ist W kann als quadratische Funktion des Green-Lagrange-Dehnungstensors geschrieben werden

Hier, E _h und ν sind Young-Modul bzw. Poisson-Zahl C ist der Steifigkeitstensor und det(F ^c ) ist die Determinante des Deformationsgradientensors für die diffusionsinduzierte Deformation.

Schließlich ist die erste Piola-Kirchhoff-Spannung gegeben durch

Kombinieren von Gl. (5), (9), (10) und (13) sind die entsprechenden Komponenten des ersten Piola-Kirchhoff (P-K) Spannungstensors

Und die erste P-K-Spannung muss die Gleichgewichtsbedingung ohne Körperkraft erfüllen

mit Anfangs- und Randbedingungen

Massentransportgleichung

Die Konzentration und der Diffusionsfluss von Lithium in Elektroden, die Funktionen von Koordinaten und Zeit sind, werden als C . bezeichnet (X , t) und J (X , t) in der Lagrange-Beschreibung, und sie sollten mit der Massentransportgleichung erfüllt sein, die geschrieben wird als

wobei Div den Divergenzoperator in der Lagrange-Beschreibung darstellt. In Anbetracht der Charakteristik der Kugelsymmetrie tritt die Diffusion nur in radialer Richtung auf und wir verwenden J (R , t), um die radiale Komponente von J . darzustellen (X , T). Im Kugelsystem gilt Gl. (18) wird

Die Diffusion von Lithium in Elektroden wird durch den chemischen Potentialgradienten angetrieben und der radiale Fluss J (R , t) ist proportional zum Gradienten des chemischen Potentials μ , als [11]

wo D ist die Diffusivität, R _g die Gaskonstante ist und T ist die Temperatur. μ ist als Abweichung der Gesamtenergiedichte von der Konzentration definiert und kann geschrieben werden als

Angenommen, die Energiedichte des Systems, , kann als Summe aus chemischer Energiedichte und Dehnungsenergiedichte beschrieben werden. Die gesamte interne Energiedichte kann also geschrieben werden als

Ersetzen von Gl. (22) in Gleichung (21), das chemische Potential μ kann gezeigt werden, dass

wobei μ ₀ (C ) und τ (E ^e , C ) sind die spannungsunabhängigen bzw. spannungsabhängigen Anteile des chemischen Potentials. Und

wobei μ ₀ eine Konstante ist, die das chemische Potential in einem Standardzustand darstellt, und γ ist der Aktivitätskoeffizient, der die Auswirkungen von Wechselwirkungen zwischen den Atomen/Molekülen darstellt. Für eine verdünnte Lösung sind Wechselwirkungen zwischen den Atomen/Molekülen vernachlässigbar; also, γ = 1.

Wir konzentrieren uns auf den stressabhängigen Teil des chemischen Potentials τ (E ^e , C), die Ableitung der Dehnungsenergiedichte W in Bezug auf die Lithiumkonzentration C. Traditionell ist Π(X , t) wird als freie Helmholtz-Energiedichte betrachtet und daher wird dieser Schritt für feste Deformation ausgeführt als [11]

Das tiefgestellte H bedeutet, dass sie durch die freie Helmholtz-Energiedichte verursacht wird. Das chemische Potenzial ist

wo σ _m ist die hydrostatische Cauchy-Spannung in der Eulerschen Beschreibung und kann erhalten werden durch

Es ist erwähnenswert, dass die Steifigkeit C des Elektrodenmaterials wird als unabhängig von der Lithiumkonzentration angenommen C in Gl. (12). Außerdem det(F ^e ) ≈ 1 wird allgemein akzeptiert, so dass es normalerweise ignoriert wird. Im Rest dieser Arbeit nennen wir Gl. (26) als traditioneller Ausdruck des chemischen Potenzials. Auf der anderen Seite (X , t) wird in einigen Studien [12, 13] zum Phasenfeldmodell als die Gibbssche freie Energiedichte angesehen, so dass wir keinen entwickelten Ausdruck von τ . erhalten können (E ^e , C) und

Das tiefgestellte G bedeutet, dass es durch die freie Energiedichte von Gibbs verursacht wird. In diesem Fall μ wird

und wir nennen Gl. (29) als der entwickelte Ausdruck des chemischen Potentials.

Die Stofftransportgleichung besteht aus Gl. (19), (20), (26) und (29) mit traditionellen und entwickelten Ausdrücken des chemischen Potenzials. Im verbleibenden Teil dieses Papiers werden wir die Auswirkungen dieser beiden Ausdrücke des chemischen Potenzials auf die diffusionsinduzierte Spannung und die Li-Konzentration bei verschiedenen Lademethoden vergleichen.

In der Thermodynamik ist die freie Helmholtz-Energie ein thermodynamisches Potenzial, das die nutzbare Arbeit misst, die aus einem geschlossenen thermodynamischen System bei konstanter Temperatur und konstantem Volumen erzielbar ist. Im Gegensatz dazu misst die freie Gibbs-Energie die maximale reversible Arbeit, die von einem thermodynamischen System bei konstanter Temperatur und konstantem Druck verrichtet werden kann. In Festkörpern mit niedrigem Spannungsniveau entspricht die Gibbssche Freie Energie ungefähr der Helmholtz-Freien Energie, da die Deformation von Festkörpern in der Regel gering ist. Diese Annahme ist aufgrund ihrer geringen diffusionsinduzierten Verformung für die meisten festen Materialien geeignet, jedoch mit Ausnahme von Silizium wegen seiner großen Volumenausdehnung während der Lithiierung. Tatsächlich finden Diffusion und Verformung gleichzeitig statt, so dass es nicht geeignet ist, davon auszugehen, dass keine Verformung stattfindet, während sich die Konzentration ändert. Trotzdem, wie aus Gl. (25) ist der traditionelle Ausdruck des chemischen Potentials immer noch genau, wenn die Deformationsrate niedrig genug ist. Es ist jedoch wahrscheinlich, dass große Fehler verursacht werden, wenn eine Si-Nanopartikel-Elektrode schnell lithiiert wird.

Die Elektrode wird mit einer konstanten Lithium-Ionen-Konzentration an ihrer Oberfläche, nämlich dem potentiostatischen Betrieb, oder mit einem konstanten Fluss an ihrer Oberfläche, nämlich dem galvanostatischen Betrieb, lithiiert. Die Randbedingungen von Gl. (19) sind

bzw. Die Anfangsbedingung wird geschrieben als

für jeden Ladevorgang. Hier, C _max ist die maximale Lithiumkonzentration des Materials und j ₀ ist eine Konstante, die den Ladestrom darstellt.

Numerische Implementierung

Es ist sehr schwierig, wenn nicht unmöglich, die analytische Lösung des obigen Systems aus partiellen Differentialgleichungen zu erhalten. Mit Gl. (1)–(3) und (13)–(18) berechnen wir die Entwicklung von diffusionsinduziertem Stress und der Lithiumkonzentration numerisch unter Verwendung der COMSOL Multiphysics Software. Die Lithiierung einer Silizium-Nanoelektrode unter potentiostatischen und galvanostatischen Operationen wird mit unterschiedlichen Ausdrucksformen des chemischen Potentials untersucht. Die Materialeigenschaften von Si und die in der Simulation verwendeten Betriebsparameter sind in Tabelle 1 aufgeführt. Der Einfachheit halber werden die entsprechenden dimensionslosen Substitutionen von Koordinaten, Spannung und Konzentration in den Abbildungen verwendet.

Um den Unterschied zwischen den verschiedenen Ausdrücken des chemischen Potentials zu verschiedenen Zeiten in der kugelförmigen Si-Elektrode zu untersuchen, wird der Ladezustand (SOC) berechnet als

Die spannungsinduzierten Diffusionsflüsse in der Lagrange-Beschreibung werden beschrieben als

repräsentiert den Fluss, der durch verschiedene chemische Potentialausdrücke verursacht wird.

Ergebnisse und Diskussion

Abbildung 1 zeigt die räumliche Verteilung der Lithiumkonzentration, Radialspannung und Ringspannung in einer kugelförmigen Si-Elektrode im galvanostatischen Betrieb an mehreren SOCs. Zum Vergleich sind die numerischen Ergebnisse sowohl mit den entwickelten als auch mit den traditionellen Ausdrücken des chemischen Potenzials enthalten und werden durch durchgezogene Linien bzw. Dreieckssymbole dargestellt. Für jeden SOC in Fig. 1a überlappt die durchgezogene Linie fast die Dreieckssymbole. Der Einfluss der unterschiedlichen Ausdrucksformen des chemischen Potentials auf die Lithiumkonzentration kann vernachlässigt werden. In Abb. 1b und Abb. 1c sind für die SOCs von 46,7% und 65,5% die durchgezogenen Linien höher als die Dreiecke in der Mitte, während sie sich außen fast überlappen, genau wie bei anderen SOCs. Insgesamt ergibt sich ein geringer Einfluss auf die Lithiumkonzentration und Spannungen im galvanostatischen Betrieb. Abbildung 2 zeigt die räumliche Verteilung der Konzentration von Lithium, radialer Spannung und Ringspannung in einer kugelförmigen Si-Elektrode unter potentiostatischem Betrieb bei mehreren SOCs. Es ist erwähnenswert, dass die Radial- und Ringspannungen sowohl in Abb. 1 als auch in Abb. 2 mit zunehmendem SOC zuerst zunehmen und dann abnehmen. Dies liegt daran, dass die Siliziumelektrode im Anfangszustand oder vollständig lithiierten Zustand spannungsfrei ist. da kein Konzentrationsgradient vorhanden ist. Im Vergleich zu Fig. 1a ist der Unterschied zwischen durchgezogenen Linien und Dreiecken in Fig. 2a größer. Aufgrund der Lithiumkonzentration an der Oberfläche ist ein konstantes C _max im potentiostatischen Betrieb ist die Aufladungsrate höher als die Deformationsrate, die des galvanostatischen Betriebs und auch die Deformationsrate. Die Gesamtverformung bei gleichem SOC ist jedoch unabhängig von der Lademethode fast gleich und dauert nur unterschiedlich lange. Es zeigt, dass der Einfluss auf die Verteilung von Lithium durch unterschiedliche Ausdrücke des chemischen Potentials nur mit der Deformationsrate und nicht mit der Deformation zusammenhängt und mit der Zunahme der Deformationsrate zunimmt. Tatsächlich zeigen bestehende Experimente, dass sich Siliziumelektroden während der Lithiierung unter bestimmten Lademodi sehr schnell verformen. Wie aus Abb. 3 [17] ersichtlich ist, ist die Si-Anode in 1 min mit einem 2-V-Potential gegenüber dem Li-Metall vollständig verformt. Unter dieser Bedingung unterscheiden sich die durch diese beiden Ausdrücke des chemischen Potentials gelösten Ergebnisse erheblich. Leider lässt sich in diesem Fall die Belastung der Elektrode nicht genau messen und kann daher nicht quantitativ mit unserem Modell verglichen werden.

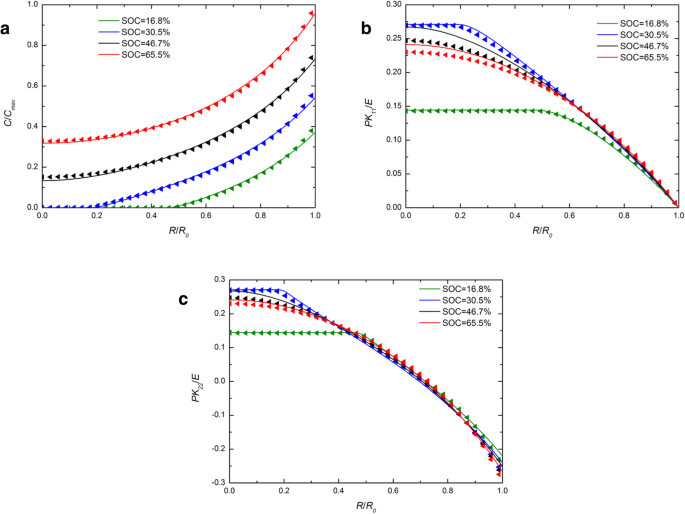
Räumliche Verteilung von (a ) die Konzentration von Lithium, (b ) Radialspannung und (c ) Ringspannung in einer kugelförmigen Si-Elektrode bei verschiedenen SOCs unter galvanostatischem Betrieb (durchgezogene Linien repräsentieren die Ergebnisse mit dem traditionellen Ausdruck des chemischen Potenzials; Dreieckslinien repräsentieren die Ergebnisse mit dem entwickelten Ausdruck des chemischen Potenzials)

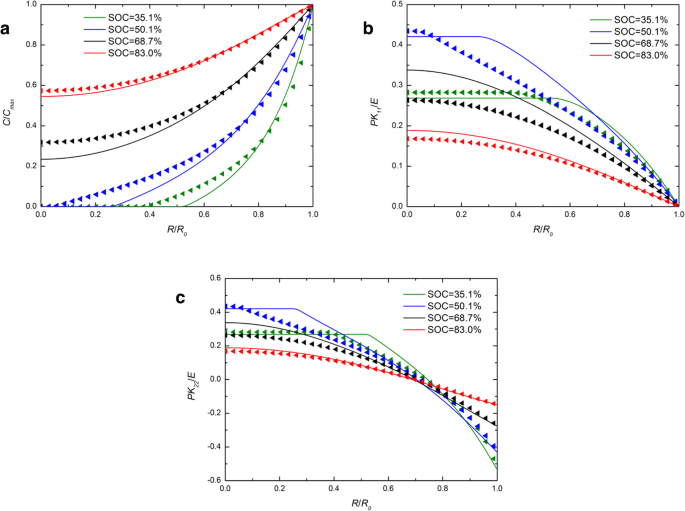
Räumliche Verteilung von (a ) die Konzentration von Lithium, (b ) Radialspannung und (c ) Ringspannung in einer kugelförmigen Si-Nanopartikel-Elektrode bei verschiedenen SOCs unter potentiostatischem Betrieb (durchgezogene Linien repräsentieren die Ergebnisse mit dem traditionellen Ausdruck des chemischen Potenzials; Dreieckslinien repräsentieren die Ergebnisse mit dem entwickelten Ausdruck des chemischen Potenzials)

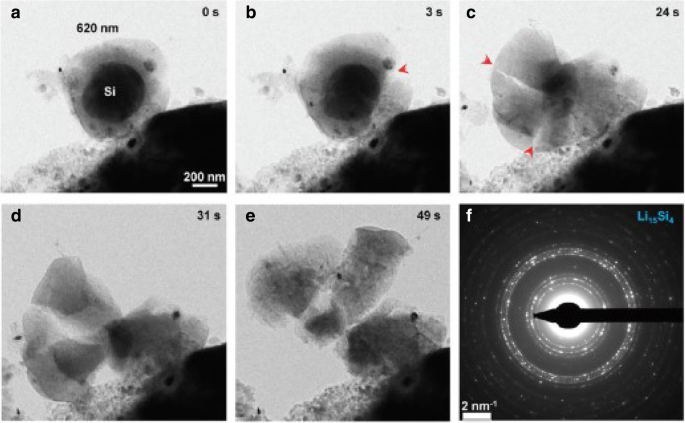
Schnelle Verformung eines freistehenden 620-nm-SiNP während der chemischen Lithiierung in 1 min. a –e Zeitlicher Ablauf der Rissbildung und des Risswachstums. f EDP ​​zeigt die Bildung von polykristallinem Li₁₅ . an Si₄ als vollständig lithiierte Phase

Abbildung 4 zeigt die räumliche Verteilung von J _H /J _G in einer kugelförmigen Si-Elektrode bei unterschiedlichen SOCs unter galvanostatischem Betrieb mit unterschiedlichen j . In Abb. 4 stimmen die durchgezogenen Linien fast mit den Dreiecken überein, was darauf hindeutet, dass unterschiedliche chemische Potentialausdrücke einen leichten Einfluss auf das Verhältnis von J . haben _H und J _G . Es ist offensichtlich, dass der Wertebereich von J _H /J _G nimmt mit steigendem Ladestrom zu. Dies liegt daran, dass der größere Ladestrom zu höheren Deformationsraten führt und daher den größeren Einfluss unterschiedlicher Ausdrücke des chemischen Potenzials verursacht. Das Verhältnis ist in der Mitte immer größer als 1 und an der Oberfläche kleiner als 1. Es deutet darauf hin, dass der Fluss, der aus der entwickelten Expression des chemischen Potenzials auf der Oberfläche erhalten wird, größer ist als der aus der traditionellen Expression erhaltene, während im Zentrum das Gegenteil zutrifft. Wir bemerken, dass sich alle durchgezogenen Linien und Dreiecke in Abb. 4 fast in einem Punkt schneiden. Außerdem beträgt das dem Schnittpunkt entsprechende Verhältnis immer ungefähr 1, unabhängig davon, mit welchem ​​Strom die Elektrode geladen wird. Es deutet darauf hin, dass es einen kritischen Radius gibt, bei dem der Fluss weniger durch die verschiedenen chemischen Potentialausdrücke beeinflusst wird. Wir nennen es die chemische Potentialunabhängige Region (CIR). Offensichtlich liegt CIR immer nahe der Oberfläche der kugelförmigen Elektrode und nähert sich der Oberfläche, wenn der Ladestrom ansteigt.

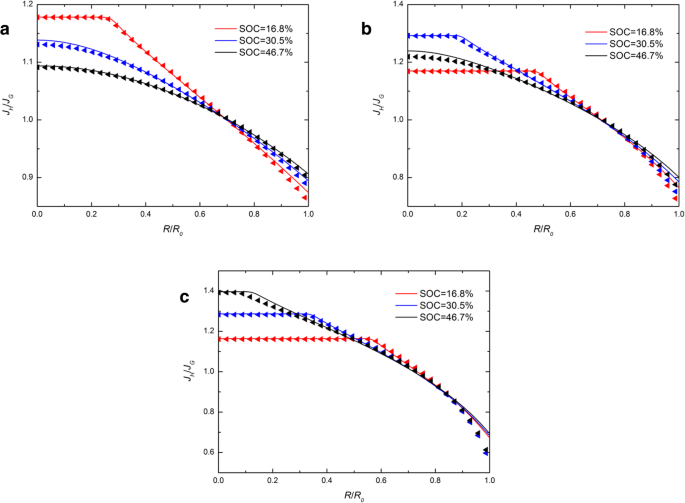
Räumliche Verteilung von J _H /J _G in einer sphärischen Si-Nanopartikel-Elektrode bei verschiedenen SOCs unter galvanostatischem Betrieb mit (a ) j =0,5j ₀ , (b ) j =j ₀ , und (c ) j =1,5j ₀ (durchgezogene Linien stellen die Ergebnisse mit dem traditionellen Ausdruck des chemischen Potenzials dar; Dreieckslinien stellen die Ergebnisse mit dem entwickelten Ausdruck des chemischen Potenzials dar)

Durch den Vergleich der traditionellen und entwickelten chemischen Potentiale in Gl. (26) und Gl. (29) ergibt sich, dass die hydrostatische Cauchy-Spannung σ_m ist der Schlüssel zum Unterschied zwischen diesen beiden Ausdrücken. Um die Ursachen von CIR zu untersuchen, wurde die räumliche Verteilung von σ_m /E in einer kugelförmigen Si-Elektrode bei verschiedenen SOCs unter galvanostatischem Betrieb mit unterschiedlichen Ausdrücken des chemischen Potentials sind in Abb. 5 und Abb. 6 dargestellt. Offensichtlich schneiden sich fast alle Kurven in einem Punkt in CIR und der hydrostatischen Cauchy-Spannung σ _m ist zu diesem Zeitpunkt nahe 0, außer zu Beginn des Ladevorgangs (SOC =6,2%). Es zeigt an, dass σ_m in CIR wird die meiste Zeit des Ladezeitraums auf einem niedrigen Niveau (fast 0) gehalten. Es kann interpretiert werden, dass die beiden chemischen Potentialausdrücke nahezu äquivalent sind, wenn die hydrostatische Spannung σ_m ist nahe 0. Dies kann teilweise erklären, warum CIR auftritt, aber es reicht nicht aus, um die Eigenschaften von Kurven auf σ_m . zu erklären . Es muss durch unsere nächste Forschung gelöst werden.

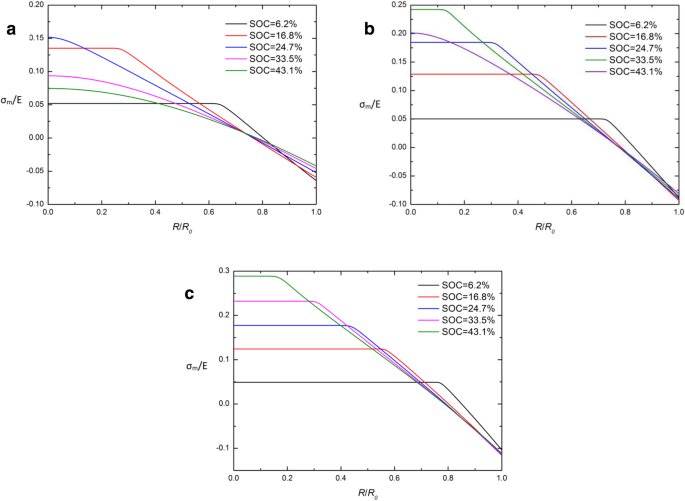
Räumliche Verteilung von σ _m /E in einer kugelförmigen Si-Nanopartikel-Elektrode an verschiedenen SOCs unter galvanostatischem Betrieb mit dem traditionellen Ausdruck des chemischen Potentials und (a ) j =0,5j ₀ , (b ) j =j _0, und (c ) j =1,5j ₀

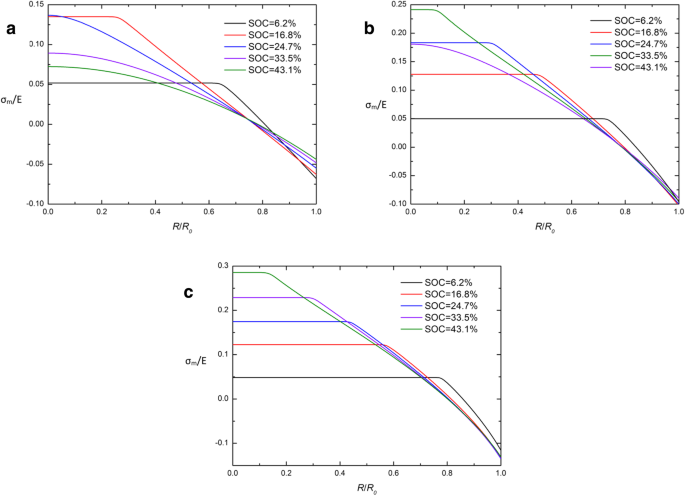
Räumliche Verteilung von σ _m /E in einer sphärischen Si-Nanopartikel-Elektrode an verschiedenen SOCs unter galvanostatischem Betrieb mit dem entwickelten Ausdruck des chemischen Potentials (a ) j =0,5j ₀ , (b ) j =j ₀ , und (c ) j =1,5j ₀ s

Schlussfolgerungen

In dieser Arbeit wird ein entwickelter Ausdruck des chemischen Potentials ohne die Annahme einer geringen Deformationsrate vorgeschlagen, der sich von dem entwickelten Ausdruck unterscheidet, der derzeit weit verbreitet ist. Der Unterschied zwischen den traditionellen und den entwickelten Ausdrücken des chemischen Potentials bei der Spannungs- und Konzentrationsverteilung in Si-Nanopartikel-Elektroden wird sowohl unter potentiostatischen als auch galvanostatischen Operationen diskutiert.

Das Ergebnis zeigt, dass der Effekt durch unterschiedliche chemische Potentialausprägungen im galvanostatischen Betrieb vernachlässigt werden kann, im potentiostatischen Betrieb jedoch signifikant ist. Es wurde festgestellt, dass der Effekt nur mit der Deformationsrate und nicht mit der Deformation zusammenhängt und mit zunehmender Deformationsrate größer sein kann. Unter Berücksichtigung der Annahme einer geringen Deformationsrate bei der traditionellen chemischen Potentialausprägung wird angenommen, dass die Ergebnisse, die durch die entwickelte chemische Potentialausprägung erhalten werden, zuverlässiger sind. In der Nähe der Nanopartikel-Elektrodenoberfläche befindet sich ein chemischer potentialunabhängiger Bereich (CIR), in dem der durch traditionelles und entwickeltes chemisches Potential verursachte Fluss während des größten Teils des lithiierten Prozesses fast gleich ist. Außerdem liegt CIR mit steigendem Ladestrom näher an der Oberfläche. Ein ähnliches Phänomen tritt auch in den hydrostatischen Spannungskurven von Cauchy auf. Die hydrostatische Cauchy-Spannung σ_m hält eine Konstante und wird höchstens auf einem niedrigen Niveau (fast 0) in CIR gehalten, unabhängig davon, welcher chemische Potentialausdruck verwendet wird. Solche Ergebnisse wurden in der Literatur noch nicht berichtet.

Verfügbarkeit von Daten und Materialien

Die im Rahmen der aktuellen Studie analysierten Datensätze sind auf begründete Anfrage beim entsprechenden Autor erhältlich.

Abkürzungen

CIR:

Eine Region, in der der durch diese beiden Ausdrücke des chemischen Potentials verursachte Diffusionsfluss nahezu gleich ist