Ein transienter Spannungsregler mit Stabilität und Verstärkung der Stromversorgungsunterdrückung

Einführung

In modernen System-on-Chip-Designs (SoC) im Nanometerbereich erfordern verschiedene Unterblöcke normalerweise unterschiedliche Versorgungsschienen, um bestimmte Funktionen zu erreichen. Außerdem muss das gesamte SoC-System möglicherweise in einem weiten Eingangsspannungsbereich betrieben werden und dennoch eine hohe Leistung bieten, die von den sich ändernden Versorgungsbedingungen unbeeinflusst bleibt [1]. Daher kann ein in Nanometer-Technologie implementierter Spannungsregler mit breitem Eingangsspannungsbereich (VR) einer der am besten geeigneten Kandidaten für diese Art von Anwendungen sein. Im Vergleich zu seinem schaltenden Gegenstück, wie Schaltregler und Ladungspumpe, hat linearer VR den Vorteil hoher Präzision, geringem Ausgangsrauschen und kompakter Größe. Die meisten linearen VRs erfüllen ihre Spannungsregelungsfunktion mit einer einzigen Spannungsversorgung, aber nur wenige können die Kombination aus breitem Stromversorgungsbereich, geringem Rauschen, schnellen Transienten, hoher Belastbarkeit und zusätzlichen Schutzfunktionen erreichen [2,3,4] .

Um einen großen Stromversorgungsbereich zu realisieren, ist die Verwendung von Transistoren erforderlich, die hohen Spannungsbelastungen standhalten. Diese Art von Transistoren nimmt jedoch normalerweise mehr Fläche ein und weist eine schlechtere Leistung im Vergleich zu den Standardtransistoren auf. Zwei der existierenden Lösungen, um den Einsatz von Hochspannungstransistoren zu reduzieren, sind das Vorreglerverfahren [5, 6] und das gestapelte Niederspannungstransistorverfahren [7, 8]. Ersteres verwendet einen zusätzlichen Vorregler, um eine interne Versorgungsspannung für den Kernregler bereitzustellen. Letztere implementiert gut konstruierte gestapelte Niederspannungstransistoren, um die Klemmenspannungen der Transistoren innerhalb der technologischen Grenzen zu halten [7]. Diese Verfahren begrenzen jedoch den Spannungsspielraum. Dieses Papier verwendet die Self-Power-Technik (SPT), um einen großen Stromversorgungsbereich zu erreichen, was bedeutet, dass die meisten Kernmodule in der Regelschleife von der geregelten Ausgangsspannung des vorgeschlagenen VR versorgt werden [9]. Ohne zusätzliche Schaltung kann die Leistung von VR durch SPT verbessert und auch die Anzahl der Hochspannungsgeräte reduziert werden.

Durch die Verwendung von SPT wird die erste Verstärkungsstufe des Fehlerverstärkers (EA) von der geregelten Ausgangsspannung des vorgeschlagenen VR versorgt. Durch sorgfältiges Entwerfen der zweiten Stufe des EA hat das Hochfrequenzrauschen der Eingangsspannung wenig Einfluss auf die Ausgangsspannung des EA. Darüber hinaus wird in diesem Papier die Architektur des N-Typ-Leistungstransistors verwendet. Daher weist der vorgeschlagene Regler eine hohe Stromversorgungsunterdrückung (PSR) und ein gutes Rauschverhalten auf [10,11,12,13,14,15].

Ein schnelles Einschwingverhalten ist auch ein wichtiger Index, um die Leistung von VRs zu messen [16,17,18,19,20], die normalerweise durch Hinzufügen einer zusätzlichen Beschleunigungsschleife erreicht wird [21]. In diesem Beitrag wird die transiente Verbesserung durch dynamische Belastungstechnik (DLT) realisiert. Während des Einschwingvorgangs führt DLT einen zusätzlichen Strom ein, der entsprechend den Lastbedingungen geändert wird, um als dynamische Last zu wirken, durch die das Über- und Unterschwingen der geregelten Ausgangsspannung unterdrückt werden kann [9].

Mit Hilfe von DLT wird die Schleifenstabilität in einem weiten Lastbereich verstärkt, da der zusätzliche Laststrom die Variation der nicht dominanten Polstellung reduzieren kann. Um die Schleife stabil zu machen, wird auch eine Miller-Kompensation mit Nullungswiderstand verwendet, um einen Niederfrequenzpol und eine zusätzliche Nullstelle zu erzeugen, um den Ausgangspol zu kompensieren. Außerdem führt eine Widerstandsreihe mit dem Ausgangskondensator eine weitere Nullstelle ein, um den Pol zu kompensieren, der durch die parasitäre Gate-Kapazität des Leistungstransistors erzeugt wird [6, 9, 22, 23].

Schließlich soll eine eingebettete Strombegrenzungsschleife Überstromschäden vermeiden und die Zuverlässigkeit des vorgeschlagenen VR verbessern [9, 24,25,26,27].

Dieses Papier ist wie folgt aufgebaut. Das Prinzip und der Mechanismus des vorgeschlagenen VR werden im Abschnitt „Methode“ erläutert, einschließlich der Überstromschutzschaltung (OCP), der DLT- und Transientenverbesserungsschaltung, der Stabilitätsverstärkungsmethode und der PSR-Analyse. Die Leistungsergebnisse und Vergleiche mit anderen verwandten veröffentlichten Literaturstellen sind im Abschnitt „Ergebnisse und Diskussion“ aufgeführt. Der Abschnitt "Schlussfolgerung" zieht die Schlussfolgerung der vorgeschlagenen VR.

Methode

Die detaillierte Schaltung des vorgeschlagenen VR ist in Abb. 1 gezeigt. Standard-Niederspannungs-MOS-Transistoren, Hochspannungs-Transistoren, BJTs, N-Typ-Verarmungs-LDMOS-(lateral diffundierte MOS)-Transistoren und Dioden werden als Mn , HVn , Qn , DNn , und Dn , bzw. in der Abbildung, wobei n ist die Sequenznummer des entsprechenden Geräts.

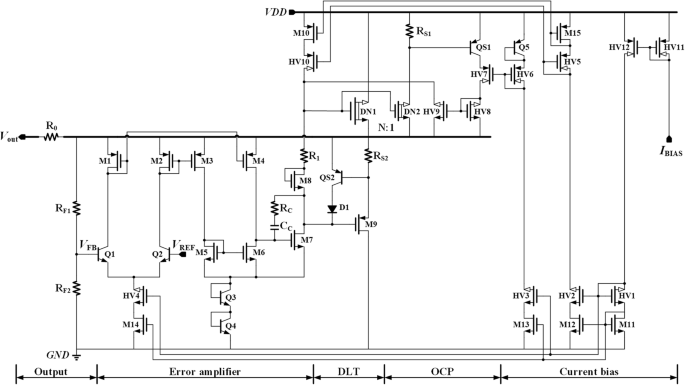
Die detaillierte Schaltung des vorgeschlagenen VR

Die vorgeschlagene VR umfasst hauptsächlich fünf Untermodule:Current Bias, OCP, DLT, EA und Ausgangsstufe. Die Stromvorspannungsschaltung liefert Vorspannungsstrom für das gesamte Reglersystem [12, 14]. Die Referenzspannung kann auf viele verschiedene Arten erzeugt werden [1], die detaillierte Schaltung ist hier nicht dargestellt. Eine eingebettete Strombegrenzungsschleife fungiert als OCP-Schaltung, um den Laststrom auf einen voreingestellten Wert zu begrenzen. Die Transientenverstärkungsschaltung, die von DLT implementiert wird, erreicht die Über- und Unterschwingungsunterdrückung durch adaptives Ändern des Laststroms während des Transientenvorgangs. Die Gegenkopplungsregelschleife wird von EA und der Ausgangsleistungsstufe gebildet, um die Ausgangsspannung einzustellen. Angenommen, die Ausgangsspannung V _AUS und damit die Rückkopplungsspannung V _FB kleiner als der gewünschte Wert wäre, würde die Gatespannung des Leistungstransistors DN1 mit Hilfe der Regelschleife hochgezogen, um die Ausgangsspannung zu erhöhen und umgekehrt. Schließlich kann sich die Ausgangsspannung bei

In Fig. 1 ist zu erkennen, dass die Ausgangsspannung des vorgeschlagenen VR auch die erste Verstärkungsstufe von EA versorgt, die als SPT bezeichnet wird. Mit dieser Power-Multiplexing-Technik können die meisten Geräte in der Regelschleife durch Niederspannungsgeräte implementiert werden. Im Vergleich zu ihren Hochspannungs-Gegenstücken haben Niederspannungsgeräte eine höhere Leistung, niedrigere Kosten und eine kleinere Fläche, wodurch die vorgeschlagene Regelschleife eine gute Regelfähigkeit viel einfacher erreicht. Was die zweite Stufe von EA betrifft, werden Q3 und Q4 hinzugefügt, um die Masseversorgungsschiene anzuheben, die verwendet wird, um die Drain-Source-Spannung von M7 zu begrenzen, V_{DS_M7} . Mit anderen Worten, Q3 und Q4 können M7 vor einem hohen Spannungsdruck schützen.

Der Einfachheit halber wird die vereinfachte Schaltung verwendet, um die Innovationsideen in der anschließenden Analyse zu veranschaulichen.

Vorgeschlagener OCP-Circuit

Abbildung 2 zeigt die vorgeschlagene OCP-Schaltung. Die vorgeschlagene Strombegrenzungsschleife kann den Betriebsmodus entsprechend unterschiedlichen Lastbedingungen automatisch ändern. Der maximale Strom des vorgeschlagenen VR kann begrenzt werden, indem die Gate-Spannung des Leistungstransistors reduziert wird, wenn eine Überlastung auftritt.

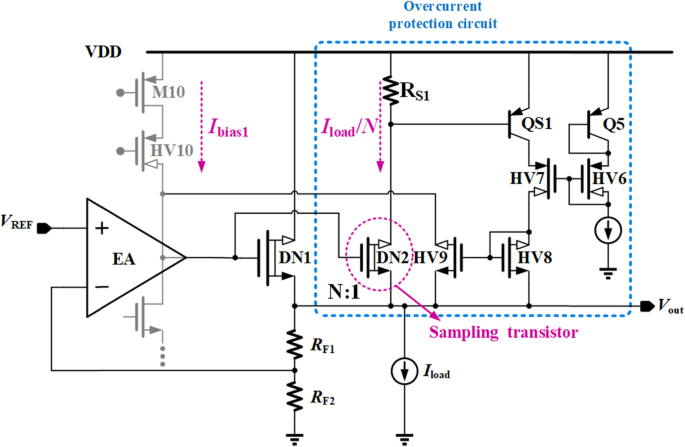
Prinzip des vorgeschlagenen OCP

Der Mechanismus des vorgeschlagenen OCP ist wie folgt. Der Abtasttransistor DN2 erfasst proportional den durch DN1 fließenden Strom, der ungefähr gleich dem Laststrom I . ist _Laden , wodurch der Spannungsabfall über R _S1 , V _RS1 , spiegeln den Laststrompegel wider. Einmal V _RS1 die Einschaltspannung von QS1, HV8 und HV9 erreicht, bildet einen Stromspiegel, um einen Strom von der zweiten Stufe von EA zu umgehen. Dann kann die Gate-Spannung von DN1 heruntergezogen werden, um den Laststrom auf einen voreingestellten Wert zu begrenzen, der ausgedrückt werden kann als

wo N ist das Größenfaktorverhältnis von DN1 zu DN2. Der Zweck von Q5 und HV6 besteht darin, HV7 eine geeignete Vorspannung bereitzustellen und somit QS1 vor Überspannungszuständen zu schützen.

Im vorgeschlagenen OCP gibt es eine eingebettete negative Rückkopplungsschleife. Die Schleifenverstärkung T und der dominante Pol p _dominant dieser Strombegrenzungsschleife kann gegeben werden durch,

wo g _{m_DN2} und g _{m_QS1} sind die Steilheit von DN2 bzw. QS1. R _{gate_OC} ≈ (g _{m_HV10} r _{o_HV10} r _{o_M10} ) || r _{o_M7} || r _{o_HV9} und C _Tor ≈ C _{gs_DN1} sind der äquivalente Ausgangswiderstand bzw. die äquivalente Kapazität am Gate-Knoten des Leistungstransistors DN1, wenn ein Überstrom auftritt. Wenn der vorgeschlagene VR normalerweise ohne Überstrom arbeitet, befindet sich HV9 im Grenzbereich und somit der äquivalente Ausgangswiderstand am Gate-Knoten von DN1 namens R _Tor kann ausgedrückt werden als [(g _{m_HV10} r _{o_HV10} r _{o_M10} ) || r _{o_M7} ].

Vorgeschlagene DLT- und Transientenverbesserungsschaltung

Abbildung 3 zeigt die Transientenverbesserungsschaltung mit DLT. Da der Laststrom proportional zu Vgs_DN1 und umgekehrt proportional zu Vsg_M9 ist, ist der durch M9 fließende Strom im Leichtlastzustand größer und unter dem Schwerlastzustand nahe Null. Daher kann, wenn der Laststrom ansteigt, ein verringerter Strom in die Gesamtausgangslast eingeführt werden. Durch diese Methode kann diese Schaltung an eine dynamische Last angeglichen werden, was sowohl für die transiente Verbesserung als auch für die Stabilitätserhöhung der Regelschleife hilfreich sein kann.

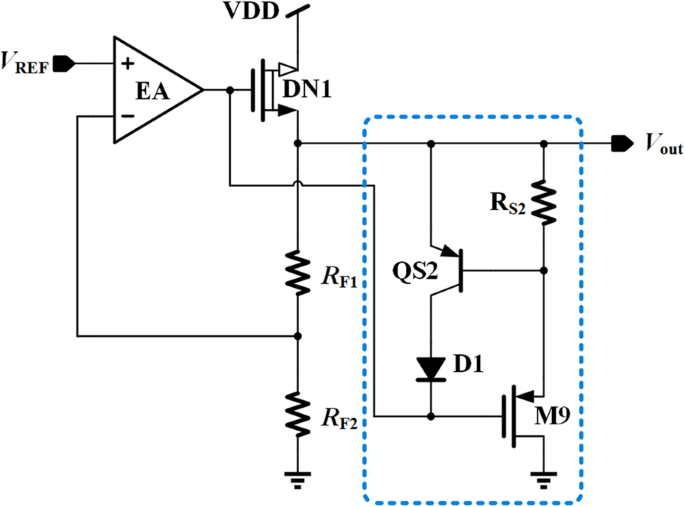
Die vorgeschlagene Schaltung zur Verbesserung der Transienten

Das detaillierte Funktionsprinzip der transienten Verbesserung ist wie folgt. Wenn der Laststrom einen plötzlichen Abfall erfährt, ändert sich der durch den Leistungstransistor DN1 fließende Strom aufgrund der begrenzten Schleifenanpassungsfähigkeit und Anstiegsgeschwindigkeit nicht sofort. Dieser Strom, in Abb. 4a als gelber Pfad dargestellt, verursacht ein Überschwingen der Ausgangsspannung und erhöht somit den Spannungsabfall an R _S2 und M9. Dann fließt ein zusätzlicher Strom durch R _S2 und M9, in Fig. 4a als blauer Pfad gezeigt, wird am geregelten Ausgang erzeugt, um den unerwünschten gelben Pfadstrom auszulöschen. Daher wird die Ausgangsspannungsspitze effektiv reduziert.

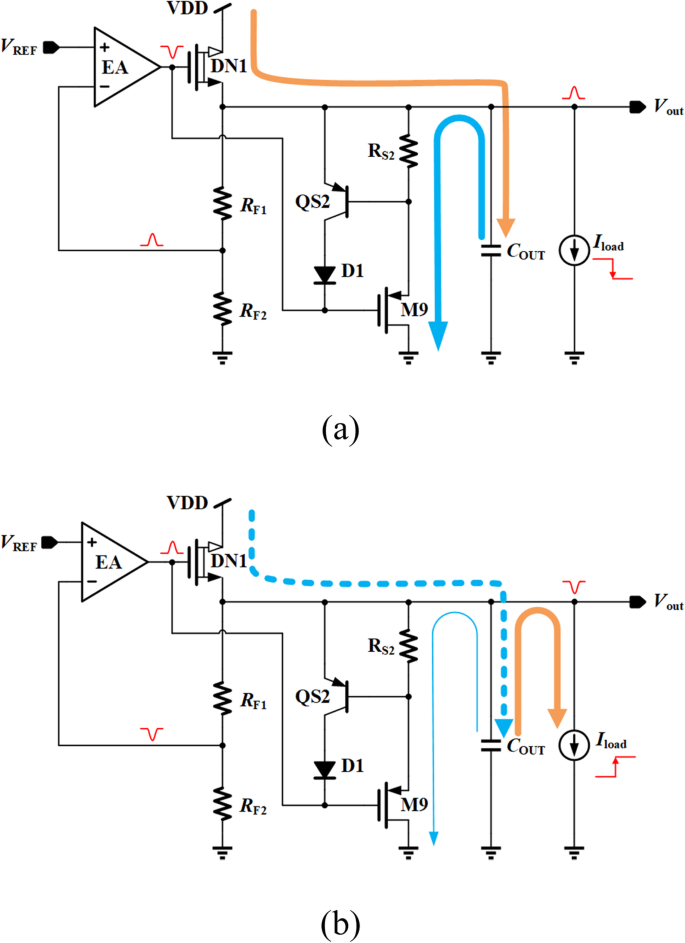
Vorübergehende Reaktion der vorgeschlagenen VR. a Stromänderung bei schwerer zu leichter Last. b Stromänderung bei leichter bis schwerer Last

Abbildung 4b zeigt den Fall einer Stromänderung von leichter zu schwerer Last, bei der ein Unterschwingen am geregelten Ausgang auftritt und dann der Strom durch R fließt _S2 und M9 nimmt ab. Dies kann einer reduzierten Strombelastung entsprechen, so dass der Nettostrom, der durch den Leistungstransistor DN1 fließt, erhöht wird und die Unterschwingungsspannungsunterdrückung erreicht werden kann.

Um M9 vor Überstrom zu schützen, werden QS2 und D1 hinzugefügt. Wenn die Spannung an R _S2 größer als die Einschaltspannung von QS2 ist, fließt der zusätzliche Strom in QS2 und D1. Der maximale Strom in M9 ist eingestellt auf

Der Zweck von D1 besteht darin, zu verhindern, dass QS2 in den umgekehrten Verstärkungsbereich fällt und ein umgekehrter Strom darin fließt, was ein anormaler Zustand der M9-Strombegrenzungsfunktion ist.

Stabilitätssteigerung der vorgeschlagenen VR

Wie in Abb. 5 gezeigt, gibt es drei Pole ω _p1 , ω _p2 , und ω _p3 , und zwei Nullen ω _z1 und ω _z2 im Regelkreis, und die Regelkreisverstärkung des vorgeschlagenen VR ist

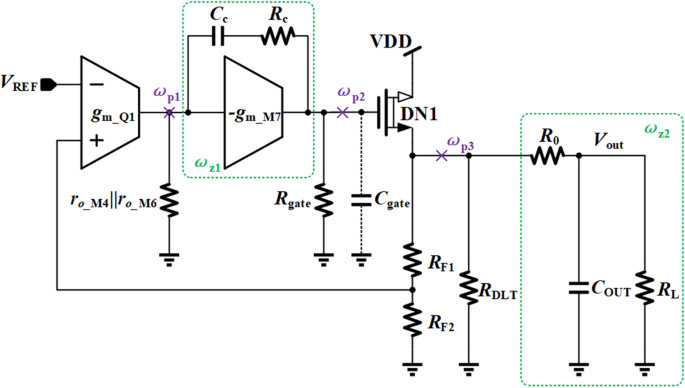
Pol- und Nullstellenverteilung der vorgeschlagenen VR

wo A _O die Open-Loop-Verstärkung des VR ist und β ist der Rückkopplungskoeffizient,

wo A _CD0 ≈ 1 ist die Niederfrequenzverstärkung der Leistungsstufe, die als Spannungsfolger arbeitet und A _E0 ist die Niederfrequenzverstärkung des EA,

Unter Berücksichtigung des Miller-Effekts und der parasitären Kapazität am Gate-Knoten von DN1 werden die Pole und Nullstellen als [13]

wo R _DLT der äquivalente Widerstand der transienten Verstärkungsschaltung ist; C _AUS ist der Ausgangskondensator des vorgeschlagenen VR.

Da der Kompensationskondensator C _C wird vergrößert um (g _{m_M7} R _Tor ) aufgrund des Miller-Effekts am Knoten p1, der Pol ω _p1 ist der dominierende Pol. Der zweite Pol sollte ω . sein _p3 , weil C _AUS liegt normalerweise im Bereich von mehreren Mikrofarad. Obwohl der parasitäre Kondensator C _Tor relativ groß ist, ist sie immer noch kleiner als sowohl die äquivalente Kapazität am Knoten p1 als auch der Ausgangskondensator. Außerdem beträgt der Widerstand am Knoten p2 nur 1/g _{m_M7} . Daher ist der Pol ω _p2 befindet sich auf hoher Frequenz. Die Null ω _z1 besteht darin, den mittleren Frequenzpol ω . auszulöschen _p3 . Der Widerstand R ₀ erzeugt eine Null ω _z2 um den internen parasitären Pol zu kompensieren ω _p2 . Die Stabilität des vorgeschlagenen VR kann als Widerstand R . verbessert werden ₀ zunehmend. Widerstand R ₀ erhöht den Fehler der Ausgangsspannung aufgrund des durch den Laststrom verursachten Spannungsabfalls. Daher Widerstand R ₀ sollte auf einen vernünftigen Wert eingestellt werden, um einen guten Kompromiss zwischen der Genauigkeit der Ausgangsspannung und der Schleifenstabilität zu erzielen.

Bei einem herkömmlichen Spannungsregler ohne DLT weist der Pol am Ausgangsknoten eine andere Frequenz auf, da sich die Laststromänderung durch die induzierte Steilheitsänderung des Leistungstransistors ändert. Wenn der Laststrom ansteigt, wird die Steilheit des Leistungstransistors g _{m _DN1} wird zunehmen, und somit bewegt sich der Ausgangspol in Richtung hoher Frequenz, während andere Nullstellen und Pole an derselben Position bleiben, wie in Fig. 6a gezeigt. Dies kann die Frequenzkompensation des Systems erschweren und das Einschwingverhalten im Leichtlastzustand verlangsamen. Im Ernst, das System könnte instabil sein.

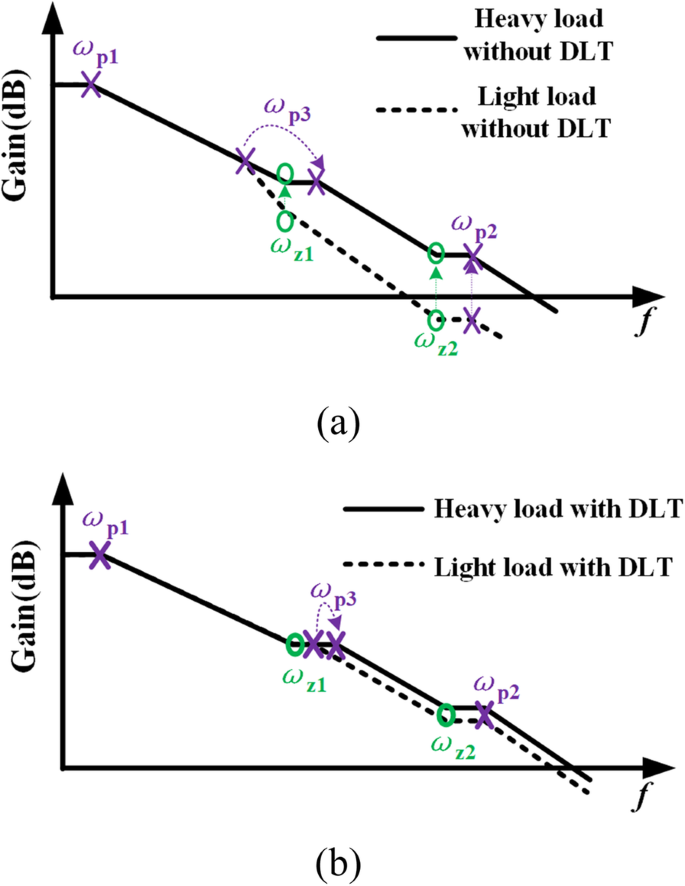
Frequenzgang des Spannungsreglers. a Spannungsregler ohne dynamische Lasttechnik. b Der vorgeschlagene Spannungsregler mit dynamischer Lasttechnik

Mit Hilfe des vorgeschlagenen DLT weist das vorgestellte VR eine bessere Stabilität bei unterschiedlichen Belastungen auf. Wie zuvor analysiert, nimmt der Strom durch den dynamischen Lastkreis ab, wenn der Laststrom im stationären Zustand ansteigt und umgekehrt. Da dieser Strom von DN1 bereitgestellt wird, kann er die Steilheitsschwankungen von DN1 innerhalb eines breiteren Laststrombereichs unterdrücken, was für die Systemstabilität und Bandbreitenkonstanz während eines breiteren Lastbereichs bei Verwendung des vorgeschlagenen DLT hilfreich ist. Der Frequenzgang des vorgeschlagenen VR ist in Abb. 6b dargestellt, was die Stabilität mit schnellem Einschwingverhalten garantieren kann.

Der Ausgangskondensator setzt die Position der Nullstelle ω _z2 . Durch eine vernünftige Platzierung des Nullpols hat das System eine bessere Stabilität bei unterschiedlichen C _AUS .

PSR-Analyse der vorgeschlagenen VR

PSR ist einer der kritischen Parameter zur Messung der Leistung von Spannungsreglern und bezieht sich auf die Unterdrückungsfähigkeit gegenüber hochfrequenten Welligkeiten und Rauschen, die von der Versorgungsspannung herrühren. In diesem Abschnitt wird die von Gupta 12 vorgeschlagene PSR-Analysemethode übernommen, deren Hauptidee darin besteht, das gesamte Reglersystem in ein Spannungsteilermodell zu vereinfachen. Wie in Abb. 7 gezeigt, gibt es zwei Rauschpfade von V _dd zu V _aus :Pfad 1 überträgt das Rauschen vom Drain des Leistungstransistors DN1 direkt auf V _aus; Pfad 2 führt von der zweiten Stufe von EA zum Gate des Leistungstransistors DN1. Die Wirkung von Pfad 2 kann ausgedrückt werden als

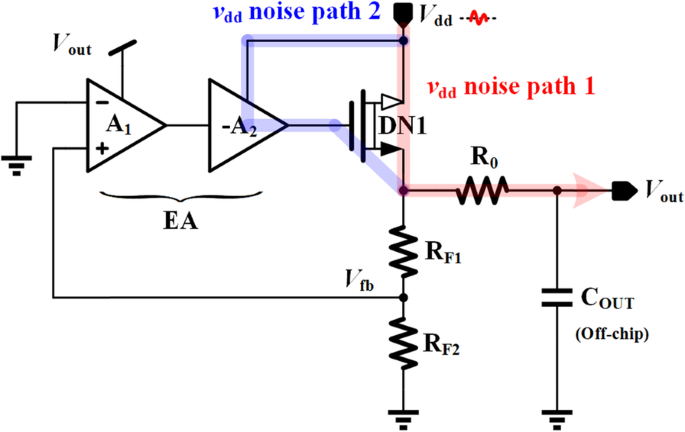
PSR-Analyse der vorgeschlagenen VR

Wie in (15) gezeigt, A _Pfad2 ist eine mit Hilfe der vorgeschlagenen SPT- und Kaskode-Stromspiegelstruktur recht kleine. Dies macht den Einfluss von Pfad 1 in der PSR-Analyse dominant.

Das vereinfachte PSR-Modell des vorgeschlagenen VR ist in Abb. 8 dargestellt, wobei r _{o_DN1} ist der Ausgangswiderstand des Leistungstransistors DN1, der den Rauschpfad 1 berücksichtigt, die gesteuerte Stromquelle stammt aus dem Rauschpfad 2, Z _B besteht aus R _F1 , R _F2 , R ₀ , und C _AUS wirkt als Filter bei hoher Frequenz und Z _{SH_FB} ist die äquivalente Impedanz einschließlich der Funktion der Gegenkopplungsschleife. Z _{SH_FB} kann gegeben werden durch

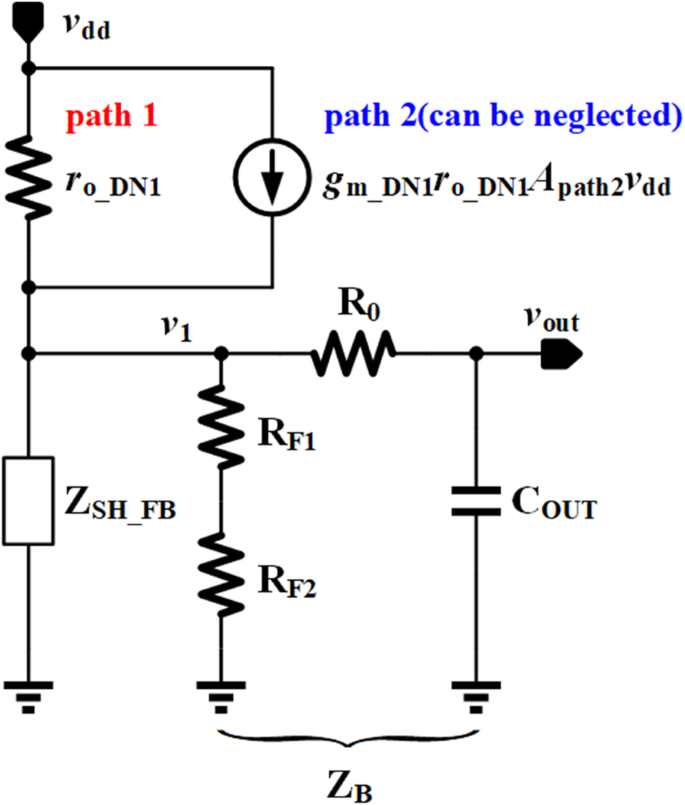
Das vereinfachte Modell der PSR

wo g _{m_DN1} ist die Steilheit des Leistungstransistors DN1. Daher kann die PSR-Übertragungsfunktion ausgedrückt werden als

$$ \mathrm{PSR}=\frac{V_{\mathrm{out}}}{V_{\mathrm{dd}}}=\frac{\left(1+{g}_{m\_\mathrm{ DN}1}{r}_{o\_\mathrm{DN}1}{A}_{\mathrm{Pfad}2}\right)\left({Z}_B\Big\Vert {Z}_{ \mathrm{SH}\_\mathrm{FB}}\right)}{r_{o\_\mathrm{DN}1}+{Z}_B\Big\Vert {Z}_{\mathrm{SH}\ _\mathrm{FB}}} $$ (17)

Durch bewusstes Einstellen der intrinsischen Verstärkung von HV10 weitaus größer als die des Leistungstransistors DN1, g _{m_DN1} r _{o_DN1} A _Pfad2 <<1 erreicht werden und somit die geregelte Stromquelle vernachlässigt werden kann. Der Ausdruck von PSR kann weiter vereinfacht werden als

$$ \mathrm{PSR}\approx \frac{Z_B\Big\Vert {Z}_{\mathrm{SH}\_\mathrm{FB}}}{r_{o\_\mathrm{DN}1}+ {Z}_B\Groß\Vert {Z}_{\mathrm{SH}\_\mathrm{FB}}} $$ (18)

Seit Z _B und Z _{SH_FB} sich mit der Frequenzänderung ändert, ist es notwendig, die Frequenzcharakteristik des PSR zu analysieren.

Die niedrige Frequenz

Bei niedriger Frequenz ist die Verstärkung von EA sehr hoch und C _AUS kann als offener Kreislauf behandelt werden. Also, Z _B>> Z _{SH_FB} und die PSR kann geschrieben werden als

$$ {\mathrm{PSR}}_{\mathrm{LF}}\approx \frac{1}{g_{m\_\mathrm{DN}1}{r}_{o\_\mathrm{DN} 1}\left(1+\beta{A}_{E0}\right)} $$ (19)

Die mittlere Frequenz

Die Impedanz von Z _{SH_FB} wird zunehmen, weil die Schleifenverstärkung bei der mittleren Frequenz abnimmt. In dieser Phase ist das Z _{SH_FB} ist immer noch klein, und der PSR wird hauptsächlich durch die Schleifenverstärkung beeinflusst. In Bezug auf (7) kann der PSR ausgedrückt werden als

$$ {\mathrm{PSR}}_{\mathrm{MF}}\approx \frac{1}{g_{m\_\mathrm{DN}1}{r}_{o\_\mathrm{DN} 1}\left(1+\beta{A}_{E0}\right)}\frac{1+s/{\omega}_p}{1+s/\left[{\omega}_p\left(1 +\beta{A}_{E0}\right)\right]} $$ (20)

Wie in (20) gezeigt, wird der PSR schlechter und das Rauschen der Ausgangsspannung wird ernster, während die Frequenz innerhalb der Verstärkungsfrequenz von Eins ansteigt.

Die Hochfrequenz

Aufgrund der zunehmenden Häufigkeit, Z _{SH_FB} wird groß und nähert sich schließlich 1/g _{m_DN1} . Die Impedanz von C _AUS wird kleiner, ist aber immer noch viel größer als R ₀ . Also R ₀ kann wie bisher weggelassen werden. Der Hochfrequenz-PSR hängt von der Spannungsteilung zwischen r _{o_DN1} und 1/g _{m_DN1} parallel zu C _AUS , die dargestellt werden kann durch

$$ {\mathrm{PSR}}_{\mathrm{HF}}\approx \frac{1}{g_{m\_\mathrm{DN}1}{r}_{o\_\mathrm{DN} 1}}\frac{1}{1+s{C}_{\mathrm{OUT}}/{g}_{m\_\mathrm{DN}1}} $$ (21)

Bei hoher Frequenz kann das Rauschen bei der Ausgangsspannung aufgrund der Wirkung von C . stark unterdrückt werden _AUS .

Wie zuvor analysiert, wird die gute Rauschunterdrückung im gesamten Frequenzbereich der vorgeschlagenen VR durch drei Aspekte garantiert. Erstens wird eine hohe Schleifenverstärkung verwendet; Zweitens bewirkt SPT, dass das Rauschen der Stromversorgung nur einen geringen Einfluss auf das Gate des Leistungstransistors hat; Drittens, der Ausgangskondensator C _AUS kann den PSR bei hoher Frequenz mit Filtereigenschaft verbessern.

Ergebnisse und Diskussion

Die vorgeschlagene VR wurde in einer standardmäßigen 0,35-μm-BCD-Technologie implementiert. Das Chipfoto des hergestellten Reglers ist in Abb. 9 gezeigt, dessen aktiver Kernbereich des VR 290 μm × 900 μm beträgt.

Das Chipfoto der vorgeschlagenen VR

Die geregelte Ausgangsspannung des vorgeschlagenen VR beträgt 5 V mit einer Versorgungsspannung von 5,5 bis 30 V. Der Ausgangskondensator ist ein kostengünstiger Keramikkondensator. Die Kapazität des Ausgangskondensators kann von 100 nF bis 3,3 μF eingestellt werden.

Abbildung 10 zeigt den Frequenzgang des vorgeschlagenen VR bei verschiedenen Lastbedingungen mit einem Ausgangskondensator von 100 nF und 3,3  μF. Der vorgeschlagene LDO kann in einem weiten Bereich von Ausgangskondensatorwerten stabil bleiben, und die Wellenform des Schleifenfrequenzgangs weist einen sehr kleinen Unterschied zwischen 0 und 30 mA Laststrom auf, was von dem zuvor analysierten vorgeschlagenen DLT profitiert.

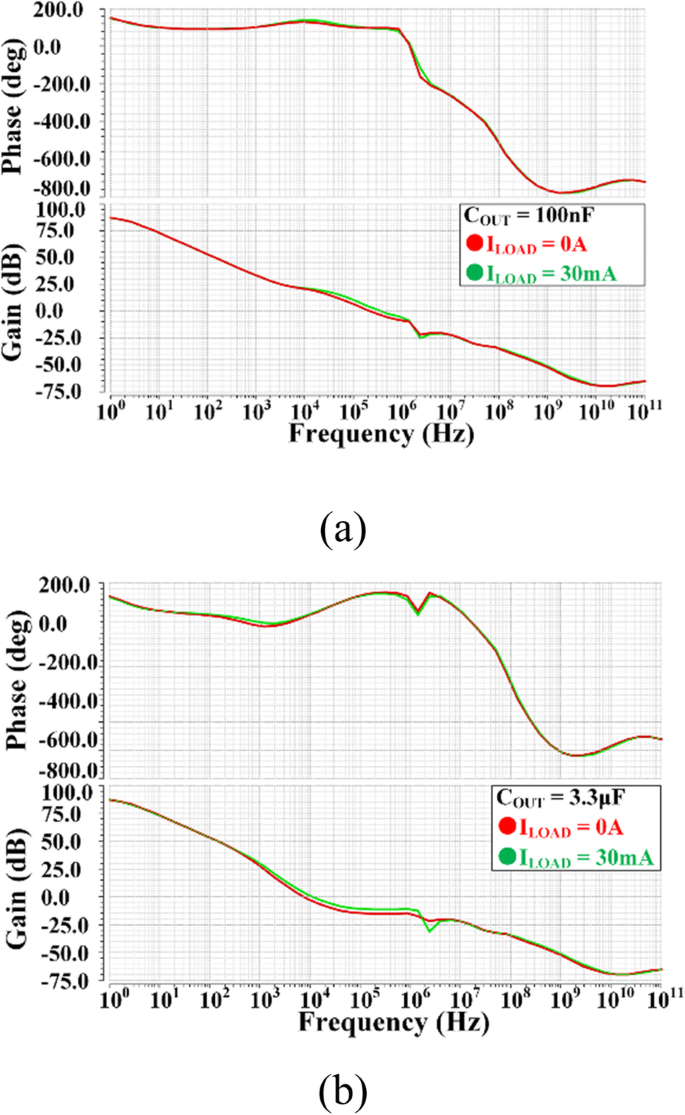
Schleifenfrequenzantworten des vorgeschlagenen VR unter einem anderen Wert von I _Laden und C _AUS Bedingungen. a C_OUT =100 nF, b C_OUT =3,3 훍F. Rote und grüne Linie stehen für I _Laden von 0 A bzw. 30 mA

Das Ergebnis der PSR-Verifizierung mit einem Ausgangskondensator von 0,1 μF ist in Abb. 11 dargestellt, wobei ein −110 dB bei niedriger Frequenz und besser als −64 dB bis zu 10 MHz erreicht werden. Bei der niedrigen Frequenz hat der vorgeschlagene VR aufgrund der hohen Schleifenverstärkung einen guten PSR. Die PSR wird aufgrund des dominierten Pols ω . innerhalb der Einheitsverstärkungsfrequenz schlecht _p . Der Ausgangskondensator C _AUS verbessert die PSR-Charakteristik bei der hohen Frequenz. Diese Ergebnisse zeigen, dass dies mit der vorherigen Analyse übereinstimmt und die vorgeschlagene VR eine bessere PSR im gesamten Frequenzbereich erzielt.

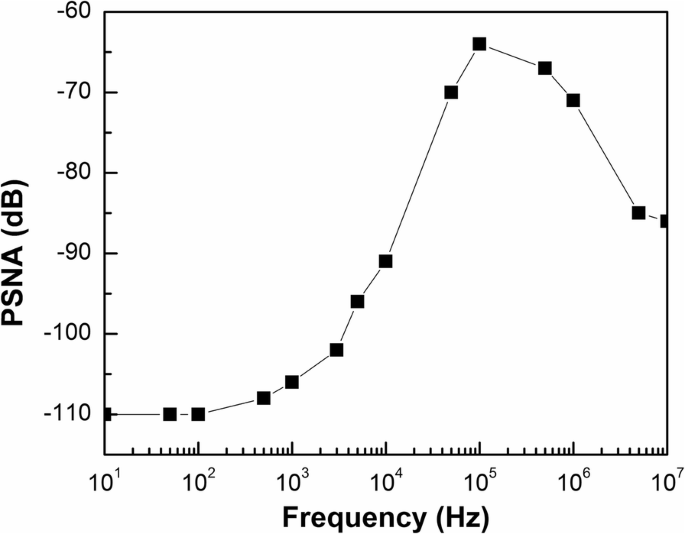
PSR der vorgeschlagenen VR

Das Ergebnis der Netzregelung des vorgeschlagenen VR ist in Abb. 12 dargestellt. Im Eingangsspannungsbereich von 5,5 bis 30 V variiert die Ausgangsspannung nur um 73,53 µV, was zu einer Netzregelung von nur 2,98 µV/V führt. Dies bestätigt die Wirksamkeit des vorgeschlagenen SPT.

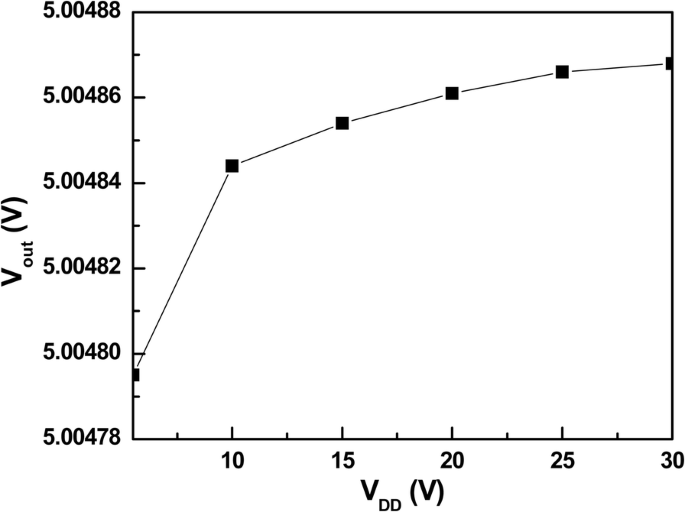
Linienregulierung der vorgeschlagenen VR

Abbildung 13 zeigt das Einschwingverhalten der Ausgangsspannung aufgrund unterschiedlicher Lastströme. Die Spannungsspitzen und -einbrüche der geregelten Ausgangsspannung betragen etwa 43 mV, 65 mV, 83 mV, wenn sich der Laststrom von 0 auf 18 mA, 28 mA bzw. 32 mA ändert. Daraus ergibt sich eine Lastregelung von 0,233 mV/mA, die hauptsächlich durch R . verursacht wird ₀ für die Stabilität mit einem breiten Ausgangskapazitätsbereich.

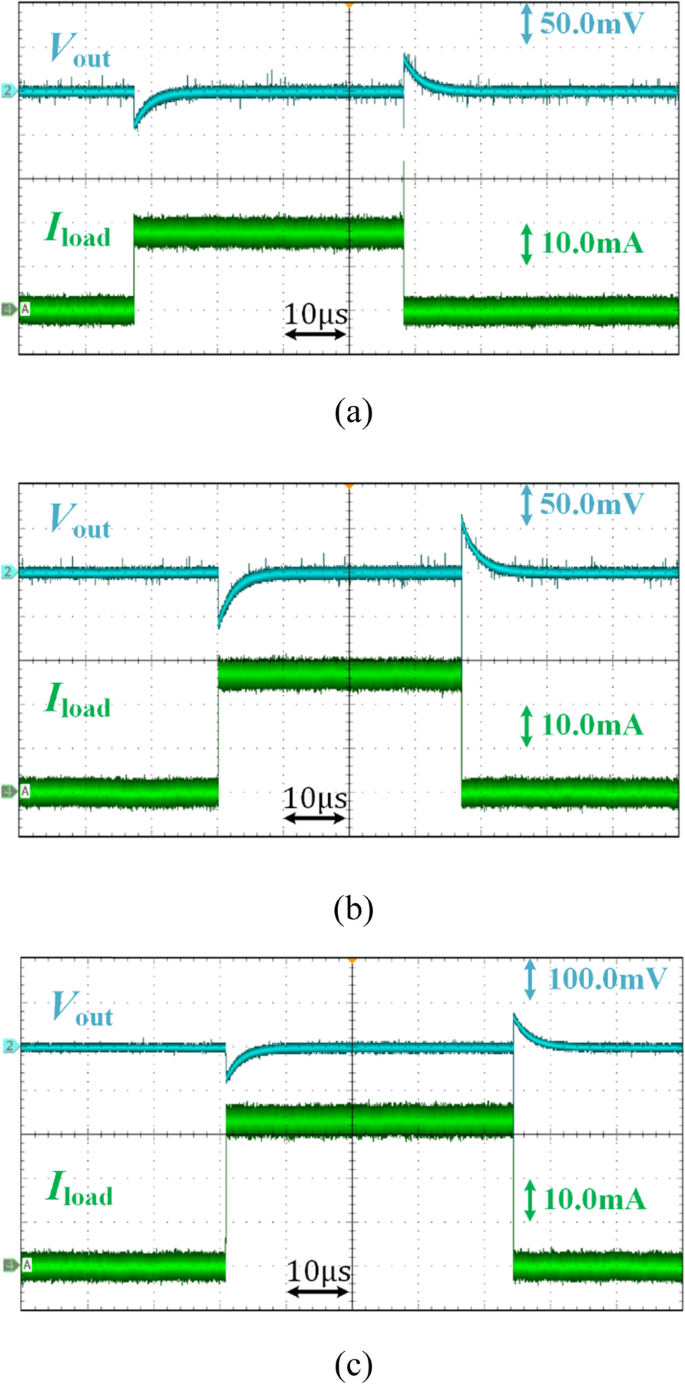
Transiente Antwortwellenform des vorgeschlagenen VR aufgrund unterschiedlicher Laststromstufen. a 0 bis 18 mA; b 0 bis 28 mA; c 0 bis 32 mA

Der gemessene OCP ist in Abb. 14 dargestellt. Um die Wirksamkeit des OCP zu verifizieren, wird in Abb. 14a ein Kurzschluss verwendet. Wie in 14a gezeigt, wird der Ausgangsstrom des vorgeschlagenen VR bei etwa 40   mA gehalten, wenn der Überstrom auftritt, während die Ausgangsspannung auf Masse gezogen wird. Abbildung 14b veranschaulicht eine Übergangsreaktion zwischen Überstrom und normaler Last, die darauf hinweist, dass der vorgeschlagene VR die Fähigkeit zur Selbstwiederherstellung besitzt, wenn die Überlast endet.

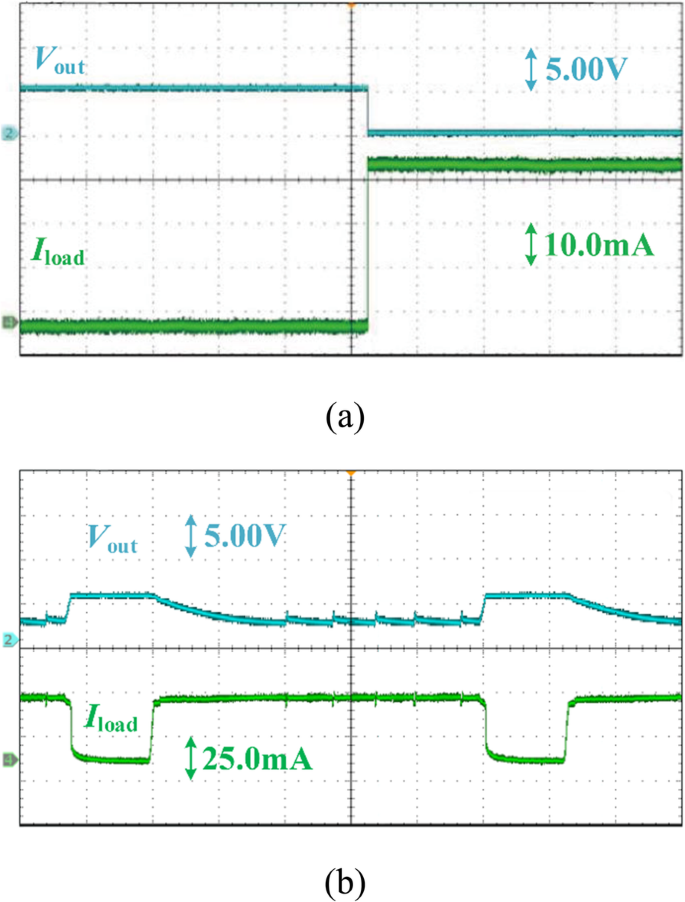
Die OCP-Messung der vorgeschlagenen VR. a Ausgangskurzschluss; b Transient zwischen Überstrom und normaler Last

Tabelle 1 bietet einen Leistungsvergleich der vorgeschlagenen LDO und einiger anderer zuvor veröffentlichter LDOs. Im Vergleich dazu hat diese LDO die beste Linienregulierung und PSR, die von der vorgeschlagenen SPT profitiert. Die aktive Fläche wird weiter reduziert, wenn sie in einem fortgeschritteneren Verfahren hergestellt wird.

Tabelle 2 bietet einen weiteren Leistungsvergleich, der sich auf die LDOs konzentriert, die ebenfalls über einen breiten Stromversorgungsbereich verfügen. Mit Hilfe des vorgeschlagenen DLT und SPT hat diese Arbeit die beste Leitungsregelung und den größten Stromversorgungsbereich im Vergleich zu anderen LDOs. Die zusätzliche OCP-Funktion macht diese Arbeit wettbewerbsfähiger und zuverlässiger.

Schlussfolgerung

Ein hochstabiler SPT VR mit DLT und OCP wird in einem standardmäßigen 0,35-μm-BCD-Prozess implementiert. Mit Hilfe von SPT wird der größte Teil der Regelschleife von einer geregelten Ausgangsspannung versorgt, was für die Stabilität und PSR-Verbesserung von Vorteil ist. Der vorgeschlagene DLT ist hilfreich für das transiente Ansprechen und die Stabilität. Außerdem kann die eingebettete OCP-Schaltung verhindern, dass die präsentierte VR durch Überlastung oder Kurzschluss beschädigt wird. Die lineare Regelung des vorgeschlagenen VR beträgt 2,98 µV/V mit VDD von 5,5 bis 30 µV, während die geregelte Ausgangsspannung 5 µV beträgt und die Lastregelung 0,233 µV/mA mit Laststrom von 0 A bis 30 µmA beträgt. Die Überschwingungs- und Unterschwingungsspannung während der Laststromänderung ist auch bei Verwendung der vorgestellten Übergangsverstärkungsschaltung gering. Der PSR bei niedriger Frequenz beträgt −110 dB und ist bis zu 10 MHz besser als −64 dB. Eine hohe Schleifenstabilität kann in einem weiten Bereich von Ausgangskondensator und Laststrom erreicht werden, und daher ist der vorgeschlagene VR für Anwendungen geeignet, die eine hohe Leistung und Zuverlässigkeit bei Schwankungen von Ausgangskondensator und Laststrom erfordern.

Verfügbarkeit von Daten und Materialien

Alle während dieser Studie generierten oder analysierten Daten sind in diesem veröffentlichten Artikel enthalten.

Abkürzungen

VR:

Voltage regulator

OCP:

Overcurrent protection

SPT:

Self-power technique

PSR:

Power supply rejection

DLT:

Dynamic load technique

EA:

Error amplifier