HOT Graphen und HOT Graphene Nanotubes:Neue niederdimensionale Halbmetalle und Halbleiter

Einführung

Kohlenstoffbasierte Systeme weisen aufgrund ihrer Bindungsflexibilität eine unbegrenzte Zahl unterschiedlicher Strukturen mit einer ebenso großen Vielfalt an physikalischen Eigenschaften auf. Diese physikalischen Eigenschaften sind zum großen Teil das Ergebnis der Dimensionalität dieser Strukturen [1]. Graphen ist eine einzelne zweidimensionale Schicht von Kohlenstoffatomen, die in einer hexagonalen Gitterstruktur [2] gebunden sind und eine Reihe einzigartiger Eigenschaften aufweisen, wie masselose Ladungsträger, hohe Fermi-Geschwindigkeit [3] und Dirac-Kegel [4, 5], die charakteristisch für zweidimensionale Dirac-Fermionen. Das Wabengitter, das aus zwei äquivalenten Kohlenstoff-Teilgittern besteht, spielt eine entscheidende Rolle bei der Bildung dieser faszinierenden Eigenschaften [2]. Enyashin und Ivanovskii [6] konstruierten 12 künstliche 2D-Kohlenstoffnetzwerke, fanden jedoch keine anderen Strukturen als das Graphin-Allotrop, die ein Graphen-ähnliches elektronisches Verhalten aufweisen. Es scheint zu implizieren, dass die Dirac-ähnlichen Fermionen in sp ² -gebundene Kohlenstoffsysteme sind von der Wabenstruktur abhängig. In der unteren Dimension ist die Kohlenstoffnanoröhre eine zu einem Hohlzylinder gewalzte Wabenstruktur mit nanometrischem Durchmesser und µm Länge [7,8,9,10]. Da es unendlich viele Möglichkeiten gibt, ein Blech zu einem Zylinder zu walzen, bietet die große Vielfalt möglicher Helixgeometrien, die die Röhrenchiralität definieren, eine Familie von Nanoröhren mit unterschiedlichen Durchmessern und mikroskopischen Strukturen [11,12,13]. Die elektronischen und Transporteigenschaften gehören sicherlich zu den bedeutendsten physikalischen Eigenschaften von Kohlenstoffnanoröhren und hängen entscheidend von Durchmesser und Chiralität ab [14,15,16,17,18]. Graphen-Nanoröhren können entweder halbmetallisch [14] oder halbleitend [19,20,21] sein, wobei die Bandlücke je nach Durchmesser und Chiralität von null bis zu einigen Zehntel eV variiert [10, 14, 16]. Darüber hinaus kann gezeigt werden, dass die Bandlücke von halbleitenden Röhren einfach auf den Röhrendurchmesser bezogen ist. Die halbmetallischen Nanoröhren behalten auch die einzigartigen Eigenschaften von Graphen bei, wie masselose Ladungsträger, hohe Fermi-Geschwindigkeit [22] und Dirac-Kegel [23]. Solche bemerkenswerten Ergebnisse können aus einer Vielzahl von Überlegungen gewonnen werden, angefangen beim sogenannten Bandfaltungsansatz, der auf der Kenntnis der elektronischen Eigenschaften der Graphenschicht basiert, bis hin zur direkten Untersuchung von Nanoröhren mit semiempirischen Tight-Binding-Ansätzen [14, 16, 18, 23]. Im Vergleich zu komplexeren Ab-initio-Berechnungen und verfügbaren experimentellen Ergebnissen sind feinere Überlegungen wie Krümmungseffekte k _F Shifting [24, 25], σ-π-Hybridisierung [26] eingeführt. Graphen und graphenähnliche Materialien [6] gelten als revolutionäres Material für die zukünftige Generation elektronischer Hochgeschwindigkeits-Logikgeräte [27, 28], thermisch und elektrisch leitfähige verstärkte Verbundwerkstoffe [29, 30], Katalysatoren [31], Sensoren [32,33,34,35], transparente Elektroden [27, 36] usw. basierend auf den oben genannten ungewöhnlichen Eigenschaften. In den letzten Jahrzehnten haben Kohlenstoffnanoröhren aufgrund ihrer außergewöhnlichen elektronischen, mechanischen und strukturellen Eigenschaften auch großes Potenzial in Logikschaltungen, Gasspeichern, Katalyse und Energiespeichern gezeigt [37,38,39]. Daher stand die Schaffung neuer Kohlenstoffallotrope (einschließlich 2D und 1D) aufgrund ihrer grundlegenden wissenschaftlichen und technologischen Bedeutung im Mittelpunkt zahlreicher theoretischer und experimenteller Untersuchungen [40]. Eine vollständige Aufklärung der Strukturen dieser spannenden Kohlenstoffphasen durch aktuelle experimentelle Technologien ist jedoch aufgrund ihrer begrenzten Menge sowie der Mischung anderer Phasen in der Regel unrealistisch. Theoretische Vorhersage ist notwendig und hat großen Erfolg gebracht [31,32,33,34,35, 40,41,42].

In dieser Studie haben wir ein neues Allotrop von Graphen entworfen, das zweidimensionale Dirac-Fermionen ohne eine ausschließlich hexagonale Struktur aufweist. Das neue Allotrop wurde aus verflochtenen Kohlenstoffsechsecken, -oktogonen und -tetragonen konstruiert und erhielt den Namen HOT Graphen. HEISS Graphen-Nanoröhren wurden auch durch Aufrollen von HOT . hergestellt Graphenblatt zusammen mit verschiedenen Richtungen. Die elektronische Eigenschaft, Krümmungseffekt, k _F Verschiebungseffekt usw. von HOT Graphen und Nanoröhren wurden mit Ab-initio-Rechnungen auf der Grundlage der Dichtefunktionstheorie (DFT) berechnet.

Berechnungsmethode

Die aktuellen Berechnungen zu HOT Graphen und HEISS Graphen-Nanoröhren wurden mit einer First-Principles-Methode basierend auf der Dichte-Funktional-Theorie (DFT) mit der generalisierten Gradienten-Approximation (GGA) in Form des Perdew-Burke-Ernzerh (PBE)-Austausch-Korrelations-Funktionals hergestellt [43], as implementiert im Wiener Ab-initio-Simulationspaket (VASP) [44, 45]. Die Wellenfunktionen wurden in ebenen Wellen bis zu einem Cutoff der kinetischen Energie der ebenen Welle von 520 eV erweitert. Die Integrale der Brillouin-Zone (BZ) wurden unter Verwendung eines Monkhorst-Pack [46]-Stichprobenschemas mit einem k -Punktnetzauflösung von 2π × 0.03 Å ^− 1 . Die Basisvektoren der Elementarzelle (die Form und Größe der Elementarzelle darstellen) und Atomkoordinaten wurden in jedem System vollständig entspannt, bis die Kräfte auf alle Atome kleiner als 0,01 eV/Å waren.

Ergebnisse und Diskussion

Geometrische und elektronische Strukturen von HOT Graphen

Die geometrische Struktur von HOT Graphen (Abb. 1a) zeigt eine kompliziertere Bindungssituation als Graphen. Die Vielfalt der Kohlenstoffpolygone in HOT Graphen führt zu verschiedenen Kohlenstoffbindungseigenschaften. Diese Polygone in HOT Graphen hat gemeinsame Kanten und die Bindungen können anhand der beiden Polygone unterschieden werden, zu denen sie gehören. Daher werden sie in unserer Forschung als 6–8 Anleihen, 4–8 Anleihen, 4–6 Anleihen, 6–6 Anleihen und 8–8 Anleihen bezeichnet. Die Bindungen 4–8 und 6–8 haben zwei verschiedene Bindungslängen:1.44 und 1.47 für 4–8 Bindungen; 1.41 Å und 1.48 Å für 6–8 Bindungen. Die 4–6 Bindungen, 6–6 Bindungen und 8–8 Bindungen haben relativ einzigartige Bindungslängen von 1.44 Å, 1.46 Å und 1.34 Å. Abbildung 1b zeigt die Bandstruktur und die Zustandsdichte (DOS) von HOT Graphen mit der entsprechenden BZ, die in Abb. 1c dargestellt ist. Der Kreuzungspunkt der Energiebänder auf dem Fermi-Niveau zeigt die Halbmetallizität von HOT . an Graphen, was durch das verschwindende DOS auf Fermi-Niveau bestätigt wird. Der Dirac-Punkt befindet sich bei (0, 0,0585, 0) neben Γ. Die 3D-Bandstruktur (Abb. 2) stellt die Bandoberflächen in der Nähe des Fermi-Niveaus dar, wo man die Dirac-Kegel sehen kann, die durch obere und untere konische Oberflächen gebildet werden, die an zwei Dirac-Punkten genau auf der Fermi-Oberfläche aufeinandertreffen. Die entsprechende Fermi-Geschwindigkeit (v_F ) der Dirac-Fermionen, berechnet aus dem Gradienten der linearen Dispersionen der Bandstrukturen, beträgt 6,27 × 10 ⁵ m/s, das ist etwas weniger als 8,1 × 10 ⁵ m/s [22] für Graphen-Nanoröhren und 8,6 × 10 ⁵ m/s [47, 48] für Graphen. Das hohe v_F impliziert eine hohe Mobilität der Träger im HOT Graphen.

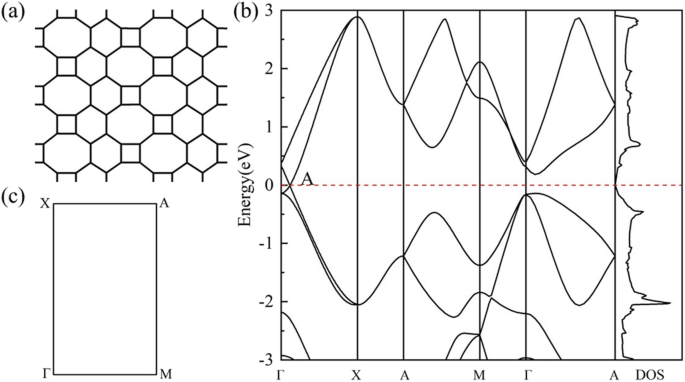
(a ) Geometrie von HOT Graphen; (b ) Bandstrukturen und DOS des HOT Graphen; (c ) die entsprechende BZ von HOT Graphen

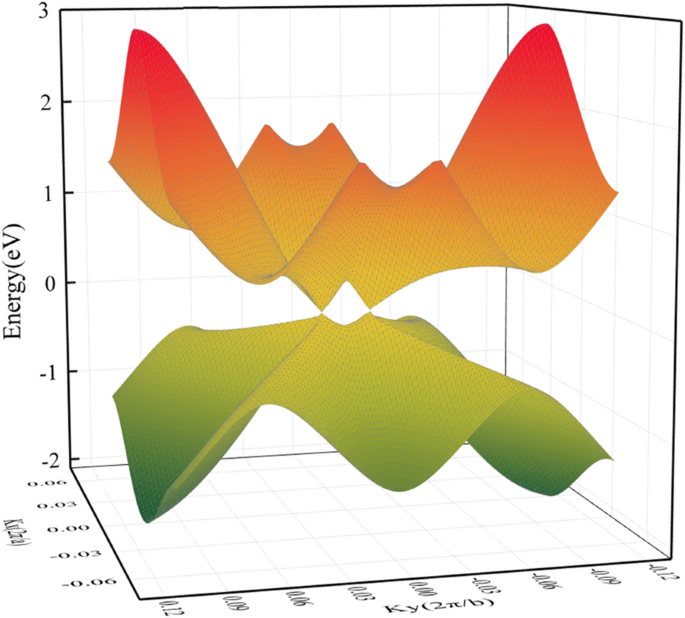
3D-Bandstruktur des HOT Graphen

Geometrische und elektronische Strukturen von HOT Graphen-Nanoröhren

Das HEISSE Graphenrohre werden aus dem HEISSEN aufgerollt Graphenblatt in verschiedene Richtungen, symbolisiert durch einen Index auf dem 2D HOT Graphengitter (Abb. 3a). Dieser Index wird als (l,m ) n basierend auf zwei Einheitsvektoren a und b . Symbol (l,m ) [18, 20, 21] steht für verschiedene Richtungen auf der HOT Graphenblatt, n steht für die Anzahl der Umfangseinheiten (Abb. 3b und c), die beim Aufrollen der Rohre verwendet werden. Unter der Raumumkehrsymmetrie des HOT Graphen-Elementarzelle, das Nanoröhrensymbol ist auf 0 ≤ l . beschränkt und 0 ≤ m um eine Viel-zu-Eins-Korrespondenz zu vermeiden. Die Anzahl der möglichen geometrischen Strukturen des HOT Graphen-Nanoröhren ist unendlich, da es sowohl für Durchmesser als auch für Rollrichtungen unendlich viele Möglichkeiten gibt. Unter einer so großen Anzahl von Nanoröhren werden in unserer Studie nur zwei Richtungen (0,1, 1,0) ausgewählt. Dies liegt daran, dass die helikale Anordnung der Atome in andere Richtungen kaum periodisch ist und eine nahezu unendliche Länge der Elementarzelle entlang der Röhrenachse besitzt. Eine so große Elementarzelle ist in unserer Berechnung unrealistisch. Unterschiedliche Rollrichtungen zwischen (1,0) n und (0,1) n Rohre führen zu den Unterschieden in Geometrie und Verbindungssituation. In den Fig. 3d und e sind zwei Rohre (1,0)6 und (0,1)4 dargestellt, um die geometrischen Unterschiede zwischen den beiden Walzrichtungen zu beschreiben. Die Anordnung von Polygonen entlang (1,0)-Richtung kann in zwei Muster unterteilt werden:C₄ –C₆ –C₈ (orange) und C₈ –C₆ –C₄ (blau), die sich genau gegenüberliegen. Diese beiden entgegengesetzten Muster wechseln sich entlang der Umfangsrichtung des Rohres ab. In Richtung (0,1) haben Polygone, die entlang der Rohrachse angeordnet sind, ebenfalls zwei Muster:C₄ –C₈ (blau) und C₆ –C₆ (Orange). Zwei C₄ –C₈ Muster wechseln sich mit einem C₆ . ab –C₆ Muster entlang der Umfangsrichtung.

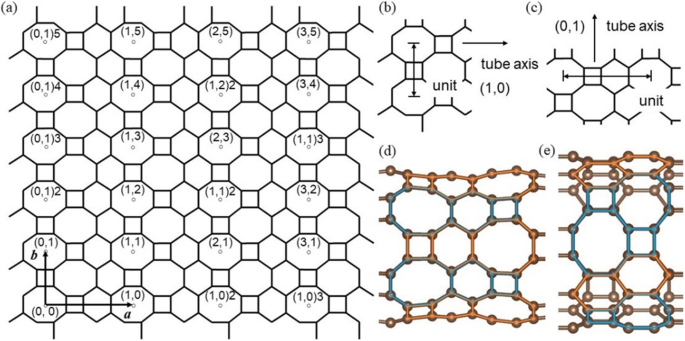
(a ) Verschiedene Röhren sind mit Symbolen gekennzeichnet (l,m ) n , mit (l,m ) steht für die Rollrichtung basierend auf dem Einheitsvektor a und b , und n für die Anzahl der Rohrdurchmessereinheiten; (b ) Durchmessereinheit in (1,0)-Richtung; (c ) Durchmessereinheit in (0,1)-Richtung; (d ) geometrische Struktur von a (1,0)6 HOT Graphen-Nanoröhre; (e ) geometrische Struktur eines (0,1)4 HOT Graphen-Nanoröhre

Um die Energiekosten beim Aufrollen eines Blechs zu Rohren aufzudecken, definieren wir die Krümmungsenergie (Abb. 4) E _aktuell als:

wobei \( {E}_{\mathrm{tube}}^{\mathrm{at}} \) die durchschnittliche Energie von Atomen in Nanoröhren ist und \( {E}_{\mathrm{sheet}}^{\ mathrm{at}} \) ist die durchschnittliche Energie der Atome im 2D-Blatt. Die (1,0) n Röhren weisen niedrigere Energiekosten auf als Graphen-Nanoröhren, während die (0,1) n Röhren sind fast die gleichen wie die Sessel-Graphen-Nanoröhren, abgesehen von einigen ultrakleinen Röhren. Solche Ergebnisse deuten auch darauf hin, dass es möglich ist, HOT . zu synthetisieren Graphen-Nanoröhren in Experimenten. Zu beachten ist, dass das Rohr (1,0)1 zu klein ist, da sein Durchmesser noch kürzer ist als die Bindungslänge von Kohlenstoff.

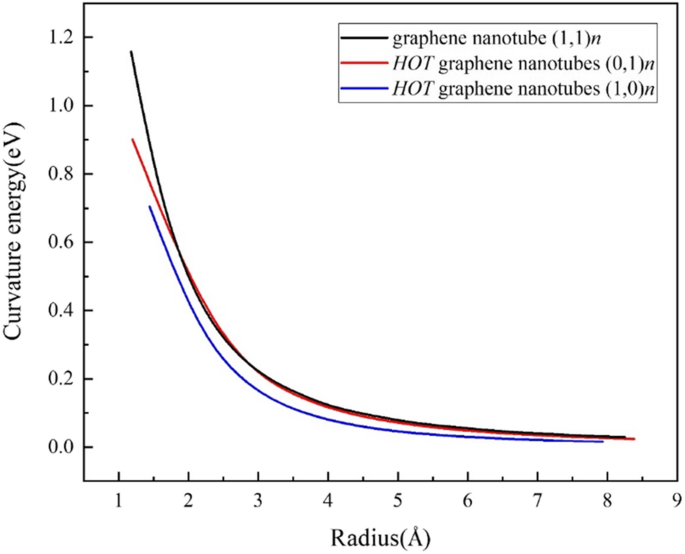
Krümmungsenergien des HOT Graphen-Nanoröhren und Graphen-Nanoröhren

Die berechnete elektronische Bandstruktur und DOS von Nanotube (0,1)6 (Abb. 5b) weisen auf einen halbmetallischen Charakter hin. Wenn die HEISSEN Graphenfolie zu einer Nanoröhre aufgerollt, reduziert sich ihr 2D BZ auf 1D BZ aufgrund der neuen periodischen Randbedingungen in Nanotubes. Die periodischen Randbedingungen entlang der Umfangsrichtung der Röhre lassen nur Wellenvektoren „um“ den Nanoröhrenumfang zu und diese Vektoren werden quantisiert [49]. Die periodischen Randbedingungen entlang der Nanoröhrenachse bleiben die gleichen wie beim 2D-Blatt, dann bleiben die Wellenvektoren entlang der Nanoröhrenachse kontinuierlich. Nach dem Zonenfaltungsschema ist die elektronische Bandstruktur einer bestimmten Nanoröhre durch die Überlagerung der elektronischen Energiebänder des entsprechenden 2D-Faltblatts entlang der spezifisch erlaubten k . gegeben Zeilen [50]. Als quantisierte Wellenvektoren in der Mitte der BZ des HOT Graphen kreuzt immer den Dirac-Punkt (Punkt F in Abb. 5a), ein nicht entarteter Dirac-Punkt (Punkt F in Abb. 5b) und Dirac-Kegel erscheint in den Bandstrukturen des (0,1) n HOT Graphen-Nanoröhren, was zur Halbmetallizität aller (0,1) n Nanoröhren. Rohr (0,1)6 wird berechnet, um die Halbmetallizität dieses Satzes von (0,1) n Nanoröhren in Abb. 5. Bandstruktur des (0,1)6 HOT Graphen-Nanoröhren zeigen einen Kreuzungspunkt von Energiebändern auf dem Fermi-Niveau und die entsprechende DOS zeigt keine Zustände auf dem Fermi-Niveau, was die Halbmetallizität des Systems bestätigt. Als Dirac-Kegel in (0,1) n Röhren stammt aus dem HOT Graphenblatt, die berechnete Koordinate des Dirac-Punktes in der (0,1)6-Nanoröhre ist die gleiche wie in HOT Graphenblatt, das (0, 0,0585, 0) ist. Die berechnete Fermigeschwindigkeit am Dirac-Punkt in (0,1)6-Nanoröhren beträgt 6,76 × 10 ⁵ m/s, nahe 6,27 × 10 ⁵ m/s im HOT Graphen-Blatt.

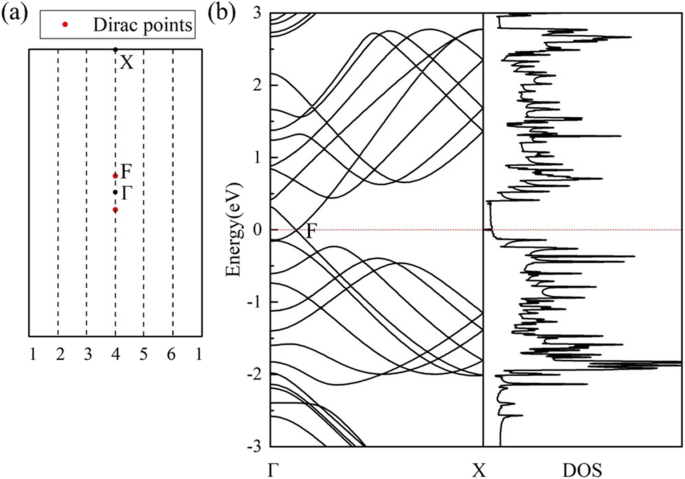
(a ) Die erste BZ der HOT Graphen mit zulässigem k Linien (gestrichelte Linien) für die (0,1)6-Nanoröhre. F ist der Dirac-Punkt. (b ) Die berechneten Bandstrukturen und DOS von (0,1)6 Nanoröhren

Die Entwicklung der Bandstruktur von (0,1) n Nanoröhren mit unterschiedlichen Röhrenradien (Abb. 6a) zeigt, dass die HEISSEN Graphen-Nanoröhren (0,1) n sind halbmetallisch (n ≥ 3) und in Metall verwandeln (n = 2) und dann zurück zum Halbmetall (n = 1). Eine solche Änderung unter einem kleinen Radius resultierte aus dem sogenannten Krümmungseffekt [26]. Bei ultrakleinen Nanoröhren (z. B. (0,1)2 und (0,1)1) hat die Krümmung einen nicht zu vernachlässigenden Einfluss auf das Zonenfaltungsschema. Bindungslänge und Bindungswinkel ändern sich innerhalb der großen Krümmung nicht unerheblich, was Einfluss auf die elektronische Bandstruktur hat. Die Bandstrukturen solcher Nanoröhren sind keine einfache Überlagerung von Energiebändern auf den erlaubten Wellenvektoren mehr. Dieser Wechsel der Anleihen verändert die Bedingungen, die die k . definieren Punkt, an dem sich besetzte und unbesetzte Bänder kreuzen (an einem Punkt bezeichnen wir k _F ) und verschiebe das k _F weg von den ursprünglichen Dirac-Punkten, die als k bezeichnet werden _F Verschiebungseffekt [24, 25]. Als Ergebnis in der (0,1) n HOT Graphen-Nanoröhren, die k _F verschiebt sich von seiner ursprünglichen Position (k _HEISS ) im HEISSEN Graphenblatt (Punkt F in Abb. 5a). Und die Verschiebungsrichtung von k _F berechnet sich entlang des zulässigen Wellenvektors (gestrichelte Linien in Abb. 5a), was zu keiner Änderung der Halbmetallizität führt (Abb. 6a (n 3)). Gemäß der berechneten Koordination von Dirac-Punkten ist das k _F Verschiebungseffekt wird bei (0,1)5 mit einem Röhrenradius von 5.988 Å nicht vernachlässigbar, dessen Dirac-Punkt (k _F ) verschiebt sich nach (0,0.0626,0) vom ursprünglichen Punkt (k _HEISS ) bei (0,0.0594,0) in HEISS Graphen-Blatt. Wenn der Rohrradius kleiner wird, ist das k _F verschiebt sich weiter und erreicht den Punkt (0,0.0712,0) in der Röhre (0,1)3. In Röhre (0,1)2 ist das k _F verschiebt sich zu (0,0.0835,0), wo sich der Dirac-Punkt unter das Fermi-Niveau bewegt, was zu einem metallischen System führt. Das Verschwinden der Halbmetallizität in (0,1)2 weist auf eine Abweichung vom k . hin _F Verschiebungseffekt im (0,1) n Nanoröhren (n 3). Außerdem wird die (0,1)1-Röhre in ihrer Bandstruktur und der DOS wieder halbmetallisch (Abb. 6b). Unsere Elektronenzustandsanalyse des (0,1) n HOT Nanoröhren zeigen π-Zustände, die sich bei n . überlappen ≥ 2, das normalerweise als Ursprung der Halbmetallizität von Graphen-Nanoröhren angesehen wird [18, 24]. Die entsprechende Elektronenzustandsanalyse des HOT Graphen-Nanoröhre (0,1)1 zeigt eine σ-π-Hybridisierung, bei der eine tiefliegende σ*-Bande das Fermi-Niveau schneidet und sich dem Dirac-Kegel anschließt (blaue Linien in Abb. 6a). Die Koordination des Dirac-Punktes, der (0,0.18345,0) ist, weist auch einen Unterschied zu anderen (0,1) n HOT auf Graphen-Nanoröhren. Die berechnete Fermi-Geschwindigkeit beträgt 4,47 × 10 ⁵ m/s, weniger als 6,27 × 10 ⁵ m/s in HEISS Graphenblatt und Werte für andere (0,1) n Nanoröhren (~6,76 × 10 ⁵ Frau). Eine offensichtlich andere Form seiner Bandstruktur ist auch in Fig. 6a gezeigt. Alle diese Zeichen bestätigen, dass die Halbmetallizität des HOT Graphen-Nanoröhre (0,1)1 stammt aus der σ-π-Hybridisierung. Zusammenfassend lässt sich sagen, dass mit zunehmender Krümmung das k _F Verschiebungseffekt tritt bei n . auf = 5, wird effektiver bei 4 ≥ n ≥ 2 und wird schließlich durch den σ-π-Hybridisierungseffekt bei n . ersetzt = 1.

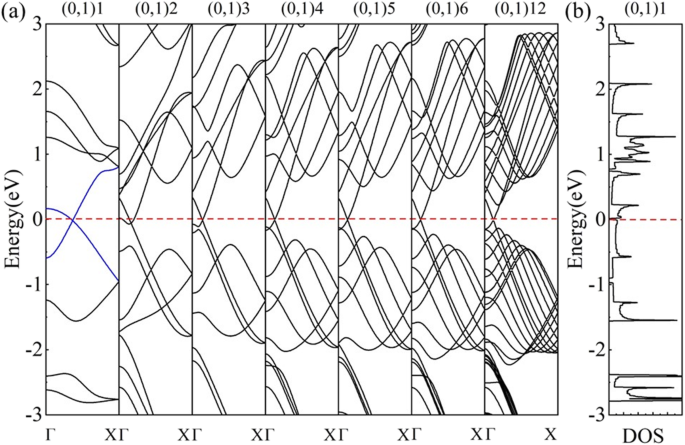
(a ) Bandentwicklung von (0,1) n Nanoröhren (n = 1, 2, 3, 4, 5, 6, 12); (b ) DOS der (0,1)1-Nanoröhre

In einer anderen Walzrichtung zeigt die berechnete Bandstruktur von (1,0)6 (Fig. 7b) Halbleiter. Die 6 Wellenvektoren (gestrichelte Linien) verlaufen parallel zu Γ-M und kreuzen den Г-Punkt in der Mitte der BZ von HOT Graphen (Abb. 7a) und öffnen eine 0,46 eV Bandlücke, wie in der DOS gezeigt (Abb. 7b). In dieser Rollrichtung enthalten die erlaubten Wellenvektoren in der Mitte der BZ niemals die Dirac-Punkte, was zu Bandlücken ungleich null in diesem Satz von Nanoröhren führt. Die Bandentwicklung zeigt eine Änderung der Bandlücken mit unterschiedlichen Radien in Abb. 8a. Die (1,0) n HEISS Graphen-Nanoröhren sind halbleitend (n 4). Das Valenzbandmaximum (VBM) und das Leitungsbandminimum (CBM) nähern sich von Röhre (1,0)6 an Röhre (1,0)4 an und kreuzen sich dann in Röhre (1,0)3 mit einem Radius von 2.17 Å. Dieser Kreuzungspunkt liegt genau auf der Fermi-Ebene bei (0.0791,0,0). Die berechnete DOS (Abb. 8b) zeigt 0-Zustände auf dem Fermi-Niveau von (1,0)3, was die Halbmetallizität bestätigt. Wenn der Röhrenradius auf (1,0)2 abnimmt, öffnet sich wieder eine Lücke von 0,848 eV. Die CBM und VBM von (1,0)2 befinden sich am -Punkt bzw. am M-Punkt, was eine indirekte Bandlücke anzeigt. Diese Änderung in VBM impliziert einen anderen Ursprung für die Halbleiter in (1,0)2. Eine weitere Untersuchung der Bandlückenänderung im (1,0) n HOT Graphen-Nanoröhren ist in Abb. 9 dargestellt. Die Entwicklung der Bandlücke als Funktion von n (3 ≤ n ≤ 23) zeigt an, dass die Bandlücke mit den Rohrgrößen einstellbar ist. Außerdem ist die Abhängigkeit der Bandlücke von der Röhrengröße nicht monoton, sondern zickzackförmig (Abb. 9 schwarze Kurve). Das globale Minimum bei (1,0)15 weist eine Bandlücke von null auf. Die Halbmetallizität von (1,0)15 wird weiter durch die Bandstruktur und DOS bestätigt (Abb. 9g). Aus dem Zonenfaltungsschema wissen wir, dass die Bandstruktur von Nanoröhren die Überlagerung der Bandstruktur der 2D-Schicht entlang des entsprechenden quantisierten k . ist Zeilen [50]. Somit zeigt die Halbmetallizität an, dass mindestens einer der zulässigen k Linien (gestrichelte Linien in Abb. 7a) schneiden die Dirac-Punkte (rote Punkte in Abb. 7a) bei n = 15. Andernfalls, wenn das zulässige k Linien haben einen Abstand von den Dirac-Punkten (k _HEISS ), erscheint eine Bandlücke in der Nanoröhre. Außerdem ist dieser Abstand zwischen k _F und das k Linien ist proportional zu den Bandlücken, da die Banddispersion in der Nähe des Dirac-Kegels linear ist [25]. Die Δk _m misst die kürzeste Distanz zwischen k _F und k _m Linien der Quantenzahl m . Wir haben diese Entfernung berechnet Δk _m zwischen den Dirac-Punkten (k _HEISS ) und das erlaubte k Zeilen im HOT Graphen und plotten Sie es (rote Linie) zusammen mit den Bandlücken (schwarze Linie) in Abb. 9. Zuerst alle zulässigen k Linien haben eine Quantenzahl m . Wenn n ≤ 7 ​​(z. B. Abb. 9a), die kürzeste Entfernung (Δk _m ) liegt zwischen den k _HEISS und das erste k Linie, k ₁ , die ständig am Γ-Punkt sitzt (Grafik (a) in Abb. 9 einfügen). In dieser Situation Δk _m ist konstant, da sowohl k ₁ und k _HEISS sind unabhängig von der Rohrgröße konstant. Da jedoch das erlaubte k Linien werden in größeren Nanoröhren dichter (7 ≤ n ≤ 17), die k ₂ wird k . am nächsten _HEISS (z. B. Abb. 9b). In dieser Situation ist die k ₂ nähert sich dem Dirac-Punkt von der äußeren BZ mit zunehmenden Rohrradien; daher zeigt es einen Rückgang von Δk _m in Abb. 9 (7 ≤ n 17). n = 17 ist ein Wendepunkt, an dem k ₂ schneidet fast den Dirac-Punkt, was zu einem lokalen Minimum der Distanz Δk . führt _m (Abb. 9c). Wenn der Radius weiter ansteigt, wird das k ₂ überqueren Sie die k _HEISS Punkt und entfernt sich weiterhin von diesem zum Г-Punkt, was zu einer erneuten Zunahme der Entfernung bei 17 ≤ n . führt ≤ 24 (z. B. Abb. 9d). Gleichzeitig k ₃ nähert sich dem Dirac-Punkt. k ₃ nähert sich k _HEISS als k ₂ und beginnt eine neue Entfernungsverringerung Δk _m um n ≥ 24. Da die Bandlücken proportional zu diesem Abstand sind Δk _m [25] zeigt die Bandlückenkurve die gleiche Form wie die Δk _m Grundstück (n 7). Und es zeigt sich, dass sich die Bandlücken zyklisch ändern:die k _m nähert sich dem Dirac-Punkt (k _HEISS ) verursacht eine Abnahme der Bandlücke, durchquert dann den Dirac-Punkt, was zu einem lokalen Minimum führt, entfernt sich dann vom Dirac-Punkt, was zu einem Anstieg der Bandlücke führt, und wird schließlich durch die nächste Linie k . ersetzt _m + 1 in den nächsten Zyklus eintreten. Zusammenfassend ist der Grund, warum sich die Bandlücken mit der Röhrengröße ändern (n ≥ 7) ist, dass das k Linien bewegen sich mit unterschiedlichen Rohrgrößen, dadurch ändert sich der Abstand Δk _m zwischen k _HEISS und das erlaubte k Linien, die proportional zu den Bandlücken sind.

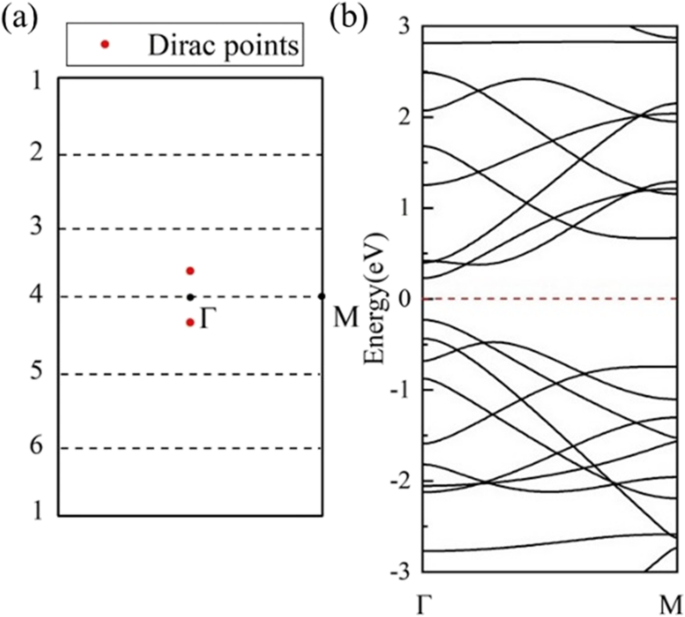
(a ) Die erste BZ der HOT Graphen mit zulässigem k Linien (gestrichelte Linien) für die (1,0)6-Nanoröhre; (b ) Bandstrukturen der (1,0)6-Nanoröhre

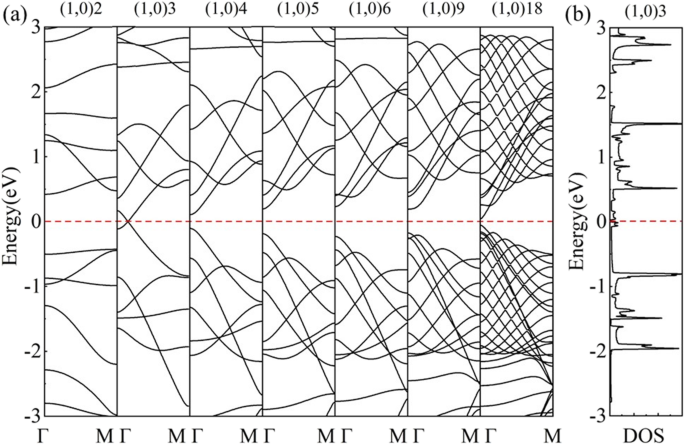
(a ) Bandentwicklung von HOT Graphen-Nanoröhren (1,0) n (n = 2, 3, 4, 5, 6, 9, 18); (b ) DOS der (1,0)3-Nanoröhre

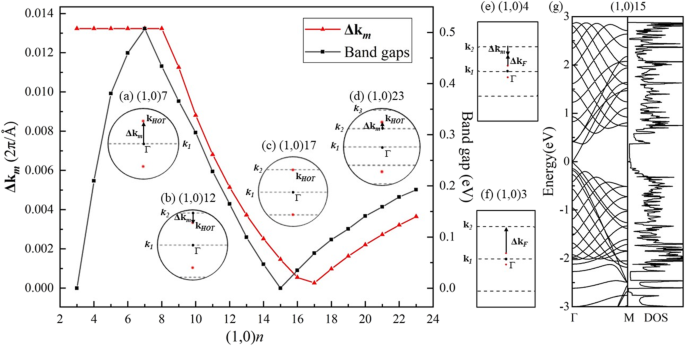
Berechnete Bandlücken (schwarze Linie) und Abstand Δk _m (rote Linie) zwischen k _HEISS und das nächste k Zeile in (1,0) n Rohre. Eingefügte Graphen sind die BZ in der Nähe des Γ-Punktes mit zulässigem k Zeilen k _m (m = 1, 2, 3) (gestrichelte Linien) und der Fermi-Punkt von HOT Graphen-Nanoröhren k _HEISS (rote Punkte) in der Tube (a ) (1,0)7, (b ) (1,0)12, (c ) (1,0)17, (d ) (1,0)23, (e ) (1,0)4 und (f ) (1,0)3. (g ) Bandstrukturen und DOS der Röhre (1,0)15

Obwohl die Δk _m Kurve und Bandlückenkurve haben Ähnlichkeiten in der Form, die Unterschiede zwischen ihnen sind auch offensichtlich, nämlich dass die Δk _m Plot zeigt eine "Verzögerung" der Änderung bei n ≥ 7 und unterscheidet sich vollständig von der Bandlückendarstellung bei 3 ≤ n ≤ 7 ​​Der Grund ist, dass der Fermi-Punkt in HOT Graphen-Nanoröhren (k _F ) hat die gleiche Koordinate wie der ursprüngliche Fermi-Punkt in HOT Graphen (k _HEISS ) im vorherigen Abschnitt, wo die Bandlückenänderung erläutert wurde. Der Fermi-Punkt (k _F ) in Nanoröhren verschiebt sich weg vom Ursprungs-Fermipunkt (k _HEISS ) in HEISS Graphenblatt unter dem Krümmungseffekt. Daher ist die k _F Verschiebung (Δk _F = k _F –k _HEISS )-Effekt trägt zu den Fehlanpassungen zwischen dem Abstand Δk . bei _m und die Bandlücken. Wie berechnet in (0,1) n Röhren (Abb. 6), die k _F in (1,0) n Rohre verschiebt sich auch zum äußeren BZ in Richtung des symmetrischen Punktes X unter der Krümmung. Wenn also das nächste k _m sitzt zwischen den k _HEISS und der Γ-Punkt, die Entfernung Δk _m unterschätzt die Bandlücke (z. B. 17 ≤ n ≤ 24 in Abb. 9d). Andernfalls das nächste k _m sitzt am äußeren k _HEISS Punkt, führt dies zu einer Überschätzung der Bandlücke (z. B. 7 ≤ n ≤ 17 in Abb. 9b). In kleinen Nanoröhren (3 ≤ n ≤ 7), die k _F der Verschiebungseffekt wird unter der großen Wachstumsrate der Krümmung verstärkt; folglich verursacht es ein drastisches k _F verschiebt und ändert die Bandlücke. Wenn der Radius kleiner wird als n = 8, das k ₁ wird dem k . am nächsten _HEISS Angabe einer konstanten Δk _m . Die k _F Der Verschiebungseffekt ist so stark, dass er das k bewegt _F weiter von k ₁ aber näher am k ₂ (Abb. 9e). Die k _F Schalteffekt gewinnt den Wettbewerb mit dem k Linien bewegen und beginnt seitdem die Bandlücken zu bestimmen (n 7). Die k _F wechselt ständig zum k ₂ mit hoher Geschwindigkeit, sodass der Abstand zwischen k _F und k ₂ wird immer kleiner. Daher nimmt die Bandlücke von (1,0)7 auf (1,0)3 ab (Abb. 9). Endlich die k _F holt k ein ₂ und überquert es bei n = 3(Abb. 9f). Diese Kreuzung eines k Linie mit dem k _F ergibt den Dirac-Punkt in der Röhre (1,0)3, der die Halbmetallizität (Abb. 8) verursacht, wie in den vorherigen Abschnitten diskutiert. Weitere Verringerung des Radius auf n = 2 öffnet eine Lücke von 0,848 eV in der Röhre (1,0)2 (Abb. 8). Diese Lücke ist so groß und wird als außerhalb der k angesehen _F Verschiebungsschema und ist daher in Abb. 9 nicht dargestellt. Zusammenfassend lässt sich sagen, dass es einen Konkurrenzmechanismus zwischen den k Linienbewegung und das k _F Verschiebung bei der Bestimmung der Bandlücken. Die k _F Schalteffekt führt in kleinen Röhren (7 ≥ n ≥ 3), während die k Linie bewegte Leitungen in großen Röhren (n ≥ 8) wobei das k _F Verschiebungseffekt wird ausgeblendet. Die Höhe der k _F Verschiebung wird auf 0,0015 2π/Å bei n . geschätzt = 15 und 0,0238 2π/Å bei n = 3, da die Bandlücken 0 eV betragen, wobei das verschobene k _F Punkt liegt auf dem erlaubten k Linien. Es ist zu erkennen, dass die k _F Die Verschiebung ist bei einem kleinen Rohr (Rohr (1,0)3) 15,86-mal größer als bei einem großen Rohr (Rohr (1,0)15).

In HEISS Graphen sind die Kohlenstoffatome alle dreifach koordiniert, daher spielt das vierte Valenzelektron eine Schlüsselrolle für dessen Leitfähigkeit. Die berechnete bandzerlegte Ladungsdichte ± 0.15 eV um das Fermi-Niveau (Abb. 10) zeigt die Verteilung der Elektronen im Dirac-Kegel. Only the electrons on the 8–8 bonds (Fig. 10a) have an overlapping and the side view (Fig. 10b) shows that the electrons distribute perpendicularly to the HOT graphene sheet, which indicates that the Dirac cone consists of π states. Therefore, the electron overlapping on the 8–8 bonds (enlarged side view in Fig. 10a) is considered to be localized π states. In big nanotubes such as (0,1)6 (Fig. 10c), the charge density is similar to the HOT graphene sheet showing localized π bonds on 8–8 bonds (enlarged side view in Fig. 10c). As the radius decreases to (0,1)2, whose conductivity transforms to metal (Fig. 6), the 8–8 bonds show several deformations (Fig. 10d). Firstly, these states are no longer symmetric with respect to the tube wall. The overlapping of the π state outside the tube wall breaks apart while the π states inside keep overlapping with each other. Besides the 8–8 π bonds, new π bonds form on 4–8 in (0,1)2. These bonds are similar to the deformed 8–8 bonds:separated π states outside the tube wall and overlapping π states inside the tube wall. Every 4–8 bond connects two 8–8 bonds adjacent to it, forming a delocalized π overlapping inside the tube along the tube axis direction. The enlarged side view in Fig. 10d shows the connection between 4 and 8 and 8–8 bonds as a segment of the whole delocalized bond. Therefore, the metallicity in tube (0,1)2 can be attributed to the delocalized π overlapping in the 4–8 and 8–8 bonds along the tube axis direction which provides a pathway for the electrons to travel along the tube. When the radius keeps decreasing, the conductivity disappears and the (0,1)1 tube becomes a semimetal again (Fig. 6). Different from all the other (0,1) n tubes, the 8–8 overlapping (Fig. 10e) in nanotube (0,1)1 is totally broken up; instead, 4–8 overlapping and 4–6 overlapping plays the major role in the Dirac cones. These two bonds belong to two opposite edges in the same carbon tetragons and are arranged parallel to the tube axis. Furthermore, they are no longer π states. Based on the electronic state analysis, a σ-π hybridization takes place at the Fermi level under such a strong curvature in nanotube (0,1)1. It is verified by the charge density which shows the electron states distribute closely to the bond axis (enlarged side view in Fig. 10e). Strongly modified low-lying σ states are introduced at the Fermi level as discussed in the preceding sections (blue line in Fig. 6). Therefore, the σ-π hybrid states in the 4–8 and 4–6 bonds are considered the reason for the semimetallicity in (0,1)1, which is essentially different from the other semimetallic tubes (0,1) n (n  ≥ 3). In another set of HOT graphene nanotubes, the band gaps show adjustability with different tube radius (Fig. 9). The charge densities also present an evolution with the tube radii in Fig. 11. The band decomposed charge density of tube (1,0)9 in Fig. 11a and b shows the localized π states overlapping in both the VBM and CBM. The VBM is contributed by π states on 6–6 bonds and 8–8 bonds (Fig. 11a). The CBM is contributed by π states on part of 4–8 and 6–8 bonds (Fig. 11b). The 4–6 bonds have no states on both of the VBM and CBM. When the (1,0) n tubes become semimetallic at some specific radii, such as n  = 15, the VBM and CBM meet with each other. Band decomposed charge density ± 0.15 eV around the Fermi level of (1,0)15 nanotube show the different distribution of electrons from the semiconductive tubes. More importantly, it exhibits a similar distribution to the semimetallic HOT graphene sheet and (0,1) n tubes. The localized π bond of (1,0)15 only locates on the 8–8 bonds. This redistribution of electron in (1,0) n tubes causes the conductivity change.

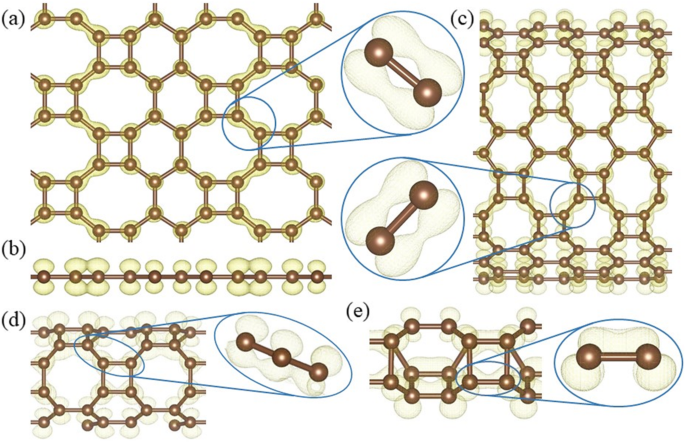
Band decomposed charge densities around the Fermi level of (a ) HOT graphene, (b ) the corresponding side view, and HOT graphene nanotubes (c ) (0,1)6, (d ) (0,1)2, and (e ) (0,1)1 with corresponding enlarged side views

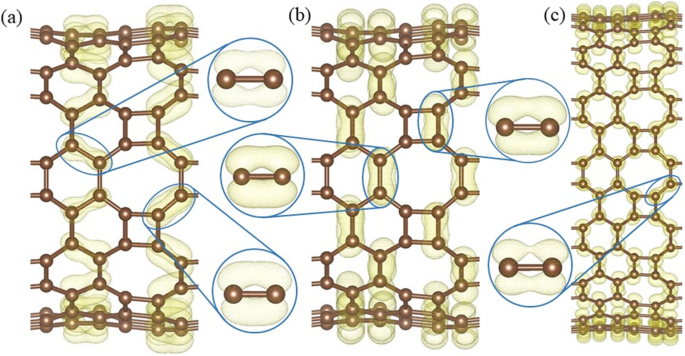
Band decomposed charge densities at (a ) VBM, and (b ) CBM of HOT graphene nanotube (1,0)9; (c ) charge densities around the Fermi level of the HOT graphene nanotube (1,0)15 with the localized π bond in the enlarged side view

Schlussfolgerung

A new graphene allotrope named HOT graphene is constructed by carbon hexagons, octagons, and tetragons showing Dirac cone and high Fermi velocity, which implies that the honeycomb structure is not an indispensable condition for Dirac fermions to exist. The semiconductivity of HOT graphene is dependent on the localized π bonding. A corresponding series of nanotubes is rolled up from the HOT graphene sheet and shows distinctive electronic structures depending on the topology. The set of (0,1) n (n  ≥ 3) HOT graphene nanotubes reveals a character of semimetallicity and Dirac cones that are composed by π states. A non-negligible k _F shifting along the allowed k line arises under the curvature effect when the tube radius gets smaller (3 ≤ n  ≤ 5). However, the ultra-small nanotube (0,1)2 begins to deviate from the π state-based k _F shifting effect showing a transformation to metallicity. Finally, an σ-π hybridization takes the place of the π states at Fermi level in nanotube (0,1)1, where a low-lying σ* band intersection appears at the Fermi level and forms a semimetallicity again. Another set of tubes (1,0) n shows various band gaps (0~ 0.51 eV), which is continuously adjustable with the tube size. The band gaps of (1,0) n (n  ≥ 3) nanotubes turn out to be determined by a competition mechanism between the k line moving and the k F shifting effect. The zone-folding approximation indicates a k line moving and results in the zigzag and periodical band gap changing curve in big tubes (n  ≥ 8), while the k F shifting effect gets stronger and causes a dramatic decrease of band gaps in small tubes (7 ≥ n  ≥ 3). Zero-gap semimetallic tubes appear periodically under the competition.

Verfügbarkeit von Daten und Materialien

Authors declare that the datasets used and/or analyzed during the current study are available to the readers and included in this article.

Abkürzungen

1D:

Eindimensional

2D:

Zweidimensional

3D:

Dreidimensional

BZ:

Brillouin zone

CBM:

Leitungsband-Minimum

DFT:

Dichtefunktionaltheorie

DOS:

Density of states

GGA:

Generalized-Gradient Approximation

HOT :

Hexagons, octagons, and tetragons

PBE:

Perdew–Burke–Ernzerh

VASP:

Vienna Ab initio Simulation Package

VBM:

Valenzband-Maximum