Untersuchung der Thermometrie in zweidimensionalem Sb2Te3 aus der temperaturabhängigen Raman-Spektroskopie

Einführung

Topologische Isolatoren (TIs) sind die neue Klasse von Quantenmaterialien mit einer breiten Energielücke im Volumen und oberflächenlückenlosen Dirac-ähnlichen Zuständen, die unter Zeitumkehrsymmetrie geschützt sind [1,2,3]. Diese Materialien sind vielversprechend für ein breites Anwendungsspektrum, darunter Feldeffekttransistoren [4, 5], Infrarot-THz-Detektoren [6], Magnetfeldsensoren [7, 8] und Thermoelektrizität [9, 10]. Die thermoelektrische Leistung jedes Materials bei einer Temperatur von T wird durch die dimensionslose Gütezahl ZT . bestimmt (ZT = S ² σT/κ , wobei S , σ und κ bezeichnen den Seebeck-Koeffizienten, die elektrische Leitfähigkeit bzw. die Wärmeleitfähigkeit [11, 12]. Die reduzierte Dimensionalität dieser Materialien hat sich als einer der gängigsten Ansätze erwiesen, um die Wärmeleitfähigkeit zu minimieren und einen hohen ZT . zu erzielen [13]. Um die Wärmeleitfähigkeit zu minimieren, ist es sehr wichtig, die Phononendynamik in diesem Materialtyp zu verstehen, insbesondere die Phonon-Phonon- und Elektron-Phonon-Wechselwirkungen, die alle einen großen Einfluss auf die Leistung thermoelektrischer Geräte haben [14, 15].

Die Raman-Streuung hat sich aufgrund ihrer zerstörungsfreien und mikroskopischen Natur als wichtiges Werkzeug zur Untersuchung der Schwingungsmoden in einem Material erwiesen [16, 17]. Es liefert auch wichtige Informationen zu Dotierung, Dehnungstechnik und Kristallphasen [18, 19]. Während die Raman-Charakterisierungen von Phononen in verschiedenen 2D-TIs bei Raumtemperatur in der Literatur gut untersucht wurden [20, 21], befinden sich die Raman-Charakterisierungen in Abhängigkeit von der Temperatur noch in den Kinderschuhen. Darüber hinaus ist bekannt, dass Temperaturänderungen die Abstände zwischen den Atomen variieren und verschiedene Phononenmoden im Kristall beeinflussen können [14]. Daher sind temperaturabhängige Raman-Spektren gut geeignet, um Informationen über die Wärmeleitfähigkeit von Materialien sowie Isotopeneffekte und Phononenlebensdauern zu erhalten [22, 23].

In dieser Arbeit präsentieren wir leistungsabhängige Raman-Spektroskopie bei Raumtemperatur und temperaturabhängige Raman-Spektroskopie im Temperaturbereich zwischen 100 und 300 K von 2D Sb₂ Te₃ Kristalle in verschiedenen Dicken. Die Variation der Raman-Peakposition und der Halbwertsbreite (FWHM ) in Bezug auf Temperatur und Leistung wurden analysiert, und die Ergebnisse werden interpretiert, um den Wärmeausdehnungskoeffizienten und die Wärmeleitfähigkeit von Sb₂ . zu bestimmen Te₃ Flocken im Rahmen der Thermometrie-Studie. Der Wert der Wärmeleitfähigkeit für Sb₂ Te₃ Flocken mit einer Dicke von 115 nm wurden geschätzt und die Rolle des Substrats bei der Verbesserung der Wärmeleitfähigkeit wurde diskutiert.

Methoden

Mechanisches Peeling wurde an hochwertigem Bulk-Sb₂ . durchgeführt Te₃ Kristall (2D Semiconductors, USA) unter Verwendung der Standard-Scotch-Tape-Technik [24], um Sb₂ . zu erhalten Te₃ Flocken unterschiedlicher Dicke (65 nm, 80 nm, 115 nm, 200 nm und 400 nm) auf 300 nm SiO₂ /Si-Substrate. Exfolierte Proben wurden mit Hilfe eines optischen Mikroskops (LV100ND-Nikon-Mikroskop) identifiziert. Die seitlichen Größen des Sb₂ Te₃ Nanoflocken werden im Bereich von 5–7 μm gefunden. Park NX-10 AFM (Atomkraftmikroskopie) wurde verwendet, um die Dicke des Sb₂ . zu messen Te₃ Flocken im kontaktlosen Modus.

Die Raman-Spektren wurden an verschiedenen Flocken unter Verwendung eines konfokalen Mikro-Raman-Systems von HORIBA LabRAM in einer Rückstreugeometrie unter Verwendung einer 632-nm-Laseranregung gemessen. Als Anregungsquelle wurde ein Laser mit einer Spotgröße ~ 1 µm und einer durchstimmbaren optischen Leistung von  ~ 0,4 bis 2,6 mW verwendet. Die Spektren wurden unter Verwendung eines Spektrometers gesammelt, das mit einer mit flüssigem Stickstoff gekühlten CCD-Kamera ausgestattet war. Die Spektren wurden im Frequenzbereich von 100 bis 200 cm ⁻¹ . aufgenommen mit einer spektralen Auflösung von 1 cm ⁻¹ . Alle Messungen wurden mit einer Integrationszeit von 10 s, einer Erfassung von 10 und einem Gitter von 1800 durchgeführt. Für Raumtemperaturmessungen (RT) wurde ein 100 × -Objektiv verwendet, während ein 50 × -Objektiv mit großem Arbeitsabstand für Niedertemperaturmessungen verwendet wurde.

Ergebnisse und Diskussion

Sb₂ Te₃ ist ein TI, das in der rhomboedrischen Kristallstruktur mit der Raumgruppe D . kristallisiert ⁵ _3d (\(R\overline{3}m\)), und seine Elementarzelle enthält fünf Atome [20]. Dieser Kristall wird durch Stapeln von Fünf-Atom-Schichten entlang der z- . gebildet Richtung, die wie in Abb. 1 als Fünffachschicht (QL) bezeichnet wird, mit einer Dicke von etwa 0,96 nm [20]. Aus dem Atomregister können wir sehen, dass das Sb-Atom zwischen zwei Te-Atomen eingeschlossen ist, mit dem Te ⁽²⁾ Atom als Inversionszentrum. Diese zentrosymmetrische Eigenschaft der Kristallstruktur führt zu voneinander unabhängigen Raman-aktiven Moden. Die Atome innerhalb einer einzelnen QL werden durch starke kovalente Kräfte zusammengehalten, während die Kraft zwischen den QLs viel schwächer und vom Typ van der Waals ist. Aufgrund der schwachen Van-der-Waal-Kraft in Richtung außerhalb der Ebene ist es möglich, dünne Schichten dieses Materials mechanisch von seinen Kristallen abzulösen. Obwohl abgeblätterte Proben die Zusammensetzung und Struktur von Volumenkristallen beibehalten, ändert sich die Phononendynamik, wenn ihre Dicke auf den Nanobereich reduziert wird [25, 26].

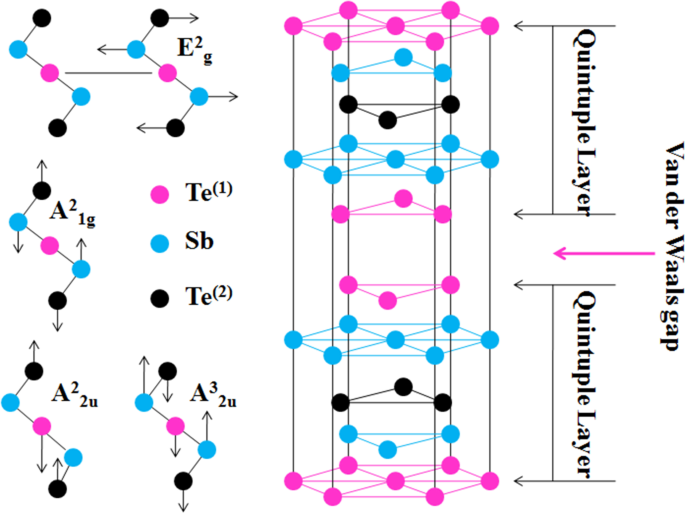
Schema von Sb₂ Te₃ Kristall, der die Anordnung der Atome und die Van-der-Waals-Lücke zeigt. Die rosa, hellblauen und schwarzen Kreise repräsentieren das Te ⁽¹⁾ , Sb und Te ⁽²⁾ Atome bzw. Das linke Feld zeigt die möglichen Phononenmodi im Frequenzbereich 100 cm ⁻¹ bis 200 cm ⁻¹ . Die Pfeile stellen die Schwingungsrichtung der konstituierenden Atome dar

Optische Schliffbilder (OM) von drei verschiedenen Sb₂ Te₃ Nanoflocken abgeblättert auf SiO₂ /Si-Substrat sind in Fig. 2a-c gezeigt. Die seitlichen Größen der Flocken liegen im Bereich von 5–7 μm, was groß genug ist, um in OM beobachtet zu werden. Man kann beobachten, dass der Farbkontrast der Flocken sehr empfindlich auf die Dicke der Flocken reagiert d. h. unterschiedliche Dicken zeigen unterschiedliche Farbkontraste. Die Dicken dieser präparierten Flocken wurden durch Rasterkraftmikroskopie (AFM) gemessen, die im unteren Feld von Abb. 2 zusammen mit ihren Querschnittshöhenprofilen (Abb. 2d–f) dargestellt sind. Die Dickenwerte dieser Flocken wurden auf 65 nm, 115 nm und 200 nm geschätzt und erwiesen sich mit Ausnahme einiger Unebenheiten als nahezu einheitlich. Alle Raman-Messungen wurden jedoch an der Position der Flocken durchgeführt, an der die Einheitlichkeit beibehalten wurde.

a-c OM-Bilder von Sb₂ Te₃ Flocken mit einer Dicke von 65 nm, 115 nm bzw. 200 nm. d-f Ihre repräsentativen AFM-Bilder und Höhenprofile.

Abbildung 3 zeigt die leistungsabhängigen Raman-Spektren von über drei bei Raumtemperatur gemessenen Flocken, die aus vier Schwingungsmoden bestehen, darunter zwei aktive Raman-Modi E ² _g und A ² _1g zugewiesen bei Frequenzen ~ 125 cm ⁻¹ und ~ 169 cm ⁻¹ , und zwei aktive IR-Modi A ² _2u und A ³ _2u zugewiesen bei ~ 115 cm ⁻¹ und ~ 144 cm ⁻¹ , bzw. [20, 27]. Es ist deutlich zu beobachten, dass es bei einer Zunahme der Laserleistung für alle Flocken (65 nm, 115 nm und 200 nm) eine Rotverschiebung sowie eine Zunahme der Spitzenintensität aller Raman-Moden gibt. Diese Veränderungen legen nahe, dass die Erhöhung der Laserleistung zu einer erheblichen Erhöhung der lokalen Temperatur an der Probenoberfläche führt [28]. Sb₂ Te₃ Flocken mit den Dicken 115 nm und 200 nm weisen alle vier Modi auf (A ² _2u , E ² _g , A ³ _2u und A ² _1g ) für niedrige Laserleistung von 0,402 mW und A ² _2u und E ² _g Moden werden bei weiterer Leistungssteigerung zusammengeführt, was an der asymmetrischen Linienbreite von A ² . zu sehen ist _2u /E ² _g Modi in Abb. 3b, c. Abbildung 3a zeigt Raman-Spektren von Sb₂ Te₃ Flocke mit einer Dicke von 65 nm bei drei unterschiedlichen einfallenden Laserleistungen und die gesamten Spektren zeigen nur zwei Raman-Moden E ² _g und A ³ _2u bei Raumtemperatur. In diesem Fall die Form von E ² _g Peaks für alle Laserleistungen sieht asymmetrisch aus, was bedeutet, dass auch beide A ² . verschmelzen _2u und E ² _g Modi ähnlich dicken Flakes (115 nm, 200 nm) bei hoher Laserleistung. Die A ² _1g fehlt für diese Dicke völlig. Wir glauben, dass dieser Modus die Charakteristik von Schwingungen außerhalb der Ebene wäre, die für diese Dicke nicht so wichtig wären.

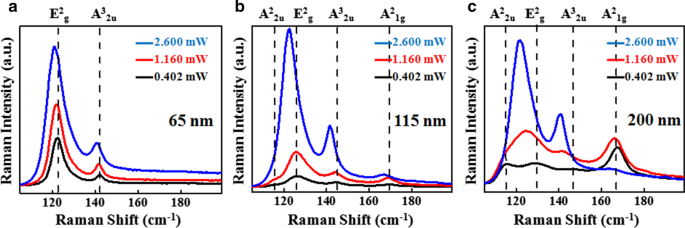
a-c Leistungsabhängige Mikro-Raman-Spektren von 65-nm, 115-nm und 200-nm Sb₂ Te₃ Flocken bzw. Die Spektren werden mit einem 632-nm-Laser mit drei verschiedenen Leistungen 0,402 mW, 1,160 mW und 2,600 mW gemessen. Die gestrichelten Linien zeigen die Position der Raman-Modi.

Der Vergleich der Raman-Spektren von drei verschiedenen Dicken (65 nm, 115 nm und 200 nm) von Proben bei einer bestimmten Laserleistung von 0,402 mW ist in Abb. 4a dargestellt. Alle beobachteten Raman-Modi und ihre Zuordnungen sind in Tabelle 1 aufgelistet. Es ist sehr interessant zu beobachten, dass A ² _1g und A ² _2u Modi für 200-nm-Flocken besitzen eine höhere Intensität als die anderen beiden Modi (E ² _g und A ³ _2u ). A ² _1g und A ² _2u Moden reagieren empfindlicher auf die Dicke, da sie Schwingungen außerhalb der Ebene und die Van-der-Walls-Wechselwirkungen zwischen den Schichten widerspiegeln. Im Fall von Sb₂ Te₃ Flocken mit einer Dicke von 65 nm und 115 nm, die Form von E ² _g Peaks für alle Laserleistungen sieht asymmetrisch aus, was darauf hindeutet, dass beide A ² . verschmelzen _2u und E ² _g Modi. Die A ² _1g fehlt für Sb₂ . völlig Te₃ Flocke mit einer Dicke von 65 nm. Dieser spezielle Raman-Modus würde aufgrund von Schwingungen außerhalb der Ebene entstehen, die für diese Dicke möglicherweise nicht ansprechen. Für E ² . wird eine Rotverschiebung beobachtet _g und A ³ _2u Phononenmoden bei dünneren Flocken, ähnlich den von Zang et al. [30], während A ² _1g Modus zeigt eine leichte Blauverschiebung (siehe Tabelle 1). Die Spitzenintensitäten von 65-nm-Sb₂ Te₃ Flocken sind bei gleicher Anregungslaserleistung stärker ausgeprägt als bei dickeren, und dieses Phänomen kann auf optische Interferenzverstärkungen zurückgeführt werden, die sowohl für den Anregungslaser als auch für die emittierte Raman-Strahlung im geschichteten TI/SiO_{2 /Si-System [30], das auch für Bi2 . berichtet wird Se3 und Bi2 Te3 [26, 31]. Aus den leistungsabhängigen Raman-Spektren von 115-nm-Sb2 Te3 Flocke (Abb. 3b), die Raman-Frequenzen von E ² g &A ² 1g Moden wurden als Funktion der Laserleistung extrahiert, wie in Abb. 4b gezeigt. Die Änderung der Phononenfrequenz mit der Änderung der einfallenden Laserleistung d. h. Leistungskoeffizient (δω/δP ) wurde aus der linearen Anpassung an die extrahierten Daten geschätzt, die zu − 1,59 cm ⁻¹ . ermittelt wurden /mW und − 1,32 cm ⁻¹ /mW entspricht E ² g und A ² 1g Modi.}

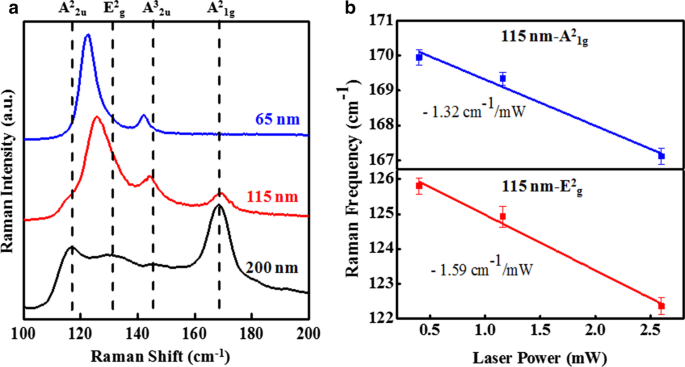
a Vergleich dickenabhängiger Mikro-Raman-Spektren von 65 nm, 115 nm und 200 nm Sb₂ Te₃ Flocken bei 0,402 mW Laserleistung. Die gestrichelten Linien zeigen die Position der Raman-Modi. b Raman-Frequenz vs. Laserleistung von E ² _g &A ² _1g Modi für 115-nm-Sb₂ Te₃ Flocke. Die durchgezogenen Linien sind die linearen Anpassungen an die experimentellen Daten (Symbole). Die berechneten Steigungen aus den linearen Anpassungen werden als Einschübe angezeigt. Die Unsicherheit bei der Raman-Frequenzmessung wurde als Fehlerbalken angezeigt

Die temperaturabhängigen Raman-Spektren wurden im Temperaturbereich von 100 bis 300 K gemäß Abb. 5 für drei verschiedene Flakes mit den Dicken 80 nm, 115 nm bzw. 400 nm bei 1,16 mW Laserleistung gemessen. Die OM-, AFM-Bilder zusammen mit Höhenprofilen von 80-nm- und 400-nm-abgeblättertem Sb₂ Te₃ Flocken sind in Zusatzdatei 1:ergänzende Informationen S1 enthalten. Bei der unteren Temperatur von 100 K, vier charakteristische Raman-Modi (A ² _2u , E ² _g , A ² _1g und A ³ _2u ) von Sb₂ Te₃ deutlich unterscheidbar sind, während A ² _2u und E ² _g Raman-Modi verschmelzen zu höheren Temperaturen, d. h. 220 K und 300 K. Rotverschiebung und Peakverbreiterung wurden in allen Raman-Modi beobachtet (A ² _2u , E ² _g , A ² _1g und A ³ _2u ) mit der Temperaturerhöhung von 100 auf 300 K. Im Allgemeinen wird die temperaturabhängige Raman-Spektroskopie häufig verwendet, um die Wärmeausdehnung, Wärmeleitung und Zwischenschichtkopplung zu untersuchen [15, 31, 32]. Darüber hinaus hat die Spitzenfrequenz eine lineare Abhängigkeit von der Temperatur, die gegeben ist durch [15],

wo ω ₀ ist die Schwingungsfrequenz dieser Phononenmoden bei absoluter Nulltemperatur und χ ist der Temperaturkoeffizient erster Ordnung dieser Phononenmoden. Es wurde berichtet, dass die thermische Expansion und Kontraktion der Kristall- und Phononenmoden zu einer Abhängigkeit der Peakposition in der Raman-Spektroskopie von der Temperatur führen kann [33].

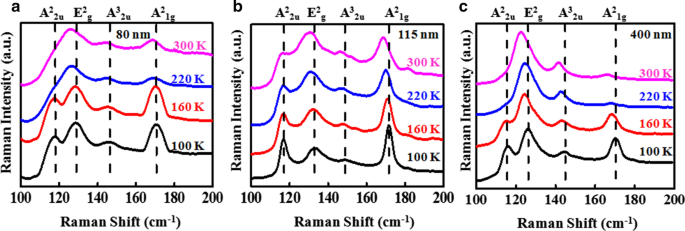
a-c Temperaturabhängige Mikro-Raman-Spektren von Sb₂ Te₃ mit einer Dicke von 80 nm, 115 nm bzw. 400 nm. Die schwarzen, roten, blauen und hellblauen Kurven repräsentieren die Raman-Spektren bei 100 K, 160 K, 220 K bzw. 300 K für eine Laserleistung von 1,16 mW. Die gestrichelten Linien zeigen die Position der Raman-Modi.

Die Peakposition im Vergleich zur Temperatur von E ² _g &A ² _1g Modi sind in Fig. 6a bzw. b für Proben unterschiedlicher Dicke gezeigt. Die Kurven der Peakposition gegen die Temperatur (Abb. 6a, b) wurden unter Verwendung von Gl. 1, um den Temperaturkoeffizienten erster Ordnung (χ ) und die Werte des Temperaturkoeffizienten erster Ordnung für E ² _g &A ² _1g Raman-Modi sind in Tabelle 2 aufgeführt. Die Erweiterung in FWHMs von E ² _g &A ² _1g Raman-Moden mit Temperaturerhöhung sind in Fig. 7a bzw. b gezeigt. Die Temperaturabhängigkeit des FWHM ist ein Maß für die Phononen-Anharmonizität und nimmt mit steigender Temperatur linear zu. Die einfachste anharmonische Näherung, bekannt als das symmetrische Drei-Phononen-Kopplungsmodell [34], berücksichtigt den optischen Phononenzerfall in zwei Phononen mit gleichen Energien und entgegengesetzten Impulsen. In der vorliegenden Arbeit haben wir den Temperaturkoeffizienten erster Ordnung (χ) . berechnet und Wärmeleitfähigkeit aus temperaturabhängigen Raman-Spektren. Wir analysieren jedoch nicht das FWHM im Kontext von ZT da es keine so direkte Relevanz dafür hat.

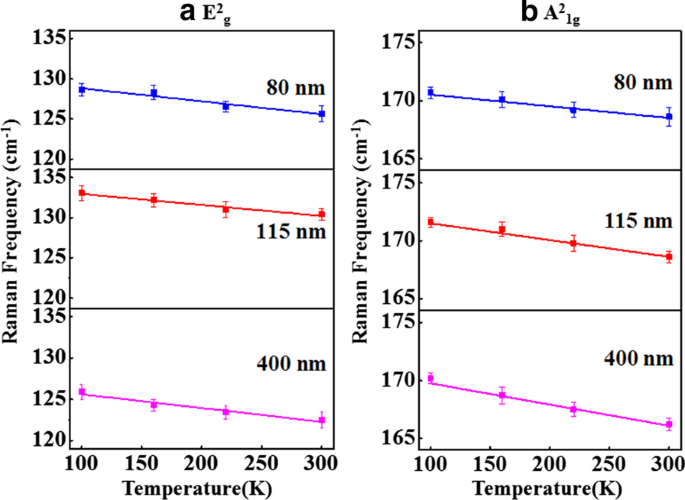
Raman-Frequenz vs. Temperatur-Diagramm von a E ² _g Modus und b A ² _1g Modus für 80-nm, 115-nm und 400-nm Sb₂ Te₃ Flocken. Die durchgezogenen Linien sind die linearen Anpassungen an die experimentellen Daten (Symbole). Die Unsicherheit bei der Raman-Frequenzmessung wurde als Fehlerbalken angezeigt

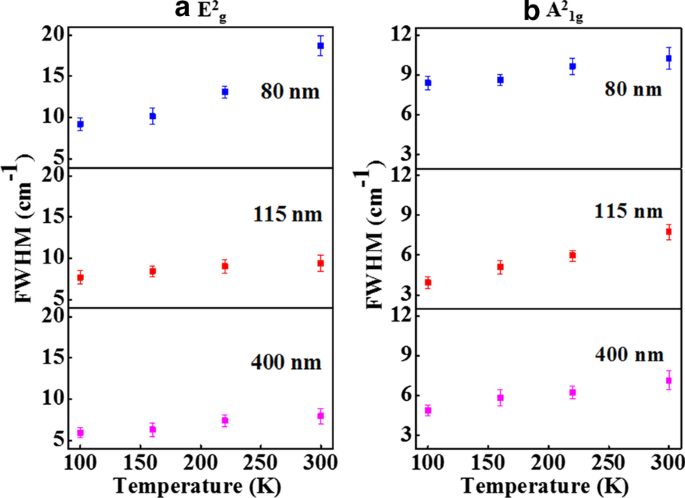
FWHM vs. Temperaturdiagramme von a E ² _g Modus und b A ² _1g Modus für 80-nm, 115-nm und 400-nm Sb₂ Te₃ Flocken. Die Unsicherheit bei der FWHM-Schätzung wurde als Fehlerbalken dargestellt

Es wird beobachtet, dass der Wert der Temperaturkoeffizienten erster Ordnung (χ ) für E ² _g und A ² _1g Modus liegt in der Größenordnung von 10 ^–2 cm ⁻¹ /K. Der Wert von χ entsprechend A ² _1g Modus verringert sich von − 2 × 10 ^–2 bis − 1 × 10 ^–2 cm ⁻¹ /K wenn die Dicke von Sb₂ Te₃ Flocke wird von 400 auf 80 nm reduziert. So niedrige χ würde eine niedrige Wärmeleitfähigkeit ergeben und eine hohe Gütezahl (ZT ). Der Wert von χ entspricht E ² _g Modus ist nahezu konstant und unabhängig von der Dicke. Jetzt haben wir einen ungefähren Wert der Wärmeleitfähigkeit von Sb₂ . berechnet Te₃ Flocke unter Verwendung der Werte des Leistungskoeffizienten und des Temperaturkoeffizienten erster Ordnung. Die Wärmeleitung durch eine Oberfläche mit der Querschnittsfläche S kann aus der folgenden Gleichung berechnet werden:\(\partial Q/\partial t =-\kappa{\oint}\nabla T.dS,\) wobei Q ist die Wärmemenge, die über die Zeit t . übertragen wird und T ist die absolute Temperatur. Unter Berücksichtigung des radialen Wärmeflusses, Balandin et al.. [40] haben einen Ausdruck für die Wärmeleitfähigkeit von Graphen abgeleitet, der gegeben ist durch

wo h ist die Dicke des 2D-Films des Materials und der lokale Temperaturanstieg ΔT liegt an der Änderung der Heizleistung ΔP . Durch Differenzieren von Gl. (1) in Bezug auf Macht und Substitution (ΔP/ΔT ) in Ausdruck (2) kann die Wärmeleitfähigkeit wie folgt geschrieben werden:

wo κ ist die Wärmeleitfähigkeit, h ist die Dicke des 2D-Films des Materials, χ der Temperaturkoeffizient erster Ordnung ist und (δω/δP ) ist die Änderung der Phononenfrequenz mit der Änderung der einfallenden Laserleistung d. h. Leistungskoeffizient bestimmter Raman-Modi. Die berechnete Wärmeleitfähigkeit beträgt  ~ 10 W/m–K für Sb₂ Te₃ Flocken mit einer Dicke von 115 nm, getragen auf 300 nm SiO₂ / Si-Substrat. Dieser Wert ist relativ höher als die berichtete Wärmeleitfähigkeit anderer TI [41]. Die leichte Verbesserung der Wärmeleitfähigkeit deutet darauf hin, dass das Trägersubstrat eine empfindlichere Rolle spielt, d. h. der Wert der Wärmeleitfähigkeit könnte von Grenzflächenladungen abhängen [42]. Diese höhere Wärmeleitfähigkeit an der substratgetragenen Probe kann auch den geringeren Temperaturanstieg bei hoher Laserleistung im Vergleich zur suspendierten Probe erklären. Der ähnliche Substrateffekt wird auch in Su et al. beschrieben. für schwarze Phosphorschichten [42]. Guo et al. berichteten auch, dass in bestimmten Regionen der Effekt der Phononenstreuung unterdrückt und die Wärmeleitfähigkeit von Nanomaterialien aufgrund der kopplungsinduzierten Verschiebung des Phononenbandes zum Niederwellenvektor überraschend erhöht werden kann [43]. Kürzlich wurde auch über eine theoretische Studie zum Substrateffekt der Wärmeleitfähigkeit von Graphen berichtet. Die Autoren fanden auch heraus, dass je nach Kopplungsbedingung sowohl die Verringerung als auch die Erhöhung der Wärmeleitfähigkeit durch das Substrat induziert werden kann [44]. Aus Gl. 3 ist die Wärmeleitfähigkeit direkt proportional zum Temperaturkoeffizienten erster Ordnung, und es ist bekannt, dass der Gütefaktor (ZT ) ist umgekehrt proportional zur Wärmeleitfähigkeit. Daher niedriger χ und κ versprechen einen hohen ZT .

Weitere Arbeiten sind in Arbeit, um Sb₂ . zu erreichen Te₃ Nanoflocken mit einer Dicke von weniger als 7 QL, was die Begrenzungsgrenze von 2D TI bei Verwendung einer Peeling-Technik mit Hilfe von speziellem Klebeband oder durch chemische Gasphasenabscheidung ist. Es wird erwartet, dass Flocken mit solch geringer Dicke einen sehr niedrigen Temperaturkoeffizienten (~ 10 ^–3 bis 10 ^–4 cm ⁻¹ /K) und ein hohes ZT . Mit hohem ZT , 2D Sb₂ Te₃ hätte großes Potenzial im Bereich thermoelektrischer Anwendungen.

Schlussfolgerungen

Zusammenfassend haben wir erfolgreich 2D Sb₂ . synthetisiert Te₃ verschiedener Dicken im Bereich von 65–400 nm mithilfe mechanischer Exfoliation und untersuchten die Thermometrie dieser Nanoflocken. Die Temperaturabhängigkeit der Peakposition und Linienbreite von Phononenmoden A ² _1g und E ² _g Die Modi wurden analysiert, um den Temperaturkoeffizienten zu bestimmen, der in der Größenordnung von 10 ^–2 . liegt cm ⁻¹ /K. Der Temperaturkoeffizient in Richtung außerhalb der Ebene nimmt mit Abnahme von Sb₂ . ab Te₃ Dicke. Ein solch niedriger Temperaturkoeffizient würde es begünstigen, einen hohen ZT . zu erreichen und ebnen den Weg, dieses Material als hervorragende Kandidaten für thermoelektrische Materialien zu verwenden. Unter Verwendung von Temperaturkoeffizienten- und Leistungskoeffizientenwerten wurde die Wärmeleitfähigkeit von 115 nm Sb₂ Te₃ Flockenunterstützt auf 300-nm-SiO₂ / Si-Substrat wurde auf  ~ 10 W/m–K geschätzt. Die etwas höhere Wärmeleitfähigkeit im Vergleich zu anderen TIs legt nahe, dass das Trägersubstrat die Wärmeableitung des Sb₂ . erheblich beeinflusst Te₃ Flocke.

Verfügbarkeit von Daten und Materialien

Die Daten, die die Ergebnisse dieser Studie stützen, sind auf begründete Anfrage beim entsprechenden Autor erhältlich.

Abkürzungen

TIs:

Topologische Isolatoren

ZT :

Verdienstzeichen

OM:

Optisches Schliffbild

AFM:

Rasterkraftmikroskopie

FWHM :

Volle Breite auf halbem Maximum

QL:

Fünffachschicht