Venn-Diagramme und -Sets

Mathematiker verwenden Venn-Diagramme um die logischen Beziehungen von Mengen zu zeigen (Sammlungen von Objekten) zueinander. Vielleicht haben Sie Venn-Diagramme bereits in Ihrem Algebra- oder anderen Mathematikstudium gesehen. Wenn ja, erinnern Sie sich vielleicht an überlappende Kreise und die Gewerkschaft und Kreuzung von Sätzen.

Wir werden die überlappenden Kreise des Venn-Diagramms überprüfen. Wir werden die Begriffe ODER und UND anstelle von Vereinigung und Schnittmenge verwenden, da dies die Terminologie ist, die in der digitalen Elektronik verwendet wird.

Das Venn-Diagramm verbindet die Boolesche Algebra aus einem vorherigen Kapitel mit der Karnaugh-Karte. Wir werden das, was Sie bereits über Boolesche Algebra wissen, auf Venn-Diagramme beziehen und dann auf Karnaugh-Karten übergehen.

Ein Satz ist eine Sammlung von Objekten aus einem Universum, wie unten gezeigt. Die Mitglieder der Menge sind die in der Menge enthaltenen Objekte. Die Mitglieder des Sets haben normalerweise etwas gemeinsam; Dies ist jedoch keine Voraussetzung.

Aus dem Universum der reellen Zahlen beispielsweise ist die Menge aller positiven ganzen Zahlen {1,2,3…} eine Menge. Die Menge {3,4,5} ist ein Beispiel für eine kleinere Menge oder Teilmenge der Menge aller positiven ganzen Zahlen. Ein weiteres Beispiel ist die Menge aller Männer aus dem Universum der College-Studenten. Fällt dir noch ein paar Beispiele für Sets ein?

Oben links haben wir ein Venn-Diagramm, das die Menge A im Kreis innerhalb des Universums U, der rechteckigen Fläche, zeigt. Wenn alles innerhalb des Kreises A ist, dann ist alles außerhalb des Kreises nicht A. Daher bezeichnen wir über der Mitte die rechteckige Fläche außerhalb des Kreises A als A-nicht statt U. Wir zeigen B und B-nicht in a ähnliche Weise.

Was passiert, wenn sowohl A als auch B im selben Universum enthalten sind? Wir zeigen vier Möglichkeiten.

Schauen wir uns jede der vier oben gezeigten Möglichkeiten genauer an.

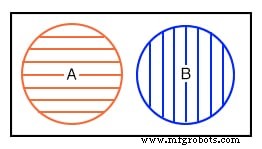
Das erste Beispiel zeigt, dass Menge A und Menge B nach dem Venn-Diagramm nichts gemeinsam haben. Es gibt keine Überlappung zwischen den kreisförmig schraffierten Bereichen A und B. Angenommen, die Mengen A und B enthalten die folgenden Elemente:

A ={1,2,3,4} setze B ={5,6,7,8}

Keines der Mitglieder von Menge A ist in Menge B enthalten, noch ist irgendeines der Mitglieder von B in A enthalten. Somit gibt es keine Überlappung der Kreise.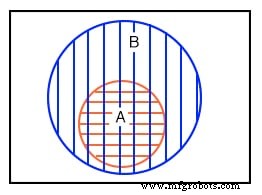

Im zweiten Beispiel im obigen Venn-Diagramm ist Menge A vollständig in Menge B enthalten. Wie können wir diese Situation erklären? Angenommen, die Mengen A und B enthalten die folgenden Elemente:

A ={1,2} setze B ={1,2,3,4,5,6,7,8}

Alle Mitglieder von Menge A sind auch Mitglieder von Menge B. Daher ist Menge A eine Teilmenge von Menge B. Da alle Mitglieder von Menge A Mitglieder von Menge B sind, wird Menge A vollständig innerhalb der Grenze von Menge B gezeichnet.

Es gibt einen fünften nicht gezeigten Fall mit den vier Beispielen. Hinweis:Es ähnelt dem letzten (vierten) Beispiel. Zeichnen Sie ein Venn-Diagramm für diesen fünften Fall.

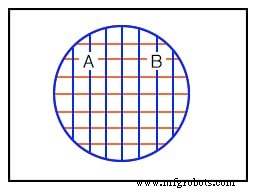
Das dritte Beispiel oben zeigt die perfekte Überlappung zwischen Menge A und Menge B. Es sieht so aus, als ob beide Mengen dieselben identischen Elemente enthalten. Angenommen, die Mengen A und B enthalten Folgendes:

A ={1,2,3,4} setze B ={1,2,3,4}

Daher

 Set A =Set B

Mengen und B sind identisch gleich, weil sie beide dieselben identischen Elemente haben. Die A- und B-Regionen innerhalb des entsprechenden Venn-Diagramms überlappen sich vollständig. Wenn Sie Zweifel haben, was die obigen Muster darstellen, sehen Sie sich die Abbildungen oben oder unten an, um sicher zu sein, wie die kreisförmigen Bereiche vor der Überlappung aussahen.

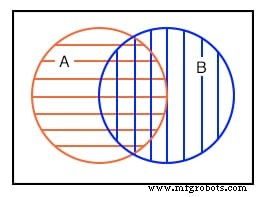
Das vierte Beispiel oben zeigt, dass zwischen Satz A und Satz B im Überlappungsbereich etwas gemeinsam ist. Wir wählen zum Beispiel willkürlich die folgenden Sätze aus, um unseren Standpunkt zu veranschaulichen:

A ={1,2,3,4} setze B ={3,4,5,6}

Set A und Set B haben beide die Elemente 3 und 4 gemeinsam. Diese Elemente sind der Grund für die gemeinsame Überlappung in der Mitte von A und B. Wir müssen uns diese Situation genauer ansehen.

Einführung in das Karnaugh-Mapping Boolesche Beziehungen in Venn-Diagrammen

Industrietechnik

Herstellungsprozess

3d Drucken

Automatisierungssteuerung System

Industrietechnik