Konvertierung von Stern zu Delta und Delta zu Stern. Y-Δ-Transformation

Stern-zu-Delta- und Delta-zu-Stern-Transformation – Y-Δ-Konvertierung

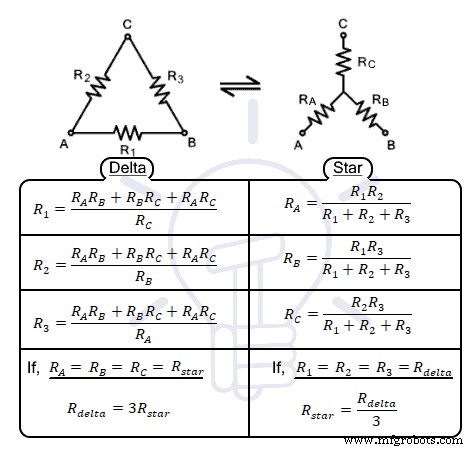
In einem elektrischen Netzwerk kann die Impedanz in verschiedenen Konfigurationen angeschlossen werden. Die gebräuchlichsten dieser Konfigurationen sind entweder stern- oder deltaverbundene Netzwerke. Um komplexe elektrische Netzwerke zu lösen oder zu vereinfachen, verwenden wir die Stern-Dreieck-Wandlungstechnik. Es ersetzt jedes sternverbundene Netzwerk durch sein äquivalentes deltaverbundenes Netzwerk und umgekehrt. Wir geben eine kurze Formelherleitung zur Lastumrechnung zwischen Stern- und Dreieckschaltung.

Stern-Delta-Konvertierung

Wir kennen die Grundlagen von Reihen-, Parallel- oder Kombination von Reihen- und Parallelschaltung, aber Y-Δ ist eine weitere etwas komplexe Konfiguration von Komponenten. Die 3-Phasen-Netze haben drei Drähte und normalerweise sind die Netze in Stern- und Dreieckskonfiguration verbunden . Die 3-Phasen-Versorgung oder die Last, die in beiden Formationen angeschlossen ist, kann in ihr äquivalentes Gegenstück umgewandelt werden. Wir verwenden eine solche Konvertierung, um die mathematischen Berechnungen zu vereinfachen, die für die Schaltungsanalyse eines komplexen elektrischen Netzwerks erforderlich sind.

Delta Connected Network

Das Delta-verbundene Netzwerk wird gebildet, wenn drei Netzwerkzweige oder Impedanzen so zu einer Schleife verbunden werden, dass ihre Köpfe mit den Enden des benachbarten Zweigs verbunden sind. Das resultierende Netzwerk bildet eine Dreiecksform, die einem griechischen Buchstaben Delta „Δ“ ähnelt, weshalb es nach ihm benannt ist. Es ist auch als π (pi)-Netzwerk bekannt, weil es nach der Neuanordnung der Zweige dem Buchstaben ähnelt. Erfahren Sie mehr über Delta Connection im vorherigen Post.

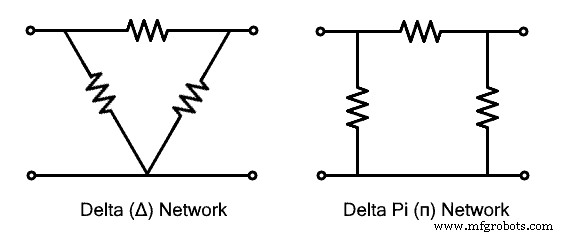
Star Connected Network

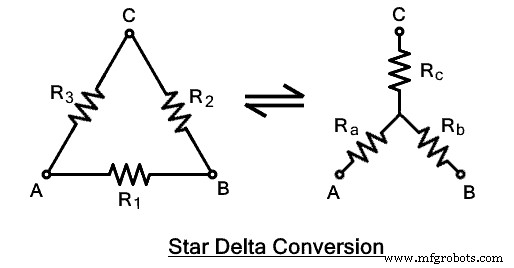
Das sternverbundene Netzwerk wird gebildet, wenn drei Zweige oder Impedanzen an einem gemeinsamen Punkt miteinander verbunden werden. Die anderen Enden der Zweignetze sind frei. Die resultierende Form ähnelt dem Buchstaben „Y“, weshalb es auch als „Y“- oder „Wye“-verbundenes Netzwerk bezeichnet wird. Aufgrund seiner Form nach der Neuanordnung der Netzwerkzweige wird es auch als „T“-verbundenes Netzwerk bezeichnet. Erfahren Sie mehr über Star Connection im vorigen Beitrag. 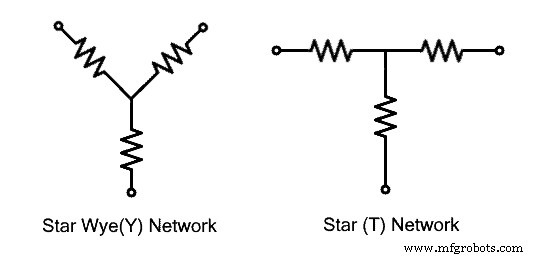Die oben angegebenen Schaltungen können mit der folgenden Transformation konvertiert werden. Bei der Transformation müssen die Klemmen A, B, C in gleicher Position bleiben, lediglich die Impedanz &ihre Anordnung ändert sich. Die folgende Abbildung veranschaulicht die oben gegebene Aussage.

Delta-zu-Stern-Konvertierung

Das Delta-verbundene Netzwerk kann mithilfe einer Reihe von elektrischen Formeln in eine Sternkonfiguration umgewandelt werden. Lassen Sie uns die Gleichung für jede Impedanz ableiten. 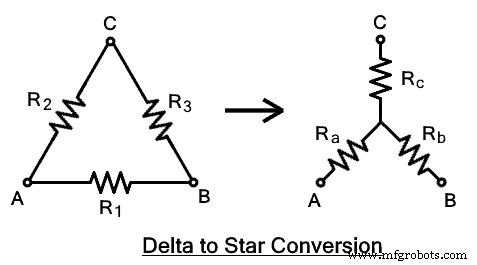Die angegebene Abbildung zeigt ein Delta-Netzwerk mit A-, B-, C-Anschlüssen mit den Impedanzen R₁ , R₂ , R₃ . Das äquivalente sternförmige Netzwerk mit R_A , R_B &R_C wo sie mit den entsprechenden Anschlüssen verbunden sind, wie in der Abbildung gezeigt.

Wie bereits erwähnt, bleiben die Anschlüsse A, B, C gleich, ebenso wie die Impedanz zwischen ihnen, muss gleich bleiben.

Die Gesamtimpedanz zwischen A-B im Delta-Netzwerk; 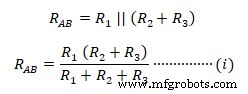In ähnlicher Weise die Impedanz zwischen den Anschlüssen B-C 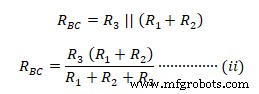Ähnlich die Impedanz zwischen A-C 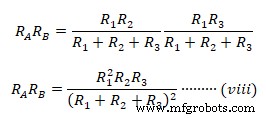Laut Sternnetzwerk;

R_AB =R_A + R_B

R_BC =R_B + R_C

R_AC =R_A + R_C

Fügen Sie nun die Gleichungen (i), (ii) und (iii) zusammen 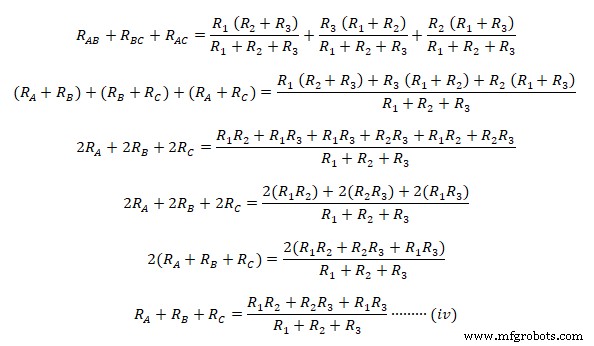Subtrahieren Sie nun Gleichung (i), (ii) und (iii) nacheinander von Gleichung (iv)

Subtrahiere zuerst (ii) von (iv) 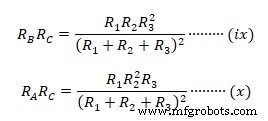Eine ähnliche Subtraktion von (i) &(iii) von (iv) ergibt 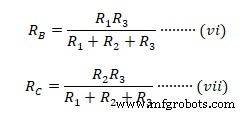Aus den abgeleiteten Gleichungen für sternäquivalente Impedanzen R_A , R_B , &R_C wir können die Beziehung zwischen Delta-zu-Stern-Umwandlungen wie folgt schließen:die äquivalente Sternimpedanz ist gleich dem Produkt der benachbarten Dreieckimpedanzen mit einer terminalen Division durch die Summe aller drei Dreieckimpedanzen.

Falls alle drei Impedanzen gleich sind in einem Delta-Netzwerk würde die äquivalente Sternimpedanz zu

werden

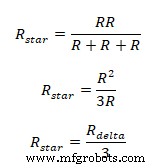Da alle Impedanzen im gesamten Delta-Netzwerk gleich sind, wäre jeder drei äquivalente Sternwiderstand 1/3 mal so hoch Delta-Impedanz.

Konvertierung von Stern zu Delta

Jetzt werden wir die sterngeschaltete Impedanz in eine deltageschaltete Impedanz umwandeln. Lassen Sie uns die Gleichungen herleiten, die für eine Stern-Delta-Umwandlung verwendet werden.

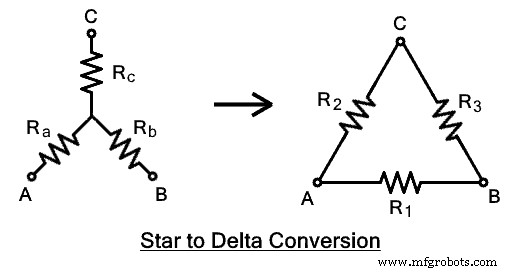Die angegebene Abbildung zeigt die sterngeschaltete Impedanz R_A , R_B &RC. Während die erforderliche Delta-Äquivalentimpedanz R₁ ist , R₂ &R₃ wie in der Abbildung gezeigt.

Um den äquivalenten Delta-Widerstand zu finden, multiplizieren Sie die vorherige Gleichung (v) &(vi) sowie (vi) &(vii) &(v) &( vii) zusammen.

 Multiplizieren von (v) &(vi) 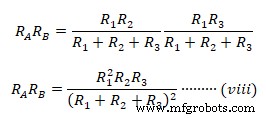In ähnlicher Weise multipliziert man (vi) mit (vii) &(v) mit (vii)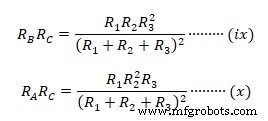

Fügen Sie nun Gleichung (viii), (ix) &(x) zusammen 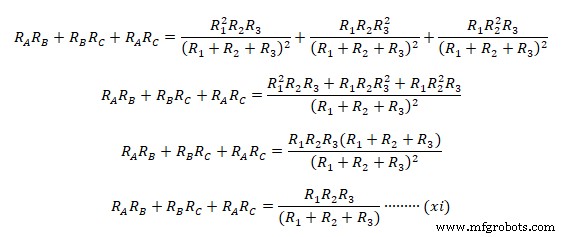Um die individuelle äquivalente Delta-Impedanz zu erhalten, dividieren wir Gleichung (xi) durch (v), (vi ) &(vii) separat wie.

Teilen von (xi) durch (v) 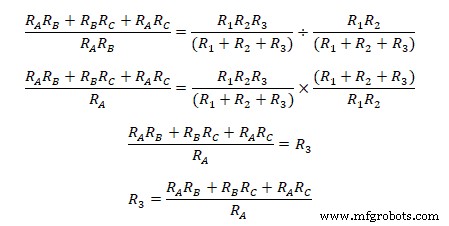Ähnlich dividiert man Gleichung (xi) durch (vi) &(vii) separat ergibt

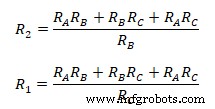Die Beziehung zwischen Stern- und Dreieck-Äquivalentimpedanz geht aus der gegebenen Gleichung hervor. Die Summe des Zweierprodukts aller Sternimpedanzen dividiert durch die Sternimpedanz der entsprechenden Klemme ist gleich der mit der Gegenklemme verbundenen Dreieckimpedanz.

Das Vereinfachen der Gleichungen führt zu 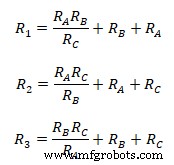Falls alle Sternimpedanzen gleich sind, wäre die äquivalente Deltaimpedanz:

Unter Verwendung der vorherigen Gleichung,

Diese Gleichung legt nahe, dass jede äquivalente Deltaimpedanz gleich dem Dreifachen der Sternimpedanz ist.