Einfluss von Oberflächenzuständen und Aluminium-Molekülfraktion auf das Oberflächenpotential und 2DEG in AlGaN/GaN-HEMTs

Methodenabschnitt und Simulations-Setup

2D-Gerätesimulationen wurden mit dem Sentaurus TCAD Version L-2016.12 von Synopsys [22] durchgeführt. Wir haben den TCAD-Simulationsaufbau kalibriert, indem wir das experimentelle Ergebnis der AlGaN/GaN-HEMT-Heterostruktur [15] reproduzierten, wie in Abb. 1b gezeigt.

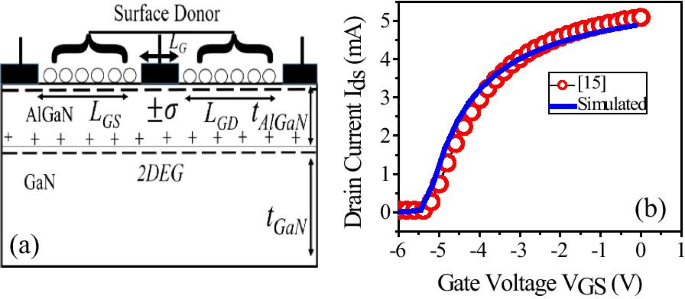
a Schema einer simulierten 2D-Struktur mit einem Al-Molenbruch von 28%. b Kalibrierung des Simulationsaufbaus durch Reproduktion der berichteten experimentellen Ergebnisse [15]

Das kalibrierte Gerät hat eine 30-nm-AlGaN-Barriereschicht auf der Oberseite der 2 μm-GaN-Pufferschicht. Schottky-Gate-Länge (L _G ) von 1 μm wird symmetrisch auf der Oberseite der AlGaN-Barriereschicht platziert. Bereich ohne Gate vom Gate zum Drain/Source (L _GD /L _GS ) hat eine Abmessung von jeweils 2,5 μm und die Breite des Geräts beträgt 150 μm.

Die Simulationsplattform befasst sich mit drei Bedingungen (Poisson-Bedingung neben Elektronen- und Lochkontinuitätsbedingung), die das Halbleiterverhalten überwacht.

Das selbstkonsistente Drift- und Diffusionstransportmodell (DD) ist ebenfalls enthalten. Lombardi Mobility und Philip Unified Mobility Model wurden herangezogen, um die Mobilitätsverschlechterung aufgrund des elektrischen Felds und der Dotierung zu erleichtern. Darüber hinaus wurden Auger- und SRH-Rekombinationsmodelle (Shockley-Read-Hall) zusammen mit Fermi-Dirac-Statistiken verwendet. Das Slotboom-Modell wird aktiviert, um der Bandlückenverengung des stark dotierten erweiterten Drain- und Source-Bereichs zu begegnen. Da diese Struktur zwei Schichten hat und wir den Aluminiumanteil in der AlGaN-Barriereschicht ändern, wird die Polarisationsladung gemäß der Gleichung von [3] eingeführt:

wo P _SP ist spontane Polarisation, e ₃₃ und e ₃₁ sind piezoelektrische Koeffizienten, C ₃₃ und C ₃₁ sind elastische Konstanten, a ist die Gitterkonstante und x ist ein Molprozentsatz von Aluminium.

Die Variation der Polarisationsladung ± σ _AlGaN (x ) mit Aluminiumanteil ist in Abb. 2a [3] dargestellt. Sobald die Polarisationsladung berechnet ist, kann die Poisson-Gleichung gelöst werden. An der AlGaN-GaN-Grenzfläche ändert sich das Leitungsband abrupt und bildet einen schmalen (1–4 nm) dreieckigen Potenzialquantentopf, in dem sich Elektronen ansammeln. Da dieser Quantenpotentialtopf sehr schmal ist, wird die reduzierte Zustandsdichte dominant. Die Schrödinger-Quantengleichung berücksichtigt den Quantenpotentialtopf, ist jedoch für ein größeres HEMT-Gerät schwer zu lösen. Um das Verhalten des Quantenpotentialtopfs zu erfassen, haben wir das eQuantumpotential-Modell im Sentaurus TCAD aufgerufen, das das Dichtegradienten-Quantenkorrekturmodell aktiviert [23] und ein gut abgestimmtes Ergebnis mit der Schrödinger-Quantengleichung für größere HEMT-Geräte (Leistungs-HEMT-Geräte) liefert. Das Dichtegradienten-Quantenmodell reduziert den Spitzenwert der Elektronendichte in 2DEG, und der Spitzenwert verschiebt sich auch weg von der AlGaN-GaN-Grenzfläche. Dadurch wird der Grenzflächenstreumechanismus reduziert und die Mobilität im Kanal verbessert, siehe Abb. 2b [20]. Das Dichtegradienten-Quantenmodell führt einen zusätzlichen Term Λ in die normale Dichteformel ein wie:

wo N _C ist die effektive Zustandsdichte, F 1/ 2 ist Fermi-Integral der Ordnung 1/ 2, E _F ist die Quasi-Fermi-Energie für Elektronen, E _C ist die Leitungsbandkante und kT stellt die thermische Energie von Elektronen dar. Λ wird berechnet durch:

wo ħ = h /2π , h ist die Plankenkonstante, m _n ist eine effektive Masse des Elektrons, γ (γ = 1.28) ist ein Anpassungsparameter und n ist die Elektronendichte.

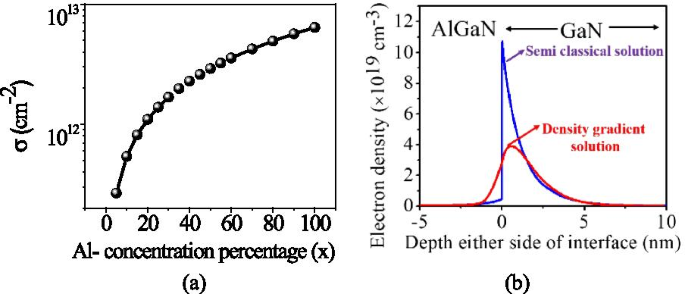
a Variation der Polarisationsschichtladung in Abhängigkeit von der Aluminiumkonzentration in der AlGaN-Sperrschicht [3]. b Einfluss der Quantengefangenschaft auf die 2DEG-Elektronendichte

Die Oberflächenfallen wurden als Donorzustand eingeführt (+ σ _D ) auf der Oberfläche von AlGaN-Barriereschichten Abb. 1a, und die Simulation wurde bei einer Temperatur von 300 K durchgeführt. Die Kalibrierung wurde mit der anfänglichen Aluminiumkonzentration von 28 % durchgeführt.

Simulationsergebnisse und Diskussion

Auswirkung des Aluminiumanteils und der Oberflächenfallen auf die 2DEG-Dichte

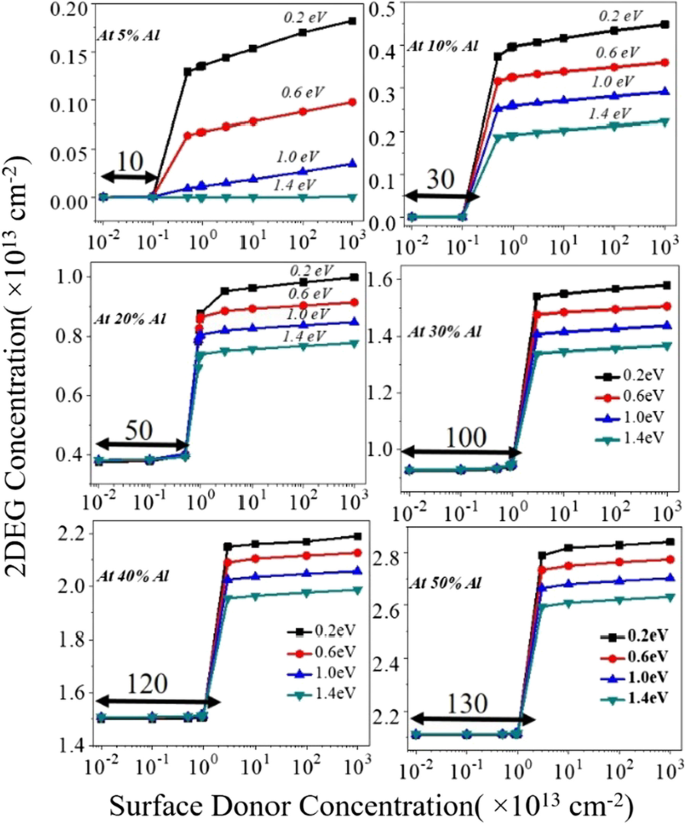
Das Gerät wurde unter Bedingungen ohne angelegte Vorspannung simuliert, um die 2DEG-Elektronendichte zu untersuchen. Während wir uns auf die 2DEG-Elektronendichte konzentrieren, gibt es für die gesamte Energie des Donorzustands bis zu einem bestimmten Wert (relativ niedrigerer Wert) der Donorfallenkonzentration keine signifikante Änderung der Elektronendichte (d. h. Region1). Die 2DEG-Elektronendichte ändert sich proportional mit der Oberflächendonatorkonzentration (zwischen Region1 und Region2). Nach einem bestimmten Schwellenwert der Oberflächendonatorfalle tritt wiederum keine Änderung der Elektronendichte (d. h. Region2) auf, siehe Abb. 3a–d. Dieser Mechanismus kann wie folgt erklärt werden:

a –d Variation der Elektronenschichtdichte in 2DEG bezüglich der Oberflächendonatorkonzentration und -energie (von flachen 0,2 eV bis zu tiefen 1,4 eV) für verschiedene Aluminiumprozentsätze. e Unterschiedliche Ladungsverteilung und elektrische Feldorientierung im Gerät

(i) Das Leitungsband der AlGaN-Barriereschicht für Region 1 hat einen größeren Abstand zum Fermi-Niveau an der Oberfläche. Wenn die Konzentration der Donorfallen von einem niedrigeren auf einen höheren Wert ansteigt, beginnt sich das Leitungsband in der Übergangsperiode (zwischen Region1 und Region2) proportional zum Fermi-Niveau zu bewegen. Somit beginnt die 2DEG-Konzentration von einem niedrigeren Wert auf einen höheren Wert anzusteigen. In der Übergangsperiode (zwischen Region1 und Region2) beginnt sich das Leitungsband proportional zum Fermi-Niveau zu bewegen, und so bewegt sich auch die Donoroberflächenenergie zum Fermi-Niveau. Für Region2 beginnt die Verbiegung des Leitungsbandes, sobald die Donorkonzentration den Schwellenwert überschreitet, so, dass die Energie der Donorfalle das Fermi-Niveau fixiert. Aufgrund des Fermi-Niveaus-Pining werden alle Donorzustände ionisiert und tragen Elektronen zum dreieckigen 2DEG-Quantenpotentialtopf bei. Sobald die Energie der Donorzustände auf das Fermi-Niveau fixiert ist, spiegelt sich keine signifikante Änderung in der Elektronendichte wider. (ii) Um Ladungsneutralität in der Vorrichtung zu finden, sind Oberflächendonatorzustände wesentlich, um den Elektronen in 2DEG entgegenzuwirken. Wenn der Oberflächendonatorzustand zunimmt, beginnt ein elektrisches Feld von der Oberfläche zum 2DEG-Quantentopf zuzunehmen. Dieses elektrische Feld wirkt dem eingebauten elektrischen Feld entgegen, das durch die Polarisationsblattladung erzeugt wird (± σ _AlGaN ). Wenn das externe elektrische Feld beginnt, das interne elektrische Feld zu überschreiten (aufgrund von ± σ _AlGaN ), senkt es das Leitungsband an der Oberfläche und trägt somit mehr Elektronen zum 2DEG-Potentialtopf bei, siehe Abb. 3e. Wenn der Aluminiumanteil von 5 auf 50 % ansteigt, nimmt auch die Ladungsdichte der Polarisationsbleche proportional zu, was zu einem hohen internen elektrischen Feld (aufgrund der Polarisation) führt. Um dieses interne elektrische Feld zu überwinden, ist eine höhere Konzentration von Oberflächen-Donatorfallen erforderlich. Daher wird der Übergangsbereich verschoben (von 10 auf 130 mal mit 10 ¹¹ cm ⁻² ) für den höheren Wert der Donorfallenkonzentration, wobei sich die 2DEG-Elektronendichte proportional zur Donorfallenkonzentration ändert, Abb. 3a–d. Die 2DEG-Konzentration für jeden Aluminiumprozentsatz in Bezug auf den Oberflächendonor (Konzentrat+ Energie) ist in Abb. 4 aufgetragen. Obwohl das Muster der 2DEG-Elektronenkonzentration für alle Aluminiumprozentsätze gleich ist, wenn die Donorfalle von flach (0,2 eV) entfernt wird zu tief (1,4 eV) (Abb. 5), ist die Änderung der 2DEG-Elektronendichte von tief nach flach immer noch ziemlich signifikant. Bei einer Aluminiumkonzentration von 5 % geht die Donorfalle von tief (1,4 eV) zu flach (0,2 eV) und trägt nicht wesentlich zur Potenzialquelle bei. Als Polarisationsladungskonzentration (± σ ) liegt in der Größenordnung von 10 ¹¹ cm ⁻² für 5 % Aluminium, siehe Abb. 2a, reicht das elektrische Feld aufgrund dieser Polarisationsladungen nicht aus, um den Leitungsbandversatz unter das Fermi-Niveau zu bringen, daher wird auf der GaN-Seite der AlGaN-GaN-Grenzflächenstruktur keine dreieckige 2DEG-Potentialmulde gebildet. Es ist auch offensichtlich, dass selbst bei der höheren Konzentration von Oberflächendonatorfallen die Sättigung der Elektronendichte nicht auftritt, wie in den Fig. 1 und 2 gezeigt. Dies gilt auch für einen Aluminiumprozentsatz von 10 %, wie in Abb. 4b gezeigt. Ab 20 % ist die Polarisationsladungskonzentration (± σ) größer als 10 ¹² cm ⁻² . Das interne elektrische Feld ist also groß genug, um den Leitungsbandversatz unter das Fermi-Niveau zu ziehen, und bildet daher die dreieckige 2DEG-Quantenpotentialmulde, siehe Abb. 6b, c. Bei einem Aluminiumanteil von 20 % und mehr nähert sich die 2DEG-Elektronendichte also ~ 10 ¹³ cm ⁻² für flache Spenderfallen, wie in Abb. 4c gezeigt. Bei einer Aluminiumkonzentration von 20 %, 30 % und mehr hat der Beitrag des Elektrons in der dreieckigen Mulde eine Dichte von 1 × 10 ¹³ bis 3 × 10 ¹³ cm ⁻² . Abbildung 5a,b zeigt die prozentuale Änderung der Elektronendichte in einer dreieckigen Vertiefung, wenn sich die Energie der Donorfallen von 1,4e auf 0,2 eV ändert. Wenn wir von 5 auf 50 % des Aluminiumprozentsatzes gehen, verringert sich die Änderung der 2DEG-Konzentration signifikant von 10,89-mal auf 1,08-mal und wird über 30 % gesättigt.

Variation eines individuellen Aluminiumprozentsatzes zur Donoroberflächenfalle von tief zu flach in Bezug auf das Leitungsband

a Prozentuale Änderung der 2DEG-Elektronendichte im logarithmischen Maßstab für die Al-Konzentration, wenn der Oberflächendonor von einem tiefen Niveau in Bezug auf das Leitungsband flach wird. b Lineare Skala

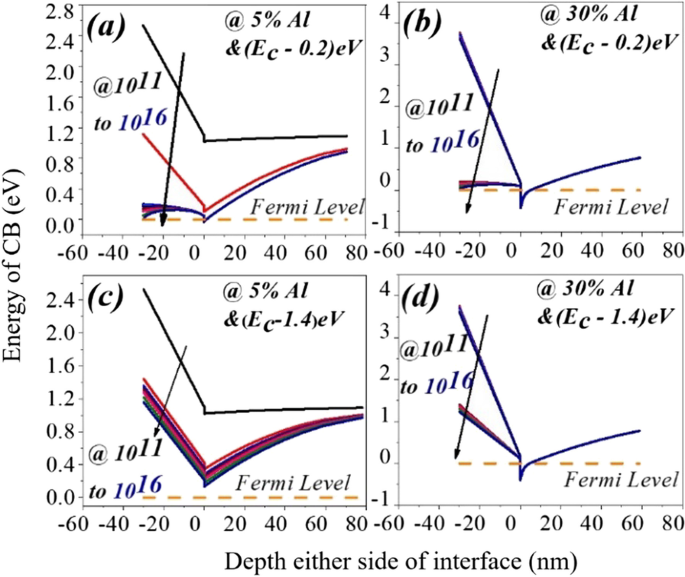
a , c Leitungsbandvariation auf beiden Seiten der AlGaN-GaN-Grenzfläche für 5 % Aluminium und b , d für 30% Aluminium. Die Oberflächenfalle in tiefer Ebene trägt nicht zur Elektronen- und positiven Schichtladung zur Potentialmulde und Oberfläche bei, wodurch die Steigung des Leitungsbandes höher wird. Selbst für einen tiefen Donoroberflächenzustand (1,4 eV) bildet sich eine 2DEG-Potentialmulde für 30 % Aluminium. Dies gilt nicht für 5% Aluminium

Auswirkung des Aluminiumanteils und der Oberflächenfalle auf das Oberflächenpotential

In einigen Literaturstellen wurde die Variation des Oberflächenpotentials aufgrund einer Änderung des Aluminiumprozentsatzes diskutiert [29]. Aber sie haben die Wirkung von Oberflächen-Donatorfallen auf das Oberflächenpotential nicht berücksichtigt. Hier berichten wir über die Variation des Oberflächenpotentials aufgrund von Oberflächendonatorfallen, sowohl in den Dimensionen Energie als auch Konzentration, siehe Abb. 7a. In dieser Studie haben wir die Oberflächendonatorkonzentration von 1 × 10 ¹² . geändert bis 1 × 10 ¹⁶ und Oberflächendonorenergie von 0,2 bis 1,4 eV. Das Oberflächenpotential wurde aus Abb. 6b berechnet. Das Oberflächenpotential pendelt sich bei 3,7 eV ein (für die Oberflächendonatorkonzentration 1 × 10 ¹² ) und 3,6 eV (für Oberflächendonatorkonzentration 1 × 10 ¹³ ). Dieses Oberflächenpotential hängt für seinen niedrigeren Wert nicht von der Energie der Oberflächen-Donorfalle ab. Das Oberflächenpotential steigt linear an, wenn der Oberflächendonor von flach (0,2 eV) in die Tiefe geht (1,4 eV). Wenn das Oberflächenpotential sinkt, nimmt die 2DEG-Elektronenkonzentration zu, da das Oberflächenpotential linear mit der Energie der Oberflächen-Donorfallen variiert. Auch der Aluminiumanteil hat einen großen Einfluss auf das Oberflächenpotential. Wenn der Aluminiumanteil von 5 auf 50 % erhöht wird, steigt die Elektronenkonzentration von 7,79 × 10 ¹¹ bis 2,75 × 10 ¹³ . Das Oberflächenpotential steigt ebenfalls von 0,49 auf 0,576 eV, wenn sich der Aluminiumanteil von 5 auf 50 % ändert, siehe Abb. 7b. Somit haben die Konzentration und Energie der Oberflächendonatorfallen zusammen mit der Aluminiumkonzentration einen großen Einfluss auf das Oberflächenpotential.

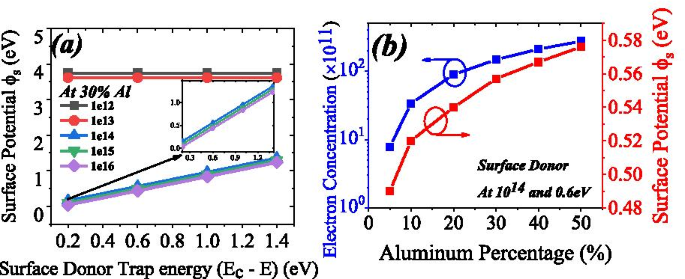
a Variation des Oberflächenpotentials in Bezug auf die Energie der Oberflächen-Donorfalle. Bei niedrigeren Konzentrationen (weniger als 1e14) gibt es keine signifikante Änderung des Oberflächenpotentials. Oberflächendonatorkonzentration über 1e13, Oberflächenpotential ändert sich proportional zur Energie des Oberflächendonors. b Elektronenkonzentration in 2DEG ändert sich von 7,79 × 10 ¹¹ bis 2,75 × 10 ¹³ für den Aluminiumanteil ändert sich von 5 % auf 50 % (blaue Linie). Das Oberflächenpotential ändert sich um etwa 0,1 eV von 5 auf 50 % des Aluminiumprozentsatzes

Auswirkung des Aluminiumanteils und der Oberflächenfalle auf das Leitungsband und die 2DEG-Potenzialquelle

Die ionisierten Oberflächenfallen tragen Elektronen zum Potentialtopf und positive Schichtladungen an der AlGaN-Oberfläche bei [6]. Im Fall einer Aluminiumkonzentration von 5 % wird die Menge der ionisierten Oberflächenfallen immer kleiner, wenn die Fallen von einem flachen Energieniveau in die Tiefe gehen. Somit trugen ionisierte Oberflächenfallen weniger Elektronen zum dreieckigen Potentialtopf und zu positiven Schichtladungen an der Oberfläche bei. Eine geringere Menge an positiven Schichtladungen und Elektronenkonzentration in 2DEG trägt nicht genügend externes elektrisches Feld bei, und daher wird die Steigung des Leitungsbandes in der AlGaN-Schicht größer, wie in Fig. 6 gezeigt. Dies gilt auch für Aluminium mit 10 % in AlGaN-Sperrschicht. Die freien Elektronen aus den Oberflächendonatorzuständen befinden sich in der 2DEG-Potentialmulde und neutralisieren die positive Schichtladung, die an der Oberfläche von AlGaN auftritt. Diese Elektronenblattladung wird berechnet nach [24]:

wo d ist die Dicke des Al_x Ga_{(1−x )} N Sperrschicht, ϕ _b ist Schottky-Barriere, E _F ist das Fermi-Niveau und ΔE _C ist der Leitungsband-Offset an der AlGaN-GaN-Grenzfläche. Aus Gl. (4) dass die Ladungsdichte der Elektronenschicht direkt proportional zum Leitungsband-Offset und den Polarisationsladungen ist, die eine Funktion des Aluminiumprozentsatzes sind. Wenn wir den Aluminiumanteil von 10 auf 50 % erhöhen, erhöht sich der Leitungsband-Offset [25] und damit die Elektronendichte in 2DEG aufgrund der Zunahme der Anzahl der Energieniveaus, siehe Abb. 8. Das interne elektrische Feld des Geräts, wenn die Aluminiumkonzentration 20 % und mehr beträgt, ist die Steigung des Leitungsbandes hoch genug, um die dreieckige Potentialmulde selbst für eine Oberflächenfallenenergie des tiefen Niveaus (1,4 eV) und eine niedrigere Oberflächendonatorfallenkonzentration zu konstruieren, wie in Fig. 6b gezeigt, d .

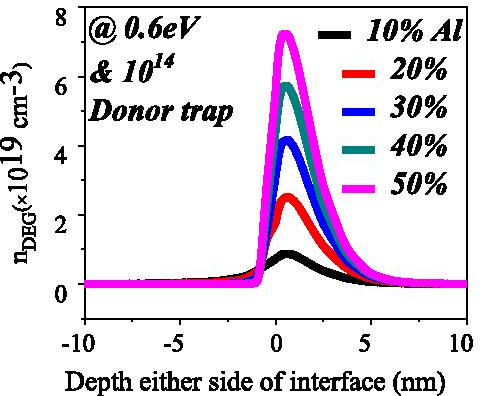
Elektronendichte im dreieckigen Quantenpotentialtopf für verschiedene Aluminiumkonzentrationen bei fester Donorkonzentration und Energie

Es ist wichtig, sich die Kerbe des dreieckigen Quantenpotentials anzusehen, die unterhalb des Fermi-Niveaus ((E _F − E) eV), wobei E ist die Energie unterhalb des Fermi-Niveaus. Zwei wichtige Parameter in der dreieckigen Quantenpotentialmulde sind die Tiefe der Potentialmulde unterhalb des Fermi-Niveaus und die Breite der Potentialmulde auf dem Fermi-Niveau. Die Eingrenzung der Elektronen in zweidimensionalen Bereichen wird als 2DEG-Quantenblatt bezeichnet. Die Zustandsdichte N (E ) ist eines der wichtigen Merkmale des 2DEG-Quantenpotentialtopfs. Die Zustandsdichte in einem zweidimensionalen Quantentopf ist definiert als [26]:

wo m* ist die effektive Masse des Elektrons und L _X ist die Breite des Brunnens. Diese Zustandsdichte im zweidimensionalen Brunnen sieht aus wie eine Stufenfunktion.

Die Anzahl der besetzten Zustände hängt vom Fermi-Niveau ab. Zum Beispiel, wenn das Fermi-Niveau höher als E . ist ₁ aber weniger als E ₂; dann nur E ₁ Teilband ist gefüllt. Wenn das Fermi-Niveau über E liegt ₂ , aber weniger als E ₃ , dann zwei untere Subbänder E ₂ und E ₁ mit Elektronen gefüllt sind, wie in Abb. 9b gezeigt. Dies bedeutet, dass, wenn die Energie an der Grenzfläche mit dem Fermi-Niveau tiefer wird, nur Elektronen in großer Zahl erwartet werden. In der AlGaN/GaN-Heterostruktur nimmt der Energieabstand ab ((E ₂ − E ₁ ) > (E ₃ − E ₂ )) für höhere Subbänder [27]. Wenn die Subbandenergie ansteigt, wird der Unterschied zwischen ihnen vernachlässigbar und sieht kontinuierlich aus. Die rigoros richtige Lösung der Wellenfunktion enthält gleichzeitig die Poisson-Gleichung und die Schrödinger-Gleichung. Das Dichtegradientenmodell erzeugt jedoch mit der Schrödinger-Gleichung das annähernd gleiche Ergebnis. Im Quantenpotentialtopf wird das Energieniveau quantifiziert, da sich dieser Topf bis zu einigen nm Längen in der GaN-Seite der AlGaN-GaN-Grenzfläche ausbildet. Die tiefere Kerbe unterhalb des Fermi-Niveaus wird sicherlich eine höhere Anzahl quantifizierter Energieniveaus aufweisen. Das quantifizierte Energieniveau unterhalb des Fermi-Niveaus ist besetzt. Daher ist die Elektronenkonzentration in 2DEG höher, je tiefer die Energie unter dem Fermi-Niveau liegt. Aus Abb. 9a ist klar, dass das Energieniveau unter dem Fermi-Niveau höher wird, wenn der Aluminiumanteil steigt, da die Polarisationsladung zunimmt und somit das interne elektrische Feld die Kerbe tiefer gehen lässt. In Bezug auf die Oberflächendonatorenergie ist aus der vorherigen Diskussion ersichtlich, dass die Ionisierung dieser Oberflächendonatoren abnimmt, wenn die Oberflächenfallen tiefer gehen (1,4 eV). Daher wird das elektrische Feld aufgrund positiver Schichtladungen an der Oberfläche erzeugt und Elektronen, die von diesen Oberflächendonatoren zu 2DEG beigetragen werden, reichen nicht aus, um das interne elektrische Feld zu überwinden. Somit verringert sich die Wirkung der Polarisationsladung in Bezug auf das elektrische Feld, was zu geringeren Energieniveaus unterhalb des Fermi-Niveaus führt. Eine Ausnahme bildet die Aluminiumkonzentration von 5 %. Aus Abb. 10a wird deutlich, dass der Wert von E _F − E negativ ist, da das Fermi-Niveau bei Null angenommen wird, für die tiefen Donorfallen (> 0,9 eV bis 1,4 eV), was bedeutet, dass die Energie E höher ist als das Fermi-Niveau (2DEG bildet sich nicht). Für flachere Oberflächen-Donorfallen (< 0,9 eV bis 0,2 eV) ist der Wert von E _F − E positiv ist, was bedeutet, dass der Wert des E niedriger als das Fermi-Niveau ist. Für den Rest der Aluminiumkonzentration (10 % bis 50 %) ist der Wert von E _F − E positiv ist, was bedeutet, dass der Wert von E niedriger als das Fermi-Niveau ist und sich für alle Arten von Oberflächendonorenergien (von 0,2 eV bis 1,4 eV) eine 2DEG-Kerbe bildet. Aus Abb. 11a ist ersichtlich, dass die prozentuale Energieänderung E mit Aluminium wird über 20 % der Aluminiumkonzentration gesättigt, was auch mit Abb. 5 übereinstimmt. Die Tiefe der Kerbe unter dem Fermi-Niveau ändert sich nach einer Aluminiumkonzentration von 20 % nicht signifikant, wenn der Oberflächendonator eine Energieänderung von tief zu flach einfängt. Abbildung 11b zeigt auch, dass bis zu einem Aluminium-Molbruch von 10 % kein signifikanter Strom vorhanden ist. Über 10 % ändert sich der Strom signifikant, wenn sich die Oberflächendonorenergie von E . ändert _C − 0,2 bis E _C − 1,4 eV und wieder über 20 % gesättigt. Dieses Ergebnis steht auch im Einklang mit den Fign. 11a und 5. Das Konturdiagramm der absoluten Stromdichte zeigt auch, dass sie über 20 % des Al-Molbruchs gesättigt ist und keine signifikante Stromdichte bis 10 % des Al-Molbruchs hat Molenbruch. Eine signifikante Menge an Elektronendichte oberhalb von 20 % des Molenbruchs beobachtet Abb. 13a. Die Verteilung des elektrischen Felds entlang des Kanals ist in Abb. 13b aufgetragen. Abbildung 13b zeigt, dass unterhalb des Gates bis 10 % des Al-Molanteils kein merklich verbessertes elektrisches Feld vorhanden ist und oberhalb von 20 % des Al-Molbruchs kein großer Unterschied im elektrischen Feld besteht, was den Strom bei einem höheren Al-Prozentsatz begrenzt.

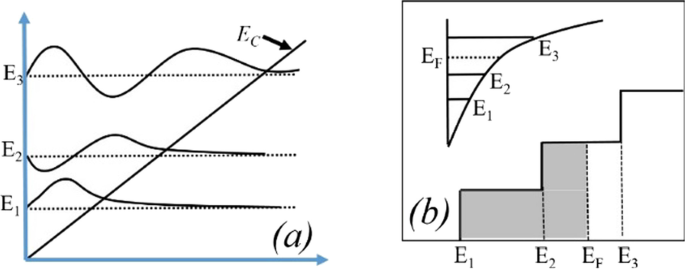
a Ein dreieckiges Potential, das Subband-Energien mit Fang-Howard Airy well gut darstellt Wellenfunktion. b Nur Subbänder mit niedrigerer Energie (E ₁ und E ₂ , niedriger als Fermi-Niveau) sind belegt [28]

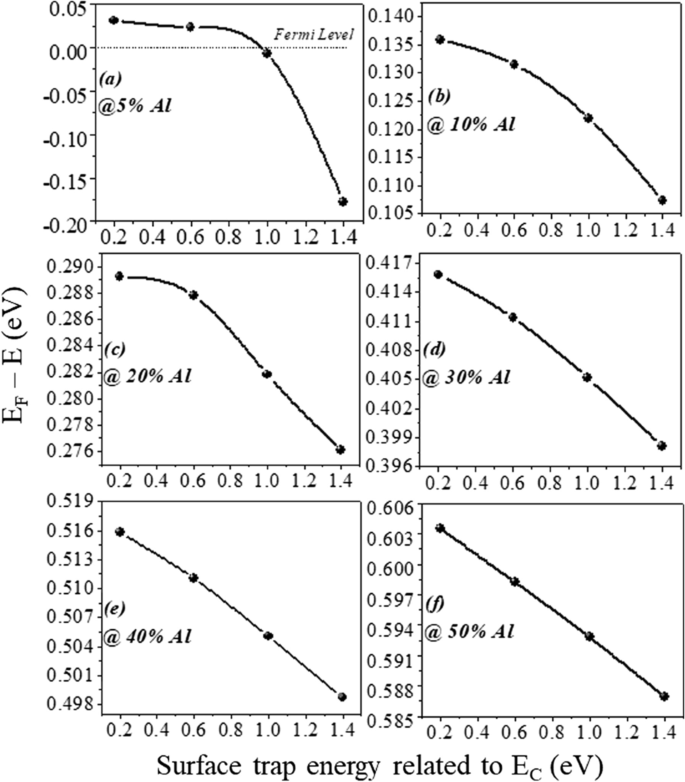
a –f (E _F  − E ) Variation mit der Oberflächendonorenergie für alle Aluminiumkonzentrationen

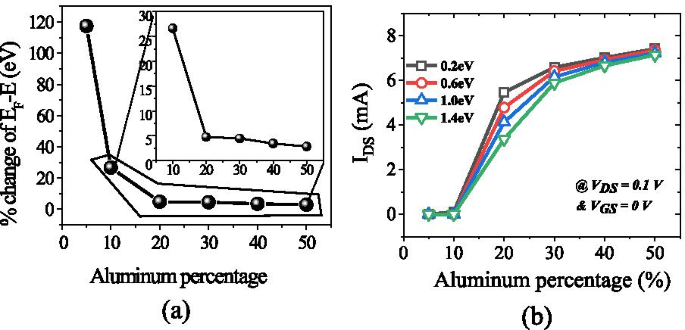
a Die prozentuale Energieänderung E mit der Aluminiumkonzentration, wenn sich die Oberflächendonatorenergie von tief nach flach ändert. b Drainstrom und V _DS = 0,1 V und V _GS = 0 V bei unterschiedlicher Energie der Donatorfallen an der Oberfläche. Bis zu 10 % kein nennenswerter Strom im Gerät beobachtet

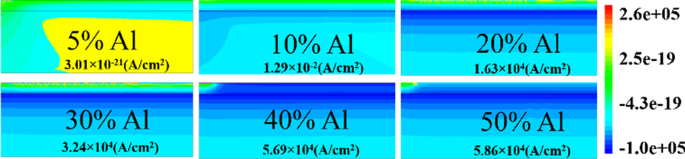
Konturdiagramm der absoluten Gesamtstromdichte für 0,6 eV Oberflächendonorenergie bei V _DS = 0,1 V und V _GS = 0 V

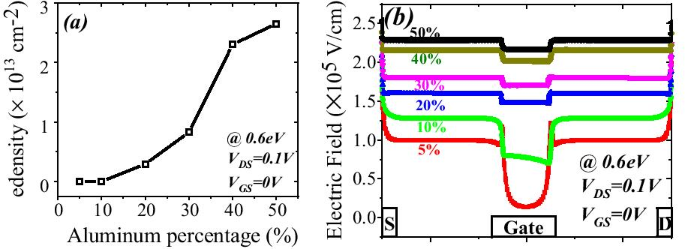
a Electron density variation with aluminum percentage and b electric field variation below gate and either side of gate for different aluminum percentage

Conclusion

In this paper, we comprehensively present the effect of surface donor traps along with aluminum percentage on electron density and quantum potential well. This manuscript demonstrated that the percentage change happens in 2DEG and notch below the Fermi level gets saturated above 20% of aluminum concentration when surface donor trap energy goes deep to shallow. The electron density in the two-dimensional quantum potential well is saturated approximately at 8%, whereas the energy below the Fermi level saturates somewhere around 2%. These two results are also in tune with each other, except 5% aluminum, having a condition for not forming two-dimensional well for relatively deep (> 0.9 eV) surface donors. Aluminum percentage above 10% forms two-dimensional quantum potential well even for deeper surface donor traps. The effect of surface donor traps on the surface potential also has been discussed in this work. The results of this paper may provide the impetus to the experimental result validation.

Verfügbarkeit von Daten und Materialien

All data are available on request.

Abkürzungen

GaN:

Gallium nitride

HEMT:

High-electron-mobility transistor

2DEG:

Two-dimensional electron gas

DD:

Drift and diffusion transport model

SRH:

Shockley–Read–Hall recombination model