Eine Studie zur Variabilität des kontaktresistiven Direktzugriffsspeichers nach dem stochastischen Vakanzmodell

Hintergrund

Resistiver Direktzugriffsspeicher (RRAM) wurde aufgrund seiner wünschenswerten Eigenschaften wie geringer Stromverbrauch, hohe P/E-Geschwindigkeit und überlegene Kompatibilität mit CMOS-Logikprozessen als vielversprechende nichtflüchtige Datenspeicherlösung angesehen [1,2,3 ,4]. Es sind jedoch noch viele Hindernisse zu überwinden, um RRAM-Speicherarrays einfach in CMOS-Schaltungen des aktuellen Stands der Technik zu implementieren [5, 6]. Eine der größten Herausforderungen bei großen RRAM-Arrays liegt in der Variation zwischen und innerhalb von Zellen [7,8,9,10]. Viele Modelle und Simulationen wurden vorgeschlagen, um den stochastischen Erzeugungs-/Rekombinationsprozess von Sauerstoffleerstellen (Vo-) in Übergangsmetalloxid(TMO)-Filmen zu beschreiben [11,12,13,14]. Kim und Brivio schlugen zufällige Leistungsschalter-Netzwerkmodelle vor, um die typischen elektrischen Eigenschaften von unipolaren bzw. bipolaren RRAM zu emulieren [11, 12]. Die Widerstände in diesen Studien wurden jedoch alle konstant eingestellt, ohne den Elektronentransport im RRAM-Film zu berücksichtigen. Außerdem wird die Variabilität des RRAM-Verhaltens in einem Array, da die vorgestellten Modelle stochastische Prozesse von RRAM auf einer einzelnen Geräteebene statt einer statistischen Analyse diskutieren, nicht gut behandelt und in früheren Arbeiten diskutiert [11,12,13,14]. Darüber hinaus wurde das Vorhandensein von Defekten in dielektrischen Filmen während der Herstellung seit vielen Jahren umfassend untersucht [15, 16], aber ihr Einfluss auf die Widerstandsschalteigenschaften in RRAM muss noch umfassend analysiert werden, damit die Technologie in großen Speichermakros angewendet werden kann. Um den Effekt der intrinsischen Vo-Verteilung auf die RRAM-Eigenschaften zu untersuchen, wird in dieser Studie ein Widerstandsnetzwerk nach dem Vorbild des Trap-assisted-Tunneling-Mechanismus zur weiteren statistischen Analyse der Variation und während des Betriebs aufgebaut [11,12,13,14, 17 ]. Außerdem wird der stochastische Erzeugungsprozess von Vo- durch die Monte-Carlo-Methode simuliert, um die Korrelation zwischen dem RRAM in seinen Anfangszuständen und den folgenden Umformeigenschaften zu ermitteln [18,19,20]. Die starke Korrelation zwischen intrinsischer Vo- und Formierspannung wird durch die Überprüfung des Simulationsergebnisses mit Messdaten an Kontakt-RRAM-Arrays nachgewiesen [21]. Schließlich werden verschiedene Arten von erzeugten leitfähigen Filamenten (CF) und Widerstandszustandsänderungen nach Umformvorgängen als Ergebnis der intrinsischen Vo-Verteilung projiziert und umfassend untersucht. Darüber hinaus wird in dieser Studie eine Lösung vorgeschlagen und demonstriert, um die Auswirkungen der Voon-Variabilität beim Vorformen zu mildern.

Methoden

Die Messdaten für die weitere statistische Analyse der Variabilität werden von 16 × 16 Contact RRAM (CRRAM)-Arrays gesammelt, die durch 28-nm-CMOS-Logikprozesse hergestellt wurden, wobei der Herstellungsprozess von CRRAM in Abb. 1 dargestellt ist [21]. Die Widerstandsschutzoxidschicht (RPO) und das Zwischenschichtdielektrikum (ILD) werden zuerst abgeschieden, nachdem der Front-End-Prozess mit den gebildeten Transistoren abgeschlossen ist. Um einen funktionalen Widerstandsschaltfilm aufzubauen, wird eine geeignete Kontaktlochgröße, Kontaktgröße von 30 nm  ×  30 nm, durchgeführt, um ein Kurzschließen des W-Steckers und des n + -Diffusionsbereichs zu verhindern. Schließlich werden die Sperrschicht, TiN und der Wolframpfropfen einzeln abgeschieden. Das Querschnitts-TEM-Bild von CRRAM ist in Abb. 2a gezeigt. Wie das Bild zeigt, ist CRRAM seriell mit einem n-Kanal-Auswahltransistor verbunden. Eine 1T1R-Struktur wird verwendet, um die richtige Auswahl in einem Array sicherzustellen und Überschwingungen zu verhindern. Abbildung 2b zeigt die Zusammensetzungszuordnung von CRRAM. Seine Übergangsmetalloxidschicht (TMO) mit einer Dicke von 9 nm, bestehend aus TiN/TiON/SiO₂ gestapelt wird zwischen den oberen Wolfram- und unteren Siliziumelektroden gebildet. Nach der Geräteherstellung werden die elektrische Analyse und die Erstellung eines physikalischen Modells in dieser Studie durch den Halbleiterparameteranalysator Aglient 4156C bzw. die MATLAB-Softwareplattform abgeschlossen.

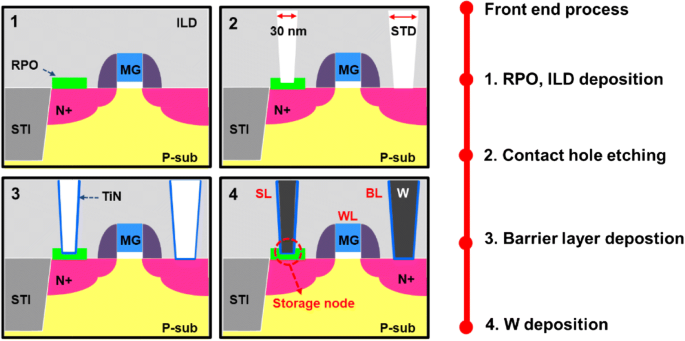
Prozessablauf eines Kontakt-RRAM auf einer 28-nm-High-k-Metall-Gate-CMOS-Logikprozessplattform. Kleinere Kontaktgröße für CRRAM wurde entwickelt, um die Ätzdicke zu kontrollieren, um eine funktionelle Widerstandsschaltschicht zu bilden

a TEM-Querschnittsbild der 1T1R-CRRAM-Struktur. b Zusammensetzungs-Mapping von CRRAM. Der Widerstandsschaltfilm besteht aus TiN/TiON/SiO₂ sandwichartig zwischen dem oberen Wolframpfropfen und der unteren Si-Elektrode

Wie in einer früheren Studie [22] berichtet wurde, findet man auf CRRAM-Arrays eine breite Verteilung von Anfangszuständen. Um den Ursprung der Anfangszustandsvariation zu untersuchen, werden in Abb. 3 zuerst die Dicken der TMO-Schicht mit unterschiedlichen Anfangswiderständen verglichen. Die Daten deuten auf keinen signifikanten Dickenunterschied zwischen den beiden Zellen mit großen Unterschieden in den anfänglichen Widerstandsniveaus hin. In vielen Studien wurde berichtet, dass Vo- in dielektrischen oder RRAM-Filmen während der Herstellung erzeugt wird [23,24,25,26], was impliziert, dass der Unterschied in Anzahl und Dichte von Vo- vermutlich für die anfänglichen Leitfähigkeitsschwankungen verantwortlich ist.

Vergleich der TMO-Schichtdicke zwischen zwei CRRAM-Zellen mit großem Anfangswiderstandsunterschied. Beide Zellen werden mit dielektrischen Schichtdicken von etwa 9 nm beobachtet

Ergebnisse und Diskussion

Intrinsisches Vakanzverteilungsmodell

Um die Wechselwirkungen zwischen intrinsischem Vo- zu emulieren, wird ein in Abb. 4a gezeigtes Widerstandsnetzwerkmodell erstellt [11,12,13,14]. Die Widerstände in jedem Gitter werden durch einen in Abb. 4b skizzierten Simulationsablauf berechnet, während die entsprechenden verwendeten physikalischen Parameter in Tabelle 1 aufgeführt sind. Basierend auf einem TEM-Bild von CRRAM, einer zweidimensionalen Struktur mit einer Breite von 30 nm und einer Dicke von 10 nm , ist zum Beschreiben der TMO-Schicht definiert, wie in Fig. 5a gezeigt. Der Widerstand der Oxidstelle, R _Oxid , und Maschengitter werden durch die Materialeigenschaft von Anatas-TiO₂ . bestimmt , das in vielen Studien als resistives Schaltmaterial verwendet wurde [27,28,29,30]. Aufgrund seiner tetragonalen Struktur sind die Gitterkonstanten von Anatas-TiO₂ mit der kristallographischen Achse variieren. Der Einfachheit halber werden die Gitternetze in unserem Modell alle auf 1 nm eingestellt, indem die Gitterkonstante in c-Richtung von Anatas-TiO₂ . eingeführt wird [31,32,33]. Darüber hinaus werden Widerstände für Gitter auch anhand des spezifischen Widerstands von Anatas-TiO₂ . bestimmt [34, 35]. Wie in Abb. 5a gezeigt, sind anfangs zufällig verteilte Vo- innerhalb des 2-D-Netzes gegeben. Die Abhängigkeiten von der Temperatur und dem elektrischen Feld des Leitungsstroms des CRRAM sind in Abb. 6a bzw. b zusammengefasst. Die Schlüsseleigenschaften des Trap-Assisted Tunneling (TAT)-Stroms werden durch seinen Schwachtemperatureffekt und die lineare Abhängigkeit zwischen ln(J) und 1/E gezeigt [17, 36]. Unter Verwendung des TAT-Leitungsmodells muss zuerst das Potentialprofil innerhalb des TMO-Films berechnet werden, um jeden lokalisierten Vo-Widerstand weiter zu erhalten. Es wird erwartet, dass die Verteilung von Vo- den leitenden Strom dominant beeinflusst, da der Tunnelabstand zwischen Sauerstoffleerstellen variiert. Der Widerstand von Vo-, R _ij , wird dann nach Gl. 1, der die Wahrscheinlichkeiten der Vo-Präsenz am Standort berücksichtigt und das TAT-Modell anwendet, um die Tunnelwahrscheinlichkeit zwischen Leerstandszuständen zu berechnen.

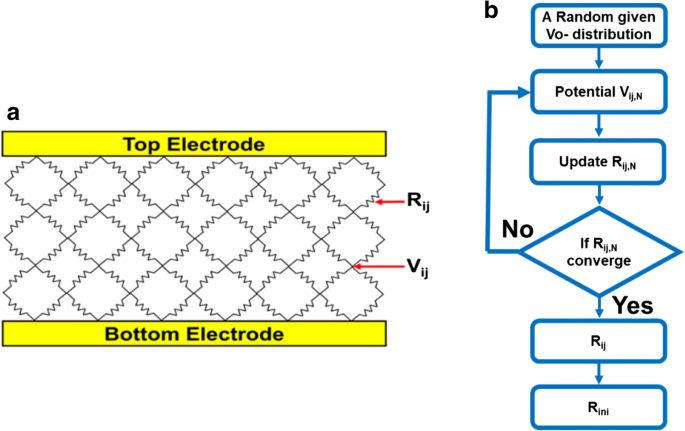
a Schema eines Widerstandsnetzwerkmodells bestehend aus einem variablen lokalisierten Widerstand von Vo-. Knoten in diesem Netzwerk sind miteinander verbunden, um die Interaktion zwischen Vo- zu simulieren. b Variabilitätssimulationsfluss des anfänglichen Widerstandsniveaus. Die stochastische Verteilung von intrinsischem Vo-emire während der Herstellung wird durch die Monte-Carlo-Methode berücksichtigt

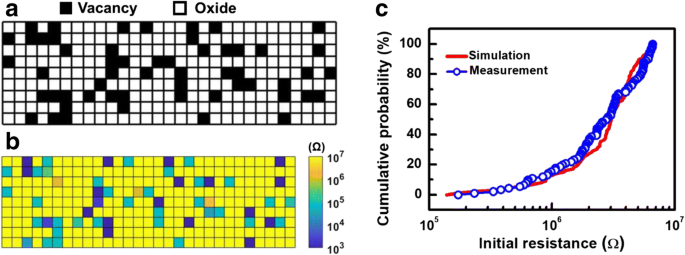
a Die zufällige Verteilung von intrinsischem Vo- ist anfänglich im RRAM-Film gegeben. b Lokalisierte Widerstandsverteilung von Vo- berechnet durch Berücksichtigung von Fallen-unterstütztem Tunneln. c R _ini Die Verteilung frischer Zellen, die von CRRAM-Arrays gesammelt wurden, stimmt gut mit den Simulationsdaten überein, wenn der TAT-Leitungsmechanismus der Vorformung von Vo-

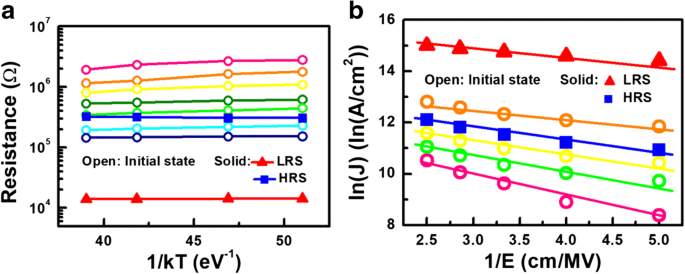
Der Leitungsmechanismus von CRRAM wird durch Überprüfung von a . bestimmt Temperaturabhängigkeit und b Abhängigkeit vom elektrischen Feld. Trap-unterstütztes Tunneln gefolgt von CRRAM wird von zwei Leitungseigenschaften angenommen, einer schwachen Temperaturabhängigkeit und einer linearen Anpassung zwischen ln(J) und 1/E

Jedes R _ij,N wird in jeder Iteration aktualisiert, bis das Ergebnis schließlich konvergiert. Als letztes R _ij Verteilung erhält man, wie in Abb. 5b dargestellt, den Gesamtwiderstand R _ini , einer frischen Zelle kann auch nachträglich projiziert werden, wie in Abb. 5c gezeigt. Wie in Abb. 5c zu sehen ist, ist die Variation des simulierten R _ini Verteilung, die durch vorgeschlagenen Simulationsfluss unter Berücksichtigung der stochastischen Verteilung und Konzentration von intrinsischem Vo- erhalten wurde, stimmt gut mit der Verteilung des R . überein _ini gemessen auf CRRAM-Arrays. Daher tragen zufällig verteilte intrinsische Vo-in-TMO-Schichten, die mehrere Tunnelpfade erzeugen, zu dem weit verbreiteten Anfangswiderstand bei, der beim Vorformen von CRRAM-Arrays gefunden wird.

Analyse des ungleichmäßigen Umformprozesses

Nach der Modellierung von Ursachen, die der Variation von Zelle zu Zelle im frischen Zustand zugeschrieben werden, wird der Formungsvorgang, der die Widerstandsschalteigenschaften initialisiert, analysiert. Der Simulationsablauf des Umformvorgangs im DC-Sweep-Modus ist in Abb. 7 [18,19,20] dargestellt. Wie in Fig. 8a dargestellt, ist eine Zelle mit einem Auswahltransistor in Reihe mit einem Kanalwiderstand von ungefähr 5 KΩ im linearen Bereich und einem Sättigungsstrom von ungefähr 80 μA verbunden. Aufgrund der niedrigen Formierspannung müssen die Leitungs- und Spannungsmechanismen des Dielektrikums im Bereich niedriger elektrischer Felder berücksichtigt werden. Basierend auf dem thermochemischen Modell, das in früheren Studien vorgeschlagen wurde, wurde eine genaue Vorhersage des dielektrischen Versagens gezeigt [37,38,39,40]. Theoretisches Abbauverhalten von TiO₂ simuliert durch das thermochemische Modell [41] zeigte ähnliche Eigenschaften wie die in CRRAM beobachteten. Daher wird die Vo-Erzeugungsrate hier basierend auf dem thermochemischen Modell erhalten [42,43,44]. Wie das thermochemische Modell nahelegt, sind die Gitterpunkte neben Vo- als Schwachstelle in der Umgebung der Defekte definiert. Die Anwesenheit von Vo- induziert auch ein lokalisiertes verstärktes Feld, wie in Abb. 8b gezeigt, und beschleunigt den Erzeugungsprozess von Vo- [45]. Betrachtet man die Zeit bis zum dielektrischen Durchbruchsprozess im thermisch-chemischen Modell mit einer Feldabhängigkeit von exp.(−E), ist die Wahrscheinlichkeit der Vo-Erzeugung P _ij wird durch die folgende Gleichung berechnet [42].

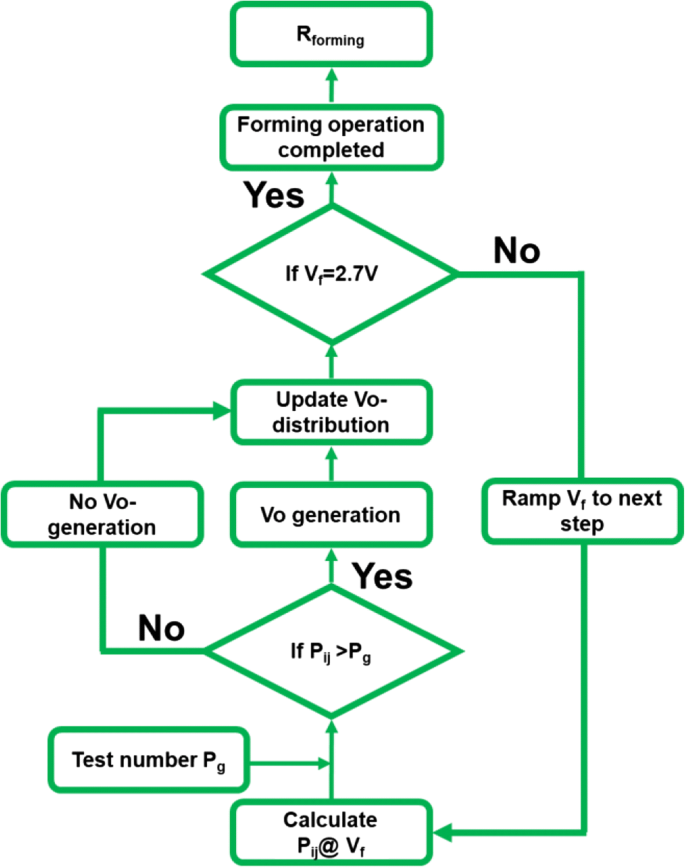
Simulationsablauf eines Umformprozesses basierend auf dem thermisch-chemischen Modell unter Annahme der dielektrischen Ausfallzeit mit Abhängigkeit vom elektrischen Feld von exp.(−E)

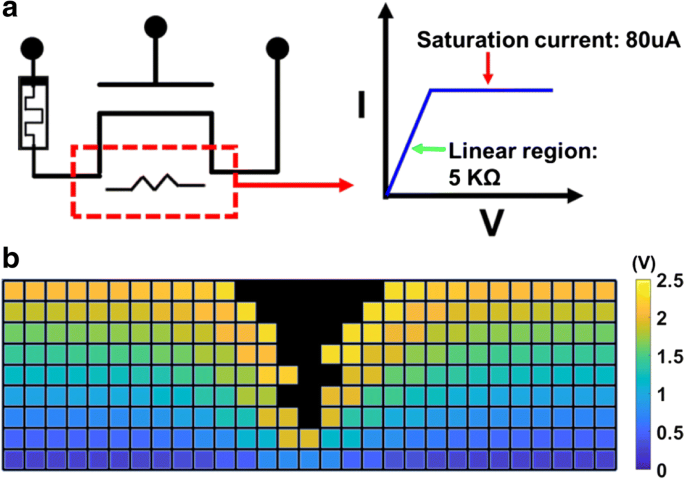
a Der Formungsvorgang wird durch einen CRRAM simuliert, der in Reihe mit einem idealen Transistor verbunden ist. b Ungleichmäßige Verteilung des elektrischen Potenzials, die aus bereits vorhandenem Vo- resultiert, induziert ein lokalisiertes Feld und beschleunigt die Erzeugung neuer Defekte

Ein kritisches Niveau, P _g , und ein Kriterium, P _ij> P _g , werden definiert, ob ein neues Vo- erzeugt wird. Ein Rampenprozess wird angewendet, um die neue Vo-Verteilung bei jeder Iteration zu aktualisieren, bis die Formungsspannung 2,7 V erreicht. Schließlich ist bei einer zufällig verteilten intrinsischen Vo- der niedrige Widerstandswert R _bilden nach dem Umformvorgang erhalten werden. Basierend auf dem obigen Modell wird der simulierte R _bilden Verteilung projizierte eine große Variation, wie in Abb. 9a gezeigt, und der berechnete I-V Eigenschaften stimmen gut mit den gemessenen Daten überein. Darüber hinaus wird auch der Zusammenhang zwischen Umformeigenschaften und Ausgangszuständen untersucht. Höhere Konzentration und örtlich verteilte Vo- beschleunigen den Umformprozess. Daher positive Korrelation zwischen Formierspannung und R _ini finden sich sowohl in den Simulationsergebnissen als auch in den gemessenen Daten, wie in Abb. 9b gezeigt.

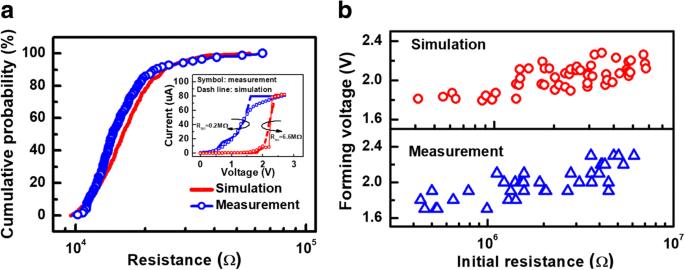
a Die simulierte Widerstandsverteilung des Umformvorgangs stimmt gut mit dem Messergebnis überein. b Positive Korrelationen zwischen Anfangswiderstand und Umformspannung finden sich sowohl in gemessenen als auch in simulierten Daten aufgrund von mehr Schwachstellen und einer höheren elektrischen Feldstärke, die durch das Vorformen erzeugt werden. Vo-

Darüber hinaus induziert beim Formgebungsvorgang erzeugtes Vo- einen leitenden Pfad und führt zu einer Änderung von CF in Zellen, wobei die Entwicklung von CF während des Formprozesses in 10 dargestellt ist. Für Zellen mit hohem R _ini , gibt es weniger intrinsische Vo- und weniger Schwachstellen, wie in Abb. 10a dargestellt. Nach dem Formungsvorgang ist es wahrscheinlicher, dass ein einzelner leitfähiger Pfad zwischen den Elektroden auftritt. Das Wachstum von CF in Zellen mit viel intrinsischem Vo-, wie in Abb. 10b gezeigt, ist jedoch tendenziell weiter verbreitet; daher werden nach dem Formen dendritische CF erzeugt. Die Korrelation zwischen verschiedenen CF-Topographien und der Vo-Verteilung im frischen Zustand wird auch durch Messdaten bestätigt. Von Vo- und CF in der TMO-Schicht ist bekannt, dass sie während des Elektroneneinfang-/Entfallervorgangs zu einem ausgeprägten zufälligen Telegraphenrauschen (RTN) führen [46]. Widerstandsschwankungen treten auf, wenn der leitfähige Pfad durch eingefangene Elektronen blockiert wird, und der Widerstand nimmt ab, wenn Elektronen ausfallen. Die RTN-Analyse von CRRAM nach der Formung ist in Abb. 11 zusammengefasst. Regelmäßige zweistufige Widerstandsfluktuation wird in Zellen mit hohem R . gefunden _ini , wenn das Einfangen/Entpacken von Elektronen in einem Gerät mit einer dominanten CF stattfindet. Auf der anderen Seite findet man mehrstufiges RTN in Zellen mit niedrigem R _ini von dem erwartet wird, dass es die dendritische CF mit mehr als einem Weg blockiert. Das statistische Ergebnis von RTN ist in Abb. 12 zusammengefasst, indem die RTN-Messung von mehr als 200 CRRAM-Zellen analysiert wird. Daten deuten darauf hin, dass Zellen mit hohem R _ini neigen dazu, nur Bi-Level-RTN zu zeigen, was eher bei Geräten mit einer dominanten CF auftrat [46,47,48,49]. Die Widerstandsschwankung nach dem Umformvorgang ist in Abb. 13 dargestellt. Die Daten legen nahe, dass sowohl in den Mess- als auch in den Simulationsergebnissen in den Zellen mit niedrigem R . eine höhere Widerstandsschwankung gefunden wird _ini . Da die weniger begrenzten CFs den Auswahltransistor früh in den Sättigungsbereich drängen, wird eine Zelle möglicherweise nicht richtig gebildet, was zu breiteren Widerstandsniveaus im niederohmigen Zustand führt.

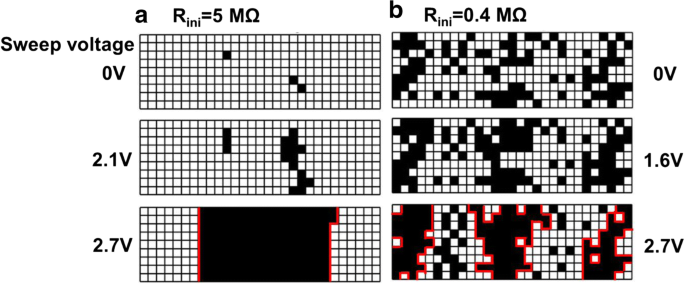
Fortschritt von CF in Zelle mit a hoher Anfangswiderstand und b geringer Anfangswiderstand. Eine höhere intrinsische Vo-Konzentration in der TMO-Schicht führt zu einer zufälligen Erzeugung von Vo- an Schwachstellen. Diese Vo- verbinden sich auch miteinander, um dendritische Pfade zu bilden

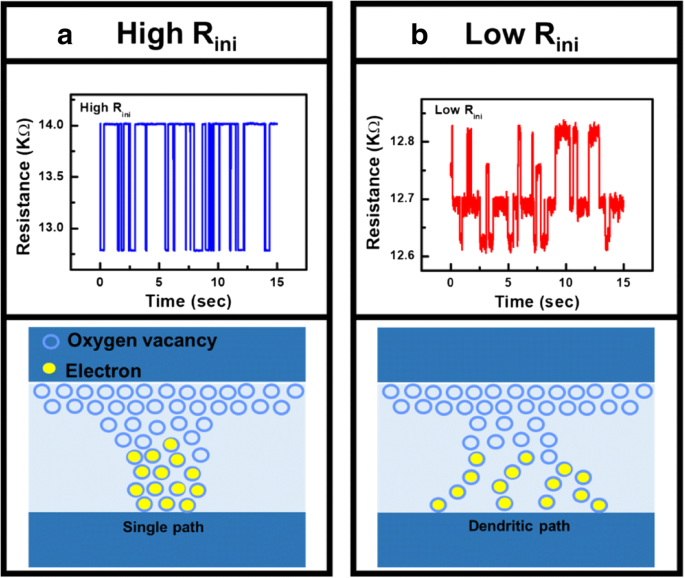
Die Topographien von CF in Zellen mit a hoher Anfangswiderstand und b niedriger Anfangswiderstand werden durch die entsprechenden RTN-Daten analysiert. Auftreten von multiplen Widerstandsfluktuationen in Zellen mit niedrigem Anfangswiderstand und mehr intrinsischem Bestätigt die Existenz von dendritischen CFs in der TMO-Schicht

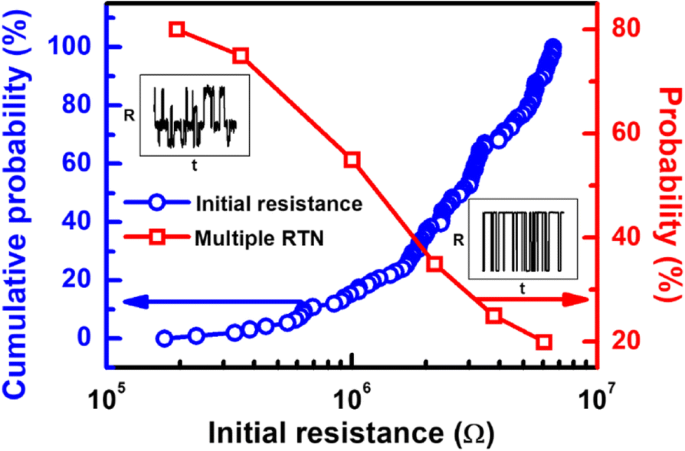
Die Korrelation zwischen dem anfänglichen Widerstandsniveau und dem RTN-Niveau bei CRAM-Zellen wird zusammengefasst. Bei Zellen mit einem dominanten Leiterpfad, die stark mit Zellen mit hohem R . korrelierten, wird eine höhere Wahrscheinlichkeit einer zweistufigen Widerstandsfluktuation erwartet _ini

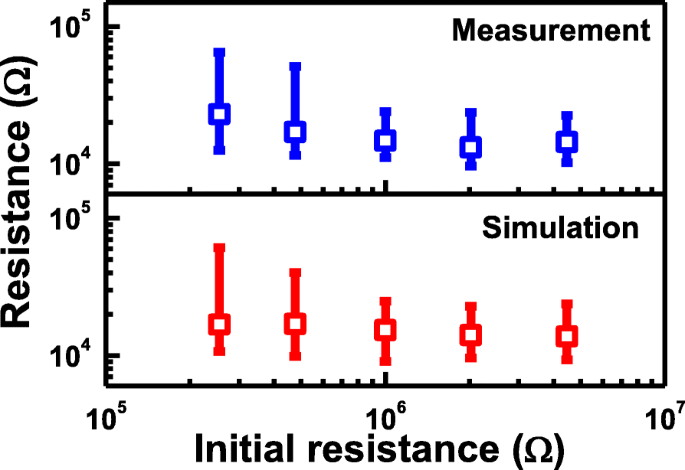
Die Analyse der Variation des Widerstandsniveaus nach dem Umformvorgang wird sowohl durch Simulation als auch durch Messung untersucht. Eine höhere Variation, die durch die dendritische CF-Erzeugung induziert wird, findet sich in Zellen mit niedrigem Anfangswiderstand

Um die durch intrinsisches Vo- in der TMO-Schicht verursachte Formungsvariabilität zu verringern, wird vorgeschlagen, dass ein Reset-Trainingsvorgang, der SL auf 1,4 V unter einer festen WL-Spannung von 2 V überstreicht, blind auf ganze Speicherzellen in einem CRRAM-Array vor dem Ausbilden angewendet wird. Es wird erwartet, dass dieser Vorgang bereits vorhandene Defekte in Zellen mit niedrigem R . vernichtet _ini und um ein besser begrenztes CF-Wachstum während des nachfolgenden Umformprozesses sicherzustellen. Aufgrund der niedrigen angelegten Spannung gibt es keine Veränderung bei Zellen mit hohem R _ini nach dem Trainingsprozess. Bei einer Trainingsoperation mit pauschalem Reset wird der Widerstand von Zellen mit niedrigem R _ini , steigt an, ohne die Zellen mit hohem R . zu stören _ini , wie in Abb. 14 gezeigt. Anschließend können gleichmäßigere Umformeigenschaften erhalten werden.

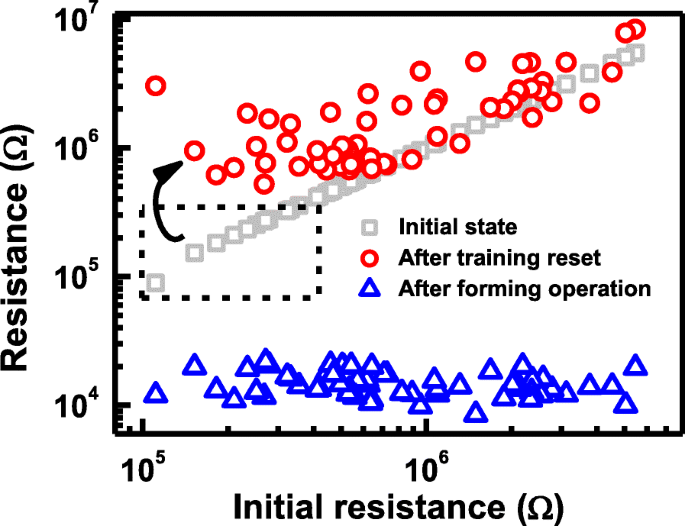
Es wird vorgeschlagen, eine Trainingsoperation mit einem pauschalen Zurücksetzen auf das CRRAM-Array anzuwenden. Widerstand in Zellen mit niedrigem R _ini wird durch die Vernichtung intrinsischer Defekte erhöht, aber Zellen mit hohem R _ini wird nicht gestört

Schlussfolgerungen

Ein Widerstandsnetzwerkmodell, das den lokalen Feldeffekt und die trap-unterstützte Tunnelleitung zwischen Vo- berücksichtigt, wurde erfolgreich etabliert. Mittels Monte-Carlo-Simulation wird die Zellvariabilität bezüglich ihres Anfangswiderstandes sowie des Umformprozesses untersucht. Die Variation in den frischen Zuständen von CRRAM kann erfolgreich durch eine zufällig gegebene Verteilung von intrinsischem Vo- erklärt werden. Die projizierte Widerstandsverteilung nach der Umformung stimmt auch gut mit dem Messergebnis überein, indem das thermochemische Modell übernommen wird. Das CF-Wachstum während der Umformung wird diskutiert und mit der in diesem Prozess beobachteten Variabilität in Verbindung gebracht. Schließlich wird ein Reset-Trainingsvorgang vorgeschlagen, um die durch intrinsische Vo- in der TMO-Schicht verursachte Formungsvariabilität weiter zu verringern. Eine starke Korrelation zwischen Anfangszuständen und Formgebungseigenschaften liefert Richtlinien für neue adaptive Operationen für die zukünftige Entwicklung von RRAM-Technologien.

Abkürzungen

CF:

Leitfähiges Filament

CRRAM:

Kontaktresistiver Arbeitsspeicher

C_Vo- :

Vo- Konzentration

d:

Tunnelentfernung

E:

Elektrisches Feld

ILD:

Zwischenschichtdielektrikum

N :

Iterationsdauer

P _g :

Schwellenwechselwahrscheinlichkeit

P _ij :

Wahrscheinlichkeit der Vo-Generation

R _bilden :

Widerstand nach Umformung

R _ij :

Lokalisierter Widerstand von Vosite

R _ini :

Anfangswiderstandszustand

R _Oxid :

Lokalisierter Widerstand der Oxidstelle

RPO:

Widerstandsschutzoxid

RRAM:

Resistiver Arbeitsspeicher

RTN:

Zufälliges Telegrafenrauschen

TAT:

Trap-assisted Tunneling

TMO:

Übergangsmetalloxid

V _f :

Umformspannung

V _ij :

Potenzial

Vo-:

Sauerstoff-Stelle

α :

Anpassungsparameter

β :

Anpassungsparameter

γ :

Anpassungsparameter

ϕ :

Elektrische Potenzialdifferenz