Eine anisotrope Mikrostrukturentwicklung in einer Festoxid-Brennstoffzellenanode

Hintergrund

Eine Festoxid-Brennstoffzelle (SOFC) ist ein elektrochemisches Gerät, das die chemische Energie von Wasserstoff direkt in Strom umwandelt. Eine einzelne Zelle hat normalerweise die Form einer flachen Platte, in der ein undurchlässiger und dichter ionenleitender Elektrolyt zwischen zwei porösen katalytischen Elektroden eingebettet ist:einer Anode und einer Kathode. Der Anodenseite wird Brennstoff zugeführt und der Kathode wird die Luft zugeführt. Die Gase können sich nicht vermischen, um eine unproduktive Verbrennung zu vermeiden. Stattdessen treffen Gase auf Katalysatormaterial, verlieren ihre Elektronen und bilden Kondensatoren auf beiden Seiten eines Elektrolyten. Da die Reaktion auf der Kathodenseite langsamer ist, tritt zwischen den beiden Elektroden eine Potentialdifferenz auf. Diese Potentialdifferenz ist zusammen mit einem Sauerstoffdruckgradienten eine treibende Kraft, die Sauerstoffionen von der Kathode zur Anode bewegt. Dabei ist die Morphologie der Elektrodenmikrostruktur von entscheidender Bedeutung. Eine typische Anode besteht aus einer Nickelphase (Ni), einer Yttriumoxid-stabilisierten Zirkonoxidphase (YSZ) und einer Porenphase. Jedes Material spielt eine wesentliche Rolle bei den Transportprozessen durch die SOFC, indem es einen Weg für verschiedene Arten bereitstellt. Im Fall einer Anode bietet die YSZ-Phase Wege zu Sauerstoffionen, die Ni-Phase für Elektronen und die Porenphase ermöglicht das Eindringen von Gasen in die Elektrode. Die elektrochemische Reaktion kann nur an der Linie ablaufen, an der sich alle drei Phasen berühren, der sogenannten Tripel-Phasen-Grenze (TPB). Die Transportphänomene durch die Zelle sind in Abb. 1 [1] schematisch dargestellt.

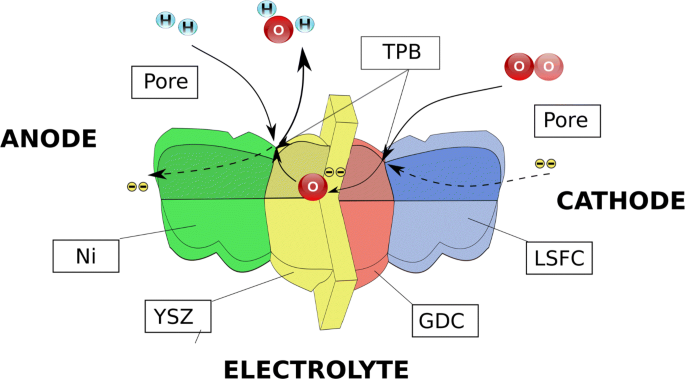
Eine schematische Ansicht des Transportphänomens durch eine typische Festoxid-Brennstoffzelle mit einer hervorgehobenen Rolle der Mikrostruktur

Aufgrund der Komplexität des Anodenverbundes wird das mikrostrukturorientierte Design zu einem entscheidenden Schritt in der SOFC-Entwicklung [2–7]. In dieser Arbeit untersuchen wir die Mikrostrukturänderungen, die in einer Festoxid-Brennstoffzellenanode über einen langen Betriebszeitraum auftreten. Für eine eingehende Analyse konzentrieren wir uns auf den anisotropen Tortuositätsfaktor, der die Komplexität der Mikrostruktur in einer bestimmten Richtung widerspiegelt. Die Strukturanalyse wird unter Verwendung eines Rasterelektronenmikroskops durchgeführt, das mit dem fokussierten Ionenstrahl gekoppelt ist. Diese Technik wurde 2006 von Wilson et al. auf dem Gebiet der SOFC eingeführt. [8]. Das Verfahren ermöglicht die direkte Beobachtung vieler nachfolgender Schnitte und wandelt die Ergebnisse in eine digitale 3D-Darstellung der Mikrostruktur um. Aus dem rekonstruierten Gefüge können die Gefügeparameter bewertet werden [9–11]. Diese Parameter, die direkt aus der realen Elektrodenstruktur gewonnen werden, sind von entscheidender Bedeutung, um die Entwicklung der Anodenmikrostruktur während der langen Laufzeit eines Brennstoffzellensystems zu verstehen. Diese Technik wurde häufig verwendet, um die numerische Modellierung zu verbessern [12–17] und in jüngerer Zeit, um die Degradationsmechanismen einer Festoxid-Brennstoffzellenanode zu verstehen [18–24]. Dies wurde zu einer wertvollen Bestätigung der jüngsten kristallographischen Studien [25, 26].

In diesem Beitrag berichten wir zum ersten Mal über den anisotropen Charakter der Mikrostrukturentwicklung während des Langzeitbetriebs eines SOFC-Stacks. Wir zeigen, dass sich die Mikrostruktur hauptsächlich durch anisotrope Migration, Wachstum und Vergröberung von Nickelpartikeln entwickelt.

Experimentelle Blenden

Modularer Stack-Teststand

Der Alterungstest wurde mit einem Modular Stack Test Bench (MSTB) durchgeführt, der von SOLID Power, einem führenden europäischen SOFC-Hersteller, entworfen und entwickelt wurde. Die schematische Ansicht des Aufbaus ist in Abb. 2 dargestellt. Der Stapel befindet sich in einem Elektroofen.

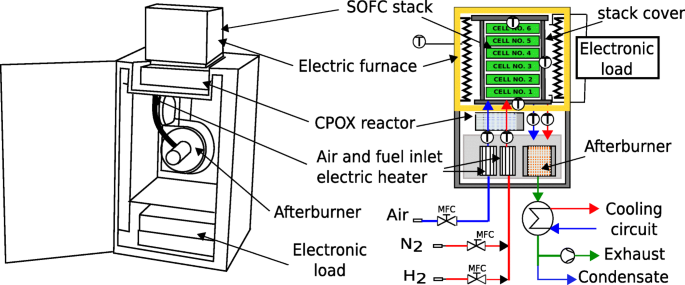
Eine schematische Ansicht des Modular Stack Test Bench

Der Brennstoff und die Luft werden dem System über Massendurchflussregler und Vorwärmer zugeführt. Sowohl Luft als auch Brennstoff werden dem katalytischen Partialoxidationsreaktor (CPOX) zugeführt (wenn der Brennstoff Methan enthält) oder umgeht ihn, wenn der Brennstoff ein Gemisch aus Wasserstoff und Stickstoff ist. Nach dem Vorheizen wird dem Kathodenkanal Luft zugeführt. Ein Teil des Sauerstoffs in der zugeführten Luft wird bei der elektrochemischen Reaktion verbraucht. Gleichzeitig wird Luft verwendet, um Wärme aus dem Zellstapel abzuführen. Dann wird dem Nachbrenner Luft zugeführt, um den ungenutzten Brennstoff aus dem Anodenkanal zu verbrennen. Auf der anderen Seite der Luftaufbereitung wird der Brennstoff oxidiert, um Strom zu erzeugen. Der Brennstoff, der in dieser Studie eine Mischung aus Wasserstoff (H₂ ) und Stickstoff (N₂ ) wird nach dem Vorwärmen dem Anodenkanal zugeführt. Der Restbrennstoff wird im Nachbrenner oxidiert. Nach dem Verbrennungsprozess wird das Gas abgekühlt, das kondensierte Wasser abgeschieden und das trockene Gas schließlich an die Umgebungsluft abgegeben.

Sieben Thermoelemente, die in Abb. 2 mit „T“ gekennzeichnet sind, überwachen die Temperaturverteilung. Jede Bipolarplatte ist mit einem Draht verbunden, der dann mit einem Potentiostaten verbunden ist. Diese Konfiguration ermöglicht es, die Strom-Spannungs-Kennlinien für jede Zelle im Stapel zu erhalten. Die Abmessungen einer Zelle betragen 60 × 80 [mm × mm]. Die für die Reaktion verfügbare aktive Zellfläche beträgt 48 [cm ² ]. Die Zelle erreicht eine Brennstoffausnutzung von bis zu 75 % und kann eine hohe Leistungsdichte von mehr als 1 [W cm ⁻² . erreichen ]. Der Stapel ist in einer Gleichstromkonfiguration organisiert, bei der Kraftstoff- und Luftstrom in die gleiche Richtung verlaufen. Als Brennstoff im System wurde ein Gemisch aus Wasserstoff und Stickstoff verwendet.

Weitere Details zum Aufbau finden Sie an anderer Stelle [27, 28].

Fokussiertes Ionenstrahl-Rasterelektronenmikroskop

Ein Doppelstrahlsystem kombiniert ein Rasterelektronenmikroskop (REM) und eine Quelle für fokussierten Galliumionenstrahl (FIB) in einer Kammer. Das REM wird zur Bildgebung verwendet und das FIB dient hauptsächlich zum Fräsen. Für eine begrenzte Situation kann FIB für die Beobachtung verwendet werden. Das System bietet die einzigartige Möglichkeit nachfolgender Schnitte einer untersuchten Probe. Die übliche Größe der Materialprobe, die im Halter platziert werden kann, beträgt 25 mm ² . Der FIB-REM-Aufbau und das Messverfahren sind schematisch in Abb. 3 dargestellt. Die Richtung der Ionenkanone ist senkrecht zur Probenoberfläche, und die Elektronenkanone ist in Bezug auf die Ionenquelle in einem gewissen Winkel geneigt, um die Beobachtung des Abschnitts einer Probe. Das interessierende Volumen der Probe, das während eines einzelnen Verfahrens beobachtet werden kann, beträgt etwa 1000 μ m ³ . Der fokussierte Ionenstrahl wird verwendet, um einen Graben herzustellen und einen Schnittpunkt einer Probe freizulegen, der die Anforderungen für die minimale repräsentative Volumengröße erfüllt. Nachdem der Graben hergestellt wurde, wird der Schnittpunkt mit niederenergetischem Ga ⁺ . poliert Strahl und das Bild wird mit einem Detektor in der Linse aufgenommen. Dies führt zu einem außergewöhnlich guten Kontrast zwischen den untersuchten Phasen:Ni, YSZ und Pore. Nachdem ein REM-Bild aufgenommen wurde, fräst die FIB-Pistole, um eine weitere Kreuzung freizulegen, und eine weitere Materialschicht wird entfernt. Das „cut-and-see“-Verfahren wird wiederholt, bis je nach interessierendem Volumen 200-300 Bilder erhalten werden. Dieses Verfahren wird als Sektionieren bezeichnet. Die Vorgehensweise lässt sich in folgenden Schritten zusammenfassen:

1. 1

   Auf dem interessierenden Volumen wird eine Kohlenstoffschicht abgeschieden.

   

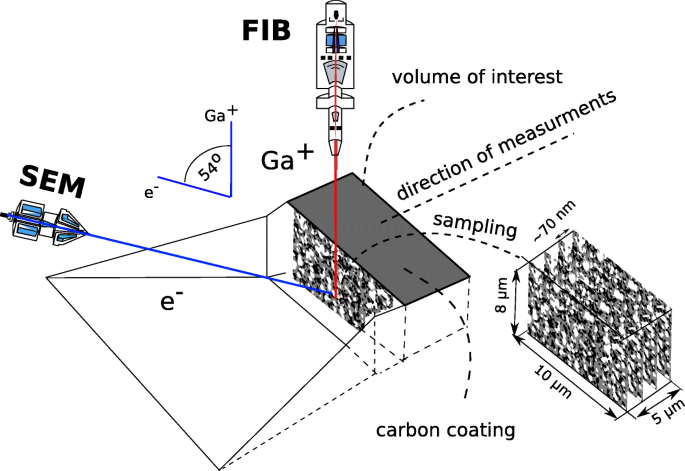
   Die Konfiguration eines Dual-Beam-Systems

2. 2

   Ein Graben wird hergestellt, um den Zugang zum Schnittpunkt der Probe zu ermöglichen.

3. 3

   Der Querschnitt wird mit dem Schwachstromstrahl poliert.

4. 4

   Ein SEM-Bild einer beobachteten Kreuzung wird unter Verwendung eines Sekundärelektronendetektors in der Linse aufgenommen.

5. 5

   Eine FIB-Pistole verwendet einen Strahl von Ga+-Ionen, um in die Probe zu fräsen, um einen weiteren Schnittpunkt freizulegen.

6. 6

   Ein „Ausschneiden und Sehen“-Verfahren wird wiederholt, um die Sequenz von 2D-Bildern zu erhalten.

Die Idee des Cut-and-See-Verfahrens ist in Abb. 3 dargestellt.

Experimentelle Methodik

Die vorgestellte Studie gliederte sich in zwei separate Teile:ein Experiment zur Stromerzeugung und eine mikrostrukturelle Studie. Die Dauerhaltbarkeitsstudie wurde durchgeführt, indem der Stapel über einen längeren Zeitraum unter konstanter Belastung gehalten wurde. Um die Testdauer zu verkürzen, wurde die Temperatur auf 800 ^{o . erhöht} C und der aufgezwungene Strom betrug 19,4 A, um zu Beginn des Experiments eine Ausgangsleistung von 90 W bereitzustellen. Der Brennstoffausnutzungsfaktor betrug 75 %. Die detaillierten experimentellen Bedingungen sind in Tabelle 1 zusammengefasst. Nach dem Alterungstest wurde der Stapel zerlegt und neun Proben für die Mikrostrukturanalyse nach dem Test ausgewählt. Drei Proben wurden aus den Zellen Nr. 1, 3 und 5 (befindet sich stromaufwärts, in der Mitte und stromabwärts von jeder Zelle) wie in 4 dargestellt. Eine zusätzliche Zelle, die sogenannte Referenzzelle, war eine neue Zelle direkt nach dem Reduktionsprozess. Die Zelle wurde vom Hersteller bereitgestellt und nahm nicht an den elektrochemischen Tests teil. Daher ist anzunehmen, dass die Mikrostruktur der Referenzzelle die Mikrostruktur vor dem Alterungstest darstellt. Alle Proben für die FIB-SEM-Analyse hatten eine Form von 5 mm × 5 mm Quadraten und wurden mit einem Diamantstift von der Zelle (6 cm × 8 cm) abgeschnitten. Vor den Gefügeuntersuchungen wurden alle Proben mit Epoxidharz imprägniert und mit Sandpapier poliert. Die Imprägnierung ist wichtig für die Erkennung der Porenphase bei der REM-Bildgebung. Alle neun Proben wurden mit der FIB-SEM-Technik analysiert.

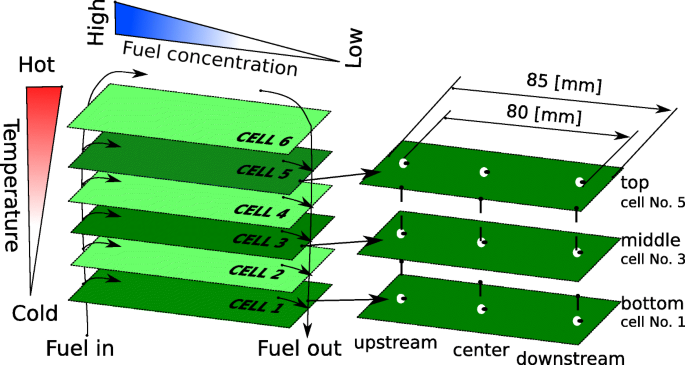
Die Positionen der ausgewählten Samples in einer Zelle und im Stapel

Der für jede Probe erhaltene Satz von SEM-Bildern durchlief den Bildsegmentierungsprozess, um jedem Bereich des SEM-Bildes eine von drei Phasen zuzuordnen. Die Segmentierung ist ein halbautomatisch durchgeführter Prozess der Kennzeichnung der Bildbereiche basierend auf ihrer Helligkeit, der bis zu einem Monat einer Bedienerarbeit pro Probe erfordert. Nach erfolgreichem Bildsegmentierungsprozess findet eine Bild-Resampling statt (siehe Abb. 5).

Der Workflow der Bildverarbeitung und Phasenbeschriftung. a Ein rohes Bild. b Manuell entfernte experimentelle Artefakte. c Filtern. d Phasenmarkierung, wobei Weiß für Nickel steht, Schwarz für Poren und Grau für YSZ steht

Die Random-Walk-Simulation, die später in diesem Artikel vorgestellt wird, erfordert das kubische Voxel. Dies bedeutet, dass der Abstand zwischen den Bildern der Pixelgröße des Bildes entsprechen sollte. Jedoch zeigen mehr Slices mehr Zeit an, die für die Segmentierung benötigt wird, was praktisch nicht durchführbar ist. In der Praxis ist der Abstand zwischen den Bildern wichtiger als die Pixelgröße, um beim zeitaufwendigsten Segmentierungsprozess Zeit zu sparen. Daher wird eine Segmentierung an den quaderförmigen Voxeln durchgeführt und während der Nachbearbeitung in ein kubisches Voxel umgewandelt. Basierend auf den neu abgetasteten Bildern wurden die Oberflächen, die die dreidimensionale Morphologie jeder Phase darstellen, durch eine dreieckige Approximation der Grenzfläche zwischen den verschiedenen Regionen erzeugt. Die Triangulation und das Resampling wurden mit der AVIZO-Software von ThermoFisher Scientific durchgeführt. Die erhaltenen dreidimensionalen digitalen Materialdarstellungen sind in Abb. 6 dargestellt.

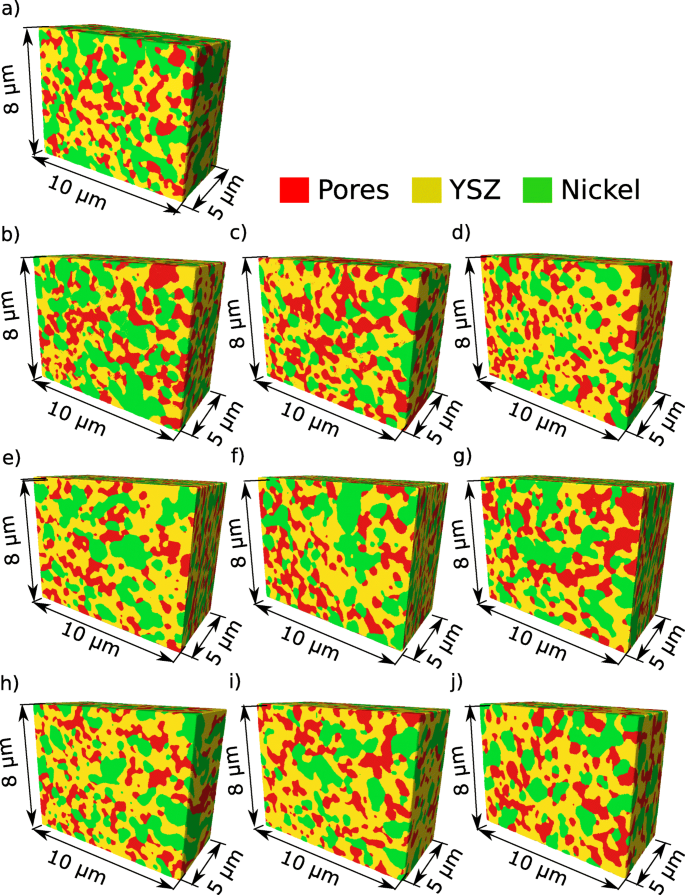
Digitale Materialdarstellung der Anodenmikrostruktur vor und nach dem Alterungstest. a Referenzprobe. b Zelle 5 stromaufwärts. c Zelle 5 zentriert d . Zelle 5 stromabwärts e Zelle 3 stromaufwärts. f Zelle 3 zentrieren g . Zelle 3 stromabwärts. h Zelle 1 stromaufwärts. ich Zelle 1 zentrieren. j Zelle 1 stromabwärts

Der Tortuositätsfaktor ist ein quantitatives Maß für die Komplexität der Mikrostruktur. Das Konzept der Tortuosität wurde von Carman [29] in die Untersuchung poröser Medien eingeführt, der eine Strömung durch ein Sandbett untersuchte. Er führte die Tortuosität als einen Faktor ein, der den verlängerten Diffusionsweg von Flüssigkeit in porösen Medien berücksichtigt. In seiner Studie nahm er an, dass ein poröses Bett der Dicke L _s könnte als ein Bündel gewundener Kapillarröhrchen mit einheitlichem Querschnitt und Länge L . betrachtet werden _e . In ähnlicher Weise kann für die Festoxid-Brennstoffzellenanode die Tortuosität als Verhältnis der tatsächlichen Diffusionsweglänge und der Elektrodendicke definiert werden. In diesem vereinfachten System ist die Tortuosität definiert als das Verhältnis der Länge des realen Diffusionsweges, L _e , zum Pfad im geraden Kanalfall, L _s (Anodendicke):

Es ist wichtig, den Unterschied zwischen Tortuosität und dem Tortuositätsfaktor im Auge zu behalten. Angesichts der Formulierung von Carman ist der Tortuosity-Faktor (τ ) ist definiert als das Quadrat der Tortuosität (τ =\(\bar{\tau}^{2}\)) und wird als Verstärkungsfaktor in einer Massendiffusionsgleichung verwendet:

wo ε ist die Porosität, D _ich ist der Diffusionskoeffizient von Gasgewürzen i in einem Gasgemisch und D _{ich ,eff} ist der effektive Diffusionskoeffizient unter Berücksichtigung des verlängerten Diffusionsweges des Fluids innerhalb des porösen Mediums.

In der Mikrostruktur einer echten Anode können die Brennstoffpfade außerordentlich kompliziert sein und Gasverbindungspfade können viele Verzweigungen bilden, sich trennen und wieder zusammenführen. Daher ist die Darstellung des Tortuositätsfaktors als Quadrat der Tortuosität eher symbolisch und die tatsächliche Beziehung zwischen Tortuosität und Tortuositätsfaktor kann nicht mit dem Kapillarmodell berechnet werden. Einige Gruppen lösen dieses Problem mit dem sogenannten M-Faktor, der die geometrische Tortuosität explizit zu einer Funktion kombiniert, den Perkolationsfaktor (P ), Konstriktionsfaktor (β ) und Phasenvolumenanteil [30]:

wo a , b , und c sind Konstanten, die aus der in Lit. beschriebenen Methodik abgeleitet wurden. [31]. Der von Peterson [32] eingeführte Einschnürungsfaktor kann als Verhältnis zwischen den Signalhörnern und den Engpässen verstanden werden. Eine umfassende Übersicht über bestehende Ansätze zur Schätzung der Tortuositätsfaktoren findet sich in einer Übersicht von Tjaden, Brett und Shearing [33].

In letzter Zeit erhalten diffusionsbasierte Algorithmen zunehmende Aufmerksamkeit, da sie keinen Einschnürungsfaktor benötigen. Dies liegt daran, dass die Engpässe und die Ausbuchtungen bei der Simulation des Diffusionsprozesses direkt berücksichtigt werden und der Messwert eine direkte Reduzierung des Diffusionskoeffizienten ist [34].

Eine der vielversprechendsten Methoden ist dabei ein Random-Walk-Prozess, der den Tortuositätsfaktor für nicht sorbierende Partikel statistisch berechnen kann. Bei diesem Verfahren wird eine große Anzahl von Markern, die Random Walker genannt werden, stochastisch in der Porenphase verteilt, die in Abb. 6 als rote Volumina dargestellt ist. Bei jedem Schritt wandert jeder Walker zufällig zu den benachbarten Voxeln derselben Phase. Gehört das für die Migration ausgewählte Voxel zu einer anderen Phase, bleibt der Walker an der aktuellen Position und wartet auf den nächsten Zeitschritt. Während dieser Vorgang wiederholt wird, kann die mittlere quadratische Verschiebung von Random Walkern berechnet werden:

wo 𝜗 die dimensionslose Zeit des Random-Walk-Verfahrens ist und n ist die Anzahl der Random Walker.

Die exakte Lösung der mittleren quadratischen Verschiebung für einen Gitterweg im freien Raum ist gegeben durch [35]:

wo D ₀ ist der Diffusionskoeffizient im freien Raum [m ² s ⁻¹ ] und t ist Zeit in [s]. Der Diffusionskoeffizient aus Gl. (5) kann als Funktion der Zeit durch Berechnung der Ableitung umgeschrieben werden:

Weil 𝜗 ist eine Funktion der Zeit t , Gl. (6) hat die folgende Form:

Aus einem Teil von Gl. (5):

geben

wo a ist die Gitterkonstante eines einfachen kubischen Gitters (d. h. die Dimension des FIB-REM-Voxels) [nm].

Der Tortuositätsfaktor τ beschreibt einen Grad der Verringerung der mittleren quadratischen Verschiebung in porösen Medien im Vergleich zum freien Raum [34, 36]:

Durch Kombinieren von Gl. (7) und (10) gelangt man zu folgender Formel:

die nach weiterer Einbeziehung von Gl. (8) und (10) wird:

Wenn das Transportphänomen nur in eine Richtung betrachtet wird, ist der folgende Ausdruck relevant:

Für die Abschätzung des anisotropen Tortuositätsfaktors wird daher Gl. (12) wird zu:

Da die Methode auf einer Statistik basiert, sind viele Wanderer und große mittlere quadratische Verschiebungen erforderlich, um den Tortuositätsfaktor richtig zu schätzen. Schließlich verlassen die Wanderer den Rechenbereich, der durch die digitale Darstellung der Mikrostruktur repräsentiert wird. Dies ist natürlich unerwünscht, da die Wanderung nicht außerhalb des Rechenbereichs fortgesetzt werden kann. Um dieses Problem zu vermeiden, wird eine Phasenspiegelung verwendet. Wenn der Wanderer die Grenze überschreitet, erscheint er vollständig in einem neuen Bereich, der die Spiegelreflexion der ursprünglichen Mikrostrukturrekonstruktion ist. Eine vollständige Kopie der digitalen Rekonstruktion zu erstellen, wenn der Wanderer die Grenze überquert, ist für den Computerspeicher zu schwer, und deshalb wurden spezielle Programmiertechniken angewendet, um Hardwareressourcen zu schonen. Die Phasenspiegelung ist die größte Einschränkung der Methode, da die berechnete Tortuosität nur die Komplexität des untersuchten interessierenden Volumens (nicht der gesamten Anode) widerspiegelt.

Basierend auf den anisotropen Tortuositäten führen wir den wie folgt definierten Anisotropiefaktor ein:

wo τ _x ,τ _y , und τ _z sind die anisotropen Tortuositätsfaktoren in x , y , und z Richtungen bzw. und τ _r ist der Tortuositätsfaktor, der für die Gesamtverschiebung des Gehwagens berechnet wird, unabhängig davon, in welche Richtung die Verschiebung erfolgt.

Ergebnisse und Diskussion

Abbildung 7 zeigt eine durchschnittliche Klemmenspannung des Stapels während des Alterungstests. Wie zu sehen ist, gibt es keine Hinweise auf eine Leistungsminderung. Außerdem nimmt die Polarisation während der ersten tausend Betriebsstunden ab. Unsere bisherigen Ergebnisse zeigten, dass die Kontaktfläche der Reaktionsoberfläche trotz fehlender Leistungsverschlechterung signifikant abnimmt [24]. Wir fanden, dass der Zerfall von TPB inhomogen war und stark von der Position im Stapel abhing [24]. In dieser Arbeit zeigen wir, dass die Entwicklung der Mikrostruktur nicht nur inhomogen, sondern auch anisotrop ist. Die Komplexität der Anode wurde basierend auf dem anisotropen Tortuositätsfaktor geschätzt, der unter Verwendung der digitalen Materialdarstellung in Abb. 6 abgeleitet wurde.

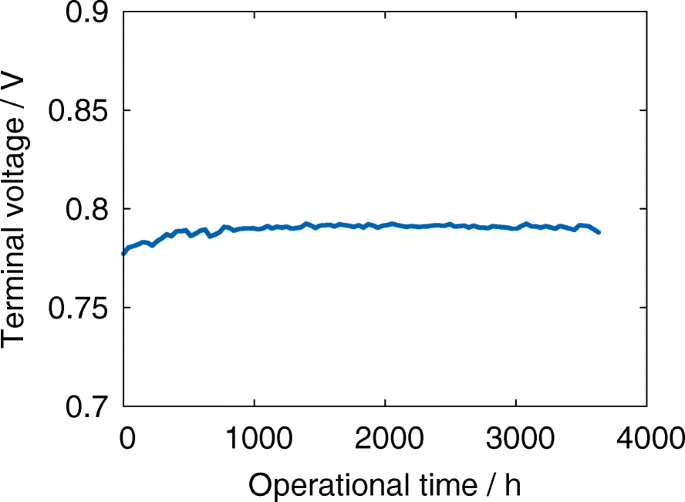
Klemmenspannung in Abhängigkeit von der Betriebsdauer im Dauerbetrieb

Anmerkung In einem realen Experiment variieren die Durchmesser des erhaltenen interessierenden Volumens aufgrund des Vorhandenseins der experimentellen Artefakte von einem zum anderen. Die gängigsten Artefakte wie Vorhangeffekte, Schattierungen und Neupositionierungen können den zugänglichen Querschnitt einschränken. Folglich ist das Volumen, das angemessen erkannt und segmentiert werden kann, für jede Messung unterschiedlich. In einigen Fällen konnten wir mehr als 10 μ . erhalten m im z Richtung; Da jedoch der Vorhang die Tonqualität beeinträchtigt, wird das Bild im y Richtung war eingeschränkt. Für andere war das Bild im y . scharf Richtung, aber wir konnten nur eine begrenzte Anzahl von Bildern korrekt ausrichten. Für die Quantifizierung betrug jedes Volumen etwa 1000 μ m ³ . Nur der Visualisierung halber haben wir die Bilder jedoch auf eine gemeinsame Größe von 10 μ . getrimmt m × 8 μ m × 5 μ m, um sie in Abb. 6 nebeneinanderstellen und vergleichen zu können.

Die Methodik der Tortuositätsfaktorschätzung wurde im Abschnitt „Experimentelle Methodik“ kurz vorgestellt. Abbildung 8 zeigt die Anisotropiefaktoren für verschiedene Stellen in der Zelle und im Stapel. Ein Vergleich mit der Referenzstichprobe wird ebenfalls präsentiert. Ein gemeinsamer Trend, der in den Ergebnissen beobachtet wurde, führte uns zu folgenden Schlussfolgerungen:

• Das Referenzanodenmaterial hat isotrope Eigenschaften, die sich während des Alterungstests zu einer starken Anisotropie entwickeln.

  

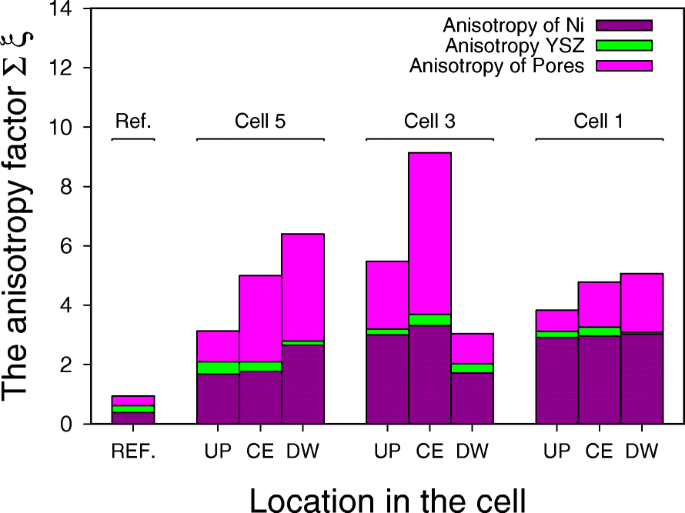
  Der Anisotropiefaktor an verschiedenen Stellen im Stapel und in einer Zelle, wobei sich UP, CE und DW jeweils auf Upstream, Center und Downstream einer Zelle beziehen und das Akronym REF der Referenzzelle entspricht

• Die allgemeine Tendenz besteht darin, dass der Anisotropiefaktor mit der Bewegung stromabwärts der Zelle zunimmt.

• Eine starke Anisotropie wurde nur für die Nickel- und Porenphasen beobachtet. Yttrium-stabilisiertes Zirkonium bleibt isotrop.

Die wahrscheinliche Ursache der Anisotropie ist die Vergröberung der Nickelpartikel [37–39] und die Migration, die in unserer bisherigen Forschung [23, 24, 40] sowie von anderen Forschungsgruppen [18, 41] beobachtet wurde. Während des Langzeitbetriebs wandern Nickelpartikel von der Anodenelektrolytgrenzfläche zur Anodenoberfläche. Da die Migration hauptsächlich in eine Richtung erfolgt, führt sie zur Anisotropie des Gefüges. Das würde auch erklären, warum Anisotropie nur die Nickel- und Porenphase betrifft. Der detaillierte Mechanismus ist unklar, aber eine mögliche Ursache für die Migration von Nickelpartikeln von der Anoden-Elektrolyt-Grenzfläche zur Anodenoberfläche ist die Verdampfung-Abscheidung der flüchtigen Nickelspezies wie Nickelhydroxid. Dies führt zu der Inhomogenität und dem diskontinuierlichen elektronischen Leitungsweg von Nickel [42].

Die meisten heute in den SOFC-Simulationen verwendeten Gasdiffusionsmodelle gehen von einer homogenen porösen Elektrode aus. Sie ist für die meisten Anwendungen genau, aber unsere Ergebnisse zeigen, dass diese homogene Annahme nach der Degradation möglicherweise nicht zutrifft. Die direkte Implikation der in diesem Artikel vorgestellten Beobachtung ist, dass wenn man mikrostrukturelle Parameter einer gealterten Probe in die numerische Simulation implementieren möchte, es wichtig ist, sich daran zu erinnern, welche Richtung der Transportphänomene im Modell berücksichtigt wird. Als Konsequenz sollten die richtigen anisotropen Eigenschaften aus den Mikrostrukturparametern extrahiert werden (wenn Anisotropie erkannt wird). Aus den erhaltenen Ergebnissen kann geschlossen werden, dass die Anisotropie bei Betrachtung der Diffusion besonders wichtig ist, da der Tortuositätsfaktor quantitativ die Reduktionsrate des Diffusionskoeffizienten ausdrückt. Beachten Sie die anisotrope Richtung bei der Gegenüberstellung der Mikrostrukturparameter verschiedener Anoden, die nach einem Langzeitbetrieb aufgenommen wurden, ein weiterer praktischer Vorschlag, der für die vorgestellte Beobachtung geeignet ist.

Allgemeine Schlussfolgerungen

In dieser Arbeit haben wir zum ersten Mal gezeigt, dass der Langzeitbetrieb von SOFC zu einer Anisotropie der Mikrostruktur in der Anode führen kann. Das Experiment zur erweiterten Stromerzeugung wurde unter Verwendung eines Short-Stack durchgeführt. Eine ortsaufgelöste Mikrostrukturanalyse wurde vor und nach dem Alterungstest mit der FIB-REM-Nanotomographie durchgeführt. Die erhaltenen 3D-Rekonstruktionen der Anodenmikrostruktur wurden in einen diffusionsbasierten Algorithmus implementiert, um den anisotropen Tortuositätsfaktor zu berechnen. Die Ergebnisse deuten darauf hin, dass der Langzeitbetrieb zu einer starken Anisotropie in der Nickel- und Porenphase der untersuchten Anode führte. Die wahrscheinliche Ursache für die anisotropen Eigenschaften der Anode nach dem Alterungstest ist Migration, Wachstum und Vergröberung der Nickelpartikel.

Verfügbarkeit von Daten und Materialien

Die Roh- und Prozessdaten, die für die Reproduktion dieser Ergebnisse erforderlich sind, können derzeit nicht weitergegeben werden, da die Daten Teil einer laufenden Studie sind.

Abkürzungen

CPOX:

Katalytische Partialoxidation

FIB:

Fokussierter Ionenstrahl

MSTB:

Modularer Stapelprüfstand

SEM:

Rasterelektronenmikroskop

SOFC:

Festoxidbrennstoffzelle

TPB:

Dreifache Phasengrenze

YSZ:

Yttriumoxidstabilisiertes Zirkonoxid