Wechselstrom-Induktorschaltungen

Widerstände vs. Induktivitäten

Induktivitäten verhalten sich nicht wie Widerstände. Während Widerstände einfach dem Stromfluss durch sie entgegenwirken (indem eine Spannung abfällt, die direkt proportional zum Strom ist), wirken Induktivitäten Änderungen entgegen im Strom durch sie, indem eine Spannung abfällt, die direkt proportional zur Änderungsrate ist des Stroms.

In Übereinstimmung mit dem Lenzschen Gesetz , diese induzierte Spannung hat immer eine solche Polarität, dass versucht wird, den Strom auf seinem gegenwärtigen Wert zu halten. Das heißt, wenn die Stromstärke zunimmt, wird die induzierte Spannung den Stromfluss "gegen" drücken; Wenn der Strom abnimmt, wird die Polarität umgekehrt und der Strom "gedrückt", um der Abnahme entgegenzuwirken.

Dieser Widerstand gegen den aktuellen Wandel wird als Reaktanz bezeichnet , statt Widerstand. Mathematisch ausgedrückt ist die Beziehung zwischen der an der Induktivität abfallenden Spannung und der Stromänderungsrate durch die Induktivität wie folgt:

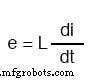
Wechselstrom in einem einfachen induktiven Stromkreis

Der Ausdruck di/dt ist eine aus der Infinitesimalrechnung, was die Änderungsrate des momentanen Stroms (i) über die Zeit in Ampere pro Sekunde bedeutet.

Die Induktivität (L) ist in Henrys angegeben und die Momentanspannung (e) natürlich in Volt. Manchmal werden Sie die Rate der Momentanspannung als „v“ anstelle von „e“ (v =L di/dt) ausgedrückt finden, aber es bedeutet genau dasselbe.

Um zu zeigen, was mit Wechselstrom passiert, analysieren wir eine einfache Induktorschaltung:

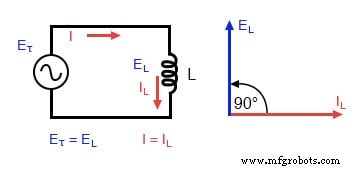
Reine induktive Schaltung:Der Induktorstrom eilt der Induktorspannung um 90° nach.

Wenn wir Strom und Spannung für diese sehr einfache Schaltung aufzeichnen würden, würde sie ungefähr so ​​aussehen:

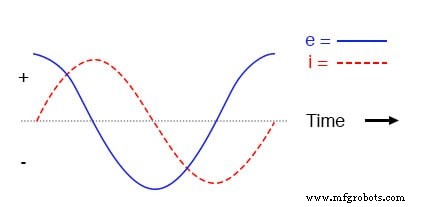
Reine induktive Schaltung, Wellenformen.

Denken Sie daran, dass die an einer Induktivität abfallende Spannung eine Reaktion auf die Änderung . ist im Strom durch sie hindurch.

Daher ist die Momentanspannung null, wenn der Momentanstrom eine Spitze hat (Nulländerung oder Pegelsteigung auf der Stromsinuswelle), und die Momentanspannung ist überall dort, wo der Momentanstrom die maximale Änderung aufweist (die Punkte von steilste Steigung der aktuellen Welle, wo sie die Nulllinie kreuzt).

Dies führt zu einer Spannungswelle, die zur Stromwelle um 90° phasenverschoben ist. Betrachtet man das Diagramm, scheint die Spannungswelle einen „Vorsprung“ gegenüber der Stromwelle zu haben; die Spannung „eilt“ dem Strom voraus und der Strom „hinkt“ der Spannung hinterher.

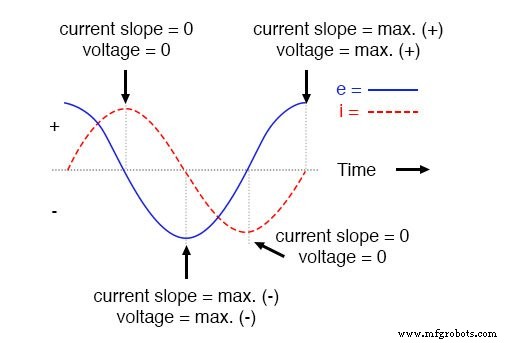
Der Strom eilt der Spannung in einem rein induktiven Stromkreis um 90° nach.

Noch interessanter wird es, wenn wir die Leistung für diese Schaltung grafisch darstellen:

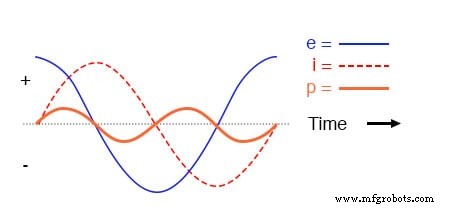
In einem reinen induktiven Stromkreis kann die Momentanleistung positiv oder negativ sein.

Da die Momentanleistung das Produkt der Momentanspannung und des Momentanstroms (p=ie) ist, ist die Leistung immer dann gleich Null, wenn der Momentanstrom oder Spannung ist null. Immer wenn der Momentanstrom und die Momentanspannung beide positiv sind (oberhalb der Linie), ist die Leistung positiv.

Wie beim Widerstandsbeispiel ist die Leistung auch positiv, wenn der Momentanstrom und die Momentanspannung beide negativ sind (unter der Linie).

Da die Strom- und Spannungswellen jedoch um 90° phasenverschoben sind, gibt es Zeiten, in denen eine positiv und die andere negativ ist, was zu gleich häufigen Auftreten von negativen Momentanleistungen führt .

Was ist negative Kraft?

Aber was bedeutet negativ Macht bedeuten? Dies bedeutet, dass der Induktor Strom an den Stromkreis abgibt, während eine positive Leistung bedeutet, dass er Strom vom Stromkreis aufnimmt.

Da die positiven und negativen Leistungszyklen im Laufe der Zeit in Größe und Dauer gleich sind, gibt der Induktor über einen vollständigen Zyklus genauso viel Leistung an den Stromkreis ab, wie er absorbiert.

Praktisch bedeutet dies, dass die Reaktanz einer Induktivität eine Nettoenergie von Null abgibt, ganz im Gegensatz zum Widerstand eines Widerstands, der Energie in Form von Wärme abgibt. Dies gilt jedoch nur für perfekte Induktivitäten, die keinen Drahtwiderstand haben.

Reaktanz vs. Widerstand

Der Widerstand einer Induktivität gegen Stromänderungen bedeutet im Allgemeinen einen Widerstand gegen Wechselstrom, der sich definitionsgemäß immer in augenblicklicher Größe und Richtung ändert.

Dieser Widerstand gegen Wechselstrom ähnelt dem Widerstand, unterscheidet sich jedoch darin, dass er immer zu einer Phasenverschiebung zwischen Strom und Spannung führt und keine Leistung verbraucht. Aufgrund der Unterschiede hat es einen anderen Namen:Reaktanz . Die Reaktanz gegenüber Wechselstrom wird in Ohm ausgedrückt, genau wie der Widerstand, außer dass das mathematische Symbol X anstelle von R ist.

Genauer gesagt wird die mit einer Induktivität verbundene Reaktanz normalerweise durch den Großbuchstaben X mit einem Buchstaben L als tiefgestelltem Index symbolisiert, wie folgt:X_L .

Da Induktoren die Spannung proportional zur Stromänderungsrate absenken, werden sie bei sich schneller ändernden Strömen mehr Spannung und bei sich langsamer ändernden Strömen weniger Spannung absenken. Dies bedeutet, dass die Reaktanz in Ohm für jede Induktivität direkt proportional zur Frequenz des Wechselstroms ist. Die genaue Formel zur Bestimmung der Reaktanz lautet wie folgt:

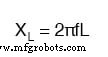
Wenn wir eine 10-mH-Induktivität Frequenzen von 60, 120 und 2500 Hz aussetzen, zeigt sie die Reaktanzen in der folgenden Tabelle.

Reaktanz einer 10-mH-Induktivität:

Frequenz (Hertz) Reaktanz (Ohm) 603.76991207.53982500157.0796

In der Reaktanzgleichung hat der Begriff „2πf“ (alles auf der rechten Seite außer dem L) eine besondere Bedeutung für sich. Es ist die Anzahl von Radianten pro Sekunde, mit der sich der Wechselstrom „rotiert“, wenn Sie sich vorstellen, dass ein Wechselstromzyklus die Drehung eines vollen Kreises repräsentiert.

Ein Radiant ist eine Winkelmaßeinheit:In einem Vollkreis gibt es 2π Radiant, genau wie in einem Vollkreis 360°. Wenn der Wechselstromgenerator eine zweipolige Einheit ist, erzeugt er einen Zyklus für jede volle Umdrehung der Wellendrehung, d. h. alle 2π Radiant oder 360°.

Wenn diese Konstante von 2π mit der Frequenz in Hertz (Zyklen pro Sekunde) multipliziert wird, ist das Ergebnis eine Zahl im Bogenmaß pro Sekunde, bekannt als die Winkelgeschwindigkeit des AC-Systems.

Winkelgeschwindigkeit in AC-Systemen

Die Winkelgeschwindigkeit kann durch den Ausdruck 2πf oder durch ein eigenes Symbol dargestellt werden, den griechischen Kleinbuchstaben omega, der unserem römischen Kleinbuchstaben „w“ ähnelt:ω. Somit ist die Reaktanzformel X_L =2πfL könnte auch als X_L . geschrieben werden =ωL.

Es muss verstanden werden, dass diese „Winkelgeschwindigkeit“ ein Ausdruck dafür ist, wie schnell die Wechselstromwellenformen zyklisch sind, wobei ein Vollzyklus 2π Radiant entspricht. Sie ist nicht unbedingt repräsentativ für die tatsächliche Wellendrehzahl des Wechselstromgenerators.

Wenn der Generator mehr als zwei Pole hat, beträgt die Winkelgeschwindigkeit ein Vielfaches der Wellendrehzahl. Aus diesem Grund wird ω manchmal in Einheiten von elektrisch . ausgedrückt Radiant pro Sekunde statt (einfacher) Radiant pro Sekunde, um es von mechanischen Bewegungen zu unterscheiden.

Wie auch immer wir die Winkelgeschwindigkeit des Systems ausdrücken, es ist offensichtlich, dass sie direkt proportional zur Reaktanz in einer Induktivität ist. Wenn die Frequenz (oder die Wellendrehzahl der Lichtmaschine) in einem Wechselstromsystem erhöht wird, wird eine Induktivität dem Stromfluss mehr Widerstand entgegensetzen und umgekehrt.

Wechselstrom in einem einfachen induktiven Stromkreis ist gleich der Spannung (in Volt) dividiert durch die induktive Reaktanz (in Ohm), genauso wie Wechsel- oder Gleichstrom in einem einfachen Widerstandskreis gleich der Spannung (in Volt) dividiert durch Widerstand (in Ohm). Eine Beispielschaltung ist hier gezeigt:

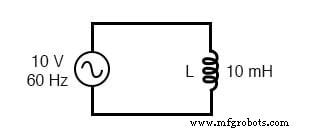
Induktive Reaktanz

Phasenwinkel

Wir müssen jedoch bedenken, dass Spannung und Strom hier nicht in Phase sind. Wie bereits gezeigt, weist die Spannung eine Phasenverschiebung von +90° gegenüber dem Strom auf. Wenn wir diese Phasenwinkel von Spannung und Strom mathematisch in Form von komplexen Zahlen darstellen, finden wir, dass der Widerstand einer Induktivität zum Strom auch einen Phasenwinkel hat:

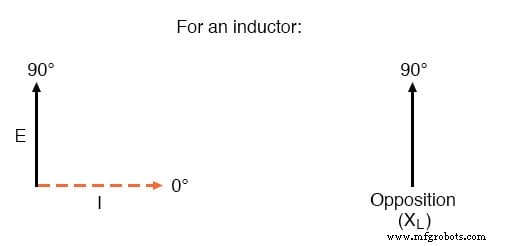
Der Strom eilt der Spannung in einer Induktivität um 90° nach.

Mathematisch sagen wir, dass der Phasenwinkel des Widerstands einer Induktivität gegen den Strom 90° beträgt, was bedeutet, dass der Widerstand einer Induktivität gegen den Strom eine positive imaginäre Größe ist. Dieser Phasenwinkel des reaktiven Widerstands gegen den Strom wird bei der Schaltungsanalyse von entscheidender Bedeutung, insbesondere bei komplexen Wechselstromkreisen, bei denen Reaktanz und Widerstand interagieren.

Es wird sich als vorteilhaft erweisen, jede zu vertreten Widerstand der Komponente zum Strom in Form komplexer Zahlen statt skalarer Größen von Widerstand und Reaktanz.

RÜCKBLICK:

• Induktive Reaktanz ist der Gegensatz, den eine Induktivität dem Wechselstrom aufgrund ihrer phasenverschobenen Speicherung und Abgabe von Energie in ihrem Magnetfeld bietet. Die Reaktanz wird durch den Großbuchstaben „X“ symbolisiert und wird ebenso wie der Widerstand (R) in Ohm gemessen.
• Induktive Reaktanz kann mit dieser Formel berechnet werden:X_L =2πfL
• Die Winkelgeschwindigkeit eines Wechselstromkreises ist eine andere Möglichkeit, seine Frequenz in der Einheit elektrisches Bogenmaß pro Sekunde anstelle von Zyklen pro Sekunde auszudrücken. Es wird durch den griechischen Kleinbuchstaben „omega“ oder ω symbolisiert.
• Induktive Reaktanz erhöht mit zunehmender Frequenz. Mit anderen Worten, je höher die Frequenz, desto mehr widersetzt sie sich dem Wechselstrom von Elektronen.

VERWANDTE ARBEITSBLÄTTER:

• Induktoren-Arbeitsblatt
• Arbeitsblatt zur induktiven Reaktanz