Dual-Mode On-to-Off-Modulation von Plasmon-induzierter Transparenz und Kopplungseffekt in gemusterter Graphen-basierter Terahertz-Metaoberfläche

Einführung

Gegenwärtig sind Oberflächenplasmonenpolaritonen (SPPs) als Träger für die Übertragung von Informationen und Energie ein Forschungsschwerpunkt in der Subwellenlängenoptik. Sie entstehen im Allgemeinen durch die Wechselwirkung zwischen den Photonen im einfallenden Lichtfeld und den Elektronen auf der Metall- oder Isolatoroberfläche [1, 2]. Die SPPs erleichtern aufgrund ihrer einzigartigen optischen Eigenschaften die Entwicklung und Herstellung hochintegrierter Optiken und photonischer Schaltungen. Erstens handelt es sich um nicht strahlende Moden mit großen Nahfeldverstärkungseffekten. Zweitens können die SPPs die traditionelle optische Beugungsbegrenzung durchbrechen und das Licht im Subwellenlängenbereich lokalisieren [3]. Drittens hängen ihre Eigenschaften von den physikalischen Parametern des umgebenden Materials ab. Daher wurden SPPs-basierte Metall-Dielektrikum-Metall-(MDM)-Wellenleiter aufgrund ihres geringen Biegeverlusts, ihrer starken lokalen Fähigkeiten und ihrer geringen Herstellungsschwierigkeiten von Wissenschaftlern umfassend untersucht. Gleichzeitig wurden viele Arten von plasmonischen MDM-Wellenleitern vorgeschlagen, wie Splitter [4, 5], Demultiplexer [6, 7], Filter [8,9,10] und Sensoren [11, 12]. Um eine bestimmte Frequenz oder Wellenlänge zu erhalten, ist es jedoch besonders unpraktisch, dass der MDM-Wellenleiter nur statisch moduliert werden kann. Graphen, da eine zweidimensionale planare Wabenstruktur die Ausbreitung der SPPs im mittleren Infrarot- und THz-Bereich unterstützen kann, wird aufgrund vieler hervorragender optischer Eigenschaften wie starke Lokalität, geringer Verlust, Nah der vielversprechendste Kandidat in vielen plasmonischen Materialien Feldverstärkung, dynamische Einstellbarkeit usw. [13, 14]. Folglich wurde die plasmonische Optik auf Graphenbasis in vielen Anwendungen verwendet, beispielsweise in der Lichterfassung [15, 16], Absorption [17, 18, 19], beim Schalten [20] und anderen faszinierenden Phänomenen wie der nichtlinearen Optik [21 , 22] und plasmoneninduzierte Transparenz (PIT) [23,24,25,26]. Der PIT-Effekt, der das Ergebnis einer destruktiven Interferenz zwischen dem Superstrahlungsmodus und dem Substrahlungsmodus ist, hat eine Vielzahl von plasmonischen Anwendungen hervorgebracht, zum Beispiel plasmonisches Schalten [20, 27], langsame Lichtausbreitung [28], holographische Bildgebung [ 29] und optischer Speicher [30]. Um eine solch komplexe Wechselwirkung zwischen Licht und Materie zu erreichen, kann die PIT in heterogenen Graphenbändern [31], einschichtigem oder mehrschichtigem Graphen [32,33,34] und graphenbasierten Metaoberflächen [35] erhalten werden. . Diese plasmonischen Geräte sind jedoch nicht nur ziemlich kompliziert im Design, sondern auch Single-Mode in Bezug auf die Modulation. Darüber hinaus wird die Resonanzfrequenz hauptsächlich durch die Manipulation des Fermi-Niveaus von Graphen bei der Modulation der meisten plasmonischen Geräte abgestimmt. Da die Transmission des PIT vernachlässigt wird, kann die On-to-Off-Modulation nicht realisiert werden.

In dieser Studie ist die vorgeschlagene PIT-Metaoberfläche, die aus den periodischen Graphenbändern und Graphenstreifen besteht, einfacher zu implementieren und herzustellen. Durch chemische Gasphasenabscheidung (CVD) [36] können die Graphenbänder und die Graphenstreifen auf der Kupferfolie aufgewachsen werden, die durch Trocken- und Nasstransfertechniken auf ein ebenes Substrat übertragen werden. Diese Technik erzeugt weniger Risse, Risse und einen geringeren Schichtwiderstand. Zweitens besteht einer der wichtigsten Vorteile darin, dass der Transmissionsabfall links (rechts) hauptsächlich durch die an die Graphenbänder (Streifen) angelegte Gatespannung beeinflusst wird, was bedeutet, dass die Dual-Mode-Ein-zu-Aus-Modulation realisiert werden kann. Drittens kann die Absorption der vorgeschlagenen Metaoberfläche sogar bei niedrigem Fermi-Niveau von Graphen 50 % erreichen, was einen außergewöhnlichen Absorber demonstriert. Schließlich, wenn die Beweglichkeit des Graphenbandes und des Graphenstreifens beide 3 m ² . beträgt /(Vs) kann die Gruppenverzögerung bis zu 0.7 ps betragen, was die vorgeschlagene Metaoberfläche repräsentiert, die auch ausgezeichnete Slow-Light-Funktionen hat. Darüber hinaus werden auch Kopplungseffekte zwischen den Graphenbändern und den Graphenstreifen in PIT-Metaoberflächen mit unterschiedlichen Strukturparametern im Detail untersucht. Daher legt diese Forschung eine solide Grundlage für den Dual-Mode-On-to-Off-Multifunktionsmodulator.

Methoden

Die Konfiguration der PIT-Metaoberfläche bestehend aus dem strukturierten einschichtigen Graphen, den Elektroden, den dünnen Metalldrähten und dem Substrat Silizium ist in Fig. 1a dargestellt. Die Graphenbänder sind mit der linken Elektrode verbunden, um ihre Fermi-Niveaus durch die Gatespannung V . zu modulieren _{g 1} . Darüber hinaus sind die Graphenstreifen mit der rechten Elektrode über dünne Metalldrähte verbunden und eine Gatespannung von V _{g 2} wird angewendet, um ihre Fermi-Niveaus zu modulieren [37, 38]. Die Gatespannungen V _{g 1} und V _{g 2} können die Fermi-Niveaus der Graphenbänder bzw. der Graphenstreifen modulieren, um die Dual-Mode-Modulation des PIT weiter zu realisieren. Bemerkenswert ist, dass der Einfluss auf den Übertragungseffekt aufgrund der geringen Größe der Anschlussdrähte vernachlässigt werden kann [39]. In Abb. 1b ist das Fermi-Niveau E _f von einschichtigem Graphen kann indirekt durch die Gatespannung moduliert werden, die wie folgt ausgedrückt werden kann [40]:

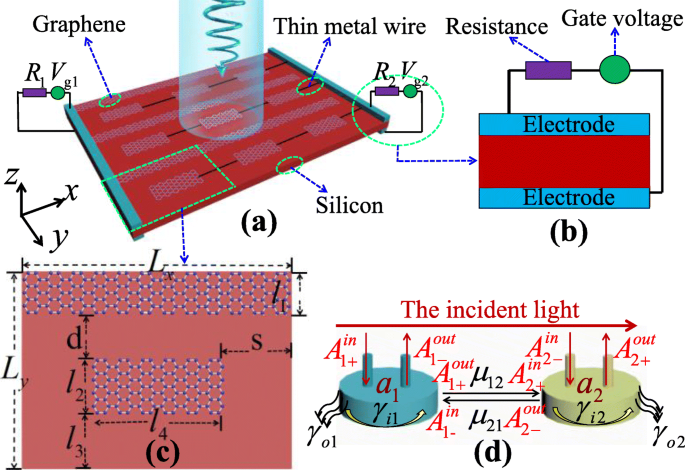
a Schema der 3 × 3-Einheiten-Struktur der PIT-Metaoberfläche. b Das modulierte Diagramm der Gatespannung. c Draufsicht auf Struktureinheit mit geometrischen Parametern L _x =6,0 μm, L _y =4,0 μm, l ₁ =1,0 μm, l ₂ =1,4 μm, l ₃ =d =0,8 μm, l ₄ =2,9 μm und S =1,55 µm. d Kopplungsdiagramm zwischen dem Graphenband und dem Graphenstreifen

Hier, ħ , ε _d , ε ₀ , e , d ₀ , und v _F sind die reduzierte Planck-Konstante, die statische Permittivität von Silizium, die Vakuum-Permittivität, die Elektronenladung, die Siliziumdicke bzw. die Fermi-Geschwindigkeit. Es ist erwähnenswert, dass die Trägerkonzentration bis zu 4 × 10 ¹⁸ . hoch ist m ⁻² in Graphenfolie wurde durch die Verwendung eines elektrolytischen Gates beobachtet, was E . bedeutet _f =1,17 eV [41]; Mit dieser Methode konnte das Fermi-Energieniveau von Graphen nach Anlegen einer hohen Vorspannung experimentell von 0,2 eV auf 1,2 eV modifiziert werden [42]. Die strukturelle Einheit der vorgeschlagenen PIT-Metaoberfläche, die aus einem Graphenband und einem Graphenstreifen besteht, die auf dem Substrat Silizium platziert sind, wie in Abb. 1c dargestellt. Die Periodizität wird als L . angenommen _x und L _y ; der Kopplungsabstand zwischen dem Graphenband und dem Graphenstreifen beträgt d; die seitliche Verschiebung des Graphenstreifens beträgt S .

Die optische Leitfähigkeit einer einschichtigen Graphenschicht besteht hauptsächlich aus Interband- und Intraband-Beiträgen [43,44,45], die ausgedrückt werden können als

$$ \varepsilon \left(\omega \right)=1+\frac{\sigma_g}{\varepsilon_0\omega \varDelta}i. $$ (2) $$ {\sigma}_g={\sigma}^{\mathrm{intra}}+{\sigma}^{\mathrm{inter}}. $$ (3) $$ {\sigma}^{\mathrm{intra}}=\frac{2i{e}^2{k}_BT}{\pi {\hslash}^2\left(\omega +i {\tau}^{-1}\right)} In\left[2\cosh\left(\frac{E_f}{2{k}_BT}\right)\right]. $$ (4) $$ {\sigma}^{\mathrm{inter}}=\frac{i{e}^2\left(\omega +i{\tau}^{-1}\right)}{ 4\pi{k}_BT}{\int}_0^{+\infty}\frac{G\left(\xi\right)}{\hslash^2{\left(\omega +i{\tau}^ {-1}\right)}^2/{\left(2{k}_BT\right)}^2-{\xi}^2} d\xi . $$ (5)

Hier, G(ξ ) =sinh(ξ )/[cosh(E _f /k _B T )+coshξ ], wobei ξ =ε /k _B T . Außerdem ω , k _B , σ _g , σ _inter , und σ _intra sind die Winkelfrequenz des einfallenden Lichts, die Boltzmann-Konstante, die Leitfähigkeit von einschichtigem Graphen, die Interband- bzw. Intraband-Beiträge. In dieser Arbeit beträgt die Raumtemperatur T =300K; die Dicke des Graphens beträgt Δ =0,34 nm. σ _inter kann wegen k . ignoriert werden _B T 2E _f im Terahertz-Band. Also, σ _g kann ausgedrückt werden als

$$ {\sigma}_g=\frac{i{e}^2{E}_f}{\pi {\hslash}^2\left(\omega +i{\tau}^{-1}\right) }. $$ (6)

Hier kann die Elektronenrelaxationszeit als τ . ausgedrückt werden =μ ₀ E _f /(ev _F ² ) [40], mit μ ₀ =1 m ² /(Vs) ist die Graphenmobilität. Außerdem ist die Ausbreitungskonstante β des auf die Graphenoberfläche einfallenden Lichts kann ausgedrückt werden als [46]

$$ \frac{\varepsilon_1}{\sqrt{\beta^2-{\varepsilon}_1{k}_0^2}}}+\frac{\varepsilon_2}{\sqrt{\beta^2-{\varepsilon} _2{k}_0^2}}=-\frac{i{\sigma}_g}{\omega {\varepsilon}_0}. $$ (7)

Hier, ε ₁ , ε ₂ , und k ₀ sind die relative Permittivität von Siliziumdioxid und Luft bzw. der Wellenvektor der ebenen Welle.

In Abb. 1d wird die Coupled-Mode-Theorie (CMT) [47] verwendet, um die Transmissions- und Absorptionsspektren numerischer FDTD-Simulationen anzupassen. Elemente A₁ und A₂ dienen als zwei Antennen, um den Kopplungseffekt zwischen dem Graphenband und dem Graphenstreifen zu beschreiben. Wenn das einfallende Licht von A beleuchtet und von B ausgestrahlt wird, kann die Beziehung erhalten werden durch

$$ \left(\begin{array}{cc}{\gamma}_1&-i{\mu}_{12}\\ {}-i{\mu}_{21}&{\gamma}_2\end {array}\right)\cdot \left(\begin{array}{c}{a}_1\\ {}{a}_2\end{array}\right)=\left(\begin{array}{cc }-{\gamma}_{o1}^{1/2}&0\\ {}0&-{\gamma}_{o2}^{1/2}\end{array}\right)\cdot \left (\begin{array}{c}{A}_{1+}^{in}+{A}_{1-}^{in}\\ {}{A}_{2+}^{in} +{A}_{2-}^{in}\end{array}\right). $$ (8)

Hier, γ ₁₍₂₎ = (iω – iω ₁₍₂₎ – γ _{ich 1(2)} – γ _{o 1(2)} ), in dem der Verlustkoeffizient γ . ist _{ich 1(2)} = ₁₍₂₎ /(2Q _{ich 1(2)} ) und der Extra-Loss-Koeffizient ist γ _{o 1(2)} = ₁₍₂₎ /(2Q _{o 1(2)} ). Außerdem Q _{ich 1(2)} =Re(n _eff )/Im(n _eff ) [29] ist der Qualitätsfaktor zwischen den Verlusten, der durch den effektiven Brechungsindex n . erhalten werden kann _eff =β /k ₀ . Der Intra-Loss-Qualitätsfaktor kann durch 1/Q . ermittelt werden _{t 1(2)} =1/Q _{ich 1(2)} + 1/Q _{o 1(2)} , mit Q_{t 1(2)} =f /Δf ist der Qualitätsfaktor des gesamten Systems (Δf ist 3 dB Bandbreite). Der Energieerhaltung folgend ist die Kopplungsbeziehung zwischen zwei Antennen wie folgt:

$$ {A}_{2+}^{\mathrm{in}}={A}_{1+}^{\mathrm{out}}{e}^{i\varphi},{A}_{ 1-}^{\mathrm{in}}={A}_{2-}^{\mathrm{out}}{e}^{i\varphi}, $$ (9) $$ {A}_{ 1+}^{\mathrm{o}\mathrm{ut}}={A}_{1+}^{\mathrm{in}}-a{\gamma}_{\mathrm{o}1}^{ 1/2},{A}_{2+}^{\mathrm{o}\mathrm{ut}}={A}_{2+}^{\mathrm{in}}-b{\gamma}_ {o2}^{1/2}, $$ (10) $$ {A}_{1-}^{\mathrm{o}\mathrm{ut}}={A}_{1-}^{\ mathrm{in}}-a{\gamma}_{\mathrm{o}1}^{1/2},{A}_{2-}^{\mathrm{o}\mathrm{ut}}={ A}_{2-}^{\mathrm{in}}-b{\gamma}_{o2}^{1/2}, $$ (11) $$ {A}_{2-}^{\ mathrm{in}}=0. $$ (12)

Dabei bedeuten die Indizes „+“ und „–“, dass die Antennen in gleiche und entgegengesetzte Richtungen beleuchtet werden; die hochgestellten Zeichen „in“ und „out“ repräsentieren das Vorzeichen des einfallenden Lichts, das in die Antennen ein- und austritt. Außerdem μ _nm (n =1, 2, m =1, 2, n ≠ m ) und φ sind die Kopplungskoeffizienten bzw. die Phasendifferenz zwischen zwei Antennen. Auf diese Weise können wir den Transmissionskoeffizienten und den Reflexionskoeffizienten der vorgeschlagenen PIT-Metaoberfläche erhalten.

$$ t=\frac{A_{2+}^{out}}{A_{1+}^{in}}={e}^{i\varphi}+\left[{\gamma}_{o1} {\gamma}_2{e}^{i\varphi}+{\gamma}_{o2}{\gamma}_1+{\left({\gamma}_{o1}{\gamma}_{o2}\right )}^{1/2}\left({\chi}_1{e}^{i\varphi}+{\chi}_2\right)\right]\cdot {\left({\gamma}_1{\ gamma}_2-{\chi}_1{\chi}_2\right)}^{-1}, $$ (13) $$ r=\frac{A_{1-}^{out}}{A_{1 +}^{in}}=\left[{\gamma}_{o1}{\gamma}_1+{\gamma}_{o2}{\gamma}_1{e}^{i\varphi}+{\left ({\gamma}_{o1}{\gamma}_{o2}\right)}^{1/2}\left({\chi}_1+{\chi}_2{e}^{i\varphi}\ rechts)\right]\cdot {\left({\gamma}_1{\gamma}_2-{\chi}_1{\chi}_2\right)}^{-1}. $$ (14)

Wo χ ₁₍₂₎ =iμ ₁₂₍₂₁₎ +(γ _{o 1(2)} γ _{o 2(1)} ) ^1/2 e ^iφ . Dann kann die Transmission und Absorption der vorgeschlagenen PIT-Metaoberfläche erhalten werden durch

$$ T={t}^2,A=1-{t}^2-{r}^2. $$ (15)

Ergebnisse und Diskussion

Vor kurzem wurden die Graphenbänder als einer der vielversprechendsten Kandidaten in der Graphenreihe aufgrund der Tatsache, dass sie experimentell sehr einfach zu erreichen sind und lokalisierte Plasmonen unterstützen können (hauptsächlich basierend auf Fabry-Perot-ähnlicher Stehwellenresonanz) [48 ,49,50] und propagieren Plasmonen [51, 52], haben auf dem Gebiet der Nanophotonik viel Aufmerksamkeit erregt. Hier nutzen wir die plasmonische Kopplung zwischen den Graphenbändern und den Graphenstreifen, um einen ausgezeichneten PIT-Effekt zu demonstrieren.

Um den physikalischen Ursprung des PIT-Effekts zu diskutieren, sind in Abb. 2a–c simulierte Transmissionsspektren von drei Graphen-Metaoberflächen und elektrische Feldverteilungen der gesamten Struktur und des Graphenstreifens bei der Resonanzfrequenz dargestellt. In Abb. 2a kann beim Bestrahlen der Metaflächen mit x-polarisiertem Licht eine subradiante Mode im Graphenband angeregt werden, die eine rote Kurve mit einer Transmission von 1 erzeugt Graphenstreifen, der eine schwarze Lorentz-Kurve mit einem Transmissions-Dip von 7,90 % bewirkt. Als Ergebnis kann der Subradiant-Modus indirekt durch den Superradiant-Modus angeregt werden, wodurch eine blaue PIT-Kurve mit einer Transmissionsspitze von 88,61 % erzeugt wird, die von der gesamten Struktur erzeugt wird. Darüber hinaus können auch elektrische Feldverteilungen der gesamten Struktur und des Graphenstreifens bei der Resonanzfrequenz den physikalischen Ursprung des PIT-Phänomens erklären. Wenn in den Struktureinheiten jeder Graphen-Metaoberfläche jedes Musters nur die Graphenstreifen vorhanden sind, befindet sich die elektrische Feldenergie um den Graphenstreifen in einem Gleichgewichtszustand, wie in Fig. 2c dargestellt. In diesem Fall wird nur das schwächere elektrische Feld um den Graphenstreifen begrenzt, was eine Lorentz-Kurve mit einem geringeren Qualitätsfaktor erzeugt. Wenn der Metaoberfläche jedoch ein Graphenband hinzugefügt wird, wird das Gleichgewicht des elektrischen Felds um den Graphenstreifen unterbrochen. Im Moment wird aufgrund des Kopplungseffekts zwischen ihnen das elektrische Feld um den Graphenstreifen verstärkt und das Graphenband wird auch durch das Nahfeld angeregt, wie in Fig. 2b dargestellt. Daher wird die elektrische Feldenergie um den Graphenstreifen und die Graphenbandoberfläche lokalisiert, wodurch eine PIT-Kurve mit höheren Qualitätsfaktoren gebildet wird.

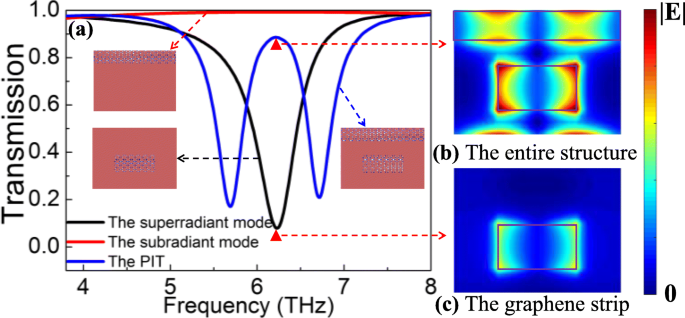
a Simulierte Transmissionsspektren von drei Graphen-Metaoberflächen. b Elektrische Feldverteilung der gesamten Struktur am Resonanzpeak. c Elektrische Feldverteilung des Graphenstreifens am Resonanzeinbruch. Hier, E _{f 1} =E _{f 2} =1,0 eV

Die Zweimoden-Ein-zu-Aus-Modulation von PIT kann durch zwei Gatespannungen erreicht werden, die an die Graphenbänder und die Graphenstreifen angelegt werden, wie in den Fig. 1 und 2 dargestellt. 3a–h. Hier werden die vier Resonanzeinbrüche mit „dip1, dip2, Dip1, Dip2“ bezeichnet. Wenn das Fermi-Niveau E . ist _{f 2} des Graphenstreifens ist auf 1.0 eV fixiert, das Fermi-Niveau E _{f 1} des Graphenbandes wird geändert, um den PIT-Effekt zu untersuchen. In Abb. 3a–d als Fermi-Niveau E _{f 1} von 0,6 eV auf 1,2 eV ansteigt, gibt es eine signifikante Änderung des dip1. Zum einen ist die Durchlässigkeit von dip1 merklich reduziert, was anzeigt, dass eine Ein-Aus-Modulation erhalten werden kann. Zum anderen weist der dip1 eine offensichtliche Blauverschiebung auf, was zeigt, dass er empfindlich auf die Änderung des Fermi-Niveaus E . reagiert _{f 1} und kann Frequenzmodulation realisieren. Außerdem, wenn das Fermi-Niveau E _{f 1} des Graphenbandes auf 1.0 eV fixiert ist, tritt ein ähnliches Phänomen in Dip2 mit dem Anstieg des Fermi-Niveaus E . auf _{f 2} . Die Blauverschiebung wird jedoch in beiden Fällen im linken Dip stärker beobachtet. Wenn die Fermi-Niveaus des Graphenstreifens und des Graphenbandes beide 1,0 eV betragen, betragen die Resonanzfrequenz der Superstrahlungsmode und die Monopolresonanzfrequenz der Substrahlungsmode im Wesentlichen 6,2 THz. Somit bildet die Kopplung zwischen ihnen ein symmetrisches PIT. Wenn das Fermi-Niveau E . ist _{f 1} des Graphenbandes von 0,6 eV auf 1,0 eV erhöht, die Monopolresonanzfrequenz der Substrahlungsmode aufgrund der Änderung der Leitfähigkeit des Graphenbandes von der linken Seite auf 6,2 THz verschoben. In diesem Fall ist die Kopplung zwischen dem Substrahlungsmodus und dem Superstrahlungsmodus aufgrund unterschiedlicher Resonanzfrequenzen schwach, wodurch ein stark asymmetrisches PIT erzeugt wird. Die offensichtliche Blauverschiebung des dip1 in Abb. 3a–d wird hauptsächlich durch die Blauverschiebung der Substrahlungsmode beeinflusst. In ähnlicher Weise wird die offensichtliche Blauverschiebung von Dip1 in Abb. 3e–h hauptsächlich durch die Blauverschiebung der Superstrahlungsmode beeinflusst. Der detaillierte Ein-Aus-Mechanismus ist in Fig. 3i dargestellt. Bei der Auslegung des On-to-Off-Modulators wird „on“ auf eine Transmission von über 0,3 eingestellt; andernfalls ist es auf „aus“ eingestellt. Somit kann die vorgeschlagene PIT-Metaoberfläche die Dual-Mode-On-Funktion im Fermi-Niveau von 0,6 eV bis 0,8 eV und die Dual-Mode-Off-Funktion im Fermi-Niveau von 0,8 eV bis 1,2 eV realisieren. Kurz gesagt, die Gatespannung V _{g 1} regelt hauptsächlich den linken Transmissions-Dip, aber der rechte Transmissions-Dip wird hauptsächlich durch die Gate-Spannung V . angepasst _{g 2} . Daher wird ein Ein/Aus-Modulator mit zwei Betriebsarten realisiert. Inzwischen ist die Dual-Mode-Modulation der plasmoneninduzierten Absorption (PIA) auch in Abb. 4a–h zu sehen. Mit dem Anstieg des Fermi-Niveaus weist der PIA eine deutliche Blauverschiebung auf. Selbst wenn das Fermi-Niveau von Graphen niedrig ist, kann die Absorption der vorgeschlagenen Metaoberfläche 50% erreichen. Dies liegt daran, dass Graphen den Verlusteigenschaften ähnlich ist, wenn das Fermi-Niveau niedrig ist, was zu einem hohen Verlust und einer hohen Absorption führt [53]. Das Phänomen bedeutet, dass ein niedrigeres Fermi-Niveau eine höhere Absorption erreichen kann, wodurch die erforderliche Spannung reduziert wird. Darüber hinaus werden die Transmissions- und Absorptionsspektren der FDTD-Simulation beide von CMT angepasst. Hier zeigt die blaue Kurve das FDTD-Simulationsergebnis an; die rot gepunktete Kurve zeigt die CMT-Anpassungsdaten an.

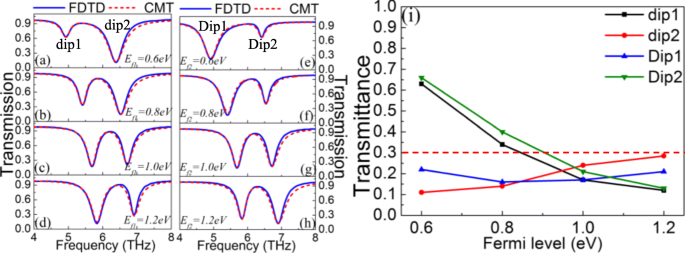
Transmissionsspektren der FDTD-Simulation und CMT-Anpassung (a –d ) für verschiedene E _{f 1} wenn E _{f 2} =1,0 eV. e –h Für verschiedene E _{f 2} wenn E _{f 1} =1,0 eV. ich Zusammenhang zwischen der Transmission des Resonanzeinbruchs und dem Fermi-Niveau

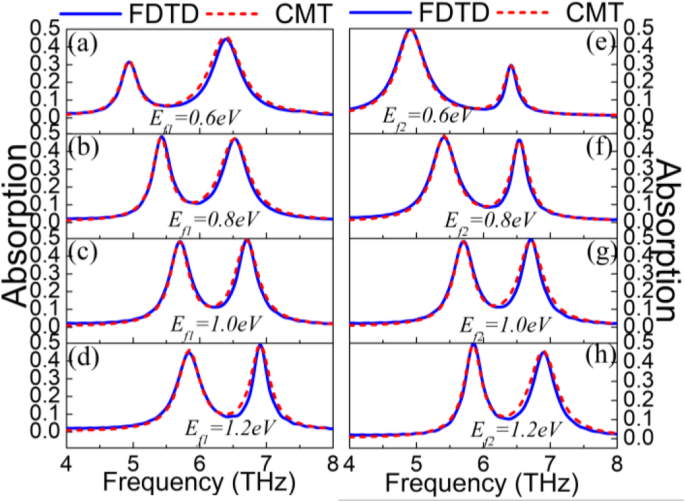
Absorptionsspektren der FDTD-Simulation und CMT-Anpassung (a –d ) für verschiedene E _{f 1} wenn E _{f 2} =1,0 eV. e –h Für verschiedene E _{f 2} wenn E _{f 1} =1,0 eV

Darüber hinaus werden auch Transmissionsspektren mit unterschiedlichen Graphenmobilitäten untersucht, wie in Fig. 5(a-c) dargestellt. Eine vollständig symmetrische PIT-Kurve wird erhalten, wenn E _{f 1} =E _{f 2} =1,0 eV. Auf dieser Basis wird die Graphenmobilität von 1,0 m ² . erhöht /(Vs) bis 3,0 m ² /(Vs) in 1,0 m ² /(Vs) Schritt. Mit zunehmender Graphenmobilität zeigen nicht nur die Transmissionsspektren eine scheinbare Rotverschiebung, sondern auch die 3 dB-Bandbreite der Transmissionsdips wird schmaler, sodass die Graphenmobilität auch zur dynamischen Modulation der PIT- und Qualitätsfaktoren von Transmissionsdips verwendet werden kann. Hier sind Transmissionsspektren von FDTD-Simulation und CMT-Anpassung noch perfekt aufeinander abgestimmt. Es ist bekannt, dass die Leistungen des Slow-Light-Effekts mit dem höheren Qualitätsfaktor des Transmissions-Dip besser sind. Daher sind in Abb. 5d–e die Transmissionsphasenverschiebung und die Gruppenlaufzeit bei unterschiedlichen Graphenmobilitäten aufgetragen. Die Gruppenverzögerung wird erreicht durch [54]:

$$ {\mathrm{t}}_g=\frac{d\phi \left(\omega \right)}{d\omega}, $$ (16)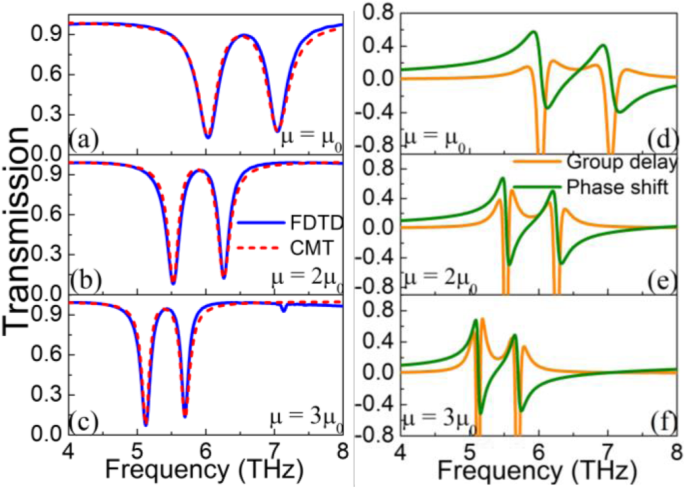

a–c Transmissionsspektren der FDTD-Simulation und CMT-Anpassung mit unterschiedlicher Graphenmobilität μ =μ ₀ , 2μ ₀ , 3μ ₀ . d, e Übertragungsphasenverschiebung und Gruppenlaufzeit bei unterschiedlicher Graphenmobilität μ =μ ₀ , 2μ ₀ , 3μ ₀ . Hier, E _{f 1} =E _{f 2} =1,2 eV

wo ϕ (ω ) ist die durch ϕ . berechnete Phasenverschiebung (ω ) =  arg (t ). Die Ergebnisse zeigen, dass sowohl die Gruppenlaufzeit als auch die Phasenverschiebung 0 sind, wenn die Transmission des Systems nahe 1 liegt. Darüber hinaus tritt die große Gruppenlaufzeit am Transmissionspeak und seiner Umgebung auf, da das Graphenband und das Graphen Streifen haben eine starke Kopplungswirkung bei der Resonanzfrequenz. Wenn die Graphenmobilität 3μ . erreicht ₀ , kann die Gruppenlaufzeit des Systems bis zu 0,7 ps betragen. Die Gruppenlaufzeit an den Sendeeinbrüchen erreicht jedoch einen großen negativen Wert, was eine schnelle Lichtausbreitung im System bedeutet. Inzwischen hat sich auch die Phasenverschiebung an den Sendeeinbrüchen dramatisch verändert. Zhanget al. hat kürzlich eine Absorptionseffizienz von 50% und eine langsame Lichtleistung mit einer gemusterten Graphenstruktur vorgeschlagen [25]. Die vorgeschlagene Struktureinheit aus Graphen-Doppelstreifen und einem komplexeren Graphen-Band kann jedoch die Dual-Mode-Ein-Aus- und Absorptionsmodulation nicht realisieren. Außerdem ist es unvernünftig, die Absorptionseffizienz zu analysieren, indem man die Beweglichkeit der Graphen-Doppelstreifen ändert, während nur das Graphen-Band mit einer Gate-Spannung beaufschlagt wird. Darüber hinaus ist der Slow-Light-Effekt, der durch den Gruppenindex analysiert wird, der stark von der Dicke des Substrats abhängt, nicht objektiv. Und der Gruppenindex, der nur 382 erreichen kann, ist schlecht.

Schließlich werden Kopplungseffekte zwischen den Graphenbändern und den Graphenstreifen in PIT-Metaoberflächen mit unterschiedlichen Strukturparametern im Detail untersucht, wie in Abb. 6a–d dargestellt. Andere Strukturparameter basieren auf Abb. 2a. Aus Abb. 6a wird mit zunehmendem Koppelweg zunächst der linke Getriebeeinbruch blau- und dann rotverschoben, während der rechte Getriebeeinbruch im Wesentlichen unverändert bleibt, d. h. eine Änderung des Koppelwegs hat einen größeren Einfluss für das linke Getriebe tauchen. Wenn die seitliche Verschiebung des Graphenstreifens zunimmt, ändert sich die Position der Transmissionseinbrüche aufgrund des x-polarisierten einfallenden Lichts nicht, wie in Fig. 6b beobachtet. Interessanterweise ist in Abb. 6c der Anstieg von l ₄ führt zu einer abgestuften Rotverschiebung im linken Transmissionseinbruch und sein Qualitätsfaktor wird kleiner, was die Abhängigkeit der Graphenstreifenlänge von den linken Transmissionsspektren anzeigt. Fig. 6d zeigt, dass die Zunahme der Graphenstreifenbreite eine leichte Rotverschiebung im linken Transmissionseinbruch und eine leichte Blauverschiebung im rechten Transmissionseinbruch bewirkt, wodurch der Abstand zwischen den Transmissionseinbrüchen vergrößert wird. Es ist erwähnenswert, dass, da die Zunahme der Länge und Breite des Graphenstreifens die Induktivität des Resonanzsystems verbessert, ein signifikantes Phänomen erzeugt wird.

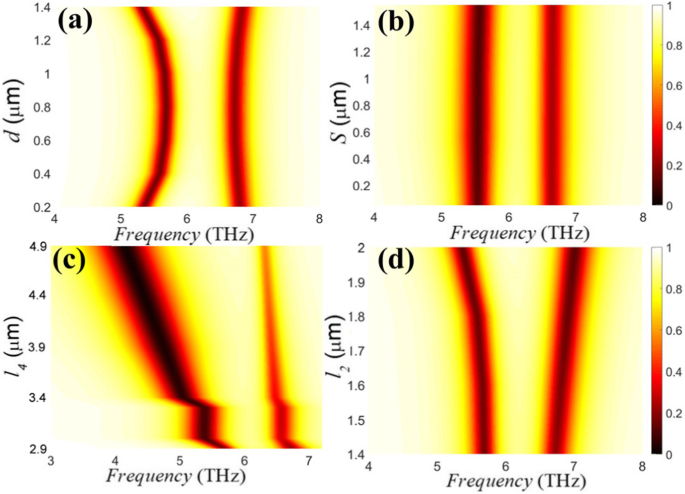
Abhängigkeit der Transmissionsspektren von verschiedenen geometrischen Parametern. a Der Kopplungsabstand, d , (b ) die seitliche Verschiebung, S , (c ) die Länge des Graphenstreifens, l ₄ , (d ) die Breite des Graphenstreifens, l ₂

Schlussfolgerung

Kurz gesagt, wir haben die PIT in der strukturierten Metaoberfläche, die aus den Graphenbändern und den Graphenstreifen besteht, numerisch simuliert und theoretisch berechnet, die durch destruktive Interferenz zwischen der Superradiant-Mode und der Subradiant-Mode verursacht wird. Interessanterweise kann die Dual-Mode-Ein-Aus-Modulation von PIT durch zwei Gate-Spannungen erreicht werden, die an die Graphenbänder und die Graphenstreifen angelegt werden. Darüber hinaus werden eine Absorptionsrate von 50% und eine Slow-Light-Eigenschaft von 0,7 ps erreicht, was zeigt, dass die vorgeschlagene PIT-Metaoberfläche wichtige Anwendungen in Absorption und Slow-Light hat. Darüber hinaus werden Kopplungseffekte zwischen den Graphenbändern und den Graphenstreifen in PIT-Metaoberflächen mit unterschiedlichen Strukturparametern im Detail untersucht. Somit bietet diese Arbeit potenzielle Anwendungen für die Implementierung von Dual-Mode-On-to-Off-Multifunktionsmodulatoren.

Verfügbarkeit von Daten und Materialien

Alle während dieser Studie generierten oder analysierten Daten sind in diesem veröffentlichten Artikel enthalten.

Abkürzungen

CMT:

Theorie der gekoppelten Mode

Lebenslauf:

Chemische Gasphasenabscheidung.

FDTD:

Zeitbereich mit endlicher Differenz

MDM:

Metall-Dielektrikum-Metall

PIT:

Plasmoneninduzierte Transparenz

SPPs:

Oberflächenplasmonenpolaritonen