Die extrem verbesserte Photostromantwort in topologischen Isolator-Nanoblättern mit hoher Leitfähigkeit

Einführung

Es ist eine ständige Aufgabe, nach Materialien mit einer höheren Photostromantwort zu suchen. Die kurze Lichteindringtiefe in Festkörpermaterialien führt dazu, dass die Photostromantwort von Oberflächenträgern dominiert wird. Ein Material mit einer größeren Menge an Oberflächenträgern ist ein besserer Kandidat als Photodetektor. Lange Zeit wurden Materialien mit hohen Oberflächen-zu-Volumen-Verhältnissen, wie Nanodrähte, umfassend untersucht [1–6]. Begleitet von der großen Photodetektionsbandbreite, niedrigdimensionalen Materialien mit linearer EK-Dispersion, wie Graphen, [7, 8] Graphen-basierte Heterostrukturen, [1–4], zweidimensionale Übergangsmetalldichalkogenide (TMDs) und topologische Materialien, haben große Aufmerksamkeit erregt [9–16].

Die jüngsten Berichte zeigen, dass die berichtete Photostromantwort in weiten Bereichen variiert [17–22]. Intuitiv schreibt man diese Verteilungen unterschiedlichen Materialwachstums- und Versuchsbedingungen zu. Die meisten Berichte konzentrieren sich auf die Anpassung der Materialkomponenten. Die potentiellen intrinsischen Mechanismen dieser Verteilungen werden weniger untersucht und diskutiert. Die Klärung des intrinsischen Mechanismus könnte helfen, potenzielle Defekte zu verbessern und die Leistung erheblich zu optimieren. Es wird angenommen, dass die Probenqualität ein kritischer Faktor sein sollte, der die Photostromantwort dominiert [17–22]. Gibt es neben der Kristallstruktur- und Bauteilanalyse noch weitere einfache physikalische Methoden zur Bestimmung der Probenqualität? Aufgrund einer Reihe von experimentellen Berichten ist uns aufgefallen, dass sich die Photoempfindlichkeit über einen weiten Bereich mit unterschiedlichem Schichtwiderstand verteilt. Die durch Photonen induzierten Transportprozesse von Elektron-Loch-Paaren folgen Streuprozessen in mesoskopischen Festkörpersystemen, sodass die Materialleitfähigkeit ein kritischer Faktor bei der Dominanz der berichteten Photostromantwort wäre. Dieser Effekt ist jedoch noch nicht gut untersucht und entsprechende experimentelle Arbeiten fehlen.

Um den Leitwerteffekt auf die Photostromantwort zu identifizieren, untersuchten wir systematisch die Photostromantwort in topologischen Isolator-Nanoblättern mit unterschiedlicher Leitfähigkeit. Der Photostrom ist linear zur Lichtleistungsintensität und der Photostrom ist proportional zum Dunkelstrom. Der höhere Photostrom wird im Nanoblatt mit höherer Leitfähigkeit beobachtet. Die Ansprechempfindlichkeit ist über zwei Ordnungen proportional zur Nanoblatt-Leitfähigkeit. Die Ansprechempfindlichkeit ist im Vakuum unabhängig von der Lichtleistungsintensität, jedoch nimmt die Ansprechempfindlichkeit in Luft bei geringer Leistungsintensität drastisch ab. Das Verhältnis der Ansprechempfindlichkeit in Luft zu der im Vakuum ist negativ proportional zum Kehrwert der Lichtleistungsintensität. Diese Verhaltensweisen werden als statistischer Photostrom in einem System mit blockierten Molekülen verstanden. Die Zeitkonstante nimmt mit zunehmender Dicke ab. Dieses Verhalten könnte als der Gleichförmigkeitsstromflussprozess verstanden werden. Die Lade- und Entladezeitkonstanten unterschiedlicher Drücke werden bestimmt. Bei niedrigerem Atmosphärendruck wird eine längere Zeitkonstante beobachtet. Die Reaktionsfähigkeit, R , ist linear mit der Nanoblatt-Leitfähigkeit. Die R bei V =0,1 V erreicht 731 bei Nanoblättern mit höherer Leitfähigkeit. Diese sind höher als alle gemeldeten Werte in (Sb, Bi)₂ (Te, Se)₃ topologische Isolatoren und niedrigdimensionale Materialien und nur niedriger als mehrere berichtete Heterostrukturen.

Experimentelle Methode

Einkristalle von Sb₂ Se₂ Te wurden in einem selbstgebauten widerstandsbeheizten Schwebezonenofen (RHFZ) gezüchtet. Die Ausgangsrohstoffe von Sb₂ Se₂ Te wurden gemäß dem stöchiometrischen Verhältnis gemischt. Zunächst wurden die stöchiometrischen Mischungen der hochreinen Elemente Sb (99,995%), Se (99,995%) und Te (99,995%) bei Temperaturen von 700 ∼ 800 °C für 20 h geschmolzen und dann langsam in ein evakuiertes Quarzglasrohr. Das resultierende Material wurde als Futterstab für das folgende RHFZ-Experiment verwendet. Nach dem Wachstum wurden die Kristalle dann im Ofen auf Raumtemperatur abgekühlt. Die gewachsenen Kristalle wurden entlang der Basalebene gespalten, wodurch eine silbrig glänzende, spiegelähnliche Oberfläche entstand, und dann für weitere Experimente präpariert. Das Raman-, EDS- und XPS-Spektrum unterstützt, dass der Kristall Sb₂ . ist Se₂ Te. Die Röntgenbeugung zeigt scharfe Peaks, die darauf hinweisen, dass Sb₂ Se₂ Te-Kristall hat eine hohe Kristallinität und Gleichmäßigkeit. Unsere bisherigen Arbeiten zeigen, dass aus ARPES extrahierte physikalische Parameter und die Quanten-SdH-Oszillation konsistent sind. Diese unterstützen die Sb₂ Se₂ Der Kristall weist eine hohe Qualität und Gleichmäßigkeit auf.

Die Sb₂ Se₂ Te-Nanoblätter wurden durch Ablösen von Bulk-Kristallen mit Dicing-Tape erhalten und dann auf dem isolierenden SiO₂ . dispergiert (300 nm)/n -Si-Schablonen mit vorstrukturierten Ti/Au-Schaltungen. Anschließend wurden auf dem ausgewählten Sb₂ . zwei Platin (Pt)-Metallkontakte abgeschieden Se₂ Te-Nanoblätter unter Verwendung der Focused-Ion-Beam-(FIB)-Technik. Abbildung 1a–c zeigt die SEM-Bilder von drei Sb₂ Se₂ Die Nanoblätter. Die Dicke der Nanoblätter wird durch Rasterkraftmikroskopie bestimmt, und die gemessene Dicke von drei synthetisierten Nanoblättern betrug 58 nm, 178 nm bzw. 202 nm. Die Leitfähigkeit dieser Nanoblätter wurde mit Keithley 4200-SCS gemessen. Der Strom wurde als Funktion der angelegten Spannung in einem Zwei-Sonden-Verfahren gemessen. Das Ich ⁺ und V ⁺ sind die gleichen Kontaktpunkte, und ich ⁻ und V ⁻ sind die gleichen Anlaufstellen. Um den intrinsischen Leitwerteffekt auf die Photostromantwort zu identifizieren, wurden drei Nanoblätter mit unterschiedlicher Leitfähigkeit für die Photostrommessung hergestellt.

a , b , und c zeige die REM-Bilder von drei Sb₂ Se₂ Die Nanoblätter. Die Nanoschichtdicke wird durch AFM gemessen. Zur Messung des Photostroms wurden zwei Pt-Kontakte auf einem Nanoblatt abgeschieden. d , e , und f offenbaren die Spannung-Strom-Beziehung, und sie ist linear. Das zeigt den ohmschen Kontakt zwischen den Pt-Elektroden und Sb₂ . an Se₂ Die Nanoblätter

Ergebnisse und Diskussion

Abbildung 1d–f zeigt eine lineare Spannungs-Strom-Beziehung. Dies zeigt die metallische Eigenschaft und die ohmschen Kontakte zwischen Pt-Elektroden und Nanoschichten an. Der gemessene Leitwert, G , sind 4 × 10 ⁻⁵ , 0,006 und 7 × 10 ⁻⁵ (S) für Nanoblätter mit Dicken von 202, 178 bzw. 58 nm. Die Leitfähigkeit liegt über 1000 (S/m), was die extrem hohe Kristallqualität unserer Nanoblätter unterstützt.

Abbildung 2a–c zeigt gemessene Ströme als Funktion der Lichtleistungsintensität. Abbildung 2d–f zeigt, dass der gemessene Strom proportional zur Lichtleistungsintensität ist [27, 28]. Die Beziehung könnte ausgedrückt werden als I _an =β P ^α +Ich _aus , wo das Ich _an sind die gemessenen Ströme mit Licht, I _aus sind die gemessenen Ströme ohne Licht, β ist eine Konstante in Bezug auf die Photostromantwort, P ist die Lichtleistungsintensität und α ist eine Konstante, die sich auf die Lichtbeleuchtungsbedingung zwischen den Geräten und dem Licht bezieht. Es ist erwähnenswert, dass das größere I _an wird im Nanoblatt mit größerem I . beobachtet _aus . Der Photostrom, I _ph , ist definiert als I _an −Ich _aus . Tabelle 1 listet das Anpassungsergebnis auf. Es zeigt, dass α ≈1 für alle Nanoblätter mit unterschiedlichen Dicken, was die konsistenten optischen Eigenschaften dieser Nanoblätter unterstützt. Es ist erwähnenswert, dass β /G ist 1,1 × 10 ⁵ ±0,2×10 ⁵ (A /WS) für alle Nanoblätter. Dies zeigt an, dass der beobachtete Photostrom proportional zur effektiven Leitfähigkeit ist. Dieser Befund bestätigt, dass neben der Systemgeometrie und der Materialbandstruktur auch die effektive Leitfähigkeit von Nanoblättern ein kritischer Faktor wäre, der die Photostromantwort dominiert.

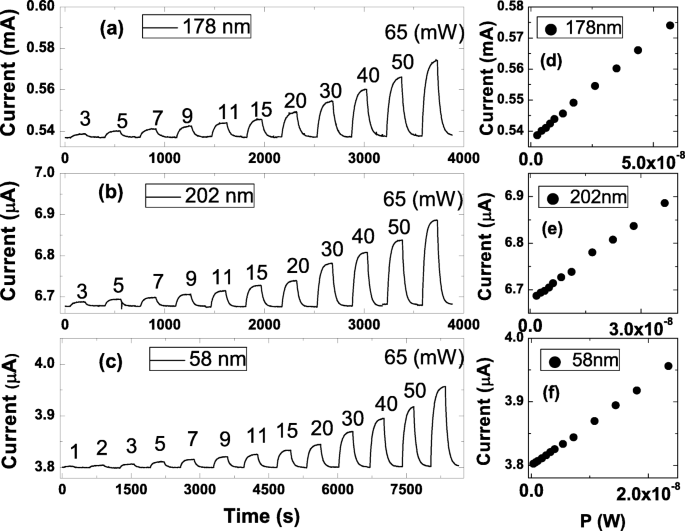
a , b , und c zeigen die gemessenen Ströme als Funktion der Lichtleistungsintensität in drei Proben mit unterschiedlichen Dicken. d , e , und f zeigen, dass die gemessenen Ströme proportional zur Lichtleistungsintensität sind. Es fällt uns auf, dass das größere I _an wird im Nanoblatt mit größerem I . beobachtet _aus

Das Ich _ph stammt von Elektron-Loch-Paaren, die durch die Wechselwirkung zwischen injizierten Photonen und Nanoblättern induziert werden. Die induzierten Elektronen und Löcher fließen bei angelegter elektrischer Vorspannung in entgegengesetzte Richtungen. Das effektive Ich _ph ist proportional zur angelegten Spannung und der Menge an Elektron-Loch-Paaren. Mehr injizierte Photonen führen zu mehr Elektron-Loch-Paaren. Die Lichteindringtiefe ist je nach Lichtleistungsintensität kurz und schwach. Es wird berichtet, dass die Lichteindringtiefe in topologischen Isolatoren etwa 20 nm beträgt, was kleiner ist als die Dicke unserer Nanoblätter [23, 24]. Das Ich _ph sollte unabhängig von der Nanoschichtdicke sein, wenn die Dicke größer als die Lichteindringtiefe ist. Die Nanoblatt-Oberfläche verteilt sich um den Faktor 3, aber das beobachtete I _ph verteilt sich über eine Differenz zweier Ordnung. Abgesehen von den effektiv induzierten Elektron-Loch-Paaren sind die beobachteten unterschiedlichen I _ph sollte von intrinsischen Eigenschaften herrühren. Um extrinsische Geometrieeffekte auf das I . auszuschließen _ph und quantitativ die Leistung dieser Nanoblätter bestimmen, die Reaktionsfähigkeit, R , wird mit der folgenden Gleichung berechnet:

wo P und S sind die Lichtleistungsintensität bzw. die effektive Fläche.

Abbildung 3 zeigt R als Funktion der Lichtleistungsintensität, anders als meist berichtet, dass der R nimmt drastisch ab, wenn die Lichtleistungsintensität in den Bi-basierten topologischen Isolatoren und niedrigdimensionalen Materialien zunimmt [25, 26]. Unsere Ergebnisse zeigen, dass die R und G sind unabhängig von der Lichtleistung im Vakuum. Dies unterstützt weiter, dass die Lichteindringtiefe unter unseren experimentellen Bedingungen kürzer als die Nanoschichtdicke sein sollte. Das größere R wird im Nanoblatt mit höherer Leitfähigkeit beobachtet. Dies belegt, dass die beobachtete höhere Photoreaktion von intrinsischen Transporteigenschaften herrührt und nicht von der Nanoblattgeometrie oder den experimentellen Bedingungen.

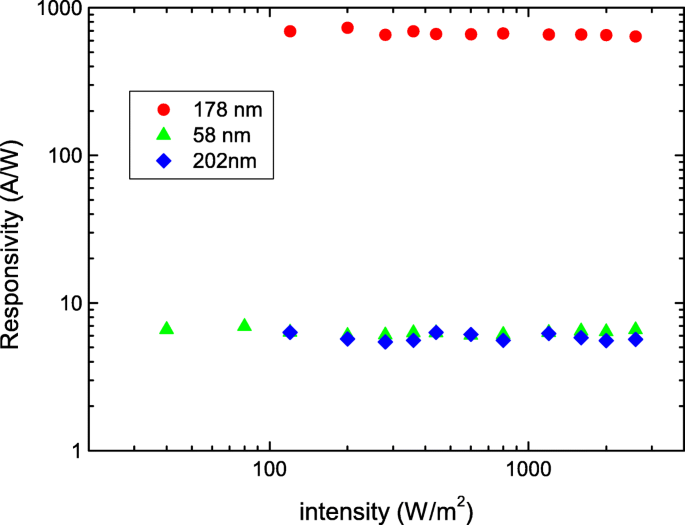
Die Reaktionsfähigkeit von drei Sb₂ Se₂ Die Nanoblätter. Es zeigt eine schwache Abhängigkeit der Lichtleistungsintensität von der Ansprechempfindlichkeit. Die höhere Empfindlichkeit wird in der Nanoschicht mit höherer Leitfähigkeit beobachtet

Wie in Abb. 1 gezeigt, unterstützt die lineare Spannungs-Strom-Beziehung, dass Nanoblätter ein metallisches Verhalten zeigen. Die lichtinduzierten Elektron-Loch-Paare würden aufgrund der angelegten Vorspannung zu zwei Elektrodenkontakten wandern [27–29]. Dem Ohmschen Gesetz folgend könnte der zugehörige Photostrom durch die Beziehung I . bestimmt werden _ph =V G wo V ist die angelegte Vorspannung zwischen zwei Elektroden. Das Ich _ph ist proportional zum G .

Abbildung 4 zeigt die R als Funktion des G in einem Log-Log-Plot. Die Datenpunkte von Sb₂ Se₂ Te sind die Messergebnisse in dieser Arbeit und Datenpunkte von Sb₂ SeTe₂ sind aus unseren früheren Arbeiten unter den gleichen Kristallwachstumsbedingungen und Messaufbauten entnommen [27]. Die Dicke von Sb₂ SeTe₂ Nanoblätter sind etwa 180 nm groß. Die Wellenlänge beträgt 532 nm. Beide Sb₂ Se₂ Te und Sb₂ SeTe₂ zeige, dass R ist unabhängig von der Lichtleistungsintensität. Diese Datenpunkte folgen der Tendenz der Punktlinie über einen weiten Bereich der Nanoblatt-Leitfähigkeit. Dies unterstützt, dass R ist proportional zum G , was mit unserem Vorschlag übereinstimmt.

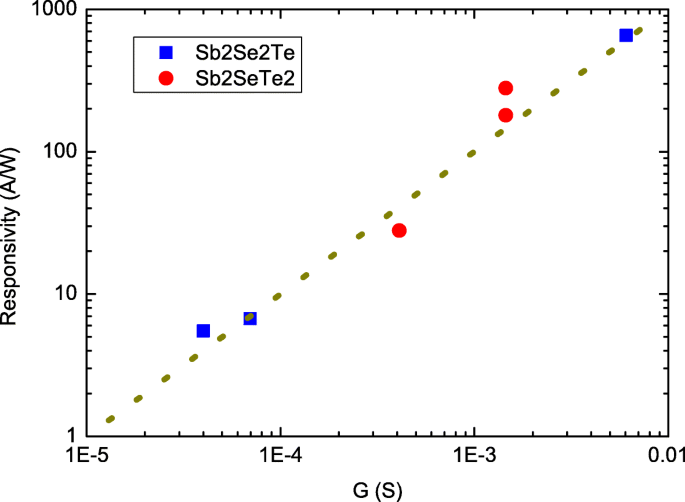
Empfindlichkeit als Funktion der Nanoblatt-Leitfähigkeit. Es zeigt, dass die Ansprechempfindlichkeit proportional zur Nanoblatt-Leitfähigkeit ist. Die Sb₂ SeTe₂ Daten stammen aus unseren gemeldeten Werten

Ein System mit einem höheren Photostrom-Ansprechverhalten wird für potentielle Anwendungen stark bevorzugt. Neben der Suche nach neuen Materialien oder Systemen mit spezifischer Bandstruktur und Bandlücke wäre auch eine geeignete Behandlung auf einem System geeignete Methoden zur Verbesserung der Photoreaktion. Unsere experimentellen Ergebnisse belegen, dass die intrinsische elektrische Leitfähigkeit ein kritischer Faktor für die Optimierung der Photostromantwort wäre. Dies kann durch geeignete Wachstumsbedingungen erreicht werden. Wie in Fig. 4 gezeigt, wird der Photostrom durch die Anpassung der Leitfähigkeit um 2 Größenordnungen verbessert. Diese Studie könnte andere Forscher bei der Erstellung einer geeigneten Richtlinie zur Auswahl eines besseren Systems für weitere experimentelle Studien durch einen einfachen elektrischen Test anleiten.

Die R und Detektivität bei V =0,1V erreicht 731 und 2,6×10 ¹⁰ am Nanoblatt mit höherer Leitfähigkeit. Diese Photoreaktionen sind größer als alle gemeldeten Werte in (Sb, Bi)₂ (Te, Se)₃ topologische Isolatoren und niedrigdimensionale Materialien [27, 28] und nur niedriger als mehrere beschriebene Heterostrukturen. In letzter Zeit haben niederdimensionale Materialien im Bereich des Photostroms große Aufmerksamkeit erregt. Es fällt uns auf, dass die berichtete Leitfähigkeit in diesen niedrigdimensionalen Materialien extrem hoch ist. Dies stimmt mit unserem experimentellen Ergebnis überein, dass die Leitfähigkeit ein kritischer Faktor ist, der die Photostromantwort dominiert.

Abbildung 5 zeigt R als Funktionen der Lichtleistungsintensität in Vakuum und Atmosphäre. Uns fällt auf das R nimmt drastisch ab, wenn die Lichtintensität weniger als 500 Wm beträgt ⁻² in Atmosphäre. Dies unterstützt, dass dieses abnehmende R bei geringer Lichtintensität in der Atmosphäre könnte vom Einfluss des adsorbierten Moleküls auf der Oberfläche unseres Sb₂ . kommen Se₂ Das Nanoblatt.

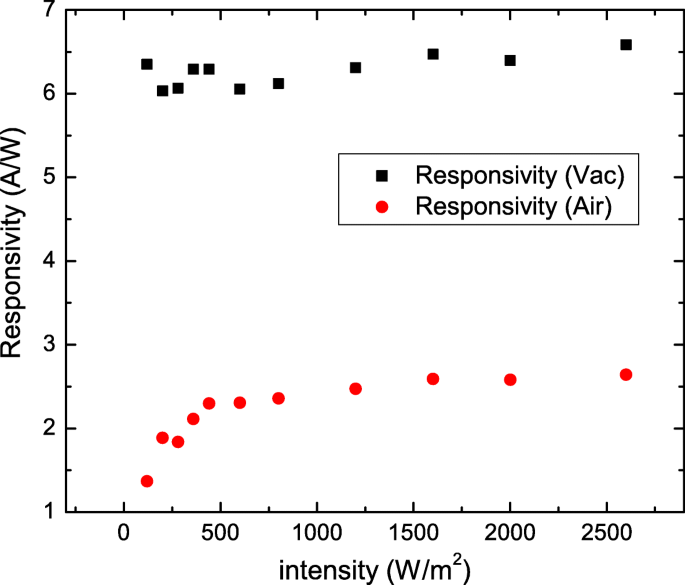
Ansprechempfindlichkeit und photoleitfähige Verstärkung als Funktion der Lichtleistungsintensität bei einer Wellenlänge von 532 nm. Die Ansprechempfindlichkeit ist im Vakuum von der schwachen Lichtleistungsintensität abhängig. Die Empfindlichkeit nimmt ab, wenn die Lichtleistungsintensität in der Atmosphäre abnimmt, wenn die Lichtleistungsintensität weniger als 500 W . beträgt /m ²

Die Photoreaktion wäre äußerst empfindlich gegenüber dem Zustand der Probenoberfläche. Neben der Verringerung des effektiven Ansprechbereichs können Oberflächendefekte und Oxidation die Ladungsträgermobilität und -lebensdauer verringern.

Kürzlich wurde berichtet, dass adsorbierte Moleküle auf der Oberfläche von Bi₂ Se₃ topologische Isolatoren verbiegen die Struktur und führen zu einem zusätzlichen 2DEG. Diese induzierte 2DEG würde die effektive Trägermobilität erhöhen [30]. Ein System mit höherer Trägermobilität könnte die Trägerlaufzeit verkürzen und einen höheren Photostrom erzeugen. Andererseits sollte die verbesserte Trägermobilität unabhängig von der Lichtleistungsintensität sein. Diese belegen, dass die beobachteten R die Unterdrückung erfolgt hauptsächlich durch den effektiv leuchtenden Bereich, nicht durch die intrinsischen Transporteigenschaften. Daher wird angenommen, dass der Abfall von R in Luft bei geringer Lichtleistungsintensität sollte eher mit dem absorbierten molekularen Schatteneffekt als mit dem intrinsischen Komplexträgerrelaxationseffekt zusammenhängen.

Die Definition der Ansprechempfindlichkeit ist das Verhältnis des induzierten Trägers zu den einfallenden Photonen und könnte auch als \(R=\eta \frac {q}{hf},\) ausgedrückt werden, wobei q , hf , und η sind die Ladungsträgerladung, die Photoenergie bzw. die Quanteneffizienz. Die η steht in direktem Zusammenhang mit den Materialeigenschaften und der Lichtwellenlänge. Um andere extrinsische und intrinsische Effekte auszuschließen und den Molekülschatteneffekt zu optimieren, wird der R (a ich r )/R (v a c ) ist als Funktion der Lichtleistungsintensität aufgetragen. Wie in Fig. 6 gezeigt, nimmt das Verhältnis mit zunehmender Leistungsintensität zu und wird bei hoher Leistungsintensität allmählich gesättigt.

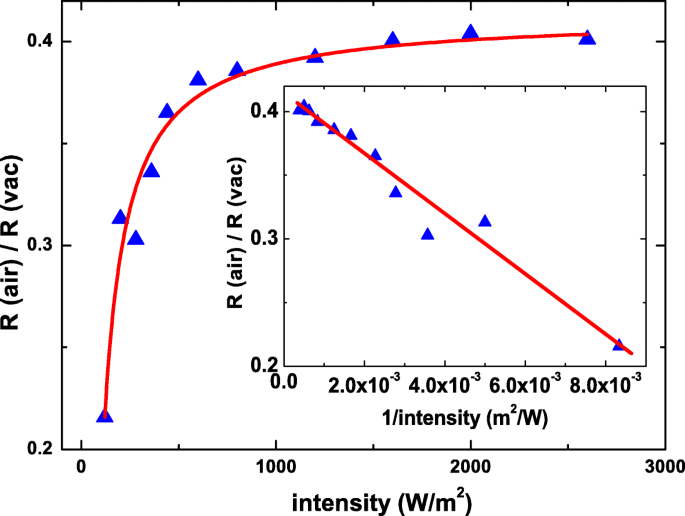
Das Verhältnis der Empfindlichkeit in Luft zu der im Vakuum als Funktion der Lichtleistungsintensität. Die Datenpunkte passen gut zur theoretischen Prädikation. Der Einschub zeigt, dass das Verhältnis der Empfindlichkeit in Luft zu der im Vakuum negativ proportional zum Kehrwert der Lichtleistungsintensität ist

Wir schlagen ein Modell vor, bei dem die einfallende Photonenzahl Y . ist , die m Photonen interagieren mit Material und n Photonen werden durch adsorbierte Moleküle auf der Oberfläche blockiert. Das heißt, Y =m +n . Das Z ist die durchschnittliche Zahl der induzierten Photostromträger durch ein Photon. Bei der extrem schwachen Lichtintensität ist die Photozahl viel kleiner als die gesamte molekulare Einheit, der effektive Photostrom sollte der statistischen Berechnung folgen und das Ergebnis unterstützt die Quanteneffizienz, η , könnte ausgedrückt werden als

Diese statische Berechnung unterstützt, dass der effektive Photostrom im Grenzbereich der schwachen Lichtleistungsintensität und der langen Relaxationszeit stark von der Lichtleistungsintensität abhängt; die Photonenzahl kann kleiner sein als der „Fototräger-Ersteller“. Der effektive Photostrom könnte ausgedrückt werden als

Das Y ist direkt proportional zur Lichtleistungsintensität. Die R (a ich r )/R (v a c ) ist negativ proportional zum Kehrwert von Y und ist schwach abhängig vom Y in der Situation des Y ≫n . Wie in 6 gezeigt, zeigt es deutlich, dass die gemessenen Datenpunkte gut mit der theoretischen Gleichung übereinstimmen, und der Einschub zeigt, dass die Datenpunkte negativ proportional zum Kehrwert der Lichtleistungsintensität sind. Diese belegen, dass der beobachtete Photostromabfall hauptsächlich auf den Schatteneffekt von adsorbierten Molekülen auf der Oberfläche zurückzuführen ist. \(\frac {R(Luft)}{R(vac)}\) beträgt bei hoher Leistungsintensität ungefähr 0,4 und dies zeigt an, dass die Oberfläche zu 40% mit adsorbierten Molekülen bedeckt ist.

Der Einschub links unten in Abb. 7 zeigt den Photostrom als Funktion der Zeit. Der Ladevorgang könnte durch das e . beschrieben werden ^{−t /k} , wobei k ist charakteristische Zeitkonstante. Unser experimentelles Ergebnis zeigt, dass der gemessene Photostrom gut zur Anpassungslinie passt. Der Einschub oben rechts zeigt die extrahierte Ladezeitkonstante als Funktion der Dicke. Es zeigt sich, dass die Zeitkonstante mit zunehmender Dicke abnimmt. Dieses Verhalten könnte als Gleichförmigkeitsstromflussprozess verstanden werden [27, 28]. Andererseits werden die Lade- und Entladezeitkonstanten unterschiedlicher Atmosphärendrücke bestimmt. Es zeigt, dass die Ladezeitkonstante ungefähr der Entladezeitkonstante entspricht und eine längere Zeitkonstante bei niedrigerem Atmosphärendruck beobachtet wird.

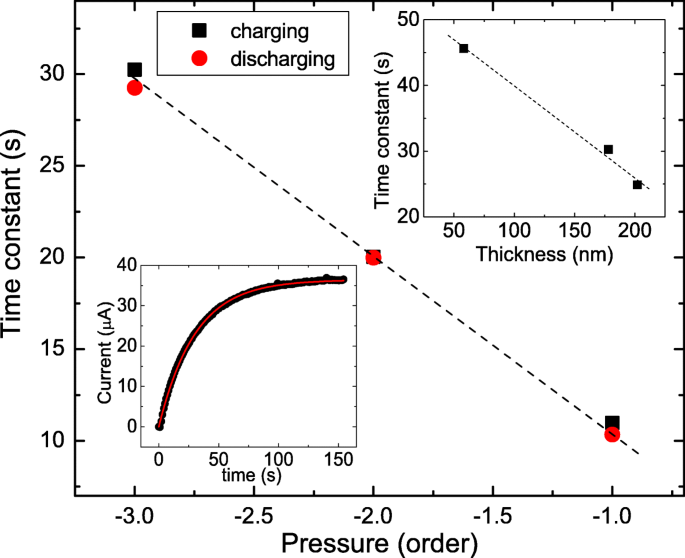
Der Einschub links unten zeigt den Photostrom als Funktion der Zeit beim Ladevorgang und passt gut zur Anpassleitung. Der Einschub oben rechts zeigt die Ladezeitkonstante als Funktion der Dicke. Die Lade- und Entladezeitkonstante als Funktion des Drucks

Schlussfolgerung

Der Photostrom wurde im Sb₂ . durchgeführt Se₂ Der topologische Isolator mit unterschiedlicher Leitfähigkeit bei einer Wellenlänge von 532 nm. Der Photostrom ist linear zur Lichtleistungsintensität und der Photostrom ist proportional zum Dunkelstrom. Im Nanoblatt mit höherer Leitfähigkeit wird ein höherer Photostrom beobachtet. Die Ansprechempfindlichkeit ist proportional zur Nanoblatt-Leitfähigkeit. Die Ansprechempfindlichkeit ist unabhängig von der Lichtleistungsintensität im Vakuum, jedoch nimmt die Ansprechempfindlichkeit bei geringer Leistungsintensität in Luft drastisch ab, dh im Gegensatz zu den meisten berichteten Ergebnissen. Das Verhältnis der Ansprechempfindlichkeit in Luft zu der im Vakuum ist negativ proportional zum Kehrwert der Lichtleistungsintensität. Diese Verhaltensweisen werden als statistischer Photostrom in einem System mit blockierten Molekülen verstanden. Nach dem theoretischen Modell ist die Oberfläche in Luft zu 40 % mit adsorbierten Molekülen bedeckt. Die Zeitkonstante nimmt mit zunehmender Dicke ab. Dieses Verhalten könnte als der Gleichförmigkeitsstromflussprozess verstanden werden. Die Lade- und Entladezeitkonstanten unterschiedlicher Drücke werden bestimmt. Bei niedrigerem Atmosphärendruck wird eine längere Zeitkonstante beobachtet. Die R und Detektivität bei V =0,1V erreicht 731 und 2,6×10 ¹⁰ am Nanoblatt mit höherer Leitfähigkeit. Diese sind höher als alle gemeldeten Werte in (Sb, Bi)₂ (Te, Se)₃ topologische Isolatoren und niedrigdimensionale Materialien und nur niedriger als mehrere berichtete Heterostrukturen.

Abkürzungen

ARPES:

Winkelaufgelöste Photoemissionsspektroskopie

EDS:

Energiedispersive Röntgenspektroskopie

SdH:

Shubnikov-de Haas

XPS:

Röntgenphotoelektronenspektroskopie