Effiziente Vorhersage und Analyse von optischem Trapping auf der Nanoskala mittels Finite-Elemente-Reiß- und Verbindungsmethode

Einführung

Plasmonische optische Pinzetten auf der Basis von Oberflächenplasmonen (SPs) ziehen viel Aufmerksamkeit auf sich und werden häufig zum Einfangen von Nanopartikeln eingesetzt [1,2,3,4,5,6]. SP ist ein Resonanzphänomen, das durch die Kopplung von einfallendem Licht mit einer bestimmten Wellenlänge und freien Elektronen an der Grenzfläche von Metallen und Dielektrika verursacht wird [7]. SPs ermöglichen es der optischen Pinzette, die Beugungsgrenze zu durchbrechen. Darüber hinaus kann die drastische lokale Feldverstärkung der SPs den Intensitätsbedarf des einfallenden Lichts reduzieren [7, 8]. SPs sind jedoch eng mit dem Material und den Abmessungen von Objekten sowie der Wellenlänge des einfallenden Lichts verbunden, was eine große Anzahl von Experimenten erfordert, um die optimalen Parameter von optischen SP-Pinzetten in der Praxis zu bestimmen. Darauf aufbauend spielt die Simulationsmethode als Hilfsmittel bei der Auslegung und Optimierung optischer SP-Pinzetten eine immer wichtigere Rolle [9]. In diesen Simulationen ist die Berechnung der optischen Kraft erforderlich, um ein stabiles Einfangen vorherzusagen. Für regelmäßige Objekte wie Kugeln kann die optische Kraft analytisch aus der verallgemeinerten Lorenz-Mie-Theorie abgeleitet werden [10, 11]. Für Objekte mit komplizierten Konfigurationen sind jedoch numerische Methoden erforderlich, die die maßgeblichen Maxwell-Gleichungen rigoros lösen, um die elektromagnetischen Felder und die anschließende optische Kraft und das Potenzial zu modellieren.

Diese numerischen Verfahren können hauptsächlich in Differentialgleichungsmethoden (DEMs) und Integralgleichungsmethoden (IEMs) eingeteilt werden [12,13,14,15]. Gegenüber den IEMs zeigen Differenzialgleichungsmethoden (DEMs) überlegene Fähigkeiten im Umgang mit komplizierten Geometrien und Bauteilen. DEMs haben auch den Vorteil einer einfachen Berechnung der Nahfeldverteilung, die bei der Analyse von SPs eine wichtige Rolle spielt. Als repräsentatives DEM wird das Finite-Difference-Time-Domain-(FDTD)-Verfahren im Zeitbereich implementiert, das leicht Breitbandinformationen und Einschwingverhalten erhalten kann [16, 17]. Die FDTD erfordert jedoch ein genaues dispersives Modell, um die frequenzabhängigen Materialeigenschaften in SPs zu beschreiben, während die Genauigkeit der FDTD-Lösung stark von der Näherungsgenauigkeit dieses dispersiven Modells abhängt [18]. Außerdem setzt das FDTD auf strukturierte Netze, die bei gekrümmten Oberflächen oft zu Treppenfehlern führen. Als ein weiteres repräsentatives DEM ist die Finite-Elemente-Methode (FEM) weit verbreitet, da sie leicht mit dispersivem Material im Frequenzbereich umgehen und den Treppenfehler durch unstrukturierte Netze eliminieren kann [19,20,21,22]. Im Vergleich zum FDTD kann die FEM gemessene Materialparameter ohne näherungsweise dispersives Modell direkt übernehmen. Allerdings erfordern drastische lokale Feldverstärkungen in den SPs feine Netze in der FEM-Diskretisierung. Außerdem erhöhen Objekte mit großen Abmessungen und mehreren Objekten die Anzahl der Unbekannten dramatisch. Diese Faktoren werden schlecht konditionierte Matrixsysteme und einen enormen Rechenaufwand verursachen, was die traditionelle FEM für die Analyse von SP-verstärktem optischem Trapping vor große Herausforderungen stellt.

In diesem Artikel wird ein effizientes Dual-Primal Finite Element Tearing and Interconnecting (FETI-DP)-Verfahren vorgestellt, um das optische Einfangen im Nanomaßstab zu simulieren. Das FETI-DP verwendet ein nicht überlappendes Domänenzerlegungsschema, das ein ursprüngliches großräumiges komplexes Problem in eine Reihe kleiner einfacher Probleme aufteilt, um es zu überwinden. Es erzwingt eine Übertragungsbedingung an den Subdomänenschnittstellen, um die Feldkontinuität sicherzustellen, und führt eine duale Variable ein, um das ursprüngliche dreidimensionale (3D) Problem durch den Lagrange-Multiplikator auf ein zweidimensionales (2D) Problem zu reduzieren. Primalvariablen an den Unterdomänenecken werden extrahiert, um die Konvergenzrate der iterativen Lösung des dualen Problems zu beschleunigen [23,24,25,26]. Zur Verbesserung der Leistung des FETI-DP wird ein niedrigrangiger Sparsification-Ansatz entwickelt. Es verwendet datensparse Algorithmen, um die Effizienz bei der Lösung der Subdomänenprobleme und des dualen Problems zu verbessern [27, 28]. Die vorgeschlagene Methode bietet vollständig entkoppelte Subdomänen, die die parallele Simulation der optischen Kraft zum Einfangen von Nanopartikeln ermöglichen. Zur Bewertung der optischen Kraft wird der Maxwell-Spannungstensor (MST) verwendet, der die Beziehung zwischen elektromagnetischem Feld und mechanischem Impuls aufzeigt [29]. Basierend auf der erhaltenen optischen Kraft kann das optische Potential für die Analyse eines stabilen Trappings weiter berechnet werden. Im Vergleich zu den IEMs ist die vorgeschlagene Methode leistungsfähiger im Umgang mit Verbundmaterialien und der Lösung des Nahfelds für das SP-basierte optische Einfangen. Verglichen mit der FDTD kann das vorgeschlagene Verfahren dispersives Metallmaterial in den SP-basierten optischen Einfangsystemen genau handhaben und den Treppenfehler für die Objekte mit Kurvenbegrenzung eliminieren. Im Vergleich zur FEM eignet sich das vorgeschlagene Verfahren für die großmaßstäbliche Berechnung von optischem Trapping. Mehrere Beispiele werden analysiert und numerische Ergebnisse demonstrieren die Genauigkeit und Effizienz der vorgeschlagenen Methode zur Vorhersage und Analyse von optischem Trapping im Nanomaßstab.

Methoden

FETI-DP-Formulierungen

Für die FETI-DP-Implementierung wird die ursprüngliche Berechnungsdomäne Ω zuerst in eine Reihe von nicht überlappenden Unterdomänen Ω ^{i . zerrissen} (ich = 1, 2, 3⋯, N _s ), wie in Abb. 1 gezeigt. In jeder Unterdomäne Ω ⁱ , kann ein Finite-Elemente-System im Unterbereich aus der Vektorwellengleichung abgeleitet werden als

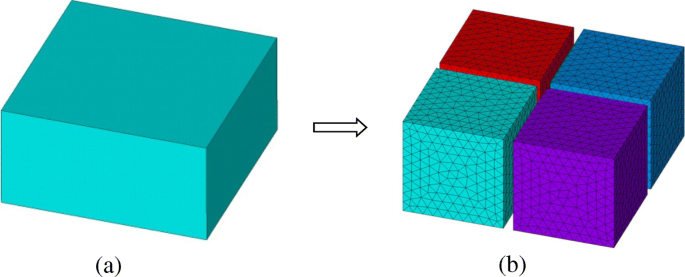
Ein Domänenteilungsschema mit nicht überlappenden Unterdomänen im FETI-DP-Verfahren. a Ursprüngliche Domäne. b Geteilte Unterdomänen und diskretisierte Netze

wo E ^ich bezeichnet das unbekannte zu lösende elektrische Feld in \({\Omega}^i\), k ₀ und η ₀ sind die Wellenzahl im freien Raum bzw. die Eigenimpedanz und \({\mathbf{J}}_i^{\mathrm{imp}}\) ist der eingeprägte Strom. \( {\Gamma}_{\mathrm{ABC}}^i \) bedeutet die absorbierende Randbedingung (ABC) zum Abschneiden des unendlich offenen Bereichs. Es sollte beachtet werden, dass k ₀ sollte durch den Wellenwiderstand im Medium ersetzt werden, wenn das umgebende Medium kein Freiraum ist, was für das optische Einfangen üblich ist. An der Subdomain-Schnittstelle Γ ⁱ , wird eine angenommene Randbedingung benötigt, um ein vollständiges Randwertproblem in Ω ^{i . zu erzeugen} . Hier eine Übertragungsbedingung vom Robin-Typ mit unbekannter Hilfsgröße Λ _ich wird auferlegt als

wobei \( {\hat{n}}^i \) den Einheitsnormalen-Auswärtsvektor an der Subdomänenschnittstelle bezeichnet Γ ⁱ , und α ^ich ist ein komplexer Parameter, der oft als jk gewählt werden kann ₀ . Alle Unterdomänen werden dann durch tetraedrische Elemente diskretisiert. In jedem Element erweitern wir E mit Vektorbasisfunktionen N und unbekannter elektrischer Feldkoeffizient E als

wo s bezeichnet die Anzahl der Vektorbasisfunktionen in jedem tetraedrischen Element. s wird für traditionelle Basisfunktionen niedriger Ordnung basierend auf der Kante zu 6 gewählt, während er für Vektorbasisfunktionen höherer Ordnung größer ist, da zusätzliche Basisfunktionen basierend auf Fläche oder Volumen eingeführt werden.

Unter Anwendung der Galerkin-Methode die FEM-Matrixgleichung in Ω ⁱ über den unbekannten elektrischen Feldkoeffizienten E ^ich erhältlich als

wobei die tiefgestellten Notationen c und r Unterscheiden Sie die Eckenfreiheitsgrade (DOFs) und die verbleibenden DOFs, wodurch die Ecken-DOFs als eine primäre Variable extrahiert werden, um das Dual-Primal-(DP)-Schema zu konstruieren. Hier, K ist die FEM-Systemmatrix und f ist der Anregungsvektor. B ist eine Boolesche Matrix, die die Schnittstellen-DOFs einer Unterdomäne extrahiert. λ ist eine duale Variable, die durch das Erweitern von Λ . erzeugt wird _ich , der auch Lagrange-Multiplikator genannt wird.

Dann können die benachbarten Unterdomänen durch Erzwingen eines tangentialen elektrischen Felds und einer magnetischen Feldkontinuität an den Grenzflächen verbunden werden. Wir bauen alle Subdomain-Schnittstellen zusammen und eliminieren alle internen Unbekannten der Subdomain E ^ich . Eine reduzierte globale Schnittstellengleichung über die duale Variable λ erhältlich als

Gleichung (6) kann durch iterative Verfahren gelöst werden, wie zum Beispiel das verallgemeinerte minimale Residuum (GMRES)-Verfahren. \({\tilde{\mathbf{K}}}_{cc}\) ist das globale Ecksystem, das die iterative Konvergenz im Primärraum beschleunigen kann. Ein geeigneter Vorkonditionierer kann verwendet werden, um die iterative Konvergenzrate zu verbessern, wie etwa eine angenäherte inverse und unvollständige LU-Zerlegung. Sobald die duale Variable λ gelöst ist, kann das elektrische Feld innerhalb jeder Unterdomäne durch (5) unabhängig bewertet werden. Für die Konstruktion der globalen Matrix \({\tilde{\mathbf{K}}}_{rr}\) muss man die numerische Greensche Unterdomänenfunktion \( {\mathbf{Z}}_{rr}^ i \) mit einer Form von

wobei die Inverse der Subdomänen-FEM-Matrix \( {\left({\mathbf{K}}_{rr}^i\right)}^{-1} \) enthalten ist. Außerdem gilt für Matrizen \( {\tilde{\mathbf{K}}}_{rc}\), \( {\tilde{\mathbf{K}}}_{cr}\) und \( {\tilde {\mathbf{K}}}_{cc} \) und Vektoren \( {\tilde{f}}_r \) und \( {\tilde{f}}_c \), die \( {\left({ \mathbf{K}}_{rr}^i\right)}^{-1} \) muss berechnet werden. Die Konstruktionen von \( {\left({\mathbf{K}}_{rr}^i\right)}^{-1} \) im Vorverarbeitungsstadium sowie deren Matrix-Vektor-Produkte (MVPs) bei iterative Lösungsstufen sind rechenaufwendig. Obwohl \( {\mathbf{K}}_{rr}^i\) spärlich ist, ist \( {\left({\mathbf{K}}_{rr}^i\right)}^{-1} \ ) sind dicht, was einen hohen Rechenaufwand bedeutet. Als nächstes wird eine Sparsifikationsmethode niedriger Ordnung eingeführt, um die Berechnung von \( {\left({\mathbf{K}}_{rr}^i\right)}^{-1} \) zu beschleunigen. Da einige Untermatrizen in dem globalen Schnittstellensystem in Matrixform mit niedrigem Rang dargestellt werden können, kann ihre Berechnung mit einem Algorithmus mit niedrigem Rang durchgeführt werden, was die Leistung des FETI-DP verbessert. Es ist ersichtlich, dass der FETI-DP unabhängige Subdomänenoperationen bereitstellt, so dass er parallele Berechnungen ausnutzen kann, um die Effizienz zu verbessern. Für ein effizientes paralleles Schema besteht ein Prinzip der Domänenaufteilung darin, die Anzahl der DOFs in jeder Unterdomäne so ausgeglichen wie möglich zu gestalten. Daher sollte sich die Größe der Unterdomänen auf die Netzdiskretisierungsdichte beziehen. Normalerweise werden kleine Unterdomänen in feinmaschigen Bereichen verwendet, während große Unterdomänen in grobmaschigen Bereichen verwendet werden.

Sparsification mit niedrigem Rang

Zur Verbesserung der FETI-DP-Effizienz wird ein niedrigrangiger Sparsification-Ansatz vorgeschlagen, um einen datensparsamen Weg bereitzustellen. Hier, Datensparse bedeutet, dass diese Matrizen tatsächlich nicht spärlich sind, aber sie sind in dem Sinne spärlich, dass bestimmte Unterblöcke von ihnen durch niederrangige Zerlegungsmatrixformen wie dargestellt werden können

wobei X und J sind in voller Matrixform und der Rang k ist viel kleiner als m und n . Die Matrix \( {\left({\mathbf{K}}_{rr}^i\right)}^{-1} \) kann durch datensparse Matrixformen dargestellt werden, da sie die Matrixeigenschaft eines Integrals besitzt Operator. Vorausgesetzt, \( {\left({\mathbf{K}}_{rr}^i\right)}^{-1} \) besitzt eine niederrangige Eigenschaft in einer gegebenen Unterdomäne, kann sie effizient berechnet und gespeichert werden in Datensparse-Formen mit dem Low-Rank-Sparsification-Ansatz, der die MVPs in der iterativen Lösung beschleunigt.

Die Prozesse des Low-Rank-Sparsification-Ansatzes können in die folgenden Schritte unterteilt werden:(1) Konstruieren eines Clusterbaums durch Unterteilen des Basisfunktionssatzes in jede Unterdomäne, (2) Konstruieren eines Blockclusterbaums durch Interaktion von zwei Clusterbäumen, ( 3) eine datensparse Form von \( {\mathbf{K}}_{rr}^i \) durch eine Zulässigkeitsbedingung erzeugen, (4) niedrigrangige formatierte Algorithmen ausführen, um die datensparse Darstellung von \( {\left({\mathbf{K}}_{rr}^i\right)}_{\mathrm{DS}}^{-1}\), und (5) geben Sie die Lösung von FETI-DP-Systemen ein durch Datensparse-Algorithmus. Geeignete Vorkonditionierer können verwendet werden, um die Lösung zu beschleunigen. Es sollte beachtet werden, dass die datensparse LU-Faktorisierung \( {\left({\mathbf{K}}_{rr}^i\right)}_{\mathrm{DS}}={\left({\mathbf {L}}_{rr}^i\right)}_{\mathrm{DS}}{\left({\mathbf{U}}_{rr}^i\right)}_{\mathrm{DS} } \) wird angenommen, um die Matrixinversion \( {\left({\mathbf{K}}_{rr}^i\right)}_{\mathrm{DS}}^{-1} \) zu ersetzen. Eine verschachtelte Dissektionstechnik wird verwendet, um die Effizienz der niederrangigen Sparsifikation weiter zu verbessern. Die verschachtelte Dissektion verwendet Trennzeichen, um große nichtdiagonale Null-Unterblöcke zu erhalten, die während der LU-Faktorisierung Null beibehalten, sodass die Auffüllungen erheblich reduziert werden können.

Um \( {\left({\mathbf{K}}_{rr}^i\right)}_{\mathrm{DS}} \ zu erzeugen, konstruieren wir zunächst einen Clusterbaum T _Ich durch rekursive Unterteilung des kantenbasierten Basisfunktionssatzes I = {1,2,……N } mit Begrenzungsrahmen. Bei der verschachtelten Sektion wird ein Cluster t innerhalb der entsprechenden Bounding Box wird in drei Nachfolger {s . unterteilt ₁ , s _September , s ₂ }, wobei s ₁ und s ₂ sind die Indexmengen der beiden getrennten Bounding Boxes und s _September ist die Indexmenge des Trennzeichens. Abbildung 2 a zeigt ein einfaches Beispiel für diesen Vorgang. Dann ein Block-Cluster-Baum T _{Ich × Ich} kann durch die Interaktion zweier Cluster-Bäume konstruiert werden T _Ich , wie in Abb. 2 b gezeigt, der als Clusterbaum des ursprünglichen kantenbasierten Basisfunktionssatzes und des Testbasisfunktionssatzes im Galerkin-Verfahren gewählt werden kann. Als nächstes müssen wir eine Zulässigkeitsbedingung basierend auf der verschachtelten Dissektion einführen, um vollständige Blöcke, niederrangige Zerlegungsblöcke und nicht-diagonale Nullblöcke in T . zu unterscheiden _{Ich × Ich} [23]. Somit kann \({\left({\mathbf{K}}_{rr}^i\right)}_{\mathrm{DS}}\) erzeugt werden, indem die entsprechenden Blöcke mit den von Null verschiedenen Einträgen von gefüllt werden \({\mathbf{K}}_{rr}^i\). Schließlich ist die datensparse LU-Faktorisierung von \( {\left({\mathbf{K}}_{rr}^i\right)}_{\mathrm{DS}}={\left({\mathbf{L }}_{rr}^i\right)}_{\textrm{DS}}{\left({\mathbf{U}}_{rr}^i\right)}_{\textrm{DS}} \ ) kann rekursiv berechnet werden aus

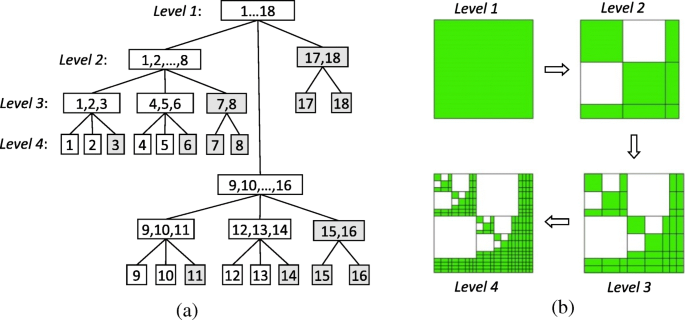
Konstruktionen eines Clusterbaums und eines Blockclusterbaums mit 4 Ebenen basierend auf verschachtelter Dissektion. a Aufbau eines Clusterbaums durch rekursive Unterteilung des kantenbasierten Basisfunktionssatzes I = {1,2,…18}. b Aufbau eines Blockclusterbaums, bei dem weiß Blöcke sind Nullmatrizen und grün Blöcke können vollständige Matrizen oder Zerlegungsmatrizen mit niedrigem Rang sein

wobei konventionelle Vollmatrixarithmetik durch ihre datensparsen Gegenstücke ersetzt wird [28]. Ein adaptiver Kürzungsfehler ε _t wird verwendet, um die Genauigkeit von Näherungen mit niedrigem Rang zu steuern. Die erhaltenen LU-Faktoren \( {\left({\mathbf{L}}_{rr}^i\right)}_{\mathrm{DS}} \) und \( {\left({\mathbf{U} }_{rr}^i\right)}_{\mathrm{DS}} \) werden gespeichert und verwendet, um \( {\mathbf{Z}}_{rr}^i \) durch

wobei \( {\mathbf{B}}_r^i{\left({\mathbf{U}}_{rr}^i\right)}_{\mathrm{DS}}^{-1} \) und \( {\left({\mathbf{L}}_{rr}^i\right)}_{\mathrm{DS}}^{-1}{\mathbf{B}}_r^i \) kann . sein berechnet durch den oberen und unteren Dreieckslöser mit geringer Datendichte. Die \( {\left({\mathbf{L}}_{rr}^i\right)}_{\mathrm{DS}} \), \( {\left({\mathbf{U}}_{ rr}^i\right)}_{\mathrm{DS}} \), und \( {\mathbf{Z}}_{rr}^i \) geben die FETI-DP-Berechnung mit Datensparse vorwärts und rückwärts ein Substitutionen (FBSs) und MVPs mit geringer Datendichte.

Optische Kraft und Potenzial

Nach der Theorie der Elektrodynamik kann die optische Kraft mit dem Maxwell-Spannungstensor (MST) bewertet werden, der die Beziehung zwischen elektromagnetischem Feld und mechanischem Impuls aufzeigt [29]. Sobald die elektromagnetische Feldverteilung um das Objekt herum erhalten ist, kann die optische Kraft durch Integrieren von MST über eine das Objekt umgebende geschlossene Oberfläche berechnet werden. Basierend auf der erhaltenen Verteilung des elektrischen Felds kann die MST an beliebigen Koordinaten konstruiert werden durch

wobei der hochgestellte Stern die Konjugation von elektrischem Feld oder magnetischem Feld bezeichnet, ε sind μ die Permittivität und Permeabilität sind und \(\overleftrightarrow{\mathbf{I}}\) eine 3 × 3-Identitätsmatrix ist. Durch das äußere Produkt von Vektoren kann die Tensorform von \(\overleftrightarrow{\mathbf{T}}\) geschrieben werden als

wobei das tiefgestellte x , y , z bezeichnet die Komponenten in drei Richtungen. Entsprechend der Erweiterung von E in (4) beschrieben, die Einträge von MST T _mn (m , n = x , y , z ) kann in der FETI-DP-Berechnung in erweiterte Formen umgewandelt werden als

wo ω die Kreisfrequenz ist; N und s wurden in Gl. (4).

Schließlich kann die auf das Objekt ausgeübte optische Kraft berechnet werden, indem die MST über eine beliebige geschlossene Oberfläche um sie herum integriert wird durch

Beachten Sie, dass die Berechnung der optischen Kraft auch parallel durchgeführt werden kann, da das Integral des MST entsprechenden Unterdomänen zugeordnet ist. Für ein stabiles optisches Einfangen besteht eine der Hauptbedingungen darin, dass die Gradientenkraft größer als die Streuungskraft sein sollte. Mit anderen Worten, die Richtung der Gesamtkraft sollte mit der der Gradientenkraft identisch sein, die immer auf die Stelle zeigt, an der die elektrische Feldstärke am stärksten ist.

Das optische Potenzial ist ein weiterer attraktiver Parameter, der die Stabilität des optischen Einfangens offenbart. Basierend auf der erhaltenen optischen Kraft ist die optische Potentialtiefe U an Position r ₀ kann berechnet werden durch

wobei der Index ∞ die Unendlichkeit bezeichnet, die als Referenzpunkt mit Nullpotential definiert ist. Der Wert von U kann durch k . dargestellt werden _B T, wobei k _B bezeichnet die Boltzmann-Konstante von 1,3806488 × 10 ⁻²³ J/K und T ist die Umgebungstemperatur. Im Allgemeinen kann das Teilchen die Brownsche Bewegung in Lösung überwinden und stabil eingefangen werden, wenn U> 1 k _B T ist zufrieden. Andernfalls kann das Teilchen nicht stabil eingefangen werden. Da die optische Gesamtkraft die konservative Gradientenkraftkomponente und die nicht konservative Streukraftkomponente enthält, beträgt die optische Gesamtkraft F aus (15) ist nicht konservativ [30, 31]. Vorausgesetzt, die Bewegung des Nanopartikels ist jedoch auf eine Dimension beschränkt, ergibt dies eine eindeutige Definition eines optischen Potentials von (16), obwohl die gesamte optische Kraft nicht konservativ ist.

Ergebnisse und Diskussion

Drei Beispiele werden vorgestellt, um die Wirksamkeit der vorgeschlagenen Methode zu demonstrieren. Da zur Anregung des Oberflächenplasmons häufig Edelmetalle verwendet werden, wählen wir für die Analysen repräsentative Gold- und Silbermaterialien aus. Das erste Beispiel berechnet die optische Kraft von Silbernanopartikeln, um die Genauigkeit der vorgeschlagenen Methode zu überprüfen. Das zweite und dritte Beispiel simulieren und diskutieren das optische Einfangen von Goldnanopartikeln. Für alle Beispiele wird der unendliche Bereich mit ABC abgeschnitten, und die Abstände zwischen ABC und den Objekten werden auf eine Wellenlänge eingestellt, was ausreichend ist, um eine akzeptable Genauigkeit zu erreichen. Alle Berechnungen werden auf einer Dell Workstation durchgeführt, die mit 3,6 GHz Intel Xeon Prozessoren ausgestattet ist.

Silber-Nanokapsel

Ein Silber-Nanokapsel-Objekt wird zuerst betrachtet, um die Genauigkeit und Effizienz der vorgeschlagenen FETI-DP-Methode bei der Vorhersage der optischen Kraft zu testen. Abbildung 3 a und b zeigt seine Konfiguration und Abmessungen. Die konstitutiven Parameter von Silber sind alle Messwerte aus [32]. Um das FETI-DP-Schema zu implementieren, wird der gesamte Analysebereich zunächst in 24 Unterbereiche unterteilt. In der Nähe der Metalloberfläche sind dichtere Netze erforderlich, um den plasmonischen lokalen Feldverstärkungseffekt zu modellieren. Für die Diskretisierung werden tetraedrische Elemente verwendet, was zu insgesamt 6.9 × 10 ⁵ . führt Unbekannte, einschließlich 4.1 × 10 ⁴ duale Unbekannte und 313 Ecken-Unbekannte. Das einfallende Licht leuchtet entlang der Richtung von +z , während die Polarisationsrichtung des elektrischen Felds −x . ist .

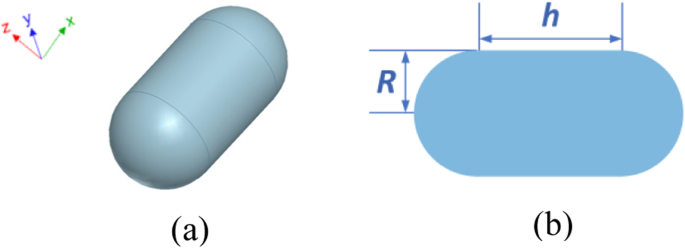
Konfiguration einer Silbernanokapselstruktur. a 3D-Ansicht. b Vorderansicht und Abmessungen, wobei R = 30 nm und h = 60 nm

Zuerst ändern wir die Wellenlänge des einfallenden Lichts λ von 200 nm bis 400 nm, um die auf die Nanokapsel ausgeübten optischen Kräfte zu simulieren. Da der FETI-DP im Frequenzbereich arbeitet, werden die optischen Kräfte an 15 Abtastfrequenzpunkten berechnet. Abbildung 4 zeigt die berechnete Kurve der auf die Silbernanokapsel ausgeübten optischen Kräfte. Um die Genauigkeit des FETI-DP anzuzeigen, werden die optischen Kraftergebnisse des FETI-DP mit denen der kommerziellen Software Lumerical FDTD Solutions [33] verglichen, und es kann eine gute Übereinstimmung beobachtet werden.

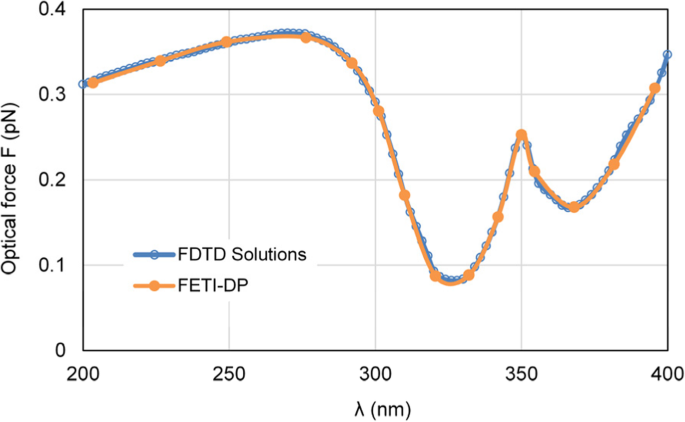
Ergebnisse der auf die Silber-Nanokapsel ausgeübten optischen Kräfte, die mit der Wellenlänge λ . variieren von einfallendem Licht, einschließlich der Ergebnisse des FETI-DP und der kommerziellen Software-FDTD-Lösungen

Then, the performance of FETI-DP is tested for different numbers of subdomains. We increase the number of subdomains from 4 to 24 by keeping the discretization density. We assign each processor to deal with one subdomain. Table 1 reports the time used for the construction of global interface Eq. (6) and the total solution time. It can be seen that the FETI-DP can fully exploit parallel computing resources and significantly improve the solution efficiency. Besides, the accuracy of the FETI-DP with the number of subdomains increasing is also examined and reported in Table 1. Here, the accuracy is defined by the 2-norm relative error of the optical force as δ _OF  = ‖OF _ich  − OF _ref ‖/‖OF _ref ‖, where OF _ich is the optical force using i subdomains and OF _ref denotes the reference optical force using two subdomains. It can be seen that the accuracy keeps almost constant with the number of subdomains increasing.

Gold Nanosphere Dimer

The second example analyzes the optical trapping of a gold nanosphere by using a gold nanosphere dimer. The plasmonic effects at the dimer gap can effectively enhance the optical force for trapping nanoparticle. Figure 5 a and b gives the configuration and dimensions of this system. The constitutive parameters of gold are all measured values taken from [32]. The surrounding medium is water with a relative refractive index of n  = 1.33. The incident light is a plane wave with the power of 10 mW/μm ² , the electric field polarization direction is +x , and the incident direction is −z . The optical force exerted on the object nanosphere is calculated by the FETI-DP method. For the FETI-DP implementation, the whole computational domain is divided into 32 subdomains and discretized by tetrahedral meshes, which results in 3.5 × 10 ⁶ unknowns, including 1.6 × 10 ⁵ dual unknowns and 1738 corner unknowns.

Configuration of an optical trapping system of a gold nansphere dimer in water. a 3D view. b Front view and dimensions, where R = 25 nm, r = 5 nm, and g = 2 nm

First, we test the parallel performance of the proposed FETI-DP by using various numbers of processors. Table 2 reports the solution time for Eq. (6) as well as the total solution time. Besides, the speedups for the parallel computation are also provided in Table 2. Here, the speedup is defined by

where \( {T}_{N_p} \) denotes the total wall-clock time using N _p processors. It can be seen that the FETI-DP significantly improves the solution efficiency and exhibits good parallel speedup. For this large number of unknowns, the total memory usage of all the processors is only 57.2 GB.

Then, the effectiveness of the low-rank sparsification approach is examined. With the low-rank sparsification, the subdomain matrix can be factorized by data-sparse algorithm and stored as data-sparse matrices. The construction time and memory usage are only 18 s and 0.5 GB, while they are 67 s and 1.7 GB by conventional matrix algorithm. It can be seen that we get 72% time saving and 70% memory compression. Related to the memory usage, the subsequent MVPs can also get 70% time-saving.

Next, the FETI-DP is tested for the optical force calculation with the wavelength λ varying from 277 nm to 818 nm. In practice, the analyses of optical force under incident light of different wavelengths are often necessary for searching the plasmonic resonance wavelength, where drastic field enhancement occurs and the strongest optical force can be obtained. Two cases are considered with the nanosphere located at (0, 0, 20 nm) and (0, 0, − 20 nm). Figure 6 a and b plots the calculated optical forces exerted on the nanosphere for different λ . It can be seen that the maximum optical force occurs at λ  = 472 nm, which is the plasmonic resonance wavelength. The optical force at this resonance wavelength enhanced by nearly 40 times as against that at non-resonance wavelength. Moreover, the optical force always points to the dimer gap, as shown in Fig. 6, where the electric field intensity is strongest. It is also the direction of gradient force to trap the object. Figure 7 a and b shows the calculated electric field enhancement distributions at the non-resonance wavelength of λ = 300 nm and the resonance wavelength of λ = 472 nm, respectively. It can be seen that the electric field intensity has been increased by almost 250 times due to the plasmonic resonance effect.

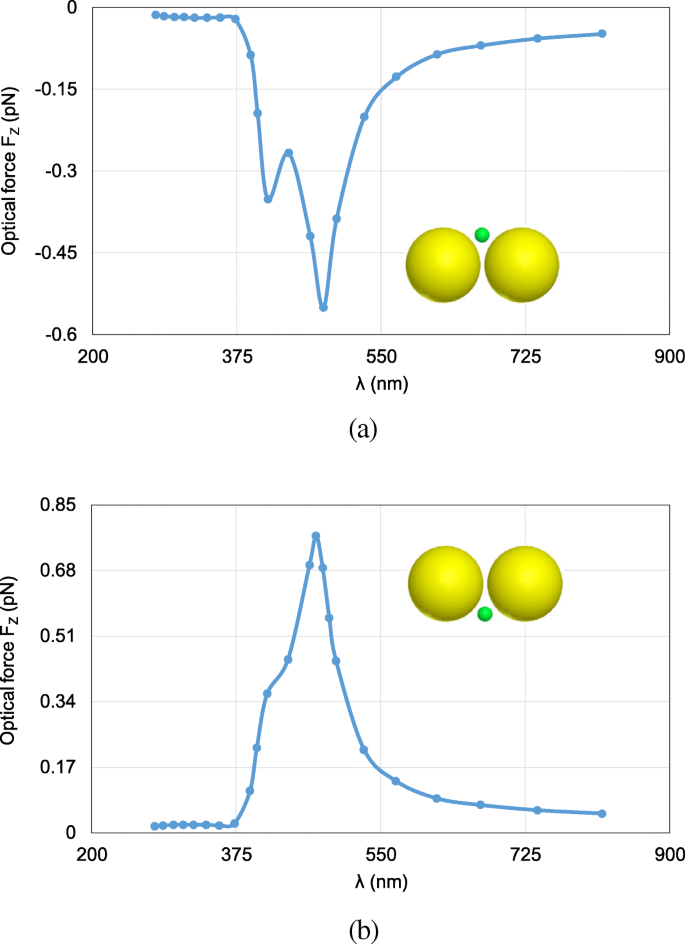
Calculated results of optical forces exerted on the nanosphere in the system of gold nanosphere dimer, varying with the wavelength λ of incident light. a The object nanosphere is located at (0, 0, 20 nm). b The object nanosphere is located at (0, 0, − 20 nm)

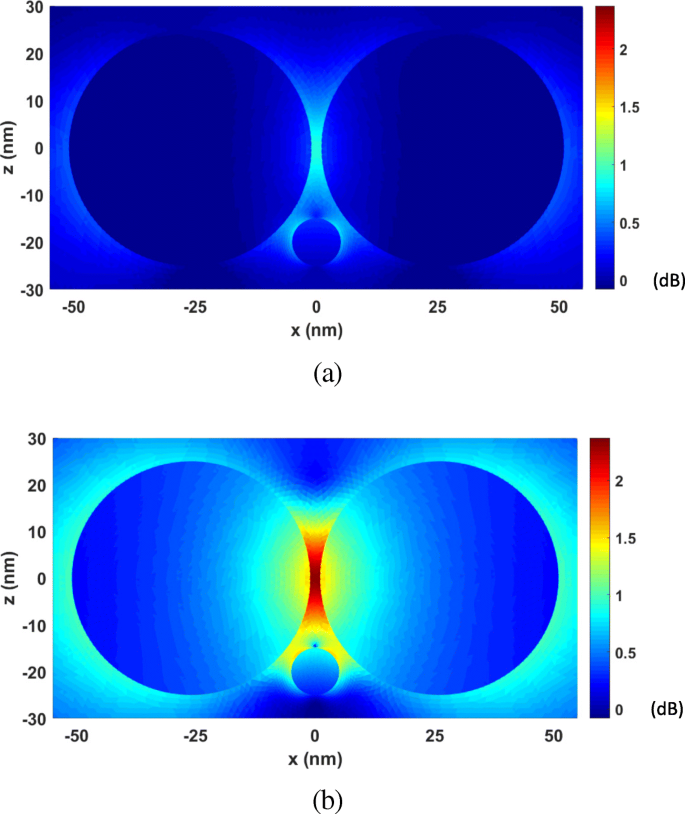
The electric field enhancement distributions on the xoz plane for the system of gold nanosphere dimer. a λ = 300 nm (non-resonance wavelength). b λ  = 472 nm (resonance wavelength)

Besides, the optical force and optical potential are calculated with the nanosphere moving from (0, 0, − 30 nm) to (0, 0, − 17 nm) along the z -Achse. Since the most typical and interesting behavior of trapping forces and potentials are those acting along z -direction, we here consider the axial trapping potential by integration along the z -Achse. Because the motion of the nanoparticle is restricted to one dimension, the definition of an optical potential is unambiguous from (16), even though the total optical force from (15) is non-conservative. As shown in Fig. 8 a, b, with the nanosphere moving to the dimer gap, the optical force and optical potential depth obviously increase. At the position of (0, 0, − 17 nm), an optical potential depth of 4.6 k _B T is produced, which is sufficient to overcome the Brownian motion in water to achieve stable optical trapping.

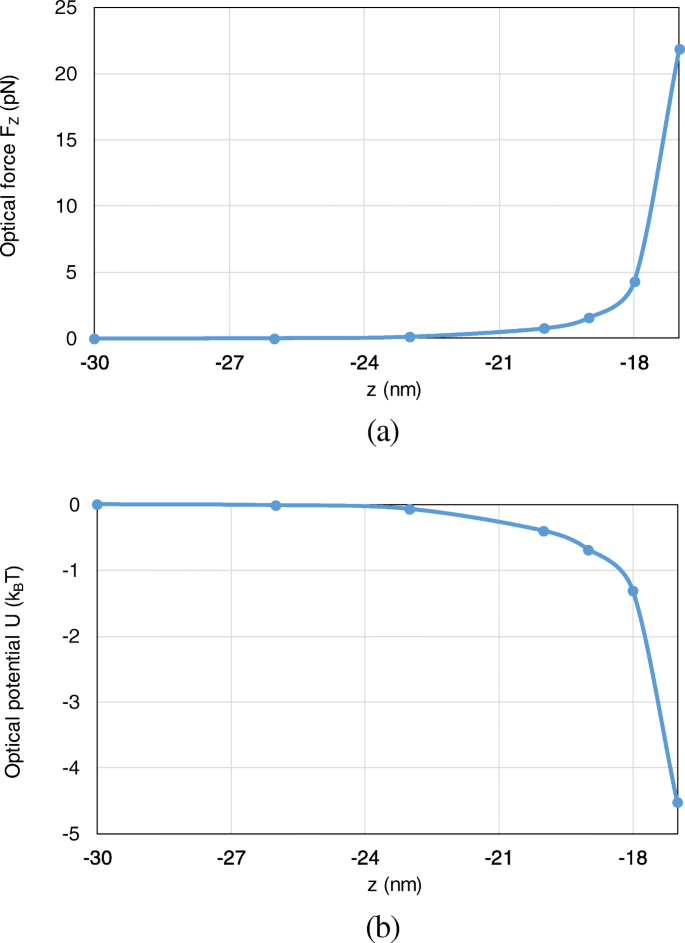
The optical forces and optical potentials exerted on the nanosphere in the system of gold nanosphere dimer, when the nanosphere moves from (0, 0, − 30 nm) to (0, 0, − 17 nm). a The optical forces. b The optical potentials

Finally, we test the effects of the dielectric substrate for this example. The optical forces are calculated with and without a substrate, respectively. For both two cases, the nanosphere is located at (0, 0, − 20 nm) and the incident wavelength is chosen as the resonance wavelength. For the case without substrate, the calculated result of the optical force is |F ₀ | = 0.769 pN. For the case with a substrate, the gold nanosphere dimer is put on a dielectric substrate with a thickness of 60 nm and a relative permittivity of ε _r = 2.25. The calculated result of the optical force is |F ₁ | = 0.761 pN. The relative error between these two results of optical forces is about 1.0 × 10 ⁻² , which is defined as |F ₁  − F ₀ |/|F ₀ |.

Gold Truncated Cone Dimer

The third example deals with the optical trapping of a gold nanosphere by using a gold truncated cone dimer. Figure 9 gives the configuration and dimensions of this system. The constitutive parameters of gold are taken from [32]. The dielectric substrate has a relative permittivity of ε _r  = 2.25. The surrounding medium is water with a relative refractive index of n  = 1.33. The incident light is plane wave with the power of 10 mW/μm ² , the electric field polarization direction is +x , and the incident direction is −z . The whole computational domain is divided into 32 subdomains and discretized by tetrahedral meshes, which leads to 3.1 × 10 ⁶ unknowns, including 1.3 × 10 ⁵ dual unknowns and 1227 corner unknowns.

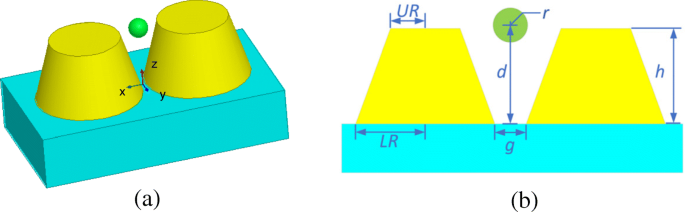
Configuration of an optical trapping system of a gold truncated cone dimer based on a dielectric substrate in water. a 3D view. b Front view and dimensions, where UR = 20 nm, LR = 30 nm, h = 35 nm, and g = 2 nm

First, we analyze the optical forces by changing λ from 277 nm to 818 nm. Figure 10 plots the calculated optical forces exerted on the nanosphere for different λ . The nanosphere is located at (0, 0, 35 nm). It can be seen that the maximum optical force occurs at λ  = 464 nm, which is the plasmonic resonance wavelength, and the optical force here is enhanced by nearly 30 times at non-resonance wavelength. Moreover, the total optical force always points to −z , as shown in Fig. 10, which is the direction of the gradient force. This confirms that the gradient force is greater than the scattering force, which is one of the conditions that the nanosphere can be stably trapped. Figure 11 a and b presents the calculated electric field distributions at the non-resonance wavelength of λ =300 nm and the resonance wavelength of λ = 464 nm, respectively. It can be seen that electric field intensity has been increased by almost 500 times due to the localized surface plasmon resonance.

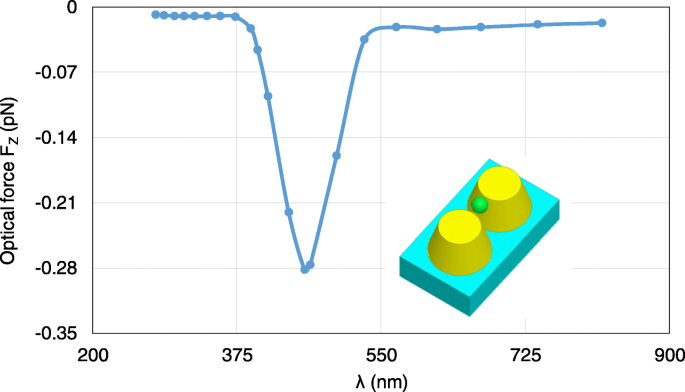
Calculated results of optical forces exerted on the nanosphere in the system of gold truncated cone dimer, varying with λ . The nanosphere is located at (0, 0, 35 nm)

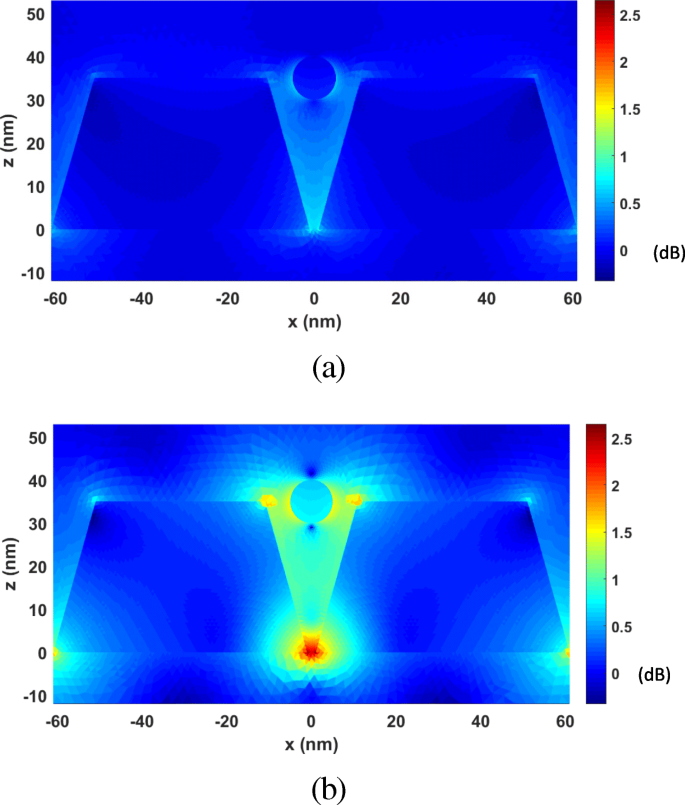
The electric field enhancement distributions on the xoz plane for the system of gold truncated cone dimer. a λ =300 nm (non-resonance wavelength). b λ =464 nm (resonance wavelength)

Then, the location of the nanosphere is changed to 0, 5, and 35 nm to observe the optical force. Figure 12 gives the calculated optical forces exerted on the nanosphere, where obvious y -component of optical force can be observed, while greater z -component of optical force exists. The total optical force still points to the position with the strongest electric field to trap the nanosphere.

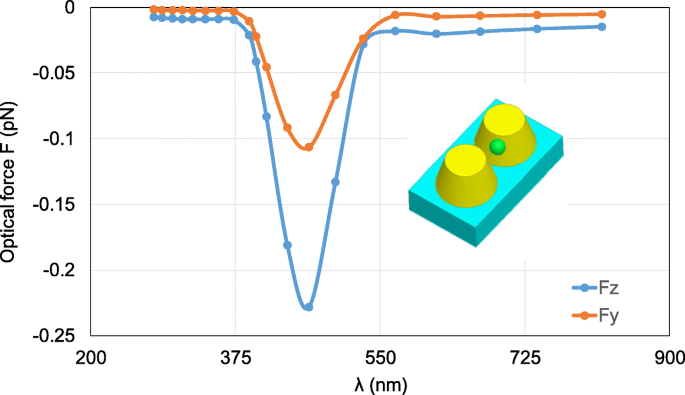
Calculated results of optical forces exerted on the nanosphere in the system of gold truncated cone dimer varying λ . The nanosphere is located at (0, 5 nm, 35 nm)

Furthermore, we analyze the optical potential with the nanosphere moving from (0, 0, 50 nm) to (0, 0, 20 nm) along the z -Achse. Here, we consider the axial trapping potential along z -direction, which restricts the motion of the nanoparticle to one dimension and leads to an unambiguous definition of optical potential. Both the optical force and potential are calculated. As can be observed from Fig. 13 a, b, with the nanosphere moving to the dimer gap, the optical force and the optical potential depth obviously increase. At (0, 0, 20 nm), an optical potential depth of 3.8 k _B T is obtained, which is sufficient to overcome the Brownian motion in water to achieve stable optical trapping.

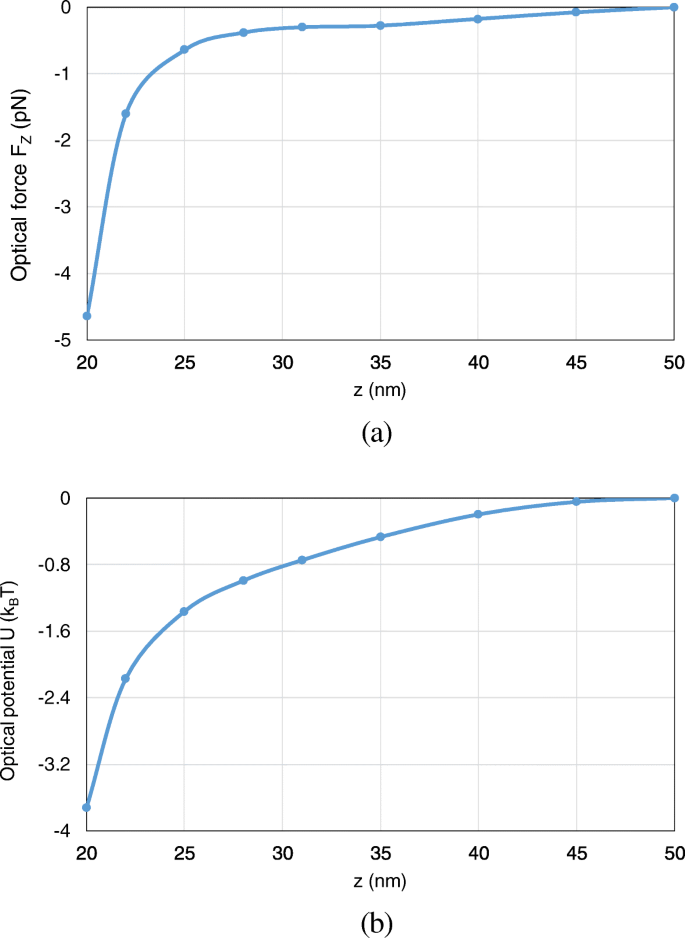
The optical forces and optical potentials exerted on the nanosphere in the system of gold truncated cone dimer, when the nanosphere moves from (0, 0, 50 nm) to (0, 0, 20 nm). a The optical forces. b The optical potentials

Finally, we test the computational costs of the FETI-DP by changing the number of unknowns from 1.0 million to 3.2 million based on different mesh size. In practice, the tests under different mesh density are usually necessary to meet different accuracy requirements. Such a large-scale complex problem brings great challenges to conventional numerical methods. However, the FETI-DP can easily handle this problem. Thirty-two processors are employed for the FETI-DP simulation, while each processor deals with a subdomain. Table 3 reports the computational costs of the FETI-DP. It can be seen that the FETI-DP exhibits high simulation efficiency and low memory requirement.

Schlussfolgerung

An FETI-DP method combined with low-rank sparsification is proposed for the prediction and analysis of optical trapping of metal nanoparticles. The proposed method provides fully decoupled subdomain problems, which converts a large-scale complex problem into a series of small-scale simple problems. It is well-suited for parallel computation and can significantly improve the efficiency of numerical simulation. Examples demonstrate that the proposed method exhibits excellent performance of large-scale computation and is well-suited for the fast and accurate simulation of optical trapping at nanoscale.

Verfügbarkeit von Daten und Materialien

Alle während dieser Studie generierten oder analysierten Daten sind in diesem Artikel enthalten.

Abkürzungen

ABC:

Absorbing boundary condition

DOF:

Degrees of freedom

FDTD:

Zeitbereich mit endlicher Differenz

FEM:

Finite-Elemente-Methode

FETI-DP:

Dual-primal finite element tearing and interconnecting

MST:

Maxwell stress tensor

MVP:

Matrix-vector product