Double-Gated Nanohelix als neuartiges abstimmbares binäres Supergitter
Zusammenfassung
Wir untersuchen theoretisch das Problem eines Elektrons, das auf eine Nanohelix zwischen zwei parallelen Gates begrenzt ist, die als geladene Drähte modelliert sind. Das Doppelgatter-Nanohelix-System ist ein binäres Übergitter mit Eigenschaften, die sehr empfindlich auf die Gate-Spannungen reagieren. Insbesondere weist die Bandstruktur bei bestimmten Kombinationen von Gatespannungen Energiebandübergänge auf, die zu quasi-relativistischen Dirac-ähnlichen Phänomenen führen könnten. Unsere Analyse für optische Übergänge, die durch linear und zirkular polarisiertes Licht induziert werden, legt nahe, dass eine Nanohelix mit Doppelgatter für vielseitige optoelektronische Anwendungen verwendet werden kann.
Einführung
Von den versteinerten spiralförmigen Schnecken, die der Erstautor in seiner Kindheit begeistert gesammelt hat, bis hin zur verschlungenen Struktur der DNA, die zweifellos einst diese prähistorischen Kreaturen definierte, ist die Helixgeometrie in der gesamten Natur verbreitet [1]. Inspiriert von den komplexen Funktionalitäten, die den Formen natürlich vorkommender Biomoleküle zugeschrieben werden [2–6], wird erwartet, dass andere Systeme mit helikalen Geometrien, die für die Nanotechnologie geeignet sind, eine reichhaltige Physik liefern und zu neuen Anwendungen beitragen werden. In den letzten drei Jahrzehnten haben bemerkenswerte Fortschritte in der Nanoherstellungstechnik zur Realisierung von Nanohelices in einer Vielzahl unterschiedlicher Systeme geführt, darunter InGaAs/GaAs [7], Si/SiGe [8], ZnO [9–11], CdS [ 12], SiO2 /SiC [13, 14] und reiner Kohlenstoff [15–20] sowie II-VI- und III-V-Halbleiter [21] (zum aktuellen Stand der Technik siehe Lit. [21–26]). Folglich wird in solchen Strukturen eine Fülle von Phänomenen erwartet, die von exotischen Transporteigenschaften wie topologisches quantisiertes Ladungspumpen [27, 28], Supraleitung [29] und Spinfilterung [30–32] bis hin zu molekularer und nanomechanischer dehnbarer Elektronik [33, 34] aufgrund von piezoelektrischen Effekten [35], Sensoranwendungen [36, 37], Energie- [38] und Wasserstoffspeicherung [39] und Feldeffekttransistoren [40, 41].
Die Faszination für Nanohelix-basierte Geräte rührt letztendlich von der inhärenten Periodizität her, die in der Topologie der Helixstruktur kodiert ist. Insbesondere führt das Aussetzen einer Nanohelix einem transversalen elektrischen Feld (senkrecht zur Helixachse) zu einem Übergitterverhalten wie der Bragg-Streuung von Elektronen an einem superperiodischen Potential, was zu einer Energieaufspaltung am Rand der Übergitter-Brillouin-Zone zwischen die niedrigsten Zustände, die durch das elektrische Feld linear abstimmbar sind [42, 43]. Dieses Verhalten kann zu Bloch-Oszillationen und negativer differentieller Leitfähigkeit führen [44, 45] und kann den spinpolarisierten Transport durch Helices betonen [31, 46] sowie zu einer Verbesserung des Circulardichroismus, die für nanophotonische chiroptische Anwendungen nützlich ist [47]. Dieses System stellt ein unäres Übergitter dar und eröffnet weiterhin die Möglichkeit, Nanohelices entweder als Tunneldioden oder Gunn-Dioden zur Frequenzvervielfachung, Verstärkung und Erzeugung oder Absorption von Strahlung im gelobten Terahertz-Bereich zu verwenden [48–51]. Während das prototypische Übergitter meist in Heterostrukturen aus alternierenden Halbleiterschichten mit unterschiedlichen intrinsischen Bandlücken realisiert wird, werden die Parameter des Nanohelix-Übergitters vollständig durch das äußere Feld gesteuert. Im Gegensatz dazu sind die Formen der ehemals konventionellen Übergitterpotentiale spezifisch für die Heterostruktur und bieten trotz ihrer Robustheit eine begrenzte Manipulationsfähigkeit im Verlauf ihrer Ausnutzung ohne die Verwendung großer externer Felder. Daher liegt der Reiz bei der Verwendung von Nanohelices als Supergitter stattdessen in ihrer größeren Abstimmbarkeit.
Andererseits kann man mit heterostrukturierten halbleitenden Übergittern (oder auch photonischen Übergitterstrukturen [52–55] und kalten Atomen in optischen Gittern [56, 57]) kompliziertere Übergitter-Elementarzellen jenseits des einfachen Quantentopfs erzeugen, der durch die elektrisches Feld entlang der Helix. Auch die Erweiterung auf ein binäres Übergitter [58–60] (wobei sich die Elementarzelle durch zwei unterschiedliche Quantensenken und/oder Barrieren auszeichnet) verspricht eine reiche Auswahl an Physik wie Bloch-Zener-Oszillationen [61], die wiederum dazu beitragen können bis hin zu abstimmbaren Strahlteiler- und Interferometeranwendungen [62]. Daher wäre es höchst wünschenswert, die externe Feldabstimmbarkeit eines Nanohelix-basierten Übergitters mit der überlegenen Funktionalität eines binären Übergitters zu kombinieren.
Im Folgenden beschreiben wir ein solches System mit einer Nanohelix, die zwischen zwei parallel gesteuerten geladenen Drähten positioniert ist, die auf die Helixachse ausgerichtet sind. Wir stellen uns die Anwendung eines zusätzlichen transversalen elektrischen Feldes vor und zeigen theoretisch, dass das Gate- und feldsteuerbare Potential ein binäres Übergitter entlang der eindimensionalen Helix bildet.
Methoden
Theoretisches Modell
Beginnen wir damit, den Fall einer kreisförmigen Einelektronen-Halbleiter-Nanohelix mit N . zu untersuchen Umdrehungen mit Radius R , Tonhöhe p , und Gesamtlänge L =Np . Die Nanostruktur ist zwischen zwei parallelen Gates positioniert, die als geladene Drähte modelliert sind, wobei ihre Helixachse entlang des z . ausgerichtet ist -Achse und mit Achse und Toren liegen alle auf derselben Ebene, wie in Abb. 1 dargestellt. Zusätzlich betrachten wir ein externes transversales elektrisches Feld senkrecht zur Ebene der Torachse \(\mathbf{E}=E_{\bot}\ Hut {\mathbf{y}}\), mit dem die Reflexionssymmetrie des Potentials oberhalb der Ebene gegenüber dem Potential unterhalb der Ebene gebrochen werden kann. Wir arbeiten in spiralförmigen Koordinaten, die parametrisch über r . beschrieben werden =(x,y ,z )=(R cos(s φ ),R Sünde(s φ ),ρ φ ), wobei die dynamische Winkelkoordinate φ =z /ρ hängt nur vom Abstand entlang der Helixachse ab mit ρ =p /2π , und s =±1 zeigt eine links- bzw. rechtsgängige Helix an. In dieser Arbeit betrachten wir eine linkshändige Helix s =1. Im Rahmen des effektiven Massenmodells ist das Energiespektrum ε ν der ν Der Eigenzustand eines Elektrons in einer Helix unter dem Einfluss solcher externen Potentiale ergibt sich aus der Schrödinger-Gleichung:
$$ -\thinspace \frac{\hbar^{2}}{2M^{*}\rho^{2}}\frac{d^{2}}{d\varphi^{2}}\psi_{\ nu} +\left[V_{g} (\varphi) + V_{\bot} (\varphi) \right]\psi_{\nu} =\varepsilon_{\nu} \psi_{\nu} $$ (1 )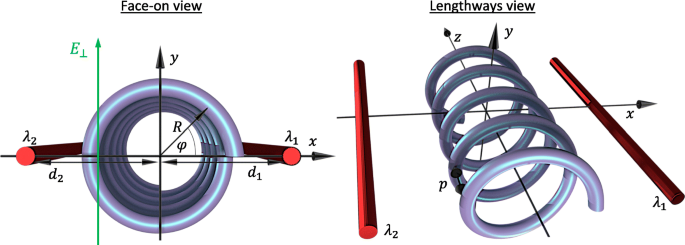
Diagramm der Geometrie und Parameter des Systems aus Sicht- und Längsperspektive. R ist der Helixradius und d 1 und d 2 sind die Abstände der geladenen Drähte von der Helixachse mit Ladungsdichten λ 1 und λ 2 , bzw. Die Raumkoordinate φ beschreibt die Winkelstellung auf der Helix von Angesicht zu Angesicht und bezieht sich auf die z -koordinieren über φ =2π z /p mit p die Steigung der Helix. Ein transversales elektrisches Feld E ⊥ wird parallel zum y . angewendet -Achse
wobei wir die effektive Elektronenmasse M . geometrisch renormiert haben e zu M ∗ =M e (1+R 2 /ρ 2 ), um alles in Form der Koordinate entlang der Helixachse auszudrücken (denken Sie daran, dass φ =z /ρ ), was für externe Potenziale bequemer ist. Hier, V ⊥ (φ )=−eE ⊥ R Sünde(φ ) ist der Beitrag des transversalen elektrischen Feldes, das entlang des y . gerichtet ist -Achse mit V ⊥ (π /2)<0. Das Potential der Gates beträgt V g (φ )=−e [Φ 1 (φ )+Φ 2 (φ )] mit dem elektrostatischen Potential, das ein Elektron entlang der Helix aufgrund eines einzelnen geladenen Drahtes spürt, gegeben durch Φ ich (φ )=−λ ich k ln(r ich /d ich ). Hier, ich =1,2 bezeichnet die Drähte, λ ich die lineare Ladungsdichte auf einem Draht und \(k =1/2\pi\tilde{\epsilon}\) mit \(\tilde{\epsilon}\) die absolute Permittivität. Der senkrechte Abstand einer Testladung von einem bestimmten Draht ist gegeben durch \(r_{i}=[d^{2}_{i}+R^{2} + 2(-1)^{i}d_{i }R\cos (\varphi)]^{1/2}\), mit d ich bezeichnet den entsprechenden Abstand des Drahtes zur Achse der Helix. Wir haben definiert, dass das Null-Gate-induzierte Potential entlang der Achse der Helix liegt. Das gesamte eindimensionale Potenzial V T (φ )=V g (φ )+V ⊥ (φ ) ist eindeutig periodisch V T (φ )=V T (φ +2π n ) mit Periode 2π im Allgemeinen (entspricht der Periode von p bezüglich der Koordinate z ). Diese Periode ist deutlich größer als der interatomare Abstand und führt zu typischen Übergittereffekten. Dieser Buchstabe unterscheidet sich von einer Nanohelix in einem transversalen elektrischen Feld (das mit V . reproduziert werden kann T (φ )=V ⊥ (φ ) hier) hauptsächlich durch Manipulation der wiederholten Elementarzelle des Übergitters über das Double-Gate-Potential V g (φ ). Das Limit nehmen p →0, kehren wir zum Teilchen auf einem Ringbild zurück, das zwei elektrostatischen Toren ausgesetzt ist [63, 64]. Näherung machen R /d ich ≪1, können wir V erweitern g (φ ) bis zur zweiten Ordnung in cos(φ ) und nach Transformation von Gl. 1 in dimensionslose Form kommen wir zu
$$ {\begin{ausgerichtet} \frac{d^{2} \psi_{\nu}}{d\varphi^{2}}+\left[\epsilon_{\nu} + 2A_{g}\cos( \varphi) + 2B_{g}\cos(2\varphi) + 2C_{\bot} \sin(\varphi) \right]\psi_{\nu} =0, \end{aligned}} $$ (2)mit den Größen in Einheiten der Energieskala \(\varepsilon_{0}(\rho) =\hbar^{2} / 2 M^{*} \rho^{2}\) definiert als
$$\begin{array}{@{}rcl@{}} A_{g} &=&\beta\frac{\left(d_{1}^{2} +R^{2}\right)}{ d_{1} R}(1-\gamma), \qquad B_{g} =\frac{\beta}{2}\left(1+\frac{\lambda_{1}}{\lambda_{2}} \gamma^{2}\right), \\ C_{\bot} &=&e E_{\bot} R /2\varepsilon_{0}(\rho), \qquad \qquad \qquad \; \epsilon_{\nu} =\frac{\varepsilon_{\nu}}{\varepsilon_{0}(\rho)}. \end{array} $$ (3)Hier gilt \(\beta =ek d_{1}^{2} R^{2} \lambda_{1} /2\left (d_{1}^{2} +R^{2}\right)^ {2}\varepsilon_{0}(\rho)\) charakterisiert den Beitrag von Gatter 1, während der Asymmetrieparameter \(\gamma =\lambda_{2} d_{2} \left(d_{1}^{2 } +R^{2}\right)/\lambda_{1} d_{1} \left (d_{2}^{2} + R^{2}\right)\) charakterisiert den relativen Beitrag von Gatter 2 , mit γ =1 entspricht gleichen Gate-Beiträgen zum Potential (was zu A g =0). Es sollte beachtet werden, dass die unvermeidliche Asymmetrie, die durch die Schwierigkeit bei der Aufrechterhaltung von d . verursacht wird, 1 =d 2 kann durch Manipulation von λ . kompensiert werden 1 und λ 2 . In diesem Brief beschränken wir uns darauf, γ . zu berücksichtigen ≤1 (das ist |Φ 1 |>|Φ 2 |) da der Asymmetrieparameter größer als eins ist, kann durch einfachen Austausch der Indizes, die die Tore beschriften, und entsprechendem Perspektivwechsel auf ein äquivalentes System unterhalb von eins abgebildet werden φ →φ ±π . Wir werden auch nur C . berücksichtigen ⊥ ≥0 wegen der Symmetrie des negativen C ⊥ bezüglich einer solchen Koordinatenverschiebung in φ , und A g ≥0, B g >0 (d.h. nur positive Ladungsdichten an den Drähten β>0), da jede potentielle Landschaft mit negativ geladenen Gates mit der richtigen Kombination von Parametern von positiv geladenen Gates reproduziert werden kann. In Abb. 2 tragen wir das dimensionslose Potential V T (φ )/ε 0 (ρ ), mit der Stärke des π -periodische Potentialkomponente fest auf B g =0,2, für mehrere Kombinationen der Störungsparameter mit doppelter Periode A g und C ⊥ . Wir sehen, dass das gesamte externe Potenzial entlang φ . ein binäres Übergitter induziert , mit einem doppelten Quantentopf (DQW) als Elementarzelle blau hervorgehoben. Dies kann qualitativ unterschiedliche Formen annehmen, indem die relativen Gate-Beiträge manipuliert werden γ und transversales elektrisches Feld E ⊥ . Die Elementarzelle ist im Wesentlichen eine einzelne Wanne unter äquivalenten Gate-Beiträgen (γ =1) und kein transversales elektrisches Feld E ⊥ =0 (wie in Abb. 2a für A g =C ⊥ =0). E reparieren ⊥ =0, mit einem stärkeren Beitrag von Gate 1 (γ <1), wird die Elementarzelle zu einem DQW mit unterschiedlichen Well-Minima und degenerierten Barriere-Maxima (Abb. 2b wobei A g =0,1 und C ⊥ =0). Im Gegensatz dazu sind symmetrische Gatebeiträge (γ =1) in einem von Null verschiedenen elektrischen Feld E ⊥ ≠0 (Abb. 2c mit A g =0 und C ⊥ =0,1). Kombinieren asymmetrischer Gate-Beiträge (γ <1) mit E ⊥ ≠0 erzeugt eine DQW mit unterschiedlichen Potentialtopf-Minima und unterschiedlichen Barrieren (wie in Abb. 2d zu sehen, wo beide A g =C ⊥ =0,1). Dies führt zu einem qualitativ unterschiedlichen und reichhaltigen Verhalten, wie wir in den folgenden Abschnitten sehen werden.
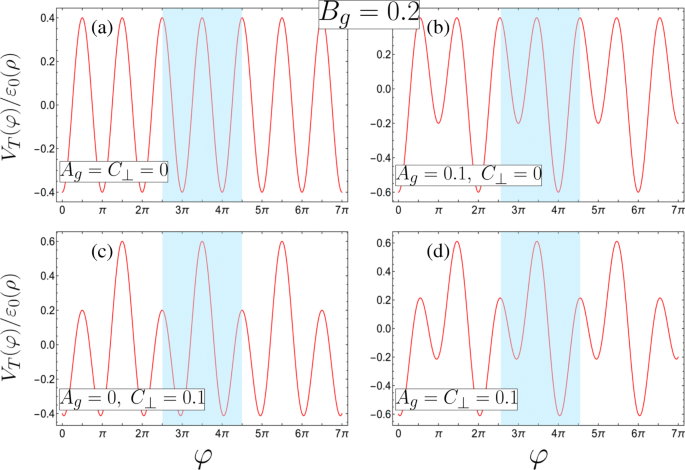
Die vier möglichen Übergitterpotentialkonfigurationen mit den blau hervorgehobenen Elementarzellen (definiert durch die dimensionslosen Parameter, siehe Gl. 3 für die entsprechenden Anforderungen der physikalischen Parameter, und alle mit B g =0,2). a Ein unäres Übergitter mit entarteten Minima und Maxima in der Elementarzelle (A g =C ⊥ =0). b –d Binäre Übergitter gebildet aus entweder b eine asymmetrische DQW mit unterschiedlichen Minima und interner Reflexionssymmetrie um jedes Minima aufgrund entarteter Maxima (A g =0,1, C ⊥ =0), c ein symmetrisches DQW mit nur entarteten Minima (A g =0, C ⊥ =0,1) oder d eine asymmetrische DQW mit unterschiedlichen Minima und Maxima (A g =C ⊥ =0,1)
Lösungen als unendliche Matrix
Lösungen zu Gl. 2 finden Sie in Bezug auf die Bloch-Funktionen
$$ \psi_{n,q}(\varphi)=(2\pi N \rho)^{-\frac{1}{2}}e^{iq \varphi}\sum_{m} c^{( n)}_{m,q} e^{im \varphi}, $$ (4)wo das q =k z ρ ist die dimensionslose Form des Quasiimpulses des Elektrons k z entlang der Achse der Helix, n gibt das Teilband an, und der Vorfaktor ergibt sich aus der Normalisierung in Bezug auf φ :\(\rho\int_{0}^{2\pi N}|\psi_{n,q}(\varphi)|^{2} d\varphi =1\). Wir nutzen die Orthogonalität der Exponentialfunktionen, indem wir den resultierenden Ausdruck mit \(e^{im^{\prime} \varphi}/2\pi\) multiplizieren und bezüglich φ . integrieren , wo m ′ ist eine ganze Zahl, so dass wir auf eine unendliche Menge simultaner Gleichungen für die Koeffizienten \(c^{(n)}_{m,q}\),
$$ {\begin{ausgerichtet} &\left[(q+m)^{2}-\epsilon_{n}\right]c^{(n)}_{m} - \left(A_{g} - i C_{\bot} \right)c^{(n)}_{m-1} - \left(A_{g} + i C_{\bot} \right)c^{(n)}_{m +1}\\ &\quad- B_{g}\left(c^{(n)}_{m+2}+c^{(n)}_{m-2} \right)=0, \ end{ausgerichtet}} $$ (5)wo zur Verdeutlichung das q -Tiefgestellte Notation wurde weggelassen, ε n,q ε n und \(c_{m}^{(n)}\äquiv. c_{m,q}^{(n)}\). Gleichung 5 stellt eine unendliche fünfeckige Matrix dar, bei der offensichtlich ist, dass das System in q . periodisch ist , und wir können unsere Betrachtungen auf die erste Brillouin-Zone beschränken, die durch − 1/2≤q . definiert ist 1/2. In Abwesenheit des Übergitterpotentials A g =B g =C ⊥ =0, die Eigenwerte werden dann aufgezählt durch m gegeben von ε m =(m +q ) 2 und wir erkennen m die Drehimpulsquantenzahl zu sein, die einem freien Elektron auf einer Helix zugeordnet ist. Wir sehen aus Gl. 5 dass wenn A g =C ⊥ =0 nur Zustände mit Δ m =±2 gemischt, wobei die Bildung einer DQW-Elementarzelle mit unterschiedlichen Well-Minima bzw. -Barrieren, erreicht über A g ≠0 und/oder C ⊥ ≠0, mischt auch Zustände mit Δ m =± 1. Interessanterweise ist das System eines Elektrons auf einer Helix unter einem externen transversalen Potential (das sich über eine Umdrehung der Helix ändert) mathematisch äquivalent zu einem Elektron auf einem Quantenring, das von einem Magnetfeld durchdrungen wird und einem Potential mit die gleiche funktionale Form variiert entlang der Winkelkoordinate; z.B. siehe Ref.-Nr. [65–67] oder vergleichen Sie zum Beispiel Lit. [42–45] mit [68–70]. Bei einem Ring die Rolle von q hier wird vom magnetischen Fluss aufgenommen. Daher ist genau die gleiche Analyse in dieser Arbeit auf das Problem eines Doppelgatter-Quantenrings [63–66] anwendbar, wenn der Ring von einem magnetischen Fluss durchdrungen wird.
Abschneiden und numerische Diagonalisierung der Matrix entsprechend Gl. 5 bietet die n Subband-Eigenenergien ε n und Koeffizienten \(c_{m}^{(n)}\) für jeden Wert von q . Wir wenden eine Kürzung bei |m . an |=10, sicher im Wissen, dass jede Zunahme der Matrixgröße keine merkliche Änderung in den niedrigsten Teilbändern ergibt.
Ergebnisse und Diskussion
Doppelgatter-Nanohelix-Bandstruktur
In Abb. 3 tragen wir die Energiedispersion der untersten Bänder für mehrere Parameterkombinationen auf. Abhängig von der Form des Übergitters finden wir eine bemerkenswerte Vielfalt im Dispersionsverhalten, und für einige spezifische Kombinationen von Parametern entdecken wir Energiebandübergänge für bestimmte Teilbänder entweder am Rand der Brillouin-Zone (Abb. 3a und c) oder am Zentrum der Brillouin-Zone (Abb. 3b und d).
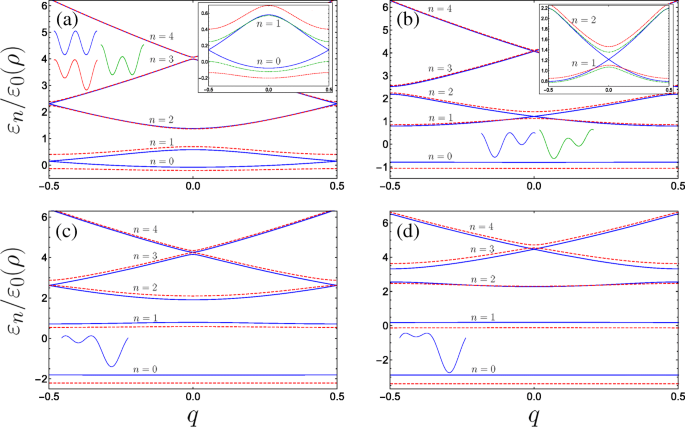
Bandstruktur für Doppelgatter-Nanohelix-System für verschiedene Kombinationen der dimensionslosen Parameter (mit B g =0,4 durchgehend fixiert):a Durchgehende blaue (gestrichelte rote) Diagramme A g =0 &C ⊥ =0 (A g =0,2 &C ⊥ =0), der Einschub zeigt zusätzlich das Verhalten der unteren beiden Teilbänder unter dem transversalen elektrischen Feld mit A g =0 &C ⊥ =0,2 als punkt-gestrichelte grüne Kurve. b Durchgehende blaue (gestrichelte rote) Diagramme A g =0,63 &C ⊥ =0 (A g =0.8 &C ⊥ =0) wobei die blaue Kurve den ersten Resonanzvorfall (siehe Text) mit sich kreuzenden Energiebändern im Zentrum der Brillouin-Zone darstellt, vergleicht der Einschub das Verhalten der unteren angeregten zwei Teilbänder mit dem Fall, bei dem A g =0,63 &C ⊥ =0,2 als punkt-gestrichelte grüne Kurve. c Durchgehende blaue (gestrichelte rote) Diagramme A g =1,26 &C ⊥ =0 (A g =1,5 &C ⊥ =0) wobei die blaue Kurve den zweiten Resonanzvorfall mit Energielücken darstellt, die sich am Rand des Brillouin für höhere Bänder schließen. d Die dritte Resonanz und die höheren Subband-Minigaps schließen sich in der Mitte, wobei durchgehend blau (rot gestrichelt) A ist g =1,9 &C ⊥ =0 (A g =2,2 &C ⊥ =0). Die Elementarzellenformen sind skizziert, n zählt die Bänder auf, und die Achsen der Einschübe sind die gleichen wie in den Hauptdiagrammen
Doppelte Periodenstörung im unteren Feld
Wenn A g =C ⊥ =0, bildet die Elementarzelle zwei äquivalente Quantentöpfe, und folglich entsteht das Auftreten von Bandenpaaren, die sich an den Rändern der Brillouin-Zone berühren, natürlich. Tatsächlich halbiert die Elementarzelle die Übergitterperiode und führt zu einer Verdoppelung der Brillouin-Zone − 1≤q 1. Wir würden dann das übliche unäre Übergitter-Banddiagramm beobachten, bei dem die Bandlücke zwischen dem Grund- und dem ersten Band bei q =1 wird hier über die Bandlücke zwischen n . angegeben =1 und n =2 bei q =0 und wäre linear in B g aus der Störungstheorie. Dennoch präsentieren wir eine Beschreibung der Bandstruktur bei |q |=1/2 im DQW-Elementarzellenbild unter Verwendung der Matrixalgebra im Anhang. Wie im Einschub von Fig. 3a zu sehen ist, öffnet die Einführung eines der Doppelperiodenpotentialterme eine Bandlücke am Rand der Brillouin-Zone. Die Elementarzelle aus symmetrischen Gatterbeiträgen (A g =0) behält die Form einer symmetrischen DQW bei Anwendung eines transversalen Feldes C ⊥ senkrecht zur Helix-Gate-Achse, wobei eine Potentialbarriere gegenüber der anderen modifiziert ist (angezeigt durch die grüne DQW-Skizze in Abb. 3a). Während C ⊥ eine Bandlücke öffnet, ist die Änderung der Dispersion deutlich weniger empfindlich als bei einer ähnlichen Größe von A g . Dies ist an der kleineren Bandlücke bei |q . zu sehen |=1/2 für die strichpunktierte grüne Linie im Einschub von Abb. 3a (mit A g =0 und C ⊥ =0,2) verglichen mit der größeren Lücke für die gestrichelte rote Kurve (die für A . gilt) g =0,2 und C ⊥ =0). Um dieses Verhalten zu unterstreichen, zeigt Abb. 4a die Größe der Energielücke bei |q |=1/2 zwischen den beiden niedrigsten Teilbändern \(\Delta\varepsilon_{01}^{(q=1/2)}/\varepsilon_{0}(\rho)\) für festes B g =0,25 als Funktion von beiden C ⊥ (mit A g =0) und A g (mit C ⊥ =0), als punkt-gestrichelte grüne bzw. gestrichelte rote Kurve. Bei einem transversalen elektrischen Feld von null und asymmetrischen Gate-Potentialen (C ⊥ =0 und A g ≠0), ist die Elementarzelle dann eine asymmetrische DQW, allerdings mit interner Reflexionssymmetrie um jedes Well-Minima aufgrund der äquivalenten Barrieren. Wir können dann die höhere Empfindlichkeit der Bandlücke gegenüber der Änderung von A . verstehen g unter Berücksichtigung der Eigenschaften der isolierten DQW-Elementarzelle, aus der das Übergitter aufgebaut ist. Mit A g =C ⊥ =0, bei |q |=1/2 (die Kanten der Brillouin-Zone) unterscheiden sich die aus dem Grund- und ersten angeregten Zustand der isolierten DQW-Elementarzelle gebildeten Bloch-Zustände (siehe blaues Schema und begleitende Wellenfunktionen in Abb. 4a) nur um an willkürliche Phase. Diese Situation entspricht der lückenlosen blauen Dispersionskurve von Fig. 3a. Wie in Abb. 4a über die grüne DQW-Skizze schematisch dargestellt, C ⊥ verringert die relativen Maxima einer der Barrieren in Bezug auf die andere, während die DQW-Minima entartet bleiben. Daher wird der Grundzustand des isolierten DQW nur durch eine leichte Zunahme seiner Wahrscheinlichkeitsverteilung unter der kleineren Potentialbarriere modifiziert (was nur eine geringe Energieabsenkung im Vergleich zum ungestörten Grundzustand ergibt), und der erste angeregte Zustand bleibt im Wesentlichen unverändert da sein Knoten unter der Barriere positioniert ist und nicht empfindlich auf seine Variation reagiert. Die aus diesen Grund- und ersten angeregten Zuständen aufgebauten Bloch-Zustände am Rande der Brillouin-Zone unterscheiden sich vom ungestörten Fall nur durch den reduzierten Zerfall der Grundzustands-Wellenfunktion unter der kleineren Barriere (vergleiche die grüne DQW mit der blauen DQW in Abb. 4a). A ändern g manipuliert die relativen Positionen der DQW-Minima, während die Barrieren degeneriert bleiben. Die Wellenfunktionen der beiden niedrigsten isolierten DQW-Zustände unterscheiden sich erheblich, wobei der Grundzustand zum lokalisierten Grundzustand der singulären tieferen Wanne tendiert und der erste angeregte Zustand zum lokalisierten Grundzustand der flacheren Wanne tendiert [71]. Während die Störung die Energie des Grundzustands senkt, wird die Energie des ersten angeregten Zustands vergleichsweise erhöht, da die Minima der flacheren Wanne mit zunehmendem A . nach oben verschoben werden g , was zu einer höheren Empfindlichkeit der Bandlückengröße in Bezug auf A . führt g . Insbesondere findet sich ein Teilchen im Bodenteilband mit zunehmendem A . schnell in der Nähe des Bodens der tiefsten Potentialmulde wieder g . Das unterste Band nähert sich daher einem dispersionsfreien Flachband schneller als im Fall des transversalen Felds, was zu elektronischen Instabilitäten und starken Wechselwirkungseffekten führen kann, die die hohe Zustandsdichte begleiten [72].
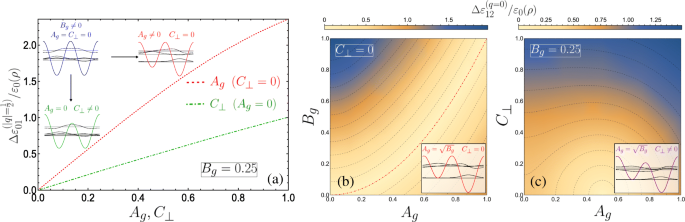
a Bandlückengröße zwischen Masse und ersten Teilbändern als Funktion von A g (C ⊥ ) rot gestrichelt (grün gepunktet), hier B g =0,25. Die Diagramme zeigen den Einfluss der verschiedenen Störungen auf die isolierte DQW-Elementarzelle und Eigenzustände. b –c Bandlückengröße zwischen ersten und zweiten Teilbändern, angegeben über eine 2D-Dichtedarstellung als Funktion von; b A g und B g für C ⊥ =0 und c A g und C ⊥ mit festem B g =0,25. b Benachbarte Isoenergie-Konturlinien zeigen eine Differenz von 0,17 an, wobei eine Lücke von Null durch die strichpunktierte rote Linie für \(A_{g}=\sqrt {B_{g}}\) gegeben ist, während c die Differenz beträgt 0.13 mit Nullspalt im Zentrum der kleinsten Halbkreiskontur (0.5,0). Die Diagramme skizzieren die isolierten DQW und Eigenzustände. Zwischen den s findet keine Hybridisierung statt -wie und p -ähnliche resonante lokalisierte einzelne Brunnenzustände in b , tut es aber in c aufgrund des elektrischen Felds, das eine Barriere in Bezug auf die andere ändert
Energiebandübergänge
Es ist bemerkenswert, dass, wenn wir C . beibehalten, ⊥ =0 und A increase erhöhen g , während anfangs alle Entartungen aufgehoben sind, kreuzen sich nachfolgende Bänder höherer Energie abwechselnd zwischen der Mitte und dem Rand der Brillouin-Zone (beobachten Sie das Verhalten der abwechselnd blauen und gestrichelten roten Kurven von Abb. 3a bis d). Physikalisch können wir die verschwindende Bandlücke als Wechselwirkungen der lokalisierten Wellenfunktionen in der Elementarzelle verstehen. Wenn das asymmetrische DQW-Potential so ist, dass der Grundzustand in der flacheren Wanne (s -ähnliches Orbital) ist in Resonanz mit dem ersten angeregten Zustand im tieferen Well (p -ähnliches Orbital), bei q =0 aufgrund der Reflexionssymmetrie um das Zentrum beider Vertiefungen verhindern die entgegengesetzten Paritäten dieser Zustände die übliche Tunnelkopplung zwischen ihnen, und folglich fallen die aus diesen Orbitalen konstruierten angeregten Zustände zusammen (blaue Kurven in Abb. 3b). Das erinnert an sogenannte s −p Resonanzen in optischen Gittern [73, 74]. Umgekehrt gilt, wenn die Parameter so sind, dass der lokalisierte Grundzustand in der flachen Wanne mit einem angeregten Zustand in der tieferen Wanne mit derselben Parität resonant ist, dann bei |q | =1/2, unterdrückt die Anwesenheit der Bloch-Phase die übliche Hybridisierung zwischen diesen beiden benachbarten lokalisierten Wannenzuständen vollständig und die Bandlücke wird geschlossen (wie in Fig. 3c für die Resonanz des Bodens mit dem zweiten angeregten Zustand gezeigt). In der Sprache der Streuung vom periodischen Potential; die Bandlücke ist aufgrund der vollständigen destruktiven Interferenz der Bragg-Streuamplituden zweiter Ordnung aus dem cos(φ ) Potential und Streuamplituden erster Ordnung aus dem cos(2φ ) Potenzial [75–77].
Wir können die Existenz von Energiebandübergängen (für ein transversales elektrisches Feld von null) sowohl im Zentrum als auch am Rand der Brillouin-Zone quantitativ zeigen, indem wir zu Gl. 2, die als Whittaker-Hill-Gleichung erkennbar ist, wenn C ⊥ =0 [78]. Die Bloch-Funktionen Gl. 4 gehorchen verdrehten periodischen Randbedingungen ψ n,q (φ +2π )=exp(2π iq )ψ n,q (φ ). Insbesondere wenn q =0 formale Lösungen zu Gl. 2 sind 2π -periodisch, während bei |q |=1/2 Lösungen sind 2π -antiperiodisch (also suchen wir nach 4π -periodische Lösungen). Insbesondere Gl. 2 mit C ⊥ =0 lässt sich auf die quasi-exakt lösbare Ince-Gleichung [79, 80] abbilden, indem man die Wellenfunktion als Produkt der asymptotischen Lösung von Gl. 2 und eine unbekannte Funktion \(\psi_{n,q}(\varphi) =\exp \left [ -2\sqrt {B_{g}}\cos(\varphi)\right ]\Phi_{n, q}(\varphi)\), so dass
$$ \frac{d^{2} \Phi_{n,q}}{d\varphi^{2}} + \frac{\xi}{2} \sin(\varphi)\frac{d\Phi_{ n,q}}{d\varphi} +\frac{1}{4}\left[ \eta_{n,q} - p\xi\cos(\varphi) \right]\Phi_{n,q} =0, $$ (6)wobei wir die Hilfsparameter \(\xi =8\sqrt {B_{g}}\) definiert haben, η n,q =4ε n,q +8F g , \(-p \xi =8A_{g}+8\sqrt {B_{g}}\), und Φ n,q (φ ) behält die notwendige verdrehte Periodizität jeder Lösung bei (beachten Sie, dass hier p ist nicht die Helixsteigung). Da das Übergitterpotential hier invariant ist unter der Transformation φ →− φ , die Lösungen für q =0 und q =1/2 kann in ungerade und gerade Parität getrennt werden, sodass die folgende trigonometrische Reihe
$$ \Phi_{n,0}^{(e)}(\varphi) =\sum_{l=0}a^{(n)}_{l}\cos(l\varphi), $$ (7a .) ) $$ \Phi_{n,0}^{(o)}(\varphi) =\sum_{l=0}b^{(n)}_{l+1}\sin[(l+1)\ varphi], $$ (7b) $$ \Phi_{n,\frac{1}{2}}^{(e)}(\varphi) =\sum_{l=0}\widetilde{a}^{( n)}_{l}\cos\left[\left(l+\frac{1}{2}\right)\varphi\right], $$ (7c) $$ \Phi_{n,\frac{1} {2}}^{(o)}(\varphi) =\sum_{l=0}\widetilde{b}^{(n)}_{l+1}\sin\left[\left(l+\frac {1}{2}\right)\varphi\right], $$ (7d)decken die formalen Lösungen ab, und wir stellen fest, dass Lösungen für q =−1/2 sind die gleichen wie für q =1/2. Hier die hochgestellten e und o bezeichne die Funktionen als gerade bzw. ungerade und n bezieht sich immer noch auf die n Subband, das auch das n ist Eigenzustand für diese angegebenen q Werte. Setzt man diese in Gl. 6 führt zu Dreiterm-Rekursionsbeziehungen für die Fourier-Koeffizienten. Das q =0 gerade Lösung ergibt
$$ -\eta_{n,0}^{(e)}a^{(n)}_{0} + \xi\left(\frac{p}{2} +1 \right) a^{( n)}_{2} =0, $$ (8a) $$ \xi pa^{(n)}_{0} + \left(4 - \eta_{n,0}^{(e)} \ rechts)a^{(n)}_{2} + \xi \left(\frac{p}{2} +2 \right)a^{(n)}_{4}=0, $$ (8b ) $$ {\begin{ausgerichtet} &\xi \left(\frac{p}{2} - l+1 \right)a^{(n)}_{2l-2} + \left(4l^{ 2} - \eta_{n,0}^{(e)} \right)a^{(n)}_{2l}\\ &\quad+\xi \left(\frac{p}{2} + l +1 \right)a^{(n)}_{2l+2} =0, \qquad (l \ge 2) \end{aligned}} $$ (8c)und die entsprechenden Rekursionsrelationen für die ungerade Lösung für q =0 ist
$$ (4 - \eta_{n,0}^{(o)})b^{(n)}_{2} + \xi \left(\frac{p}{2} +2 \right)b ^{(n)}_{4} =0, $$ (9a) $$ {\begin{ausgerichtet} &\xi \left(\frac{p}{2} - l+1 \right)b^{ (n)}_{2l-2} + \left(4l^{2} - \eta_{n,0}^{(o)} \right)b^{(n)}_{2l} +\xi \left(\frac{p}{2} + l +1 \right)b^{(n)}_{2l+2}\\ &=0. \qquad (l \ge 2) \end{aligned} } $$ (9b)Das q =1/2 gerade Lösung ergibt
$$ \left[ 1 -\eta_{n,\frac{1}{2}}^{(e)} +\frac{\xi}{2}(p+1)\right]\widetilde{a} ^{(n)}_{1} +\frac{\xi}{2}(p+3)\widetilde{a}^{(n)}_{3}=0, $$ (10a) $$ {}{\begin{ausgerichtet} &\frac{\xi}{2}(p-2l +1)\widetilde{a}^{(n)}_{2l-1}+\left[(2l+1 )^{2} - \eta_{n,\frac{1}{2}}^{(e)}\right]\widetilde{a}^{(n)}_{2l+1}\\ &\ quad+ \frac{\xi}{2}(p+2l+3)\widetilde{a}^{(n)}_{2l+3}=0, \qquad (l\ge 1) \end{ausgerichtet} } $$ (10b)und das q =1/2 ungerade Lösung ergibt
$$ \left[ 1 -\eta_{n,\frac{1}{2}}^{(e)} -\frac{\xi}{2}(p+1)\right]\widetilde{b} ^{(n)}_{1} +\frac{\xi}{2}(p+3)\widetilde{b}^{(n)}_{3}=0 $$ (11a) $$ { }{\begin{aligned} &\frac{\xi}{2}(p-2l+1)\widetilde{b}^{(n)}_{2l-1}+\left[(2l+1) ^{2} -\eta_{n,\frac{1}{2}}^{(e)}\right]\widetilde{b}^{(n)}_{2l+1}\\&\quad + \frac{\xi}{2}(p+2l+3)\widetilde{b}^{(n)}_{2l+3}=0. \qquad (l \ge 1) \end{aligned}} $$ (11b)Consider then Eqs. (8c) and (9b) for the q =0 solutions. The series solutions (7a) and (7b) can clearly be made to terminate if p is 0 or an even positive integer. The resulting polynomials are referred to as Ince polynomials. The remaining solutions for higher eigenvalues are simultaneously double degenerate and correspond to the energy crossings observed at q =0 for certain parameters. The existence of these degeneracies can be seen by looking at the diagonalizable matrices describing the recursion relations for a l und b l :
$$ \boldsymbol{\mathcal{A}} =\left[ \begin{array}{ccccc} 0 &\xi\left(\frac{p}{2} +1 \right) &0 &0 &\hdots \\ \xi p &4 &\xi\left(\frac{p}{2} +2 \right) &0 &\hdots \\ 0 &\xi\left(\frac{p}{2} - 1 \right) &16 &\xi\left(\frac{p}{2} +3 \right) &\hdots \\ \vdots &\vdots &\vdots &\vdots &\ddots \end{array} \right]\!, $$ (12)and
$$ \boldsymbol{\mathcal{B}} =\left[ \begin{array}{ccccc} 4 &\xi\left(\frac{p}{2} +2 \right) &0 &0 &\hdots \\ \xi\left(\frac{p}{2} - 1 \right) &16 &\xi\left(\frac{p}{2} +3 \right) &0 &\hdots \\ 0 &\xi\left(\frac{p}{2} -2 \right) &36 &\xi\left(\frac{p}{2} +4 \right) &\hdots \\ \vdots &\vdots &\vdots &\vdots &\ddots \\ \end{array} \right]\! $$ (13)bzw. Either of the above tridiagonal matrices can be broken into tridiagonal sub-matrices if a leading off-diagonal matrix element is equal to zero, i.e. if p is an even number. The matrices will decompose into two tridiagonal blocks, one smaller finite matrix \(\boldsymbol {\mathcal {A}_{1}}\) (\(\boldsymbol {\mathcal {B}_{1}}\)) and a remaining infinite matrix \(\boldsymbol {\mathcal {A}_{2}}\) (\(\boldsymbol {\mathcal {B}_{2}}\)). From the theory of tridiagonal matrices the corresponding eigenvalue spectra for each matrix is then \(\eta (\boldsymbol {\mathcal {A}}) =\eta (\boldsymbol {\mathcal {A}_{1}}) \cup \eta (\boldsymbol {\mathcal {A}_{2}})\) and \(\eta (\boldsymbol {\mathcal {B}}) =\eta (\boldsymbol {\mathcal {B}_{1}}) \cup \eta (\boldsymbol {\mathcal {B}_{2}})\). The smaller finite matrices are analytically diagonalizable in principle, giving exact eigenvalues, and their corresponding finite length eigenvectors define the fourier coefficients yielding Ince polynomials via Eq. 7. We can see that for a given even integer p , the remaining infinite tridiagonal matrices are the same \(\boldsymbol {\mathcal {A}_{2}}=\boldsymbol {\mathcal {B}_{2}}\equiv \boldsymbol {\mathcal {D}}\) which results in the double degenerate eigenvalues. To be clear, we provide an example of when p =2 in the Appendix.
In the same way, when p is a positive odd integer the series solutions (7c) and (7d) can be made to terminate, and the matrices corresponding to \(\widetilde {a}_{l}\) and \(\widetilde {b}_{l}\) share eigenvalues resulting in the closing of higher subbands at the edge of the Brillouin zone q =± 1/2. From the definitions of the auxiliary parameters in Eq. 6, we have
$$ A_{g} =(p+1)\sqrt{B_{g}}, $$ (14)which defines the condition for exactly-solvable solutions for the lower lying solutions and simultaneously the existence of higher double degenerate eigenvalues above the p th subband, with p =0 or an even positive integer corresponding to crossings at the centre of the Brillouin zone, while crossings at the edge require p to be an odd positive integer. Figure 4b plots the size of the band gap between the first and second subbands \(\Delta \varepsilon _{12}^{(q=0)}/\varepsilon _{0}(\rho)\) as a function of A g und B g , with the dot-dashed red contour line corresponding to Eq. 14 for p =0. The schematic indicates the appropriate eigenstates of the isolated DQW at the p =0 resonance.
The application of a small transverse field C ⊥ breaks the reflection symmetry of the system, permitting hybridization of the localized well states of the isolated DQW which results in a significant change at points of degeneracy, as can be seen by comparing the schematic depicted in Fig. 4b with that in c (see also inset of Fig. 3b). We plot in Fig. 4c the behaviour of the band gap between the first and second subbands as a function of A g und C ⊥ . Here we see that the band gap is more sensitive to C ⊥ due to the significant change in the isolated DQW eigenstates by lowering one barrier with respect to the other. This behaviour is notably the converse of the parameter sensitivity for the band gap between the ground and first subbands. By degenerate perturbation theory, it can be shown that this induced band gap is linear in C ⊥ for the lowest crossing bands when p =0, and to higher order with increasing p . Finally, within the vicinity of the crossings, e.g. for small q about q =0 in Fig. 3a, the dispersions could be approximated as a quasi-relativistic linear dispersion yielding Dirac-like physics, which could permit superfluiditiy [81] for example. The advantage in using nanohelices lies in introducing such phenomena to portable nanostructure based devices, while also exhibiting unusual responses of the charge carriers to circularly polarized radiation [44, 45, 82–85] (or indeed magnetic fields [86, 87]) due to the helical spatial confinement.
Optical transitions
In order to understand how our double-gated nanohelix system interacts with electromagnetic radiation, we study the inter-subband momentum operator matrix element \(T^{g\rightarrow f}_{j} =\langle {f}|\boldsymbol {\hat {j}} \cdot \boldsymbol {\hat {P}}_{j} |{g}\), which is proportional to the corresponding transition dipole moment, and dictates the transition rate between subbands ψ f and ψ g . Here, \(\boldsymbol {\hat {j}}\) is the projection of the radiation polarization vector onto the coordinate axes (j =x,y ,z ) and the respective self-adjoint momentum operators are [44, 45, 82–84]
$$ \boldsymbol{\hat{P}}_{x} =\boldsymbol{\hat{x}}\frac{i \hbar R}{\rho^{2} +R^{2}}\left[\sin(\varphi)\frac{d}{d\varphi} + \frac{1}{2}\cos(\varphi) \right], $$ (15a) $$ \boldsymbol{\hat{P}}_{y}=-\boldsymbol{\hat{y}}\frac{i \hbar R}{\rho^{2} +R^{2}}\left[\cos(\varphi)\frac{d}{d\varphi} - \frac{1}{2}\sin(\varphi) \right], $$ (15b) $$ \boldsymbol{\hat{P}}_{z}=-\boldsymbol{\hat{z}}\frac{i \hbar \rho}{\rho^{2} +R^{2}}\frac{d}{d\varphi}. $$ (15c)In terms of the dimensionless position variable φ , we are required to evaluate \(T^{g\rightarrow f}_{j} =\rho \int _{0}^{2\pi N}\psi _{f}^{\ast } P_{j} \psi _{g} d\varphi \), and upon substituting in from Eq. 4 we find
$$ {\begin{aligned} T^{g\rightarrow f}_{x} &=\frac{i \hbar R}{2\left(\rho^{2} + R^{2} \right)}\sum_{m} c_{m}^{\ast (f)} \left[ c_{m-1}^{(g)} \left(q+m-\frac{1}{2}\right)\right.\\ &\quad\left.-c_{m+1}^{(g)} \left(q+m+\frac{1}{2}\right) \right], \end{aligned}} $$ (16a) $$ {\begin{aligned} T^{g\rightarrow f}_{y} &=\frac{\hbar R}{2\left(\rho^{2} + R^{2} \right)}\sum_{m} c_{m}^{\ast (f)} \left[ c_{m-1}^{(g)} \left(q+m-\frac{1}{2}\right)\right.\\&\left.\quad+c_{m+1}^{(g)} \left(q+m+\frac{1}{2}\right) \right], \end{aligned}} $$ (16b) $$ T^{g\rightarrow f}_{z} =\frac{\hbar \rho}{\left(\rho^{2} + R^{2} \right)} \sum_{m} c_{m}^{\ast (f)} c_{m}^{(g)} (q+m). $$ (16c)We see from Eqs. 16a and 16b that light linearly polarized transverse to the helix axis couples coefficients with angular momentum differing by unity Δ m =± 1, whereas from Eq. 16c, linear polarization parallel to the helix axis couples only Δ m =0. In Fig. 5, we plot the absolute square of the momentum operator matrix element between the lowest three bands for linearly polarized light propagating perpendicular to the helix axis (i.e. with z -Polarisation). Initially, for A g =C ⊥ =0, transitions between the ground and first bands are forbidden (as is to be expected for a unit cell with two equivalent wells resulting in a doubling of the first Brillouin zone, so it is in fact the same band). As the strength of the doubled period potential A g is increased with respect to B g , transitions become allowed away from q =0 as can be seen from Fig. 5a (following behaviour from the dotted red curve through to the solid blue curve). The parameters are swept through a resonance as we go from the solid to the dashed blue curve, wherein the situation changes drastically. To understand this behaviour, we must consider the special case of q =0. As we traverse this resonance, the energy of the Bloch function with q =0 constructed from the first excited state of the deeper well in the DQW unit cell (p -like) passes below the Bloch function constructed from the ground state in the shallower well (s -like). Consequently, the parity with respect to φ (which is a good quantum number only for q =0 or |q |=1/2) of the two excited states is exchanged resulting in the rapid switch from forbidden to allowed at q =0, wherein the z -polarized inter-subband matrix element becomes non-zero due to the operator \(\boldsymbol {\hat {P}}_{z}\) (see Eq. 15c) now coupling the even ground state with the odd first excited state. We therefore see the opposite behaviour for transitions between the ground and second band in Fig. 5b about q =0. While initially increasing A g allows transitions at q =0 between the ground state and the second excited state when it is p -like, beyond resonance (when the order of the s -like and p -like excited states are swapped) transitions are suppressed. See for example Ref. [88] for a clear picture of this interchange between the ordering of the even and the odd parity excited states. For transitions between the first and second band (Fig. 5c), we observe a large transition centred about q =0 due to the lifting of the m =± 1 degenerate states of the field-free helix by the superlattice potential. The presence of symmetry-breaking C ⊥ ruins the pristine parities of the states at the centre of the Brillouin zone and all transitions are allowed, as shown in the insets of Fig. 5.
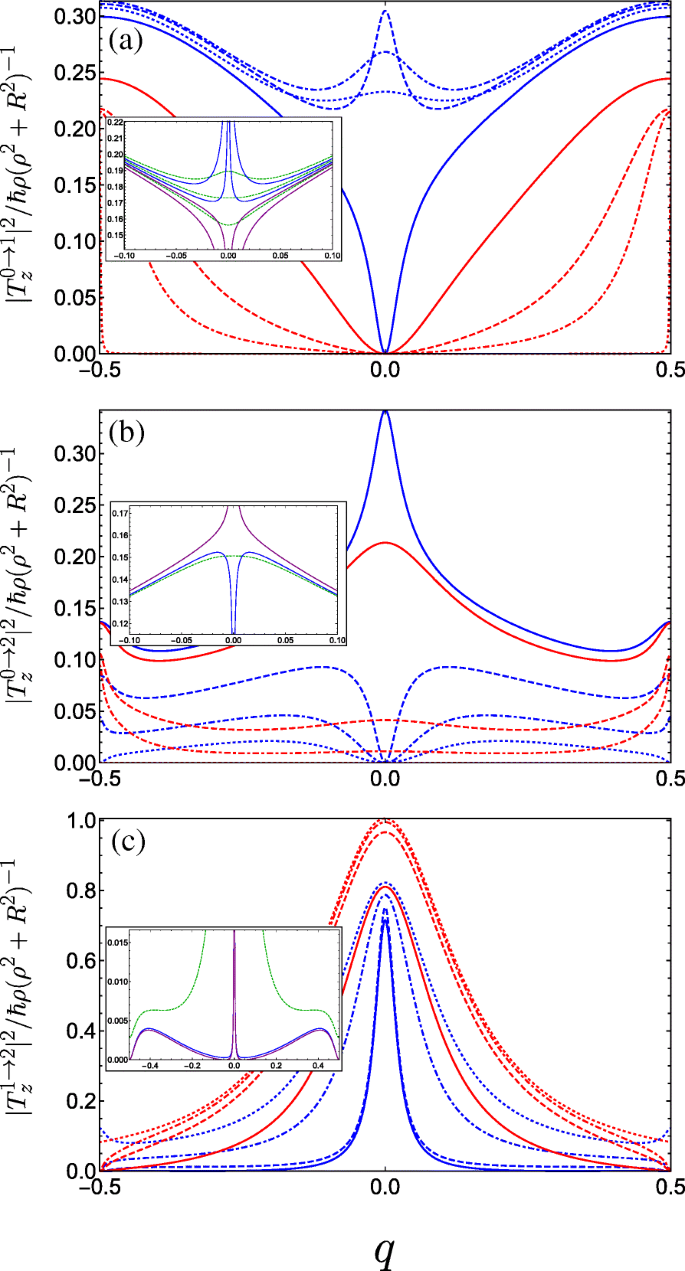
Square of the dimensionless momentum operator matrix element between the g th and f th subbands in the first Brillouin zone as a function of the dimensionless wave vector q of the electrons photoexcited by linearly z -polarized radiation and for a variety of parameter combinations spanning the first incident of resonance. The different blue curves keep A g =0.5 and C ⊥ =0 fixed and vary B g =0.1, 0.2, and 0.3 corresponding to dot-dashed, dashed, and solid. The different red curves keep B g =0.3 and C ⊥ =0 fixed while varying A g =0.05, 0.1 and 0.3 as dot-dashed, dashed, and solid, while the dotted blue (dotted red) plots the limiting case A g =0.5 &B g →0 (A g →0 &B g =0.3). a Transitions between the ground and first bands. The inset plots the behaviour for fixed A g =0.5 and changing B g crossing the resonant condition at B g =0.25 (see text) in a reduced q -range, ranging from upper blue B g =0.245, lower blue B g =0.249, upper purple B g =0.251, to lower purple B g =0.255. The dashed green curves are for small non-zero transverse field C ⊥ =0.05 ranging from B g =0.245 (upper curve) to B g =0.255 (lower curve) in increments of 0.05. b Plots transitions between the ground and second bands, the inset plots the behaviour close to resonance when A g =0.5; blue is B g =0.249, purple is B g =0.251, and dark green is at resonance with C ⊥ =0.05. c Plots transitions between the first and second bands, the parameters for the inset are the same as those in (b )
In Fig. 6, we plot the absolute square of the momentum operator matrix element for right-handed circularly polarized light which propagates along the helix axis, given by |T x +iT y | 2 . Notably, we observe a large anisotropy between the two halves of the first Brillouin zone, while the result for left-handed polarization is a mirror image to what we see in Fig. 6. Physically, this can be attributed to the conversion of the photon angular momenta to the translational motion of the free charge carriers projected onto the direction of the helix axis, with an unequal population of the excited subband in a preferential momentum direction controlled by the relative handedness of both the helix and the circular polarization of light. An intuitive mechanical analogue would be the rotary motion of Archimedes’ screw being converted into the linear motion of water along the direction of the screw axis dictated by the handedness of the thread. As such, our system of a double-gated nanohelix irradiated by circularly polarized light exhibits a photogalvanic effect, whereby one can choose the net direction of current by irradiating with either right- or left-handed circularly polarized light [44, 45, 89]. This differs from conventional one-dimensional superlattices, wherein the circular photogalvanic effect stems from the spin-orbit term appearing in the effective electron Hamiltonian and is consequently a weaker and hard-to-control phenomenon [90, 91]. The electric current induced by promoting electrons from the ground subband to an excited subband f via the absorption of circularly polarized light can be understood from the equation for the electric current contribution from the f th subband
$$ j_{f} =\frac{e}{2 \pi \rho} \int dq \left[ v_{f}(q) \tau_{f}(q) - v_{g}(q) \tau_{g} (q) \right] \Gamma_{CP}^{g \rightarrow f}(q), $$ (17)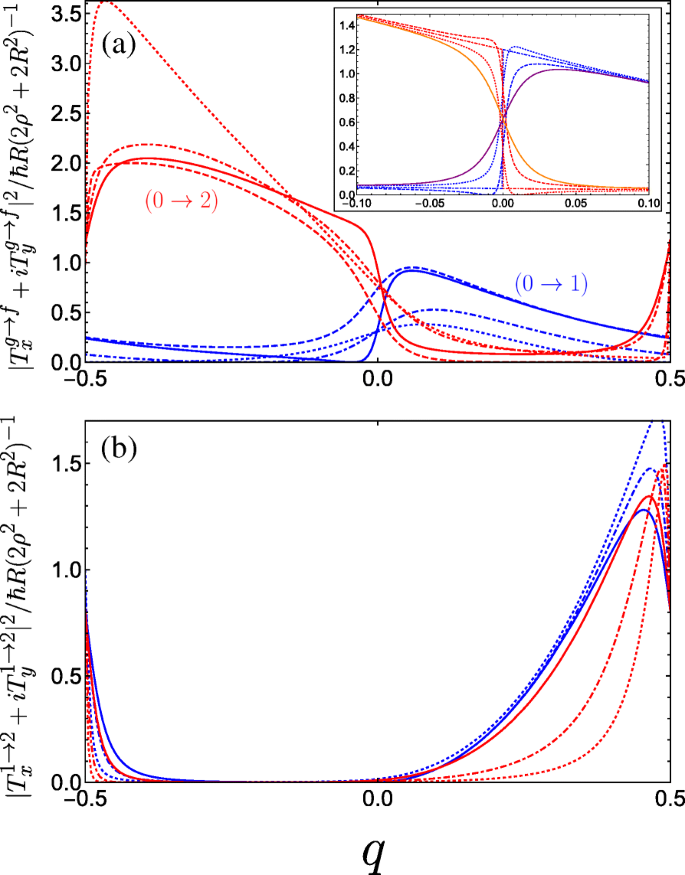
Square of the dimensionless momentum operator matrix element between the g th and f th subbands in the first Brillouin zone as a function of the dimensionless wave vector q of the electrons photoexcited by right-handed circularly polarized radiation |T x +iT y | 2 and for a variety of parameter combinations spanning the first incident of resonance. a The blue curves denote transitions between the ground and first band while the red curves denote transitions between the ground and second band, both with the following parameters:A g =0.5 and B g =0.3 for solid curves, A g =0.5 and B g =0.1 for dashed curves, A g =0.3 and B g =0.3 for dot-dashed curves, and A g =0.01 and B g =0.3 for dotted curves (as A g →0 the maximum of the 0→2 increases rapidly as it approaches q =− 1/2). The inset plots the behaviour as B g is tuned through resonance for A g =0.5; dotted is B g =0.24, dot-dashed is B g =0.25, and dashed is B g =0.26. The solid purple (orange) curve denotes transitions between the ground and first (second) band at resonance with C ⊥ =0.05 applied. b Plots transitions between the first and second bands. The different blue curves keep A g =0.5 fixed and vary B g =0, 0.2, and 0.3 corresponding to dotted, dot-dashed, and solid. The different red curves keep B g =0.3 fixed while varying A g =0.05, 0.1, and 0.3 as dotted, dot-dashed, and solid. We have omitted plots for C ⊥ ≠0 here as it yields no great qualitative change to the matrix elements
where \(v_{g,f}(q)=(\rho /\hbar)\partial \varepsilon _{g,f}/\partial q \) is the antisymmetric electron velocity v (q )=− v (− q ) (which we can deduce from the symmetric dispersion curves), τ g,f (q ) is a phenomenological relaxation time, and \(\Gamma _{CP}^{g \rightarrow f}(q)\) is the transition rate resulting from the optical perturbation of the electron system. Given that \(\Gamma _{CP}^{g \rightarrow f}(q) \propto |T_{x}^{g \rightarrow f} + i T_{y}^{g \rightarrow f}|^{2}\) for right-handed circularly polarized light where T x und T y are given by Eqs. 16a and 16b, respectively. The anisotropy present in Fig. 6a enters Eq. 17 to yield a non-zero photocurrent. This current flows in the opposite direction for left-handed polarization. Such a circular photogalvanic effect is also exhibited in chiral carbon nanotubes under circularly polarized irradiation [92, 93], although tunability predominantly stems from manipulating the nanotube physical parameters, which are hard to control. The double-gated nanohelix system offers superior versatility by fully controlling the landscape of the superlattice potential, which can be used to tailor the non-equilibrium asymmetric distribution function of photoexcited carriers (as shown in Fig. 6 for inter-subband transitions between the three lowest subbands).
On a side note, we expect that (as with chiral carbon nanotubes [93–95]) the application of a magnetic field along the nanohelix axis can take up the role played by circularly polarized radiation, whereby the current is induced by a magnetic-field-induced asymmetric energy dispersion—which in turn produces an anisotropic electron velocity distribution across the two halves of the Brillouin zone.
Schlussfolgerungen
In summary, we have shown that the system of a nanohelix between two aligned gates modelled as charged wires is a tunable binary superlattice. The band structure for this system exhibits a diverse behaviour, in particular revealing energy band crossings accessible via tuning the voltages on the gates. The application of an electric field normal to the plane defined by the gates and the helix axis introduces an additional parameter with which to open a band gap at these crossings. Engineering the band structure in situ with the externally induced superlattice potential along a nanohelix provides a clear advantage over conventional heterostructure superlattices with a DQW basis [96, 97]. Both systems can be used as high-responsivity photodetectors, wherein tailoring the band structure (to the so-called band-aligned basis [98–100]) can lead to a reduction in the accompanying dark current. Here control over the global depth of the quantum wells also permits versatility over the detection regime, which can lie within the THz range. We have also investigated the corresponding behaviour of electric dipole transitions between the lowest three subbands induced by both linearly and circularly polarized light, which additionally allows this system to be used for polarization sensitive detection. Finally, the ability to tune the system such that a degenerate excited state is optically accessible from the ground state, along with the inherent chirality present in the light-matter interactions, may make this a promising system for future quantum information processing applications [101]. It is hoped that with the advent of sophisticated nano-fabrication capabilities [102], fully controllable binary superlattice properties will be realized in a nanohelix and will undoubtedly contribute to novel optoelectronic applications.
Appendix
Touching energy bands at Brillouin zone boundary when A g =C ⊥ =0
Here, we show using matrix algebra that in the picture of a binary superlattice pairs of subbands touch at the Brillouin zone edges if A g =C ⊥ =0 and B g ≠0, as seen from the solid blue curves in Fig. 3a. Equation 5 is equivalent to the following N -by-N pentadiagonal matrix Hamiltonian with zeros on the leading sub- and superdiagonals:
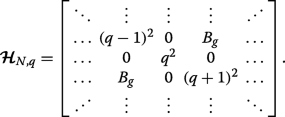 (18)
(18) Let us consider q =1/2 (we could alternatively take q =− 1/2) which makes the leading diagonal symmetric. We can then express this matrix Hamiltonian \(\widetilde {\mathcal {\boldsymbol {H}}}_{N} \equiv \boldsymbol {\mathcal {H}}_{N,q=1/2} \) in block form as
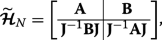 (19)
(19) wo
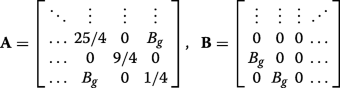 (20)
(20) are both of dimension N /2-by- N /2, and J is the exchange matrix. We may construct a matrix via permuting \(\boldsymbol {\mathcal {H}}_{N}\) with the N -by-N permutation matrix \(\boldsymbol {\mathcal {P}}_{N}\),
$$ \boldsymbol{\mathcal{P}}_{N} =\left[ \begin{array}{cccccc} 1 &0 &\hdots &\hdots &\hdots &0 \\ 0 &\hdots &\hdots &\hdots &\hdots &1 \\ 0 &1 &\hdots &\hdots &\hdots &0 \\ 0 &\hdots &\hdots &\hdots &1 &0 \\ \vdots &&&&&\vdots \\ 0 &\hdots &\hdots &1 &\hdots &0 \\ \end{array} \right], $$ (21)such that the permutation-similar matrix is
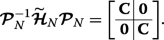 (22)
(22) Hence, the eigenvalues of \(\boldsymbol {\mathcal {P}}_{N}^{-1}\widetilde {\boldsymbol {\mathcal {H}}}_{N} \boldsymbol {\mathcal {P}}_{N}\), which are the same as the eigenvalues \(\widetilde {\boldsymbol {\mathcal {H}}}_{N}\), are double degenerate with the values given by the eigenvalue spectrum of the tridiagonal matrix C
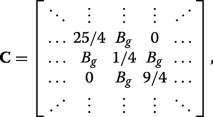 (23)
(23) which can also be expressed succinctly in terms of the previously defined matrices via \(\mathbf {C}=\boldsymbol {\mathcal {P}}_{N/2}^{-1}\mathbf {A}\boldsymbol {\mathcal {P}}_{N/2}+\boldsymbol {\mathcal {P}}_{N/2}^{-1}\mathbf {B}\mathbf {J}\boldsymbol {\mathcal {P}}_{N/2}^{4}\). We can see that applying C ⊥ ≠0 (inset of Fig. 3a) or both C ⊥ und A g ≠0 (inset of Fig. 3b) ruins the symmetry in the matrix Hamiltonian and prevents the existence of eigenvalues with multiplicity beyond unity, resulting in the appearance of band gaps.
Energy crossing at centre of Brillouin zone between third and forth subbands
As an example, let us specifically consider the case where p =2, wherein the matrices (12) and (13) become:
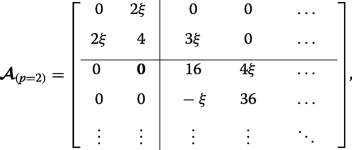 (24)
(24) and
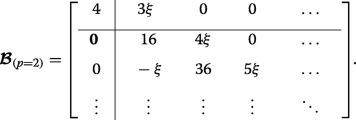 (25)
(25) This case corresponds to the crossings of the blue curves at the edge of the Brillouin zone in Fig. 3d (whereas p =0 results in crossings at q =0 in Fig. 3b). The lower eigenvalues are found exactly by diagonalizing each of the two finite matrices and they interlace, yielding \(\eta _{0,1,2} =2-\sqrt {4+4\xi ^{2}}, 4, 2+\sqrt {4+4\xi ^{2}}\). The infinite lower-right-hand block tridiagonal matrices coincide, thus the remaining double degenerate eigenvalues are found by approximately or numerically solving Det[D −η I ]=0.
Verfügbarkeit von Daten und Materialien
The data for the figures all stem from numerically diagonalizing the matrix described by Eq. 5 and can readily be achieved in any numerical software package. With this in mind, the datasets used and/or analyzed during the current study are available from the corresponding author on reasonable request.
Nanomaterialien



