Abstimmbarer und anisotroper Dual-Band-Metamaterial-Absorber mit elliptischen Graphen-Schwarz-Phosphor-Paaren

Einführung

Graphen ist ein zweidimensionales Material mit in einem Wabengitter angeordneten Kohlenstoffatomen [1, 2]. In den letzten Jahren wurden aufgrund ihrer ultrakompakten Größe und der einzigartigen Licht-Graphen-Wechselwirkung verschiedene photonische Geräte auf Graphenbasis entwickelt [3,4,5,6]. Als eine ihrer wichtigsten Anwendungen haben Metamaterial-Absorber auf Basis von Graphen aufgrund ihrer starken und einstellbaren plasmonischen Reaktion auf wachsendes Interesse geweckt [7,8,9,10]. Einige Anwendungen, die ein hohes Ein-Aus-Verhältnis erfordern, sind jedoch aufgrund der Bandlücke von Graphen von null oder nahe null eingeschränkt [11]. Als alternatives zweidimensionales Material hat in letzter Zeit auch schwarzer Phosphor (BP), eine Monoschicht aus Phosphoratomen, die in einem hexagonalen Gitter mit einer gefalteten Struktur angeordnet sind, [12] ein starkes Forschungsinteresse gefunden. Es besitzt außergewöhnliche optische und elektronische Eigenschaften wie In-Plane-Anisotropie, dickenabhängige abstimmbare Bandlücke [13] und hohe Ladungsträgerdichte und Mobilität [14]. In den letzten Jahren haben Forscher im Infrarotbereich zahlreiche Strukturen untersucht, um die Licht-BP-Wechselwirkungsstärke in dem auf BP basierenden Metamaterial zu verbessern [15,16,17]. Trotzdem ist die plasmonische Resonanz von BP-basierten Absorbern kaum flexibel und effektiv abzustimmen, und sie leiden normalerweise unter einer relativ niedrigen Absorptionsrate bei moderatem Dotierungsniveau. Dies wird der Tatsache zugeschrieben, dass die Resonanzstärke in Monolayer-BP eher schwach ist, was seine anisotropen Potentiale begrenzt. Daher wurden plasmonische Absorber auf Graphen-BP-Basis vorgeschlagen, die die Hybridisierung von Graphen und BP nutzen, um eine starke und anisotrope plasmonische Absorption zu erreichen [18, 19, 20]. Die zuvor beschriebenen Absorber auf Graphen-BP-Basis erfordern jedoch im Allgemeinen eine relativ komplizierte Herstellungstechnik oder besitzen eine einzelne Absorptionsbande, was ihre weiteren Anwendungen für Bildgebungs-, Biosensor- und Kommunikationssysteme behindert.

In unserer Arbeit wird ein anisotroper Dualband-Infrarotabsorber numerisch vorgeschlagen, der periodische elliptische Graphen-BP-Paare verwendet, was eine einfache Herstellung ist. Die unabhängige Abstimmbarkeit der Resonanz durch geometrische Größe und Dotierungsniveau wird demonstriert. Elektrische Feldverteilungen werden aufgetragen, um den physikalischen Mechanismus aufzuzeigen. Die Toleranz des Einfallswinkels und die Polarisationsempfindlichkeit werden ebenfalls veranschaulicht.

Methoden

Der vorgeschlagene Absorber besteht aus transversalen und longitudinalen elliptischen Graphen-BP-Paaren, die auf einem SiO₂ . abgeschieden sind Schicht wie in Abb. 1 gezeigt. Zwischen Monolayer-Graphen und BP wird eine hexagonale Bornitrid (hBN)-Schicht als isolierender Spacer eingefügt, um den Ladungsträgertransport zwischen ihnen zu verhindern und eine hohe Ladungsträgermobilität zu gewährleisten. Die Parameter von SiO₂ und hBN werden aus Lit. 21 und Ref.-Nr. 22 bzw. Die Simulationen werden von COMSOL Multiphysics durchgeführt, um die Dualband-Eigenschaften zu untersuchen, die auf der Finite-Elemente-Methode (FEM) im Frequenzbereich basieren. Wir verwenden Floquet-Periodizität als Randbedingungen in beiden x - und y - Richtungen. Ein Port mit Infrarotwellenanregung wird auf der oberen Oberfläche der Rechendomäne eingestellt, während die Randbedingung des perfekten elektrischen Leiters (PEC) auf der unteren Oberfläche eingestellt wird. Für die gesamte Domäne werden tetraedrische Netze mit einer vom Benutzer gesteuerten Netzdichte angewendet.

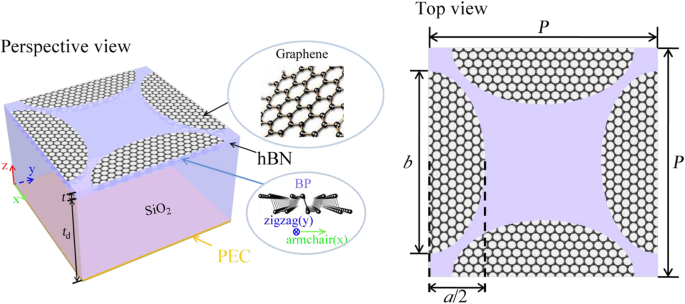
Eine Elementarzelle des vorgeschlagenen Absorbers basierend auf elliptischen Graphen-BP-Paaren. t _d und t die Dicken der dielektrischen bzw. Isolatorschicht sind. a und b sind die kurze Achse und die lange Achse der Ellipse. P ist die periodische Seitenlänge der quadratischen Elementarzelle

In der Simulation werden sowohl Graphen als auch SP als zweidimensionale Oberflächen mit Oberflächenleitfähigkeiten anstelle von Schüttgütern mit Permittivitätstensoren behandelt. Diese Annahme löst die Probleme der Dickendefinition für ultradünne Materialien und eine geringe Recheneffizienz [23].

Zur Beschreibung der Oberflächenleitfähigkeit von Graphen σ (ω ), verwenden wir die bekannten Kubo-Formeln wie folgt [24]:

Nach Gl. 1, σ (ω ) besteht aus den Intraband- und Interband-Gegenstücken, nämlich σ _intra und σ _inter . ω ist die Bogenfrequenz, μ_c ist das chemische Potential, Г ist die Streurate und T ist die Kelvin-Temperatur. ħ , e , ξ , und k _B sind die reduzierte Planck-Konstante, Elektronenladung, Elektronenenergie bzw. Boltzmann-Konstante.

Da im Infrarotbereich das einfallende Photon den Interband-Übergang kaum anregen kann, wird die Licht-Graphen-Wechselwirkung vom Intraband-Übergang dominiert. Insbesondere wenn μ_c k _B T , Kubo-Formeln können weiter zu Gl. 5:

Somit hängt die Oberflächenleitfähigkeit von Graphen von den Werten von ω . ab , Г , und μ _c . Hier, Г wird mit 0,3 meV und μ . angenommen _c wird gemäß der vorherigen Arbeit [25, 26] mit 0.7 eV angenommen.

Andererseits berechnen wir die Oberflächenleitfähigkeit σ _j von BP mit einem einfachen halbklassischen Drude-Modell [27]:

wo n _s die Ladungsträgerdichte in Bezug auf das Dotierungsniveau ist. Wir wählen n _s = 1,9 × 10 ¹³ cm ⁻² und Г _BP = 10 meV gemäß der vorherigen Referenz [16]. j ist die betreffende Richtung, also σ _x und σ _y werden durch die Elektronenmasse entlang x . bestimmt - und y -Richtung bzw. m _x und m _y kann weiter berechnet werden durch:

wo m ₀ die Standardelektronenmasse ist und Δ und a sind die Bandlücke bzw. die Skalenlänge für die BP-Monoschicht. Durch Ersetzen der Gl. 10–12 in Gl. 8 und Gl. 9 erhält man die Elektronenmasse entlang des Sessels (x -) und Zickzack (y .) -) Richtung. Die Diskrepanz zwischen ihnen trägt zur anisotropen Oberflächenleitfähigkeit von SP bei.

Ergebnisse und Diskussion

Um die anisotrope Absorptionscharakteristik des vorgeschlagenen Absorbers zu veranschaulichen, simulieren und vergleichen wir zunächst die Absorptionsspektren mit einzelnen Graphenschichten, einzelnen BP-Schichten und Graphen-BP-Paaren. Wie in Abb. 2a zu sehen ist, ist die plasmonische Reaktion von Graphen isotrop mit zwei offensichtlichen Absorptionspeaks bei 9,9 µm und 15,4 µm, unabhängig von der Polarisation. Auf der anderen Seite ist die Plasmonenresonanz von BP zwar anisotrop, aber ihre Stärke ist entweder für TE (< 12,7%) oder TM (< 0,7%) ziemlich schwach. Durch die Kombination der Vorteile von Graphen und BP zeigen Graphen-BP-Paare sowohl starke als auch anisotrope plasmonische Antworten. Für die TE-Inzidenz liegen die beiden Absorptionspeaks bei 8,8 µm und 14,1 µm, mit Absorptionsraten von mehr als 90 %. Für den TM-Einfall sind die Wellenlängen der maximalen Absorption auf 9,5 µm bzw. 15,4 µm verschoben. Das Polarisations-Extinktionsverhältnis kann definiert werden als PER = 10 × log(R ₁ /R ₀ ), wobei R ₁ und R ₀ das Reflexionsvermögen (R = 1-A , A stellt die Absorption dar) verschiedener Polarisationen bei derselben Wellenlänge, dann kann das maximale PER jeder Resonanz bis zu 23 dB und 25 dB bei λ . erreichen = 9.5 μm und λ = 14,1 μm. Daher kann der vorgeschlagene Absorber als reflektierender Dualband-Polarisator mit hoher Leistung verwendet werden.

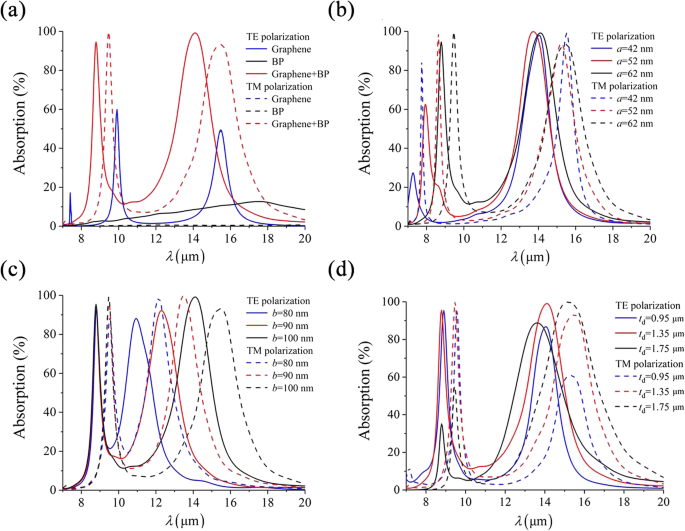
a Vergleich der plasmonischen Reaktionen zwischen Monolayer-Graphen (blaue durchgezogene Kurve und blaue gestrichelte Kurve überlappen), Monolayer-BP und Graphen-BP-Paaren und Absorptionsspektren mit unterschiedlichen a (b ), b (c ) und t _d (d ). Die Standardparameter sind a = 62 nm, b = 100 nm, t _d = 1,35 μm, t = 5 nm und P = 250 nm, bei normalem Einfall

Als nächstes analysieren wir die Absorptionsspektren mit verschiedenen geometrischen Konfigurationen, um die abstimmbare Dualband-Absorptionseigenschaft in Abb. 2b–d zu demonstrieren. In Abb. 2b haben die ersten Absorptionspeaks Rotverschiebungen als a steigt für beide Polarisationen von 42 auf 52 nm an, während die zweiten Resonanzfrequenzen nahezu unverändert bleiben. Andererseits, wie in Abb. 2c gezeigt, durch Erhöhen der Längsachsenlänge b , sind die zweiten Resonanzen ebenfalls rotverschoben, während die ersten Absorptionspeaks für TE- und TM-Polarisation konstant bleiben. Daher können die dualen Absorptionspeaks unabhängig durch Variieren der entsprechenden Achsenlänge in den elliptischen Graphen-BP-Paaren abgestimmt werden. Darüber hinaus spielt die Dicke der dielektrischen Schicht auch eine kritische Rolle für die Leistung des vorgeschlagenen Bauelements, das als Fabry-Perot-Resonator fungiert, der aus der Graphen-BP-Metaoberfläche und dem PEC-Substrat gebildet wird. Somit sind die Absorptionsspektren mit unterschiedlichen t _d sind in Fig. 2d aufgetragen. Als t _d von 0,95 auf 1,75 µm ansteigt, fallen die ersten Absorptionspeaks für TE- und TM-Polarisation dramatisch ab, während die zweiten Peaks zuerst ansteigen und dann stark abfallen. Folglich gibt es eine optimale Dicke t _d das maximiert die dualen Absorptionspeaks des vorgeschlagenen Absorbers.

Um die physikalische Erkenntnis zu verdeutlichen, zeigen wir in Abb. 3 weiterhin die Verteilungen der elektrischen Feldstärke bei verschiedenen Wellenlängen. Bei TE-Einfall befindet sich das elektrische Feld im Sessel (x -) Richtung. Am ersten Gipfel (λ = 8,8 μm) kann das einfallende Infrarotlicht Elektronen in Graphen und BP zu Schwingungen in Querrichtung anregen, was zu einer Konzentration des elektrischen Feldes an den kurzen Achsenenden der Längsellipse führt, wie in Abb. 3a gezeigt. Bei λ = 14.1 μm wird das lokalisierte elektrische Feld an den Längsachsenenden der Querellipse verstärkt. Andererseits TM-Einfall mit elektrischem Feld im Zickzack (y -) Richtung kann Elektronen zu Schwingungen entlang der Längsrichtung beim Absorptionspeak von 9,5 µm anregen, was zu konzentrierten Feldverteilungen an den kurzen Achsenenden der Querellipse führt. Außerdem bei λ = 15,4 μm ist die Verstärkung des elektrischen Felds auf die Längsachsenenden der Längsellipse fokussiert. Daher stehen die Resonanzwellenlängen in direktem Zusammenhang mit der endlichen Oszillationslänge der induzierten Dipole sowohl in transversalen als auch in longitudinalen elliptischen Graphen- und BP-Paaren.

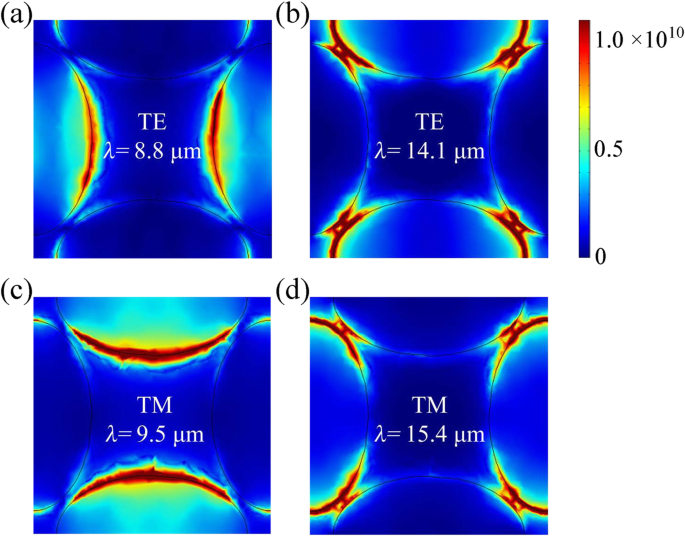
Verteilung der elektrischen Feldstärke bei verschiedenen Wellenlängen für a , b TE und c , d TM-Polarisation, wobei a = 62 nm, b = 100 nm, t _d = 1,35 μm, t = 5 nm, P = 250 nm, bei normalem Einfall

Man kann die anisotrope Dualband-Absorptionsleistung effektiv einstellen, indem man die geometrischen Abmessungen variiert, wie in Abb. 2b–d gezeigt. Inzwischen können die Oberflächenleitfähigkeiten von Graphen und BP auch durch Variation von μ_c . manipuliert werden und n _s nach Graphen- und BP-Modellformeln wie oben erwähnt. μ _c und n _s stellen das Dotierungsniveau von Graphen und BP dar, das nach der geometrischen Herstellung verändert werden kann. Somit sind die Leistungen des vorgeschlagenen Absorbers mit unterschiedlichen μ _c und n _s sind in Abb. 4 dargestellt. Unter Berücksichtigung der praktischen Situation μ _c wird zwischen 0,4 und 0,8 eV aus der durch Experimente verifizierten früheren Arbeit gewählt [28]. In der früheren veröffentlichten Arbeit [29] wurde der maximale theoretische Wert für n _s von BP wurde mit 2,6 × 10 ¹⁴ . nachgewiesen cm ⁻² , also ein gemäßigtes n _s wird zwischen 10 ¹³ . gewählt cm ⁻² und 10 ¹⁴ cm ⁻² in der Simulation. In Abb. 4a, wenn μ _c = 0,4 eV liegt der erste Absorptionspeak bei 10,9 μm und der zweite bei 17,1 μm. Als μ _c auf 0,8 eV ansteigt, sind die beiden Resonanzwellenlängen auf 8,4 μm und 13,4 μm blauverschoben. Ähnlich sind bei der TM-Polarisation die dualen Absorptionspeaks von 12,4 und 19,8 µm auf 8,9 bzw. 14,4 µm mit µ . blauverschoben _c Erhöhung von 0,4 auf 0,8 eV, wie in Fig. 4b gezeigt. Für individuell gemusterten BP ist die Resonanzwellenlänge λ _p kann berechnet werden als \( {\lambda}_p\propto \sqrt{L/{n}_s} \), wobei L ist die effektive Schwingungslänge [27]. Wenn also L fixiert ist, zeigen die Absorptionsspektren eine offensichtliche Blauverschiebung als n _s nimmt für die TE-Polarisation zu, wie in Fig. 4c aufgetragen. Bei der TM-Polarisation sind die Absorptionspeaks ebenfalls leicht blauverschoben als n _s erhöht sich von 10 ¹³ cm ⁻² bis 10 ¹⁴ cm ⁻² wie in Abb. 4d gezeigt.

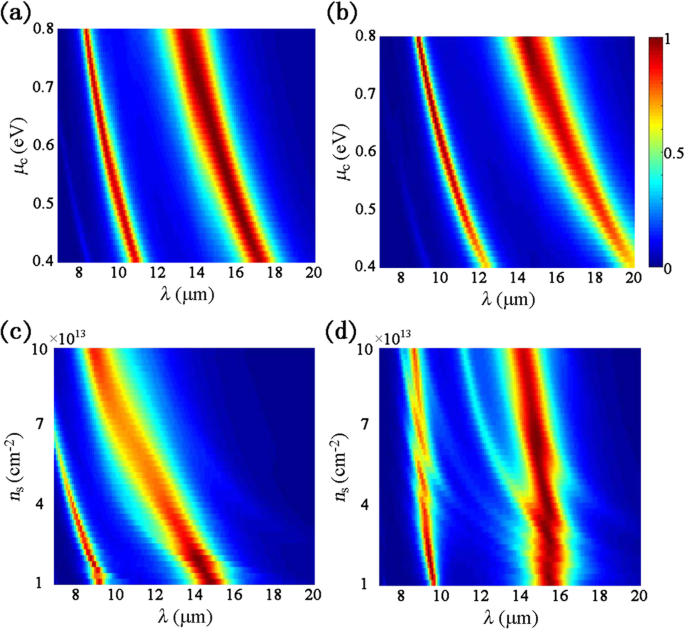
Absorptionsspektren gegen verschiedene Dotierungsniveaus bei normalem Einfall:a und b für verschiedene chemische Potentiale von Graphen, c und d für unterschiedliche Trägerdichten von BP, a und c für TE-Polarisation und b und d für TM-Polarisation, wobei a = 62 nm, b = 100 nm, t _d = 1,35 μm, t = 5 nm und P = 250 nm

Bei den praktischen Anwendungen wird für Infrarotabsorber die Toleranz gegenüber weiten Einfallswinkeln bevorzugt. Daher werden Absorptionsspektren unter schrägem Einfall erstellt. In Fig. 5a wird beobachtet, dass für die TE-Polarisation der erste Absorptionspeak größer als 80% bleibt, wenn θ steigt auf 52° an, während der zweite Absorptionspeak über 80% bleibt, selbst wenn θ erhöht sich auf 80°. Wenn θ> 46°, die zweite Resonanzwellenlänge wird allmählich als θ . rotverschoben wird größer. Bei TM-Inzidenz, wenn θ kleiner als 62° ist, bleibt die Absorptionsrate beim ersten Peak größer als 90%, während die Resonanzwellenlänge konstant bei λ . bleibt = 9,5 μm wie in Abb. 5b gezeigt. Außerdem bleibt die Spitzenabsorption für die zweite Resonanz größer als 80% mit θ bis 60°, fällt dann mit der Zunahme von θ . leicht ab . Die hervorragende Winkelstabilität ergibt sich aus dem gemeinsamen Merkmal von Fabry-Perot-Resonatoren, die robust gegenüber schrägen Einfallswinkeln sind [30].

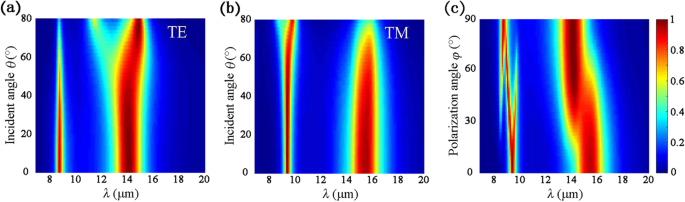
Absorptionsspektren unter verschiedenen Einfallswinkeln für a TE und b TM-Polarisation und c verschiedene Polarisationswinkel bei senkrechtem Einfall. Geometrische Parameter sind die gleichen wie in Abb. 4

Absorptionsspektren bei senkrechtem Einfall mit unterschiedlichen Polarisationswinkeln φ sind in Abb. 5c dargestellt, um die Polarisationsabhängigkeit des vorgeschlagenen Absorbers zu untersuchen. Wir nehmen an, dass der Polarisationswinkel der TE-Polarisation 0° beträgt. Aus Abb. 5c ist ersichtlich, dass als φ von 0 auf 90° zunimmt, ist das Absorptionsspektrum das gleiche wie die TM-Polarisation in Abb. 2a. Bei 0° < φ < 90°, der Einfall regt Elektronen in BP an, aufgrund seines x . sowohl in Sessel- als auch in Zickzack-Richtung zu schwingen - und y - Komponenten des einfallenden elektrischen Feldes. Folglich können Oberflächenplasmonenresonanzen gleichzeitig in Sessel- und Zickzack-Richtung von BP induziert werden.

Schlussfolgerungen

Zusammenfassend haben wir einen anisotropen Dualband-Infrarotabsorber vorgeschlagen, der aus periodischen transversalen und longitudinalen Graphen-BP-Ellipsen besteht. Der maximale PER bei jeder Resonanz kann bis zu 23 dB und 25 dB erreichen. Die dualen anisotropen Resonanzen werden den induzierten elektrischen Dipolen zugeschrieben, die sich an den Enden der kurzen und langen Achsen befinden. Durch Einstellen der Längen der kurzen Achse und der langen Achse können die ersten und zweiten Absorptionspeaks jeweils unabhängig abgestimmt werden. Darüber hinaus können die Resonanzabsorptionsbanden auch durch Ändern des entsprechenden Dotierungsniveaus von Graphen und BP abgestimmt werden. Außerdem können bei schrägem Einfall für jede Polarisation hohe Absorptionsraten an beiden Peaks erreicht werden. Der vorgeschlagene Absorber kann als abstimmbarer reflektierender Polarisator und neuartiger Infrarotsensor verwendet werden.

Verfügbarkeit von Daten und Materialien

Alle Daten sind uneingeschränkt verfügbar.

Abkürzungen

BP:

Schwarzer Phosphor

FEM:

Finite-Elemente-Methode

hBN:

Hexagonales Bornitrid

PEC:

Perfekter elektrischer Leiter

TE:

Quer elektrisch

TM:

Quermagnetisch