Magnetisierungsdynamik moduliert durch Dzyaloshinskii-Moriya-Wechselwirkung in der Spin-Transfer-Torque-Magnettunnelverbindung mit Doppelschnittstelle

Einführung

Magnetischer Direktzugriffsspeicher (MRAM) ist aufgrund seines geringen Stromverbrauchs, seiner hohen Dichte, seiner schnellen Zugriffsgeschwindigkeit, seiner nahezu unendlichen Lebensdauer und seiner guten Kompatibilität mit der CMOS-Technologie einer der vielversprechendsten Kandidaten für den nichtflüchtigen Speicher der nächsten Generation [1, 2]. Das elementare Bauelement des MRAM ist der magnetische Tunnelübergang (MTJ), der aus einer Tunnelbarriere besteht, die zwischen zwei ferromagnetischen Schichten (genannt gepinnte Schicht und freie Schicht) eingebettet ist. Ausgehend von den Fortschritten bei der senkrechten Anisotropie wurde die Strukturgröße des MTJ unter 40 nm oder sogar 1× nm skaliert [3,4,5]. Eine Herausforderung für den MTJ unter 40 nm besteht jedoch darin, die angemessene thermische Stabilitätsbarriere E . aufrechtzuerhalten = μ ₀ M _s H _k V /2. (mit μ ₀ die magnetische Vakuumpermeabilität, M _s die Sättigungsmagnetisierung, H _k das Anisotropiefeld, V das Volumen der freien Schicht). Wie diese Gleichung zeigt, ist E nimmt mit der Skalierung des MTJ ab, was zu einer Verkürzung der Datenaufbewahrungszeit führt. Um diese Herausforderung zu meistern, wurden MTJs mit doppelter Schnittstelle vorgeschlagen, um ein ausreichend hohes E . zu erreichen am Sub-40 nm-Technologieknoten [6,7,8,9,10]. Durch die Verwendung von zwei gekoppelten ferromagnetischen Schichten als zusammengesetzte freie Schicht wird das äquivalente Volumen (V ) in der Doppelschnittstelle MTJ erhöht, um die thermische Stabilitätsbarriere zu verbessern. Währenddessen wird die Dämpfungskonstante verringert, um einen niedrigen Schaltstrom zu halten.

Bei den Doppelschnittstellen-MTJs spielt die Ferromagnet/Heavy-Metal (FM/HM)-Struktur eine wichtige Rolle bei der Leistungsoptimierung. Einerseits erhöht die FM/HM-Struktur die Spin-Bahn-Kopplung (SOC), um die senkrechte Anisotropie zu induzieren. Andererseits wirkt das Schwermetall als Abstandshalter zwischen zwei ferromagnetischen Schichten der zusammengesetzten freien Schicht, um die Ruderman-Kittel-Kasuya-Yosida (RKKY)-Wechselwirkung [11] bereitzustellen, die die Magnetisierungen der beiden ferromagnetischen Schichten ferromagnetisch koppelt damit sie sich wie eine identische Schicht verhalten. Außerdem zeigen neuere Arbeiten, dass der starke SOC des Schwermetalls in Kombination mit den Atomspins des Ferromagneten eine antisymmetrische Austauschkopplung bilden könnte, die als Dzyaloshinskii-Moriya-Wechselwirkung (DMI) bezeichnet wird [12, 13]. Daher wird der DMI natürlicherweise im Doppelschnittstellen-MTJ mit FM/HM-Strukturen induziert. DMI begünstigt die chiralen magnetischen Texturen (z. B. Spinspiralen, Skyrmionen und Domänenwände vom Neel-Typ) und beeinflusst die Magnetisierungsdynamik dramatisch, wie durch aktuelle Studien bestätigt [14,15,16,17,18,19,20,21 ,22,23,24,25]. Es ist wichtig zu erwähnen, dass die Rolle von DMI im Doppelschnittstellen-MTJ komplizierter wird, da zwei FM/HM-Schnittstellen zusammen mit einer zusätzlichen RKKY-Interaktion betrachtet werden müssen. Daher ist es von Bedeutung, die Wirkung von DMI auf das Doppelschnittstellen-MTJ aufzuzeigen.

In diesem Brief untersuchen wir zum ersten Mal den Schaltprozess der Doppelschnittstellen-MTJs unter den Einwirkungen der DMI- und RKKY-Interaktion. Der Doppelschnittstellen-MTJ wird durch das Spin-Transfer-Torque (STT) geschaltet, was ein Mainstream-Ansatz für das Datenschreiben des MRAM ist. Kürzlich wurde berichtet, dass sich der DMI nachteilig auf das STT-Switching auswirkt [21, 22]. Hier zeigen unsere Ergebnisse, dass in Doppelschnittstellen-MTJs der schädliche Effekt von DMI durch die RKKY-Wechselwirkung unterdrückt werden könnte, was zu einem schnellen Schalten und einer gleichmäßigeren Dynamik führt. Unsere Arbeit beweist die Robustheit des STT-MTJ mit Doppelschnittstelle gegenüber dem negativen Grenzflächeneffekt.

Methoden

Die in dieser Arbeit untersuchte Vorrichtung ist in Abb. 1a dargestellt, mit einer FM/HM/FM-Struktur als freier Verbundschicht. Die HM-Schichtdicke wird auf einen geeigneten Wert eingestellt, damit die induzierte RKKY-Wechselwirkung zwei FM-Schichten ferromagnetisch koppelt. Eine der FM-Schichten ist magnetisch weicher, was als FL1 (freie Schicht 1) bezeichnet wird, während die andere magnetisch härter ist und als FL2 (freie Schicht 2) bezeichnet wird. Um die Magnetisierung der zusammengesetzten freien Schicht umzuschalten, wird ein Strom an den Doppelschnittstellen-MTJ angelegt und erzeugt die STT. In dieser Arbeit betrachten wir nur die übertragene STT von der Referenzschicht nach FL1, während die anderen Drehmomente zwischen FL1 und FL2 vernachlässigt werden. Dieses vereinfachte Modell stimmt mit den zuvor berichteten Arbeiten überein [26,27,28]. Die DMIs werden sowohl in FM/HM- als auch in HM/FM-Grenzflächen induziert und haben aufgrund der unterschiedlichen Chiralität die entgegengesetzten Vorzeichen [29].

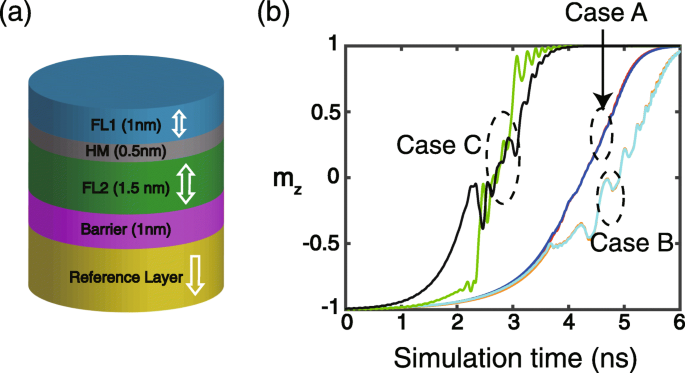
a Schematischer Aufbau des in dieser Arbeit untersuchten Gerätes. Die anderen Schichten sind der Übersichtlichkeit halber nicht gezeigt. b Typische Ergebnisse des zeitabhängigen m _z (Senkrechte-Komponente der Einheitsmagnetisierung). Fall A:σ = 1 × 10 ⁻³ J/m ² , D ₁ =D ₂ = 0 (rot für FL1, blau für FL2). Fall B:σ = 1 × 10 ⁻³ J/m ² , D ₁ = 1 mJ/m ² , D ₂ =−1 mJ/m ² (orange für FL1, cyan für FL2). Fall C:σ = 1 × 10 ⁻⁴ J/m ² , D ₁ =D ₂ = 0 (grün für FL1, schwarz für FL2)

Die Magnetisierungsdynamik von FL1 und FL2 im Doppelschnittstellen-MTJ wird durch mikromagnetische Simulation untersucht. Die zeitliche Entwicklung des Einheitsmagnetisierungsvektors wird durch die folgende Landau-Lifshitz-Gilbert (LLG)-Gleichung bestimmt. Wir wählen das OOMMF-Paket, ein Open-Source-Tool zur mikromagnetischen Simulation [30], um die Gerätestruktur zu modellieren und die LLG-Gleichung zur Analyse der Magnetisierungsdynamik zu lösen.

wo γ ist das gyromagnetische Verhältnis, m ist der Einheitsvektor entlang der Magnetisierung, z ist der Einheitsvektor entlang der Dickenrichtung, H _eff ist das effektive Feld einschließlich einachsiger senkrechter Anisotropie, 6-Nachbar-Austauschenergie, DMI-Feld, RKKY-Wechselwirkung, Entmagnetisierungsfeld, dipolarer Wechselwirkung und STT. Andere Parameter und ihre Standardwerte sind in Tabelle 1 aufgeführt, sofern nicht anders angegeben. Diese Parameterwerte entsprechen dem Stand der Technik. Was die DMI-Größe angeht, betrachten wir eine freie CoFeB/W/CoFeB-Kompositschicht im Doppelgrenzflächen-MTJ [10, 31, 32, 33]. Die berichteten experimentellen DMI-Ergebnisse von W/CoFeB variieren von 0,12 mJ/m ² bis 0,73 mJ/m ² [34,35,36]. In unserer Simulation erweitern wir den Bereich der DMI-Größe auf ±2 mJ/m ² für ein allgemeines Studium.

Die RKKY-Energie zwischen einem Paar magnetischer Momente m _ich und m _j ist definiert als E _ij = σ [1 − m _ich ∙ m _j ]/∆ _ij , wobei m _ich und m _j sind magnetische Momente von FL1 bzw. FL2. σ ist der bilineare Oberflächenaustauschkoeffizient zwischen zwei Oberflächen. ∆ _ij ist die diskrete Zellengröße in Richtung von Zelle i in Richtung Zelle j . In dieser Arbeit sind FL1 und FL2 ferromagnetisch gekoppelt, dann σ> 0, was bedeutet, dass die RKKY-Interaktion dazu neigt, m _ich parallel zu m _j . Der DMI wirkt auf die benachbarten Atomspins S ₁ und S ₂ durch ein drittes Atom mit großem SOC. Der entsprechende DMI-Hamiltonian wird als H . ausgedrückt _DM =  − D ₁₂ ∙ (S ₁ × S ₂ ), wobei D ₁₂ ist der DMI-Vektor [37]. Daher verschlechtert der DMI die Einheitlichkeit zwischen S ₁ und S ₂ , die mit der RKKY-Interaktion konkurriert.

Ergebnisse und Diskussion

Zunächst typische Simulationsergebnisse des zeitabhängigen m _z (senkrechte Komponente der Einheitsmagnetisierung) sind in Fig. 1b gezeigt. Wenn die RKKY-Wechselwirkung ausreichend stark ist (z. B. σ = 1 × 10 ⁻³ J/m ² in Fall A und Fall B) sind FL1 und FL2 miteinander gekoppelt und somit ist ihre Magnetisierungsdynamik nahezu identisch, egal ob der DMI berücksichtigt wird oder nicht. Es ist auch ersichtlich, dass die Einführung von DMI den Prozess der Magnetisierungsumschaltung verzerrt (siehe Fall B), was mit den berichteten Ergebnissen übereinstimmt [21,22,23] und auf den antisymmetrischen Austausch von DMI zurückgeführt werden kann. Wenn die RKKY-Wechselwirkung nicht stark genug ist, kann die Magnetisierungsdynamik von FL1 und FL2 nicht ideal gekoppelt werden, sodass ein signifikanter Unterschied zwischen ihnen beobachtet wird (siehe Fall C). Im Folgenden werden die Simulationsergebnisse unter einer ausreichend starken RKKY-Wechselwirkung erhalten, sofern nicht anders angegeben.

Anschließend untersuchen wir die Schaltgeschwindigkeit unter den verschiedenen RKKY-Interaktionen. Die Schaltgeschwindigkeit spiegelt sich in einer Zeit wider, in der m _z 0 erreicht (definiert als Schaltzeit). Das D ₁ und D ₂ werden auf positive bzw. negative Werte gesetzt [29]. Die entsprechenden Ergebnisse sind in Abb. 2 dargestellt. In Abwesenheit von DMI erhöht sich die Schaltzeit mit der verstärkten RKKY-Interaktion, in Übereinstimmung mit den anderen berichteten Ergebnissen [26,27,28, 38]. Der Grund dafür ist, dass die stärkere RKKY-Wechselwirkung die Magnetisierungsdynamik von FL1 und FL2 kohärenter macht, was entsprechend die Anisotropie der freien Verbundschicht erhöht. Allerdings wird die Abhängigkeit der Schaltzeit von der RKKY-Stärke in Gegenwart von DMI chaotischer. Dieses Chaos wird hauptsächlich auf die Inkonsistenz der Anisotropie zwischen FL1 und FL2 zurückgeführt. Weitere Erläuterungen werden später gezeigt. Diese Ergebnisse belegen den nicht zu vernachlässigenden Effekt von DMI auf das Schaltverhalten des Doppelschnittstellen-MTJ.

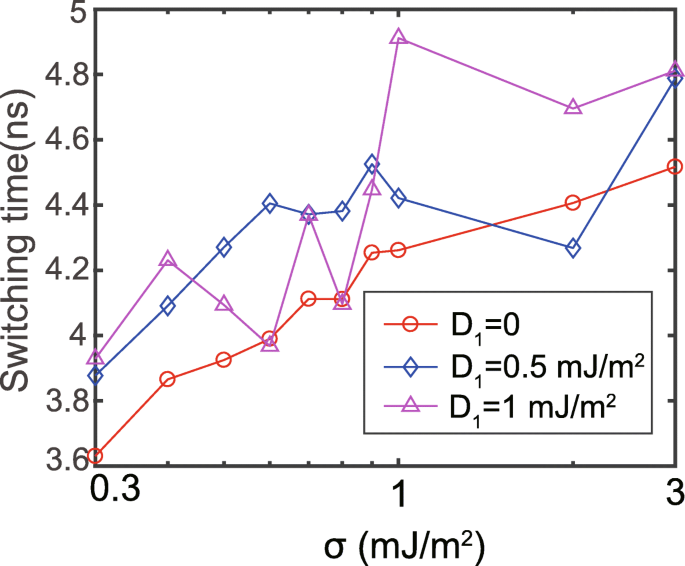
Schaltzeit in Abhängigkeit von der RKKY-Stärke, wobei σ in der logarithmischen Skala dargestellt ist. D ₁ und D ₂ werden auf die gleichen Werte gesetzt, jedoch mit entgegengesetzten Vorzeichen

Als nächstes untersuchen wir die Wirkung von DMI genauer. Abbildung 3 zeigt die Schaltzeit in Abhängigkeit von der DMI-Stärke. Es ist wichtig zu erwähnen, dass D ₁ und D ₂ sind in Fig. 3a absichtlich auf die gleichen positiven Werte gesetzt, obwohl sie in Wirklichkeit die entgegengesetzten Vorzeichen haben. Mit anderen Worten, Abb. 3a entspricht einem virtuellen Fall, den wir untersuchen, um das Simulationsmodell zu verifizieren. Aus Sicht der physikalischen Theorie werden die schädlichen Wirkungen zweier positiver DMIs unter der Wirkung der ferromagnetisch gekoppelten RKKY-Wechselwirkung kumuliert. Daher wird erwartet, dass die Schaltzeit mit zunehmendem D . ansteigt ₁ und D ₂ , wie in den vorherigen Arbeiten berichtet [21, 22]. Diese Analyse stimmt gut mit den in Abb. 3a gezeigten Ergebnissen überein. Damit wird die Rationalität des Simulationsmodells validiert. Im Gegensatz zu Abb. 3a könnten die schädlichen Auswirkungen von DMI abgemildert werden, wenn D ₁ und D ₂ haben die entgegengesetzten Vorzeichen, wie in Fig. 3b gezeigt, wo die Änderung der Schaltzeit im Vergleich zu Fig. 3a viel kleiner ist. Beachten Sie, dass in Fig. 3b die Kurve nicht genau monoton ist, die lokale Fluktuation wird später erklärt. Bemerkenswerterweise konnten die Auswirkungen von DMIs an zwei Schnittstellen durch eine geeignete Abstimmung der Größen von D . ausgeglichen werden ₁ und D ₂ , wie in Abb. 3c gezeigt. Diese Ergebnisse können mit Chiralitätstheorien wie folgt erklärt werden.

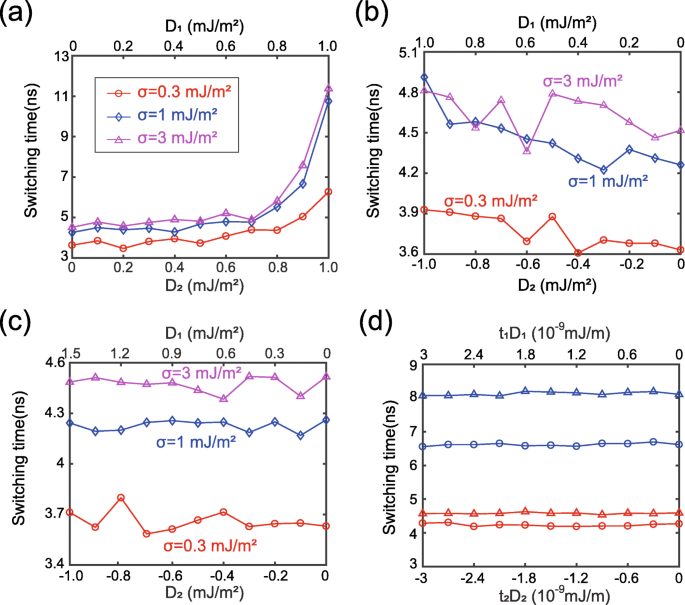
Schaltzeit in Abhängigkeit von der DMI-Stärke. a D ₁ und D ₂ werden auf den gleichen positiven Wert gesetzt. b D ₁ und D ₂ werden auf den gleichen Wert gesetzt, jedoch mit entgegengesetzten Vorzeichen. c D ₁ und D ₂ sind so konfiguriert, dass sie t . erfüllen ₁ D ₁ + t ₂ D ₂ = 0. d Zusätzliche Ergebnisse beim Ändern der Dicke oder Anisotropie konstant, während t . beibehalten wird ₁ D ₁ + t ₂ D ₂ = 0. blaue Linie:t ₁ wird auf 2 nm geändert; rote Linie:t ₁ wird auf 1,5 nm geändert. Dreiecksdaten:σ = 3 × 10 ⁻³ J/m ² . Kreisdaten:σ = 1 × 10 ⁻³ J/m ²

Die DMI-Energie wird als E . ausgedrückt _DM = t ∬ D [m _x (∂m _z /∂x ) − m _z (∂m _x /∂x ) + m _y (∂m _z /∂y ) − m _z (∂m _y /∂y )]d ² r = tDε _DM [39], wobei D ist die kontinuierliche DMI-Konstante, t ist die Dicke der ferromagnetischen Schicht. Wie oben erwähnt, ist die Magnetisierungsdynamik von FL1 und FL2 bei ausreichend starker RKKY-Wechselwirkung nahezu identisch. In diesem Fall das gleiche ε _DM wird in FL1 und FL2 erhalten. Dann könnte die gesamte DMI-Energie von FL1 und FL2 berechnet werden durch E _tot = (t ₁ D ₁ + t ₂ D ₂ )ε _DM . Daher durch Einstellen von D ₁ /D ₂ =  − t ₂ /t ₁ , könnten die DMI-Effekte von FL1 und FL2 bei einem ausreichend großen σ vollständig ausgeglichen werden, in Übereinstimmung mit Abb. 3c. Diese Schlussfolgerung wird weiter durch die zusätzlichen Ergebnisse in Abb. 3d bestätigt, wo die anderen Parameter absichtlich variiert werden, während D . beibehalten wird ₁ /D ₂ =  − t ₂ /t ₁ .

Die äquivalente DMI-Größe (D _eq ) der zusammengesetzten freien Schicht kann als D . ausgedrückt werden _eq = (t ₁ D ₁ + t ₂ D ₂ )/(t ₁ + t ₂ ), die zur quantitativen Analyse der Wirkung von DMI auf das Doppelschnittstellen-MTJ verwendet werden könnte. Um die Wirksamkeit dieser Gleichung zu validieren, zeigen wir in Abb. 4a zwei Gruppen von Simulationsergebnissen, wobei zwei Kurven unter dem gleichen D . erhalten wurden _eq aber mit zwei Paaren unterschiedlicher {D ₁ , D ₂ }-Werte. Obwohl es einen kleinen Unterschied zwischen den beiden Kurven gibt, sind ihre Gesamttrends ähnlich und bestätigen die nachteilige Wirkung von DMI auf die STT-Umschaltung. Hier könnte der Unterschied zwischen zwei Kurven wie folgt erklärt werden. FL1 und FL2 haben unterschiedliche Anisotropiekonstanten, was zu der lokal unsicheren Oszillation der Magnetisierungsdynamik führt, wie in Abb. 4c gezeigt. Das gleiche Phänomen wird auch in Fig. 2 und Fig. 3b beobachtet. Stattdessen ist in Fig. 4b, d ein Idealfall dargestellt, bei dem die Anisotropiekonstanten von FL1 und FL2 auf die gleichen Werte eingestellt sind. Offensichtlich ist eine gute Übereinstimmung zwischen den beiden Kurven erkennbar, was darauf hinweist, dass der obige Ausdruck von D _eq könnte den äquivalenten DMI-Effekt des Doppelschnittstellen-MTJ gut beschreiben.

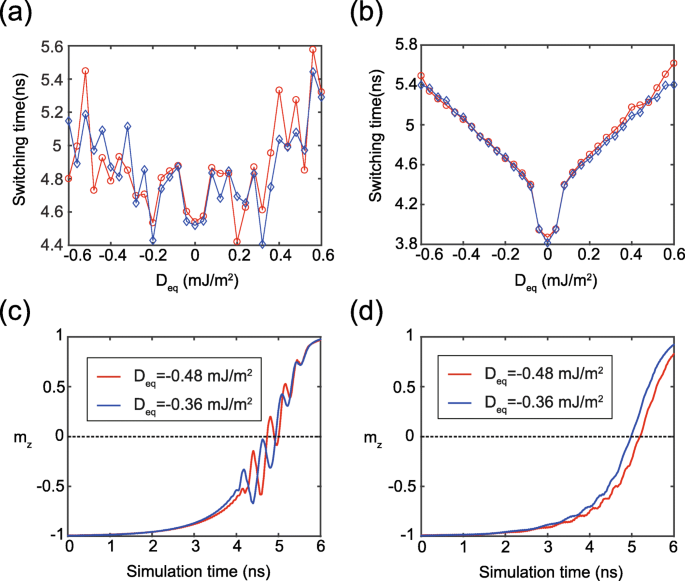
a , b Schaltzeit in Abhängigkeit von D _eq . Jedes D _eq erhält man mit zwei Paaren unterschiedlicher {D ₁ , D ₂ } Werte nach D _eq = (t ₁ D ₁ + t ₂ D ₂ )/(t ₁ + t ₂ ). Rote Kurve:D ₁ ist mittlerweile abwechslungsreich D ₂ ist auf 1 mJ/m ² festgelegt . Blaue Kurve:D ₁ und D ₂ werden immer auf den gleichen Wert gesetzt. Hier = 1 × 10 ⁻² J/m ² . In a , die anderen Parameter sind als Tabelle 1 konfiguriert. In b , K _{du 1} = K _{du 2} = 0,7 mJ/m ³ für einen Idealfall. c , d Typische Ergebnisse von zeitabhängigem m _z entspricht a und b , bzw.

Schließlich analysieren wir die zeitliche Entwicklung der Magnetisierungsdynamik genauer. Bild 5 zeigt die zeitabhängige Energie beim Magnetisierungswechsel. Die DMI-Energien von FL1 und FL2 werden akkumuliert oder aufgehoben, je nach Vorzeichen und Größe von D ₁ und D ₂ . Dieser Trend stimmt gut mit den obigen theoretischen Modellen überein. Darüber hinaus werden die RKKY-Energien auf niedrigen Werten gehalten, was bestätigt, dass die magnetischen Momente von FL1 und FL2 synchron angetrieben werden. Die Verteilungen von RKKY- und DMI-Feldern sind in Abb. 6 dargestellt, wobei das RKKY-Feld in verschiedenen Fällen unterschiedliche Rollen spielt. Erstens ist im Fall von DMI ungleich Null (siehe Fall 2 und Fall 3) das RKKY-Feld viel stärker im Vergleich zu dem Fall von Null DMI (siehe Fall 1). Es versteht sich, dass das RKKY-Feld die zusätzliche Ungleichmäßigkeit der magnetischen Texturen in Gegenwart von DMI überwinden muss. Zweitens, wenn D ₁ und D ₂ das entgegengesetzte Vorzeichen hat, widersteht das RKKY-Feld den DMI-Feldern sowohl in FL1 als auch in FL2 (siehe Fall 2). Als Ergebnis wird der DMI geschwächt, so dass die Magnetisierungsdynamik gleichmäßiger wird. Im Gegensatz dazu einmal D ₁ und D ₂ das gleiche Vorzeichen haben, widersteht das RKKY-Feld dem DMI-Feld in einer ferromagnetischen Schicht, unterstützt es jedoch in der anderen ferromagnetischen Schicht (siehe Fall 3). Somit hat das gesamte DMI-Feld immer noch einen gewissen Einfluss auf die Magnetisierungsdynamik, was bestätigt, dass das DMI nicht aufgehoben werden kann, wenn D ₁ und D ₂ haben das gleiche Vorzeichen.

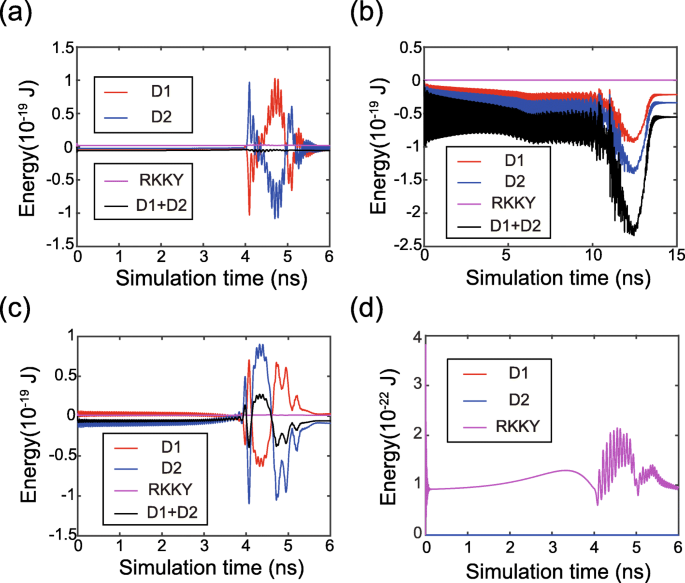
Zeitliche Entwicklung der DMI- und RKKY-Energien. a D ₁ = 1,5 mJ/m ² , D ₂ =  − 1 mJ/m ² , d. h. der DMI-Effekt wird aufgehoben. b D ₁ = D ₂ = 1 mJ/m ² , d. h. der DMI-Effekt wird akkumuliert. c D ₁ = 1 mJ/m ² , D ₂ =  − 1 mJ/m ² d. h. der DMI-Effekt wird abgeschwächt, aber nicht aufgehoben. d D ₁ = D ₂ = 0

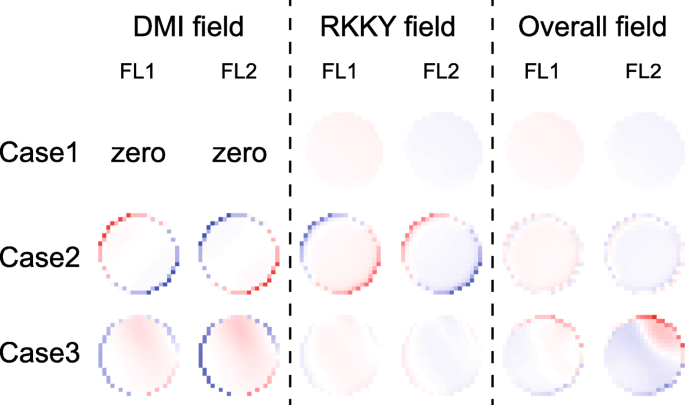
Räumliche Verteilungen der DMI- und RKKY-Felder. Hier wird für jeden Fall ein typisches Ergebnis zu einem bestimmten Zeitpunkt angezeigt. Die Schlussfolgerung bleibt zu den anderen Zeitpunkten unverändert. Fall 1:D ₁ = D ₂ = 0. Fall 2:D ₁ = 1,5 mJ/m ² , D ₂ =  − 1 mJ/m ² d. h. der DMI-Effekt wird aufgehoben. Fall 3:D ₁ = D ₂ = 1 mJ/m ² , d. h. der DMI-Effekt wird akkumuliert

Abbildung 7 zeigt die mikromagnetischen Konfigurationen von FL1 und FL2 während der Magnetisierungsumschaltung. Obwohl die Domänenwand in allen Fällen erscheint, konnten zu bestimmten Zeitpunkten unterschiedliche Merkmale beobachtet werden. Es ist bekannt, dass der DMI die ungleichmäßigen magnetischen Texturen bevorzugt. Nichtsdestotrotz wird in Abb. 7 auch in Gegenwart von DMI noch eine gleichmäßige Magnetisierung gebildet (siehe die Zeit, wenn m _z =  − 0.5 im Fall 2), solange der DMI-Effekt aufgehoben wird. Auch dieses Ergebnis bestätigt das obige theoretische Modell. Darüber hinaus ist auch ersichtlich, dass die Magnetisierungsdynamik ungleichmäßiger ist, wenn D ₁ und D ₂ haben das gleiche Vorzeichen (siehe Fall 3, wo die Domänenwand immer erscheint), im Einklang mit der obigen Analyse. Wir zeigen auch einige Ergebnisse, die mit kleineren MTJ simuliert wurden (siehe die letzten beiden Zeilen in Abb. 7). Der Unterschied der mikromagnetischen Konfigurationen zwischen Fall 2 (DMI wird nicht aufgehoben) und Fall 3 (DMI wird nicht aufgehoben) ist bemerkenswerter.

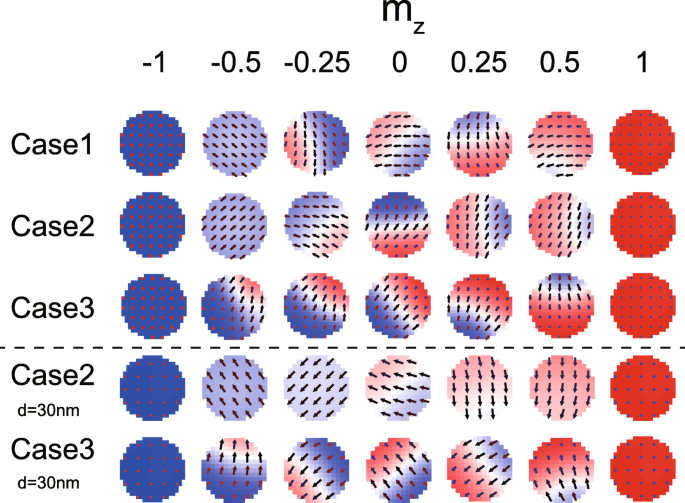
Mikromagnetische Konfigurationen während der Magnetisierungsumschaltung. Hier werden die Fälle 1~3 mit den gleichen Parametern wie in Abb. 6 konfiguriert

Schlussfolgerung

Wir haben die Wirkung von DMI auf die Doppelschnittstelle STT-MTJ umfassend untersucht. Bekanntlich wurde das Double-Interface MTJ zur Erhöhung der thermischen Stabilitätsbarriere entwickelt. In dieser Arbeit beweisen unsere Ergebnisse einen weiteren Vorteil von Double-Interface-MTJ, nämlich die Unterdrückung der schädlichen Wirkung von DMI. Die DMIs in zwei ferromagnetischen Schichten könnten unterdrückt oder sogar ausgelöscht werden, wenn sie mit entsprechenden Werten und entgegengesetzten Vorzeichen konfiguriert werden, was natürlich von der STT-MTJ-Struktur mit Doppelschnittstelle erfüllt wird. Theoretische Modelle wurden vorgeschlagen, um die Schlussfolgerung zu erklären. Die Ergebnisse der mikromagnetischen Simulation wurden diskutiert, um die Rolle von DMI in der Magnetisierungsdynamik aufzuzeigen. Unsere Arbeit bietet einen praktikablen Ansatz zur Minimierung des DMI im STT-MTJ mit doppelter Schnittstelle.

Verfügbarkeit von Daten und Materialien

Alle Daten sind uneingeschränkt verfügbar.

Abkürzungen

DMI:

Dzyaloshinskii-Moriya-Interaktion

FL:

Kostenlose Ebene

FM/HM:

Ferromagnet/Schwermetall

MRAM:

Magnetischer Direktzugriffsspeicher

MTJ:

Magnetischer Tunnelübergang

RKKY:

Ruderman–Kittel–Kasuya–Yosida

SOC:

Spin-Bahn-Kopplung

STT:

Spin-Transfer-Drehmoment