Riesiger abstimmbarer Zirkulardichroismus von großflächigen extrinsischen chiralen Metall-Nanocrescent-Arrays

Einführung

Ein Objekt ist chiral, wenn sich seine Struktur von seinem Spiegelbild-Enantiomer unterscheidet [1]. Chiralität ist eine allgegenwärtige Eigenschaft einer Vielzahl von Verbindungen, wie etwa biologischen und chemischen Substanzen oder künstlichen Metamaterialien [2]. Diese strukturelle Eigenschaft wird in vielen Bereichen wie Physik, Biologie, Chemie und Medizin häufig verwendet [3,4,5,6]. Chirale Edelmetall-Nanostrukturen wurden in den letzten Jahrzehnten aufgrund ihrer abstimmbaren optischen Eigenschaften, zu denen optische Rotation, asymmetrische Transmission von zirkular polarisiertem Licht und außergewöhnlicher Zirkulardichroismus (CD) gehören, umfassend untersucht [7,8,9,10,11 ,12,13,14]. Diese außergewöhnlichen Eigenschaften werden der starken optischen Reaktion dieser Strukturen zugeschrieben und sie wird durch lokalisierte Oberflächenplasmonenresonanzen (LSPRs) erzeugt. Dieses Phänomen ist empfindlich gegenüber Form, Größe und Umgebung der Metallnanostrukturen [15,16,17]. Aus diesen Gründen können chirale Metall-Nanostrukturen in vielen Anwendungen eingesetzt werden, beispielsweise bei der negativen Brechung [18,19,20], bei der Manipulation der Polarisation einer Lichtquelle [21,22,23] und bei der chiralen Molekülsensorik [ 24, 25].

Optische Chiralität kann auch in achiralen Metamaterialien erzeugt werden, indem die Spiegelsymmetrie der Versuchsanordnung durch schräge Beleuchtung gebrochen wird. Dieses Phänomen wird aufgrund des Fehlens der zweizähligen Rotationssymmetrie der Verbindung als „extrinsische Chiralität“ bezeichnet. Die extrinsische Chiralität wurde 1945 von Bunn eingeführt und nachgewiesen. Zheludev und Mitarbeiter entdeckten die extrinsische chirale Reaktion, die durch extrinsische Chiralität in einem Metallspaltring induziert wird. Darüber hinaus untersuchten sie den Wechselwirkungsmechanismus zwischen dem elektrischen Dipol und dem magnetischen Dipol dieser Strukturen [26, 27]. Kürzlich haben Leon et al. [28] demonstrierten experimentell und theoretisch den großen Circulardichroismus in einer Metaoberfläche aus Metallspaltringanordnungen. Im Vergleich zu chiralen Metallnanostrukturen sind extrinsische chirale Metallnanostrukturen mit einer großen Oberfläche einfacher herzustellen [29,30,31,32,33,34]. Darüber hinaus zeigen sie noch stärkere chirale optische Eigenschaften wie CD, was bedeutet, dass die Verbindung unterschiedliche Transmissionen aufweist, wenn sie mit linkszirkular polarisierten (LCP) oder rechtszirkular polarisierten (RCP) einfallenden Wellen wechselwirkt [35, 36]. In einer früheren Arbeit derselben Forschungsgruppe wurde eine großflächige zufällig verteilte metallische sichelförmige Nanostruktur hergestellt, deren hohe optische Chiralität nachgewiesen wurde [37]. Aufgrund der geringen Dichte der zufällig verteilten Nanosicheln war der im Experiment erhaltene CD-Koeffizient jedoch niedriger als erwartet. Darüber hinaus wies die Gleichmäßigkeit der zufällig verteilten metallischen Halbmond-Nanostrukturen mehrere Mängel auf, die den Einsatz dieser Verbindung in Anwendungen verhinderten. Da die Array-Struktur eine große Zelldichte und eine gute Gleichmäßigkeit bietet. Die Entwicklung einfacher, bekannter und kostengünstiger Herstellungsverfahren zur Herstellung großflächiger, einheitlicher, extrinsischer chiraler Metallarraystrukturen stellt eine neue Herausforderung dar, um die Verwendung von Metallchiralität in Anwendungen zu fördern.

In dieser Arbeit wurde ein periodisches Array von metallischen Halbmond-Nanostrukturen mit Gitterkonstanten im Bereich von 500–1000 nm unter Verwendung von Polystyrol (PS)-Mikrosphären-Arrays als Templat hergestellt. Der Maximalwert der CD (0,51) wurde bei 1270 nm für eine Gitterkonstante von 800 nm gemessen. Simulationen der vorgeschlagenen Struktur wurden implementiert und stimmen hervorragend mit den experimentellen Messungen überein. Den Simulationen zufolge ist der Hauptmechanismus, der diesem intensiven CD-Effekt zugrunde liegt, die selektive Anregung der LSMs durch das zirkular polarisierte Licht. Darüber hinaus wurde die Abstimmbarkeit des CD-Effekts experimentell durch Änderung der Gitterkonstanten der Struktur überprüft. Da die PS-Mikrosphären kommerziell erhältlich sind, kann die extrinsische Chiralität der periodischen Anordnung metallischer Halbmond-Nanostrukturen über einen weiten Spektralbereich moduliert werden, der vom sichtbaren bis zum Infrarotbereich reicht. Die vorgeschlagene Probe hat die Vorteile eines hohen Dichroismus, einer einfachen Herstellung und der Kompatibilität mit Standard-Fertigungstechniken, was zu Bildgebungs- und Sensoranwendungen von zirkular polarisiertem Licht führen könnte.

Methoden

Die großflächigen, gleichseitigen Dreiecksgitterarrays aus metallischen Halbmond-Nanostrukturen mit unterschiedlichen Gitterkonstanten wurden unter Verwendung von PS-Nanosphären unterschiedlicher Größe als Template hergestellt. Die Durchmesser der in dieser Arbeit verwendeten PS-Nanosphären betragen 500, 650, 800, 850 und 1000 nm. Der Herstellungsprozess ist in Fig. 1a gezeigt. Zunächst wurde auf einer vorbehandelten Quarzoberfläche durch den Selbstorganisationsprozess eine einschichtige hexagonale dicht gepackte Anordnung von PS-Kugeln gebildet [38]. Die dicht gepackte kolloidale Monoschicht wurde dann durch Bildung eines Argonplasmas für 6 min (PDC-32G-2) geätzt, um ein nicht dicht gepacktes Templat zu erhalten [39, 40]. Die Probe wurde auf einem Druck von 0,2 mbar gehalten und die Eingangsleistung des Lichts wurde auf 100 mW eingestellt. Anschließend wurde eine 50 nm dünne Goldschicht durch Ionenstrahlsputtern mit einem Neigungswinkel von 45° abgeschieden. Der Goldfilm wurde durch den Ionenstrahl vertikal geätzt. Schließlich wurde das Nanokügelchen-Templat mit Aceton entfernt und die großflächigen, gleichseitigen Dreiecksgitteranordnungen aus metallischen Halbmond-Nanostrukturen gebildet. Nach grundlegenden geometrischen Überlegungen kann der Halbmonddurchmesser durch die Wahl eines anderen Durchmessers der PS-Nanosphären angepasst werden. Darüber hinaus ist die Filmdicke direkt zugänglich, indem die auf der Probe abgeschiedene Goldmenge und die maximale Halbmondbreite w . kontrolliert werden des Metalls ist gegeben als

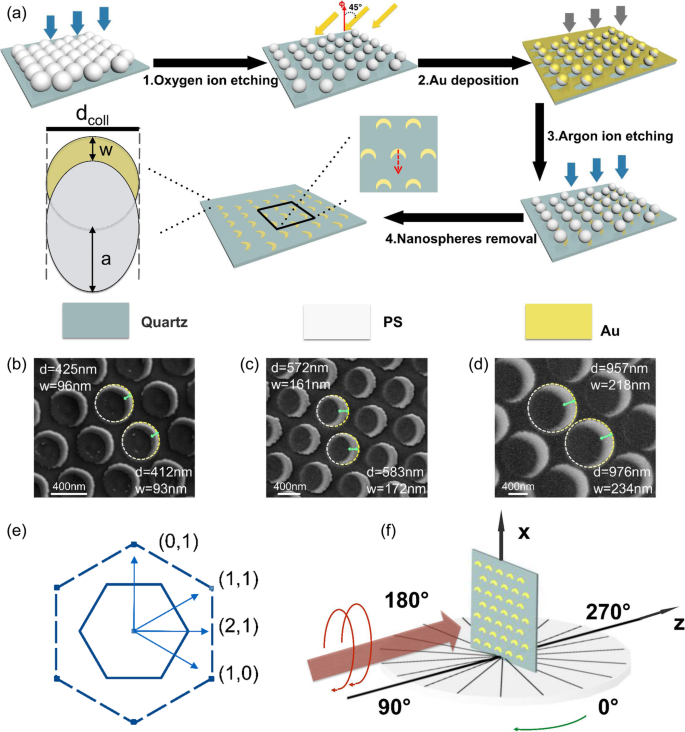
a Skizze des Halbmond-Präparationsprozesses und der Partikelgeometrie mit Angabe des Durchmessers d _{Zusammenfassung} des Maskierungskolloids und der maximalen Halbmondbreite w des Metalls. Der rote Pfeil zeigt die positive Richtung der Spiegelachse von Nanosicheln an; b –d REM-Aufnahmen der Struktur mit Gitterkonstanten:b 500 nm, c 800 nm, d 1000 nm. Die Länge des grünen Pfeils repräsentiert die maximale Breite der halbmondförmigen Struktur w . Die gestrichelte Linie repräsentiert den Durchmesser der sichelförmigen Struktur nach der Anpassung an einen Kreis (geätzte PS-Nanosphären); e Das reziproke Gitter wird von den Basisvektoren (1, 0) und (0, 1) aufgespannt. Die reziproken Vektoren (1, 1) und (2, 1) werden angezeigt. Die durchgezogenen und gestrichelten Linien im Diagramm des reziproken Gitters stellen die Grenzen der ersten bzw. zweiten Brillouin-Zone dar. f Schematischer Aufbau des Experiments

Ersetzen von Φ =45°, verwendet in den hier diskutierten Studien, in der obigen Gleichung ergibt

Dabei ist zu beachten, dass es in der Realität zu Abweichungen von der in Abb. 1a vorgeschlagenen idealisierten Geometrie kommt. Die w , zu sehen in den Rasterelektronenbildern, Abb. 2b–d, ist etwas kleiner als der Idealfall. Als zusätzliche systematische Unsicherheiten sollten das Ätzen und die Aggregation von Kolloiden berücksichtigt werden. Der rote Pfeil in Fig. 1a definiert die positive Richtung der Spiegelachse von Nanocrescents, die in Richtung der Öffnungsrichtung von Nanocrescents verläuft. Wie in Abb. 1b–d gezeigt, ist die Richtung der Spiegelachse von Nanosicheln konsistent und konnte über den Kippprozess bestimmt werden und wurde künstlich kontrolliert. Die metallischen Nanocrescents ordnen sich regelmäßig in einem relativ großen Bereich an. Die Orientierung des Gitters ist jedoch aufgrund von Fertigungsfehlern außerhalb des optischen Messbereichs, der einige Quadratmillimeter misst, schwer zu kontrollieren. Daher ist die relative Orientierung zwischen der Richtung der Metallnanosicheln und dem gleichseitigen Dreiecksgitter zufällig.

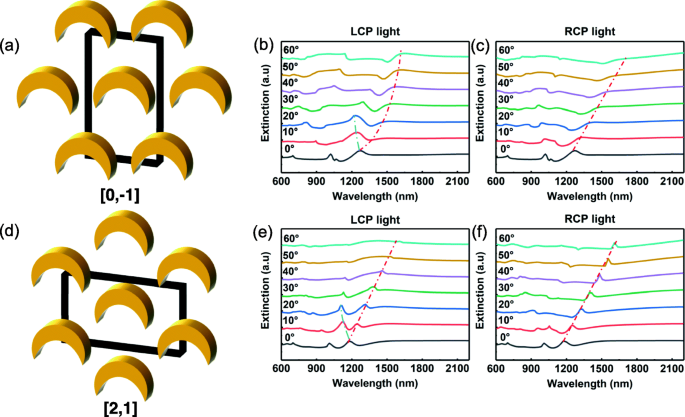
a , d Schema des Gitters, bei dem die Spiegelachse von Nanosicheln auf die [0, − 1]- bzw. [2, 1]-Kristallachse ausgerichtet ist (die Blöcke repräsentieren die Kristallzelle); b , c Extinktionsspektren, die unter Verwendung eines einfallenden Lichts mit linker bzw. rechter zirkularer Polarisation aufgezeichnet wurden. Die Spiegelachse von Nanosicheln ist in Richtung [0, − 1] des Kristallgitters gerichtet; e , f Extinktionsspektren, die unter Verwendung eines einfallenden Lichts mit linker bzw. rechter zirkularer Polarisation aufgezeichnet wurden. Die Spiegelachse von Nanosicheln ist in die [2, 1]-Richtung des Kristallgitters gerichtet

Die Probe mit extrinsischer chiraler Antwort wurde mit einem Maxwell-Gleichungslöser modelliert, der auf der Finite-Difference-Time-Domain (FDTD)-Methode basiert. Die Metall-Nanohalbmond-Array-Struktur mit einer Gitterkonstante von 800 nm (d. h. die Probe, die mit PS-Mikrokügelchen von 800 nm Durchmesser gebildet wurde) wurde ausgewählt, um die Simulation durchzuführen. Während im Experiment die relative Orientierung zwischen der Spiegelachse von Nanocrescents und dem Gitter zufällig ist, wurde in der Simulation die Spiegelachse von Nanocrescents in Richtung der [0, − 1] und [2, 1] Kristallachse gewählt, wie in gezeigt Abb. 2a, d, der Einfachheit halber. Hier bildet der Quarz das Substrat und das Au das Metall, wie im Modell von Johnson und Christy. Entlang des x . wurden periodische Randbedingungen angewendet - und y -Richtungen. Die FDTD-Maschenweite wurde auf 2 nm eingestellt, um eine genaue Berechnung des plasmonischen Effekts zu ermöglichen. Durch Richten von linkszirkular und rechtszirkular polarisiertem Licht auf die Probe und gleichzeitiges Rotieren der Probe um die Rotationssymmetrieachse des Metall-Nanohalbmonds kann der Einfallswinkel verändert werden, wie in Abb. 1e gezeigt.

Ergebnisse und Diskussion

Die Oberflächengitterresonanzen (SLRs) in einer zweidimensionalen Anordnung von Nanopartikeln wurden umfassend untersucht. Die Extinktionsmerkmale im Spektrum resultieren aus den Gitteroberflächenmoden (LSMs), die durch streifende Beugungsordnungen oder Rayleigh-Anomalien (RAs) erzeugt werden [28, 41]. In dieser Arbeit wird die Größe der Nanopartikel durch die Gitterkonstante angenähert. Aus diesem Grund können die im Spektrum vorhandenen Extinktionsmerkmale, die aus den LSMs resultieren, noch beobachtet werden, obwohl die Umgebungsbrechungsindexasymmetrie durch Hinzufügen des Quarzsubstrats eingeführt wurde [42]. Darüber hinaus kann eine signifikante Rotverschiebung beobachtet werden, die aufgrund der starken Kopplung der LSPR mit den benachbarten Metallpartikeln aus der Rayleigh-Anomaliebedingung stammt [43]. Diese Phänomene werden in den folgenden Abschnitten dieser Arbeit detailliert vorgestellt.

Wenn die Spiegelachse von Nanosicheln in Richtung der [0, − 1]-Gitterkristallachse zeigt und der Einfallswinkel des Lichts 0° beträgt, überlappen sich die von den beiden zirkular polarisierten Lichts erzeugten Extinktionsspektren. Darüber hinaus weist jedes Spektrum drei Extinktionspeaks auf, die bei 697 nm, 1019 nm bzw. 1265 nm liegen (Abb. 2b, c). Aufgrund der geringen Intensität des Extinktionspeaks bei 697 nm und seines geringen Beitrags zum CD-Effekt wurden keine weiteren Untersuchungen zu diesem Merkmal durchgeführt. Der bei 1265 nm lokalisierte Extinktionspeak wird hauptsächlich von den LSMs (± 1, 0), (1, 1) und (− 1, − 1) induziert, während das bei 1019 nm erscheinende Merkmal hauptsächlich von den LSMs erzeugt wird (2 , 1) und (− 2, − 1). Die Einführung der Sichelstruktur beseitigt die Entartung, da sie durch einen relativ geringen Symmetriegrad gekennzeichnet ist. Als Ergebnis teilt sich der Extinktionspeak bei 1019 nm auf, wenn er mit einem Licht mit einem Einfallswinkel von 0° beleuchtet wird. Wenn der Einfallswinkel θ zunimmt und die Spiegelachse parallel zur [0, − 1]-Richtung des Kristallgitters ist, kann die Resonanzgleichung der LSMs wie folgt geschrieben werden:

\( {\lambda}_{RA}^{\pm}\left(\theta \right)=\frac{\sqrt{3}}{2}\varLambda n\left[1\pm \frac{\sqrt {3}}{2}\sin\left(\theta\right)\right]\) für die Modi (±1, 0), (1, 1) und (−1, −1);

\( {\lambda}_{RA}^{\pm}\left(\theta \right)=\frac{1}{2}\varLambda n\left[1\pm \sin \left(\theta \right )\right] \) für die Moden (2, 1), (−2, −1). wo Λ ist die Gitterkonstante des gleichseitigen Dreiecksgitters, die 800 nm misst; das Symbol ± (positiv oder negativ) hängt von der ersten Ziffer der LSMs ab; n ist der effektive Brechungsindex der Umgebung des gleichseitigen Dreiecksgitters, der für jede LSM nahezu identische Werte (1,25) annimmt. Durch Einführen dieser Werte in die obigen Ausdrücke sollte der durch die LSMs (± 1, 0), (1, 1) und (− 1, − 1) induzierte Extinktionspeak bei 866 nm erscheinen, während das durch die LSMs induzierte Merkmal (2, 1) und (− 2, − 1) bei 500 nm. Die Simulationsergebnisse zeigen jedoch, dass diese Peaks bei 1265 nm und 1019 nm liegen, was bedeutet, dass sie gegenüber den berechneten stark rotverschoben sind. Die Rotverschiebung wird durch die starke Kopplung der LSPR-Moden mit den benachbarten Metallnanopartikeln verursacht [43]. Die Kopplungsstärke der LSPR-Moden mit den benachbarten Metall-Nanohalbmonden ist für verschiedene geometrische Konfigurationen und Moden unterschiedlich, was eine Rotverschiebung in ihrer optischen Reaktion induziert. In dieser Arbeit sind die unterschiedlichen Werte der Rotverschiebungen abhängig vom effektiven Brechungsindex, n , in der Resonanzgleichung. Der effektive Brechungsindex, der gemessen wird, wenn die Spiegelachse von Nanosicheln in Richtung der [0, − 1]-Kristallachse und θ . liegt =0° ist 1,46 für die LSMs (± 1, 0), (1, 1) und (− 1, − 1) und 2,04 für die LSMs (2, 1) und (− 2, − 1). Wenn der Einfallswinkel zunimmt, wird die Entartung beseitigt und die Extinktionspeaks bei 1265 nm und 1019 nm werden breiter oder gespalten. Die Beseitigung der Entartung ist ein sehr komplizierter Prozess, da sich die Anregungseffizienzen der LSPR-Moden mit unterschiedlichen Trends mit der Zunahme von θ . ändern . Daher konzentriert sich diese Arbeit auf den Hauptfaktor, der den enormen CD-Effekt verursacht. Wie in Fig. 2b, c gezeigt, wird der bei 1265 nm befindliche Extinktionspeak bei Zunahme des LCP-Lichteinfallswinkels blauverschoben, aber dieses Phänomen wird in den Extinktionsspektren nicht beobachtet, wo RCP-Licht verwendet wird. Diese Ergebnisse zeigen einen signifikanten Unterschied zwischen den Extinktionsspektren, die mit RCP- und LCP-Einfallslicht gemessen wurden, und dies kann mit dem großen gemessenen CD-Effekt zusammenhängen; während LCP-Licht die (− 1, 0) und (− 1, − 1) LSMs anregen kann, passiert dies bei RCP-Licht nicht.

Wenn die Spiegelachse von Nanosicheln mit der [2, 1]-Achse des Gitters ausgerichtet ist, werden ähnliche Ergebnisse erhalten. Wie in Abb. 2e, f gezeigt, wenn θ =0°, überlappen sich die Extinktionsspektren für die beiden Arten von zirkular polarisiertem einfallendem Licht. Darüber hinaus weist jedes Spektrum auch drei Extinktionspeaks auf, die sich bei 697 nm, 1019 nm bzw. 1171 nm befinden. Der bei 697 nm liegende Extinktionspeak wurde bei der folgenden Analyse nicht berücksichtigt. Die Beobachtungen legen nahe, dass der Extinktionspeak bei 1171 nm hauptsächlich durch die LSMs (0, ± 1) induziert wird, während der bei 1019 nm positionierte von den LSMs (− 1, 1), (1, − 1) erzeugt werden kann. , (1, 2) und (− 1, − 2). Bei Zunahme des Einfallswinkels θ , und wenn die Spiegelachse parallel zur [2, 1]-Richtung des Gitters ist, kann die Resonanzgleichung der LSMs wie folgt geschrieben werden:

\( {\lambda}_{RA}^{\pm}\left(\theta\right)=\frac{\sqrt{3}}{2}\varLambda n\left[1\pm \sin\left( \theta \right)\right] \) für die (0, ±1)-Modi;

\( {\lambda}_{RA}^{\pm}\left(\theta\right)=\frac{1}{2}\varLambda n\left[1\pm \frac{\sqrt{3}} {2}\sin\left(\theta\right)\right]\) für die Moden (−1, 1), (1, −1), (1, 2) und (−1, −2).

Das Vorzeichen ± (positiv oder negativ) hängt von der zweiten Ziffer der LSMs ab. Wenn θ =0°, n beträgt 1,35 für die LSMs (0, ± 1), während sie 2,04 für die LSMs (− 1, 1), (1, − 1), (1, 2) und (− 1, − 2) beträgt. Wenn der Einfallswinkel zunimmt, werden die Extinktionspeaks bei 1171 nm und 1019 nm breiter oder gespalten. Wenn die Spiegelachse von Nanosicheln parallel zur [0, – 1]-Kristallachse ist, ist der signifikanteste Unterschied zwischen den Extinktionsspektren, die mit RCP- und LCP-Einfallslicht aufgenommen wurden, eine Reihe von Extinktionspeaks. Sie sind im Vergleich zum Peak bei 1171 nm blauverschoben. Außerdem erscheinen sie bei Vergrößerung des Einfallswinkels nur in den Extinktionsspektren, die über das LCP-Einfallslicht gemessen werden, was jedoch bei Verwendung von RCP-Licht nicht beobachtet werden kann. Diese Beobachtung könnte den gemessenen großen CD-Effekt erklären, da nur das LCP-Licht das (0, − 1) LSM anregen kann. Die selektive Anregung der LSMs durch links- und rechtszirkular polarisiertes Licht könnte dann für den großen CD-Effekt verantwortlich sein, der in extrinsischen chiralen Array-Strukturen beobachtet wird, und diese Beobachtung stimmt mit Lit. [28].

Eine experimentelle Messung wurde durchgeführt, um die Extinktionsspektren und die CD-Spektren der Proben zu erhalten. Ein Messsystem, das ein Ultraviolett-sichtbares-nahes Infrarot-Spektrophotometer darstellt, wurde entwickelt. Das Licht wird durch ein Glan-Taylor-Prisma und eine Breitspektrum-Viertelwellenplatte geleitet, um sicherzustellen, dass eine zirkulare Polarisation erreicht wird und die Probe unter einem bestimmten Winkel bestrahlt wird. Dieser Winkel kann durch Drehen des Probentisches präzise gesteuert werden. Der CD-Koeffizient kann mit der folgenden Gleichung berechnet werden:

wo L _ext und R _ext sind die Extinktionsintensitäten der Metall-Nanocrescents, gemessen mit dem Spektrophotometer über LCP-Licht bzw. RCP-Licht. Die Ergebnisse sind in Abb. 3d, e dargestellt, während die CD-Spektren in Abb. 3f dargestellt sind. Um die Simulationen den experimentellen Bedingungen anzunähern, wurden die Extinktionsspektren der beiden Konfigurationen überlagert (Abb. 3a, b) und die simulierten CD-Koeffizienten berechnet (Abb. 3c). Die Simulationen stimmen gut mit den experimentellen Ergebnissen überein, insbesondere bei den CD-Spektren. Wie in Abb. 3d, e gezeigt, wenn θ =0°, sind die Extinktionsspektren, gemessen von LCP und RCP-Einfallslicht, nahezu identisch. Darüber hinaus sind zwei markante Extinktionspeaks bei 696 nm und 1838 nm vorhanden. Die Ergebnisse legen nahe, dass der Extinktionspeak bei 696 nm durch den LSPR-Modus höherer Ordnung erzeugt wird. Der Extinktionspeak bei 1838 nm kann stattdessen aufgrund der LSMs (± 1, 0), (1, 1), (–1,– 1), (0, ± 1) und des LSPR-Dipolmodus entstehen. Bei Zunahme von θ , nimmt der Extinktionspeak bei 696 nm zunächst ab und steigt dann wieder an, obwohl seine Intensität in den LCP- und RCP-Spektren unterschiedlich ist. Diese Beobachtung steht im Einklang mit den Schlussfolgerungen der bisherigen Arbeiten dieser Forschungsgruppe. Der Extinktionspeak bei 1838 nm zeigt nur eine geringfügige Änderung und ein neuer Extinktionspeak bei 1390 nm entsteht bei einem Anstieg von θ und wenn LCP-Einfallslicht verwendet wird. Dies führt zur Anregung der (− 1, 0), (− 1, − 1) und (0, − 1) LSMs. Wenn die Probe durch einfallendes RCP-Licht angeregt wird, verschiebt sich der Extinktionspeak bei 1838 nm rot und seine Intensität wird schwächer als θ steigt. Obwohl sich bei 1390 nm keine Extinktionspeaks befinden, tritt bei 1080 nm ein neues Merkmal auf, wenn θ wird erhöht und dies kann durch die LSPR-Modi erzeugt werden. Wie in Abb. 3f gezeigt, wird bei einem Anstieg von θ , entsteht ein großer CD-Peak und eine Rotverschiebung. Wenn θ =30°, kann der Maximalwert des CD-Koeffizienten (0,51) bei 1270 nm gemessen werden. Die selektive Anregung der (− 1, 0), (− 1, − 1) und (0, − 1) LSMs durch das zirkular polarisierte Licht löst den Mechanismus aus, der für den riesigen CD-Effekt verantwortlich ist. Aufgrund der Mängel im Produktionsprozess sind die im Experiment erhaltenen Extinktions- und CD-Peaks im Vergleich zu den simulierten etwas breiter.

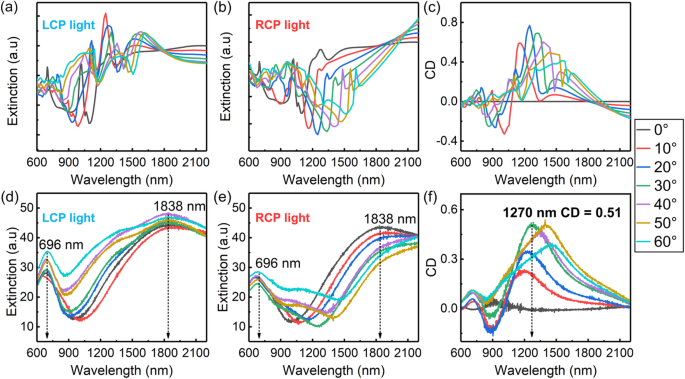
Simulierte und gemessene Extinktions- und CD-Spektren. a –c Simulierte additive Extinktionsspektren für verschiedene Einfallswinkel des zirkular polarisierten Lichts:a LCP, b RCP und die CD-Spektren. d –f Gemessene Extinktionsspektren für verschiedene Einfallswinkel des zirkular polarisierten Lichts:d LCP, e RCP und die CD-Spektren

Darüber hinaus zeigt diese Arbeit, dass die extrinsische Chiralität des Arrays von metallischen Halbmond-Nanostrukturen durch Anpassen des Durchmessers der PS-Mikrokügelchen eingestellt werden kann. Abbildung 4 zeigt die CD-Spektren mehrerer Metall-Nanohalbmond-Arrays mit unterschiedlichen Gitterkonstanten (d. h. Durchmesser der PS-Nanosphären) im Bereich von 500–1000 nm mit θ =30°. Bei Zunahme der Gitterkonstante verschiebt sich der Peak der CD-Spektren von 1019 auf 1799 nm rot, und der CD-Koeffizient bleibt relativ groß (> 0,25). Da PS-Mikrosphären mit Durchmessern zwischen 50 nm und 10 µm kommerziell erhältlich sind, kann die extrinsische Chiralität der Struktur für ihre Anwendung über einen weiten Wellenlängenbereich von sichtbarem bis infrarotem Bereich moduliert werden.

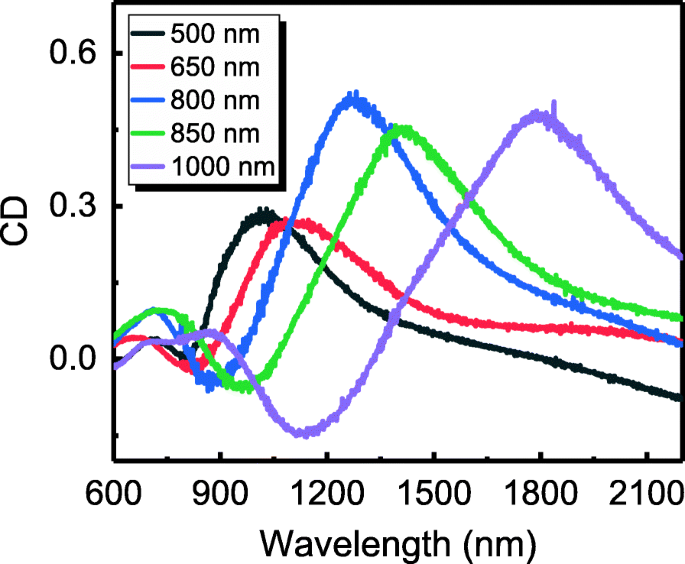
CD-Spektren von metallischen Nanocrescent-Arrays mit Durchmessern im Bereich von 500–1000 nm; der Einfallswinkel der Lichtquelle beträgt 30°

Schlussfolgerungen

Zusammenfassend haben wir gezeigt, dass die großflächigen Metall-Nanohalbmond-Array-Strukturen einen beträchtlichen extrinsischen chiralen Effekt sowie eine hohe Modularität und ein einfaches Herstellungsverfahren aufweisen. Proben mit unterschiedlichen Gitterparametern wurden erfolgreich hergestellt und der CD-Effekt theoretisch und experimentell untersucht. Der größte CD-Koeffizient (> 0,5) wurde bei 1270 nm unter Verwendung eines Einfallswinkels von 30° in einer Metallsichelanordnung mit einer 800-nm-Periode gemessen. Darüber hinaus kann das CD-Spektrum solcher Strukturen umfassend abgestimmt werden, während eine große Peakintensität beibehalten wird, indem der Durchmesser der PS-Mikrokügelchen geändert wird. Die Orte der CD-Peaks variieren von 1019 bis 1799 nm bei einer Änderung der Gitterkonstante im Bereich von 500–1000 nm. Die Simulationen stimmen gut mit den experimentellen Ergebnissen überein und der große und einstellbare extrinsische chirale Effekt der Proben kann auf die selektive Anregung der LSMs durch LCP und RCP zurückgeführt werden. Die demonstrierte Struktur könnte in der Fernerkundung und Polarisationsbildgebung nützlich sein.

Verfügbarkeit von Daten und Materialien

Alle während dieser Studie generierten oder analysierten Daten sind in diesem veröffentlichten Artikel enthalten.

Abkürzungen

LCP:

linkszirkular polarisiert

RCP:

rechtszirkular polarisiert

CD:

Zirkulardichroismus

LSPRs:

lokalisierte Oberflächenplasmonenresonanzen

LSMS:

Gitteroberflächenmoden

SLRS:

Oberflächengitterresonanzen

SEM:

Rasterelektronenmikroskop