Stehende Wellen und Resonanz

Immer wenn die Impedanz zwischen Übertragungsleitung und Last nicht übereinstimmt, treten Reflexionen auf. Wenn das einfallende Signal eine kontinuierliche AC-Wellenform ist, vermischen sich diese Reflexionen mit einem größeren Teil der einfallenden einfallenden Wellenform, um stationäre Wellenformen zu erzeugen, die als stehende Wellen bezeichnet werden .

Die folgende Abbildung zeigt, wie eine dreieckförmige einfallende Wellenform beim Erreichen des nicht abgeschlossenen Endes der Leitung in eine spiegelbildliche Reflexion übergeht. Die Übertragungsleitung in dieser veranschaulichenden Sequenz ist der Einfachheit halber als einzelne, dicke Linie und nicht als ein Paar Drähte dargestellt.

Die einfallende Welle läuft von links nach rechts, während die reflektierte Welle von rechts nach links läuft:(Abbildung unten)

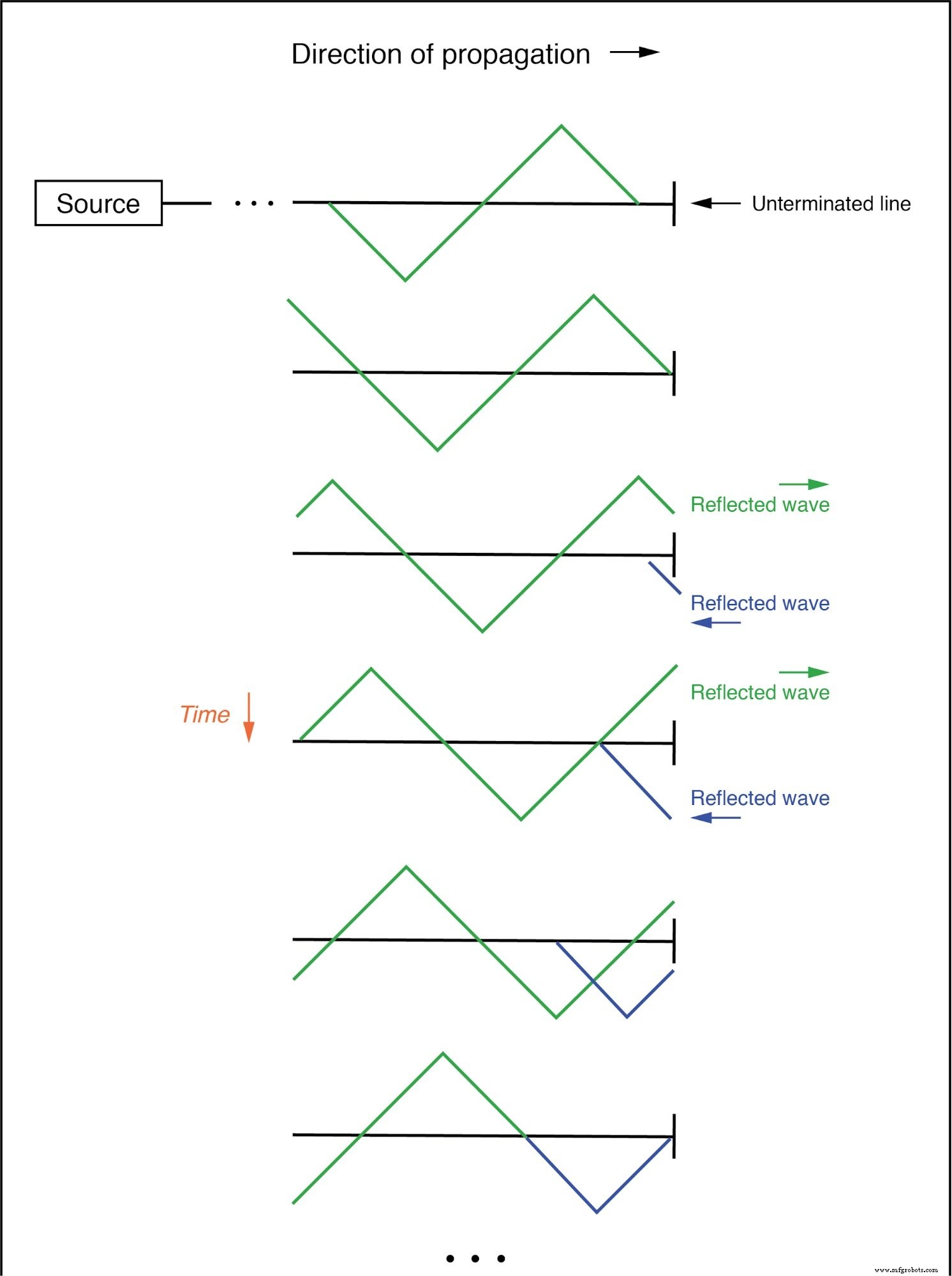
Einfallende Welle reflektiert am Ende einer nicht abgeschlossenen Übertragungsleitung.

Wenn wir die beiden Wellenformen addieren, stellen wir fest, dass eine dritte, stationäre Wellenform entlang der Länge der Linie erzeugt wird:(Abbildung unten)

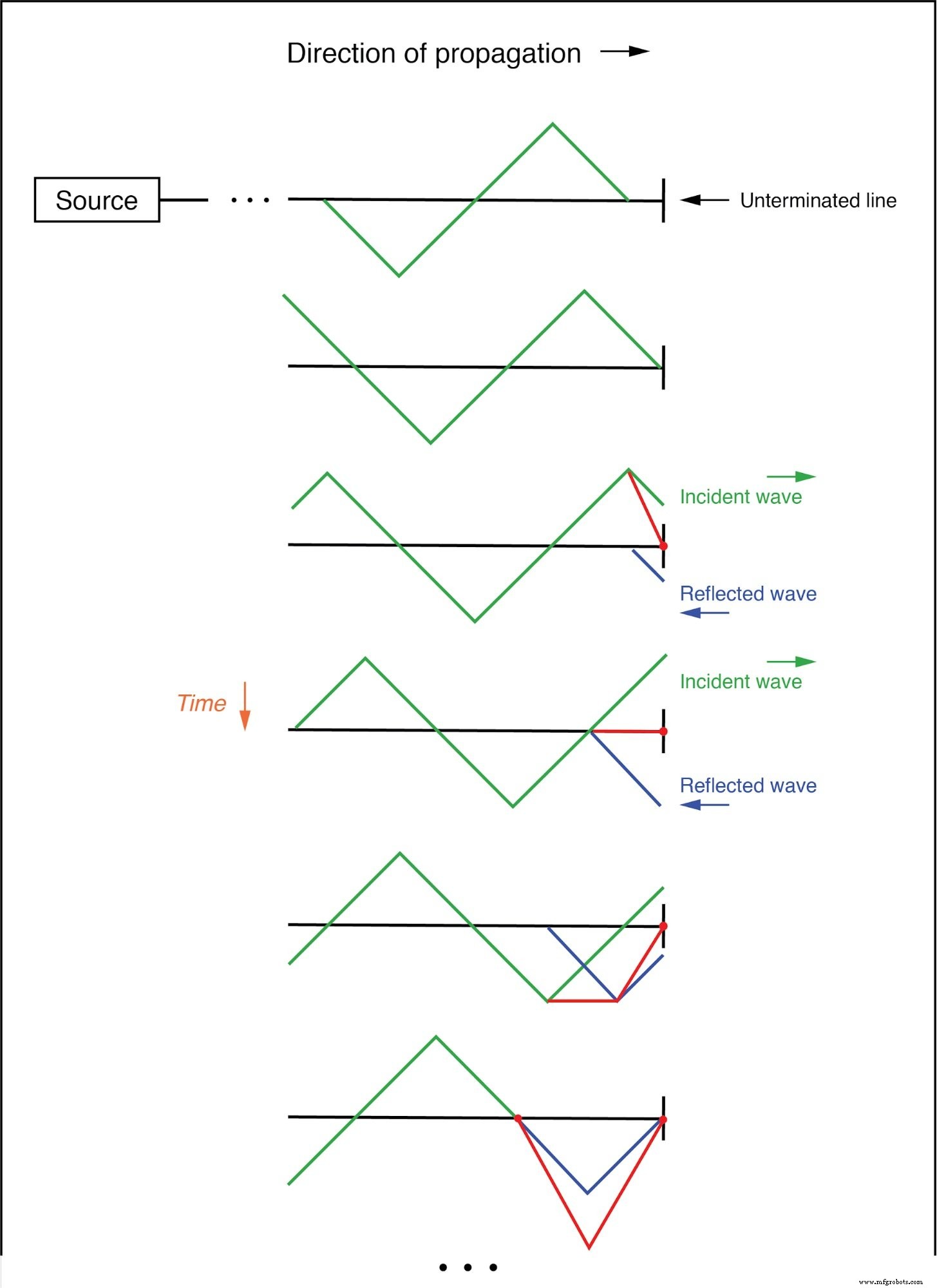
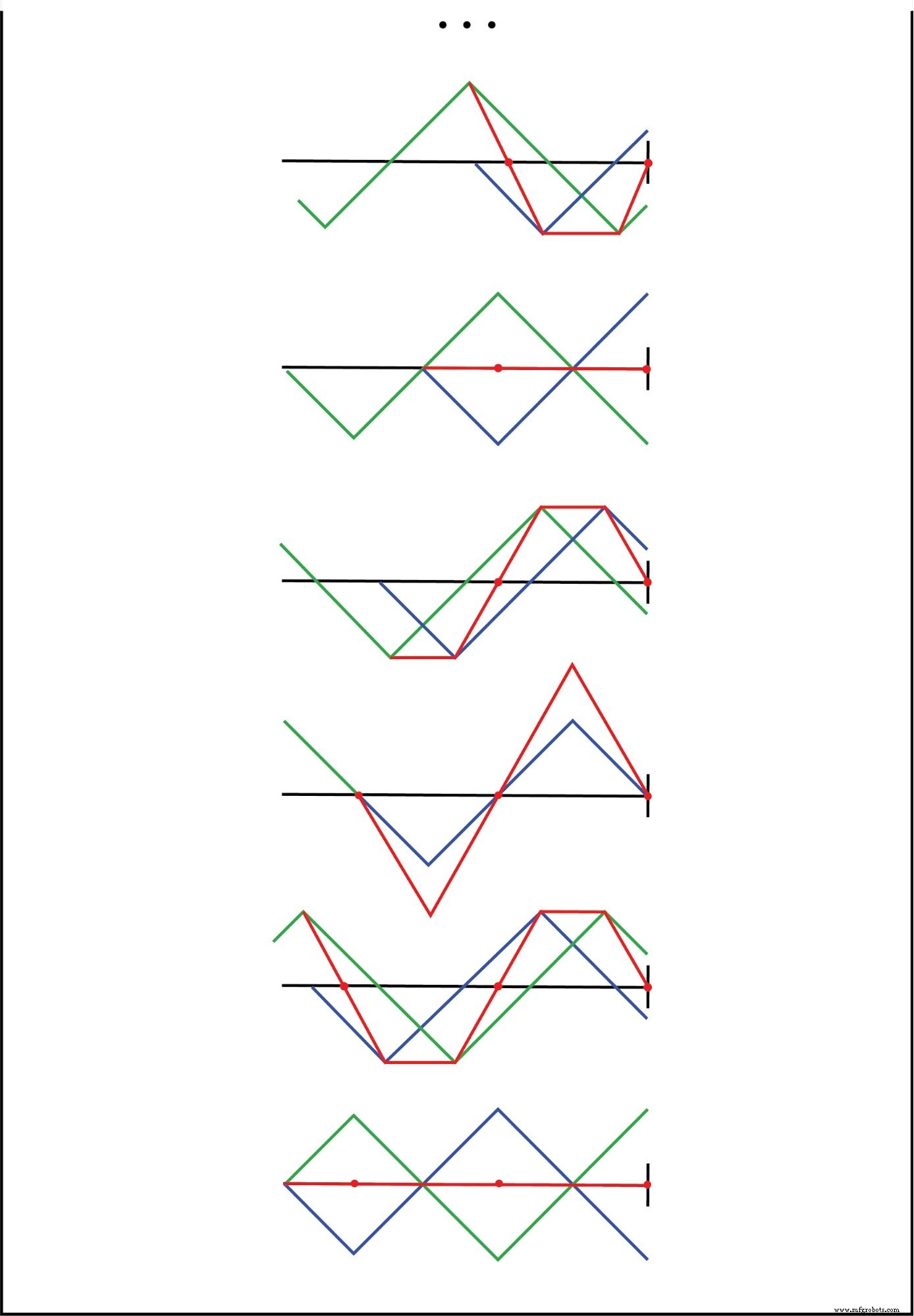
Die Summe der einfallenden und reflektierten Wellen ist eine stehende Welle.

Diese dritte, „stehende“ Welle stellt tatsächlich die einzige Spannung entlang der Leitung dar, da sie die repräsentative Summe der einfallenden und reflektierten Spannungswellen ist. Es schwingt in augenblicklicher Größe, breitet sich jedoch nicht über die Länge des Kabels aus, wie es die einfallenden oder reflektierten Wellenformen verursachen.

Beachten Sie die Punkte entlang der Linienlänge, die die „Null“-Punkte der stehenden Welle markieren (wo sich die einfallenden und reflektierten Wellen gegenseitig aufheben) und wie diese Punkte ihre Position nie ändern:(Abbildung unten)

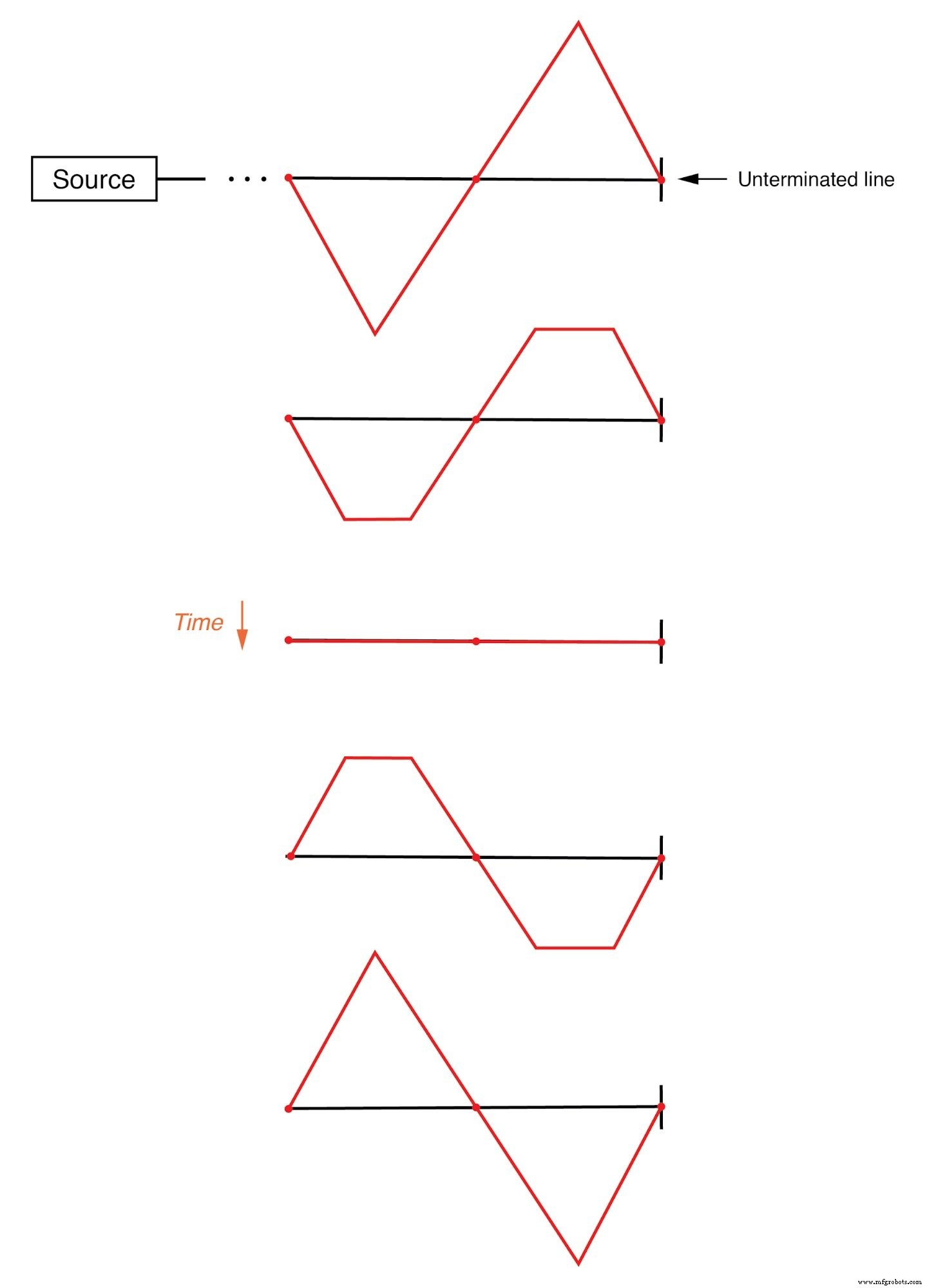
Die stehende Welle breitet sich nicht entlang der Übertragungsleitung aus.

Fälle, in denen eine stehende Welle erzeugt wird

Stehende Wellen sind in der physischen Welt ziemlich häufig. Betrachten Sie eine Schnur oder ein Seil, das an einem Ende geschüttelt und am anderen festgebunden ist (nur ein halber Zyklus der Handbewegung gezeigt, sich nach unten bewegend):(Abbildung unten)

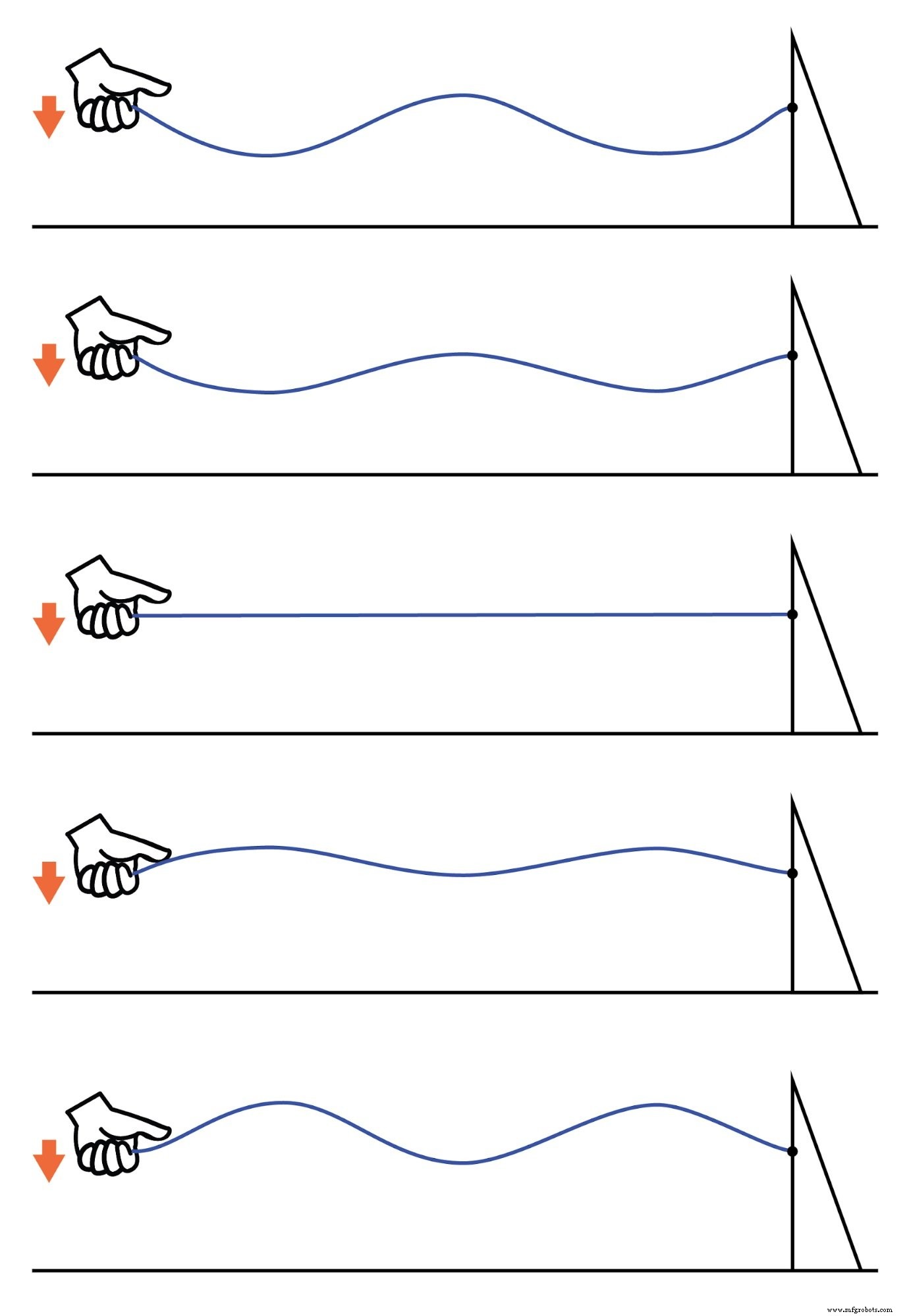
Stehende Wellen an einem Seil.

Sowohl die Knoten (Punkte mit geringer oder keiner Vibration) als auch die Bäuche (Punkte mit maximaler Vibration) bleiben entlang der Länge der Schnur oder des Seils fixiert.

Der Effekt ist am ausgeprägtesten, wenn das freie Ende mit genau der richtigen Frequenz geschüttelt wird. Gezupfte Saiten weisen das gleiche Verhalten einer „stehenden Welle“ auf, mit „Knoten“ von maximaler und minimaler Schwingung entlang ihrer Länge.

Der Hauptunterschied zwischen einer gezupften Saite und einer geschüttelten Saite besteht darin, dass die gezupfte Saite ihre eigene „richtige“ Schwingungsfrequenz liefert, um den Stehwelleneffekt zu maximieren:(Abbildung unten)

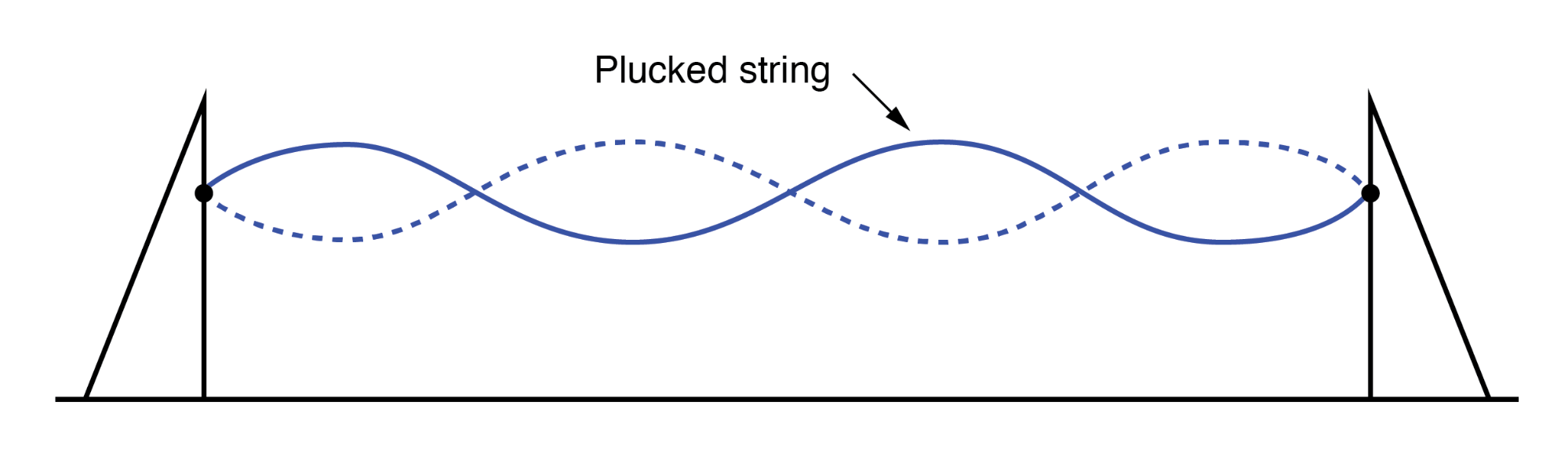
Stehende Wellen an einer gezupften Schnur.

Wind, der über ein Rohr mit offenem Ende bläst, erzeugt auch stehende Wellen; diesmal handelt es sich bei den Wellen eher um Schwingungen von Luftmolekülen (Schall) in der Röhre als um Schwingungen eines festen Objekts. Ob die stehende Welle in einem Knoten (minimale Amplitude) oder einem Schwingungsbauch (maximale Amplitude) endet, hängt davon ab, ob das andere Ende der Röhre offen oder geschlossen ist:(Abbildung unten)

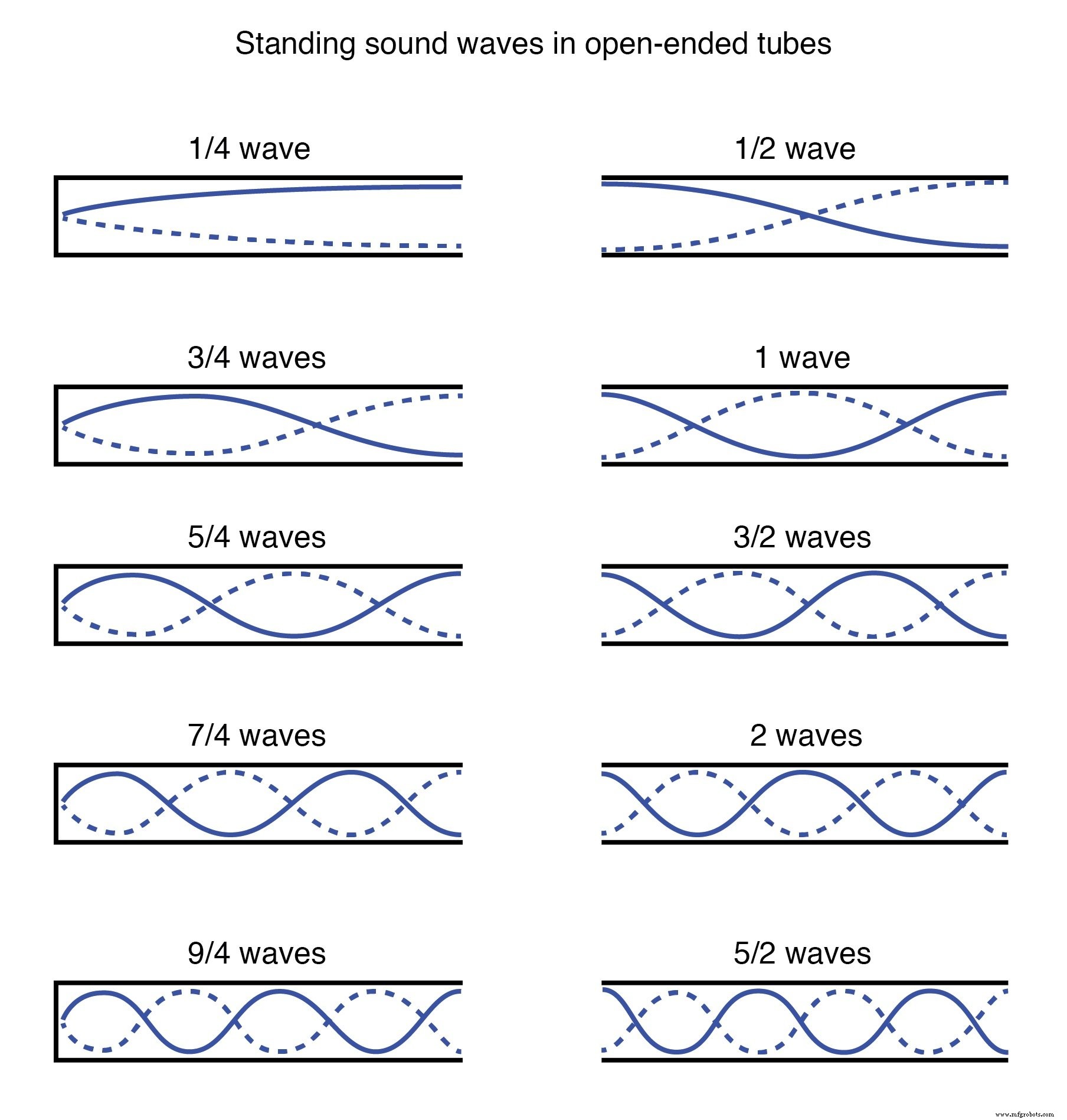
Stehende Schallwellen in Rohren mit offenem Ende.

Ein geschlossenes Rohrende muss ein Wellenknoten sein, während ein offenes Rohrende ein Schwingungsbauch sein muss. Analog dazu muss das verankerte Ende einer schwingenden Saite ein Knoten sein, während das freie Ende (sofern vorhanden) ein Schwingungsbauch sein muss.

Progression der Harmonischen von Resonanzfrequenzen

Beachten Sie, dass es mehr als eine Wellenlänge gibt, die geeignet ist, stehende Wellen vibrierender Luft in einer Röhre zu erzeugen, die genau den Endpunkten der Röhre entspricht.

Dies gilt für alle Stehwellensysteme:Stehwellen schwingen mit dem System für jede Frequenz (Wellenlänge) in Resonanz, die mit den Knoten-/Bäuchenpunkten des Systems korreliert. Anders ausgedrückt, es gibt mehrere Resonanzfrequenzen für jedes System, das stehende Wellen unterstützt.

Alle höheren Frequenzen sind ganzzahlige Vielfache der niedrigsten (Grund-)Frequenz für das System. Der sequentielle Verlauf der Obertöne von einer Resonanzfrequenz zur nächsten definiert den Oberton Frequenzen für das System:(Abbildung unten)

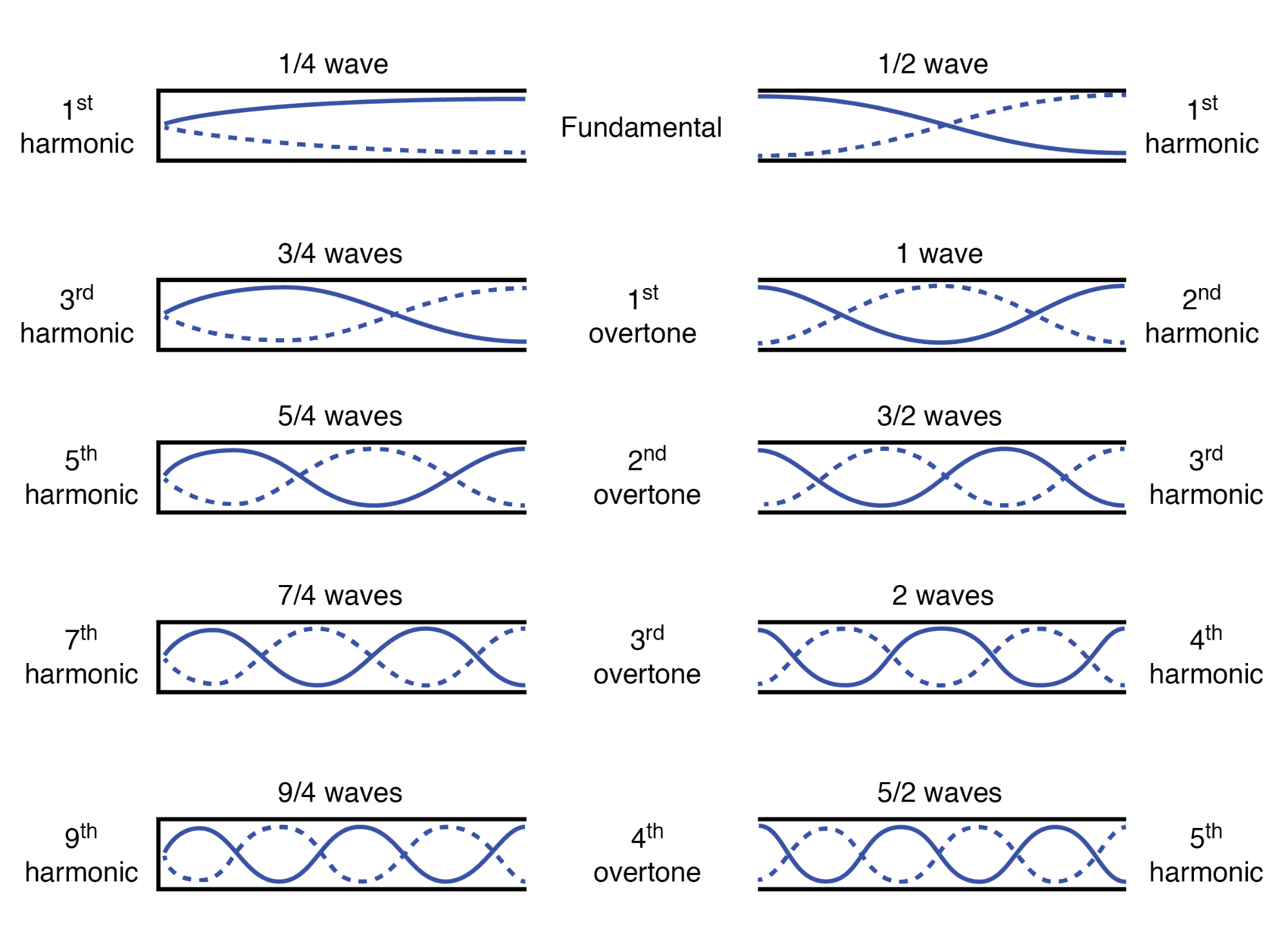
Obertöne (Obertöne) in offenen Pfeifen

Die tatsächlichen Frequenzen (gemessen in Hertz) für jede dieser Harmonischen oder Obertöne hängen von der physikalischen Länge der Röhre und der Ausbreitungsgeschwindigkeit der Wellen ab, die der Schallgeschwindigkeit in Luft entspricht.

Simulation einer Übertragungsleitungsresonanz mit SPICE

Da Übertragungsleitungen stehende Wellen unterstützen und diese Wellen zwingen, je nach Art der Abschlussimpedanz am Lastende Knoten und Bäuche zu besitzen, weisen sie auch Resonanzen bei Frequenzen auf, die durch physikalische Länge und Ausbreitungsgeschwindigkeit bestimmt werden.

Die Resonanz der Übertragungsleitung ist jedoch etwas komplexer als die Resonanz von Saiten oder von Luft in Röhren, da wir sowohl Spannungswellen als auch Stromwellen berücksichtigen müssen.

Diese Komplexität wird durch Computersimulation leichter verständlich gemacht. Lassen Sie uns zunächst eine perfekt aufeinander abgestimmte Quelle, Übertragungsleitung und Last untersuchen. Alle Komponenten haben eine Impedanz von 75 Ω:(Abbildung unten)

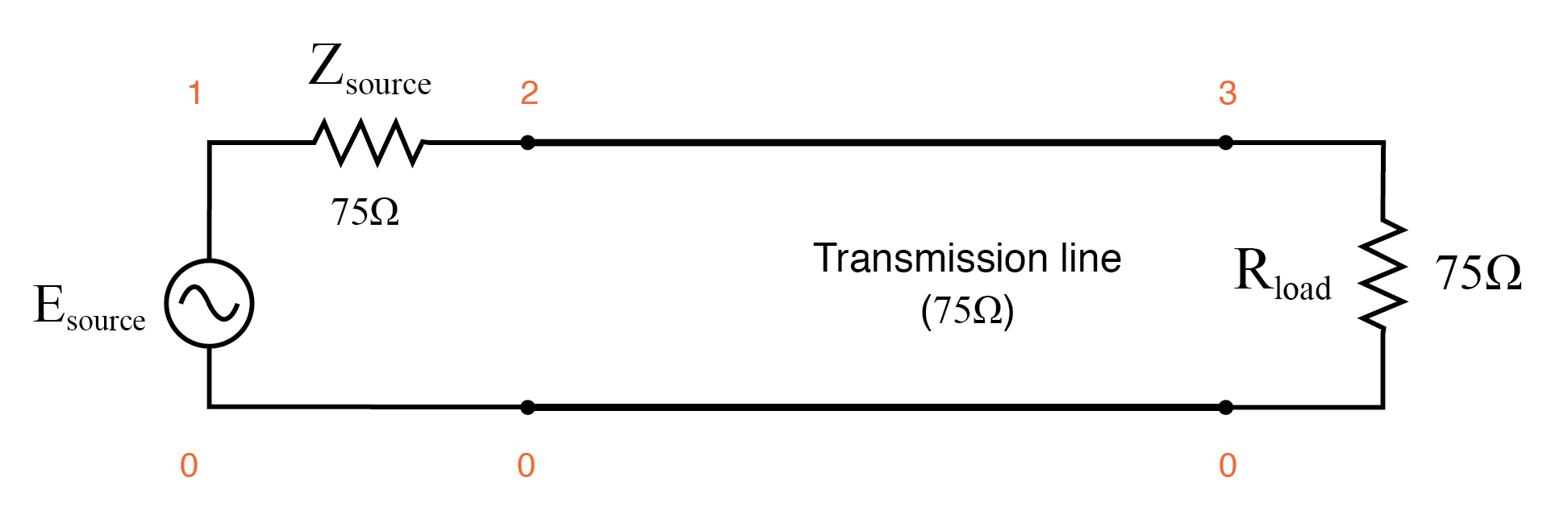
Perfekt abgestimmte Übertragungsleitung.

Mit SPICE zur Simulation der Schaltung spezifizieren wir die Übertragungsleitung (t1 ) mit 75 Ω Wellenwiderstand (z0=75 ) und einer Ausbreitungsverzögerung von 1 Mikrosekunde (td=1u ). Dies ist eine bequeme Methode, um die physikalische Länge einer Übertragungsleitung auszudrücken:die Zeit, die eine Welle braucht, um sich über ihre gesamte Länge auszubreiten.

Wenn dies ein echtes 75--Kabel wäre – vielleicht ein Koaxialkabel des Typs „RG-59B/U“, der üblicherweise für die Kabelfernsehverteilung verwendet wird – mit einem Geschwindigkeitsfaktor von 0,66 wäre es etwa 200 m lang.

Da 1 µs die Periode eines 1-MHz-Signals ist, werde ich die Frequenz der Wechselstromquelle von (fast) null bis zu diesem Wert durchstreichen, um zu sehen, wie das System reagiert, wenn es Signalen im Bereich von Gleichstrom bis 1 Wellenlänge ausgesetzt ist.

Hier ist die SPICE-Netzliste für die oben gezeigte Schaltung:

Übertragungsleitung v1 1 0 ac 1 sin Quelle 1 2 75 t1 2 0 3 0 z0=75 td=1u rload 3 0 75 .ac lin 101 1m 1meg * Verwenden des Programms „Muskatnuss“ zum Plotten der Analyse .Ende 

Wenn wir diese Simulation ausführen und den Quellenimpedanzabfall (als Anzeige des Stroms), die Quellenspannung, die Spannung am Quellenende der Leitung und die Lastspannung grafisch darstellen, sehen wir, dass die Quellenspannung – angezeigt als vm(1) (Spannungsgröße zwischen Knoten 1 und der implizierte Massepunkt von Knoten 0) im grafischen Diagramm – zeigt konstant 1 Volt an, während jede andere Spannung konstant 0,5 Volt anzeigt:(Abbildung unten)

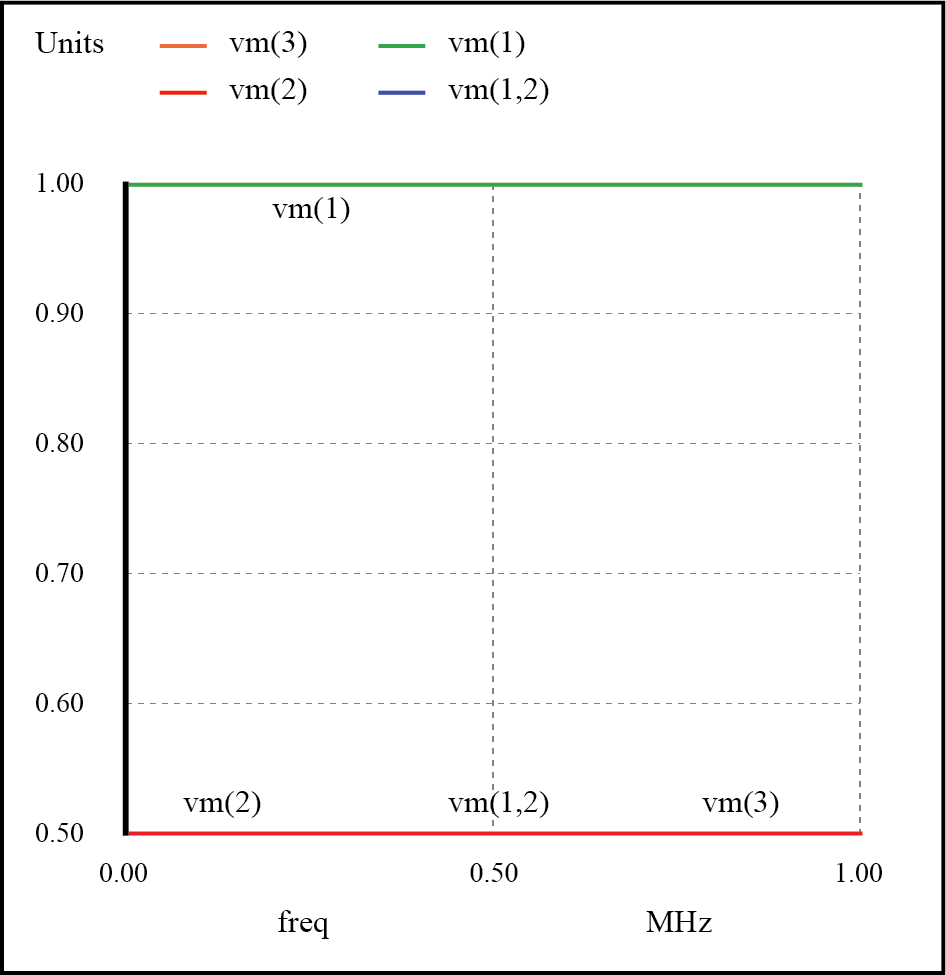
Keine Resonanzen auf einer passenden Übertragungsleitung.

In einem System, in dem alle Impedanzen perfekt aufeinander abgestimmt sind, kann es keine stehenden Wellen und daher keine resonanten „Spitzen“ oder „Täler“ im Bode-Diagramm geben.

Ändern wir nun die Lastimpedanz auf 999 MΩ, um eine Übertragungsleitung mit offenem Ende zu simulieren. (Abbildung unten) Wir sollten jetzt definitiv einige Reflexionen auf der Leitung sehen, da die Frequenz von 1 MHz auf 1 MHz gesweept wird:(Abbildung unten)

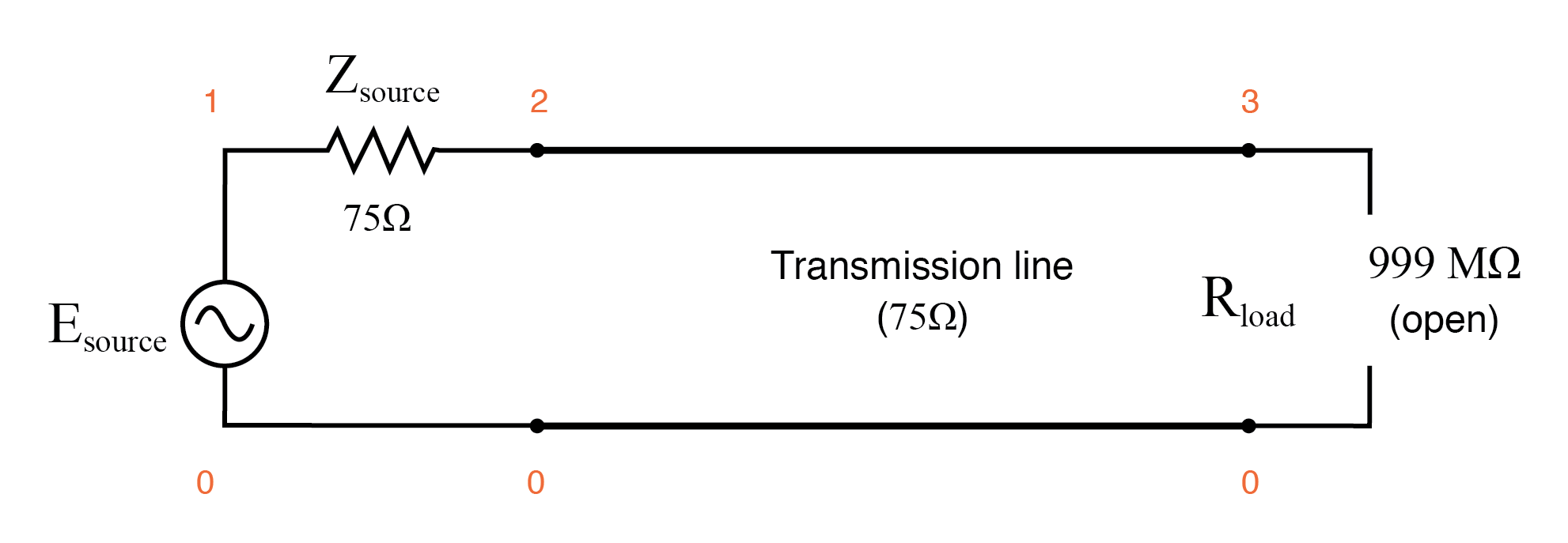
Offene Übertragungsleitung.

Übertragungsleitung v1 1 0 ac 1 sin Quelle 1 2 75 t1 2 0 3 0 z0=75 td=1u rload 3 0 999meg .ac lin 101 1m 1meg * Verwenden des Programms „Muskatnuss“ zum Plotten der Analyse .Ende 

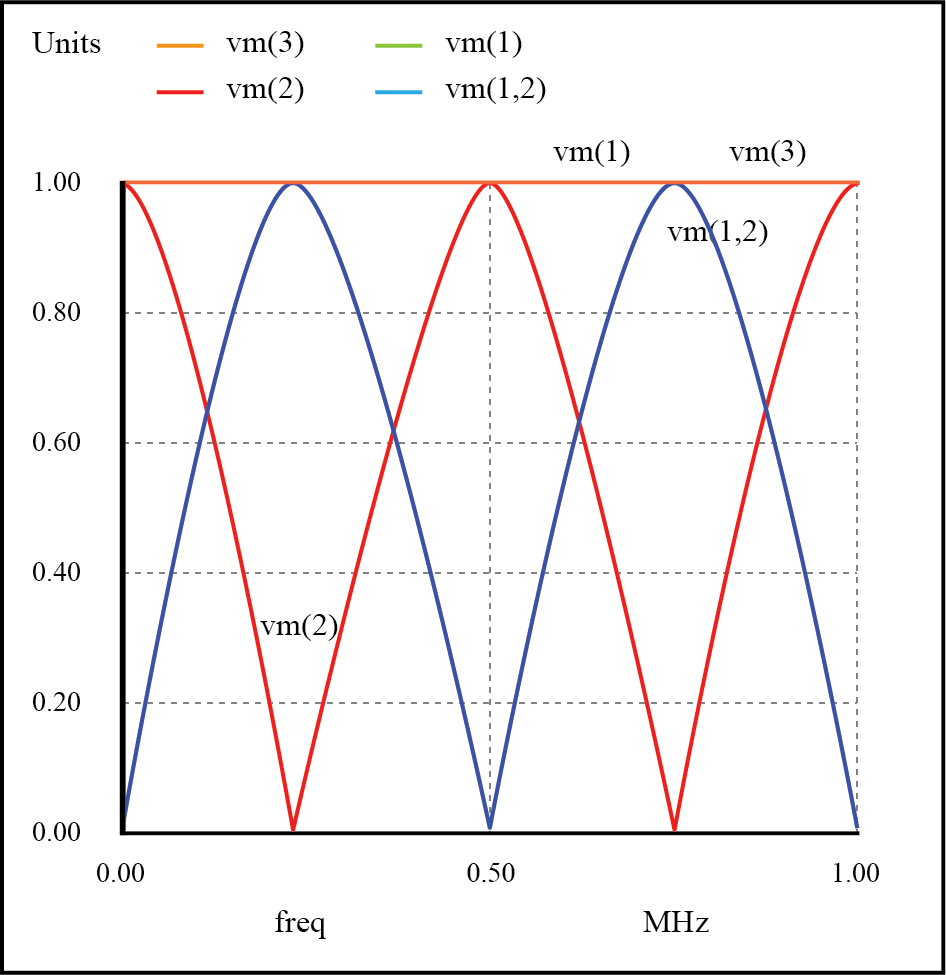
Resonanzen auf offener Übertragungsleitung.

Hier ist sowohl die Versorgungsspannung vm(1) und die lastseitige Spannung der Leitung vm(3) konstant bei 1 Volt bleiben. Die anderen Spannungen fallen bei unterschiedlichen Frequenzen entlang des Sweep-Bereichs von 1 mHz bis 1 MHz ab und spitzen sich hoch.

Entlang der horizontalen Achse der Analyse gibt es fünf interessante Punkte:0 Hz, 250 kHz, 500 kHz, 750 kHz und 1 MHz. Wir werden jeden einzelnen in Bezug auf Spannung und Strom an verschiedenen Stellen des Stromkreises untersuchen.

Bei 0 Hz (eigentlich 1 mHz) ist das Signal praktisch Gleichstrom und die Schaltung verhält sich ähnlich wie bei einer 1-Volt-Gleichstrom-Batteriequelle.

Es fließt kein Strom im Stromkreis, was durch einen Spannungsabfall von null über der Quellenimpedanz angezeigt wird (Z_Quelle :vm(1,2) ) und volle Quellenspannung am Quellenende der Übertragungsleitung (Spannung gemessen zwischen Knoten 2 und Knoten 0:vm(2) ). (Abbildung unten)

Bei f=0:Eingabe:V=1, I=0; Ende:V=1, I=0.

Bei 250 kHz sehen wir Nullspannung und maximalen Strom am Quellenende der Übertragungsleitung, aber immer noch volle Spannung am Lastende:(Abbildung unten)

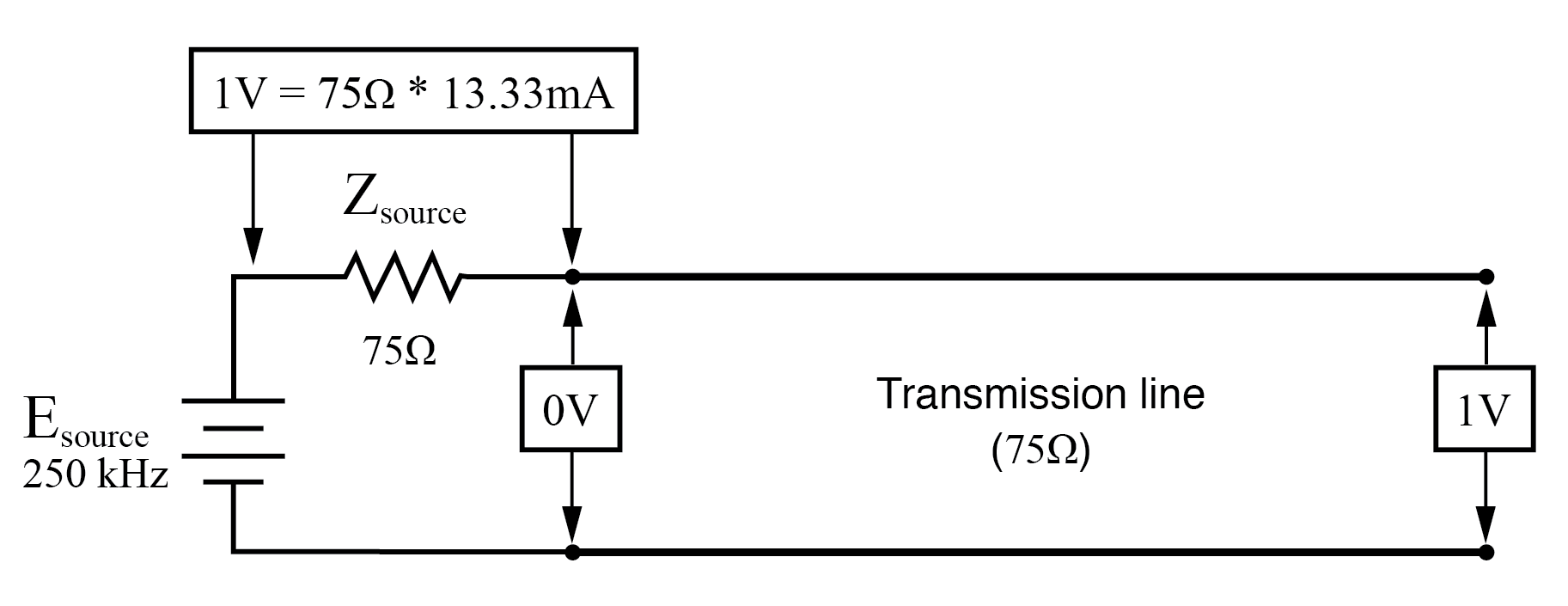
Bei f=250 KHz:Eingang:V=0, I=13,33 mA; Ende:V=1 I=0.

Sie fragen sich vielleicht, wie kann das sein? Wie können wir die volle Quellenspannung am offenen Ende der Leitung erhalten, während am Eingang keine Spannung anliegt?

Die Antwort liegt im Paradoxon der stehenden Welle. Bei einer Quellfrequenz von 250 kHz ist die Länge der Leitung genau richtig, damit 1/4 Wellenlänge von einem Ende zum anderen passt. Bei offenem Lastende der Leitung kann kein Strom, aber Spannung vorhanden sein.

Daher ist das Lastende einer offenen Übertragungsleitung ein Stromknoten (Nullpunkt) und ein Spannungsbauchknoten (maximale Amplitude):(Abbildung unten)

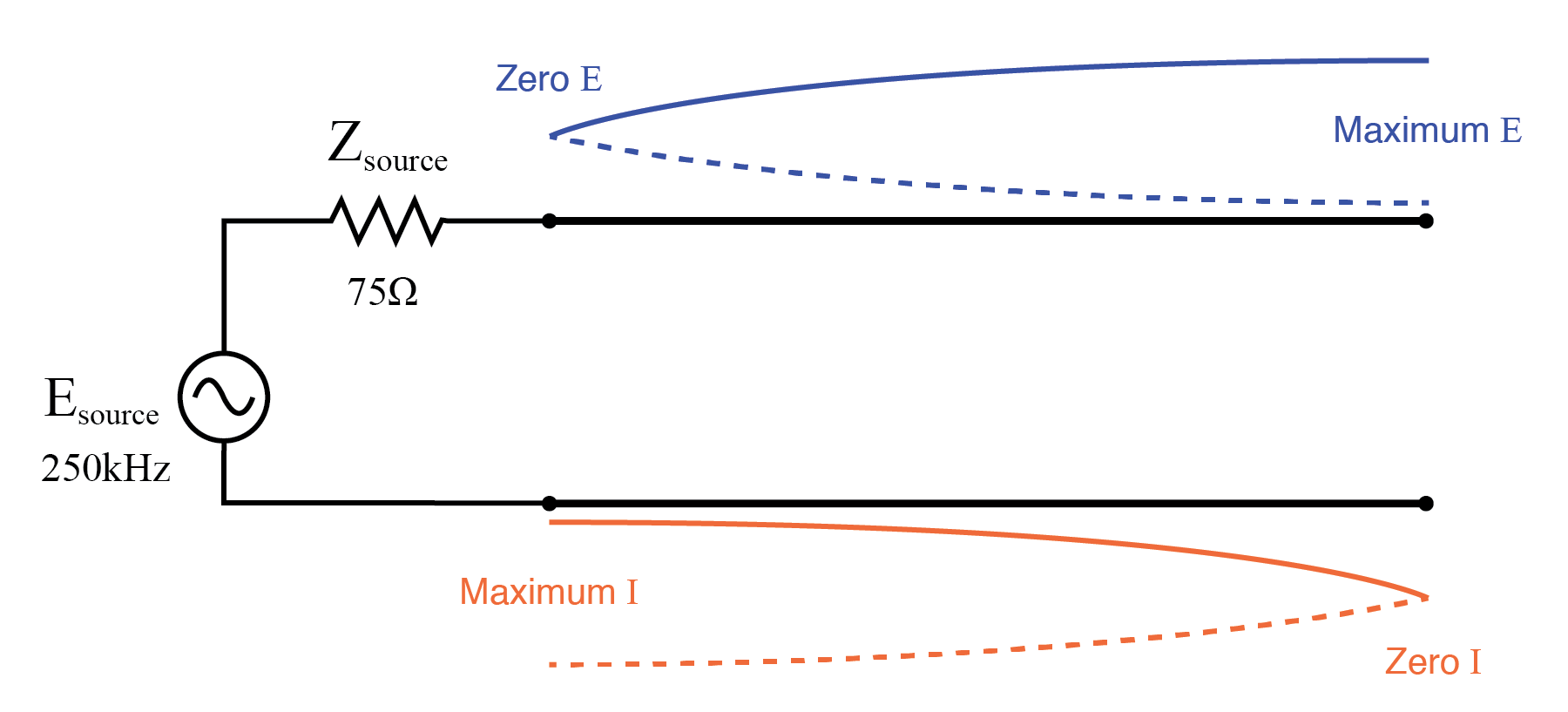
Offenes Ende der Übertragungsleitung zeigt aktuellen Knoten, Spannungsbauch am offenen Ende.

Bei 500 kHz ruht genau die Hälfte einer stehenden Welle auf der Übertragungsleitung, und hier sehen wir einen weiteren Punkt in der Analyse, an dem der Quellenstrom auf Null abfällt und die Quellen-Endspannung der Übertragungsleitung wieder auf die volle Spannung ansteigt :(Abbildung unten)

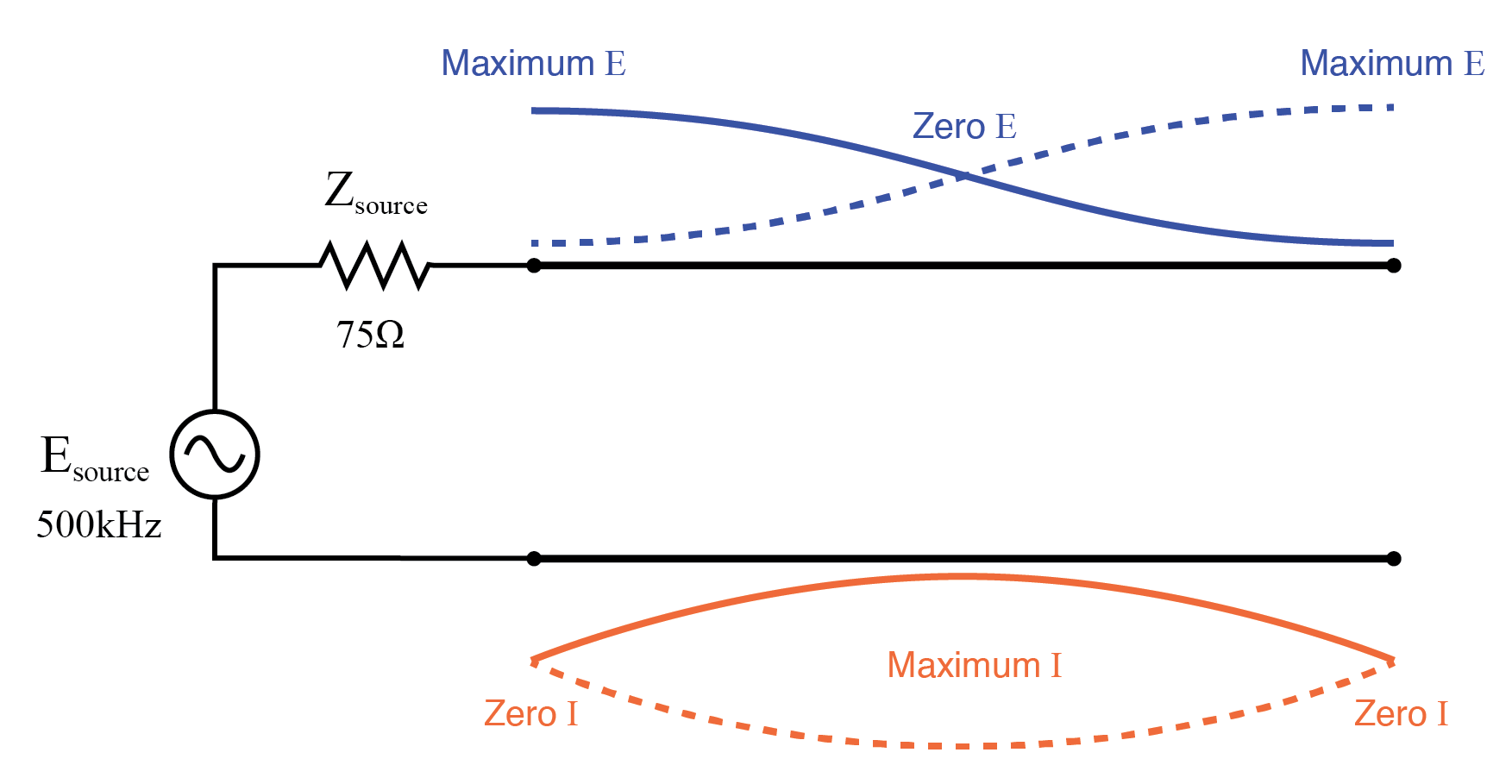
Volle stehende Welle auf halber offener Übertragungsleitung.

Bei 750 kHz sieht das Diagramm sehr ähnlich aus wie bei 250 kHz:Null Spannung am Quellenende (vm(2)) und maximaler Strom (vm(1,2)). Dies ist darauf zurückzuführen, dass 3/4 einer Welle entlang der Übertragungsleitung schweben, was dazu führt, dass die Quelle einen Kurzschluss „sieht“, wo sie mit der Übertragungsleitung verbunden ist, obwohl das andere Ende der Leitung offen ist:(Abbildung unten)

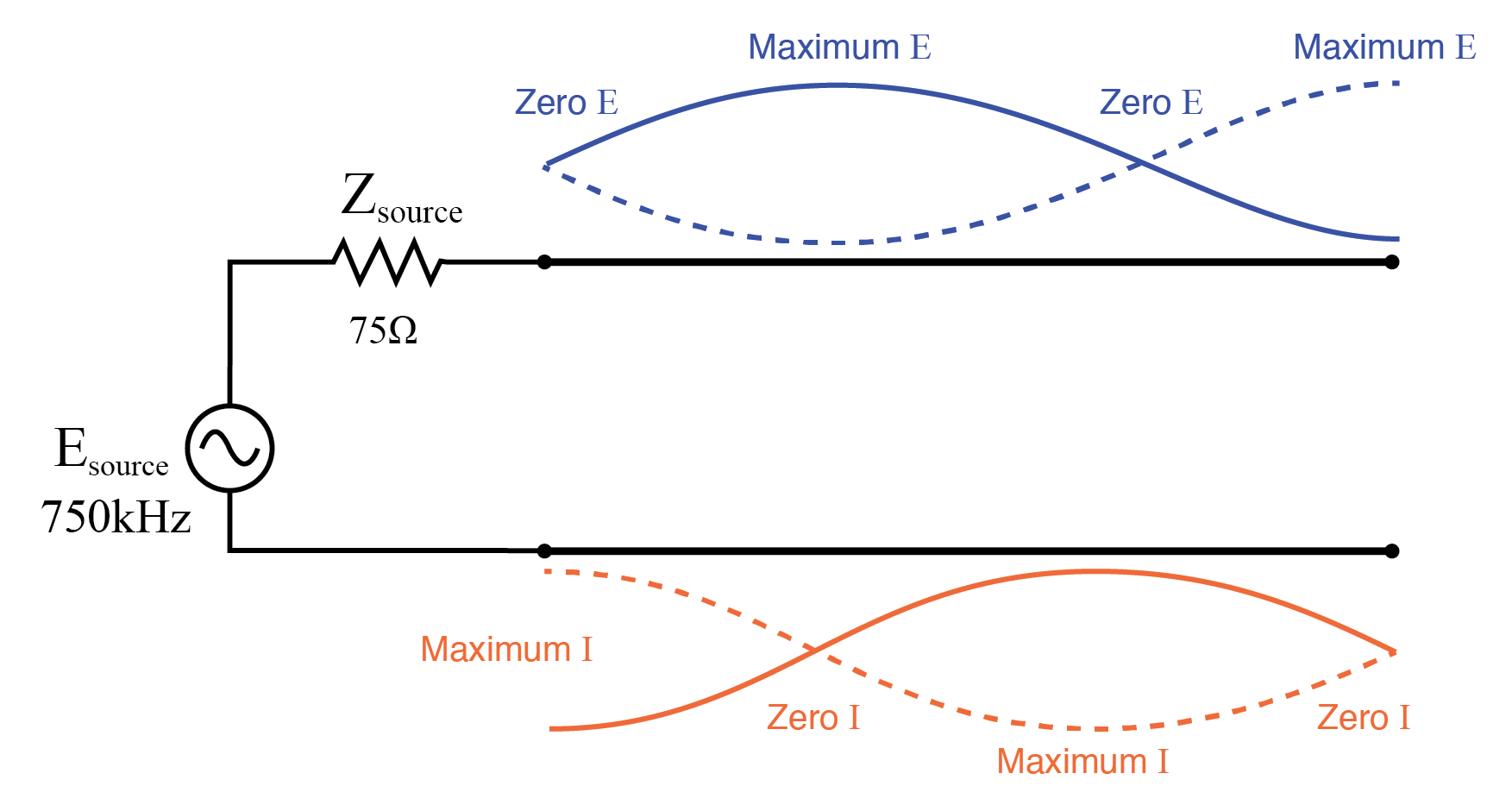
1 1/2 stehende Wellen auf einer offenen 3/4-Wellen-Übertragungsleitung.

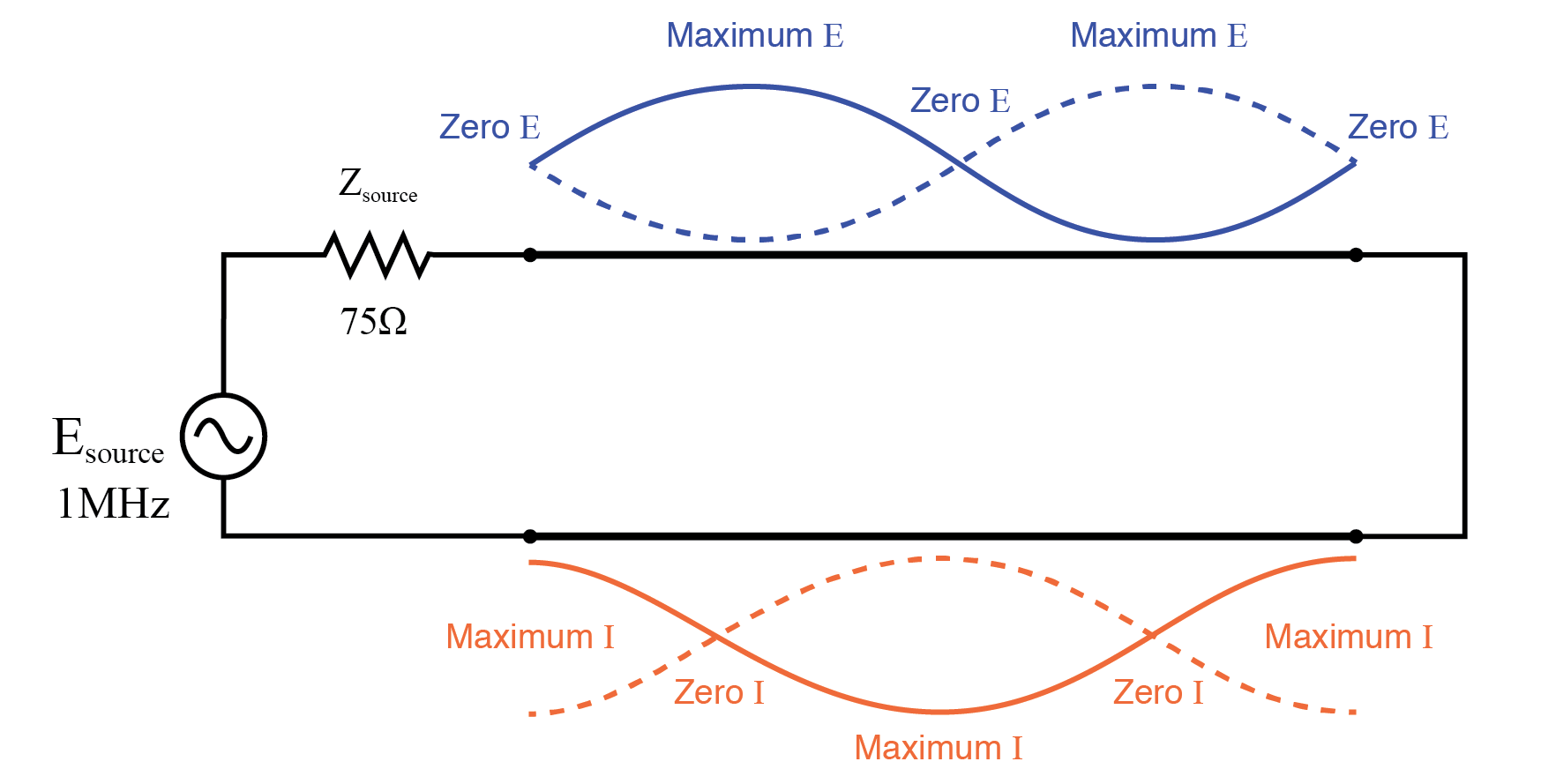
Wenn die Versorgungsfrequenz bis zu 1 MHz durchläuft, existiert eine volle stehende Welle auf der Übertragungsleitung. An diesem Punkt erfährt das Quellenende der Leitung die gleichen Spannungs- und Stromamplituden wie das Lastende:volle Spannung und Nullstrom. Im Wesentlichen „sieht“ die Quelle an der Stelle, an der sie mit der Übertragungsleitung verbunden ist, einen offenen Stromkreis. (Abbildung unten)

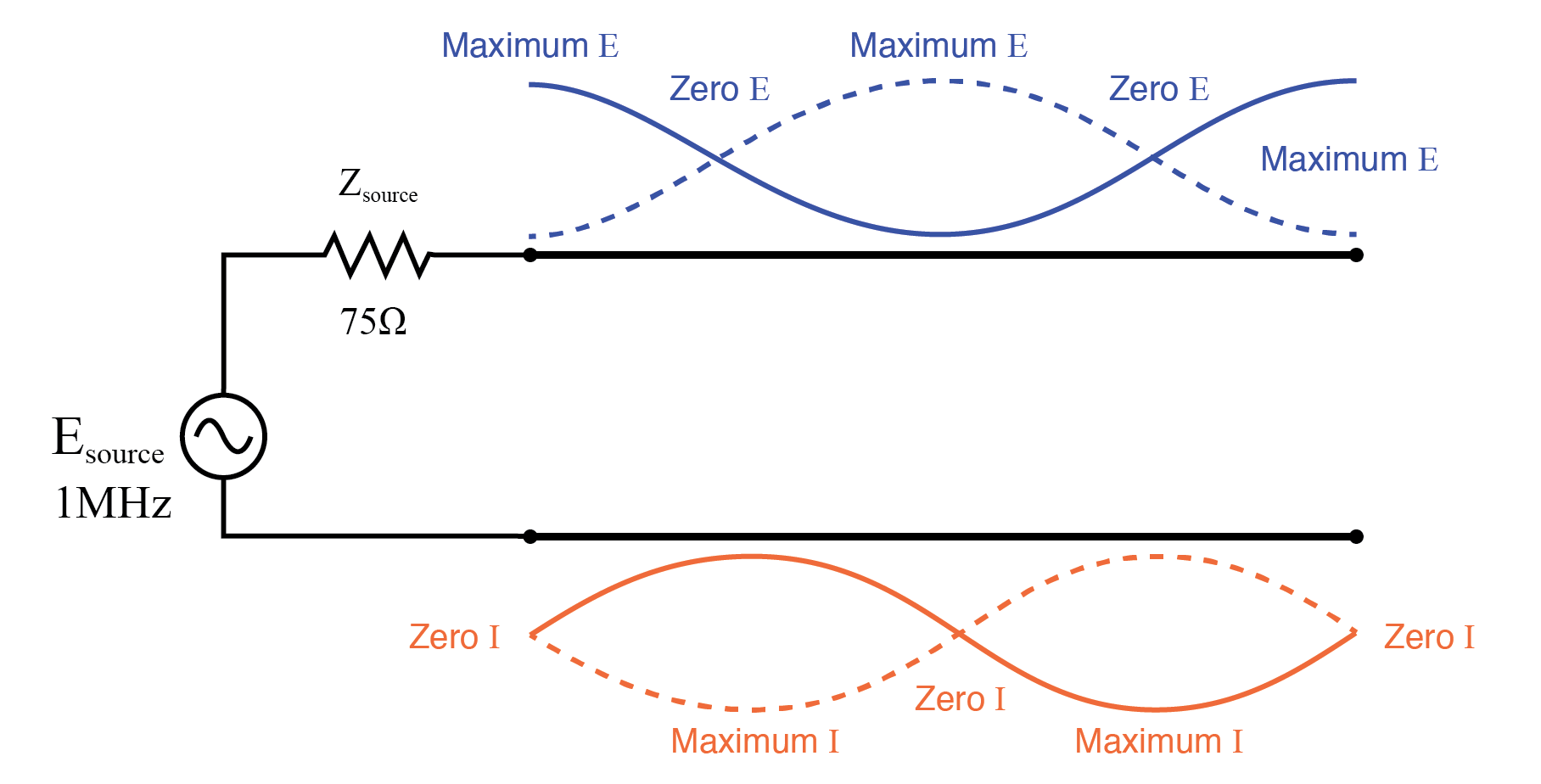
Doppelte stehende Wellen auf einer offenen Vollwellenübertragungsleitung.

In ähnlicher Weise erzeugt eine kurzgeschlossene Übertragungsleitung stehende Wellen, obwohl die Knoten- und Baukastenzuordnungen für Spannung und Strom vertauscht sind:Am kurzgeschlossenen Ende der Leitung gibt es keine Spannung (Knoten) und maximalen Strom (Bausteine). . Was folgt, ist die SPICE-Simulation und Abbildungen dessen, was bei allen interessanten Frequenzen passiert:0 Hz , 250 kHz , 500 kHz , 750 kHz und 1 MHz . Die Kurzschlussbrücke wird durch eine Lastimpedanz von 1 µΩ simuliert:

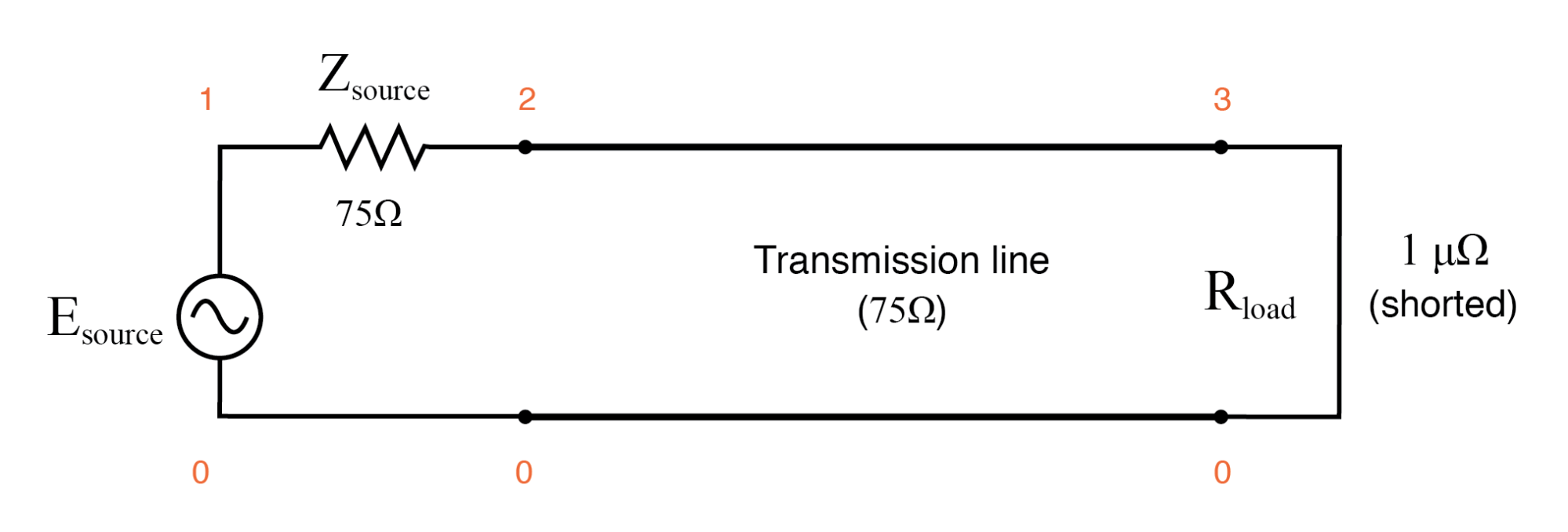
Kurze Übertragungsleitung.

Übertragungsleitung v1 1 0 ac 1 sin Quelle 1 2 75 t1 2 0 3 0 z0=75 td=1u rload 3 0 1u .ac lin 101 1m 1meg * Verwenden des Programms „Muskatnuss“ zum Plotten der Analyse .Ende 

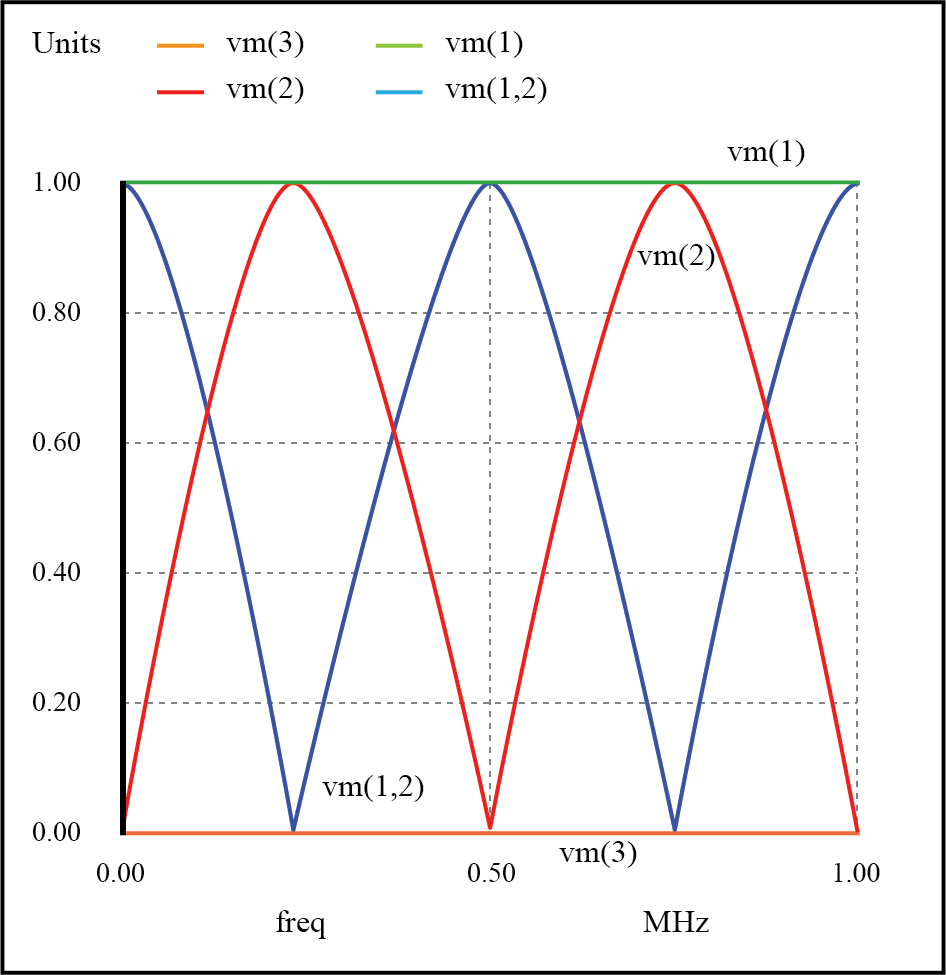
Resonanzen auf kurzgeschlossener Übertragungsleitung

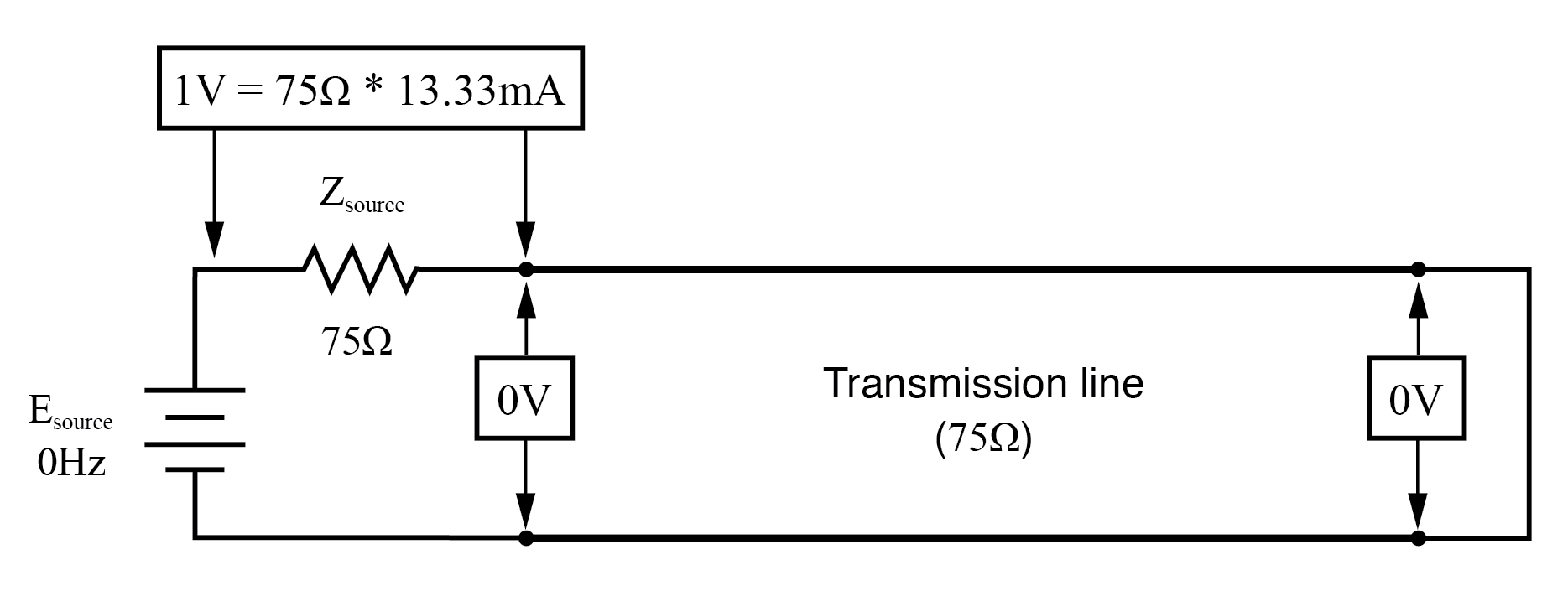
Bei f=0 Hz:Eingang:V=0, I=13,33 mA; Ende:V=0, I=13,33 mA.

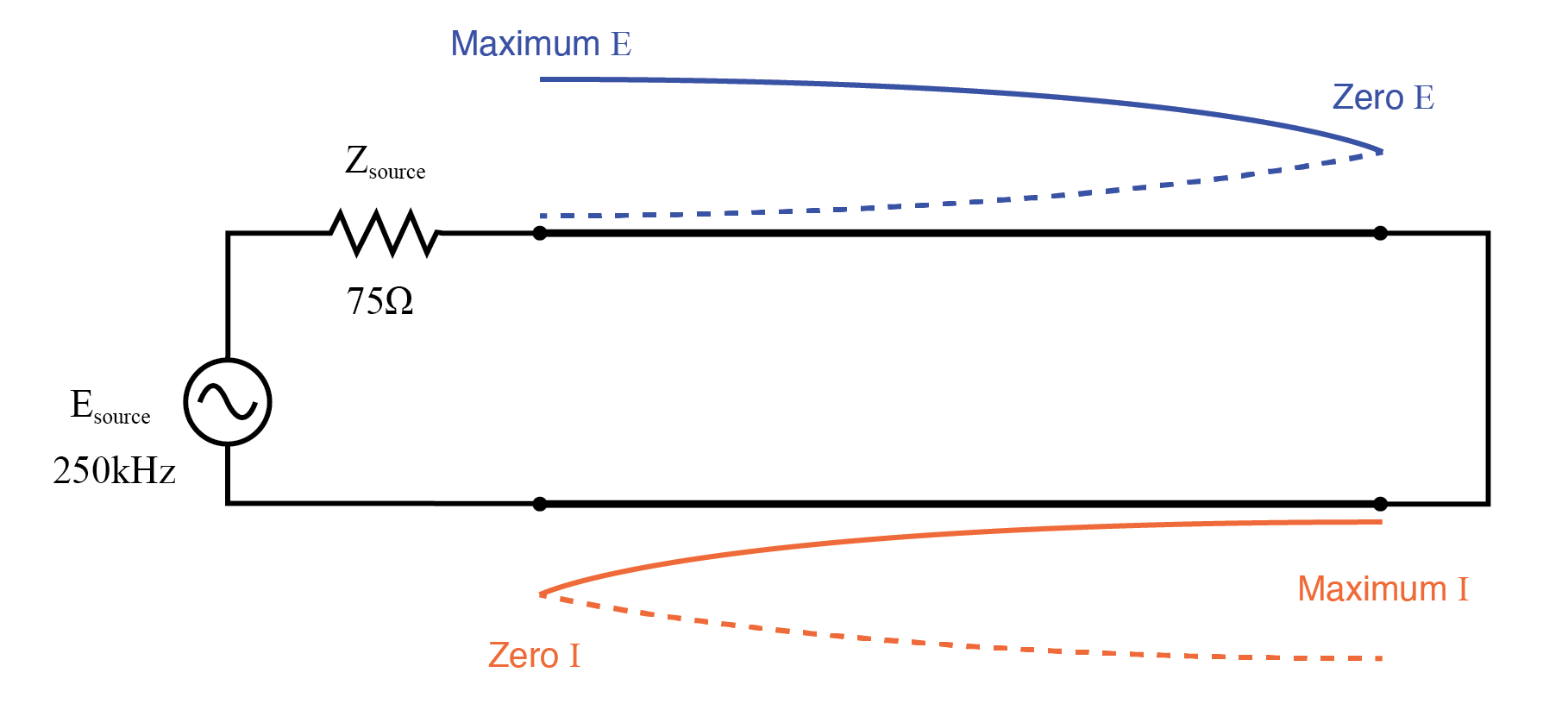
Stehwellenmuster einer halben Welle auf einer kurzgeschlossenen 1/4-Welle-Übertragungsleitung.

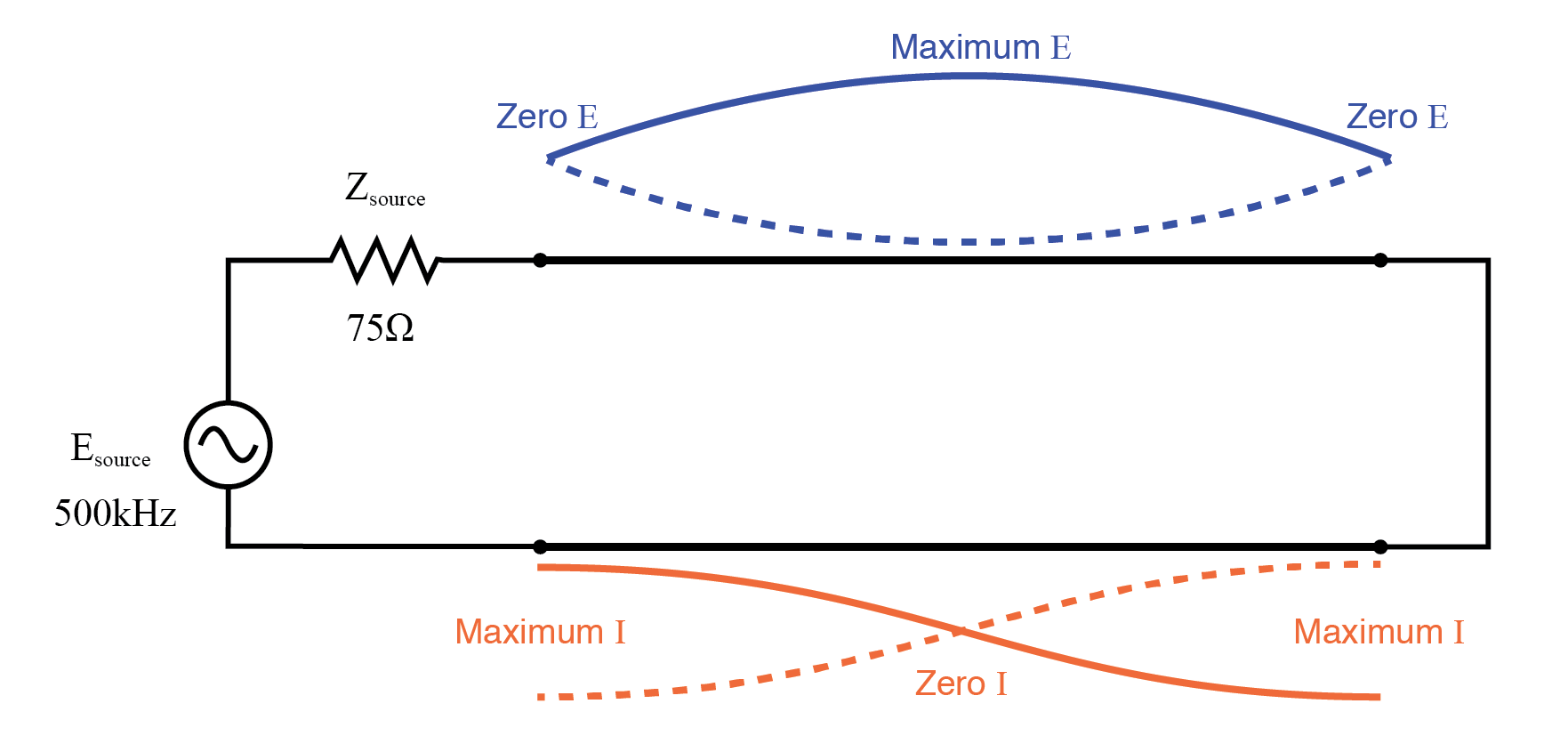
Stehwellenmuster der vollen Welle auf einer kurzgeschlossenen Übertragungsleitung mit halber Welle.

1 1/2 stehendes Wellenmuster auf einer 3/4 Welle kurzgeschlossener Übertragungsleitung.

Doppelte stehende Wellen auf einer Vollwellenkurzschluss-Übertragungsleitung.

In beiden Schaltungsbeispielen, einer unterbrochenen Leitung und einer kurzgeschlossenen Leitung, ist die Energiereflexion total:100 % der einfallenden Welle, die das Ende der Leitung erreicht, wird zurück zur Quelle reflektiert.

Wenn die Übertragungsleitung jedoch mit einer anderen Impedanz als einer Unterbrechung oder einem Kurzschluss abgeschlossen wird, sind die Reflexionen weniger intensiv, ebenso wie der Unterschied zwischen den minimalen und maximalen Werten von Spannung und Strom entlang der Leitung.

Angenommen, wir würden unsere Beispielleitung mit einem 100--Widerstand anstelle eines 75--Widerstands terminieren. (Abbildung unten) Untersuchen Sie die Ergebnisse der entsprechenden SPICE-Analyse, um die Auswirkungen einer Impedanzfehlanpassung bei verschiedenen Quellfrequenzen zu sehen:(Abbildung unten)

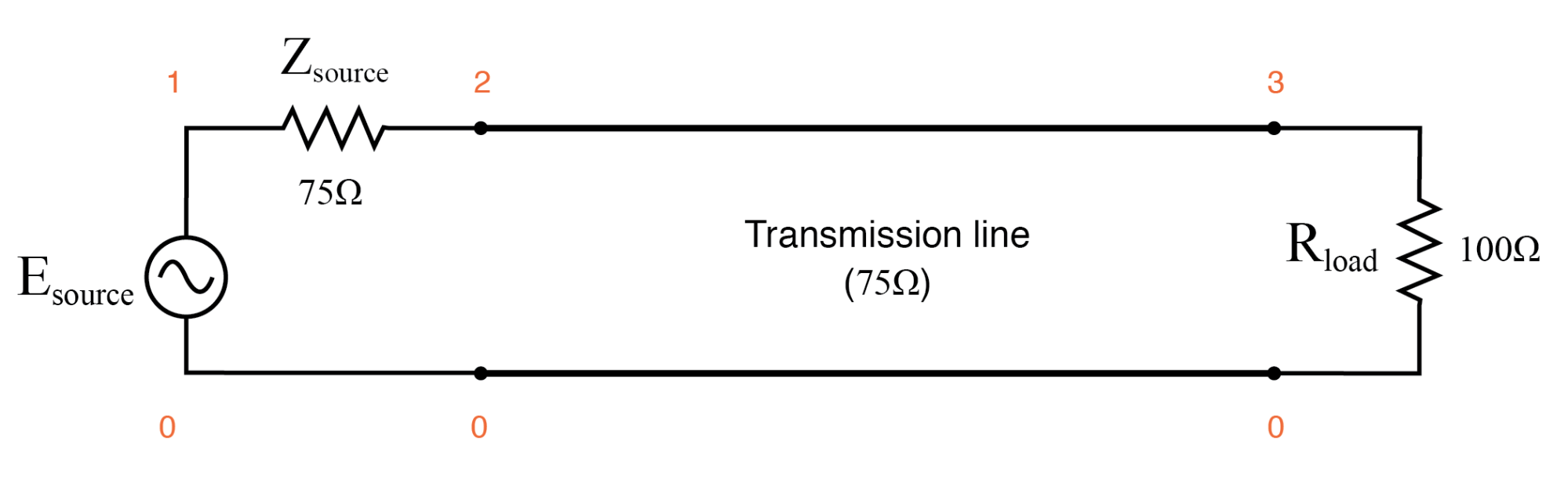
Übertragungsleitung in einer Nichtübereinstimmung beendet

Übertragungsleitung v1 1 0 ac 1 sin Quelle 1 2 75 t1 2 0 3 0 z0=75 td=1u rload 3 0 100 .ac lin 101 1m 1meg * Verwenden des Programms „Muskatnuss“ zum Plotten der Analyse .Ende 

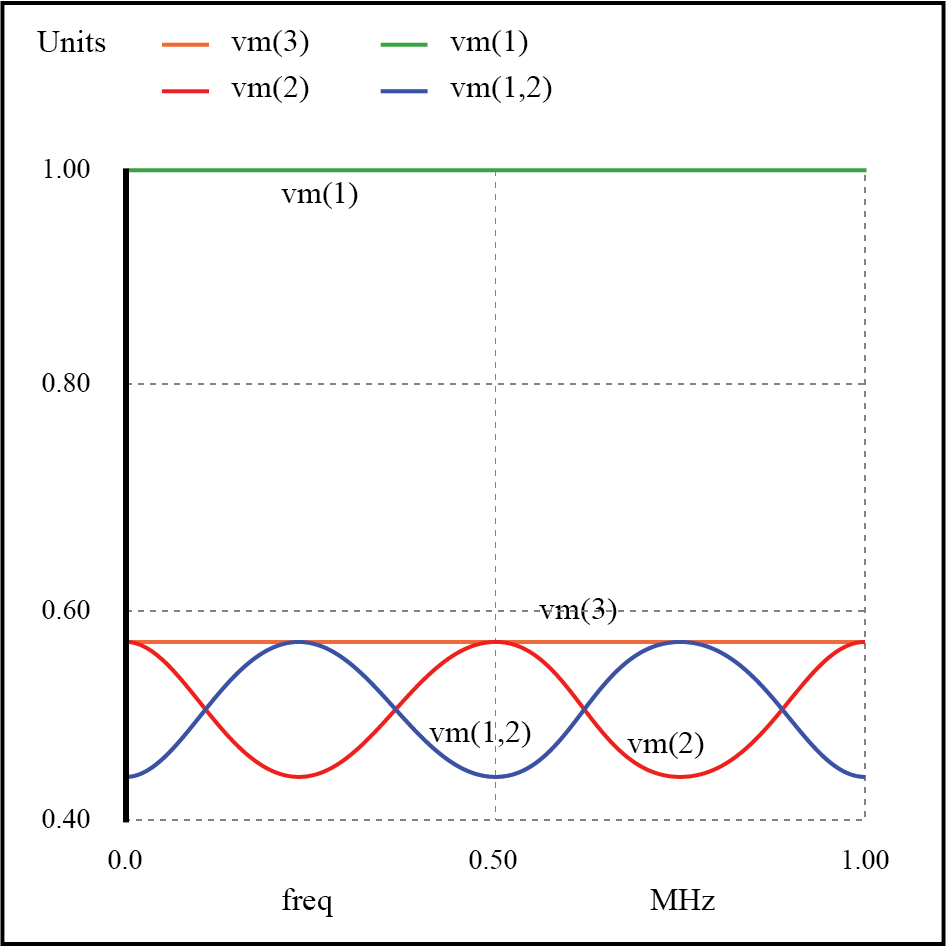
Schwache Resonanzen auf einer nicht übereinstimmenden Übertragungsleitung

Wenn wir eine weitere SPICE-Analyse durchführen und diesmal numerische Ergebnisse drucken, anstatt sie darzustellen, können wir genau herausfinden, was bei allen interessanten Frequenzen passiert:

Übertragungsleitung v1 1 0 ac 1 sin Quelle 1 2 75 t1 2 0 3 0 z0=75 td=1u rload 3 0 100 .ac lin 5 1m 1meg .print ac v(1,2) v(1) v(2) v(3) .Ende 

Frequenz v(1,2) v(1) v(2) v(3) 1.000E-03 4.286E-01 1.000E+00 5.714E-01 5.714E-01 2.500E+05 5.714E-01 1.000E+00 4.286E-01 5.714E-01 5.000E+05 4.286E-01 1.000E+00 5.714E-01 5.714E-01 7.500E+05 5.714E-01 1.000E+00 4.286E-01 5.714E-01 1.000E+06 4.286E-01 1.000E+00 5.714E-01 5.714E-01 

Bei allen Frequenzen ist die Quellenspannung v(1) , bleibt konstant bei 1 Volt, wie es sollte. Die Lastspannung, v(3) , bleibt ebenfalls konstant, jedoch bei einer geringeren Spannung:0,5714 Volt. Sowohl die Netzeingangsspannung (v(2) ) und der Spannungsabfall über die 75 Ω Impedanz der Quelle (v(1,2) , was den aus der Quelle entnommenen Strom anzeigt) variieren mit der Frequenz.

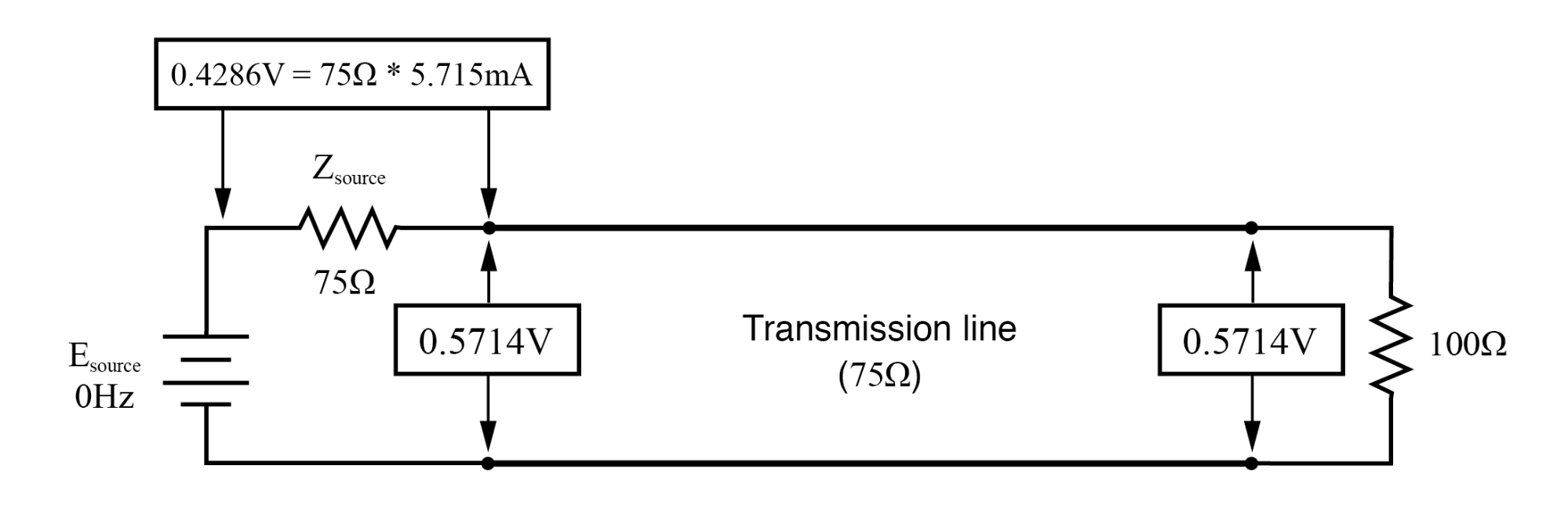
Bei f=0 Hz:Eingang:V=0.57.14, I=5.715 mA; Ende:V=0.5714, I=5.715 mA.

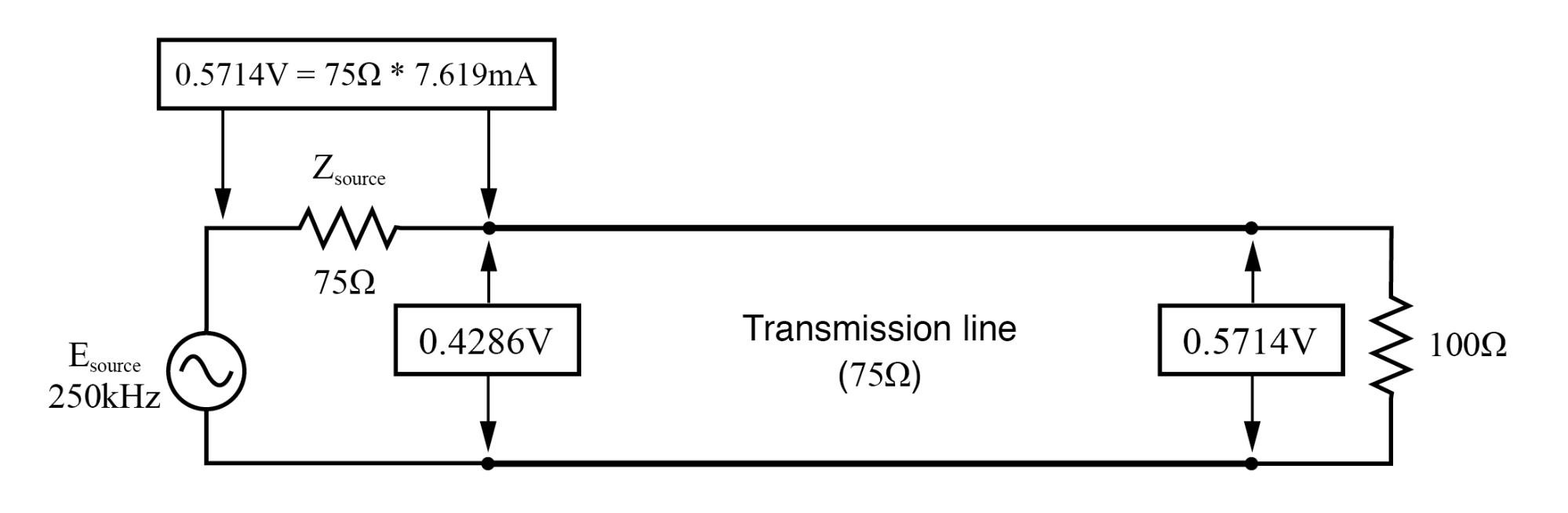
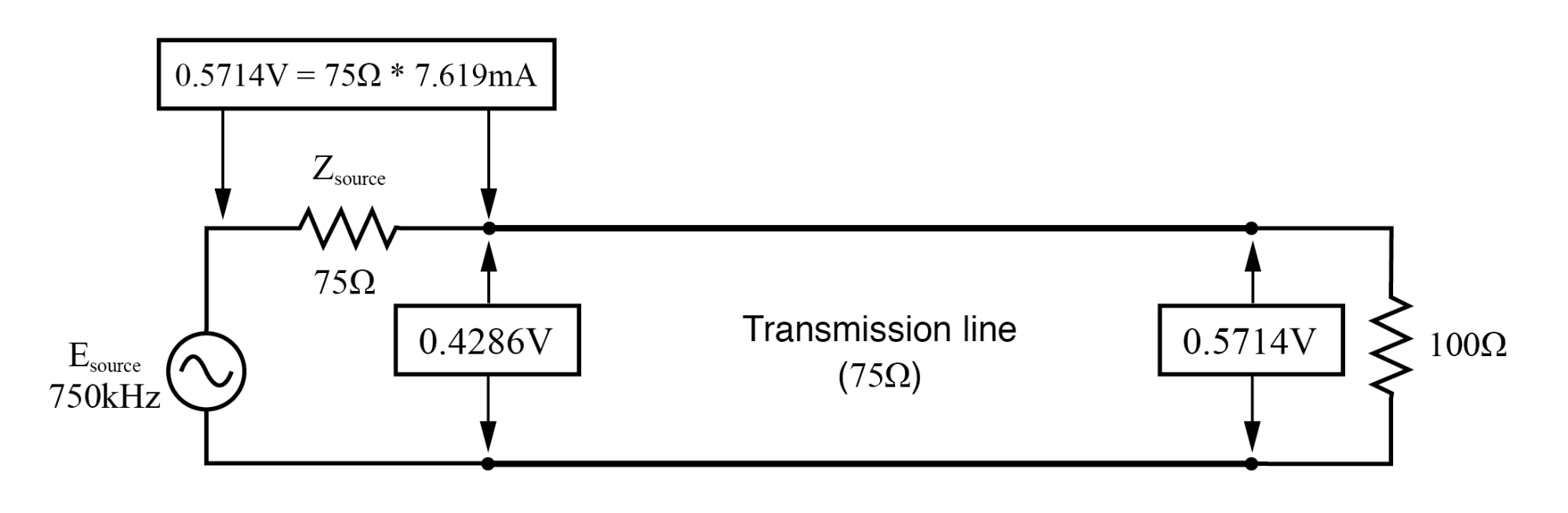
Bei f=250 KHz:Eingang:V=0.4286, I=7.619 mA; Ende:V=0.5714, I=7.619 mA.

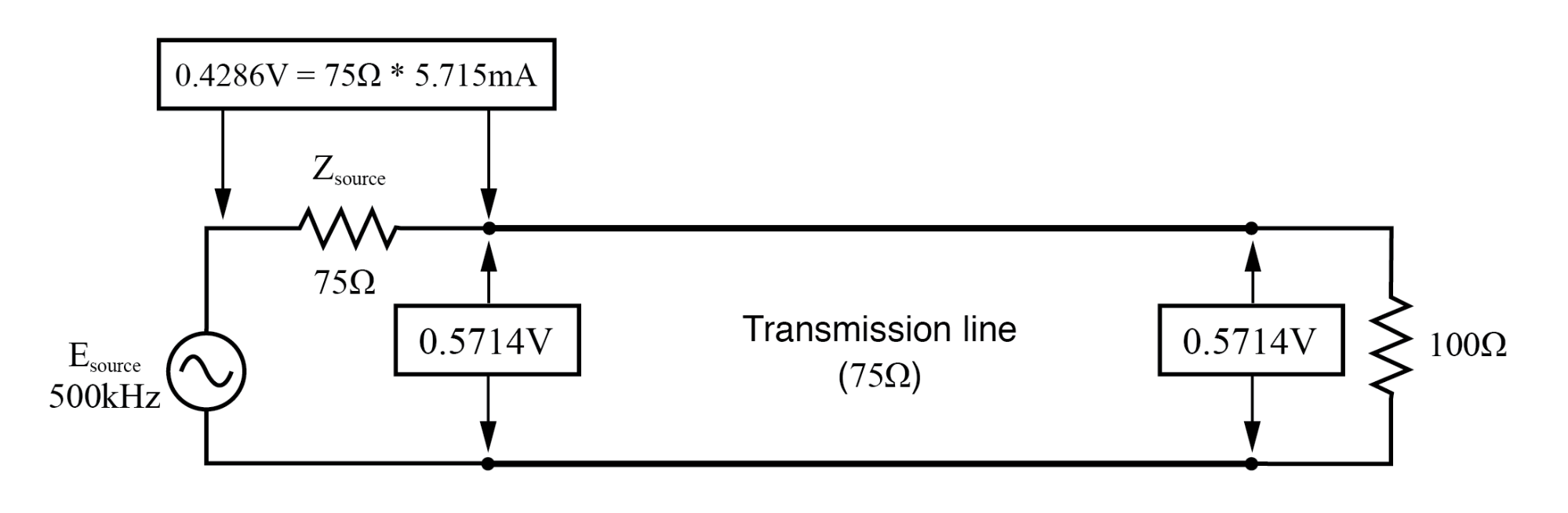
Bei f=500 KHz:Eingang:V=0.5714, I=5.715 mA; Ende:V=5.714, I=5.715 mA.

Bei f=750 KHz:Eingang:V=0.4286, I=7.619 mA; Ende:V=0.5714, I=7.619 mA.

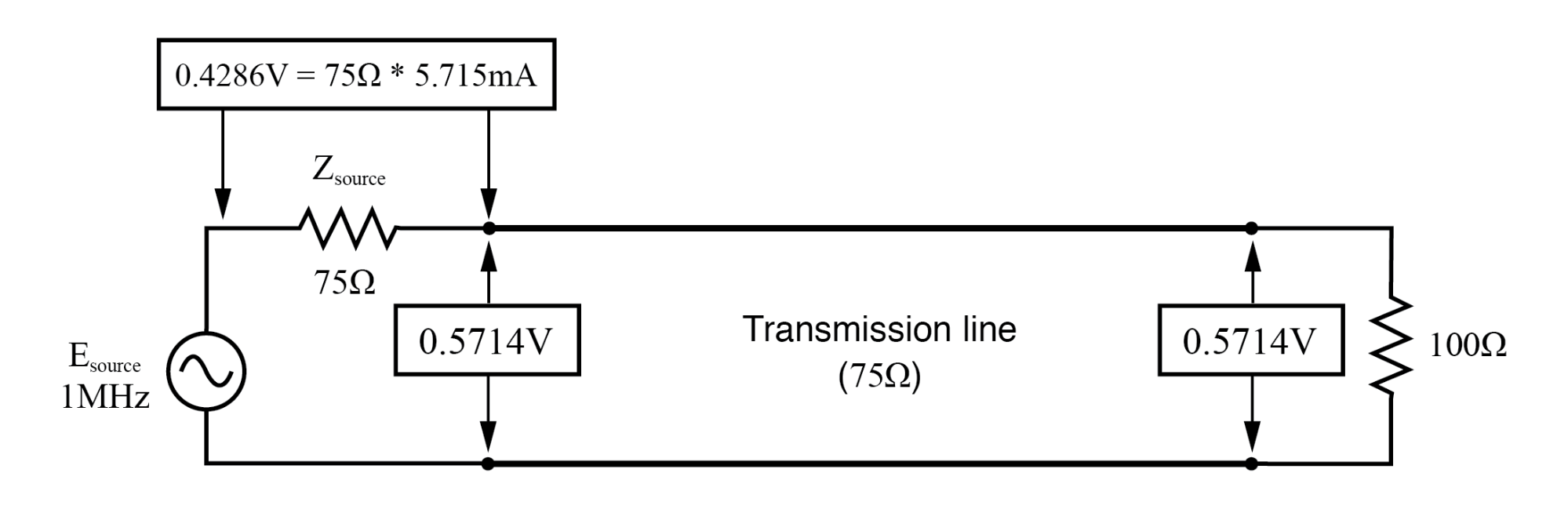
Bei f=1 MHz:Eingang:V=0.5714, I=5.715 mA; Ende:V=0.5714, I=0.5715 mA.

Bei ungeraden Harmonischen der Grundfrequenz (250 kHz, Abbildung 3 oben und 750 kHz, Abbildung oben) sehen wir unterschiedliche Spannungspegel an jedem Ende der Übertragungsleitung, da bei diesen Frequenzen die stehenden Wellen an einem Ende in einem Knoten enden und am anderen Ende in einem Schwingungsbauch.

Im Gegensatz zu den Beispielen mit offener und kurzgeschlossener Übertragungsleitung erreichen die maximalen und minimalen Spannungspegel entlang dieser Übertragungsleitung nicht die gleichen Extremwerte von 0 % und 100 % Quellenspannung, aber wir haben immer noch Punkte von „Minimum“ und „ maximale“ Spannung.

(Abbildung 6 oben) Das gleiche gilt für Strom:Wenn die Abschlussimpedanz der Leitung nicht mit der charakteristischen Impedanz der Leitung übereinstimmt, haben wir an bestimmten festen Stellen auf der Leitung Punkte minimalen und maximalen Stroms, die den Knoten der stehenden Stromwelle entsprechen bzw. Bäuche.

Stehwellenverhältnis

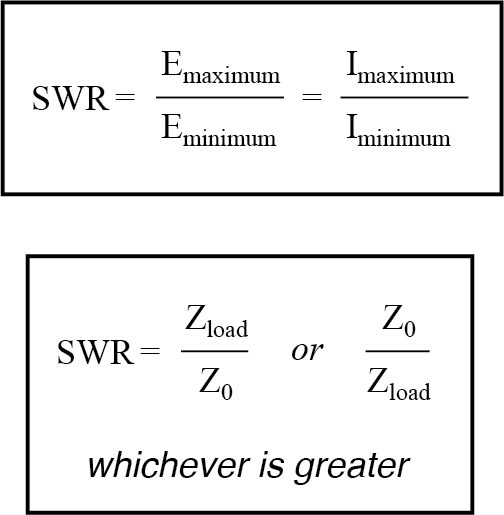
Eine Möglichkeit, die Schwere stehender Wellen auszudrücken, ist das Verhältnis von maximaler Amplitude (Bäuche) zu minimaler Amplitude (Knoten), für Spannung oder für Strom.

Wenn eine Leitung durch eine Unterbrechung oder einen Kurzschluss endet, ist dieses Stehwellenverhältnis , oder SWR wird mit unendlich bewertet, da die minimale Amplitude null ist und jeder endliche Wert geteilt durch null einen unendlichen (eigentlich „undefinierten“) Quotienten ergibt.

In diesem Beispiel mit einer 75--Leitung, die mit einer 100--Impedanz abgeschlossen ist, ist das SWR endlich:1,333, berechnet aus der maximalen Leitungsspannung bei entweder 250 kHz oder 750 kHz (0,5714 Volt) und Division durch die minimale Leitungsspannung ( 0,4286 Volt).

Das Stehwellenverhältnis kann auch berechnet werden, indem man die Abschlussimpedanz der Leitung und den Wellenwiderstand der Leitung nimmt und den größeren der beiden Werte durch den kleineren dividiert. In diesem Beispiel ergibt die Abschlussimpedanz von 100 Ω geteilt durch die charakteristische Impedanz von 75 Ω einen Quotienten von genau 1,333, was der vorherigen Berechnung sehr gut entspricht.

Eine perfekt abgeschlossene Übertragungsleitung hat ein SWR von 1, da die Spannung an jeder Stelle entlang der Länge der Leitung gleich ist, ebenso wie für den Strom.

Auch dies wird normalerweise als ideal angesehen, nicht nur weil reflektierte Wellen Energie darstellen, die nicht an die Last geliefert wird, sondern weil die hohen Spannungs- und Stromwerte, die von den Bäuchen stehender Wellen erzeugt werden, die Isolierung der Übertragungsleitung (Hochspannung) überbeanspruchen können und Leiter (Hochstrom) bzw..

Außerdem neigt eine Übertragungsleitung mit einem hohen SWR dazu, als Antenne zu fungieren, die elektromagnetische Energie von der Leitung weg abstrahlt, anstatt sie vollständig zur Last zu leiten. Dies ist normalerweise unerwünscht, da sich die abgestrahlte Energie mit nahegelegenen Leitern „koppeln“ kann, was zu Signalstörungen führt.

Eine interessante Fußnote zu diesem Punkt ist, dass Antennenstrukturen – die typischerweise offenen oder kurzgeschlossenen Übertragungsleitungen ähneln – oft für den Betrieb bei hohen . ausgelegt sind Stehwellenverhältnisse, um die Signalabstrahlung und den Empfang zu maximieren.

Das folgende Foto (Abbildung unten) zeigt eine Reihe von Übertragungsleitungen an einem Verbindungspunkt in einem Funksendersystem. Die großen Kupferrohre mit keramischen Isolierkappen an den Enden sind starre koaxiale Übertragungsleitungen mit 50 Ω Wellenwiderstand.

Diese Leitungen führen HF-Leistung von der Funksenderschaltung zu einem kleinen hölzernen Unterstand am Fuß einer Antennenstruktur und von diesem Unterstand zu anderen Unterständen mit anderen Antennenstrukturen:

Flexible Koaxialkabel verbunden mit starren Leitungen.

An die starren Leitungen angeschlossene flexible Koaxialkabel (ebenfalls mit 50 Ω Wellenwiderstand) leiten die HF-Leistung zu kapazitiven und induktiven „Phasing“-Netzwerken innerhalb des Shelters. Der weiße Kunststoffschlauch, der zwei der starren Leitungen miteinander verbindet, leitet „Füllgas“ von einer versiegelten Leitung zur anderen.

Die Leitungen sind mit Gas gefüllt, um zu vermeiden, dass sich darin Feuchtigkeit ansammelt, was für eine Koaxialleitung ein definitives Problem wäre. Beachten Sie die flachen, kupfernen „Bänder“, die als Überbrückungsdrähte verwendet werden, um die Leiter der flexiblen Koaxialkabel mit den Leitern der starren Leitungen zu verbinden.

Warum Flachbänder aus Kupfer und keine Runddrähte? Wegen des Skin-Effekts, der den größten Teil der Querschnittsfläche eines Rundleiters bei Hochfrequenzen unbrauchbar macht.

Wie viele Übertragungsleitungen werden diese bei niedrigen SWR-Bedingungen betrieben. Wie wir im nächsten Abschnitt sehen werden, ist das Phänomen der stehenden Wellen in Übertragungsleitungen jedoch nicht immer unerwünscht, da es für eine nützliche Funktion ausgenutzt werden kann:Impedanztransformation.

RÜCKBLICK:

• Stehende Wellen sind Spannungs- und Stromwellen, die sich nicht ausbreiten (d. h. stationär sind), sondern das Ergebnis einer Interferenz zwischen einfallenden und reflektierten Wellen entlang einer Übertragungsleitung sind.
• Ein Knoten ist ein Punkt auf einer stehenden Welle von Minimum Amplitude.
• Ein Baustein ist ein Punkt auf einer stehenden Welle von maximal Amplitude.
• Stehende Wellen können in einer Übertragungsleitung nur existieren, wenn die Abschlussimpedanz nicht mit der charakteristischen Impedanz der Leitung übereinstimmt. In einer perfekt abgeschlossenen Linie gibt es keine reflektierten Wellen und daher überhaupt keine stehenden Wellen.
• Bei bestimmten Frequenzen korrelieren die Knoten und Bäuche von stehenden Wellen mit den Enden einer Übertragungsleitung, was zu einer Resonanz führt .
• Der Resonanzpunkt mit der niedrigsten Frequenz auf einer Übertragungsleitung ist dort, wo die Leitung eine Viertelwellenlänge lang ist. Resonanzpunkte existieren bei jeder harmonischen (ganzzahligen) Frequenz der Grundwelle (Viertelwellenlänge).
• Stehwellenverhältnis , oder SWR , ist das Verhältnis von maximaler Stehwellenamplitude zu minimaler Stehwellenamplitude. Sie kann auch berechnet werden, indem die Abschlussimpedanz durch die charakteristische Impedanz geteilt wird oder umgekehrt, je nachdem, was den größten Quotienten ergibt. Eine Linie ohne stehende Wellen (perfekt abgestimmt:Z_load zu Z₀ ) hat ein SWR von 1.
• Übertragungsleitungen können durch die hohen maximalen Amplituden stehender Wellen beschädigt werden. Spannungsbäuche können die Isolierung zwischen Leitern zerstören und Strombäuche können Leiter überhitzen.