Pseudospin-abhängige Einwegübertragung in Graphen-basierten topologischen plasmonischen Kristallen

Hintergrund

Photonische topologische Isolatoren [1,2,3,4], optische Materialien einer nichttrivialen topologischen Phase, die die Lichtdurchlässigkeit in ihrem Inneren verbieten, aber die Ausbreitung entlang ihrer Kanten ermöglichen, wurden nach der Entdeckung des Quanten-Hall-Effekts (QHE) in kondensierten Angelegenheit. Eine wichtige Manifestation der topologischen Physik ist das Vorhandensein von Kantenzuständen, die robust gegenüber strukturellen Defekten oder lokalen Störungen sind. Insbesondere durch die Verwendung der Bulk-Kanten-Korrespondenz [5, 6] kann man verschiedene topologische Phasen untersuchen, indem man Kantenzustände oder topologische Invarianten der Kanten untersucht. In den letzten Jahren wurden topologische Randzustände in vielen photonischen topologischen Bandlückensystemen vorhergesagt und beobachtet, wie z [12, 13] und photonische Floquet-Gitter [14, 15], bei denen verschiedene physikalische Mechanismen vorgeschlagen werden, um topologischen Schutz zu bieten. Bemerkenswert ist, dass ein doppelter Dirac-Kegel geöffnet wurde, um eine topologisch nicht triviale Bandlücke in einem bekannten photonischen Wabengitterkristall zu erhalten, der die Pseudozeitumkehrsymmetrie bewahrt, was zu einer pseudospinabhängigen unidirektionalen Transmission von Kantenzuständen führt [16, 17]. Neben den photonischen Systemen wurden pseudospinabhängige Kantenzustände in phononischen Systemen untersucht [18,19,20]. Die Analogie zu den plasmonischen Nanostrukturen wurde jedoch noch nicht beschrieben, was auf den enormen ohmschen Verlust der Plasmonen zurückzuführen ist, die sich entlang der traditionellen plasmonischen Materialien wie Au und Ag ausbreiten.

Oberflächenplasmonenpolaritonen (SPPs) [21], durch Photonen gekoppelte Elementaranregungen und Freie-Elektronen-Oszillationen an einer Grenzfläche zwischen einem Metall und einem Dielektrikum, gelten als vielversprechender physikalischer Mechanismus, um die Beugungsbegrenzung zu umgehen und die Miniaturisierung der Bauelemente voranzutreiben . Iurov et al. untersuchten die Rückwirkung und Hybridisierung der Plasmonenmoden und fanden die induzierte optische Polarisation durch Dirac-Elektronen in Graphen [22]. Memmiet al. berichteten über die starke Kopplung zwischen SPPs und Molekülschwingungen [23]. Während häufig verwendete Edelmetalle wie Gold und Silber plasmonische Eigenschaften hauptsächlich im sichtbaren und nahen Infrarotbereich des Spektrums aufweisen, hat sich Graphen in letzter Zeit als vielversprechende Alternative herausgestellt, die in der Lage ist, den Bereich der Plasmonik auf Infrarot und Terahertz (THz) auszudehnen. Wellenlängen. Noch wichtiger ist, dass Graphenplasmonen im Gegensatz zu Edelmetallen durch elektrostatische Vorspannung dynamisch abgestimmt werden können [24, 25], was eine neue Generation rekonfigurierbarer plasmonischer Bauelemente ermöglicht. Darüber hinaus können in hochwertigem Graphen angeregte SPPs bemerkenswert lange intrinsische Relaxationszeiten erreichen und eine beispiellose Feldbegrenzung bieten [26]. Diese außergewöhnlichen Eigenschaften machen Graphen zu einem idealen Kandidaten für die vollständig integrierten topologischen plasmonischen Komponenten. Vor kurzem haben Jin et al. realisierten topologisch geschützte Einweg-Kantenplasmonen in einem periodisch gemusterten Monolayer-Graphen, wobei die Bandtopologie von Graphen-Plasmonen unter einem die Zeit umkehrenden Magnetfeld im Detail untersucht wurde [27]. Und Panet al. demonstrierten das substantielle nichtreziproke Verhalten an den Übergitterübergängen unter moderaten statischen Magnetfeldern, was zur Entstehung topologisch geschützter Randzustände und lokalisierter Volumenmoden führte [28].

In dieser Arbeit untersuchen wir theoretisch die topologischen Eigenschaften von zweidimensionalen (2D) plasmonischen Graphenkristallen (GPCs), die aus periodisch angeordneten Graphen-Nanoscheiben aufgebaut sind. Dirac-Kegel an den Ecken der Brillouin-Zone (BZ) werden unter Verwendung des Zonenfaltmechanismus zu einem doppelten Dirac-Kegel in der BZ-Mitte gefaltet. Um topologische Bandlücken zu erhalten, nehmen wir weitere Verformungen am Wabengitter vor. Durch das Schrumpfen oder Expandieren der Graphen-Nanoscheiben wird der doppelte Dirac-Kegel geöffnet und die Bandinversion zwischen Pseudospin-Dipol- und Quadrupol-Moden tritt auf, was weiter zu einem topologischen Phasenübergang zwischen nichttrivialen und trivialen Zuständen führt. Darüber hinaus wird die unidirektionale Ausbreitung von Kantenzuständen entlang einer durch triviale und nichttriviale GPCs konstruierten Grenzfläche numerisch simuliert, was die Pseudospin-Eigenschaften und die topologische Robustheit unserer entworfenen plasmonischen Kristalle weiter demonstriert.

Methoden

Wir untersuchen die Bandtopologie von SPPs in einem 2D-Plasmonenkristall einer Anordnung periodisch angeordneter Graphen-Nanoscheiben, die von derselben Graphenschicht mit unterschiedlichem chemischem Potential umgeben sind, wie in Abb. 1a gezeigt. Die Gitterkonstante a = 40 nm, μ _c1 , und r sind das chemische Potenzial und die Radien der Graphen-Nanoscheiben; μ _c2 bezeichnet das chemische Potential des umgebenden Graphens. Durch Lösen der Maxwells-Gleichungen mit Randbedingungen erhalten wir die Dispersionsbeziehung für transversal magnetisch (TM)-polarisierte SPP-Moden, die auf der von Luft und Siliziumdioxid umgebenen Graphenschicht unterstützt werden [29]:

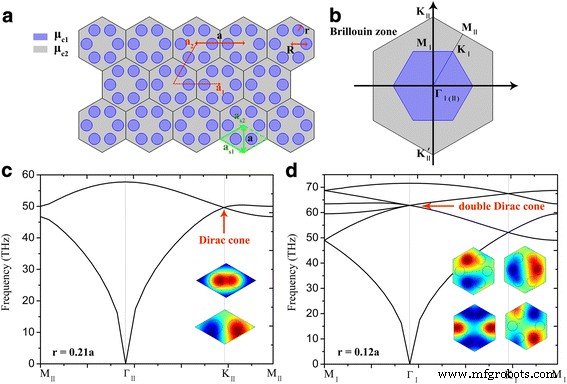
a Schemata der 2D-GPCs. b Die Brillouin-Zonen. c Bandstruktur des Gitters basierend auf der mit grünen gestrichelten Linien gekennzeichneten rhombischen primitiven Elementarzelle, die Einschübe zeigen die eigenelektrischen Feldverteilungen des Dirac-Punktes. d Bandstruktur des Gitters basierend auf der hexagonalen Elementarzelle, die Einschübe zeigen die eigenelektrischen Feldverteilungen des doppelten Dirac-Punktes. Die anderen Parameter sind als μ . eingestellt _c1 = 0,3 eV, μ _c2 = 0.6 eV, τ = 1 ps, die Gitterkonstante a = 40 nm

Hier, ε ₀ ist die Vakuumpermittivität des freien Raums, k ₀ = 2π/λ die Wellenzahl im freien Raum ist und λ ist die Betriebswellenlänge im Vakuum. Im mittleren Infrarotbereich werden die Dielektrizitätskonstanten von Luft und Siliciumdioxid, die Super und Substraten entsprechen, als ε . angenommen _Luft = 1 und ε _SiO2 = 3,9 bzw. [30]. Im nicht verzögerten Regime mit β » k ₀ , die Gl. (3) kann vereinfacht werden zu [31].

wobei β ist die Ausbreitungskonstante SPPs auf der Graphenschicht und der effektive Brechungsindex n _eff des SPP-Modus kann abgeleitet werden von n _eff = β /k ₀ . σ _g ist die Oberflächenleitfähigkeit von Graphen, die sich aus den Beiträgen von Intraband und Interband zusammensetzt, d. h. σ _g = σ _intra + σ _inter [29, 30]. Die Intraband-Leitfähigkeit σ _intra entsprechend dem Intraband-Elektronen-Photonen-Streuungsprozess ist gegeben durch

wobei μ _c ist das chemische Potential bezogen auf die Elektronendichte, e ist die Elektronenladung, ω ist die Kreisfrequenz des Plasmons, ℏ und k _B sind die reduzierte Planck-Konstante bzw. die Boltzmann-Konstante, T ist die Temperatur und τ repräsentiert die Elektronenimpulsrelaxationszeit aufgrund von Ladungsträgerstreuung. Für ℏω » k _B T und |μ _c | » k _B T , die Interband-Leitfähigkeit σ _inter entsprechend Interband-Elektronenübergängen kann näherungsweise ausgedrückt werden als

Ergebnisse und Diskussion

Die Energiebandstrukturen der vorgeschlagenen plasmonischen Kristalle werden durch den Einsatz der Finite-Elemente-Methode (FEM) basierend auf der kommerziell erhältlichen Software COMSOL Multiphysics erhalten. In Abb. 1a sehen wir, dass sowohl die rhombische Elementarzelle zweier Graphen-Nanoscheiben (grüne gestrichelte Raute definiert durch die Vektoren a _s1 und a _s2 ) und die hexagonale Elementarzelle von sechs Graphen-Nanoscheiben (mit Gittervektoren a ₁ und a ₂ ) können die plasmonischen Kristalle mit Wabengitter bilden. Abbildung 1b zeigt die BZs für die rhombischen und hexagonalen Elementarzellen mit den irreduziblen Zonen von M_II -Γ _II - K_II - M_II und M_I -Γ _Ich - K_I - M_Ich bzw. Beachten Sie, dass die hexagonale Elementarzelle dreimal größer ist als die rhombische Grundzelle. Daher ist die erste BZ der rhombischen primitiven Elementarzelle dreimal größer als die der hexagonalen (blauer Bereich in Abb. 1b). Wenn man eine rhombische primitive Elementarzelle nimmt, zeigt dieser plasmonische Kristall eine Dirac-Kegel-Dispersion bei K_II und K_II ` Punkte in den BZ-Ecken wie in Abb. 1c gezeigt. Die Einschübe in Abb. 1c zeigen die Eigenverteilungen des elektrischen Feldes der beiden entarteten Zustände am Dirac-Punkt. Ähnlich den Pseudospins in klassischen photonischen und akustischen Systemen [17, 19, 20] sollte der Freiheitsgrad auf zweifache Zustände erhöht werden, um das Analogon der Pseudospins in plasmonischen Systemen nachzuahmen. Daher werden vierfach degenerierte Doppel-Dirac-Kegel in der plasmonischen Bandstruktur benötigt. Durch den Einsatz des Zonenfaltmechanismus [18] können die Dirac-Kegel bei K<sub>II</sub> und K<sub>II</sub> ` Punkte werden bei Γ . zu einem doppelten Dirac-Kegel gefaltet Punkt in der BZ-Mitte, wenn man die größere hexagonale Elementarzelle nimmt (wie in Abb. 1d dargestellt). Die Einschübe in Abb. 1d zeigen die vierfach entarteten Eigenzustände mit Dipol- und Quadrupolmoden. Die von uns verwendeten relativen Parameter sind μ _c1 = 0,3 eV, μ _c2 = 0,6 eV und τ = 1 ps, die mäßig aus den vorherigen Untersuchungen für praktisches Graphen ausgewählt wurden [32, 33].

Die vierfach degenerierten Doppel-Dirac-Kegel, die aus zwei dipolaren und zwei quadrupolaren Moden bestehen, sind mit zwei irreduziblen 2D-Darstellungen eines C_6v . verbunden Punktgruppe, nämlich E₁ Modi ungerader räumlicher Parität und E₂ Modi gleichmäßiger räumlicher Parität. In Anlehnung an die in der Quantenmechanik weit verbreitete konventionelle Notation [34] können wir diese Moden in die p . klassifizieren _x /p _y und d _x2-y2 /d _xy Moden nach ihrem Eigen E _z Feldverteilungen in Abb. 2. Um als nächstes eine nichttriviale topologische Bandlücke am Γ nehmen wir weitere Modifikationen vor (d. h. die Verformung des Wabengitters von a /R = 3) auf der hexagonalen Elementarzelle, um die Symmetrie zu brechen. Beim Schrumpfen der Graphen-Nanoscheiben auf a /R = 3.2, der vierfach entartete Doppel-Dirac-Kegel spaltet sich in zwei zweifach entartete Zustände auf und eine Volumenbandlücke öffnet sich von 62,1 bis 63,5 THz, wie in Abb. 2a gezeigt. Das E _z Felder der unteren Bänder haben ein Paar von Dipolmoden mit p _± Zeichen, während die oberen Bänder ein Paar Quadrupolmoden aufweisen, die d . aufweisen _± Zeichen um das Γ Punkt, der mit der klassischen photonischen Theorie übereinstimmt, dass die Dipolmoden eine niedrigere Frequenz aufweisen müssen als die Quadrupolmoden höherer Ordnung. Allerdings findet eine Bandinversion statt, wenn die Graphen-Nanoscheiben auf a . erweitert werden /R = 2,9, d. h. die Dipolmoden steigen über die Quadrupolmoden an, was die topologische nichttriviale Bandlücke von 62,4 bis 63,3 THz bewirkt, wie in Abb. 2c gezeigt. Abbildung 2d, e veranschaulicht den Prozess des topologischen Übergangs zwischen p _± und d _± Zustände und die mit p . verbundenen Magnetfelder in der Ebene _± und d _± sind mit weißen Pfeilen gekennzeichnet. Die Drehimpulse der Wellenfunktion von E _z Felder p _± = (p _x ± ip _y )/\( \sqrt{2} \) und d _± = (d _x2-y2 ± id _xy )/\( \sqrt{2} \) bilden weiterhin den Pseudospin in den vorliegenden plasmonischen Kristallen [17, 18].

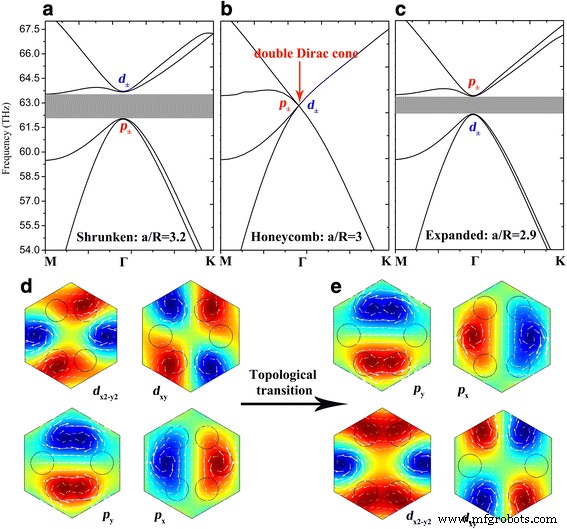
Bandstrukturen der GPCs mit a a /R = 3.2, b a /R = 3 und c a /R = 2.9. d , e Das E _z Feldverteilungen von Dipolmoden und Quadrupolmoden des p _± und d _± Staaten in a und c bzw. Die weißen Pfeile stellen das mit E . verbundene Magnetfeld in der Ebene dar _z Feld

Um die topologische Eigenschaft der in Abb. 2a, c gezeigten Bandlücken weiter zu untersuchen, wird sie im Allgemeinen auf eine effektive Hamiltonsche Beschreibung und topologische Zahlen bezogen. Durch Anwendung der \( \overset{\rightharpoonup }{k}\cdot \overset{\rightharpoonup }{p} \)-Störungstheorie wird der effektive Hamilton-Operator H _eff (k ) rund um die Γ Punkt auf der Grundlage [p ₊ , d ₊ , p ₋ , d ₋ ] kann ausgedrückt werden als [17, 35].

wo k _± = k _x ± ik _y , und A kommt von nichtdiagonalen Elementen des Störungsterms erster Ordnung \( {M}_{\alpha \beta}=\left\langle {\Gamma}_{\alpha}\left|\overset{\rightharpoonup }{k }\cdot \overset{\rightharpoonup }{p}\right|{\Gamma}_{\beta}\right\rangle\) mit α = 1, 2 und β = 3, 4. Der effektive Hamiltonoperator H _eff (k ) hat eine ähnliche Form wie das Bernevig-Hughes-Zhang (BHZ)-Modell für das CdTe/HgTe/CdTe-Quantentopfsystem [36] und impliziert eine topologische Bandlücke, wenn die Bandinversion stattfindet. Basierend auf dem Hamilton-Operator, der in Gl. (5) können wir die Spin-Chern-Zahlen der topologischen plasmonischen Kristalle als [36] auswerten.

Hier, M = (E _p – E _d )/2 ist die Frequenzdifferenz zwischen E ₂ und E ₁ Vertretungen bei der Γ Punkt. B wird durch die Diagonalelemente des Störungsterms zweiter Ordnung bestimmt und ist typischerweise negativ [19]. Also, C _± = 0 wird erhalten, wenn eine normale Bandordnung vorliegt, wie in Fig. 2a dargestellt. Und wir schließen daraus, dass die geöffnete Bandlücke trivial ist. Jedoch M wird positiv, wenn eine Bandinversion auftritt. Daher C _± = ±1 wird einfach erhalten, und die Lücke in Fig. 2c ist nicht trivial.

Durch Überlappen der Bandlücken mit unterschiedlichen Topologien (d. h. topologisch trivial und topologisch nicht trivial) kann man Kantenzustände erzeugen, die räumlich um die Grenzfläche zwischen zwei plasmonischen Kristallen begrenzt sind. Hier betrachten wir ein Band eines topologisch nichttrivialen plasmonischen Kristalls (mit der in Abb. 2c gezeigten Bandstruktur), dessen beiden Kanten von zwei topologisch trivialen plasmonischen Kristallen (mit der in Abb. 2a gezeigten Bandstruktur) im gleichen Frequenzfenster umhüllt sind. Die zwei trivialen Bereiche verhindern, dass mögliche Kantenzustände in den freien Raum eindringen. In Abb. 3a präsentieren wir die berechneten projizierten Bandstrukturen entlang des Γ K-Richtung für ein solches Band, bei dem eine Volumenbandlücke von zusätzlichen topologischen Kantenzuständen überspannt wird, wie durch die doppelt entarteten roten Kurven angezeigt. Abb. 3b zeigt die Verteilungen des elektrischen Feldes, die um die Grenzfläche begrenzt sind, die von zwei charakteristischen Kristallen aufgebaut ist, entsprechend den Punkten A (mit k _x = − 0.05π/a ) und B (mit kx = 0,05π/a ) in Abb. 3a markiert. Die Pseudo-Spin-Up- und Spin-Down-Eigenschaften werden durch Phasenwirbel im Gegenuhrzeigersinn und im Uhrzeigersinn gezeigt, wie im rechten Feld von Fig. 3b dargestellt.

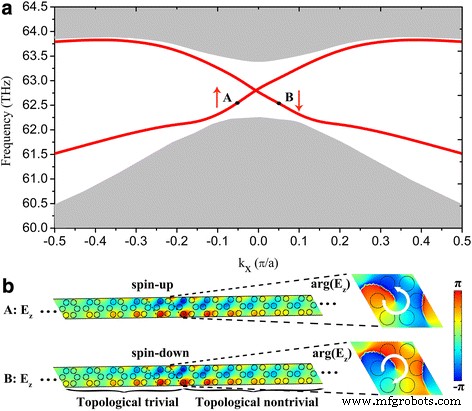
a Projizierte Bandstruktur für eine Superzelle bestehend aus 16 nichttrivialen Elementarzellen, die auf beiden Seiten von 12 trivialen Elementarzellen umhüllt sind. b Elektrische Feldverteilungen um die Grenzfläche zwischen den trivialen und nichttrivialen plasmonischen Kristallen an den Punkten A und B, d. h. bei k _x = − 0,05π/a bzw. 0,05π/a

Die pseudospinabhängige unidirektionale Übertragung von Kantenzuständen wird auch in einem endlichen 20a . demonstriert × 18a Gitter aus trivialen und nichttrivialen Kristallen aufgebaut. Wie in Abb. 4a, b gezeigt, Einwegausbreitung der SPP-Welle nach links (rechts) bei Anregung durch eine Pseudo-Spin-Up-(Spin-Down)-Quelle S ₊ (S ₋ ) der gegen den Uhrzeigersinn (im Uhrzeigersinn) zirkularen Polarisation des in der Ebene liegenden Magnetfelds. Eines der charakteristischsten Merkmale topologischer Kantenzustände ist, dass sie robust gegenüber Störungen/Imperfektionen sind. Um diese Robustheit zu verifizieren, konstruieren wir scharfe Krümmungen, wie in Abb. 4c gezeigt, wo die unidirektionale Übertragung der SPP-Welle durch eine Pseudo-Spin-Down-Quelle S . angeregt wird ₋ . Die SPP-Welle verschwand schließlich nach einer langen Strecke entlang der scharfen Kurven aufgrund des intrinsischen Verlusts von Graphenmaterial. Um diese topologische Transmission weiter zu bestätigen, zeigen wir auch die Verteilung der elektrischen Feldstärke, indem wir den intrinsischen Verlust von Graphen zum Vergleich ignorieren. Wie aus Fig. 4d ersichtlich ist, folgt die SPP-Welle der entworfenen Route und behält die Ausbreitung in eine Richtung mit geringer Rückstreuung bei.

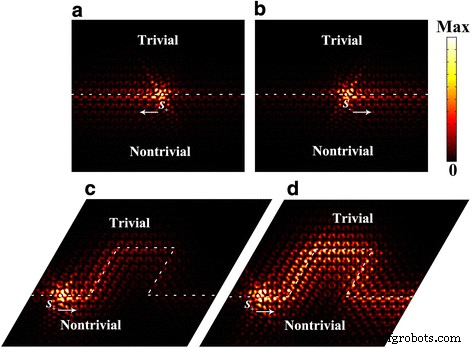
a Nach links und b Einweg-Kantenzustände nach rechts, angeregt durch ein in der Ebene liegendes Magnetfeld mit einer Phasendifferenz von π/2:\( {S}_{\pm }={H}_0\left(\overset{\rightharpoonup }{x}\mp i\overset{\rightharpoonup }{y}\right) \). c Topologische Kantenzustände, die sich entlang scharfer Kurven bewegen. d Die Verteilung der elektrischen Feldstärke der topologischen Einwegübertragung ohne Berücksichtigung des intrinsischen Verlusts von Graphenmaterial

Schlussfolgerungen

Zusammenfassend haben wir systematisch die Bandtopologien der GPCs untersucht, die aus periodisch gemusterten Graphen-Nanoscheiben aufgebaut sind. Durch den Zonenfaltmechanismus werden die Dirac-Kegel an der BZ-Ecke zu einem doppelten Dirac-Kegel in der BZ-Mitte gefaltet. Darüber hinaus werden topologische Bandlücken durch Verformung der Wabengitter-GPCs realisiert. Basierend auf dem effektiven Hamilton-Operator, der von der \(\overset{\rightharpoonup }{k}\cdot \overset{\rightharpoonup }{p}\)-Störungstheorie abgeleitet wird, werden die Spin-Chern-Zahlen berechnet. Die Pseudospineigenschaften, die durch Phasenwirbel im Gegenuhrzeigersinn und im Uhrzeigersinn nachgewiesen werden, werden erfolgreich verwendet, um die unidirektionale Übertragung von Kantenzuständen entlang einer Grenzfläche zu realisieren, die aus zwei topologischen trivialen und nichttrivialen plasmonischen Kristallen besteht. Die entworfene GPC bietet einen neuen Weg zur Erforschung topologischer Phänomene und könnte potenzielle Anwendungen im Bereich der topologischen Plasmonik finden. Es könnte auch die Erforschung der Pseudospin-Plasmonik und der Technik des Pseudospin-Multiplexens in hochdichten nanophotonischen integrierten Schaltkreisen auslösen.

Abkürzungen

BHZ:

Bernevig-Hughes-Zhang

BZ:

Brillouin-Zone

FEM:

Finite-Elemente-Methode

GPC:

Plasmonischer Graphenkristall

QHE:

Quanten-Hall-Effekt

QSHE:

Quantenspin-Hall-Effekt

SPPs:

Oberflächenplasmonenpolaritonen