Änderung der Oberflächenleitfähigkeit von elastisch verformten p-Si-Kristallen, die mit Röntgenstrahlen bestrahlt werden

Zusammenfassung

In dieser Arbeit wurden Leitfähigkeitsänderungen von bestrahlten und unbestrahlten p-Si-Einkristallen unter dem Einfluss von elastischer einachsiger mechanischer Spannung untersucht. Ein analytischer Ausdruck wurde vorgeschlagen, um die Abhängigkeit der Oberflächenleitfähigkeit als Funktion der mechanischen Belastung und der Röntgenbestrahlungsdosis zu beschreiben. Es wurde gezeigt, dass 4-eckige Nanopartikel auf der Oberfläche von „solarem“ Silizium die Änderungen der elektrischen Leitfähigkeit unter mechanischer Belastung beeinflussen. Es wurde festgestellt, dass Röntgenbestrahlung zur Erzeugung von Punktdefekten in Silizium führt. Diese Defekte unterdrücken die Versetzungsbewegung. Es wurde gezeigt, dass der spezifische Widerstand von zuvor bestrahlten Proben von „elektronischem“ Silizium nur geringfügig empfindlich gegenüber dem Einfluss einachsiger Kompression bei einer bestimmten Verformungsrate ist.

Hintergrund

Eine weit verbreitete Verwendung von Halbleiterbauelementen im Bereich moderner elektronischer Technologien erfordert die Untersuchung neuer halbleitender Materialien, die eine hohe Stabilität gegenüber äußeren Einflüssen wie Röntgenstrahlung und mechanischer Verformung aufweisen. Heutzutage wird Silizium aktiv in hochempfindlichen Detektoren und anderen Halbleitersensoren verwendet, die in Strahlungsfeldern arbeiten [1].

Die meisten Artikel widmen sich dem Einfluss der plastischen Verformung auf die Leitfähigkeit von n-Si [2, 3]. Daher gilt der Einfluss der elastischen Verformung auf die Eigenschaften von p-Si-Kristallen nach wie vor als wichtige wissenschaftliche Aufgabe. Die Umverteilung der Ladungsträgerkonzentration und der Verunreinigungen in verformten Kristallen ist oft durch das Vorhandensein von Versetzungen gekennzeichnet, die wirksame Getter von Defekten sind, insbesondere auf der Oberfläche des Kristalls [4, 5]. Es ist bekannt [3, 6], dass die Anregung kristallelektronischer Subsysteme auch mit entsprechenden Änderungen der Versetzungsbeweglichkeit einhergeht. Die Erregung der elektronischen Subsysteme kann durch äußere Einflüsse wie Strahlung und elektrostatische Felder erfolgen. Ein charakteristisches Merkmal von Versetzungen in Siliziumkristallen ist das Vorhandensein von Punktdefekten (Cottrell-Wolke) mit einer hohen Konzentration um Versetzungen herum.

Die Oberfläche der Kristalle ist am empfindlichsten gegenüber ionisierender Strahlung. Daher wird die Untersuchung strahlungsinduzierter Prozesse an den Randschichten von Siliziumkristallen nach wie vor als relevant erachtet. Die Oberfläche mit den abgeschiedenen Al-Kontakten ist ein effektiver Getter für die Strukturfehler [5,6,7]. Unterhalb des abgeschiedenen Metallfilms treten die mechanischen Spannungen aufgrund von Inkonsistenzen in den Gitterparametern des Films und des Halbleiters auf [5, 7]. Diese Spannungen stimulieren die Prozesse des Getterns von Defekten (Fremdatome, interstitielle Siliziumatome und Leerstellen) in der Kontaktschicht.

Methoden

Silizium-Einkristalle mit p-Leitfähigkeit, gezüchtet nach der Czochralski-Methode (ρ = 10–20 Ω cm), wurden in der Forschungsarbeit verwendet. Diese Einkristalle sind von zwei Arten:(1) Silizium für die Elektronik – die sogenannten versetzungsfreien (oder elektronischen) Einkristalle auf deren Oberfläche (111), deren Konzentration an dreieckigen Ätzgruben 10<. nicht überschreitet sup> 2 cm⁻² (Abb. 1a und 2), und (2) „solare“ Einkristalle aus Silizium, auf deren Oberfläche (111) die Defekte in Form von 4-eckigen Pyramiden (Abb. 1b) aufgrund einer relativen hohe Konzentration des Hintergrundkohlenstoffs (≈5 × 10¹⁶ cm⁻³ ) und Sauerstoff (≈1.8 × 10¹⁸ cm⁻³ ) Verunreinigungen. Viereckige Pyramiden sind auf die gleiche Weise angeordnet. Die Pyramidenbasis hat eine Größe von 10 nm bis 10 μm.

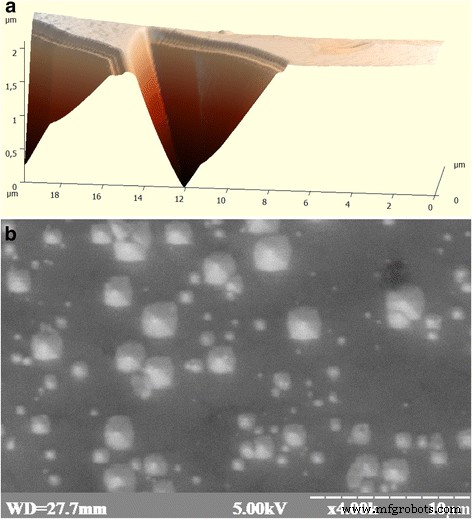
Das Aussehen der Oberfläche der Versuchsproben:a Auftreten von Versetzungsätzgruben auf der Oberfläche des p-Si-Kristalls, erhalten im Bereich des Rasterkraftmikroskops und b Aussehen der submikroskopischen Oberfläche (111) von Sonnenkristallen

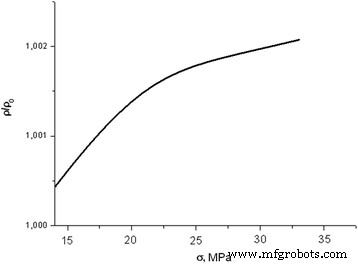
Abhängigkeit des Längswiderstands der primär versetzungsfreien Probe während der elastischen Verformung mit der Verformungsrate 8 μm/min

Es wurde gezeigt [8, 9], dass bei der Bildung von Clustern, denen 4-Winkel-Pyramiden-Ätzlöcher entsprechen, Oxidschichten von Silizium, Punktdefekte und Schichten mit unterschiedlichen Strukturzuständen von Silizium, insbesondere Alpha-Silizium, teilnehmen können.

Experimentelle Proben erhielten nach dem Schleifen und chemischen Polieren Abmessungen von 4 Zoll × 3,7 Zoll × 7,6 mm. Ohmsche Kontakte in Form von zwei 1,5 mm breiten Streifen an den Enden der Probenoberflächen (111) wurden durch thermisches Verdampfen von Aluminium im Vakuum (10⁻⁴ Pa) bei einer auf 593 K erhitzten Probe. Die Messung der elektrischen Leitfähigkeit wurde in einem Vakuumkryostaten bei einem Restgasdruck von 10^–3 . durchgeführt Pa bei der Anwendung von einachsiger Kompression auf die Enden (in Richtung [$ 11\overline{2} $]) mit einer Leistung von 15 bis 40 MPa und einer Verformungsrate von 8 oder 32 μm/min. Die Proben wurden mit einer vollständigen Röntgenstrahlung (W -Anode, 50 kV, 10 mA), beidseitig, auf denen Aluminiumkontakte beschichtet wurden. Der Abstand zwischen der Röntgenquelle und den Kristallen war minimal (1–2 mm). Es wurde festgestellt, dass die absorbierte Dosis alle 30 Minuten um 130 Gy ansteigt. In der Arbeit haben wir zunächst die Versuchsproben bestrahlt und anschließend den Widerstand beim Verformungsprozess gemessen.

Ergebnisse und Diskussion

Das Forschungsergebnis zur Änderung der induzierten mechanischen Leitfähigkeit entlang der Verformungsrichtung (ρ (σ )) von „versetzungsfreien“ Proben der p-Leitfähigkeit unter dem Einfluss einachsiger Spannungen (σ ) ist in Abb. 2 dargestellt. Die Erhöhung der Last von 0 auf 40 MPa (bei einer Verformungsrate von 8 μm/min) dauert 45 min.

Bei der Verformung nimmt der Widerstand versetzungsfreier Proben leicht zu. Es ist zu beachten, dass bei unbestrahlten Kristallen die Änderung der Deformationsrate praktisch keinen Einfluss auf die allgemeine Betrachtung der Abhängigkeiten hatte ρ (σ ) [10, 11]. Ähnliche Abhängigkeiten wurden für bestrahlte Proben erhalten (Abb. 3). Nach Einwirkung von Röntgenstrahlung wurde eine Widerstandserhöhung beobachtet. Die Art der Abhängigkeit ρ (σ ) war etwas anders als bei unbestrahlten Proben.

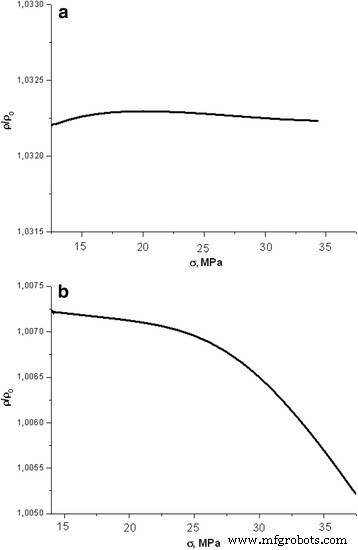
Abhängigkeit des Längswiderstands von eingestrahltem (D = 130 Gy) versetzungsfreie Siliziumprobe bei elastischer Verformung mit wachsender Kompressionsstärke bei einer Geschwindigkeit von 8 μm/min (a .) ) und 32 μm/min (b )

Es ist zu erkennen, dass der Widerstand während der Kompression mit einer Geschwindigkeit von 8 μm/min durch die Einwirkung der Röntgenstrahlung praktisch unveränderlich bleibt (Abb. 3a). Die Diagramme der Abhängigkeiten von Proben, die 260 und 480 Gy ausgesetzt waren, sahen ähnlich aus. In früheren Studien [11] wurde gezeigt, dass der Widerstand während des Bestrahlungsprozesses proportional zur Quadratwurzel der Energiedosis zunahm.

Eine Vervierfachung der Kompressionsrate (von 8 auf 32 μm/min) führt zu einer veränderten Art der Abhängigkeit des spezifischen Widerstands von der Last (Abb. 3b). Der Widerstand der bestrahlten Proben während des Kompressionsprozesses nimmt geringfügig (<0,2%) ab. Anzumerken ist, dass alle Messungen zu Leitfähigkeitsänderungen mit hoher Genauigkeit (±0,045 %) durchgeführt wurden, sodass kleine Widerstandsänderungen im Experiment korrekt analysiert werden konnten.

Es ist zu beachten, dass die in Abb. 3 gezeigte Abhängigkeit 7 Tage nach der Messung der Änderungen des Längswiderstands (D = 130 Gy) versetzungsfreier Proben bei einer Geschwindigkeit von 8 μm/min (Abb. 3a). Im angegebenen Zeitraum erreichte der Widerstand fast wieder seinen ursprünglichen Wert, d. h. den Widerstandswert, der nach der Bestrahlung und der mechanischen Belastung beobachtet wurde.

Ähnliche Studien zur Messung der Widerstandsabhängigkeit von der Einwirkung elastischer Kompression und nach Bestrahlung wurden auch für experimentelle Proben auf Basis von „solarem Silizium“ mit p-Leitfähigkeit durchgeführt (Abb. 4), denen inhärente 4-eckige Pyramiden auf die Oberfläche (111).

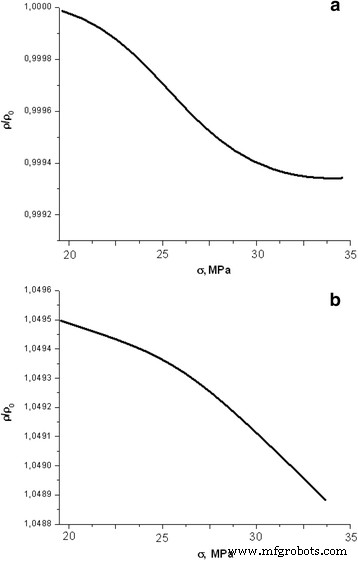
Abhängigkeit des Längswiderstandes von Solarsilizium bei elastischer Verformung mit zunehmender Druckstärke:a D = 0 Gy, Kompressionsgeschwindigkeit 32 μm/min; b D = 130 Gy Kompressionsgeschwindigkeit 8 μm/min

Zunächst wurde festgestellt, dass die Art der Widerstandsänderung von "solarem" Silizium vom p-Si-Typ auf die Größe der mechanischen Spannung unabhängig von der Kompressionsgeschwindigkeit ist. Ein ähnliches Merkmal wurde sowohl bei unbestrahlten als auch bei bestrahlten Proben beobachtet. Die Abhängigkeiten des Längswiderstands von der mechanischen Belastung ändern sich um einen relativ kleinen Wert (<0,5 %) und nehmen bei steigender Belastung leicht ab (Abb. 4a).

Die Bestrahlung von Versuchsproben mit Röntgenstrahlen (480 Gy) beeinflusst die allgemeine Natur der Änderung des Längswiderstands von „solarem“ Silizium während der elastischen Verformung praktisch nicht (Abb. 4b). Bei elektronischen Proben ist der Widerstand proportional zur Quadratwurzel der Energiedosis [11]. Während der mechanischen Belastung sinkt der spezifische Widerstand um einen sehr kleinen Wert (±0,1%).

Wie in unseren früheren Studien [12, 13] gezeigt wurde, ist der dielektrische Film SiO₂ hat eine positive Ladung. Daher ist die an Löchern verarmte Raumladungsoberflächenschicht (mit hohem Widerstand) und mit einer Dicke von w (Abb. 5) wird in Silizium hergestellt. Je näher Si-SiO₂ zur Schnittstelle, desto weniger Löcher gibt es.

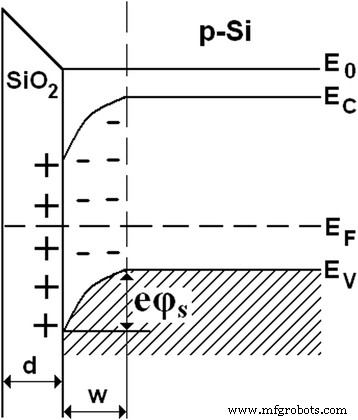
Verzerrung der Energiebänder im p-Leiter unter bereitgestellter positiver Ladung an der Grenzfläche Halbleiter-Isolator

Die Konzentration von Löchern in der Oberflächenschicht von Silizium und folglich seine Leitfähigkeit ändert sich bei einer Änderung des Oberflächenpotentials (φ _S ). Betrachten wir eine ebene quadratische Platte (Abb. 6). Lassen Sie den Strom parallel zur Plattenebene in Richtung einer ihrer Kanten fließen.

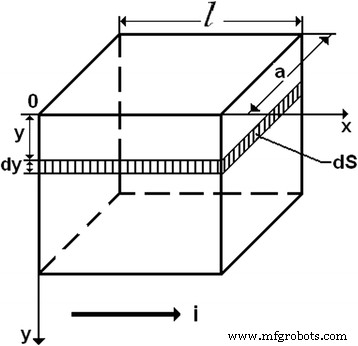
Berechnungen der Leitfähigkeit

Es wurde eine dünne parallele Schicht mit der Dicke dy . aufgenommen und Querschnittsfläche dS [14] in einiger Entfernung (y ) von der Oberfläche. Diese Schicht kann als homogener Halbleiter betrachtet werden, dessen Widerstand nach folgender Formel bestimmt werden kann:

$$ d R=\rho \frac{l}{dS}, $$ (1) $$ d S=a d y. $$ (2)

Da die Platte quadratisch ist (l = a ), die Leitfähigkeit der Schicht ist

$$ d\lambda =\frac{1}{dR}=\sigma d y, $$ (3)

wobei $\sigma=\frac{1}{\rho}$ die elektrische Leitfähigkeit der Schicht mit dy . ist Dicke bei y Abstand von der Oberfläche. Für einen Halbleiter vom p-Typ kann die Leitfähigkeit geschrieben werden als $ \sigma \approx e p(y){\mu}_p $. Dann bekommen wir

$$ d\lambda =e p(y){\mu}_p dy. $$ (4)

Finden wir die gesamte Oberflächenleitfähigkeit (λ ). Sie müssen den letzten Ausdruck im Bereich von Null bis zu einer Dicke von mehreren nachhaltigen Debye-Rastern integrieren oder beispielsweise die Breite der Raumladungszone w . einschränken :

$$ \lambda ={\displaystyle \underset{0}{\overset{w}{\int }} ep(y){\mu}_p dy=e{\mu}_p{\displaystyle \underset{0}{ \overset{w}{\int}} p(y) dy}}. $$ (5)

Im Allgemeinen hängt die Konzentration von Löchern in der verarmten Oberflächenschicht nicht nur von den Koordinaten (y ) sondern auch von der aufgebrachten mechanischen Belastung (σ _meh ). Es wird durch zwei Komponenten bestimmt:p (y , σ _meh ) = p ₁ (y ) − p ₂ (σ _meh ), wobei p ₁ (y ) ist eine Komponente, die einer Änderung der Ladungsträgerkonzentration mit der Änderung des Abstands von der Oberfläche des Halbleiters entspricht und p ₂ (σ _meh ) ist eine Komponente, die anzeigt, um wie viel sich die Konzentration von Löchern aufgrund ihres Einfangens an Versetzungen während der mechanischen Belastung verringert. Außerdem ist die Beweglichkeit von Löchern kein konstanter Wert. Das hängt von der mechanischen Belastung ab. Daher kann der Ausdruck für die Gesamtoberflächenleitfähigkeit in der folgenden Form geschrieben werden:

$$ \lambda =e{\mu}_p\left({\sigma}_{meh}\right){\displaystyle \underset{0}{\overset{w}{\int }}\left({p} _1(y)-{p}_2\left({\sigma}_{meh}\right)\right) dy}. $$ (6)

Mechanisch induzierte Änderung der Leitfähigkeit kann wie folgt geschrieben werden:

$$ \lambda \left({\sigma}_{meh}\right)=e{\mu}_p\left({\sigma}_{meh}\right)\cdot \Big({\displaystyle \underset{ 0}{\overset{w}{\int}}{p}_1(y) dy-{\displaystyle \underset{0}{\overset{w}{\int}}{p}_2\left({\ sigma}_{meh}\right) dy}\Big)=e{\mu}_p\left({\sigma}_{meh}\right)\cdot \left\{{\beta}_1-{\beta }_2\left({\sigma}_{meh}\right)\right\}}, $$ (7)

wobei $ {\beta}_1={\displaystyle \underset{0}{\overset{w}{\int}}{p}_1(y) dy;\kern1em {\beta}_2\left({\sigma }_{meh}\right)={\displaystyle \underset{0}{\overset{w}{\int}}{p}_2\left({\sigma}_{meh}\right) dy}}={p}_2\left({\sigma}_{meh}\right){\displaystyle \underset{0}{\overset{w}{\int}} dy=} w\cdot {p}_2\left( {\sigma}_{meh}\right) $.

Es sollte beachtet werden, dass da p ₁ (y ) und p ₂ (σ _meh ) hängen auch von der Bestrahlungswirkung ab, die Faktoren β ₁ , β ₂ , und μ _p hängen von der Dosis der Röntgenstrahlung ab. Daher ist die Formel für die Oberflächenleitfähigkeit vor (λ (σ _meh ,0 )) und nach (λ (σ _meh ,D )) Bestrahlung kann wie folgt geschrieben werden:

$$ \lambda \left({\sigma}_{meh},0\right)=e{\mu}_p\left({\sigma}_{meh},0\right)\cdot \Big({\ displaystyle \underset{0}{\overset{w}{\int}}{p}_1\left( y,0\right) dy- w\cdot {p}_2\left({\sigma}_{meh} ,0\right)\Big)=e{\mu}_p\left({\sigma}_{meh},0\right)\cdot \left\{{\beta}_1(0)-{\beta} _2\left({\sigma}_{meh},0\right)\right\}}. $$ (8) $$ \lambda \left({\sigma}_{meh}, D\right)=e{\mu}_p\left({\sigma}_{meh}, D\right)\cdot \Big({\displaystyle \underset{0}{\overset{w}{\int }}{p}_1\left( y, D\right) dy- w\cdot {p}_2\left({\sigma }_{meh}, D\right)\Big)=e{\mu}_p\left({\sigma}_{meh}, D\right)\cdot \left\{{\beta}_1(D) -{\beta}_2\left({\sigma}_{meh}, D\right)\right\}}. $$ (9)

Wenn die Probe eine rechteckige Form mit einer Länge (l ) und Breite (a ) können wir die endgültige Formel für die gesamte Oberflächenleitfähigkeit wie folgt schreiben:

$$ \lambda \left({\sigma}_{meh}, D\right)=\frac{a}{l} e{\mu}_p\left({\sigma}_{meh}, D\right )\left\{{\beta}_1(D)-{\beta}_2\left({\sigma}_{meh}, D\right)\right\}, $$ (10)

$$ {\beta}_1(D)={\displaystyle \underset{0}{\overset{w}{\int}}{p}_1\left( y, D\right) dy,\kern1em }{\ beta}_2\left({\sigma}_{meh}, D\right)=w\cdot {p}_2\left({\sigma}_{meh}, D\right). $$ (11)

Die Änderung der Oberflächenleitfähigkeit bestrahlter p-Si-Kristalle unter Einfluss mechanischer Spannung wird hauptsächlich durch die Änderung von drei Parametern bestimmt:β ₁ , β ₂ , und μ _p .

Nach unseren früheren Studien [10,11,12,13] wird die Wirkung der Röntgenstrahlung des elektronischen Siliziums von einer leichten Zunahme der positiven Ladung in der dielektrischen Oberflächenschicht von SiO₂ . Als Ergebnis ist der Faktor β ₁ :β ₁ (D ) > β ₁ (0 ) leicht erhöht. Für das „solare“ Silizium werden entgegengesetzte Abhängigkeiten beobachtet:β ₁ (D ) < β ₁ (0 ).

Zum Faktor β ₂ , seine Änderungen werden hauptsächlich durch die Änderung von p . bestimmt ₂ (σ _meh , D ) unter Strahlungseinwirkung. Diese Änderungen sind viel stärker als die Änderung des Parameters β ₁ . Röntgenbestrahlung löst die Erzeugung von Punktdefekten im Silizium aus, die als Stopper für die Versetzungsbewegung wirken. Dadurch wird nach der Strahlenexposition der Faktor β ₂ für diese Proben nimmt p-Si stark ab (reduziert die Anzahl der durch Versetzungen eingeschlossenen Löcher) für beide Arten von Experimentproben p-Si:β ₂ (D ) < β ₂ (0 ).

In unbestrahlten Kristallen aus „solarem“ Silizium spielen die vorhandenen Defekte, denen 4-eckige pyramidenförmige Ätzgruben entsprechen, die Rolle von Stoppern für die Versetzungsbewegung. Durch Bestrahlung erzeugte zusätzliche Defekte spielten vor dem Hintergrund einer starken Konzentration vorhandener Oberflächendefekte keine signifikante Rolle.

Durch die Zunahme der Streuung an Strahlungsdefekten nimmt die Beweglichkeit von Löchern bei Bestrahlung leicht ab:μ _p (D ) < μ _p (0 ). Durch diesen Mechanismus lässt sich die experimentell bestätigte Abnahme der Leitfähigkeit bestrahlter Siliziumproben erklären. Somit bestätigt eine Analyse der Formeln (8) und (9) das Anwachsen des Widerstands bei Zunahme des Wertes der absorbierten Dosis der Röntgenstrahlung hauptsächlich durch Verringerung der Mobilität (μ _p (D ) < μ _p (0 )) und die Konzentration freier Ladungsträger – Löcher (β ₂ (D ) < β ₂ (0 )).

Betrachtet man die Gleichungsdaten bei einer festen Dosis, können wir folgende Schlussfolgerungen ziehen, die die oben angegebenen experimentellen Abhängigkeiten der Beständigkeit gegen mechanische Beanspruchung bestätigen:

1.
Der Widerstand von nicht bestrahlten Proben aus elektronischem Silizium erhöht sich unter Kompression (Abb. 2). Dies geschieht aufgrund des signifikanten Wachstums von Faktor β ₂ unter Einwirkung von mechanischer Belastung. Während der Kompression wird die Änderung (Wachstum) des Faktors β ₂ die Änderung (Erhöhung) der Beweglichkeit von Löchern bei zunehmender mechanischer Belastung deutlich übersteigt. Zum Parameter β ₁ , sein Wert hängt nicht von σ . ab _meh .

In unserem Fall lässt sich also die Widerstandserhöhung (Kompression) und Abnahme (Dekompression) der Belastung für unbestrahlte Kristalle auf Basis von elektronischem Silizium durch die Bewegung von Versetzungen erklären, die die Hauptträger übernehmen. Im elastisch verformten Kristallgitter treten Kräfte auf, die eine Bewegung von Defekten, die Koagulation von Clustern und die Kondensation von Clustern an Versetzungen verursachen [15]. Defekte werden zu Zentren des Einfangens von Hauptträgern, während sie zu größeren Clustern wie Mikroporen, Clustern von Internodien-Silizium und Verunreinigungen koagulieren. Die Ansammlung von Defekten in der Oberflächenschicht von Silizium neigt dazu, deren Leitfähigkeit zu verringern. Es wird durch den entsprechenden Wachstumsfaktor β . angezeigt ₂ in der Formel für die Oberflächenleitfähigkeit.
2.
Der Widerstand von bestrahlten Proben aus elektronischem Silizium ändert sich unter Druck geringfügig (Abb. 3a). Dies wird durch die Verringerung der Veränderung (Wachstum) des Faktors β . verursacht ₂ , aufgrund einer behinderten Versetzungsbewegung. Mit anderen Worten, gegenseitig konkurrierende Änderungen von Parametern β ₂ und μ _p sind unter Kompression von bestrahlten Proben von elektronischem Silizium angemessen.

Die Widerstandsreduktion elektronischer Siliziumkristalle in Kombination mit einer Spannungserhöhung (Abb. 3b) erfolgt aufgrund der Abnahme der longitudinalen effektiven Masse schwerer Löcher [16, 17] und einer entsprechenden Erhöhung ihrer Beweglichkeit unter Kompression. Dies wird durch entsprechende Mobilitätssteigerung μ . angezeigt _p in der Formel für die Oberflächenleitfähigkeit.
3.
Der Widerstand von bestrahlten und unbestrahlten Proben von Solarsilizium nimmt unter Kompression leicht ab (Abb. 4). Der Versetzungsbewegungsprozess ist für diese experimentellen Proben sehr schwierig. Darüber hinaus leisten zusätzliche Defekte, die sich von der Mitte zur Oberfläche des Siliziums bewegen, den unwesentlichen Beitrag zum Stromtransport vor dem Hintergrund der hohen Konzentration vorhandener Oberflächendefekte in Kristallen von Solarsilizium. Die Strahlungseinwirkung erhöht zusätzlich die Konzentration von Oberflächendefekten in Kristallen aus Solarsilizium. Somit können sich gegenseitig konkurrierende Parameteränderungen β ₂ und μ _p sind unter Kompression von bestrahlten und unbestrahlten Proben von Solarsilizium angemessen.

Strahlungswirkung (Abb. 4b) erhöht zusätzlich die Konzentration von Oberflächendefekten in Kristallen aus Solarsilizium. Daher tragen zusätzliche Defekte, die sich durch Gettering bewegen, einen geringen Beitrag zum Stromtransport als bei unbestrahlten Kristallen.

Schlussfolgerungen

Bei der mechanischen Belastung müssen zwei Hauptfaktoren berücksichtigt werden, die den Widerstand des p-Si-Kristalls beeinflussen. Der erste Faktor ist eine Zunahme des Widerstands bei Zunahme der Last (Kompression) und eine Abnahme des Widerstands bei Abnahme der Last (Entklammerung) aufgrund des Prozesses der Versetzungsbewegung, der die Hauptträger übernimmt. Der zweite Faktor ist die Abnahme des Widerstands von Siliziumkristallen mit einer Zunahme der Last aufgrund der Abnahme der effektiven Masse der Löcher und einer entsprechenden Zunahme ihrer Beweglichkeit.

Röntgenbestrahlung verursacht die Bildung von Leerstellen und Zwischengitteratomen im Silizium, die als Stopper für die Bewegung von Versetzungen wirken. Aufgrund der Zunahme der Streuung von Strahlungsdefekten nimmt die Beweglichkeit von Löchern während der Röntgenbestrahlung leicht ab. In unbestrahlten Kristallen aus Solarsilizium spielen die vorhandenen Defekte die Rolle von Stoppern für die Bewegung von Versetzungen.

Vorbestrahlte experimentelle p-Si-Kristalle (elektronisches und „solarbasiertes“ Silizium) haben die Eigenschaft, ihren spezifischen Widerstand (±0,2%) unter dem Einfluss einachsiger Kompression (Geschwindigkeit der Spannungszufuhr 8 μ/min) innerhalb der elastische Verformung entlang des Stroms [$ 11\overline{2} $].

Bei den vorbestrahlten elektronischen p-Si-Proben hängt die Abhängigkeit des Widerstands von einachsiger mechanischer Belastung signifikant von der Kompressionsrate ab. Bei geringer Geschwindigkeit der Spannungszufuhr (8 μm/min) steigt der Widerstand mit zunehmender mechanischer Belastung; bei hohen Geschwindigkeiten (32 μm/min) nimmt ab. Bei Kristallen auf der Basis von Solar-p-Silizium ist die Widerstandsabhängigkeit bei mechanischer Belastung unabhängig von der Kompressionsrate.

Abkürzungen

ρ (σ ):: Die Änderung der induzierten mechanischen Leitfähigkeit entlang der Verformungsrichtung

Mit Titanat-Nanoröhren dekorierte Graphenoxid-Nanokomposite:Vorbereitung, Flammhemmung und Photoabbau Verbundmembranen mit Nanopartikeln von anorganischen Ionenaustauschern für die elektrodialytische Entsalzung von Glycerin

Nanomaterialien