Hocheffiziente plasmonische dritte Generation mit Graphen auf einem Beugungsgitter aus Silizium im mittleren Infrarotbereich

Einführung

Harmonische Erzeugung ist ein nichtlinearer optischer Prozess, bei dem N Photonen mit derselben Frequenz ω die mit einem nichtlinearen Material interagieren, werden kombiniert, um neue Photonen mit der Frequenz Nω . zu erzeugen . Als Mittel zur Erweiterung kohärenter Lichtquellen auf kurze Wellenlängen hat die Erzeugung der dritten Harmonischen (THG) enormes Forschungsinteresse auf sich gezogen. Herkömmlicherweise wird eine hocheffiziente harmonische Erzeugung in exotischen Kristallen realisiert, was jedoch die photonische Integration mit hoher Dichte beeinträchtigt [1]. Als optischer Informationsträger zur Übertragung von Lichtsignalen in hochintegrierten photonischen Schaltkreisen hat sich Silizium zu einem ausgereiften Material entwickelt. Nichtlineare optische Effekte wie die stimulierte Raman-Streuung [2] und THG [3,4,5] haben großes Potenzial, die Funktionalitäten der Siliziumphotonik zu erweitern. Die effiziente Lichtemission durch die Verwendung von Silizium bleibt jedoch aufgrund seiner indirekten Bandlücke eine Herausforderung. Die Verwendung nichtlinearer optischer Wechselwirkungen wie THG scheint ein vielversprechender Ansatz zu sein, um kohärentes Licht für die Siliziumphotonik bereitzustellen. Im Allgemeinen kann der THG-Umwandlungswirkungsgrad (CE) für einen optischen Wellenleiter verbessert werden, indem eine Phasenanpassung zwischen dem Grundmodus und dem Modus der dritten Harmonischen verwendet wird. Dieses Verfahren erfordert typischerweise komplizierte Konfigurationen, die in praktischen Situationen normalerweise schwer zu implementieren sind. Eine effektive und robuste Methode zur Verbesserung des THG-CE kann durch Erhöhen der Lichtintensität innerhalb des nichtlinearen Materials geschaffen werden, was uns die Möglichkeit bietet, die strengen Anforderungen an die Phasenanpassungsbedingung zu lockern. Dies wurde kürzlich durch die Verwendung von photonischen Siliziumkristallen mit ultrahohem Qualitätsfaktor für langsames Licht [3,4,5], Silica-Mikrostäbchen mit kleinem modalem Volumen [6] und Oberflächenplasmonen [7,8,9,10] realisiert. Es wurde berichtet, dass photonische Siliziumkristalle den THG-CE auf die Größenordnung von ~ 10 ⁻⁷ . verbessert haben aufgrund der reduzierten Gruppengeschwindigkeit von c/40 [4]. Erst kürzlich wurde nachgewiesen, dass Oberflächenplasmonen den THG-CE auf eine Größenordnung von 10 ⁻⁵ . erhöhen können aufgrund der engen elektrischen Feldverstärkung [7].

In den letzten Jahren hat sich die Betriebswellenlänge der Siliziumphotonik aufgrund vieler potenzieller Anwendungen wie der chemischen und biologischen Sensorik auf den mittleren und fernen Infrarotbereich (IR) ausgedehnt [11]. Der Einsatz von Plasmonik im mittleren und fernen Infrarotbereich ist attraktiv, weil der Ausbreitungsverlust eines plasmonischen Wellenleiters bei längeren Wellenlängen dramatisch abnimmt und auch weil der Modenquerschnitt solcher Wellenleiter im Subwellenlängenbereich liegt, was Licht-Materie-Wechselwirkungen wie z THG-Umwandlung [7,8,9,10, 12, 13]. Jüngste Studien haben bewiesen, dass Graphen als ausgezeichnetes nichtlineares optisches Material dient, um den nichtlinearen Effekt zu verstärken, was zu verschiedenen Anwendungen führt, darunter Vierwellenmischung [14, 15], THG [16, 17, 18], rein optisches Schalten [19], und optische Bistabilität [20, 21] aufgrund seiner großen nichtlinearen optischen Suszeptibilität dritter Ordnung. Insbesondere die beobachtete Schwelle der optischen Bistabilität kann dank der großen nichtlinearen optischen Suszeptibilität von Graphen dritter Ordnung stark reduziert werden [20, 21]. Interessanter ist, dass Graphen-Plasmonen (GPs) im Gegensatz zum Plasmonenmodus in Metallen signifikant größere Wellenvektoren sowie eine viel höhere Lichteingrenzung aufweisen, was auf die Fähigkeit hindeutet, den CE von THG weiter zu verbessern [13]. Eine direkte Kopplung zwischen den Grundfrequenz-(FF)-GPs und Strahlungswellen wird jedoch aufgrund ihrer Impulsfehlanpassung verhindert, was die Implementierung dieses Schemas in der Praxis zu einem schwierigen Problem macht. Aus diesem Grund haben die Forscher die geführte Modenresonanz von Gittern verwendet, um das Kopplungsproblem anzugehen [12, 18, 20]. Das vorgeschlagene Schema in Ref. [18] wurde absichtlich entwickelt, um die FF-GPs direkt anzuregen und somit die CE von Freiraumwellen der dritten harmonischen Frequenz (THF) im Terahertz-Bereich zu verbessern.

In diesem Artikel haben wir auch die geführte Modenresonanz von Gittern verwendet, um die FF-GPs auf den Graphenblättern effizient anzuregen. Abweichend von der Konfiguration in Ref. [18] Wo die GPs verwendet werden, um die CE von THF-Freiraumwellen im Terahertz-Bereich zu verbessern, werden die GPs hier verwendet, um THF-GPs bei Infrarotfrequenzen auf einem Siliziumchip zu erzeugen. Die riesige Feldstärke von FF-GPs in Kombination mit der großen nichtlinearen Suszeptibilität von Graphen dritter Ordnung führt zu einem merklich erhöhten CE von THF-GPs auf dem Graphenblatt im mittleren und fernen Infrarotbereich. Wir weisen auf eine frühere Studie zur Verwendung von Quasi-Phasenanpassungsbedingungen hin, um den CE von THF-GPs auf einer Graphenoberfläche zu verbessern [13]. Wir betonen hier jedoch, obwohl in Lit. ein hoher CE zwischen FF und THF GP erreichbar ist. [13] fehlt eine direkte Kopplung zwischen Strahlungswellen und GPs. Im Gegensatz dazu kann das vorgestellte Schema nicht nur direkt mit den räumlichen FF-Wellen gekoppelt werden, sondern kann auch hocheffizient die THF-GPs erzeugen, was den Vorschlag für die Integration auf einer photonischen Siliziumplattform geeignet macht. Darüber hinaus haben die vorgestellten plasmonischen Frequenzumrichter die Vorteile der Kompaktheit und des hohen CE, während sie eine geringe Einfallsleistung erfordern [22, 23].

Methoden

Die Oberflächenleitfähigkeit von Graphen kann durch die weit verbreitete Kubo-Formel unter der Annahme des chemischen Potentials (auch als Fermi-Energie bezeichnet) abgeschätzt werden, μ _c . In den Infrarot- und Terahertz-Frequenzen mit |μ _c | k _B T (k _B ist die Boltzmann-Konstante und T die Temperatur ist), könnte die Oberflächenleitfähigkeit von Graphen angenähert werden als

wo e ist die Elektronenladung, ℏ ist die reduzierte Planck-Konstante, ω ist die Radiantfrequenz und τ ist die Impulsrelaxationszeit, die den Verlustmechanismus darstellt. In unserer Studie wird eine Arbeitstemperatur von T . angenommen = 300 K. Nimmt man die einzelne Graphenschicht als nicht wechselwirkende Monoschicht, beträgt die optische Leitfähigkeit von mehrschichtigem Graphen nσ _g [24], wobei n ist die Anzahl der Graphenschichten (n < 6). Wir modellieren Graphen als anisotropes Material und die effektive Permittivität in der Ebene kann als [25, 26] geschrieben werden.

wo η ₀ (=377 Ω) ist die Impedanz von Luft, k ₀ ist der Wellenvektor in der Luft und d _g ist die Gesamtdicke von n -Schicht Graphenplatten. Die Permittivität von Graphen außerhalb der Ebene, ε _y , wird unabhängig vom Fermi-Niveau konstant auf 2,5 gehalten [27, 28].

Ergebnisse und Diskussion

Anregung von FF-GPs mit einem Siliziumgitter

Zunächst betrachten wir die Anregung der FF-GPs und die Erzeugung der THF-GPs auf Graphenschichten, die von dielektrischen Gittern (GSSDG) getragen werden, wie in Abb. 1 gezeigt. Unter Berücksichtigung der praktischen Situation, dass die Fläche von Graphen Hunderte Male größer sein kann als Im Gitterabschnitt wird angenommen, dass die Graphenschichten auf der Oberseite der Gitter flach sind und sich nicht an die Gitter anpassen. Wir haben einige Forschungsstudien zu GP festgestellt, die von Graphenschichten unterstützt werden, die von Gittern getragen werden, wobei angenommen wird, dass die Graphenschichten flach sind [12, 13]. Insbesondere stellen wir fest, dass die experimentellen Ergebnisse gut mit den Simulationsergebnissen übereinstimmen, bei denen angenommen wird, dass die Graphenschichten in der Modellierung flach sind [12]. Es wird angenommen, dass die GSSDG entlang x . unendlich ist Richtung und periodisch entlang z Richtung. Die Dicke der Siliziumgitterschicht unter den Graphenschichten wird mit 2 µm angenommen. In diesem Fall kann die Gitterschicht bei der Modellierung als unendlich dick angesehen werden, da das Siliziumsubstrat unter dem Gitter die Feldverteilung der GPs im Luft-Graphen-Gitter-Modell nicht beeinflusst. Die dispersive Beziehung der GPs, die von dieser Konfiguration unterstützt werden, kann ausgedrückt werden als [29].

wobei β ist die Ausbreitungskonstante der GPs entlang z- Achse, ε ₀ die Permittivität in der Luft ist und ε _{r 1} (=1) und ε _{r 2} sind die Dielektrizitätskonstanten der dielektrischen Medien oberhalb bzw. unterhalb der Graphenschichten. Da die Gitterperiode viel kleiner ist als die Lichtwellenlänge in der Luft, kann das Siliziumgitter näherungsweise als effektives Medium mit der äquivalenten Permittivität modelliert werden [30].

wo ε _Silikon (=11.9) ist die Permittivität von Silizium bei Infrarot- und Terahertz-Frequenzen [31] und f (=w /p ) ist der Füllgrad des Siliziums (f ist in dieser Arbeit auf 0,5 festgelegt).

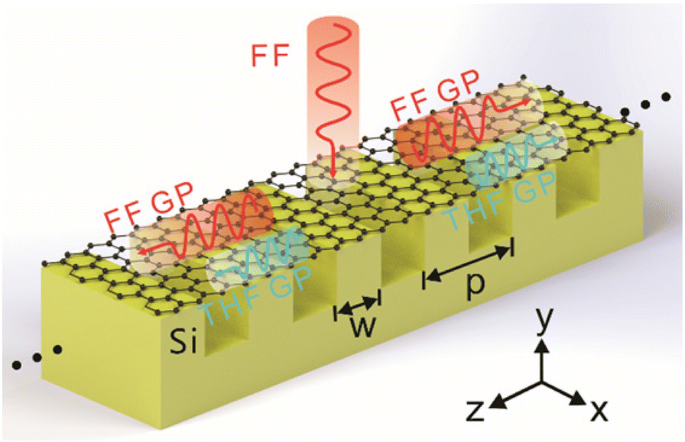
Das Schema des GSSDG als THG-Wellenlängenwandler. Die FF-GPs (rote Kurven) werden mit einer normal einfallenden x-polarisierten ebenen Welle von FF angeregt und erzeugen dann aufgrund der Siliziumgitter unter den Graphenschichten die THF-GPs (blaue Kurven). Die Gitterperiode beträgt p , und w bezeichnet die Breite von Silizium

Die Dispersionsrelation der GPs auf der GSSDG für verschiedene Parameter (τ , μ _c , undd _g ) ist in Abb. 2 dargestellt. In der gesamten Arbeit wird eine zweidimensionale Finite-Differenz-Zeitdomäne (FDTD) mit einer kommerziellen Software von Lumerical FDTD Solution durchgeführt, um die numerische Modellierung durchzuführen. Bei der Simulation dieses Teils werden die perfekt angepassten Schichtgrenzen und periodischen Grenzen im y . verwendet und z Richtungen, während angenommen wird, dass die gesamte Struktur entlang der x . unendlich ist Richtung. Die Maschenweiten mit 0,1 nm entlang y Richtung und 10 nm entlang z Richtung werden verwendet, um das Graphen zu beschreiben, während ungleichmäßige Netze mit einem maximalen Wert von 20 nm entlang y Richtung und gleichmäßiges Netz von 10 nm entlang z Richtung werden in den Regionen neben den Graphenschichten eingenommen. Aus Abb. 2a, d, g ist ersichtlich, dass im betrachteten Wellenlängenbereich der Wellenvektor der GPs dutzendemal größer ist als der der Luft, was darauf hindeutet, dass das optische Feld der GPs stark auf die Graphen-Oberfläche. Die Phasenfehlanpassung zwischen den GPs und den Strahlungswellen verhindert jedoch die direkte Kopplung zwischen ihnen. Das Beugungsgitter aus Silizium unter den in Fig. 1 gezeigten Graphenschichten kann einen zusätzlichen Impuls liefern, um die Wellenvektordifferenz zu überwinden, so dass die FF-GPs mit einem ebenen Welleneinfall effizient angeregt werden können. Die Gitterperiode, p , muss die Phasenanpassungsgleichung als

wobei β _FF ist die Ausbreitungskonstante der FF-GPs entlang z -Achse, j die Beugungsordnung ist und θ ist der Einfallswinkel. Anregung der FF-GPs mit einer effektiven Wellenlänge von λ _FF mit der fundamentalen Beugungsordnung j = 1 unter der Bedingung des normalen Einfalls θ = 0, der folgende Ausdruck sollte erfüllt sein

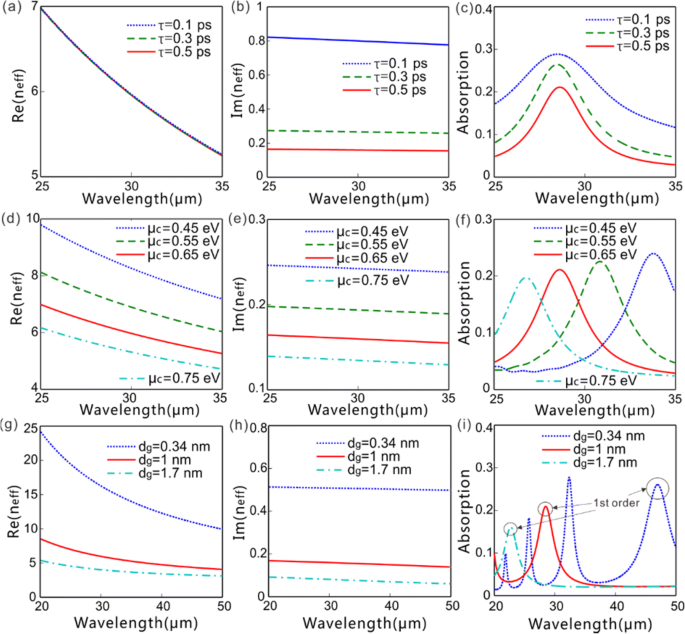
Die echte [Re(n _eff )] und imaginär [Im(n .) _eff )] Teile des effektiven Index und Absorption gegenüber der Wellenlänge mit unterschiedlichen Werten von μ _c , τ , und d _g . a –c Re(n _eff ), Im(n _eff ) und Absorption gegen Wellenlänge (τ =0,1, 0,3 und 0,5 ps, verbunden mit μ = 0,14, 0,42, 0,69 m ² V ⁻¹ s ⁻¹ ) mit μ _c = 0,65 eV und d _g = 1 nm. d –f Re(n _eff ), Im(n _eff ) und Absorption gegenüber der Wellenlänge (μ _c =0,45, 0,55, 0,65 und 0,75 eV) mit τ = 0.5 ps und d _g =1 nm. g –ich Re(n _eff ), Im(n _eff ) und Absorption gegen Wellenlänge [d _g =0,34 nm (n = 1), 1 nm (n = 3) und 1,7 nm (n = 5)] mit μ _c = 0,65 eV und τ = 0,5 ps. Für alle Fälle ist die Gitterperiode auf p . festgelegt = 4 μm

Abbildung 2 zeigt die Abhängigkeit des reellen [Re(n _eff )] und imaginär [Im(n .) _eff )] Teil der effektiven Indizes und Absorption bei der Lichtwellenlänge mit unterschiedlichen Werten von τ , μ _c , undd _g . Es erklärt anscheinend, wie die Parameter von Graphen die angeregten FF-GPs unter Beleuchtung einer x-polarisierten ebenen Welle mit normalem Einfall beeinflussen, wobei die Gitterperiode auf 4 µm festgelegt ist. Sowohl die echten [Re(n _eff )] und Imaginärteile [Im(n .) _eff )] der effektiven Brechungsindizes der FF-GPs nimmt mit zunehmender Lichtwellenlänge innerhalb des betrachteten Wellenlängenbereichs ab (Abb. 2a, b, d, e, g, h). Dies bedeutet, dass GPs bei einer kürzeren Lichtwellenlänge stärker um Graphenschichten begrenzt sind, was zu einer größeren Ausbreitungskonstante und einem höheren Ausbreitungsverlust führt. Die Absorption ist sehr wellenlängenempfindlich und nimmt stark zu, wenn sich die einfallende Wellenlänge der Resonanzwellenlänge nähert (Abb. 2c, f, i). Die Trägerstreuzeit τ bestimmt die Trägermobilität μ in Graphen als \( \tau ={\mu \mu}_c/e{\nu}_F^2 \) mit der Fermi-Geschwindigkeit von ν _F = 9.5 × 10 ⁴ Frau. Wenn man bedenkt, dass eine Trägermobilität von μ> 10 m ² V ⁻¹ s ⁻¹ wurde experimentell in hochqualitativem suspendiertem Graphen erreicht [32], was zu τ . führt> 1.5 ps, unsere Einstellung von τ ≤ 0.5 ps kann den praktischen Transportverlust von Graphen konservativ widerspiegeln. Die τ , verbunden mit der Trägermobilität μ , beeinflusst sanft die Re(n _eff ) und die Anregungswellenlänge von FF-GPs, beeinflusst aber stark die Im(n _eff ) und Absorption (Abb. 2a–c). Die verbesserte μ _c verringert Re(n _eff ) und Im(n _eff ) gleichzeitig, reduziert daher die Resonanzwellenlänge von FF-GPs entsprechend (Abb. 2d–f). Die Re(n _eff ), Im(n _eff ) und die Resonanzwellenlänge von FF-GPs nimmt mit zunehmender Graphendicke ab, entsprechend der Anzahl der Graphenschichten (Abb. 2g–i).

Im Folgenden nehmen wir τ = 0,5 ps, μ _c = 0,65 eV und d _g = 1 nm als Beispiele. Die Dispersionsbeziehung der GPs auf dem GSSDG ist in Abb. 3a dargestellt, wo die berechneten Dispersionskurven gut mit den Simulationsergebnissen der kommerziellen Software Lumerical FDTD Solutions übereinstimmen. Abbildung 3b zeigt die optische Reaktion der Graphenschichten mit und ohne Siliziumgitter. Es ist deutlich zu erkennen, dass die Absorptionseffizienz (über 20%) bei λ . deutlich verbessert ist = 28,62 μm, wenn das Gitter beteiligt ist (p = 4 μm). Im Gegensatz dazu wird die Absorptionseffizienz über den gesamten betrachteten Spektralbereich auf einem niedrigen Niveau (unter 2 %) gehalten, wenn das Gitter nicht berücksichtigt wird. Die merklich verstärkte Absorption für den ersteren Fall kann auf die Anregung der GPs bei λ . zurückgeführt werden = 28,62 µm. Wir finden aus dem |E | Ausschüttungen bei λ = 28,62 μm (Abb. 3c), dass die angeregten GPs die fundamentale geführte Wellenresonanzmode ist (j = 1). Aus Fig. 3d kann man sehen, dass die Resonanzwellenlänge der Grundmode in Bezug auf die Gitterperiode aus den numerischen Simulationen gut mit dem theoretischen Ergebnis übereinstimmt, das durch Gl. (6).

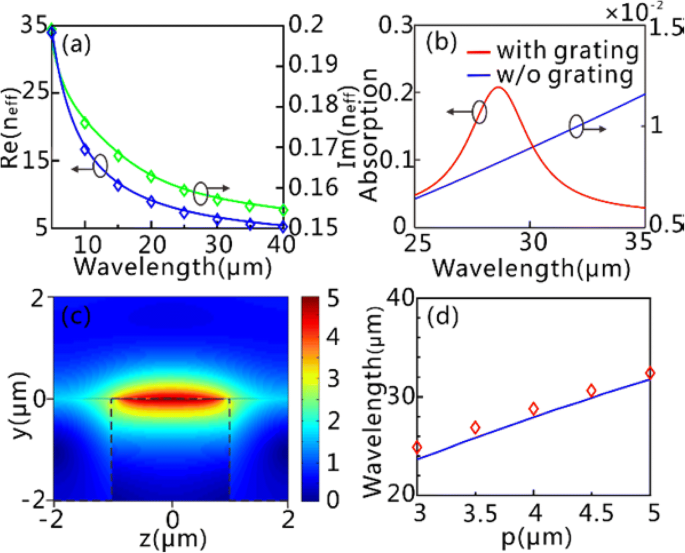
FF GPs und Felderweiterung auf der GSSDG. a Ausbreitungskurven der GPs auf der GSSDG. Die blauen und grünen durchgezogenen Linien entsprechen dem reellen [Re(n _eff )] und imaginär [Im(n .) _eff )] Teil des aus Gl. (3), während die blauen und grünen Rauten aus numerischen Simulationen stammen. b Absorptionsspektren mit Gittersubstrat (rote Linie) und reinem Siliziumsubstrat ohne Gitter (blaue Linie). c Das normalisierte |E | Verteilungen des fundamentalen GPs-Modus bei 28,62 μm. Die schwarzen gestrichelten Linien umreißen die Siliziumschicht. d Die Anregungswellenlänge des fundamentalen GPs-Modus gegenüber der Gitterperiode. Die blaue Linie wird aus Gl. (6), und die roten Rauten stammen aus numerischer Simulation. In b und c , P wird auf 4 µm eingestellt. Alle Simulationsergebnisse werden von der kommerziellen Software Lumerical FDTD Solutions abgerufen

Es sollte beachtet werden, dass aufgrund der signifikanten Verringerung der Gruppengeschwindigkeit der FF-GPs (dutzende Male kleiner als die Lichtgeschwindigkeit in der Luft) ein stark verstärktes plasmonisches Feld auf der Graphenoberfläche auftritt. Das plasmonische Feld erfährt eine elektrische Feldverstärkung, die 5-mal so hoch ist wie die der beleuchtenden ebenen Wellen, von der erwartet werden kann, dass sie THF-GPs mit einem signifikant erhöhten CE in Kombination mit der großen optischen Nichtlinearität dritter Ordnung von Graphen erzeugt [16, 17]. Die nichtlineare Reaktion von Graphen kann durch den nichtlinearen Leitfähigkeitskoeffizienten beschrieben werden, der als [17] definiert ist.

wobei die Fermi-Geschwindigkeit ν _F = 9.5 × 10 ⁴ m/s.

Generierung von THF-GPs

Anschließend vergleichen wir die elektrische Feldstärke der THF-GPs auf der Graphenoberfläche, wenn die Graphenschichten mit und ohne Gitter gehalten werden. Die Randbedingungen in FDTD-Simulationen sind die gleichen wie in den Fign. 2 und 3. Die normalisierte elektrische Feldstärke (NEFI) als Funktion der Wellenlänge ist in Abb. 4a dargestellt, wenn die Graphenschichten mit normal einfallendem Dauerstrichlicht (CW) mit einer Leistungsdichte von 0,11 MW/cm . beleuchtet werden ² und die zentrale Wellenlänge von 28,62 µm. Hier wird der NEFI durch Normierung der elektrischen Feldstärke auf ihren Wert bei 28,62 µm (FF) mit der Gitterstruktur erhalten. Es kann beobachtet werden, dass im NEFI-Spektrum mit Gitterstruktur (GSSDG) ein scheinbarer Peak bei THF auftritt, verglichen mit dem NEFI-Spektrum ohne beteiligtes Gitter. Definition des CE als \( {\int}_0^p{P}_y^{THF} dz/\left({P}^{FF}p\right) \), wobei \( {P}_y^{THF } \) ist das y Komponente des Poynting-Vektors bei THF und P ^FF die Leistungsdichte des einfallenden Lichts ist, erreicht die CE bis zu 5,71 × 10 ⁻⁷ für die GSSDG. Es kann leicht gefolgert werden, dass die Anregung der FF-GPs zur Erhöhung des CE von THF-GPs beiträgt. Die Feldverteilungen des Realteils von E _y bei THF, wie in Abb. 4b gezeigt, validieren die Erzeugung von THF-GPs auf der Graphenoberfläche.

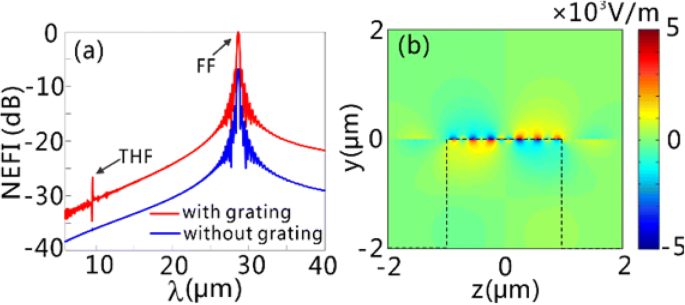
Generierung von THF GPs auf der GSSDG. a Der NEFI für die Struktur mit (rote Linie) und ohne (blaue Linie) Gitter, die normalerweise mit CW-Licht mit einer Leistungsdichte von 0,11 MW/cm ² . beleuchtet werden und die zentrale Wellenlänge von 28,62 µm. Die beiden Spitzen in der roten Linie bezeichnen die FF GPs (λ = 28,62 μm) und die generierten THF-GPs (λ = 9,54 μm). b Die Verteilung des Realteils von E _y für die generierten THF GPs. Die schwarze gestrichelte Linie in b stellt die Umrisse der Siliziumschicht dar. Die strukturellen Parameter von GSSDG sind die gleichen wie in Abb. 3

Die GSSDG als Lichtquelle für die Siliziumphotonik im mittleren Infrarot

Als nächstes betrachten wir die Verwendung des plasmonischen Wellenlängenkonverters GSSDG, um direkt eine Lichtquelle für die integrierten photonischen Schaltkreise aus Silizium bereitzustellen. Als Beispiel in Abb. 5a sind zwei Graphen-Silizium-Plasmonenwellenleiter (GSPWs) auf beiden Seiten an der GSSDG angebracht. Die GSPWs werden so gewählt, dass sie in der Lage sind, GPs über ein breites Spektralband zu führen, das die FF- und THF-GPs abdeckt. Da die modalen Feldverteilungen der FF- und THF-GP-Moden in der GSSDG (asymmetrisch in Bezug auf die Graphenoberfläche) eine starke Ähnlichkeit mit den auf dem GSPW unterstützten GP-Moden aufweisen, kann man daraus schließen, dass, sobald der Gitterabschnitt mit Normaleinfall beleuchtet wird FF-Wellen können die erzeugten FF- und THF-GPs oberhalb des Gitterbereichs auf beiden Seiten effizient an die GSPWs gekoppelt werden. Wir haben FDTD-Simulationen durchgeführt, um unsere Vorhersage zu validieren. Die Präfektenübereinstimmungsebenengrenzen werden in beiden y und z Richtungen in der Modellierung. Wir simulierten eine FF-Lichtwelle mit normalem Einfall, die auf den Gitterabschnitt trifft, und zeigten die elektrischen Feldverteilungen für die FF- und THF-GPs (Abb. 5b, c). Um sicherzustellen, dass in der Simulation nur der Gitterabschnitt mit Auflicht beleuchtet wird [33]. Eine perfekt angepasste absorbierende Grenze wurde verwendet, um alle Lichtwellen, die die Grenze des Berechnungsbereichs erreichen, vollständig zu absorbieren. Abbildung 5b zeigt, dass die FF-GPs auf der Graphenoberfläche über dem Gitter angeregt werden und sich dann entlang der GSPWs auf beiden Seiten ausbreiten. Aus Abb. 5c können wir außerdem das Aussehen der THF-GPs auf der Graphenoberfläche sowohl im Gitterschnitt als auch in den GSPWs finden. Hier ist das CE definiert als

wobei \( {P}_z^{\mathrm{THF}} \) die z . ist -Komponente des Poynting-Vektors bei THF, \( \int {P}_z^{\mathrm{THF}}\mathrm{dz} \) ist die Ausgangsleistungsdichte von THF GP im GSPW, P ^FF die Leistungsdichte der einfallenden FF-Lichtwellen ist und N _p ist die Zahl der Gitterperioden. Aus Abb. 5d ist ersichtlich, dass der CE von THG den Maximalwert von 3,68 × 10 ⁻⁷ . erreicht (− 64,3 dB) an der Gittergrenze und schwächt sich aufgrund des ohmschen Absorptionsverlusts von Graphen exponentiell entlang der Ausbreitungsrichtung ab.

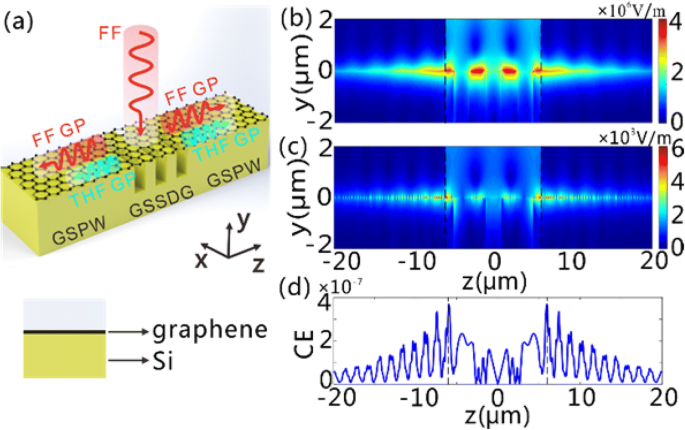
Generierung von FF- und THF-GPs auf der GSSDG und den angeschlossenen GSPWs. a Die Schemata des GSSDG und der verbundenen GSPWs auf beiden Seiten, wenn eine normal einfallende x-polarisierte ebene Welle von FF die Struktur beleuchtet. Die THF-GPs werden erzeugt und entlang der beiden GSPWs geführt, nachdem die FF-GPs in der GSSDG angeregt wurden. Der Querschnitt des GSPW ist in der Abbildung unten dargestellt, in der die Graphenschichten und die Si-Schicht bezeichnet sind. b , c Das |E | Verteilungen von b FF und c THF GPs im y -z Ebene, da der Gitterabschnitt mit CW-Licht mit einer Leistungsdichte von 0,19 MW/cm ² . beleuchtet wird bei 28,62 µm. d Der CE von THG entlang der z Richtung. Die schwarzen gestrichelten Linien in b –d stellen die Schnittstellen zwischen der GSSDG und den GSPWs dar. In b –d , N _p ist auf drei eingestellt

Es ist wichtig, die Faktoren zu diskutieren, die den THG-CE beeinflussen, der für die Bewertung der Geräteleistung eines THG-Wellenlängenwandlers von entscheidender Bedeutung ist. Bei einem THG-Verfahren erwartet man immer, mit einer relativ kleinen Pumpleistung den größten CE zu erreichen. Frühere Studien zeigten, dass eine Erhöhung der lokalen Feldstärke in den nichtlinearen Materialien dritter Ordnung zu einer bemerkenswerten Verbesserung des CE von THG bei einer signifikant reduzierten Pumpleistung führt [3, 4, 7]. Abbildung 6a zeigt den Einfluss der Leistungsdichte einfallender Lichtwellen auf den maximalen CE in den GSPWs, der mit der Leistungsdichte erhöht wird. Beachten Sie, dass der maximale CE bis zu 3,68 × 10 ⁻⁷ . beträgt selbst wenn die Leistungsdichte der einfallenden Lichtwellen nur 0,19 MW/cm ² . beträgt , die 6–7 Größenordnungen kleiner ist als die im gleichen Spektralband [22, 23]. Wir zeigen in Abb. 6b, dass die verwendete Anzahl der Gitterperioden, N _p , betrifft auch das CE in den GSPWs. Wenn N _p erhöht wird, erreicht ein reduzierender Anteil der THF-GPs, die in der Mitte des Gitters erzeugt werden, die GSPWs aufgrund des erhöhten Ausbreitungsverlusts, der durch die Graphen-Absorption induziert wird. Trotzdem ist die Eingangsleistung, verbunden mit N _p , zeigt eine lineare Verbesserung. Daher nimmt der maximale CE der THF-GPs mit zunehmendem N . ab _p . Wir betonen hier, dass die absolute Ausgangsleistungsdichte von THF-GPs aussagekräftiger sein sollte, um das Design eines THG-Wellenlängenwandlers für praktische Anwendungen zu leiten, sobald die einfallende Leistungsdichte festgelegt ist. Obwohl der maximale CE der THF GPs bei N . liegt _p = 2 In unserem Fall nähert sich die Ausgangsleistungsdichte von THG dem Maximum an, wenn N _p ≥ 3 (Abb. 6b). Daher haben wir 3 Gitterperioden verwendet, um die Erzeugung von THF-GPs in den GSPWs zu demonstrieren. Für zukünftige experimentelle Implementierungen mit dem aktuellen Design überschreitet die Fläche der Eingangs-FF-Quelle den Gitterbereich und wird konstant gehalten, wenn THF GP mit unterschiedlichen Gitterzahlen erzeugt wird. In diesem Fall sollte das CE geschrieben werden als

wobei der Bereich der FF-Quelle, S , ist konstant. Somit ist die Ausgangsleistungsdichte proportional zum CE, und daher muss die optimale Gitterzahl richtig ausgewählt werden, um die Ausgangsleistungsdichte von THF GP zu maximieren.

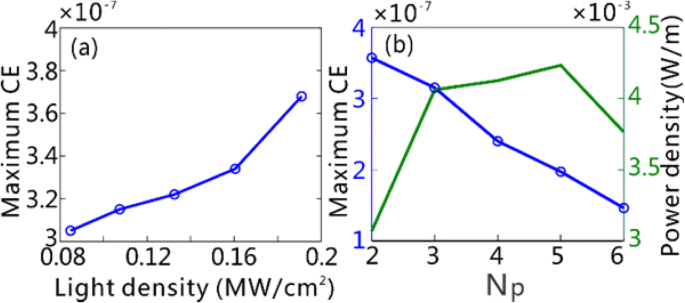
a Der maximale CE von THG als Funktion der einfallenden Leistungsdichte für N _p = 3. b Die maximale CE und die maximale Ausgangsleistungsdichte von THG als Funktion der Anzahl der Gitterperioden N _p verwendet bzw. Die einfallende Leistungsdichte ist auf 0,11 MW/cm ² . festgelegt

Die physikalischen Eigenschaften von Graphen können auch die Geräteleistung von THF-GPs beeinflussen, sobald die in Fig. 5a gezeigte untersuchte Struktur fertig ist. Die Fermi-Energie, μ _c , und die Anzahl der Graphenschichten wird die Resonanzwellenlänge von FF-GPs signifikant ändern (Abb. 2f, i) und daher auch die Erzeugungswellenlänge von THF-GPs beeinflussen. Im Gegensatz dazu ist die τ , verbunden mit der Trägermobilität μ , beeinflusst die Resonanzwellenlänge von FF-GPs sowie die Erzeugungswellenlänge von THF-GPs kaum (Abb. 2c). Der Ausbreitungsverlust von FF-GPs und THF-GPs kann jedoch durch die Verwendung eines viel größeren τ . reduziert werden (Abb. 2b), wodurch der CE von THF-GPs deutlich erhöht wird. Wenn man bedenkt, dass eine Trägermobilität von μ> 10 m ² V ⁻¹ s ⁻¹ (τ> 1,5 ps) ist im Experiment erreichbar [32], unsere Simulationsergebnisse (τ = 0,5 ps), wie in (Fig. 3, 4, 5 und 6) gezeigt, kann die Geräteleistung des THF-GP-Generators in Fig. 5a konservativ darstellen.

Schließlich lohnt es sich, die Einflüsse der Oberflächenrauheit von Graphenplatten auf die Geräteleistung zu diskutieren. Die Oberflächenrauhigkeit von Graphen könnte möglicherweise Plasmonen streuen, und daher wird der Plasmonenverlust verstärkt [34]. Der in Fig. 5 gezeigte vorgeschlagene THF-GP-Generator kann basierend auf der aktuellen Mikro-/Nano-Fertigungstechnologie hergestellt werden. Auf das Siliziumsubstrat kann man zunächst ein 270 nm dickes Polymethylmethacrylat (PMMA) aufschleudern. Die PMMA-Schicht wird nach einem anschließenden Elektronenstrahl-Lithographieprozess mit MIKE\IPA entwickelt. Danach wird eine 60 nm dicke Cr-Schicht auf dem Resist mittels Elektronenstrahlverdampfungsverfahren abgeschieden. Das Siliziumgittersubstrat kann mit Ätztechniken wie etwa einer induktiv gekoppelten Plasmamaschine gebildet werden. Nach dem Nassätzverfahren wird die restliche Cr-Schicht durch das Nassätzverfahren entfernt. Schließlich werden die Graphenschichten auf das Siliziumgitter übertragen, um die in Abb. 5 gezeigte endgültige Struktur zu bilden.

Schlussfolgerung

Wir haben die Erzeugung der THF-GPs in einer Graphenschicht auf Siliziumgittern mit den normal einfallenden ebenen Wellen im mittleren und fernen Infrarot numerisch demonstriert. Es wurde gezeigt, dass THF-GPs auf der Graphenoberfläche erzeugt und übertragen werden, und die CE wird aufgrund der signifikant erhöhten Feldintensität der angeregten FF-GPs in Kombination mit der großen nichtlinearen Suszeptibilität dritter Ordnung von Graphen dramatisch verbessert. Die erzeugten THF-GPs können bequem an ein GSPW gekoppelt werden, was die Integration des Graphen-basierten Wellenlängenwandlers auf einer Siliziumplattform erheblich erleichtert. Our proposal can stimulate making graphene-based light sources for mid- and far-infrared photonics on a silicon platform and hence broaden the functionalities of silicon photonics, such as signal processing, spectroscopy, and sensing.

Abkürzungen

CE:

Conversion efficiency

CW:

Dauerwelle

FDTD:

Zeitbereich mit endlicher Differenz

FF:

Fundamental frequency

GP:

Graphene plasmon

GSPW:

Graphene-silicon plasmon waveguide

GSSDG:

Graphene sheets sustained by dielectric grating

PMMA:

Polymethylmethacrylat

THF:

Third-harmonic frequency

THG:

Third-harmonic generation