Verbesserter nichtlinearer optischer Effekt in hybriden Flüssigkristallzellen basierend auf photonischen Kristallen

Hintergrund

Einer der Hauptvorteile optischer Verarbeitungssysteme ist ihre Fähigkeit, die hohe zeitliche und räumliche Bandbreite der Photonik zu nutzen. Eine grundlegende Komponente in diesen Systemen ist ein Gerät, das Licht moduliert. Räumliche Lichtmodulatoren (SLM), die optischen Datenfeldern in optischen Informationsverarbeitungssystemen Informationen aufprägen, wurden lange Zeit als wesentlich für die effiziente Ausnutzung der Geschwindigkeit, Parallelverarbeitung und Verbindungsfähigkeiten, die der Optik innewohnen, angesehen. Diese Geräte verändern im Allgemeinen die Phase, Polarisation, Amplitude und/oder Intensität einer räumlichen Lichtverteilung in Abhängigkeit von elektrischen Antriebsinformationen oder der Intensität einer anderen Lichtverteilung [1]. Zu den Vorteilen elektrooptischer Flüssigkristallmaterialien für SLMs gehören ihre hohe Doppelbrechung und der Niederspannungsbetrieb. In den frühen 1980er Jahren wurde vorgeschlagen, Flüssigkristalle auf integrierten Siliziumschaltkreisen zu platzieren, um Handheld-Displays herzustellen [2]. Aufgrund der umfangreichsten Herstellung von integrierten Siliziumschaltkreisen, die Fotodetektoren, Verstärker und Speicherelemente enthalten können, wurden die elektrooptischen Flüssigkristall-auf-Silizium-SLMs (LCoS) in den meisten optischen Labors zu einem Standardwerkzeug. Der nächste und sehr erwünschte Schritt schlägt das rein optische Informationshandling vor, das durch lichtgesteuerte Modifikation der optischen Eigenschaften des Mediums erreicht werden könnte. Viele optisch adressierte SLMs haben die grundlegende Sandwich-Struktur übernommen, bei der der Fotoleiter eine an das Sandwich angelegte Vorspannung auf ein modulierendes Material überträgt, z. B. Flüssigkristalle im Flüssigkristall-Lichtventil (LCLV) [3].

Fast alle existierenden nichtlinearen optischen Effekte wurden in farbstoffdotierten LC-Zusammensetzungen beobachtet, in denen die absorbierenden Farbstoffmoleküle die LC-Director-Umorientierung auslösen [4]. Alternativ beeinflusst die Lichteinwirkung auf die lichtempfindlichen Moleküle den Ordnungsparameter von LC, was wiederum zu erheblichen und schnellen Änderungen der lokalen Brechungsindizes der LC führt [5]. Im letzten Jahr wurden die beliebten lichtempfindlichen Zentren zu Nanopartikeln, die in das LC-Volumen eingebettet sind [6]. Nicht absorbierende LC-Systeme haben auch als photorefraktive rein-nematische LC-Lichtventile großes Interesse geweckt. Der wichtigste nichtlineare optische Mechanismus in LC ist die kollektive Neuorientierung von Molekülen in einem Großteil der LC unter Laseranregung, die oft bei angelegtem elektrischem Feld auftritt. In der vorliegenden Arbeit verwenden wir rein nematische LC. Der nichtlineare optische Mechanismus in solchen LC-Zellen deutet auf einen oberflächeninduzierten photorefraktiven Effekt hin, der die Orientierung der LC-Moleküle in der Masse, initiiert von der Oberfläche, ändert. Dieser Effekt wurde in LC-Zellen mit unterschiedlichen Oberflächenmaterialien wie photorefraktiven Polymerschichten [7, 8], leitfähigen Schichten mit eingebetteten Verunreinigungen [9], Edelmetallplatten [10] und photorefraktiven Kristallen [11] untersucht. In der Regel war die anfängliche Orientierung der Moleküle auf einer Oberfläche die planare. Eine andere Art von Zellen, die einen oberflächeninduzierten photorefraktiven Effekt aufweisen, bestehen aus einfachen Glassubstraten, die mit ITO-Elektroden bedeckt und mit einem rein nematischen LC gefüllt sind, aber das untersuchte Hauptmerkmal ist die homöotrope Orientierung von Molekülen [12, 13]. Ein solcher Effekt wird in der vorliegenden Arbeit untersucht. Wir verwenden jedoch Hybridzellen, bei denen eines der Substrate ein photonischer Kristall aus Silizium ist. Die Verbesserung der physikalischen Eigenschaften von Materialien, die in nano- oder mikrostrukturierten Oberflächen abgeschieden sind, einschließlich optischer, elektrischer und anderer Eigenschaften, wird zu einer vorrangigen Richtung der grundlegenden Nanowissenschaften. In unserer Forschung untersuchen wir die Möglichkeit, den nichtlinearen optischen Effekt in einer LC-Zelle zu verstärken, der auf den Einfluss einer mikrostrukturierten Oberfläche eines Substrats, das die Zelle bildet, zurückzuführen ist.

Um die nichtlinearen optischen Eigenschaften in hybriden LC-Zellen mit reflektierender Oberfläche zu untersuchen, wenden wir die dynamische holographische Technik an, die auf der Zweiwellenmischung von Laserstrahlen in der Reflexionsgeometrie basiert [14]. Es ist bekannt, dass die dynamische Holographie auf drei Haupteffekten basiert, die gleichzeitig wirken:(1) Erzeugung eines periodischen Interferenzmusters innerhalb eines nichtlinearen Mediums mit Hilfe von zwei oder mehr kohärenten Laserstrahlen; (2) Modulation des Brechungsindex unter Einwirkung dieses Interferenzmusters; in unserem Fall bedeutet dies, ein phasendynamisches Gitter in einem nichtlinearen Medium zu induzieren; (3) Selbstbeugung der Aufzeichnungsstrahlen auf dem dynamischen Gitter. Bisher ist die Wellenmischung als effektive Technik für viele Anwendungen in der nichtlinearen Optik bekannt (siehe zB [15]). Es genügt, das räumliche Multiplexen und Schalten von Laserstrahlen, die rein optische Kontrolle der Parameter der Strahlen, den dynamischen optischen Speicher, die Logik usw. zu erwähnen. In der vorliegenden Arbeit zeigen wir, dass diese Methode auch als einfache experimentelle Technik auf bestimmen nichtlineare optische Eigenschaften von dünnen Filmen. Wir haben einen mathematischen Ansatz entwickelt, um den nichtlinearen Brechungskoeffizienten in einem Kerr-ähnlichen Medium zu berechnen, aus dem die nichtlineare optische Suszeptibilität bestimmt werden kann. Das mathematische Modell umfasst die Selbstbeugung von Wellen im Raman-Nath-Regime, also für den Zustand eines dünnen Gitters. Dieser Ansatz wird im Allgemeinen für die Mehrheit dünner Proben erfüllt, die typischerweise eine Dicke von bis zu mehreren zehn Mikrometern aufweisen. Solche Medien umfassen auch LC-Zellen. Beachten Sie, dass eine alternative Methode zur Bestimmung der optisch nichtlinearen Suszeptibilität transparenter Materialien die z-Scan-Technik ist [16]. Wir zeigen jedoch, dass die Zweiwellenmischmethode für die experimentelle Realisierung recht einfach ist und sich sehr gut für die Untersuchung dynamischer Medien eignet, auch die nur in der Reflexionsgeometrie funktioniert.

Methoden

Materialien und Muster

Die Struktur der Hybrid-LC-Zellen ist in Fig. 1 gezeigt. Die Hybridzelle hat einen sandwichartigen Typ, wird aus Glas- und Siliziumsubstraten gebildet und mit nematischem LC gefüllt; seine Kanten sind geklebt. Die Dicke der nematischen LC-Schicht beträgt 20 µm. Das flache Glassubstrat ist mit einer ITO-Elektrode bedeckt. Das zweite Substrat wird aus einem phosphordotierten Siliziumwafer geschnitten, seine Abmessungen betragen 17 × 17mm ² . Sein spezifischer Widerstand beträgt 4,5 cm, seine Dicke 380 µm und seine Orientierung 〈100〉. Das Siliziumsubstrat enthält zwei Bereiche, nämlich eine Oberfläche mit einem periodischen mikrostrukturierten Teil, der eigentlich ein photonischer Kristall im Mikrometerbereich ist, und einen flachen Teil der Oberfläche.

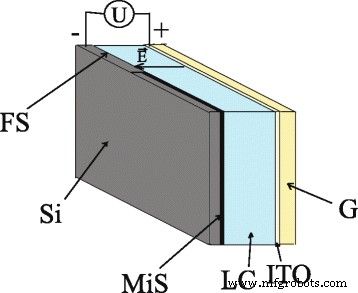
Aufbau einer Hybrid-LC-Zelle:Siliziumsubstrat (Si ); mikrostrukturierte Siliziumoberfläche (MiS ); flache Silikonoberfläche (FS ); Flüssigkristalle (LC ); Glassubstrat (G ); ITO-Elektrode (ITO ); angelegte Spannung (U ); elektrischer Feldvektor (\( \overrightarrow{E} \))

Die drei in unserer Untersuchung verwendeten Si-Substrate sind in Abb. 2 dargestellt. Die Mikrostrukturen stellen geätzte Pits dar, die in einer quadratischen Matrix (die Substrate 1 und 2) oder in einer dreieckigen Matrix (das Substrat 3) angeordnet sind. Die Pits sind quadratische Mikropyramiden, die sich durch Form, Größe und Anordnung unterscheiden. Es gibt (1) regelmäßige Pyramiden, (2) Pyramidenstümpfe (Gruben) und (3) leicht abgeschnittene Pyramiden. Regelmäßige Mikropyramiden haben eine Höhe von 2 µm, eine gleiche Basisseite von 2 µm und eine Periodizität von 3 µm. Gruben haben ähnliche Parameter, sind aber dicht beieinander. Leicht abgeschnittene Pyramiden haben eine Grundseite von 1,5 µm und eine Periodizität von 3,5 µm. Die Mikrostrukturen wurden auf der polierten Seite des Siliziumwafers durch eine standardmäßige photolithographische Technik gebildet, gefolgt von anisotropem Ätzen für die Substrate 1 und 3 oder durch Plasmaätzen für das Substrat 2.

Bilder einer mikrostrukturierten Siliziumoberfläche im Lichtmikroskop. Mikropyramiden haben die folgenden Formen:regelmäßige Pyramiden (1), Gruben (2) und leicht abgestumpfte Pyramiden (3)

Zwei nematische LC wurden verwendet:reines nematisches 5CB (4×-(n -Pentyl)-4-cyanobiphenyl) und nematische Mischung E7. In allen Fällen ist die molekulare Orientierung in einer Flüssigkristallschicht homöotrop und tritt spontan an ITO- und Siliziumoberflächen auf, wobei die Verarbeitungstemperatur nicht höher als 50 °C gehalten wird. Wir haben vier Proben untersucht, die sich durch die Form der Mikrostruktur und durch das verwendete LC unterscheiden. Die Proben mit Siliziumsubstrat 1 und 2 bestehen aus zwei Teilen:Ein Teil enthält eine fehlstrukturierte Oberfläche, der zweite Teil ist eine Fläche. In solchen Proben haben wir die Möglichkeit, die nichtlineare Reaktion in einer flachen Zelle (die einen flachen Teil des Si-Substrats enthält) und in einer mikrostrukturierten Zelle (die einen mikrostrukturierten Teil des Si-Substrats enthält) zu vergleichen.

Auf diese Weise haben wir in unseren Experimenten die folgenden Hybridzellen:

1. 1)

   abgekürzt M1:Glassubstrat + ITO/5CB/Si Substrat 1, mikrostrukturierte Oberfläche

2. 2)

   abgekürzt F1:Glassubstrat + ITO/5CB/Si Substrat 1, flache Oberfläche

3. 3)

   abgekürzt M2:Glassubstrat + ITO/5CB/Si Substrat 2, mikrostrukturierte Oberfläche

4. 4)

   abgekürzt F2:Glassubstrat + ITO/5CB/Si Substrat 2, flache Oberfläche

5. 5)

   abgekürzt M3:Glassubstrat + ITO/5CB/Si Substrat 3, mikrostrukturierte Oberfläche

6. 6)

   abgekürzt M4:Glassubstrat + ITO/E7/Si Substrat 3, mikrostrukturierte Oberfläche

Experimenteller Aufbau

Abbildung 3 zeigt das Schema des Versuchsaufbaus, der auf der dynamischen holographischen Methode mit Zweiwellenmischung basiert. Kontinuierlicher Halbleiter-Nd:YAG-Laser (Frequenzverdopplung, λ = 532 nm, P = 52 mW, Single-Mode-Erzeugung) ist eine Lichtquelle. Mittels Strahlteiler BS und Spiegel M wird die Laserstrahlung in zwei Strahlen aufgespalten B ₀ und B ₁ , konvergiert auf der Zelle unter einem kleinen Winkel θ ≈ 0,01 rad. Die Eingangsintensitäten I ₀ und ich ₁ werden mit Hilfe des Filters F1 entzerrt und in unserem Fall I ₀ = Ich ₁ = 3,3 W/cm ² . Ein Laserspotdurchmesser auf einer Zelle beträgt 1 mm.

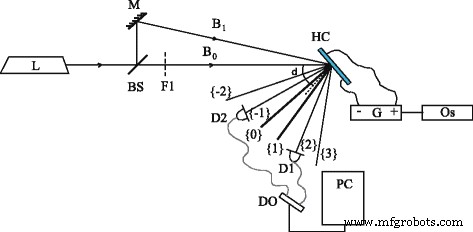
Schema Versuchsaufbau:Laser (L ); Spiegel (M ); Strahlteiler (BS ); optischer Filter (F1 ); Balken (B ₀ ) und (B ₁ ); Fotodioden (D1 ) und (D2 ); Hybrid-LC-Zelle (HC ); Oszilloskop (Os ); Generator (G ); digitaler Oszillograph (DO ); Computer (PC ). Die ausgegebenen Beugungsordnungen sind {0} und {1} die Hauptordnungen; {−1} und {2} die ersten Beugungsordnungen; {−2} und {3} die zweiten Beugungsordnungen. δ ist der Drehwinkel der Zelle

Zwei Laserstrahlen B ₀ und B ₁ bilden ein Interferenzmuster innerhalb der Probe. Beide einfallenden Strahlen haben ein lineares p Polarisation. So wird das Intensitätsmodulations-Interferenzmuster erzeugt. Die normale LC-Zelle macht den Winkel δ mit der Winkelhalbierenden von B ₀ und B ₁ . Das elektrische Gleichstromfeld wird aufgrund der Quelle G . angelegt mit der Spannung U im Bereich von 0 bis 15 V gesteuert. Als positive Elektrode wird das ITO-Glassubstrat eingesetzt. Wir haben Intensitäten der ersten Beugungsordnungen {−1} und {2} mit den Photodioden D1 und D2 über ein computergesteuertes digitales Oszilloskop DO gemessen. Die Winkel der Zellrotation wurden angepasst, um das Beugungssignal zu maximieren und schienen δ . zu sein ≈ 40 − 55 ⁰ für verschiedene Proben. Diese Ergebnisse decken sich mit den Experimenten anderer Gruppen (zB [9, 12]); der Grund für einen solchen Effekt liegt außerhalb des Rahmens unserer Studie.

Modell der Selbstbeugung von Wellen in der Raman-Nath-Approximation

Die Selbstbeugung von Wellen wurde in mehreren Arbeiten berücksichtigt [17, 18]. Wenn die Selbstbeugung zweier Eingangswellen an dem photoinduzierten dünnen Brechungsindexgitter stattfindet, erscheinen viele Beugungsordnungen am Ausgang. Durch Messung der Intensitäten in den ersten Beugungsordnungen kann man die Modulationstiefe des Gitters berechnen (Δn ). Da im Kerr-ähnlichen Medium die Bedingung Δn = n ₂ Ich ₀ gültig ist (wobei ich ₀ ist die Intensität des Anregungsstrahls), der Koeffizient der nichtlinearen Brechung n ₂ ist kalkulierbar.

In diesem Abschnitt suchen wir nach der Lösung für die Beugungseffizienz der ersten Beugungsordnungen bei nicht verschobenem sinusförmigem Brechungsindexgitter. Dann sind die Intensitäten in symmetrischen Ordnungen gleich. Die Modellierung geht von der Wellengleichung aus, in der sowohl das elektrische Feld \( \overrightarrow{E} \) als auch der modulierte Anteil der dielektrischen Permittivität Δε die sich aus dem Kerr-ähnlichen nichtlinearen Effekt ergeben, hängen von der Koordinate z ab (entlang der Wellenausbreitung):

wo c ist die Lichtgeschwindigkeit im Vakuum, \( {\varepsilon}_0={n}_0^2 \) repräsentiert die dielektrische Permittivität eines Mediums und n ₀ ist sein Brechungsindex. Wir suchen die Lösung der Wellengleichung (1) in der Summe aller Beugungsordnungen, die in Richtung der Achse \(\overrightarrow{y}\) polarisierte ebene Wellen sind:

wo ω ₀ ist die Frequenz der Laserstrahlung, \( \overrightarrow{r} \) ist die Koordinate und „c. c .“ bezeichnet den komplex konjugierten Term. In unserer Darstellung ist es zweckmäßig, den Dämpfungskoeffizienten als α . auszudrücken = α _Bauchmuskeln + α _sc , die die Verluste der Laserstrahlung sowohl bei der Absorption α . berücksichtigt _Bauchmuskeln und Streuung von α _s . Abbildung 4 zeigt das Wellenvektordiagramm der Selbstbeugung in Raman-Nath-Näherung. Es zeigt, dass die Welle des m --te Beugungsordnung entspricht der durch den Wellenvektor \({\overrightarrow{k}}_m\) beschriebenen Raumrichtung. Beugungsordnungen m = 0 und m = 1 gehören zu zwei Anregungsstrahlen B ₀ und B ₁ . Der Wellenvektor des m -te Beugungsordnung ist \( {\overrightarrow{k}}_m={\overrightarrow{k}}_0- m\overrightarrow{K} \), und \( \overrightarrow{K} \) ist der Wellenvektor von das photoinduzierte Gitter. Die Permittivitätsmodulation Δε ist in Form eines Gitters definiert:

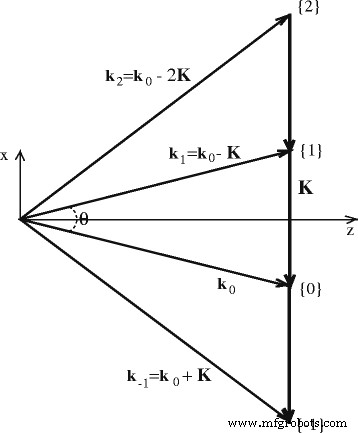
Wellenvektordiagramm der Selbstbeugung zweier kohärenter Wellen (beschrieben durch \( {\overrightarrow{k}}_0 \) und \( {\overrightarrow{k}}_1 \)) in der Raman-Nath-Näherung

Durch Einsetzen von Lösung (2) und (3) in Gl. (1) erhält man die Beziehung für eine langsame variable Amplitude A _m der m -te Ordnung:

wo k _υ = 2π /λ ist der Wellenvektor im Vakuum, und das Zeichen „∗“ bezeichnet die komplexe Konjugation. Da in unserer Darstellung die Hauptaufnahmebalken der Ordnungen m = 0 und m = 1 am Eingang sowie über die gesamte Dicke der Probe identisch sind, folgt daraus ε ₁ ist reell und hängt nicht von der Koordinate z ab (siehe [18]):\( {\varepsilon}_1(t)={\varepsilon}_1^{*}(t) \). Zur weiteren Transformation von Gl. (4) führen wir eine neue Funktion \( {U}_m\left( z, t\right)={A}_m\left( z, t\right) \exp \left(-\frac{1}{ 2}\alpha z\right) \exp \left( im\frac{\pi}{2}\right) \), bezeichne T = exp(−αz ) die Verluste der Lichtintensität im Medium und definieren \( {\varepsilon}_1=T{\tilde{\varepsilon}}_1 \). Durch Einführung einer neuen Variablen \( \tilde{z}={k}_{\upsilon}/\left({n}_0 \cos\left(\theta /2\right)\right)\cdot \left(1 - T\right)/\left(2\alpha \right)\), wobei θ ist der Konvergenzwinkel, Gl. (4) kann geschrieben werden als:

wobei Parameter ϕ ist definiert durch \(\phi=T{\tilde{\varepsilon}}_1/\left(2{n}_0^2{\sin}^2\left(\theta/2\right)\right)\) .

Unter den Bedingungen der Raman-Nath-Näherung kann der letzte Term im rechten Teil der Gl. (5) (Ref. [18]), d. h. 2m (m − 1)/ϕ < < 1 für jedes m . Dann erhalten wir durch Einführung einer neuen Variablen \(\zeta=\tilde{z}{\tilde{\varepsilon}}_1(t)\) unsere Hauptgleichung in der Raman-Nath-Näherung:

Diese Relation ist formal eine wohlbekannte Darstellung für die Bessel-Funktion, daher kann ihre Lösung mit Hilfe von Bessel-Funktionen in der Form ausgedrückt werden:

Die Gl. (6) erfüllt die Symmetrieeigenschaften \( {U}_0{U}_0^{*}={U}_1{U}_1^{*} \) für das Paar der Hauptträger sowie für alle Paare der gebeugten Strahlen (\( {U}_2{U}_2^{*}={U}_{-1}{U}_{-1}^{*} \)). Beachten Sie, dass bei z = 0, E ₀ (0, t ) = E ₁ (0, t ) ≠ 0, aber E _m (0, t ) = 0 für m ≠ 0, 1 und dann Ausgabeintensitäten der ersten Beugungsordnungen I _{−1} (d , t ) und ich _{2} (d , t ) ist gleich und durch eine Formel definiert (siehe auch [18]):

wo d die Dicke eines nichtlinearen Mediums ist; Ich ₀ die Intensität eines Laserstrahls ist; J ₁ und J ₂ sind die Besselfunktionen erster Art erster bzw. zweiter Ordnung. Da in unserem Fall die Intensitäten I ₀ und ich ₁ gleich sind, d. h. 2I ₀ = Ich _Laser , folglich der Wert von ζ kann geschrieben werden als:

In einem Kerr-ähnlichen Medium Δn = n ₂ Ich ₀ , wobei n ₂ stellt den nichtlinearen Brechungskoeffizienten dar, dann der Endwert von ζ hat eine einfachere Form:

Die Beugungseffizienz η der ersten Beugungsordnung wird bestimmt als η = Ich _{−1} /(TI ₀ ). Andererseits kann die Beugungseffizienz experimentell durch Messen der Intensität I . erhalten werden _{−1} und der Transmissionskoeffizient einer Zelle T . Die allgemeine Formel (8) ist gültig, um die Beugungseffizienz in einem großen Bereich zu berechnen. Für kleinere Beugungseffizienzen η ≤ 2%, die gute Näherung ist nur der erste Polynomterm von (8):η ζ ² /4. Folglich erhält man eine einfache Beziehung für n ₂ :

Es sollte beachtet werden, dass die abgeleitete Gl. (11) hat die gleiche Form wie die Gleichung, die herkömmlich für den Fall der Beugung nur eines Probenstrahls an einem gegebenen Brechungsindexgitter erhalten wird (siehe z. B. Lit. [19]). Aber für große Werte von η , das für LC-Zellen üblich ist, sollten genauere Beziehungen (8) und (10) verwendet werden, um die Werte ζ . zu berechnen und n ₂ .

Den Wert n kennen ₂ , kann man die nichtlineare Suszeptibilität des Mediums mit Hilfe des Ausdrucks definieren:

wo ε _e ist die elektrische Konstante. Im Fall von nematischem 5CB verwenden wir den Brechungsindex für die homöotrope Orientierung von Molekülen n ₀ = n _⊥ =  1,51 als der des gewöhnlichen Brechungsindex; ähnlich für nematische Mischung E7, n ₀ = n _⊥ = 1,5268.

Der entwickelte theoretische Ansatz ist für dünne Filme mit Kerr-ähnlicher optischer Nichtlinearität gültig, wenn die Lichtverluste sowohl bei der Absorption als auch bei der Streuung groß sind. Da die Selbstbeugungsmethode keine zusätzliche Laserquelle als Sonde benötigt, wird die Zweiwellenmischung zu einer einfachen Methode zur Diagnose der optischen Nichtlinearität von dünnen Medien einschließlich LC-Zellen.

Ergebnisse und Diskussionen

Wir vermuten, dass der nichtlineare optische Mechanismus in Hybrid-LC-Zellen ein oberflächeninduzierter photorefraktiver Effekt ist, der die Orientierung der LC-Moleküle in der Masse, initiiert von der Oberfläche, ändert [12, 13]. Bei den Zweiwellen-Mischexperimenten wird die Probe durch ein periodisches Lichtinterferenzmuster beleuchtet, das von zwei kohärenten Laserstrahlen gebildet wird. Dieses Muster erzeugt eine räumliche Ladungsmodulation an der LC-Substrat-Grenzfläche. Die resultierende periodische Verteilung des elektrischen Feldes auf der Oberfläche stimuliert die Modulation der Direktorenorientierung auf dem Substrat. Die Umorientierung der Moleküle beginnt an der Oberfläche und breitet sich in das LC-Volumen aus.

Eine typische experimentelle Leistung der Zweiwellenmischung mit Hybrid-LC-Zellen ist in Abb. 5 gezeigt. In Abwesenheit eines elektrischen Feldes beobachten wir eine regelmäßige zweidimensionale Struktur der Hauptlaserstrahlen, die von einem mikrostrukturierten Substrat der Zelle reflektiert werden (Abb. 5a .). ). Nach Anlegen einer Gleichspannung treten viele Beugungsordnungen neben jedem Paar der Hauptstrahlen aufgrund der Anregung des Brechungsindexgitters innerhalb der Zelle auf (Abb. 5b). Bei den Flachzellen F1 und F2 gibt es kein Mehrfachstreumuster, wir beobachten nach Anlegen der Spannung nur eine Mittellinie. Wir haben die Intensitäten in den ersten Beugungsordnungen {−1} und {+2} in der Mittellinie im stationären Zustand für alle Zellen gemessen:flache Zellen und Zellen mit mikrostrukturierter Oberfläche. Dann berechneten wir die Beugungseffizienz gemäß η = Ī _{−1} /(TI ₀ ), wobei Ī _{−1} ist die durchschnittliche Intensität zweier erster Beugungsordnungen (Ī _{−1} = (ich _{−1} + Ich _{2} )/2) und T ist der Transmissionskoeffizient der Zelle.

Typische Streumuster für zwei interferierende Laserstrahlen, die durch eine hybride nichtlineare LC-Zelle mit mikrostrukturierter Oberfläche gebildet werden. a Streumuster einer Hybridzelle ohne angelegtes elektrisches Feld. b Bildung vieler Beugungsordnungen (die Raman-Nath-Selbstbeugung) beim Anlegen einer elektrischen Gleichspannung. Die Mittellinie wird in (b ) durch eine Strichlinie

Beachten Sie, dass der oberflächeninduzierte photorefraktive Effekt, der in unseren Experimenten ausgenutzt wurde, stark vom Rotationswinkel der Probe relativ zur Winkelhalbierenden des Konvergenzwinkels zwischen zwei Eingangswellen abhängt (siehe z. B. [9, 12, 13]). Somit werden bei normaler Position der Probe, wenn die Platte der Probe senkrecht zur Winkelhalbierenden der Wellen steht, keine Beugungsordnungen beobachtet. Gleichzeitig scheint in unserem Fall, wenn die Probe relativ zu dieser Winkelhalbierenden gedreht wird, das photoinduzierte Brechungsindexgitter relativ zum Lichtinterferenzmuster verschoben zu sein. Dieser Effekt sollte sich in der existierenden Energieübertragung zwischen Beugungsordnungen manifestieren. Bei unseren Hybridzellen und zwei Laserstrahlen mit gleichen Eingangsintensitäten haben wir beobachtet, dass der Unterschied der Intensitäten in den ersten Beugungsordnungen 10 % nicht überschreitet. Wir haben einen Mittelwert zwischen diesen beiden gemessenen Intensitäten gebildet, der für weitere Berechnungen des Koeffizienten der nichtlinearen Refraktion verwendet wird. Dieser Wert gehört zum Genauigkeitsbereich unserer Schätzungen der nichtlinearen optischen Koeffizienten. Beachten Sie auch, dass das entwickelte mathematische Modell auf eine ziemlich einfache resultierende Formel reduziert ist und die Änderungen der Wellenphasen in einem Volumen einer nichtlinearen Schicht nicht berücksichtigt. Der Effekt der nichtlokalen Reaktion im Medium und die Energieübertragung zwischen den Wellen werden in unseren nächsten Arbeiten sorgfältig betrachtet.

In Tabelle 1 sammeln wir experimentelle Parameter, die für die Hybrid-LC-Zellen gemessen wurden. Der Transmissionskoeffizient ist definiert als T = Ich ^aus /Ich ₀ , wo ich ₀ die Intensität eines einzelnen einfallenden Strahls ist und I ^aus ist die Intensität des Ausgangsstrahls. T enthält zwei Teile:T = R _s T _a , wobei R _s berücksichtigt den Intensitätsverlust für die Streuung von der mikrostrukturierten Oberfläche, um ein periodisches Lichtmuster zu bilden; und T _a = exp(−αd _eff ) beschreibt den Intensitätsverlust bei der Absorption während der Lichtausbreitung in einem Bulk einer LC-Zelle. In Tabelle 1 präsentieren wir auch die Werte d _eff , die eine effektive Dicke für einen sich ausbreitenden Strahl in einer Zelle ist. Beachten Sie, dass wir bei unseren Messungen die Verluste bei der Lichtreflexion von der Eingangsglasgrenze einer Zelle vernachlässigen.

Gemessene Beugungseffizienzen für alle Zellen in Abhängigkeit von der angelegten Spannung sind in Abb. 6 dargestellt. Man sieht, dass die Beugungseffizienz ihr Maximum für eine bestimmte Spannung erreicht, die in verschiedenen Zellen unterschiedlich ist; diese Spannung ist bei mikrostrukturierten Zellen höher als bei flachen (vergleiche F1 und M1, F2 und M2); ebenso ändert sich diese Spannung in Abhängigkeit von einer Form der Mikrostruktur (vgl. M1, M2, M3, M4). Wir betonen auch, dass die Beugungseffizienzen in LC-Zellen ziemlich große Werte erreichen (bis zu 9% für die Zellen M1 und F1). Wir verwenden Messwerte von η um nichtlineare optische Eigenschaften von untersuchten LC-Zellen zu berechnen, nämlich den nichtlinearen Brechungskoeffizienten n ₂ und effektive nichtlineare Suszeptibilität χ ⁽³⁾ , wobei berücksichtigt wird, dass die LC-Zellen eine Kerr-ähnliche optische Nichtlinearität besitzen.

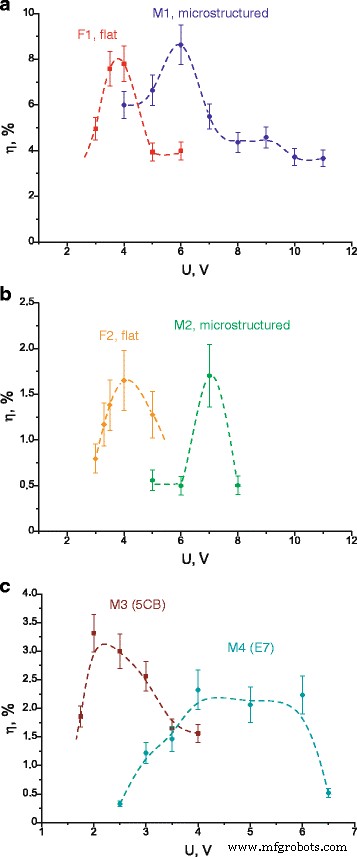
Beugungseffizienz der ersten Beugungsordnung in Abhängigkeit von der angelegten Spannung. a Zellen M1 und F1. b Zellen M2 und F2. c Zellen M3 und M4. Gestrichelte Linien nur zur Visualisierung präsentiert

Aus experimentellen Messungen der Beugungseffizienz berechnete nichtlineare Brechungskoeffizienten sind in Fig. 7 für alle Zellen gezeigt. Bei den Zellen M1 und F1 sowie M3 und M4 gilt n ₂ berechnet sich aus den Hauptformeln (8) und (10) als gemessener Beugungswirkungsgrad η> 3,5 %. Wir verwenden die Näherungsformel (12) für die Zellen M2 und F2, da das erhaltene η < 2%. Wir erhalten, dass der maximale nichtlineare Brechungskoeffizient in einer Zelle mit mikrostrukturiertem Substrat höher ist als in flachen Zellen (siehe Abb. 7a, b). Tabelle 2 zeigt die Werte der nichtlinearen Suszeptibilität, berechnet aus den Maximalwerten von n ₂ in Abb. 7. Die nichtlineare Suszeptibilität schien bei den Zellen mit mikrostrukturiertem Substrat im Vergleich zu den Zellen aus flachen Substraten wesentlich erhöht (um 30–100%) zu sein. Gründe, die zu einer zunehmenden Modulationstiefe des dynamischen Gitters in den in den Zellen enthaltenen mikrostrukturierten Substraten führen, sind Gegenstand weiterer Forschung. Wir nehmen an, dass dieser Effekt mit der anfänglichen Umorientierung von Molekülen verbunden ist, die auf einer mikrostrukturierten Oberfläche entstehen.

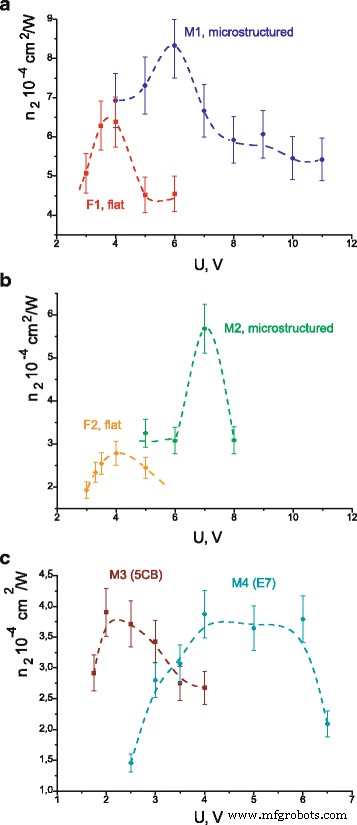
Calculated coefficients of nonlinear refraction in dependence on applied voltage for cells M1 and F1 (a ); M2 and F2 (b ); M3 and M4 (c ). Dashed lines are for the visualisation only

Conclusions

We have investigated the nonlinear optical effect in novel hybrid LC cells based on a silicon photonic crystal. The cell consists of two different materials separated by a thin LC layer with homeotropic orientation of molecules. One material is a glass substrate with ITO electrode. The second one is silicon substrate with periodic microstructured surface. Microstructures in a shape of periodically arranged micro-pyramids are etched on the silicon surface by applying the chemical photolithography method or plasma etching one.

We apply the dynamic holography method with two-wave mixing to define the efficiency of self-diffraction of the dynamic grating induced in LC layer. A theoretical model for the Raman-Nath self-diffraction, offered for calculating the diffraction efficiency in the first diffraction orders, have allowed us to determine the nonlinear refraction coefficient n ₂ , and nonlinear susceptilibity χ ⁽³⁾ of the cells. We have also made a comparative analyses of nonlinear parameters obtained for cells with and without microstructures. Nonlinear susceptibility appeared to be essentially enhanced (by 30 − 100%) in the microstructured cells with respect to the cells made of flat surfaces. The underlying mechanism of the optical nonlinearity is the surface-induced photorefractive effect in the pure nematic LC. The increased modulation depth of the refractive index might be connected with initial reorientation of the molecules arising on the microstructured substrate.

The developed theoretical approach could be valid for determination of nonlinear optical characteristics of thin films possessing Kerr-like optical nonlinearity, in which the losses on the both absorption and scattering are large, as well as in the either transmission or reflection geometries. Photorefractive hybrid LC cells are perspective as new samples of electro-optical microsystems, including multi-channel SLMs. Additionally, two-wave mixing technique in such nonlinear cells may be successfully implemented in multi-channel couplers, switches, and optical communication lines. They may be also applied in networks, if to ensure the independent control of each channel in LCD structures.

Abkürzungen

5CB:

4′-(n -pentyl)-4-cyanobiphenyl

E7:

Liquid crystal mixture

F1:

Hybrid LC cell, composed by flat part of Si plate 1/5CB/glass plate covered by ITO

F2:

Hybrid LC cell, composed by flat part of Si plate 2/5CB/glass plate covered by ITO

ITO:

Conductive layer of indium-tin-oxide

LC:

Liquid crystals

M1:

Hybrid LC cell, composed by microstructured part of Si plate 1/5CB/glass plate covered by ITO

M2:

Hybrid LC cell, composed by microstructured part of Si plate 2/5CB/glass plate covered by ITO

M3:

Hybrid LC cell, composed by microstructured part of Si plate 3/5CB/glass plate covered by ITO

M4:

Hybrid LC cell, composed by microstructured part of Si plate 4/E7/glass plate covered by ITO

Si:

Silicon