Durch Defekte und Dotierung entwickeltes Penta-Graphen zur Katalyse der Wasserstoffentwicklungsreaktion

Hintergrund

Aufgrund des Klimawandels und der Umweltverschmutzung durch die Nutzung fossiler Brennstoffe sind die Nutzung und Nutzung sauberer und erneuerbarer Energie heute der Mittelweg [1,2,3,4]. Als saubere, erneuerbare und umweltfreundliche Energiequelle ist Wasserstoff (H₂ ) hat erhebliche Aufmerksamkeit auf sich gezogen, um den zukünftigen Energiebedarf der Menschheit zu decken [5, 6]. Wasserelektrolyse ist eine nachhaltige und saubere Methode zur Herstellung von H₂ , und Elektrokatalysatoren können die Effizienz der Wasserspaltung beobachtbar steigern [7, 8]. Für die Wasserstoffentwicklungsreaktion (HER) gelten Platin-basierte Nanomaterialien aufgrund einer kleinen Tafel-Steigung, einer geringen Überspannung und einer leicht negativen Gibbs-Freien Energie (ΔG .) als die besten Elektrokatalysatoren _H ) und eine hohe Austauschstromdichte [9, 10], aber die Knappheit und die hohen Kosten erschweren ihre Anwendungen im industriellen Maßstab [11]. Daher ist die Entwicklung effektiver, auf der Erde reichlich vorhandener und kostengünstiger Elektrokatalysatoren für die HER unerlässlich [12,13,14].

Tatsächlich wurde eine breite Palette von auf der Erde reichlich vorhandenen Elektrokatalysatoren untersucht und für HER entwickelt [15,16,17]. Unter diesen Materialien bieten zweidimensionale (2D) Nanomaterialien aufgrund ihrer überzeugenden strukturellen und elektronischen Eigenschaften neue Möglichkeiten für die HER. Bis heute sind die Übergangsmetalldichalkogenide (TMDs) und die Graphen-basierten Materialien die größten und am intensivsten untersuchten Gruppen von 2D-Elektrokatalysatoren für die HER [18,19,20,21,22,23]. Die HER-Katalysatoren der TMDs haben ein niedriges Überpotential und eine kleine Tafel-Steigung, ungewöhnliche elektronische Eigenschaften und eine hohe Luftstabilität, zeigen eine hohe HER-Leistung, und verschiedene Methoden wurden verwendet, um ihre katalytische Leistung zu verbessern [24, 25]. Die Graphen-basierten HER-Katalysatoren haben aufgrund ihrer besonderen strukturellen Vorzüge, wie hoher elektrischer Leitfähigkeit, großer Oberfläche und guter chemischer Stabilität, beträchtliche Aufmerksamkeit und anhaltende Untersuchungen auf sich gezogen [26, 27]. Zur Steigerung der katalytischen Aktivität wurden viele Methoden wie Heteroatom-Dotierung und Defektions-Engineering angewendet [28, 29]. Inzwischen wurde auch intensiv an anderen neuen 2D-Kohlenstoffallotropen geforscht, wie zum Beispiel Graphdiin [30] und Penta-Graphen (PG) [31]. Als 2D-Kohlenstoffallotrop besteht PG nur aus Kohlenstoffpentagonen und erbt viele außergewöhnliche Eigenschaften von 2D-Materialien, wie z Anwendungen wie andere 2D-Graphen-basierte Materialien [32,33,34,35]. Da es nur Anwendungen in der Gasadsorption gibt [36,37,38], H₂ Lagerung [39, 40], Anodenmaterialien derzeit [41, 42], über die Anwendung bei HER wurde bisher kein Bericht gefunden. Daher ist die HER-Forschung von PG von großer Bedeutung und kann nicht nur eine solche Lücke schließen, sondern auch den Anwendungsbereich von Graphen-basierten HER-Katalysatoren erweitern. Es wurde jedoch festgestellt, dass das reine PG für die HER mit einem relativ großen ΔG . inert ist _H , was bedeutet, dass die Wasserstoffadsorption schwierig ist und die HER hemmt. Dies ähnelt den Problemen, auf die reines Graphen stößt (ΔG _H = 1,85 eV [43]). Heteroatomdotierungen in graphenbasierten Materialien könnten ihre elektronischen und katalytischen Eigenschaften anpassen, was sie zu vielversprechenden Katalysatoren für praktische Anwendungen macht [3]. Daher gelang es uns, die katalytische Aktivität von PG durch Dotierung mit Heteroatomen [44,45,46] und Defektionstechnik [47, 48] anzupassen.

In diesem Artikel haben wir mithilfe von First-Principles-Rechnungen einen Defekt und N-, S-, P-dotiertes PG entworfen und demonstriert und ihre Stabilität und elektronischen Eigenschaften untersucht und ihre Leistung als HER-Elektrokatalysatoren bewertet. Unsere Ergebnisse zeigen, dass der Defekt und das dotierte PG offensichtlich die katalytische Aktivität gegenüber HER im Vergleich zum reinen PG erhöhen können. Es wird auch gezeigt, dass die ΔG _H kann 0 eV mit C2-Leerstellen und P-Dotierung an den aktiven C1-Zentren betragen, was die optimale Leistung für einen HER-Katalysator sein sollte, also hat P-dotiertes PG das optimale ΔG _H und Aktivierungsenergiebarriere für den geschwindigkeitsbestimmenden Schritt unter den drei Gegenstücken und zeigt eine günstigere Leistung. Wir zeigen weiterhin, dass die katalytische Aktivität von den eingebauten Dotieratomen herrührt, die einen effizienten Weg für den Ladungstransport während der Elektrolyse bieten können, was zu einer Reduzierung von ΔG . führt _H . Wir zeigen auch, dass der Volmer-Heyrovsky-Mechanismus für HER auf defektem und dotiertem PG bevorzugter ist. Wir haben unsere Ergebnisse mit denen anderer Graphen-Forscher verglichen und es lässt sich feststellen, dass die Defekt- und Dotierungstechnik für PG bei der Katalyse von HER effektiver ist. Daher machen unsere Bemühungen zu defektem und dotiertem PG es zu einem vielversprechenden Elektrokatalysator für die HER, und unsere Ergebnisse liefern ein tiefes Verständnis für die Entwicklung effizienter und langlebiger Elektrokatalysatoren. Diese Methode kann auch auf andere Materialien auf Graphenbasis angewendet werden.

Rechenmethoden

Unsere First-Principles-Berechnungen wurden mit dem Vienna Ab initio Simulation Package (VASP) durchgeführt [49]. Die projizierten Augmented-Wave-(PAW)-Potentiale wurden verwendet, um die Wechselwirkungen zwischen Kernelektronen und Valenzelektronen zu analysieren [50,51,52]. Die Elektronenaustausch-Korrelations-Wechselwirkungen wurden mit dem Perdew-Burke-Ernzerhof-(PBE)-Funktional innerhalb der generalisierten Gradienten-Approximation (GGA) beschrieben [53]. Das DFT-D3-Austausch-Korrelations-Funktional wurde in die Strukturoptimierung eingeführt, um die Van-der-Waals-Wechselwirkung zu berücksichtigen. Der Vakuumraum entlang der z -direction wurde auf 20 Å gesetzt, um die Interaktionen zwischen PG und seinen periodischen Bildern zu eliminieren.

Der Energiegrenzwert für ebene Wellen wurde auf 500 eV festgelegt. Das Konvergenzkriterium wurde als 10 ⁻⁵ . festgelegt eV für eine Gesamtenergie. Alle atomaren Positionen und Gitterstrukturen wurden mit dem Schwellenwert einer maximalen Kraft von 0,02 eV Å ⁻¹ . vollständig entspannt . Um die Genauigkeit und Effizienz der Berechnung zu gewährleisten, wurde für alle betrachteten Strukturen nach dem Konvergenztest ein Gamma-zentriertes k-Punkt-Netz mit einer Monkhorst-Pack-Methode 5 × 5 × 1 verwendet [54]. Das Ausmaß des Ladungstransfers zwischen den C-Atomen und H-Atomen wurde nach dem Bader-Code [55] berechnet. Wir berechneten auch H*-Adsorptionsenergiebarrieren mit der Methode des Climbing Image-Nudged Elastic Band (CI-NEB) [56, 57]. Der CI-NEB ist eine effiziente Methode, um den minimalen Energiepfad und Sattelpunkte zwischen einer gegebenen Anfangs- und Endposition zu bestimmen [58,59,60], und in unseren CI-NEB-Berechnungen wurden die Anfangs- und die Endstruktur vollständig optimiert.

Die Adsorptionsenergie (ΔE _H ) ist definiert als

wo E (*H) und E (*) sind die Gesamtenergien von Strukturen mit bzw. ohne Wasserstoffadsorption und E (H₂ ) ist die Gesamtenergie eines H₂ Molekül.

Die freie Gibbs-Energie (ΔG _H ) ist definiert als:

wobei ΔE _H ist die Adsorptionsenergie, ΔE _ZPE ist die Differenz der Nullpunktsenergie, T ist die Temperatur (298,15 K) und ΔS _H ist die Entropiedifferenz von adsorbiertem H und H in der Gasphase. Wir haben die Entropie der Wasserstoffadsorption angenähert als \(\Delta S_{{\text{H}}} \approx \frac{1}{2}(S_{{{\text{H}}_{2} }}^ { \circ } )\), wobei \(S_{{{\text{H}}_{2} }}^{ \circ }\) die Entropie der Gasphase H₂ . ist unter Standardbedingungen, T ΔS _H wurde nach der Berechnung in dieser Studie auf − 0.202 eV festgelegt.

Ergebnisse und Diskussion

Struktur und katalytische Aktivität von defektem und dotiertem PG

Die optimierte Struktur von PG ist in Abb. 1 dargestellt. Zur Vereinfachung der Diskussion gruppieren wir im Folgenden die sp ³⁻ und sp ²⁻ hybridisierte C-Atome als C1 bzw. C2. Der Abstand zwischen C1 und C2 beträgt 1,55 Å und die C2-C2-Bindungslänge beträgt 1,34 Å, was mit dem experimentellen Ergebnis übereinstimmt [31].

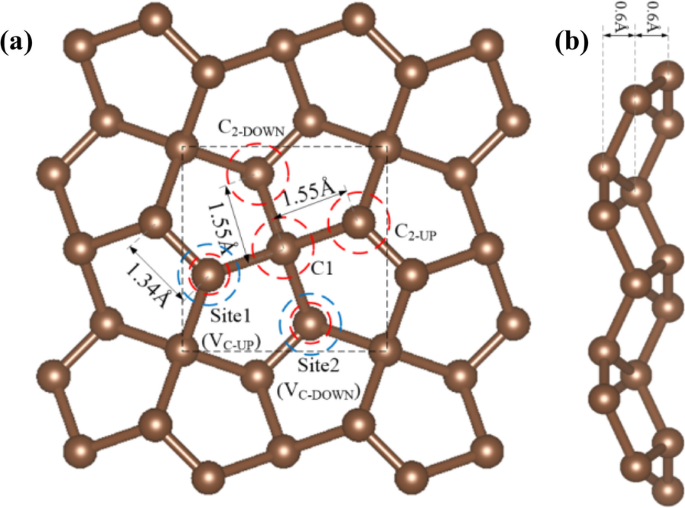
a Oben und b Seitenansichten der optimierten Struktur von PG. Das schwarze gestrichelte Rechteck zeigt die Elementarzelle an, die blauen gestrichelten Kreise zeigen zwei C-Leerstellen an, die roten gestrichelten Kreise zeigen die in dieser Veröffentlichung verwendeten Dotierungsstellen an

Zu Beginn untersuchten wir zunächst die Stellen C1 und C2 in der Basalebene von reinem PG für HER, das berechnete ΔG _H Werte sind 2,43 eV bzw. 2,72 eV. Unsere Berechnungen zeigen also, dass das unberührte PG für die HER mit einem relativ großen ΔG . inert ist _H von H, was bedeutet, dass die Wasserstoffadsorption schwierig ist und die HER gehemmt wird. Daher gelang es uns, einige Methoden zu verwenden, um die katalytische Aktivität von PG zuzuschneiden. Wir untersuchten die möglichen aktiven Zentren für die Dotierung und wir untersuchten auch die aktiven Zentren für C1 und C2 mit N-, S- bzw. P-Dotierung. Die Berechnungsergebnisse zeigen, dass keine offensichtliche Verbesserung der HER erreicht werden kann, wenn nur die Dotierungstechnik eingeführt wird. Im Fall der P-dotierten Struktur ist das berechnete ΔG _H Die Werte der C1- und C2-Sites betragen 1,24 eV bzw. 1,40 eV. Schließlich untersuchten wir das defekte PG mit C-Leerstellen. Die Berechnungsergebnisse zeigen, dass die C1-Leerstellenstruktur die HER-Leistung nicht verbessern kann, die C2-Leerstellenstruktur jedoch verringern kann ΔG _H Offensichtlich verwenden wir in dieser Studie die C2-Leerstellenstruktur. Die optimierten Strukturen mit V_C-UP und V_C-DOWN C2-Leerstellenstellen sind in Abb. 2 gezeigt. Die Leerstellendefekte werden durch Entfernen von C2-Atomen aus C_2-UP . aufgebaut oder C_2-DOWN Stelle in einer 24-atomigen Superzelle. Das berechnete ΔG _H Werte sind in Tabelle 1 gezeigt, wobei C1 und C2 die aktiven Zentren für die Wasserstoffadsorption sind.

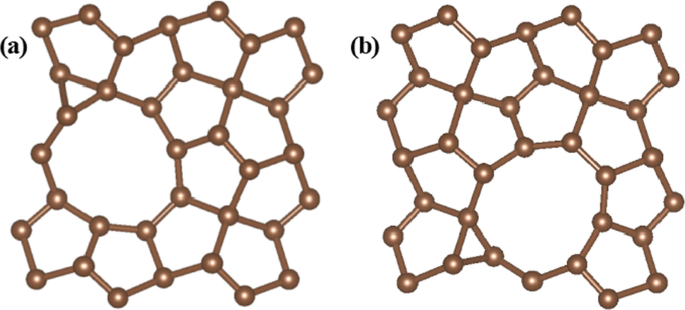
Die optimierten Strukturen von PG mit zwei verschiedenen C2-Leerstellenplätzen. a V_C-UP C2-Stellenangebot, b V_C-DOWN C2-Stellenangebot

Obwohl durch unsere Rechnungen bestätigt wird, dass C2-Leerstellen effizient sind, um die HER-Aktivität zu erhöhen, ist PG mit C2-Leerstellenstruktur noch nicht optimal für einen HER-Katalysator. Daher haben wir den Defekt weiter untersucht und PG für HER dotiert. Wir haben PG mit C2-Leerstelle als Ausgangsstruktur verwendet, die in Abb. 2 gezeigt ist, und dann alle verschiedenen möglichen aktiven Zentren mit N-, S-, P-Dotierung untersucht, einschließlich C1, C_2-UP und C_2-DOWN Websites. Als Ergebnis fanden wir, dass eine bessere HER-Leistung mit einer Kombination aus C2-Leerstelle und Heteroatom-Dotierung erreicht werden kann. Wir haben alle möglichen Strukturen untersucht und die Ergebnisse zeigten, dass es zwei Strukturen gibt, die eine bessere HER-Leistung erreichen können, eine Struktur ist eine Kombination aus C_2-UP Leerstelle und Heteroatom-Dotierung im C_2-DOWN Site, und die andere ist eine Kombination aus C_2-DOWN Leerstelle und Heteroatom-Dotierung im C_2-UP Seite? ˅. Also haben wir uns auf diese beiden Strukturen konzentriert und festgestellt, dass sie das ΔG . verschieben können _H Werte näher an Null. Die optimierten Strukturen sind in Abb. 3 dargestellt und die berechneten Bindungslängen sind in Tabelle 2 zusammengefasst.

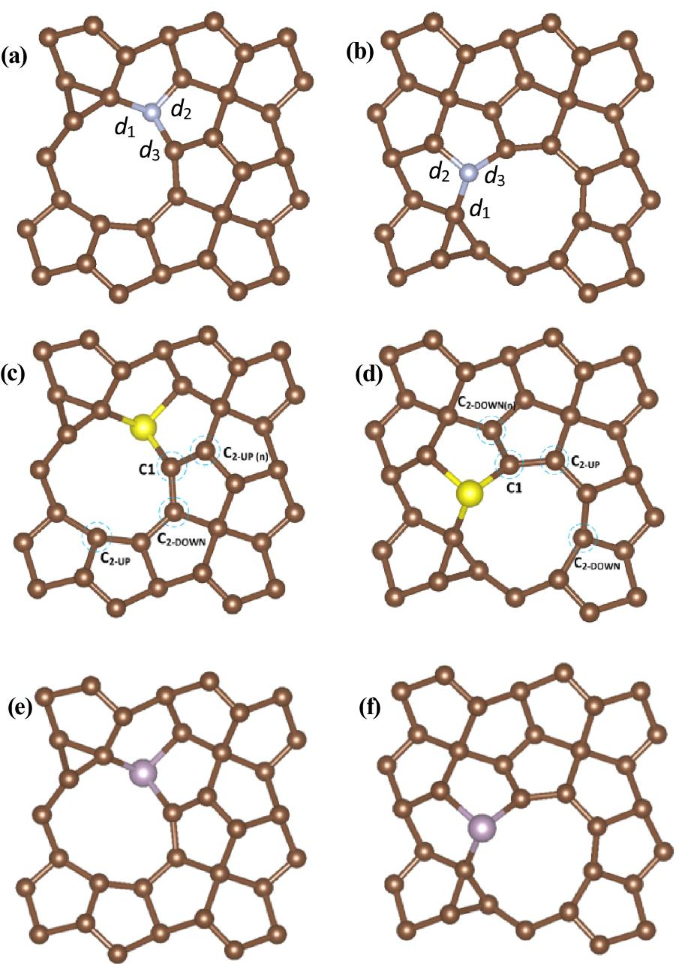
Die optimierten Strukturen für den Defekt und das dotierte PG mit den zwei verschiedenen C2-Leerstellenplätzen, a V_C-UP N-dotiert, b V_C-DOWN N-dotiert, c V_C-UP S-dotiert, d V_C-DOWN S-dotiert, e V_C-UP P-dotiert, f V_C-DOWN P-dotiert, die blauen gestrichelten Kreise zeigen mögliche aktive Zentren für die Wasserstoffentwicklung an

Wir können sehen, dass es einen leichten Unterschied zwischen den entsprechenden Bindungslängen von N-dotiertem PG und denen von reinem PG gibt. Aufgrund des großen Radius der S- und P-Atome unterliegen diese beiden Strukturen einer viel stärkeren Verzerrung, aber sie können beide die Struktur von PG beibehalten.

Um die Stabilität von PG mit C2-Leerstelle und Heteroatom-Dotierung zu untersuchen, berechneten wir die Bildungsenergie, die definiert ist als

wo E _t die Gesamtenergie des Defekts und des dotierten Systems ist und E _V ist die Energie der C2-Leerstelle PG, E _C ist die durchschnittliche Energie pro C-Atom des reinen PG, E _d ist die Energie der Dotierungsatome,\(\mu_{{\text{H}}}\) wird aus der Gesamtenergie des H₂ Molekül bzw. Eines unserer Berechnungsergebnisse zu den Bildungsenergien der beiden vorhergehenden Strukturen mit aktiven C1-Zentren für HER ist in Abb. 4 dargestellt. Wir können sehen, dass negative Bildungsenergien energetisch günstige und machbare Defekt- und S-, P-dotierte PG anzeigen. Ebenso E _f Werte von N-dotierten Strukturen mit aktiven Zentren für HER sind alle positiv. Wir haben alle möglichen aktiven Zentren untersucht und ähnliche Ergebnisse wie in Abb. 4 erhalten, daher werden wir nur das S- und P-dotierte PG untersuchen. Laut Definition ist ein negativeres E _f Wert zeigt eine höhere Stabilität der Struktur an, daher hat P-dotiertes PG eine ausgezeichnete Stabilität sowie eine gute HER-Leistung.

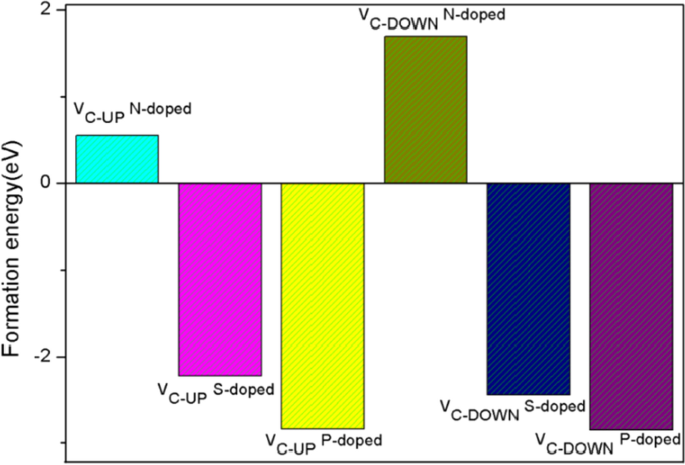
Bildungsenergie von zwei anfänglichen Defekt- und dotierten PG-Strukturen mit aktiven C1-Zentren für HER, negativerer Wert zeigt eine höhere Stabilität der Struktur an

Ursprung der HER-katalytischen Aktivität

DOS und Bandstrukturen

Um ein tieferes Verständnis der Natur der C2-Leerstellen und des Dotierungs-Engineerings in der HER-Aktivität zu erlangen, untersuchten wir die gesamte und die projizierte DOS, die elektronische Bandstruktur des Defekts und S-, P-dotiertes PG. Abbildung 5 ist eines unserer Berechnungsergebnisse über elektronische Bandstrukturen, Gesamt- und projizierte DOS von reinem PG, V_C-UP , V_C-UP S-dotiert und V_C-UP P-dotiertes PG.

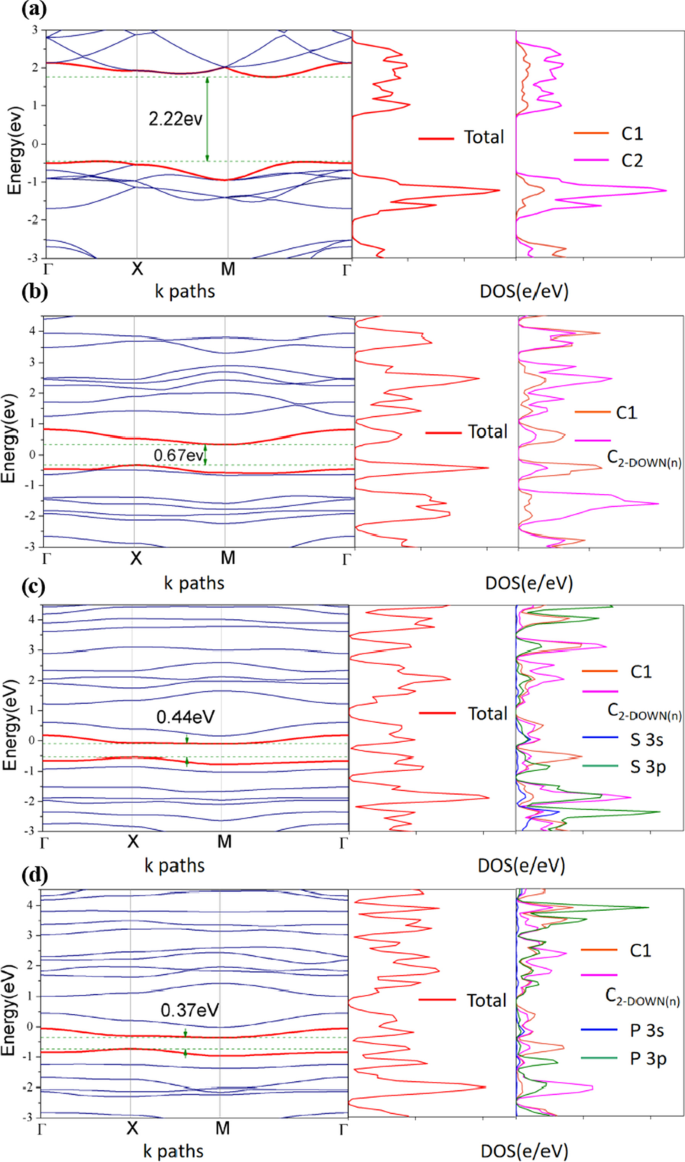
Elektronische Bandstruktur, Gesamt- und projizierte DOS des Defekts und dotiertes PG. a Makelloses PG, b V_C-UP C2-Stellenangebot, c V_C-UP S-dotiert und d V_C-UP P-dotiert bzw. Die Strukturen von c und d wie in Abb. 3 gezeigt. Sie werden mit dem PBE-Funktional berechnet, das Fermi-Niveau wird auf 0,00 eV verschoben

Aus der Abbildung können wir sehen, dass bei Einführung einer C2-Leerstelle einige neue Defektzustände, die durch rote Kurven hervorgehoben sind, im verbotenen Band in der Nähe des Fermi-Niveaus erscheinen. Offensichtlich ergeben sich diese neuen Zustände aus der C2-Leerstelle. Wenn eine S, P-Heteroatom-Dotierung eingeführt wird, wird außerdem die Bandlücke kleiner (von 2,22 eV [31] auf 0,37 eV) und die Anzahl neuer Defektzustände in der Nähe des Fermi-Niveaus nimmt zu, was möglicherweise die H*-Adsorptionsstärke verbessern kann.

Wir haben jedoch festgestellt, dass die DOS von V_C-UP nahe der Fermi-Ebene ist viel größer als die von unberührtem PG. Darüber hinaus ist die Elektronendichte nahe dem Fermi-Niveau von C2-Leerstellen und S-, P-dotiertem PG im Vergleich zu reinem PG weiter erhöht. Wir fanden auch, dass die S 3p- und P 3p-Orbitale eine signifikante Hybridisierung mit den C1- und C2-Zuständen eingehen, was zu starken Wechselwirkungen zwischen den Heteroatomen und C sowie zur Bildung von S-C- und PC-Bindungen führt. Diese Ergebnisse zeigen, dass die Kombination der C2-Leerstelle und der S, P-Heteroatom-Dotierung eine bessere Technik zur Verbesserung der HER-Aktivität sein kann.

Elektronendichtedifferenz und Ladungstransfer

Um die Bindungswechselwirkung zwischen dem H-Atom und PG zu untersuchen, berechneten wir außerdem die Unterschiede der Elektronenladungsdichte für defektes und S-, P-dotiertes PG mit unterschiedlichen aktiven Zentren für die Wasserstoffentwicklung. Eines unserer Berechnungsergebnisse über die Elektronenladungsdichtedifferenz und die Bader-Ladungsanalyse für ein C_2-DOWN Leerstelle und P-dotiertes PG mit H*, das an den verschiedenen aktiven Zentren für die Wasserstoffadsorption adsorbiert ist, ist in Abb. 6 dargestellt. Die gelben und blauen Farben stehen für Ladungsakkumulation bzw. -reduzierung. Es wird gezeigt, dass sich die Elektronen um H-Atome ansammeln und um die an H-Atome gebundenen C-Atome reduzieren, was auf einen Ladungstransfer von PG zu H* hinweist. Die Ladungsübertragung wird auch durch die Bader-Gebührenanalyse bestätigt. Die Berechnungsergebnisse zeigen, dass an C1, C_2-DOWN . 0,18, 0,04, 0,02 und 0,01 Elektronen auf H* übertragen werden , C_2-DOWN(n) und C_2-UP Websites bzw. Wir zeigen weiter, dass je größer der Ladungstransfer von PG zu H* ist, desto näher ΔG _H Null ist, was die optimale Leistung für einen HER-Katalysator bedeutet, wie in Abb. 7 gezeigt. Aus Abb. 6 ist ersichtlich, dass Elektronen von PG auf H* übertragen werden, was zu einer Erhöhung der Ladungsdichte der Bindungen führt, was bedeutet, dass die Stabilisierung der H*-Spezies in der HER-Leistung von der erhöhten Ladungsdichte von P-dotierten C-Atomen herrühren könnte, was darauf hindeutet, dass P-Atome von Natur aus vorteilhafter bei der Wechselwirkung mit H-Atomen als mit C-Atomen sind. Wir haben auch festgestellt, dass H* an C statt an P absorbiert wird, was darauf hindeutet, dass die erhöhte Ladungsdichte zum Elektrokatalysator am H-Atom beitragen kann. Unsere Rechnungen zeigen also, dass eine P-Dotierung in das PG zu einer verstärkten Adsorption von H* an C-Atomen führen kann. Wie oben erwähnt, legten die DFT-Rechnungen auch nahe, dass die P-Dotierung in PG die HER-Aktivität viel effizienter steigern könnte als die der S-Dotierung.

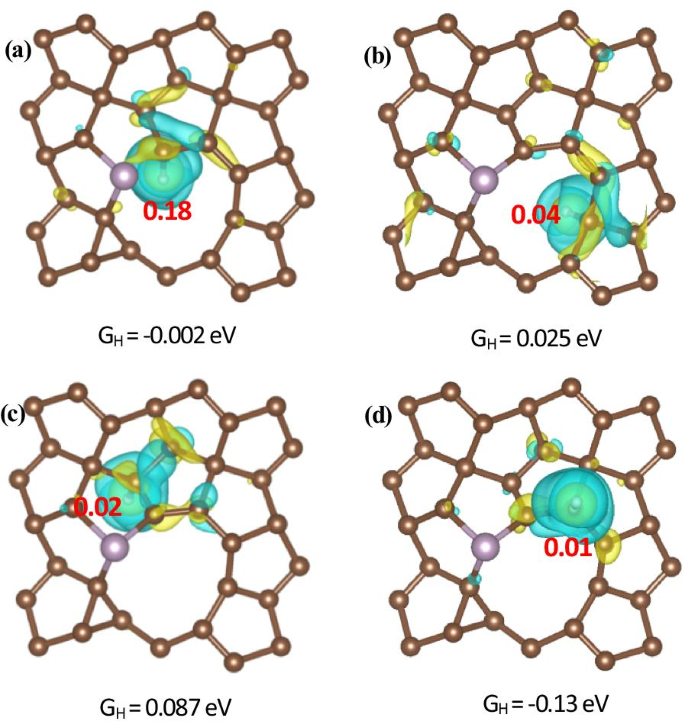
Draufsichten der Elektronenladungsdichtedifferenz und Bader-Ladungsanalyse für ein C_2-DOWN Leerstelle und P-dotiertes PG mit H adsorbiert am a C1, b C_2-DOWN , c C_2-DOWNn und d C_2-UP Websites. Der Isooberflächenpegel beträgt 0,004 e/Bohr ³ . Die gelben und blauen Farben stehen für Ladungsakkumulation bzw. -reduzierung

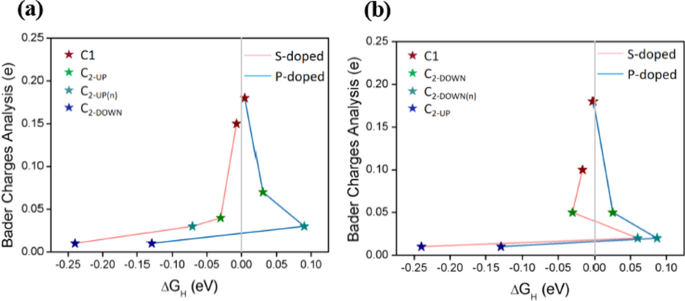
Beziehung zwischen ΔG _H und Bader berechnet Analyse für a V_C-UP S-dotiert, V_C-UP P-dotiert und b V_C-DOWN S-dotiert, V_C-DOWN P-dotierte Strukturen. Das ΔG _H Werte und aktive Zentren sind in Tabelle 3 gezeigt

Aktivität von Defekt und gedopter PG gegenüber IHR

Gibbs Free Energies of IHR

Das ΔG _H ist der entscheidende Deskriptor der HER für eine Vielzahl von Elektrokatalysatoren, der optimale ΔG _H der Wert für einen Elektrokatalysator null ist, sodass die H*-Adsorption und -Desorption spontan ohne Aktivierungsenergiebarriere erfolgen kann [61, 62]. Um die HER-Aktivität des PG zu bewerten und die Defekt- und Dotierungstechnik zu untersuchen, haben wir den ΔG . berechnet _H ihrer. Eines unserer Berechnungsergebnisse zu ΔG _H gegen die Reaktionskoordinate der HER für PG ist in Abb. 8 dargestellt, wobei C1 und C2 innerhalb der Klammern aktive Zentren für die Wasserstoffadsorption sind.

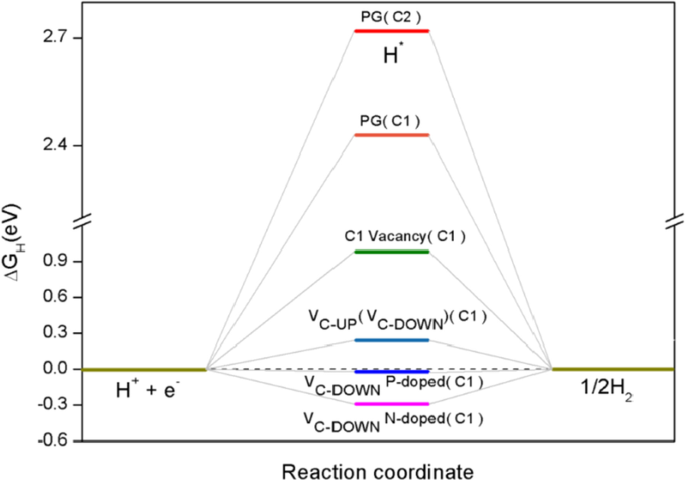
Freie Gibbs-Energie versus Reaktionskoordinate der HER für PG, wobei C1 und C2 innerhalb der Klammern aktive Zentren für die Wasserstoffadsorption sind

Unsere Berechnungen zeigen, dass das reine PG für die HER mit einer relativ großen freien Gibbs-Energie von H* (ΔG _H = 2,72 eV(C2), ΔG _H = 2,43 eV(C1)). Bei der Einführung von Stellen gibt es zwei verschiedene C-Stellenangebote, C1-Stellplatz und C2-Stellplatz. Wir haben den ΔG . berechnet _H an den beiden Standorten und stellte fest, dass die C2-Leerstelle ΔG . deutlich verringern kann _H (ΔG _H = 0.24 eV), was darauf hinweist, dass H* bevorzugt an C2-Leerstellenstrukturen adsorbiert. Die optimierten Strukturen mit C2-Leerstandsplätzen (V_C-UP und V_C-DOWN ) sind in Abb. 2 dargestellt. Obwohl C2-Leerstellen eine deutliche Verbesserung gegenüber dem reinen PG zeigen, sind sie immer noch nicht optimal für die Wasserstoffadsorption, sodass Dotierungstechniken untersucht werden, um die HER-Leistung zu verbessern. Wir zeigen unsere Auswirkungen von C2-Leerstellen und S, P-Heteroatom-Dotierung auf die HER-Aktivität und optimieren die HER-Leistung. Das ΔG _H Werte sind in Tabelle 3 zusammengefasst und die aktiven Zentren für die Wasserstoffentwicklung sind in Abb. 3 dargestellt.

Die Berechnungsergebnisse zeigen, dass ΔG _H deutlich ab, was zeigt, dass die Defektions- und Dotierungstechnik sehr effektiv bei der Reduzierung von ΔG . sind _H . Bemerkenswerterweise haben wir festgestellt, dass die ΔG _H Werte der aktiven Zentren C1, C_2-UP und C_2-UP(n) für V_C-UP , aktive Sites C1, C_2-DOWN und C_2-DOWN(n) für V_C-DOWN liegen sehr nahe bei Null, insbesondere für zwei C1-Standorte, was bedeutet, dass optimale Bedingungen erreicht werden können, die dem reinen PG deutlich überlegen sind. Und wir haben unsere Ergebnisse mit früheren Arbeiten anderer Forscher zu Graphen verglichen, zum Beispiel Graphen mit C-Leerstelle (ΔG _H = − 2.108 eV) [28], Graphen mit N-dotiertem (ΔG _H = − 0.693 eV) [28], Graphen mit C-Leerstelle und N-dotiert (ΔG _H = − 0.595 eV) [28], Graphen mit S-dotiertem (ΔG _H = − 0.30 eV) [29] und Graphen mit N/S co-dotiert (ΔG _H = − 0,12 eV) [29]. Wir können feststellen, dass die Defekt- und Dotierungstechnik für PG effektiver ist. Somit legen unsere Ergebnisse eindeutig nahe, dass die ΔG _H von PG kann durch Anwendung von Defektions- und Dotierungstechniken manipuliert werden, um die optimale HER-Aktivität zu erreichen.

Die Reaktionswege von defektem und dotiertem PG

Die HER verläuft in einem mehrstufigen elektrochemischen Prozess über einen von zwei Reaktionswegen, die als Volmer-Tafel- und Volmer-Heyrovsky-Mechanismen bekannt sind. Der erste Schritt der HER ist die H*-Adsorption an der Elektrokatalysatoroberfläche (d. h. Volmer-Reaktion), die durch H ⁺ . beschrieben wird + e ⁻ → H*. Dann wird H* mit H ⁺ . kombiniert und ein Elektron (e ⁻ ) um ein H₂ . zu bilden Molekül, bekannt als Heyrovsky-Schritt, der beschrieben wird durch H* + H ⁺ + e ⁻ → H₂ . Alternativ H₂ Molekül kann über den Tafel-Schritt gebildet werden, d. h. die Kombination von zwei H* auf der Elektrokatalysatoroberfläche, die beschrieben wird durch 2H* → H₂ [63].

Um die Defekt- und Doping-Engineering-Effekte auf PG zu untersuchen und den Mechanismus der überlegenen HER-Aktivität, die Energiebarrieren von Tafel- und Heyrovsky-Reaktionen mit C_2-UP . weiter zu verstehen und C_2-DOWN Leerstellen, S-, P-dotiertes PG für die C1-Stelle wurden berechnet. Der Anfangszustand (IS), der Endzustand (FS) und der Übergangszustand (TS) sind in Abb. 9 mit den entsprechenden Energiebarrieren dargestellt. Für die Tafel-Reaktion zeigt die Rekombination von 2H* Energiebarrieren von 1,51 eV (S-dotiert) bzw. 1,32 eV (P-dotiert). Während die Freisetzung eines H₂ -Molekül in der Heyrovsky-Reaktion, das an einem Proton beteiligt ist, das mit einem adsorbierten H* reagiert, muss die Energiebarrieren von 1,01 eV (S-dotiert) bzw. 0,99 eV (P-dotiert) überwinden. Die Ergebnisse zeigen, dass die Energiebarrieren der Tafel-Reaktion deutlich höher sind als die der Heyrovsky-Reaktion. Daher bevorzugt die HER bei defektem und dotiertem PG den Volmer-Heyrovsky-Mechanismus.

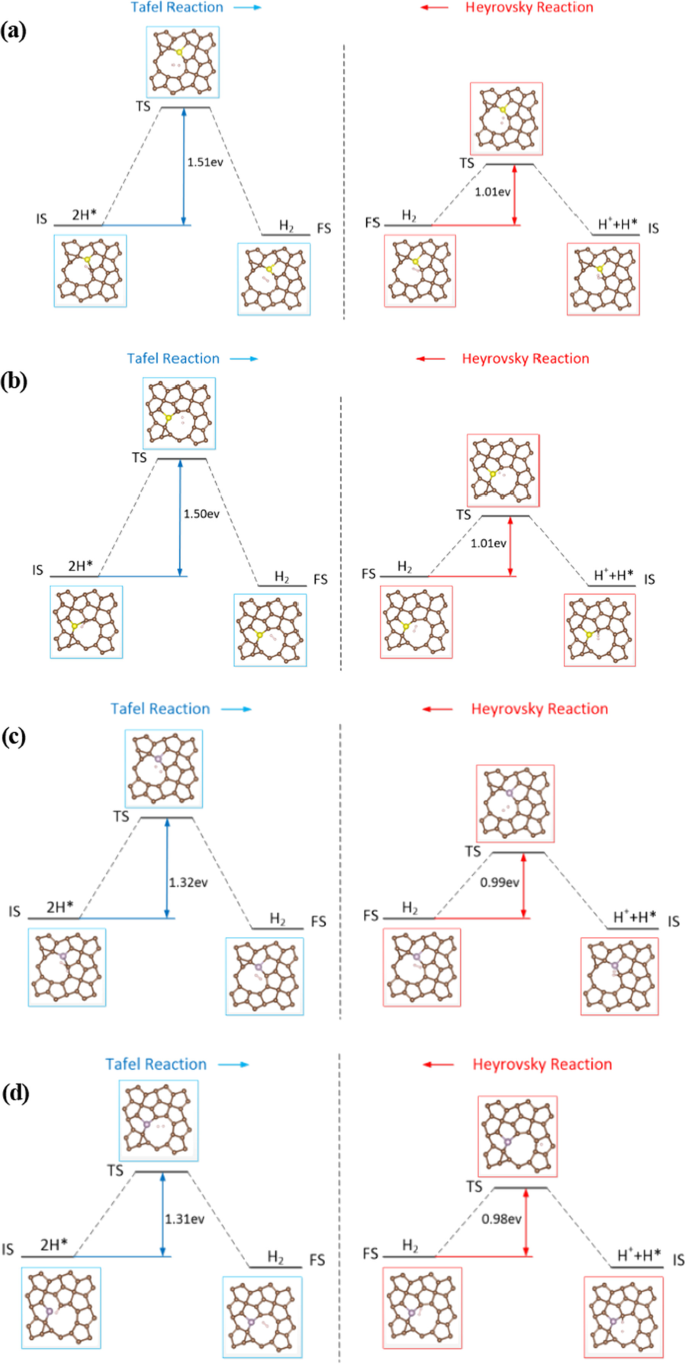
Schematische Pfade für die HER. Energieprofile für die Tafel- und Heyrovsky-Reaktion mit a C_2-UP Leerstand und S-dotiertes PG, b C_2-DOWN Leerstand und S-dotiertes PG, c C_2-UP Leerstelle und P-dotiertes PG, d C_2-DOWN Leerstelle und P-dotiertes PG. Der Anfangszustand (IS), der Übergangszustand (TS) und der Endzustand (FS) sind im Diagramm mit den entsprechenden Energiebarrieren gekennzeichnet

Schlussfolgerungen

Wir haben theoretisch eine C-Leerstelle und N-, S-, P-dotiertes PG entworfen und ihre Stabilität und einzigartige Rolle als Elektrokatalysator für HER systematisch untersucht. Wir stellen fest, dass Defektions- und Doping-Engineering eine überlegene HER-Leistung gegenüber dem reinen PG aufweisen. Wichtig ist, dass die optimale HER-Aktivität mit C2-Leerstellen und S, P-Heteroatom-Dotierung erreicht werden kann, was darauf hindeutet, dass die katalytischen Eigenschaften des Defekts und des dotierten PG einfach und effektiv eingestellt werden können. Unsere Berechnungen zeigen, dass ΔG _H nimmt mit C2-Leerstellen und S, P-Heteroatom-Dotierung signifikant ab, und die optimalen Bedingungen können mit P-Dotierung an aktiven C1-Zentren erreicht werden, für die Defekte oder Dotierungstechnik allein die optimalen Bedingungen nicht erreichen können. Die elektronische Strukturanalyse zeigt, dass bei Einführung von C2-Leerstellen und S, P-Heteroatom-Dotierung mehrere neue Defektzustände näher an das Fermi-Niveau rücken, was zu einer engeren Bandlücke und einer Verbesserung der Wasserstoffadsorptionsstärke führt. Wir finden auch den Ladungstransfer von PG zu H* durch Berechnung der Elektronenladungsdichteunterschiede, je größer der Ladungstransfer zu H*, desto näher ΔG _H Werte auf Null unter Verwendung der Bader-Ladungsanalyse, die die optimale Leistung für einen HER-Katalysator anzeigt. Und wir zeigen weiter die HER auf Defekt und dotiertes PG bevorzugt den Volmer-Heyrovsky-Mechanismus. Unsere Studie zeigt also, dass der entworfene Defekt und das dotierte PG gegenüber dem HER-Elektrokatalysator stark aktiviert sind, die optimale HER-Aktivität erreicht werden kann und reichlich katalytische Aktivitätszentren bereitgestellt werden. Es wird erwartet, dass die in diesem Papier entwickelten Strategien zum Design von 2D-Graphen-basierten Elektrokatalysatoren für kostengünstige und leistungsstarke HER-Anwendungen angewendet werden können.

Verfügbarkeit von Daten und Materialien

Die Datensätze, die die Schlussfolgerungen dieses Artikels stützen, sind in dem Artikel enthalten, und weitere Informationen zu den Daten und Materialien können dem Interessenten auf begründete Anfrage an den korrespondierenden Autor zur Verfügung gestellt werden.

Abkürzungen

IHR:

Wasserstoffentwicklungsreaktion

PG:

Penta-Graphen

2D:

Zweidimensional

ΔG _H :

Die kostenlose Gibbs-Energie

TMDs:

Die Übergangsmetalldichalkogenide

VASP:

Wien Ab-initio-Simulationspaket

PAW:

Projizierte erweiterte Welle

PBE:

Der Perdew–Burke–Ernzerhof

GGA:

Die verallgemeinerte Gradienten-Approximation

CI-NEB:

Das Kletter-Bild-angestoßene Gummiband

IS:

Ausgangszustand

FS:

Der Endzustand

TS:

Der Übergangszustand