Karnaugh-Karten, Wahrheitstabellen und boolesche Ausdrücke

Wer hat die Karnaugh-Karte entwickelt?

Maurice Karnaugh, ein Telekommunikationsingenieur, entwickelte die Karnaugh-Karte 1953 in den Bell Labs, während er auf digitaler Logik basierende Telefonschaltkreise entwarf.

Die Verwendung der Karnaugh-Karte

Nachdem wir die Karnaugh-Karte mit Hilfe von Venn-Diagrammen entwickelt haben, verwenden wir sie nun. Karnaugh-Karten reduzieren Logik funktioniert im Vergleich zur Booleschen Algebra schneller und einfacher. Mit reduzieren meinen wir vereinfachen, die Anzahl der Gatter und Eingänge reduzieren.

Wir vereinfachen die Logik gerne zu einem geringsten Preis Form, um durch den Wegfall von Bauteilen Kosten zu sparen. Wir definieren die niedrigsten Kosten als die niedrigste Anzahl von Gattern mit der niedrigsten Anzahl von Eingängen pro Gatter.

Wenn sie die Wahl haben, machen die meisten Schüler eine logische Vereinfachung mit Karnaugh-Karten anstelle von Boolescher Algebra, sobald sie dieses Werkzeug kennen.

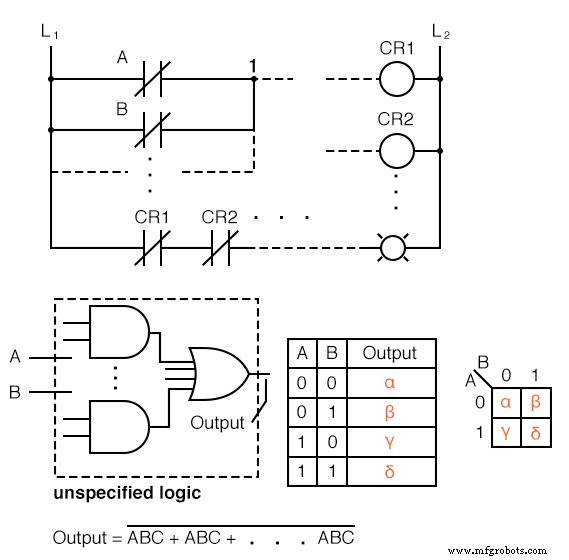
Wir zeigen oben fünf einzelne Elemente, die nur unterschiedliche Darstellungsweisen derselben Sache sind:eine beliebige digitale Logikfunktion mit 2 Eingängen. Zuerst gibt es eine Relaisleiterlogik, dann logische Gatter, eine Wahrheitstabelle, eine Karnaugh-Karte und eine Boolesche Gleichung.

Der Punkt ist, dass alle diese gleichwertig sind. Zwei Eingänge A und B kann Werte von entweder 0 . annehmen oder 1 , hoch oder niedrig, offen oder geschlossen, wahr oder falsch, je nachdem. Es gibt 2 ² =4 Kombinationen von Eingaben, die eine Ausgabe erzeugen. Dies gilt für alle fünf Beispiele.

Diese vier Ausgänge können an einer Lampe in der Relaisleiterlogik oder an einer Logiksonde im Gate-Diagramm beobachtet werden. Diese Ausgaben können in der Wahrheitstabelle oder in der Karnaugh-Karte aufgezeichnet werden. Betrachten Sie die Karnaugh-Karte als eine neu geordnete Wahrheitstabelle.

Die Ausgabe der Booleschen Gleichung kann nach den Gesetzen der Booleschen Algebra berechnet und auf die Wahrheitstabelle oder Karnaugh-Karte übertragen werden.

Welche der fünf äquivalenten logischen Beschreibungen sollten wir verwenden? Diejenige, die für die zu erledigende Aufgabe am nützlichsten ist.

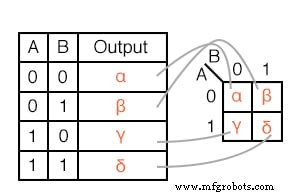
Die Ausgaben einer Wahrheitstabelle entsprechen auf einer Eins-zu-Eins-Basis Karnaugh-Karteneinträgen. Beginnend an der Spitze der Wahrheitstabelle erzeugen die Eingaben A=0, B=0 eine Ausgabe α.

Man beachte, dass dieselbe Ausgabe α in der Karnaugh-Karte an der Zelladresse A=0, B=0, obere linke Ecke der K-Karte gefunden wird, wo sich die A=0-Reihe und die B=0-Spalte schneiden. Die anderen Wahrheitstabellenausgaben β, χ, von den Eingängen AB=01, 10, 11 werden an entsprechenden K-Map-Positionen gefunden

Unten zeigen wir die benachbarten 2-Zellen-Regionen in der 2-Variablen-K-Map mit Hilfe des vorherigen rechteckigen Venn-Diagramms wie Boolesche Regionen.

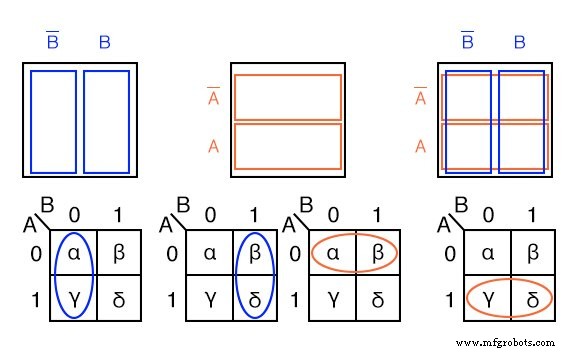
Die Zellen α und sind in der K-Map als Ellipsen in der ganz linken K-Map unten benachbart. Bezogen auf die vorherige Wahrheitstabelle ist dies nicht der Fall. Dazwischen befindet sich ein weiterer Wahrheitstabelleneintrag (β). Was uns zum eigentlichen Punkt der Organisation der K-Map in ein quadratisches Array bringt, müssen Zellen mit allen gemeinsamen Booleschen Variablen nahe beieinander liegen, um ein Muster darzustellen, das uns ins Auge springt.

Für die Zellen α und χ haben sie die boolesche Variable B’ gemeinsam. Wir wissen das, weil B=0 (wie B’ ) für die Spalte über den Zellen α und χ. Vergleichen Sie dies mit dem quadratischen Venn-Diagramm über der K-Karte.

Eine ähnliche Argumentation zeigt, dass β und δ ein boolesches B . haben (B=1) gemeinsam. Dann haben α und β das Boolesche A’ (A=0) gemeinsam. Schließlich haben χ und δ das boolesche A (A=1) gemeinsam. Vergleichen Sie die letzten beiden Karten mit dem mittleren quadratischen Venn-Diagramm.

Zusammenfassend suchen wir nach Gemeinsamkeiten von Booleschen Variablen zwischen Zellen. Die Karnaugh-Karte ist so organisiert, dass wir diese Gemeinsamkeit erkennen können. Versuchen wir es mit einigen Beispielen.

Beispiele

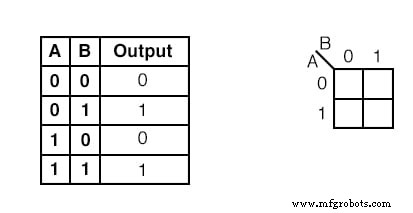
Beispiel:

Übertragen Sie den Inhalt der Wahrheitstabelle auf die Karnaugh-Karte oben.

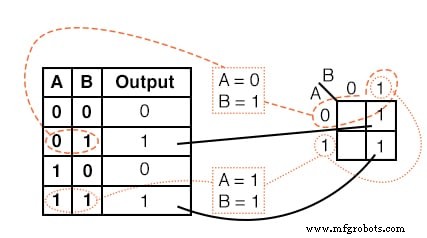
Lösung:

Die Wahrheitstabelle enthält zwei 1 S. die K-Map muss beides haben. suche die erste 1 in der 2. Zeile der Wahrheitstabelle oben.

• Notieren Sie sich die AB-Adresse der Wahrheitstabelle
• lokalisieren Sie die Zelle in der K-Map mit derselben Adresse
• platziere eine 1 in dieser Zelle

Wiederholen Sie den Vorgang für die 1 in der letzten Zeile der Wahrheitstabelle.

Beispiel:

Schreiben Sie für die Karnaugh-Abbildung in der obigen Aufgabe den booleschen Ausdruck. Die Lösung ist unten.

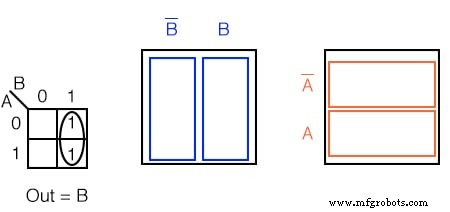
Lösung:

Suchen Sie nach benachbarten Zellen, d. h. über oder neben einer Zelle. Diagonale Zellen sind nicht benachbart. Benachbarte Zellen haben eine oder mehrere boolesche Variablen gemeinsam.

• Gruppieren (kreisen) Sie die beiden 1 s in der Spalte
• Suchen Sie die Variable(n) top und/oder side, die für die Gruppe gleich sind. Schreiben Sie dies als boolesches Ergebnis. Es ist B in unserem Fall.
• Variable(n) ignorieren, die für eine Zellgruppe nicht identisch sind. In unserem Fall variiert A, ist sowohl 1 als auch 0, ignorieren Sie das Boolesche A.
• Ignoriere alle Variablen, die nicht mit Zellen verknüpft sind, die 1s enthalten. B' hat niemanden darunter. Ignoriere B’
• Ergebnis Aus =B

Dies ist möglicherweise leichter zu erkennen, wenn Sie die Venn-Diagramme rechts vergleichen, insbesondere das B Spalte.

Beispiel:

Schreiben Sie den booleschen Ausdruck für die Karnaugh-Karte unten.

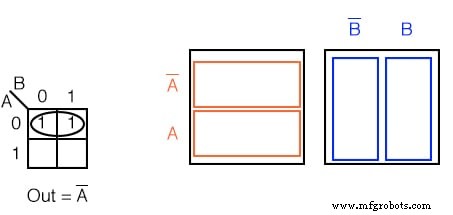
Lösung: (oben)

• Gruppieren (kreisen) Sie die beiden Einsen in der Reihe
• Finden Sie die gleiche(n) Variable(n) für die Gruppe, Out =A’

Beispiel:

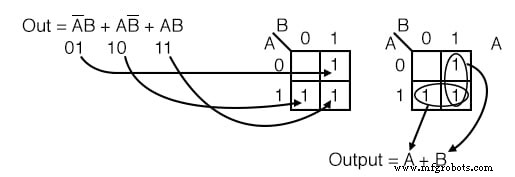
Übertragen Sie für die Wahrheitstabelle unten die Ausgaben an den Karnaugh und schreiben Sie dann den booleschen Ausdruck für das Ergebnis.

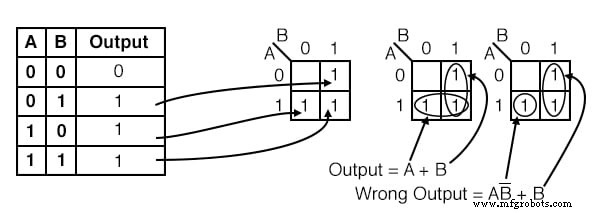
Lösung:

Übertragen Sie die 1 s von den Orten in der Wahrheitstabelle zu den entsprechenden Orten in der K-Karte.

• Gruppieren (kreisen) Sie die beiden Einsen in der Spalte unter B=1
• Gruppieren (kreisen) Sie die beiden Einsen in der Reihe rechts von A=1
• Produktbegriff für erste Gruppe schreiben =B
• Produktbegriff für zweite Gruppe schreiben =A
• Summe-Of-Products der obigen zwei Begriffe schreiben Output =A+B

Die Lösung der K-Map in der Mitte ist die einfachste oder kostengünstigste Lösung. Eine weniger wünschenswerte Lösung ist ganz rechts. Nach der Gruppierung der beiden 1 s, machen wir den Fehler, eine Gruppe von 1-Zellen zu bilden. Dies ist aus folgenden Gründen nicht wünschenswert:

• Die einzelne Zelle hat einen Produktbegriff von AB’
• Die entsprechende Lösung ist Ausgabe =AB’ + B
• Dies ist nicht die einfachste Lösung

So holen Sie sich diese Single 1 ist eine Zweiergruppe mit der 1 . zu bilden rechts davon, wie in der unteren Zeile der mittleren K-Karte gezeigt, obwohl dies 1 wurde bereits in die Spaltengruppe aufgenommen (B ). Wir dürfen Zellen wiederverwenden, um größere Gruppen zu bilden. Tatsächlich ist es wünschenswert, weil es zu einem einfacheren Ergebnis führt.

Wir müssen darauf hinweisen, dass eine der obigen Lösungen, Ausgabe oder Falsche Ausgabe, logisch korrekt ist. Beide Schaltungen liefern die gleiche Leistung. Es geht darum, dass die erstere Schaltung die kostengünstigste Lösung ist.

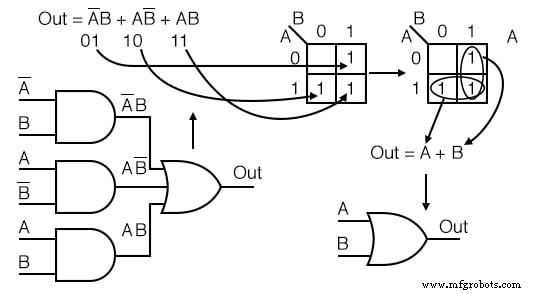
Beispiel:

Füllen Sie die Karnaugh-Map für den booleschen Ausdruck unten aus und schreiben Sie dann den booleschen Ausdruck für das Ergebnis.

Lösung: (oben)

Der boolesche Ausdruck hat drei Produktterme. Es wird eine 1 geben für jeden Produktbegriff eingegeben. Obwohl im Allgemeinen die Anzahl von 1 s pro Produktterm variiert mit der Anzahl der Variablen im Produktterm im Vergleich zur Größe der K-Map.

Der Produktbegriff ist die Adresse der Zelle, in der die 1 eingetragen ist. Der erste Produktbegriff, A’B , entspricht dem 01 Zelle in der Karte. Ein 1 wird in diese Zelle eingetragen. Die anderen beiden P-Terme werden für insgesamt drei 1en eingegeben

Fahren Sie als Nächstes mit dem Gruppieren und Extrahieren des vereinfachten Ergebnisses wie im vorherigen Wahrheitstabellenproblem fort.

Beispiel:

Vereinfachen Sie das folgende Logikdiagramm.

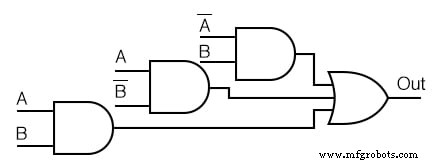
Lösung: (Abbildung unten)

• Schreiben Sie den booleschen Ausdruck für das ursprüngliche Logikdiagramm wie unten gezeigt
• Übertragen Sie die Produktbedingungen auf die Karnaugh-Karte
• Bilden Sie Zellengruppen wie in den vorherigen Beispielen
• Schreiben Sie einen booleschen Ausdruck für Gruppen wie in den vorherigen Beispielen
• Vereinfachtes Logikdiagramm zeichnen

Beispiel: Vereinfachen Sie das folgende Logikdiagramm.

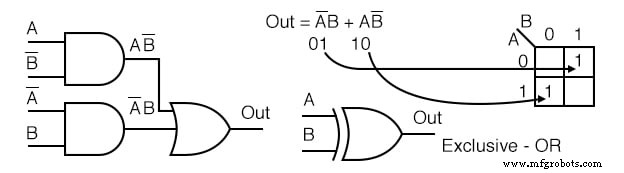
Lösung:

• Schreiben Sie den booleschen Ausdruck für das oben gezeigte ursprüngliche Logikdiagramm
• Übertragen Sie die Produktbegriffe auf die Karnaugh-Karte.
• Es ist nicht möglich, Gruppen zu bilden.
• Es ist keine Vereinfachung möglich; lass es so wie es ist.

Für das obige Diagramm ist keine logische Vereinfachung möglich. Dies passiert manchmal. Weder die Methoden der Karnaugh-Maps noch die Boolesche Algebra können diese Logik weiter vereinfachen.

Wir zeigen oben ein schematisches Exklusiv-ODER-Symbol; Dies ist jedoch keine logische Vereinfachung. Es macht nur ein schematisches Diagramm schöner.

Da es nicht möglich ist, die Exklusiv-ODER-Logik zu vereinfachen und sie weit verbreitet ist, wird sie von den Herstellern als integrierter Basisschaltkreis (7486) bereitgestellt.

VERWANDTE ARBEITSBLÄTTER:

• Karnaugh-Mapping-Arbeitsblatt
• Arbeitsblatt zur Booleschen Algebra
• Grundlegendes Logic Gates-Arbeitsblatt