Theoretische Untersuchung von biaxial zugbelasteten Germanium-Nanodrähten

Hintergrund

Als Element der Gruppe IV besitzt Germanium (Ge) die Überlegenheit sowohl in der Optoelektronik als auch in der Elektronik und weist eine hohe Kompatibilität mit der Silizium-(Si)-Photonik auf. Ein wesentliches Merkmal von Ge ist, dass seine direkte Bandlücke etwa 0,8 eV beträgt (1,55 μ m) bei 300 K. Die Beweglichkeit von Elektron und Loch in Ge ist viel höher als in Si. Daher wurde Ge in Hochgeschwindigkeitsvorrichtungen in aktuellen integrierten Schaltungen auf Si-Basis verwendet [1, 2]. Interessanterweise bietet zugbelastetes Ge eine Optimierung in den obigen Aspekten. Ge ist ein Halbleiter mit indirekter Bandlücke mit einem geringen Unterschied von 136 meV zwischen L-Tal und Γ -Tal [3]. Es wird theoretisch vorhergesagt, dass über ∼4,0 % uniaxial entlang 〈111〉 [4] oder ∼1,6–2,0 % biaxial [5, 6] Zugdehnung die Γ . senken kann -Tal unterhalb des L-Tals, wodurch Ge in ein Material mit direkter Bandlücke umgewandelt wird, was einen neuen Weg für die Lichtemission von Materialien der Gruppe IV eröffnet. Ein weiterer wichtiger Punkt ist, dass zugbelastetes Ge eine signifikante Verbesserung der Ladungsträgermobilität bietet [7, 8], um Hochgeschwindigkeits-Komplementärmetalloxid-Halbleiterbauelemente zu realisieren.

Nanodrähte (NWs) weisen aufgrund des großen Oberfläche-zu-Volumen-Verhältnisses und der Beschränkung sowohl von Trägern als auch Photonen in zwei Dimensionen (2D) attraktive elektronische und optische Eigenschaften auf [9]. In den letzten Jahren wurden Ge-NWs (GeNWs) auf Si [10] oder Ge/Si-Kern/Schale-NWs [11] aufgrund ihres Potenzials in Metalloxid-Halbleiter-Feldeffekttransistoren (MOSFETs) für die Si-Mikroelektronik intensiv untersucht. Sowohl die skalierte Steilheit als auch der Einschaltstrom wurden im Vergleich zu herkömmlichem Si p . um das Drei- bis Vierfache verbessert -MOSFET [12]. Somit wurde erwartet, dass epitaktisches Wachstum von lateralen GeNWs direkt auf Si Hochleistungs-MOSFETs herstellt. Zhanget al. adressierten, dass ultradünne GeNWs auf Si (001) mit Facetten von {105} [13] exponiert werden, die die niedrigste vorhergesagte Oberflächenenergie aufweisen [14]. Darüber hinaus wurde gezeigt, dass ein verspannter Ge-MOSFET auf einem virtuellen SiGe-Substrat die Lochbeweglichkeit verbessert [1]. Obwohl laterale GeNW auf Si mit Druckspannung wie angenommen eine deutliche Verbesserung des Ladungsträgertransports aufweisen können, lassen sie sich nicht in eine direkte Bandlücke umwandeln. Zur Einführung von Zugspannungen in GeNWs werden GeSn-Legierungen [15] und III-Sb-Verbindungen [16] benötigt, die eine größere Gitterkonstante als die von Ge aufweisen. Obwohl dieses mechanische Verfahren zur Herstellung von einachsig verspannten GeNWs angewendet wurde [17, 18], kann der Komplex dieser Herstellungstechnik kaum für die monolithische Integration in Si-basierter Photonik und Elektronik geeignet sein. Darüber hinaus wird die Belastung in freistehenden NWs leicht freigesetzt, während laterale GeNWs selbst viel hohe Belastung aufnehmen können. Daher sind epitaktisch gewachsene laterale GeNWs mit hoher biaxialer Zugspannung erforderlich, um einen direkten Bandlückenübergang sowie eine Verbesserung der Trägermobilität zu erreichen.

Bis heute haben versetzungsfreie und hoch biaxial zugbelastete Ge-Quantenpunkte auf InP (001) Potenziale für eine direkte Bandlückenemission, simuliert durch die Finite-Elemente-Methode (FEM) gezeigt [19]. In ähnlicher Weise sagen wir in dieser Arbeit theoretisch die Morphologie der exponierten Oberflächen und die Wachstumsrichtung von biaxial zugbelasteten GeNWs auf einem entspannten GaSb-Templat voraus, das direkt auf Si mit einer AlSb-Pufferschicht aufgewachsen werden kann [16, 20]. Wir wählen {110}, {105} und {111} als exponierte Oberflächen lateraler GeNWs und vergleichen die Gesamtenergieänderung im stationären System. Der Einfachheit halber ignorieren wir den Einfluss von Luxation und Fraktur [21] in diesem stark belasteten System. Die auf FEM basierende Simulation zeigt, dass eine kritische Menge an Ge existiert. Unterhalb des kritischen Wertes werden GeNWs durch {105} exponiert, während sie über dem kritischen Wert durch {110} exponiert werden. Fast die gesamte GeNW-Region kann in eine direkte Bandlücke umgewandelt werden, die die Differenz der Leitungsbandminima und der Lichtlochbandmaxima am Γ . ist -Punkt. Außerdem analysieren wir auch qualitativ die Änderung der dehnungsabhängigen effektiven Trägermasse am Γ -zeigen, um indirekt die Verbesserung der Elektronen- und Lochmobilität vorherzusagen.

Methoden

Laterale NWs weisen normalerweise einen dreieckigen Querschnitt auf [22, 23]. Dank der in Abb. 1a gezeigten 1D-Eigenschaft von NW kann ein endliches NW-Modell ähnlich dem von Zhang et al. im ergänzenden Material von Ref. [13] kann für Simulationen verwendet werden, bei denen sowohl Anfangs- als auch Endflächen fixiert sind, wie in Abb. 1b gezeigt. Wegen des Randeffekts diskutieren wir nur den mittleren Teil des NW und nehmen an, dass der Querschnitt dieses Teils die Situation in einem unendlich langen NW darstellt. FEM wird verwendet, um die Verteilung der Zugspannung in GeNW mit 7,7% Gitterfehlanpassung zu GaSb zu simulieren. Wir berechnen das Gesamtsystemenergieinkrement nach Abscheidung der gleichen Menge Ge im stationären Zustand in drei Situationen:(i) [100] Wachstumsrichtung mit {110} Facetten exponiert (Situation A), (ii) [100] Wachstumsrichtung aber mit {105} Facetten exponiert (Situation B) und (iii) [110] Wachstumsrichtung mit {111} Facetten exponiert (Situation C). Die Querschnitte dieser drei Situationen sind in Abb. 1c gezeigt. Die Querschnittsflächen bleiben gleich und repräsentieren gleiche Mengen an Ge.

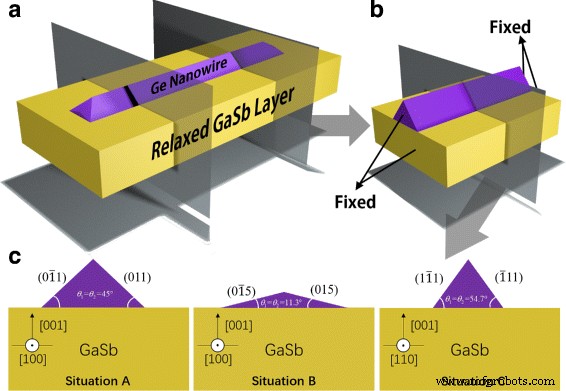
Schemata von GeNW auf GaSb:a 3D-Modell, b vereinfachtes endliches Modell und c Querschnitte von GeNW mit verschiedenen Facetten

Die Gesamtsystemenergieänderung pro Längeneinheit (J/nm) beinhaltet die Gesamtdifferenz der Dehnungsenergie, Oberflächenenergie und Kantenenergie [24] und kann wie folgt angegeben werden:

Der erste Begriff Δ E _{s t r a ich n} stellt die Dehnungsenergiedifferenz des stationären Systems vor und nach der Ge-Abscheidung dar und wird in Volumeneinheiten ausgedrückt,

Ergebnisse und Diskussionen

Wir gehen davon aus, dass das System aufgrund der großen Gitterfehlanpassung von 7,7% zwischen Ge und GaSb anfänglich unter voller Zugspannung steht. Abbildung 2 zeigt die 2D-Restdehnungsverteilung einschließlich Dehnung in der Ebene ε _xx , Schubdehnung ε _xy , und vertikale Dehnung ε _zz der Situation A mit der Basisbreite von w =40 nm zum Beispiel im stationären Zustand nach Relaxation. Die Stammdefinition hier ist (a _Ges −a _Ge )/a _Ge , wobei a _Ges und a _Ge sind Gitterkonstanten von gespanntem bzw. relaxiertem Ge. Wie in Abb. 2a zu sehen ist, ε _xx hat den Maximalwert von ca. 15,4% an zwei basalen Kanten, der viel größer ist als die anfängliche Dehnung, aber von der Kante zur Mitte mit dem Minimalwert von ca. 3,3% stark abfällt. In z -Richtung von unten nach oben von GeNW, ε _xx sinkt auch durch die Lockerung von GeNW. Die Verteilung von ε _zz hat ähnliche Eigenschaften wie ε _xx in Abb. 2b. Im Gegensatz zur biaxialen Dehnung in Ge-Dünnfilmen zeigt Abb. 2c, dass die asymmetrisch verteilte Scherdehnungskomponente von GeNW eine bedeutende Rolle beim direkten Bandlückenübergang spielt. Die Dehnungsverteilung ist in drei Situationen ziemlich ähnlich. Dennoch unterscheiden sich die Werte der Dehnungskomponenten in drei Situationen aufgrund des unterschiedlichen Breiten-Höhen-Verhältnisses (W /H ) durch seine Form induziert. Situation B mit GeNW exponiert durch {105} Oberflächen hat das größte W /H von 10 und zeigt eine hohe Dehnung ähnlich der in der Ge-Dünnschicht. Situation C mit exponierten {111}-Oberflächen zeigt ebenfalls eine hohe Dehnung, da die NW-Wachstumsorientierung entlang der [110] ein unveränderlicher Dehnungswert bleibt, was den Wert von ε . erhöht _xx und ε _yy gleichzeitig. Somit kann die Belastung in der Ebene kaum entspannt werden.

Restspannungsverteilung eines GeNW in Situation A mit der basalen Breite von 40 nm:a x Komponentendehnung ε _xx , b z-Komponentendehnung ε _zz , und c Schubdehnung in x-y-Ebene ε _xy . Die Zickzackform unten bezeichnet die partielle Substratschicht (das Folgende hat die gleiche Bedeutung)

Entsprechend der Dehnungsverteilung kann das Dehnungsenergieinkrement erhalten werden. Wie zuvor besprochen, enthält Situation B das höchste Dehnungsenergie-Inkrement, während Situation A das niedrigste hat. Für die Oberflächenenergieänderung liefert Situation B jedoch mit zunehmender Querschnittsfläche abnehmende negative Werte und die anderen beiden Situationen zeigen sehr ähnliche positive Werte unter derselben Fläche. Das Gesamtenergieinkrement ohne Kantenenergieänderung ist in Fig. 3a gezeigt. Das Ergebnis zeigt, dass es weniger wahrscheinlich ist, dass nur in Situation C GeNWs gebildet werden, da das Energieinkrement nie das niedrigste ist. Es gibt zwei verschiedene Konsequenzen des Energiezuwachses mit der Vergrößerung der Fläche, und die vertikale gestrichelte Linie ist markiert, um den kritischen Wert der Fläche darzustellen, A _c =136,2 nm ² , was die Mengen von Ge bedeutet. Wenn die Fläche weniger als 136,2 nm beträgt ² , GeNWs neigen dazu, die Form in Situation B zu bilden, aber in Situation A, nachdem mehr Ge abgeschieden wurde. Das Berechnungsergebnis sagt voraus, dass zugbelastete GeNWs auf GaSb es vorziehen könnten, hohe W . zu bilden /H Dreiecksform im Querschnitt, wenn eine geringe Menge an Ge abgeschieden wird, während ein niedriges W . gebildet wird /H einmal nach Überschreiten des kritischen Wertes. Abbildung 3b–e zeigt die Verteilungen der hydrostatischen Dehnung und die Summe der Absolutwerte der Scherdehnungskomponenten in Situation A und B unter dem kritischen Bereich. Vergleicht man Situation A mit B, hält trotz dieser Situation A den größeren Maximalwert sowohl der hydrostatischen Dehnung als auch |ε _xy |+|ε _yz |+|ε _xz |, Situation B hat eine größere durchschnittliche hydrostatische Dehnung, aber einen kleineren Durchschnittswert von |ε _xy |+|ε _yz |+|ε _xz |. In der Zwischenzeit zeigt Situation B einen kleinen Unterschied in der räumlichen Verteilung sowohl der hydrostatischen Dehnung als auch |ε _xy |+|ε _yz |+|ε _xz |. Diese Eigenschaften sind denen der Ge-Dünnschicht sehr ähnlich und werden ihrem hohen W . zugeschrieben /H Wert. Als Ergebnis unter Bezugnahme auf Gl. (5) und (6), Situation B weist einen kleineren Wert von Δ . auf E _DT als in Situation A, was zu einer hohen Wahrscheinlichkeit führt, Ge in ein Material mit direkter Bandlücke umzuwandeln.

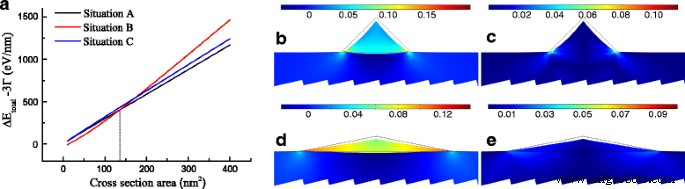
a Die Gesamtenergieänderung ohne die Kantenenergieänderung 3 Γ im Vergleich zur Querschnittsfläche (die gestrichelte Linie ist der kritische Wert der Minima ungefähr 136,2 nm ² in verschiedenen Situationen). b –e hydrostatische Belastung und |ε _xy |+|ε _yz |+|ε _xz | in b , c Situation A und d , e Situation B beim kritischen Wert

Aufgrund der hohen Zugspannung in GeNW kann fast die gesamte Region von GeNW in direkte Bandlücke umgewandelt werden. Abbildung 4a zeigt die Verteilung von Δ E _DT mit zunehmender Größe von GeNW. Der Wert von Δ E _DT fällt in GeNWs von oben nach unten. Interessanterweise ist das Minimum von Δ E _DT befindet sich in Situation B am unteren Rand des Querschnitts, in Situation A jedoch in der unteren Mitte. Der Grund für diese unterschiedliche Verteilung ist, dass die signifikante Schubdehnung am unteren Rand in Situation A mehr zu \(\Delta E_ {c}^{\mathrm {L}}\) als in Situation B. Für GeNW in Situation B unterhalb des kritischen Bereichs ist der Durchschnitt Δ E _DT ist viel niedriger als in Situation A über dem kritischen Bereich, wie in Fig. 4b gezeigt. Am kritischen Punkt ist der Durchschnitt von Δ E _DT steigt plötzlich vom Wert von −0,308 auf −0,137 eV an. Außerdem sind für dieselbe Form die Verteilung und der Durchschnitt von Δ E _DT sind grundsätzlich ähnlich, ohne offensichtlichen Bezug zur Größe. Um die inhärente Beziehung zur Dehnung in GeNW aufzudecken, tragen wir die hydrostatische Dehnungskomponente an der GeNW-Basis mit Basisbreite in Abb. 5 auf. Die Kurven der hydrostatischen Dehnungskomponente mit unterschiedlichen Größen gegenüber der relativen Position der Basis in einem GeNW fast überlappen mit Ausnahme des Unterschieds in der Randregion. Die konsequenten Konsequenzen finden sich in ε _xx und die Summe der absoluten Scherkomponenten. Somit ist der dehnungsinduzierte Wert von Δ E _DT besitzt die identische Verteilung in GeNW mit der gleichen Form.

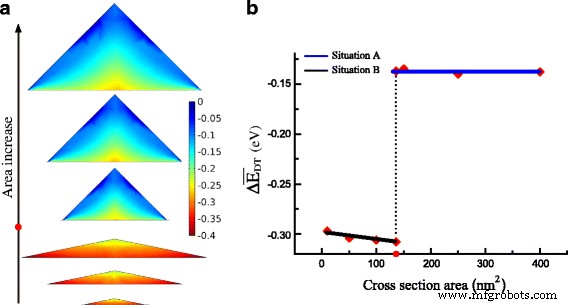
a Die Verteilung von Δ E _DT mit Vergrößerung der Fläche (der Farbbalken bezeichnet den Wert von Δ E _DT ). b Der Durchschnitt von Δ E _DT gegen die Gegend. Der kritische Wert ist mit rotem Punkt gekennzeichnet in der Bereichsachse

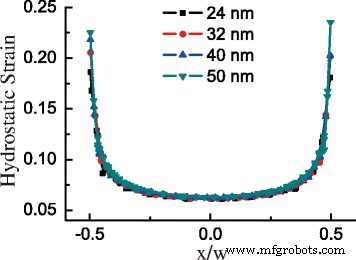
Hydrostatische Dehnungskomponente an der Basis von GeNW vs. x/w mit unterschiedlichen Basalbreiten

Darüber hinaus simulieren wir die dehnungsinduzierte Bandlückenabbildung im Querschnitt des in Abb. 6a gezeigten 40 nm breiten GeNW. Die räumliche Verteilung der Bandlücke wird aus dem variablen Wert der dehnungsabhängigen Bandkanten am Γ . abgeleitet -Punkt. Abbildung 6b zeigt die Bandkantenenergie bei Γ -zeige entlang der z -Richtung des GeNW. Wir stellen fest, dass sich sowohl die Leitungsband- als auch die Valenzbandkanten, einschließlich des leichten Lochbandes und des schweren Lochbandes, in den ersten 15 nm signifikant und dann geringfügig ändern. Die Spitzen des leichten und des schweren Lochbandes trennen sich und neigen dazu, sich mit zunehmender Zugspannung in entgegengesetzte Richtungen zu verschieben. Aus Fig. 6a, b nimmt die Bandlücke in den ersten 15 nm signifikant zu und erreicht etwa 0,30 eV, ändert sich dann geringfügig um einen Wert von 0,24 eV, was die Bandlücke in den meisten GeNW-Regionen ist. Da das Bandmaxima der leichten Löcher höher ist als das des Bandes der schweren Löcher am Γ -Punkt im GeNW, Löcher im Valenzband bevorzugen die Lage an den Maxima des leichten Lochbandes. Somit findet die Elektron-Loch-Rekombination zwischen dem Leitungsbandminimum und dem Leichtlochbandmaximum bei Γ . statt -Punkt, wenn wir die Überlappung der raumabhängigen Elektronen- und Lochwellenfunktionen vernachlässigen. Interessanterweise bewegen sich die Lichtlochbandmaxima sogar über die Leitungsbandminima im Bereich des NW-Bodens, der in Abb. 6a als schwarze Kurve markiert ist, bei einer hydrostatischen Dehnung von mehr als ∼5,0%. Die negative Bandlücke, die wir unter hoher Zugbelastung berechnen, kann komplizierte Folgen haben, wie etwa eine halbmetallische [31] oder invertierte [32] Bandstruktur.

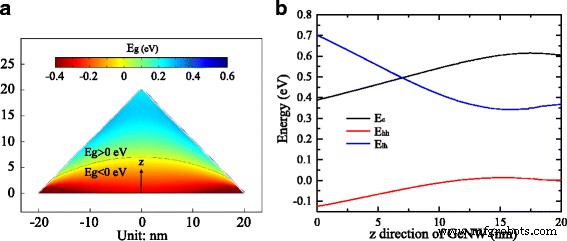
a Die spannungsabhängige Bandlücke im GeNW, verteilt nach Positionen. b Die spannungsabhängigen Bandkantenenergien entlang z Richtung in der GeNW

Schließlich wird die Mobilität von Elektronen und Löchern unter solch einer hohen Zugspannung im GeNW verbessert. Bei relaxiertem Ge wird der Elektronentransport hauptsächlich von im L-Tal beheimateten Elektronen beigesteuert. Wenn Ge unter Zugspannung steht, so dass das Γ -Tal unterhalb des L-Tals liegt, wie in Abb. 3a gezeigt, der Hauptbeitrag des Elektronentransports stammt vom Γ -Schlucht. Andererseits ist die dominierende Beteiligung von Löchern am Transport vom leichten Lochband am Γ -Punkt unter hoher Zugspannung, während das schwere Lochband im entspannten Fall die Valenzbandmaxima einnimmt. Aufgrund der viel kleineren effektiven Elektronenmasse am Γ -Punkt als am L-Punkt, sowie die verringerte effektive Masse von den Bandmaxima der schweren Löcher zu den Bandmaxima der leichten Löcher kann die Beweglichkeit nicht nur von Elektronen, sondern auch von Löchern verbessert werden. Theoretisch kann vorhergesagt werden, dass die Zugspannung die effektive Masse von Elektronen und Löchern am Γ . reduziert -Punkt in einem Quantenpunktmodell von Califeno und Harrison [29]. Obwohl die quantitative Berechnungsmethode für unser NW-Modell ungeeignet ist, gehen wir qualitativ davon aus, dass die Zugspannung die effektive Masse bei k . modifizieren kann =0 durch Erhöhen der Krümmung der Dispersionsrelation für kleine k in der Nähe des Γ -Punkt. Somit kann die Beweglichkeit sowohl von Elektronen als auch von Löchern in zugbelasteten GeNWs verbessert werden. Die sich aufspaltenden Valenzbänder induzieren außerdem eine starke Elektron-Phonon-Kopplung und Intraband-Streuung [33], was die Lochmobilität auf einen geringeren Wert als die Elektronenmobilität begrenzt.

Schlussfolgerungen

Zusammenfassend haben wir zugbelastete GeNWs auf GaSb vorgeschlagen und drei verschiedene Situationen über die Gesamtenergieänderung vor und nach der Ge-Abscheidung verglichen. Das Ergebnis zeigt, dass das GeNW geneigt ist, {105}-Oberflächen entlang der 〈100〉-Wachstumsrichtung vor dem kritischen Betrag zu bilden, während es durch {110}-Oberflächen nach dem kritischen Betrag exponiert ist. Die Restdehnungsfeld- und Bandlückenanalyse hat gezeigt, dass dieselbe Form eine ähnliche Verteilung sowohl in der Dehnung als auch in Δ . aufweist E _DT unabhängig von der Größe. Darüber hinaus nehmen die Belastung in der Ebene und die hydrostatische Belastung nicht nur von den Rändern zur Mitte, sondern auch von unten nach oben in allen Situationen ab. Aufgrund der hohen Zugspannung kann in den beiden möglichen Situationen fast das gesamte GeNW auf GaSb in ein direktes Bandgap-Material umgewandelt werden. Außerdem nehmen die leichten Löcher hauptsächlich an der Elektron-Loch-Rekombination und dem elektrischen Transport am Γ . teil -Punkt, weil die Maxima des leichten Lochbandes bei hoher Zugspannung zu den Maxima des Valenzbandes werden. Die Beweglichkeit nicht nur von Elektronen, sondern auch von Löchern kann aufgrund der Abnahme der effektiven Ladungsmasse am Γ . erhöht werden -Punkt bestimmt durch die Zugspannung. Die theoretisch vorhergesagte attraktive Leistung impliziert, dass zugbelastete GeNWs vielversprechend für die Optoelektronik als Lichtquelle und Mikroelektronik für Hochgeschwindigkeitsbauelemente in der Si-Photonik bzw. in der Elektronik sind.