Design von Strain-Engineered GeSn/GeSiSn-Quantenpunkten für direkte Bandlückenemission im mittleren IR-Bereich auf Si-Substrat

Hintergrund

Kürzlich hat die Demonstration von Materialien der Gruppe IV mit direkter Bandlücke durch das Legieren von Ge [1, 2] und SiGe [3, 4] mit Zinn zu intensiven Forschungsaktivitäten geführt, da die realen und praktisch umsetzbaren Möglichkeiten für Photonik und Elektronik effizienten On-Chip Integration. Tatsächlich hat sich gezeigt, dass die GeSn-Legierung eine direkte Bandlücke jenseits einer bestimmten Zusammensetzung durch die schnellere Abnahme von Γ im Vergleich zum L-Tal aufweist [5,6,7,8]. Obwohl die berichteten Ergebnisse sehr ermutigend sind, sind die Materialeigenschaften und Anwendungsmöglichkeiten noch nicht vollständig erforscht. Tatsächlich umfasst der tatsächlich verfügbare Hauptweg zur Erhöhung der Betriebswellenlänge von GeSn-basierten Halbleiterlasern in Richtung des Atmosphärentransparenzfensters, das sich mit absorbierenden Linien verschiedener Gase überlappt [9], die Erhöhung des Sn-Gehalts in den GeSn-Schichten [10, 11 ]. Aufgrund der großen Gitterfehlanpassung zwischen Ge und Sn (14 %) erscheint jedoch die Erhaltung der kristallographischen Qualität des Materials als die größte Herausforderung, die dieses Ziel verhindert [12, 13]. Eine potenziell interessante Lösung, um die Emissionswellenlänge zu erhöhen und eine bessere Trägereingrenzung zu gewährleisten, beruht auf niederdimensionalen Strukturen wie Nanodrähten [14,15,16], Nanostäben [17] und Quantenpunkten [18]. Innerhalb der spezifischen Direktheitskriterien ist die direkte Bandlücken-Interband-Emissionswellenlänge theoretisch auf 4,3 μm begrenzt [19]. Um diese Einschränkungen zu überwinden, ist es notwendig, einen zusätzlichen Freiheitsgrad in die Konzeption von Gruppe-IV-basierten Quantenstrukturen einzuführen. Dies kann durch die Verwendung einer ternären GeSiSn-Schicht [20,21,22] als umgebendes Material für GeSn-Quantenpunkte (QD) gewährleistet werden, die die Möglichkeit des Strain Engineering durch Einbau geeigneter Si- und Sn-Zusammensetzungen bietet. Dementsprechend wird erwartet, dass die Verwendung einer GeSiSn-Verspannungsschicht um die GeSn-QD einen größeren Bereich zugänglicher direkter Bandlücken-Emissionswellenlängen bietet.

In diesem Zusammenhang berichten wir über die theoretische Untersuchung des Effekts von Strain Engineering durch Variation der Sn-Zusammensetzung in der GeSiSn-Schicht, die die GeSn-QD umgibt, auf die direkte Bandlücken-Zwischenband-Emissionswellenlänge.

Methoden

Da die Bandverschiebungen zwischen binären und ternären Sn-haltigen Legierungen der Gruppe IV und Ge experimentell nicht bekannt sind, wird die relative Bandausrichtung zwischen den verschiedenen an dieser Arbeit beteiligten Halbleitern der Gruppe IV in Bezug auf die Valenzbandkante von Ge bewertet. unter Verwendung der vereinfachten Theorie der Bandverschiebungen von Jaros [23], wie von D'Costa et al. [24]. Die Spannungseffekte, die aus der Gitterfehlanpassung zwischen Ge-Substrat und GeSiSn-Schicht und zwischen der GeSn-QD und dem umgebenden GeSiSn-Material resultieren, wurden für die Leitungs- und Valenzbandkanten untersucht.

Tatsächlich ist die Leitungsbandkante um \(\delta{E}_c^i\) und die des Valenzbandes um δE . verschoben _v wie in Gl. (1) und (2):

wo ich bezeichnet L- oder Γ-Tal, a _c und a _v sind das Leitungs- bzw. Valenzbanddeformationspotential und b ist das Schubverformungspotential. \( {\varepsilon}_{xx}={\varepsilon}_{yy}=\varepsilon =\left(\frac{a_s-{a}_{\mathrm{l}}}{a_{\mathrm{l }}}\right) \) ist die Dehnung im Plan und \( {\varepsilon}_{zz}=-2\frac{C_{12}}{C_{11}}{\varepsilon}_{xx} \) ist die Dehnung in Wachstumsrichtung. a _s und a _l sind jeweils der Gitterparameter des Substrats und der verspannten Schicht. C ₁₁ und C ₁₂ sind die Steifigkeitskonstanten.

Die binären und ternären Legierungsmaterialparameter werden aus denen von Ge, Si und Sn durch lineare Interpolation abgeleitet. Diese Parameter stammen aus Referenz [11].

Die zusammensetzungsabhängigen gedehnten Bandlücken können bewertet werden, indem die entsprechenden spannungserzeugten Energieverschiebungen zu der in Gl. (3) für GeSn und Gl. (4) für GeSiSn:

wo b ist der entsprechende Bandgap-Bowing-Parameter der binären Legierungen, die in Tabelle 1 zusammengefasst sind.

Um die eingeschlossenen Zustände der Träger zu bestimmen und die Übergangsenergien zwischen den Bändern abzuleiten, wurde die Schrödinger-Gleichung der effektiven Einzelbandmasse in kartesischen Koordinaten durch die Finite-Elemente-Methode gelöst, die von der COMSOL Multiphysics-Software bereitgestellt wird [25]:

E stellt die Energie des Trägers dar und ψ ist die entsprechende Wellenfunktion. m* ist die effektive Masse des Trägers, ћ ist die reduzierte Planck-Konstante, \( \overrightarrow{r} \) ist der dreidimensionale Koordinatenvektor und V ist das Begrenzungspotential des Trägers (Banddiskontinuität). Um das Berechnungsverfahren der elektronischen QD-Struktur zu vereinfachen, haben wir die Constant-Strain-Approximation [26, 27] anstelle des rechenaufwendigen atomaren Simulationsansatzes verwendet, der offensichtlich mehr Präzision im Dehnungsverteilungsprofil liefern könnte [28, 29]. Tatsächlich halten wir das Ladungsträger-Begrenzungspotential in der kompressionsverspannten QD für ausreichend tief, um den Einfluss der Spannungsungleichförmigkeit auf die elektronenbegrenzten Zustände zu minimieren [27]. Darüber hinaus werden die Leitungsbandkanten, die die wichtigsten Parameter in dieser Arbeit sind, die es ermöglichen, die Bandlückendirektheit zu untersuchen, nur dadurch verschoben, dass die hydrostatische Dehnung weniger empfindlich auf die Dehnungsungleichmäßigkeit ist, insbesondere wenn eine relativ geringe Gitterfehlanpassung berücksichtigt wird [30].

Ergebnisse und Diskussion

Da uns hauptsächlich der Einfluss der Spannung um das GeSn-QD herum interessiert, wird die Sn-Zusammensetzung des QD auf 28% und die Si-Zusammensetzung des GeSiSn auf 35% festgelegt; die studie konzentriert sich daher auf die auswirkungen der zusammensetzung der sn-barriere (x _b ) Schwankung zwischen 6 und 22 %. Die resultierende Dehnung im Plan entweder in der GeSiSn-Schicht oder in der GeSn-QD ist in Abb. 1a angegeben.

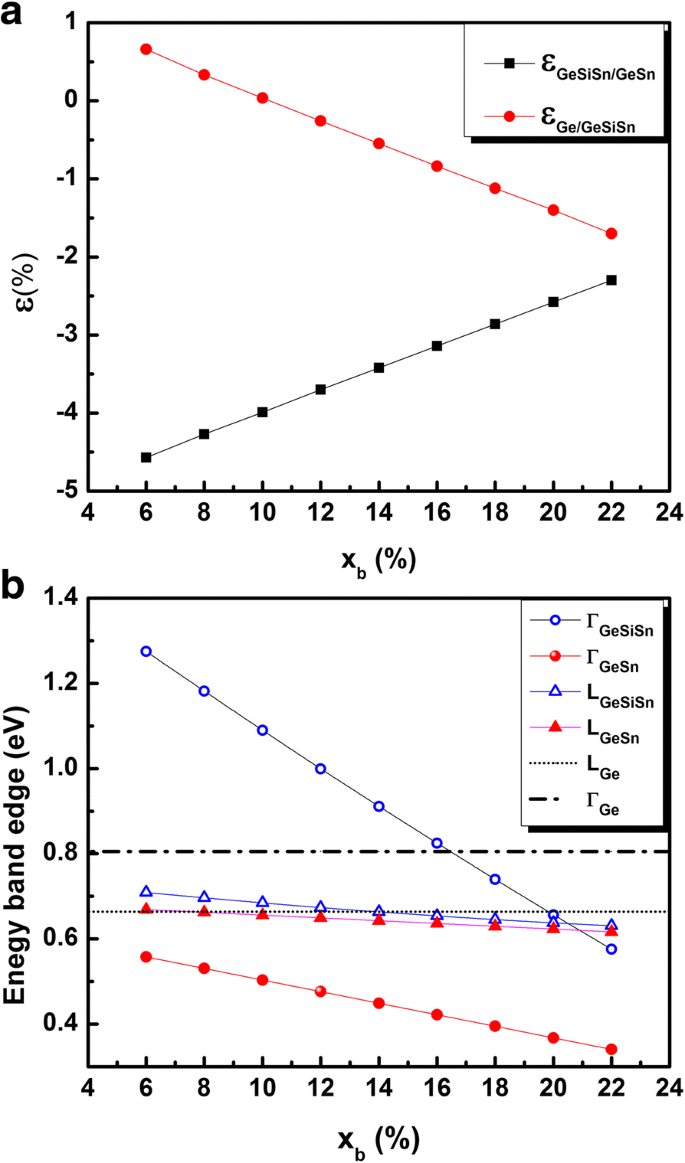
a Gitterfehlanpassung zwischen Ge_0.65-xb Si_0,35 Sn _xb und Ge (ausgefüllte Kreise) und zwischen Ge_0,72 Sn_0,28 und Ge_0.65-xb Si_0,35 Sn _xb (gefüllte Quadrate) als Funktion von x _{b .} b Bandkanten in L- und G-Tälern für Ge_0.65-xb Si_0,35 Sn _xb , Ge_0,72 Sn_0,28 , und Ge als Funktion von x _b

Die Dehnung in der Ebene in der zweidimensionalen Schicht aus GeSiSn-Material variiert zwischen 0,6% (x _b = 6%) und − 1,7% (x _b = 22%). Wir nehmen an, dass diese Schicht pseudomeorphisch gespannt bleibt, wodurch die entworfene Struktur experimentell realisierbar bleibt. Das GeSn wird so gewählt, dass es innerhalb des umgebenden GeSiSn-Materials mit einer Gitterfehlanpassung im Bereich von − 2,3 bis − 4,5% kompressiv verspannt wird, wodurch günstige Bedingungen für die Bildung von selbstorganisiertem GeSn-QD gewährleistet werden.

Abbildung 1b zeigt die Abhängigkeit der gespannten Bandlücke an den Punkten L und Γ von Ge_0.72 Sn_0,28 und Ge_{(0.65-xb )} Si_0,35 Sn _xb als Funktion von x _b . Das Γ-Tal von Ge_0.72 Sn_0,28 Material bleibt unterhalb der L-Täler, was seinen Typ I für den gesamten untersuchten Bereich der Zinn-Barriere-Zusammensetzung bezeugt. Unter Berücksichtigung des Elektroneneinschlusses nimmt die effektive Bandlücke zu und der QD-Größeneffekt wird entscheidend [18] insbesondere für hoch gespannte QD. Tatsächlich sollte bei Quanteneinschluss die Grundzustandsenergie anstelle des Minimums des Γ-Bandes berücksichtigt werden. Dementsprechend wird erwartet, dass QD mit kleinerer Größe höhere begrenzte Energieniveaus im -Tal haben, die das L-Tal (und/oder Grundzustandselektronenenergieniveau im L-Tal) überschreiten können. Daher ist es wichtig, den Bereich der QD-Größe unter Einhaltung der spezifischen Direktheitskriterien zu untersuchen.

Die modellierte Struktur ist in Abb. 2 schematisch dargestellt. Die Ge_0.72 Sn_0,28 QD hat eine Kuppelform mit einer kreisförmigen Basis des Durchmessers D im Bereich von 15 bis 40 nm und einem festen Verhältnis von Höhe zu Durchmesser von 0,25. Der QD ist innerhalb einer 15 nm dicken GeSiSn-Schicht mit einer Si-Zusammensetzung von 35% und einer abstimmbaren Sn-Zusammensetzung positioniert. Diese Struktur soll auf einem Ge-gepufferten Substrat gebildet und mit einer Ge-Schicht bedeckt werden.

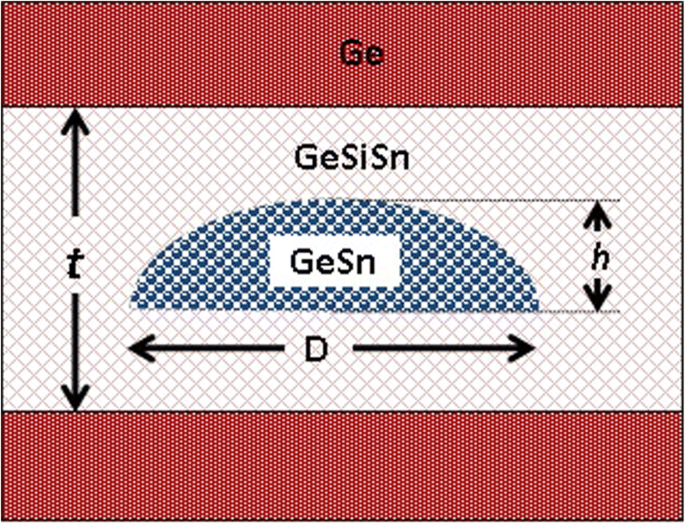
Schematische Darstellung des modellierten GeSn QD der Höhe (h ) und Durchmesser (D ) innerhalb einer spannungsreduzierenden GeSiSn-Schicht in einer Ge-Matrix

Um ein konsistentes QD-Design für einen besseren Betrieb der lichtemittierenden Vorrichtung zu gewährleisten, wurde ein geeigneter Direktheitsparameter eingeführt, der den Energieabstand zwischen der niedrigsten QD-begrenzten Energieniveauposition in L- und G-Tälern berücksichtigt [18]. Dieser Parameter wird mit GS_L . bezeichnet -GS_Γ und sollte höher als die Wärmeenergie bei Raumtemperatur sein, um den Verlust von Ladungsträgern durch thermische Aktivierung zu vermeiden, wobei GS_L (GS_Γ ) repräsentiert das Energieniveau des Grundzustands der Elektronen im L-Tal (Γ-Tal) in Bezug auf das Valenzbandmaximum. Die Bewertung von GS_L -GS_Γ ist im Einschub von Fig. 3 schematisch dargestellt.

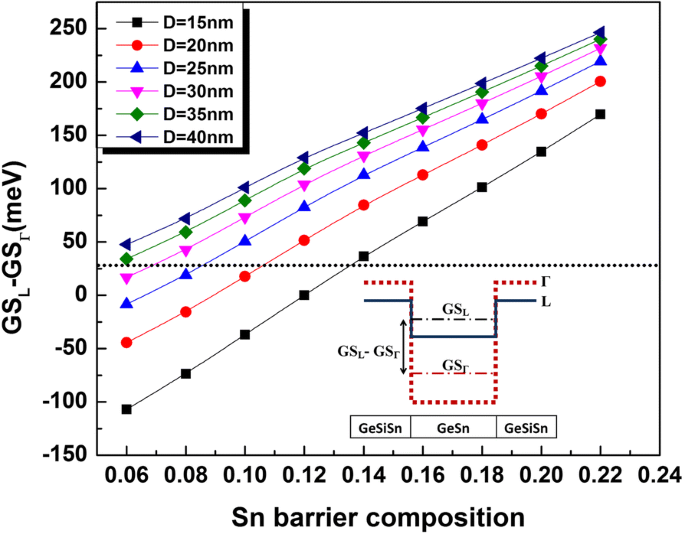
Direktheitsparameter (GS_L -GS_Γ ) Variation als Funktion von Ge_0,72 Sn_0,28 QD-Größe und Sn-Zusammensetzung von Ge_0.65-x Si_0,35 Sn _x umgebende Schicht. Die gestrichelte Linie gibt die Wärmeenergie bei Raumtemperatur an. Der Einschub stellt eine schematische Definition des Direktheitsparameters dar.

Die Berechnung der GeSn-QD-Elektronenenergieniveaus in Γ- und L-Tälern für verschiedene Durchmesser in Abhängigkeit von der Sn-Zusammensetzung in GeSiSn ermöglicht es, den entsprechenden Direktheitsparameter (GS_L -GS_Γ ). Die Ergebnisse sind in Abb. 3 aufgetragen. Für ein gegebenes x _b , der Wert von GS_L -GS_Γ wird hauptsächlich durch die QD-Größe bestimmt. Dementsprechend erfordern die kleineren Punkte mit offensichtlich höheren eingeschlossenen Energiezuständen eine niedrigere Bandlückenenergie durch Dehnungsverringerung, um die Direktheitskriterien zu erfüllen. Wie in Abb. 3 gezeigt, sind größere Punkte (D> 25 nm) erfüllen GS_L -GS_Γ> 26 meV für x _b höher als 8%. Für höhere Werte von x . wurde jedoch festgestellt, dass eine effiziente direkte Bandlücke von QD mit kleiner Größe gewährleistet ist _b (x _b ≥ 14 % für D = 15 nm).

Innerhalb der in dieser Arbeit angenommenen Parameter, und insbesondere der Biegeparameter der binären Materialien, reduziert die Erhöhung des Sn-Gehalts des GeSiSn-Materials die Verfärbung um die QD herum und verringert auch die umgebende Materialbandlücke. Tatsächlich ist, wie in Abb. 1b gezeigt, der Anstieg von x _b von 6 auf 22% reduziert die Leitungsbanddiskontinuität im Γ-Tal von 0,72 eV auf 0,23 eV. Tatsächlich ist, wie in Abb. 4 gezeigt, die quadratische Wellenfunktion \({\left|\uppsi\left(\overrightarrow{r}\right)\right|}^2\) des Grundzustandselektrons in Quantenpunkten von Durchmesser 35 nm ist im xy-Plan für eine Sn-Barrierezusammensetzung von 6 % und 22 % gezeigt, die Elektronen sind unabhängig von der Barrierezusammensetzung (Diskontinuität des Leitungsbandes) vollständig innerhalb der QD lokalisiert. Die stark eingeschlossenen Elektronen weisen auf eine höhere Zuverlässigkeit des untersuchten QD als aktives Medium für Lichtemitter auf Si-Substrat hin.

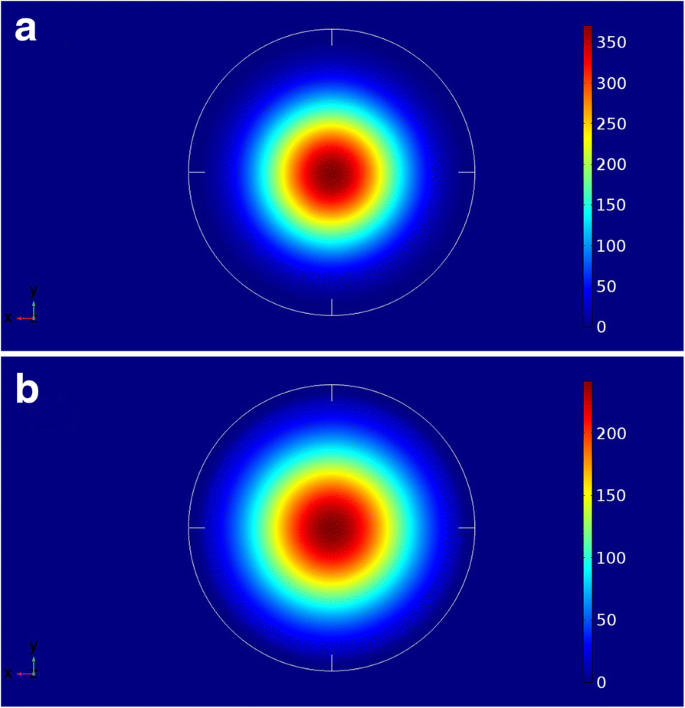
Quadratische Elektronen-Grundzustands-Wellenfunktion für Ge_0,72 . mit einem Durchmesser von 35 nm Sn_0,28 QD für a Xb = 6 % und b Xb = 22%

Durch Begrenzung der QD-Größen für ein gegebenes x _b für diejenigen, die eine effiziente direkte Bandlückenemission erzeugen, haben wir die QD-Grundzustands-Interband-Emissionswellenlänge abgeschätzt. Die Ergebnisse sind in Abb. 5 dargestellt, in der die Emissionswellenlänge gegen x . aufgetragen ist _b für verschiedene QD-Größen. Es ist erwähnenswert, dass die größte in dieser Arbeit betrachtete QD-Größe (D = 40 nm) hat einen geringen Energieabstand zwischen dem Elektronengrundzustand und dem ersten angeregten Zustand (unter 26 meV) gezeigt und wurde daher in dieser Studie ignoriert. Die ausgewertete Emissionswellenlänge als Funktion von x _b wurde in Abb. 5 mit einer gestrichelten Linie gehalten.

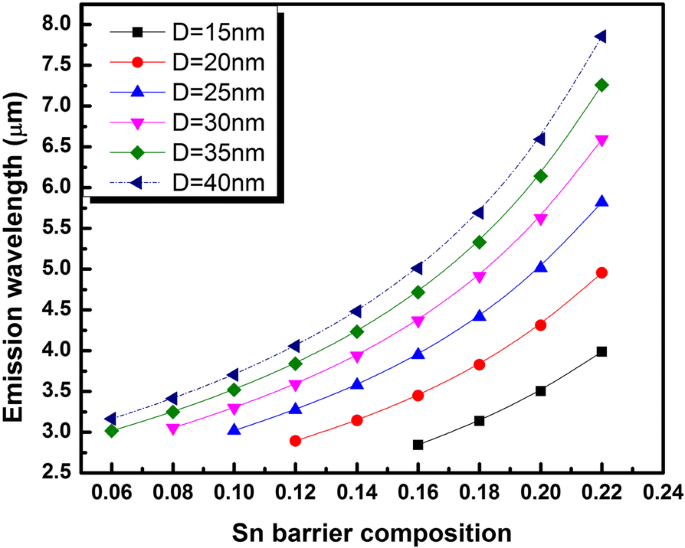
Grundzustandsemissionswellenlänge bei Raumtemperatur von der direkten Bandlücke Ge_0,72 Sn_0,28 QD als Funktion von Größe und Sn-Zusammensetzung des Ge_0.65-xb Si_0,35 Sn _xb umgebende Schicht

Der Wellenlängenbereich, der durch das vorgeschlagene QD-Design abgedeckt werden soll, reicht von 3 bis 7 μm. Der abgegebene Bereich ist für Gassensoranwendungen äußerst wichtig. Die experimentelle Implementierung dieser Struktur könnte zum ersten Mal die Möglichkeit bieten, den gesamten mittleren IR-Bereich mit einem vollständig kompatiblen Material mit bestehender Mikroelektronik-Technologie abzudecken, was den Weg zu neuen Perspektiven in der CMOS-kompatiblen QD-basierten Mid-IR-Optoelektronik ebnet.

Schlussfolgerungen

GeSn-QD in GeSiSn-Strain-Engineering-Schichten auf Ge-Matrix wurden als Funktion der QD-Größe und der Gitterfehlanpassung mit dem umgebenden Material untersucht. Es wurde festgestellt, dass die Verringerung der Spannung um den GeSn-QD durch Variieren der Sn-Zusammensetzung des GeSiSn-Barrierematerials die Emissionswellenlänge vom Typ I mit direkter Bandlücke von 3 auf 7 μm erhöht. Die entworfene Struktur eröffnet neue Perspektiven für Lichtemitter im mittleren IR-Bereich, die vollständig mit der Si-Technologie kompatibel sind.

Abkürzungen

CMOS:

Komplementärer Metalloxid-Halbleiter

GS_L :

Grundzustandselektronenniveau im L-Tal

GS_Γ :

Grundzustandselektronenniveau im Γ-Tal

QD:

Quantenpunkte