Entwicklung der Kontaktfläche bei Normallast für raue Oberflächen:von atomaren zu makroskopischen Skalen

Hintergrund

Die meisten makroskopischen Oberflächen gelten als rau und fraktal [1, 2]. Das Kontaktverhalten zwischen rauen Oberflächen ist viel komplizierter als das von vollkommen glatten Oberflächen [3, 4]. Die reale Kontaktfläche wird durch ein großes Ensemble diskreter Kontaktbereiche (Cluster) gebildet, das viel kleiner ist als die scheinbare Oberfläche. Die Normalkraft und die Größe, Form und Verteilung der Kontaktcluster sind der Schlüssel zur Aufdeckung des Kontaktverhaltens, das für die folgenden Reibungsstudien von wesentlicher Bedeutung ist [5,6,7].

Um den Zusammenhang zwischen Kontaktfläche und Belastung zu ermitteln, wurden seit den 1960er Jahren zahlreiche Modelle vorgeschlagen [1, 8,9,10,11,12,13,14]. Unter ihnen ist das Asperity-Modell das einfachste und beliebteste. In einer der frühen Anwendungen des Unebenheitsmodells beschreiben Greenwood und Williamson [8] die Rauheit der Kontaktgrenzfläche unter der Annahme, dass Unebenheiten dieselben Radien, aber unterschiedliche Höhen aufweisen. Seitdem hat sich das Asperity-Modell durchgesetzt und es ist eine Vielzahl von Literatur auf diesem Gebiet erschienen. Whitehouse und Archard [15] entwickelten das Modell von Greenwood und Williamson (G-W), indem sie die zufälligen Krümmungsradien der Unebenheitsspitzen berücksichtigten. Nayak [16,17,18] führte die Techniken der Random-Process-Theorie [19, 20] in die Analyse der Gaußschen Rauheit ein, die später von Bush et al. [9] bei Kontakt mit rauer Oberfläche.

Eine der Grundannahmen im Unebenheitsmodell ist, dass die Wechselwirkung zwischen den Unebenheiten vernachlässigt werden kann, was darauf hindeutet, dass die potentiellen Kontaktunebenheiten durch die Oberflächengeometrie im Voraus bestimmt werden können. Diese Annahme kann jedoch zu ungenauen Schätzungen der Kontaktkraft und Kontaktfläche führen. Um die Evolution der sich berührenden Cluster und die Wechselwirkung zwischen ihnen zu ermitteln, verwenden wir die molekulare Dynamik der Greenschen Funktion (GFMD) [21,22,23], um die fraktale raue Oberfläche zu untersuchen.

Diese Arbeit soll die Lücke zwischen der atomaren und der makroskopischen Skala für normales Kontaktverhalten schließen. Die Entwicklung der Kontaktfläche von atomaren zu makroskopischen Skalen wird an numerischen Beispielen unter Berücksichtigung der Rauheitswechselwirkungen demonstriert. In der anschließenden Diskussion stellen wir zunächst kurz unsere Ansätze für die fraktale Oberflächengenerierung, das GFMD-Modell, den Contacting-Cluster-Detektionsalgorithmus und das numerische experimentelle Design vor. Anschließend konzentrieren wir uns auf die Bildung und Entwicklung des Kontaktierungsclusters und den Einfluss dieser Prozesse auf das Verhalten der Schnittstelle.

Methoden

Erzeugung rauer fraktaler Oberflächen

Um das Kontaktverhalten der rauen Oberfläche zu untersuchen, müssen wir die Oberfläche für das numerische Modell generieren. Für fraktale Oberflächen wurden mehrere Algorithmen verwendet [24]. In dieser Arbeit verwenden wir die Fourier-Transformationsmethode, um fraktale raue Oberflächen zu erzeugen, wie in Abb. 1 zu sehen. Vier Parameter sind erforderlich, um die fraktale raue Oberflächengeometrie zu bestimmen. Dies sind die maximalen Frequenzen (w _H ), die Mindestfrequenz (w _L ), der Hurst-Exponent (H ) und die Standardabweichung der Amplitude (P ). Die grundlegenden statistischen Parameter der Oberfläche, wie RMS (root mean square) Höhe \( \left(\sqrt{M_0}\right) \), RMS-Steigung \( \left(\sqrt{M_2}\right) \) _, und RMS-Krümmung \( \left(\sqrt{M_4}\right) \), sind die Schlüsselparameter für das Verhalten der Schnittstelle, wobei M _ich ist das i Radialmoment des Oberflächenspektrums [19, 20]. Es ist erwähnenswert, dass der statistische Oberflächenparameter M _ich bezieht sich auf die statistischen Profilparameter m _ich durch die folgende Gleichung:\( {M}_0={m}_0,{M}_2=2{m}_2,{M}_4=\frac{4}{3}{m}_4\). Es ist bekannt, dass die Unebenheitsdichte n (Oberflächengipfel oder -täler) können durch die folgende Gleichung bestimmt werden:

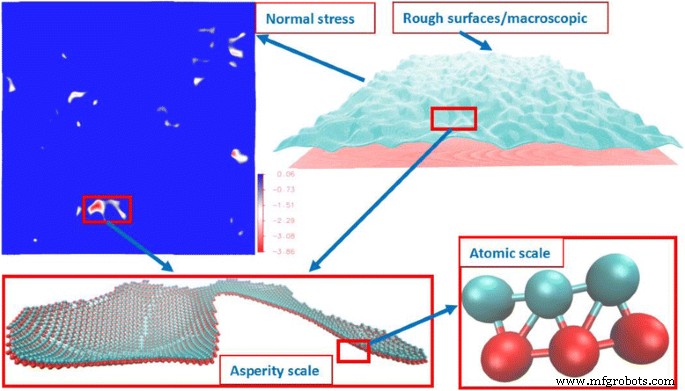
Das GFMD-Modell auf verschiedenen Skalen, von atomarer bis makroskopischer Skala (in σ )

Zusätzlich ist die Gesamthöhe der Gipfel/Talzahl N wird ausgedrückt durch

wo A ₀ ist die scheinbare Oberfläche. Für die selbstaffine fraktale Oberfläche beziehen sich die statistischen Oberflächenparameter auf die Eingabeparameter (w , H , P ) durch die folgende Gleichung:

wo B ist die Oberflächenrauheitskonstante, die sich auf P . bezieht . Gleichungen (3) und (2) zeigen, dass die Gipfel-/Talzahl der fraktalen Oberfläche von der Wellenlänge und dem Hurst-Exponenten abhängt. Ausführliche Diskussionen zu den statistischen Eigenschaften fraktaler Oberflächen finden sich in der Literatur [25, 26].

Im Fourier-Transformationsalgorithmus setzen wir als typisches Beispiel die Hurst-Komponente auf H = 0.5, die maximale Frequenz darf w . sein _L = 1/(24σ ), muss die Mindestfrequenz w . sein _H = 1/(256σ ), beträgt die Standardabweichung der Frequenzamplitude P = 0,69, und die Systemgröße soll 512 × 512 Atome betragen (mit einem Anfangsabstand von 1,12σ ). Diese Eingabeparameter erzeugen anschließend die Fläche mit den folgenden statistischen Parametern:Fläche RMS Steigung \( \sqrt{M_2}=0,077 \) und RMS Krümmung \( \sqrt{M_4}=0,0077 \) . Die Gesamtzahl der Oberflächengipfel/-täler beträgt 150 nach Gl. (2), während durch numerisches Zählen die Oberflächengipfelnummer 158 und die Talnummer 159 beträgt. Der Fehler liegt innerhalb von 5%, was darauf hindeutet, dass die Systemgröße im statistischen Sinne akzeptabel ist. Wenn wir die Systemgröße auf 2048 × 2048 Atome erhöhen (mit einem anfänglichen Abstand von 1,12σ ), stimmen die Ergebnisse für die statistischen Parameter mit denen des kleineren Systems überein.

GFMD-Modell

Die Inter-Partikel-Wechselwirkung ist experimentell sehr schwer zu erfassen [6, 27]. Kürzlich wurde Molekulardynamik verwendet, um die Wechselwirkung zwischen Partikeln zu simulieren, mit dem Ziel, die molekularen Ursprünge des Kontakt-/Reibungsmechanismus zu untersuchen. Allerdings ist der Rechenaufwand für groß angelegte Molekulardynamiksimulationen beträchtlich hoch. Daher wird GFMD aufgrund seiner hohen Effizienz eingeführt, um die Oberfläche zu simulieren. GFMD verwendet Molekulardynamik, um die Wechselwirkung der Atome der Grenzfläche (hier zwei Schichten) zu simulieren, während die Nicht-Grenzflächen-Schicht, die normalerweise elastisches Verhalten zeigt, durch die Green-Funktion simuliert wird. Somit reduziert es das große Atomsystem auf zweischichtige Atome an der Grenzfläche (wie in Abb. 1 zu sehen), was den Rechenaufwand drastisch reduziert. Ausführliche Diskussionen zu GFMD sind in der Literatur zu finden [21,22,23, 28]. Im GFMD-Modell wird das Lennard-Jones (LJ)-Potential verwendet, um die Inter-Partikel-Wechselwirkung zu simulieren. Die Gleichung wird geschrieben als

wo ε ist die Tiefe des Potentialtopfes, σ ist der endliche Abstand, bei dem das Zwischenteilchenpotential Null ist, und r ist der Abstand zwischen den Teilchen. Wir nehmen ε , σ , und ε /σ als Energie-, Distanz- und Krafteinheit. Nach dem LJ-Potenzial wissen wir, dass wenn r = 2 ^1/6 σ ≈ 1.12σ , ist die Kraft zwischen den Teilchen null. Wenn r> 1.12σ , die Kraft zwischen den Teilchen ist anziehend; wenn r < 1.12σ , ist die Kraft zwischen den Teilchen abstoßend. Da wir in dieser Arbeit die Adhäsion nicht berücksichtigen, wird der Cutoff-Abstand auf 1,12σ . eingestellt . Die für die Atomschicht verwendete Kristallstruktur ist kubisch flächenzentriert (FCC). Aus Symmetriegründen verwenden wir nur die Schicht der Grenzfläche, um die Oberflächengeometrie zu bilden, wie in Abb. 1 gezeigt, und der elastische Block unter der flachen Oberfläche wird durch die Green-Funktion simuliert.

Clustererkennungsmethode kontaktieren

In der Grenzfläche werden drei Skalen beobachtet, wie in Abb. 1 zu sehen:(1) atomare Skala, die durch das LJ-Potential simuliert wird; (2) Unebenheitsskala, die der Gruppeneffekt von Kontaktatomen ist; und (3) makroskopischer Maßstab, der der Gruppeneffekt von Kontaktclustern ist. Größe, Form, Lage und Verteilung der Kontaktcluster sind die kritische Brücke zwischen molekularem Verhalten und Grenzflächeneigenschaften. Auf der Nanoskala ist die atomare Kontaktregion schwer zu definieren [6]. Wir definieren hier ein Kontaktatom durch seine Normalkraftkomponente fz > 0 Anschließend werden die verbundenen Kontaktatome als Kontaktcluster definiert. Die Markierungstechnik [29, 30] wird verwendet, um den Kontaktierungscluster zu durchsuchen. Hier verwenden wir einen modifizierten Algorithmus zur Beschleunigung, der den rekursiven Suchprozess vermeidet. Das Flussdiagramm des Algorithmus ist in Abb. 2 dargestellt, in der Atomkraftdaten aus der Molekulardynamiksimulation der Greenschen Funktion extrahiert werden. Der Algorithmus ist wie folgt in acht Schlüsselschritte unterteilt.

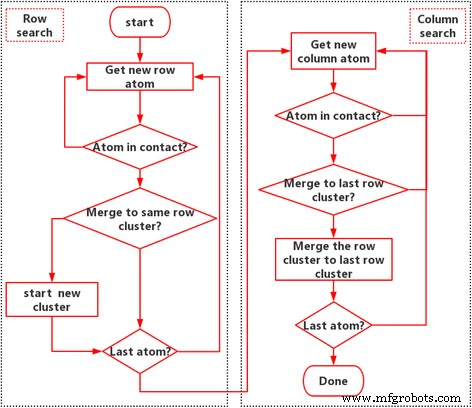
Algorithmus zur Erkennung von Kontaktclustern:die Kennzeichnungstechnik

Schritt 1. Starten Sie die Zeilensuche und rufen Sie die neuen Atomdaten ab, dh durchsuchen Sie die Atome von Zeile zu Zeile.

Schritt 2. Stellen Sie fest, ob das Atom Kontakt hat. Wenn es keinen Kontakt hat, gehen Sie zurück zu Schritt 1. Wenn es Kontakt hat, fahren Sie mit dem nächsten Schritt fort.

Schritt 3. Vergleichen Sie das aktuelle Atom mit dem vorherigen Atom in derselben Reihe. Wenn das vorherige Atom auch in Kontakt ist, füge das Atom zu dem Cluster zusammen, zu dem das vorherige Atom gehört, und beschrifte das Atom dann mit der gleichen Nummer wie das vorherige Atom. Wenn das vorherige Atom keinen Kontakt hat, beschrifte das Atom mit einer neuen Zahl, die der vorherigen Zahl plus eins entspricht.

Schritt 4. Bestimmen Sie, ob es das letzte Atom ist; wenn nicht, gehen Sie zurück zu Schritt 1 oder gehen Sie zum Spaltensuchprozess.

Schritt 5. Starten Sie die Spaltensuche und rufen Sie die neuen Atomdaten ab, dh durchsuchen Sie die Atome von Spalte zu Spalte.

Schritt 6. Stellen Sie fest, ob das Atom Kontakt hat. Wenn es keinen Kontakt hat, gehen Sie zurück zu Schritt 5. Wenn es Kontakt hat, fahren Sie mit dem nächsten Schritt fort.

Schritt 7. Vergleichen Sie das aktuelle Atom mit dem vorherigen Atom in derselben Spalte. Wenn das vorherige Atom auch in Kontakt ist und zu einem anderen Cluster gehört, fügen Sie den aktuellen Cluster in den Cluster ein, zu dem das vorherige Atom gehört, beschriften Sie die Atome dann mit der gleichen Nummer und speichern Sie sie. Wenn das vorherige Atom keinen Kontakt hat oder zu demselben Cluster gehört, fahren Sie mit dem nächsten Schritt fort.

Schritt 8. Bestimmen Sie, ob das aktuelle Atom das letzte Atom ist; wenn nicht, gehen Sie zurück zu Schritt 5 oder der Suchvorgang ist abgeschlossen.

Numerisches experimentelles Design

Es ist bekannt, dass das Problem des Kontakts zweier rauher Oberflächen als ein Problem mit einer starren rauen Verbundoberfläche und einer flachen elastischen Oberfläche vereinfacht werden kann, indem der äquivalente Elastizitätsmodul E* . eingeführt wird , die geschrieben wird als

wo E ₁ und E ₂ sind der Elastizitätsmodul der oberen Fläche bzw. der unteren Fläche. Der Einfachheit halber betrachten wir eine starre raue Oberfläche in Kontakt mit einer elastischen glatten Oberfläche und untersuchen dann die Bildung und Entwicklung des kontaktierenden Clusters und sein Kraft-Flächen-Verhalten. In der folgenden Diskussion verwenden wir die oben erzeugte Oberfläche (die obere Oberfläche ist starr und rau (E ₁ = ∞), und die Unterseite ist glatt und elastisch (E ₂ = 3ε /σ ³ )) um das Kontaktverhalten zu untersuchen, wobei beide von v ₁ und v ₂ sind auf 0,5 eingestellt. Unsere Systemgröße beträgt 512 × 512 Atome (mit einem Anfangsabstand von 1,12σ ) und periodische Randbedingungen werden im x . verwendet -y Flugzeug. Die Tiefe des elastischen Blocks wird auf 1024 Atomlagen eingestellt (mit einem anfänglichen Abstand von 1,12σ ). In einer regulären Molekulardynamiksimulation besteht das System aus 268.697.600 Atomen; das GFMD-Modell reduziert die Zahl auf 524.288 (zwei Schichten von Atomen), wie in Abb. 1 zu sehen ist. Wir schieben die raue Oberfläche (oben) allmählich in die flache elastische Oberfläche. Die Belastung der starren Fläche wird durch die Verschiebung gesteuert. Jeder Verschiebungsladeschritt ist auf 0,01σ . eingestellt , und der GFMD-Algorithmus aktualisiert die Position jedes Atoms, bis die Atomkraft die Konvergenzkriterien L . erfüllt ¹ -norm = 0.01ε/σ. Die maximale Iterationszahl ist auf 50.000 festgelegt, um eine Endlosschleife zu vermeiden.

Ergebnisse und Diskussion

Kontaktaufnahme mit der Verteilung und Entwicklung von Clustern

Das Unebenheitsmodell betrachtet die Unebenheit entweder als kugelförmig oder elliptisch und berücksichtigt nicht die Wechselwirkung zwischen den sich berührenden Unebenheiten. In dieser Arbeit werden die Unebenheiten, die im Unebenheitsmodell verwendet werden, aus der oben erzeugten Oberfläche extrahiert. Im Rauhigkeitsmodell können die potentiellen Kontaktunebenheiten durch die Oberflächengeometrie vorab anhand ihrer Höhen bestimmt werden; das heißt, die Oberflächengipfel/-täler bilden sich entsprechend ihrer Höhe als Kontaktcluster. In Wirklichkeit hat die Unebenheit jedoch eine unregelmäßige Form, und normalerweise können mehrere benachbarte Unebenheiten zu einer großen verschmelzen, wie in Abb. 2 gezeigt. Es wird beobachtet, dass es am Anfang sechs unabhängige Unebenheiten gibt, und als Kontaktkraft zunimmt, verschmelzen sie schließlich zu einem großen Kontaktcluster (Abb. 3). Dies deutet darauf hin, dass die Annahme, dass der Abstand zwischen den Unebenheiten weit genug ist, damit sich Unebenheiten nicht gegenseitig beeinflussen, zu ungenauen Ergebnissen führen kann.

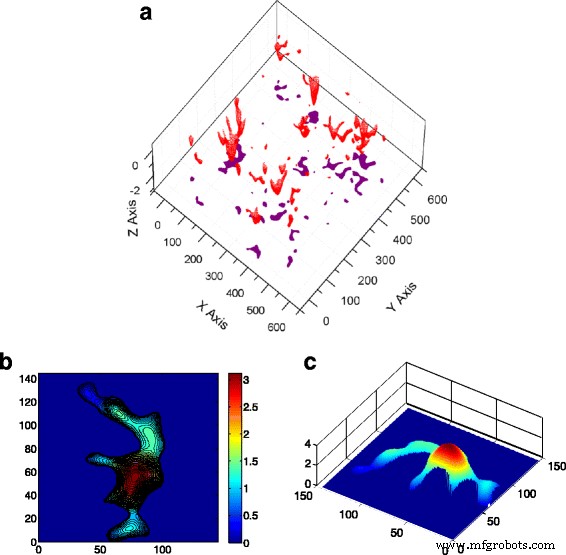
Die Form der Cluster und der Verschmelzungseffekt. a Die 3D-Ansicht von Kontaktclustern und ihre Projektion auf das x -y Flugzeug (in σ ). b Ein typischer Kontaktcluster mit sechs unabhängigen Unebenheiten. c Die 3D-Ansicht der Geometrie des Kontaktclusters (in σ )

Abbildung 4 zeigt, dass die Clusteranzahl mit zunehmender Kontaktfläche zuerst zu- und dann abnimmt, während die Oberflächenunebenheit mit zunehmender Kontaktfläche immer zunimmt. Dies ist auf den in Abb. 3 erläuterten Zusammenführungseffekt zurückzuführen.

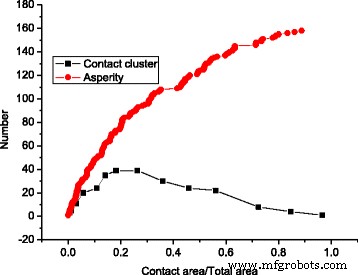
Oberflächentäler und Clusteranzahl unter verschiedenen Kontaktbereichen

Der Verschmelzungseffekt von Kontaktclustern wurde sowohl im Rauhigkeitsmodell als auch im GFMD-Modell beobachtet. Bei gleicher Kontaktfläche ist die Anzahl der Kontaktcluster im GFMD-Modell jedoch viel größer als die des Unebenheitsmodells, wie in Abb. 5 zu sehen ist. Es wird beobachtet, dass die Anzahl der Kontaktcluster im GFMD-Modell fast doppelt so hoch ist im Unebenheitsmodell, wie in Abb. 5 gezeigt. Der Hauptgrund dafür ist, dass das Unebenheitsmodell die Interaktion zwischen den Unebenheiten nicht berücksichtigt. Im GFMD-Modell beeinflussen sich die Kontaktcluster jedoch gegenseitig. Die von den Kontaktclustern erzeugten Verschiebungsfelder sind über die gesamte Fläche durchgehend. Die Verschiebung des großen Ensembles von Clustern führt zu einer neuen Geometrie auf der elastischen Oberfläche, die sich auf die Bildung neuer Kontaktcluster auswirkt. Daher basiert die Bildung der Kontaktcluster nicht nur auf der Höhe der starren rauen Oberfläche, sondern kann auch durch Verformungen in der glatten elastischen Oberfläche beeinflusst werden. Dies ist auch in Abb. 6 zu sehen, die die Kontaktclusterverteilung in verschiedenen Bereichen für das Rauhigkeitsmodell bzw. das GFMD-Modell zeigt. Wie in Abb. 6 gezeigt, betragen die Kontaktclusternummern bei einer Kontaktfläche von 5 % 17 bzw. 34 für das Rauhigkeitsmodell und das GFMD-Modell, während bei einer Kontaktfläche von 10 % ihre Kontaktclusternummern 24 und 52 werden , bzw. Dies deutet darauf hin, dass die Kontaktcluster im GFMD-Modell diskreter sind als die im Unebenheitsmodell. Im GFMD-Modell ist die durchschnittliche Clustergröße kleiner, aber die meisten Cluster fallen mit den Gipfeln/Tälern zusammen, wie in Abb. 7 zu sehen ist. Darüber hinaus betrachtet das Unebenheitsmodell entweder die Täler oder die Gipfel als potenzielle Unebenheiten ( je nachdem, welche Seite in Kontakt ist). In Abb. 8 haben wir jedoch festgestellt, dass mit zunehmender Kontaktfläche sowohl die Gipfel als auch die Täler in Kontakt sein können. In Abb. 8 sind die meisten Kontaktunebenheiten die Oberflächentäler, wenn die Kontaktfläche klein ist. Wenn die Kontaktfläche jedoch größer als 10 % der Oberfläche ist, können sich auch immer mehr Gipfel als Kontaktcluster bilden.

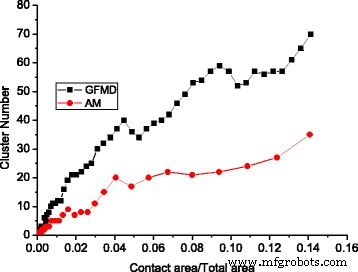
Die Clusterentwicklung für verschiedene Modelle

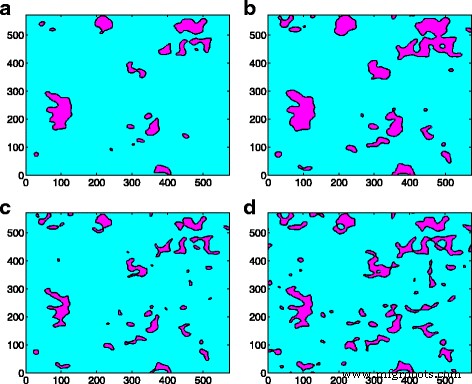
Die Kontur der Clusterverteilung (in σ ) an unterschiedlichen Kontaktflächen für das Rauheitsmodell bzw. das GFMD-Modell. a Asperity-Modell mit 5% Kontaktfläche. b Rauheitsmodell mit 10 % Kontaktfläche. c GFMD-Modell mit 5% Kontaktfläche. d GFMD-Modell mit 10 % Kontaktfläche

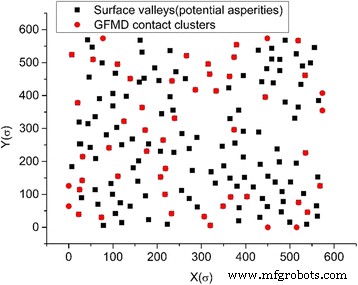
Die Lage der Kontaktcluster und der Oberflächentäler bei 10 % Kontaktfläche

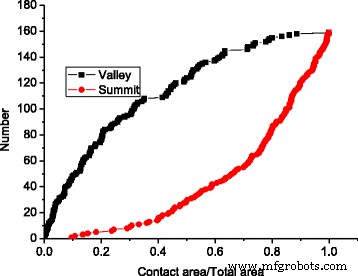
Die Anzahl der Oberflächentäler und Gipfel wächst in verschiedenen Bereichen

Kontaktbereich-Last-Beziehung

Wesentlich für das Kontaktverhalten ist die Kraft-Flächen-Beziehung unter Normalbelastung. In den früheren Modellen werden Unebenheiten normalerweise als kugelförmig und elliptisch betrachtet. Reale Kontaktcluster sind jedoch viel komplizierter. In diesem Abschnitt haben wir die Kontaktkraft-Flächen-Beziehung von drei Modellen verglichen:(1) das GFMD-Modell; (2) das Unebenheitsmodell (als AM gekennzeichnet), bei dem die Unebenheit direkt aus der Oberfläche extrahiert wird, bevor wir GFMD verwenden, um diese Unebenheiten in die flache elastische Oberfläche zu drücken (dies stellt sicher, dass es während des Kontakts nicht zu unerwarteter Kontaktclusterbildung kommt); und (3) das Modell von Greenwood und Williamson (als G-W gekennzeichnet), bei dem die Unebenheit in die äquivalente Kugel umgewandelt wird. Der Kugelradius wird erhalten durch

Für das GFMD-Modell und das Unebenheitsmodell mit exakt aus der Oberfläche extrahierten Unebenheiten können die Gesamtkräfte in der Grenzfläche durch Summieren der aus GFMD extrahierten Kräfte jedes Kontaktclusters erhalten werden. Für das Greenwood- und Williamson-Modell verwenden wir die Hertz-Theorie für jede Rauheitskraft (mit derselben Materialeigenschaft wie im GFMD-Modell), was bedeutet, dass die Gesamtkraft F kann ausgedrückt werden als

wobei Z _ich ist die Unebenheitshöhe, d die auf die starre Fläche aufgebrachte Verschiebung ist und f ist die Rauhigkeitskontaktkraft basierend auf der Hertz-Kontakttheorie.

In Abb. 9 haben wir die Kraft-Flächen-Beziehungen der drei Modelle verglichen, die lineare Beziehungen aufweisen. Es wird beobachtet, dass die Gesamtkraft bei GFMD viel kleiner ist als die des Rauhigkeitsmodells und des G-W-Modells. F im Asperity-Modell ist das 1,80-fache der von GFMD vorhergesagten und F im G-W-Modell ist das 1,54-fache der von GFMD vorhergesagten. Dies kann durch die RMS-Steigung der Kontaktcluster erklärt werden. Es ist bekannt, dass die Normallast proportional zur RMS-Steigung ist, also \( L\propto \sqrt{M_2}\). Im GFMD-Modell besteht die Kontaktfläche aus einer größeren Anzahl von Clustern, deren Durchdringungen flacher sind als die des Unebenheitsmodells. Da die Steigung der Unebenheitsspitze kleiner ist, ist auch die RMS-Steigung für den Kontaktcluster im GFMD-Modell kleiner. Abbildung 10 zeigt die RMS-Steigungen des Kontaktclusters für die drei Modelle. Es ist ersichtlich, dass die RMS-Steigung der Kontaktcluster in GFMD geringer ist als die RMS-Steigung der Oberfläche von 0,077, während die RMS-Steigung der beiden anderen Modelle der Kontaktcluster größer ist als die RMS-Steigung der Oberfläche.

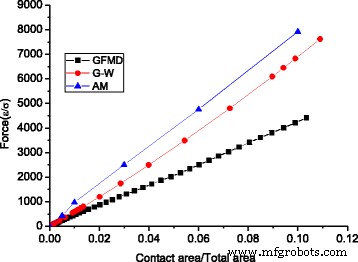
Verhältnis von Kontaktfläche und Belastung für verschiedene Modelle

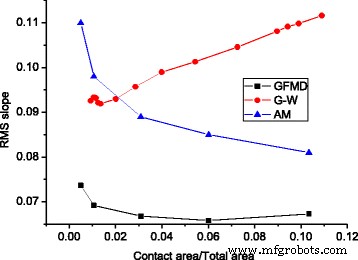
Die RMS-Steigung der Kontaktcluster mit unterschiedlichen Kontaktflächen für verschiedene Modelle, wobei die Oberflächen-RMS-Steigung 0,077

Schlussfolgerungen

Um die Entwicklung der Kontaktfläche von der atomaren zur makroskopischen Skala zu finden, wurde das Kontaktproblem der rauen fraktalen Oberfläche mit dem GFMD-Modell untersucht. Wir haben den atomaren Kontakt durch die Existenz einer Kraft größer Null definiert und drei verschiedene Längenskalen im gleichen System untersucht. Es wurde festgestellt, dass die Wechselwirkung zwischen den Asperitäten für die Bildung eines Kontaktclusters wesentlich ist. Einige Cluster sind nah genug, dass sie zu einem großen verschmelzen können. Der reale Kontaktbereich ist aufgrund der elastischen Verformung in der elastisch glatten Oberfläche weitaus komplizierter als der von der Oberflächengeometrie vorhergesagte. Die meisten Kontakt-Cluster-Standorte fallen mit den Oberflächengipfeln/-tälern zusammen. Die Größe des Clusters ist jedoch kleiner und seine Bildung wird nicht durch die Höhen der Oberflächenunebenheiten bestimmt. Mit zunehmender Kontaktfläche können sich sowohl Gipfel als auch Täler als Kontaktcluster ausbilden. Beim GFMD-Modell ist die Kraft viel kleiner als beim Rauheitsmodell, während die Kontaktclusterzahl beim GFMD-Modell viel größer ist. Die RMS-Steigung der Kontaktcluster im GFMD-Modell ist kleiner als die des Rauhigkeitsmodells, was erklärt, warum das Rauhigkeitsmodell zu einem höheren Druck führt. Unsere Ergebnisse legen nahe, dass die tatsächliche Kontaktfläche nicht allein durch die Oberflächengeometrie vorhergesagt werden kann. Die tatsächliche Kontaktfläche mit der Normallast ist für die folgende Reibungsforschung von Bedeutung.