Hohe Photonenabsorption von Quantenpunkt-Infrarot-Photodetektoren durch den Oberflächenplasmoneneffekt von Metall-Nanoloch-Arrays

Hintergrund

Halbleiter-Infrarot-Photodetektoren können verwendet werden, um Infrarotlicht zu detektieren, und haben große vielversprechende Anwendungen auf den Gebieten der wissenschaftlichen Forschung, der digitalen Bildgebung, der optischen Kommunikation und des Militärs. Bis heute haben die Quantenpunkt-Infrarot-Photodetektoren (QDIPs) in den letzten Jahren aufgrund ihrer hervorragenden Lichtempfindlichkeitseigenschaften und der Trends zur Miniaturisierung von Geräten zunehmende Aufmerksamkeit auf sich gezogen [1,2,3]. Obwohl Wissenschaftler in Jahrzehnten anhaltender Bemühungen große Fortschritte bei der Entwicklung von Technologien zum Erhalt von Hochleistungs-QDIPs gemacht haben, müssen noch weitere Verbesserungen vorgenommen werden, um den Herausforderungen der Miniaturisierung von Geräten [4] und den praktischen Anforderungen gerecht zu werden. Es wird darauf hingewiesen, dass die Kopplung von Metallgittern auf der quantenpunktbasierten aktiven Region als effektiver Ansatz zur Leistungssteigerung der QDIPs angesehen werden könnte [5, 6], die durch die lokale Photokopplung von plasmonenverstärkten einen hohen Photoabsorptionskoeffizienten erzielen können Wirkung.

Berichten zufolge gibt es zwei Hauptarten von Metallgitterstrukturen, die verwendet werden, um die Leistung der QDIPs zu verbessern. Eine ist die Metall-Loch-Array-Struktur und die andere ist die lochlose Metall-Array-Struktur. Konkreter kombinierte Changs Gruppe bei der Anwendung der Metallloch-Array-Struktur das periodische Metallloch-Array mit der Quantenpunktschicht im QDIP im Jahr 2007, was zur übernormalen Lichtdurchlässigkeit des Photodetektors führte [7]. Im Jahr 2009 haben Lee et al. schlugen eine Methode für eine QDIP mit hoher Detektionskraft durch die Integration metallischer photonischer Kristalle mit einer 3,6-μm-Periode eines Locharrays (100 nm Dicke) vor [8]. Die Forschungsergebnisse zeigen, dass die Methode die Spitzenreaktion des Photodetektors bei einer Wellenlänge von 11,3 µm realisieren kann und eine bis zu 30-mal höhere Detektivität als ohne den photonischen Metallkristall liefert. Anschließend diskutierten sie die Leistung der QDIP-Abhängigkeit vom einfallenden Licht und ihre Anwendung im Fokalebenen-Array [9, 10]. Eine ähnliche Leistungssteigerung kann auch in den Berichten durch die Verwendung des Loch-Metall-Array-Kopplungsgitters gefunden werden [11,12,13,14]. Es werden auch lochfreie Metall-Array-Strukturen vorgeschlagen. Im Jahr 2011 verwendeten Huang und seine Mitarbeiter die selbstorganisierte Plasmon-Silber-Nanopartikel-Schicht, um die breite spektrale Empfindlichkeit des QDIP zu verbessern, und erzielten eine 2,4- bis 3,3-fache Verstärkung [15]. 2014 berichtete Chens Gruppe, dass die Leistung des Photodetektors durch den Nahfeldeffekt der Au-Nanopartikel verbessert werden kann [16]. 2015 schlugen Dings Gruppe und Wangs Gruppe die Wellenleiterkopplungsstrukturen bzw. den einzelnen Resonanzhohlraum des verteilten Prager Reflektors vor [17, 18]. Neben den oben genannten Strukturen wurden auch andere Metallstrukturen, beispielsweise das Antennenstreifen-Array und das Nano-Disk-Array diskutiert und analysiert [19,20,21].

Diese No-hole-Array-Verfahren können jedoch auch eine verbesserte Wirkung in der Photoantwort der QDIPs aufweisen, aber ihr Herstellungsprozess mit kostengünstigen und einfachen Methoden bleibt im Vergleich zur typischen Hole-Array-Struktur eine Herausforderung. Für die typischen Loch-Array-Strukturen ist die Größe des Loch-Arrays im Mikromaßstab üblich. Die Verbesserung der Photoreaktion erfolgt durch den Plasmoneneffekt an der Grenzfläche zwischen der Luft in den mikroskaligen Metalllöchern und dem darunter liegenden Halbleiter. Die Größe des Metallloch-Arrays kann weiter auf die erwartete nanoskalige Anpassung an die Größe des Quantenpunktes im nanoskaligen QDIP verringert werden, unabhängig davon, ob die Hochleistungs-QDIPs mit entsprechendem Verstärkungseffekt realisiert werden können oder nicht. Gleichzeitig sind weitere theoretische Arbeiten notwendig, um die Mechanismen, die diesen Phänomenen zugrunde liegen, aufzuklären. In dieser Studie werden, um das Phänomen deutlich zu machen, die QDIPs mit nanoskaligen Metall-Loch-Array-Strukturen entworfen, und wichtiger im Vergleich zu den herkömmlichen mikroskaligen QDIPs wird der Verstärkungseffekt durch die Analyse der optischen Übertragungsbedingungen und der Verteilung des elektrischen Feldes erklärt . Die Ergebnisse zeigen, dass die QDIPs mit nanoskaligen Metall-Array-Strukturen aufgrund der Photon-Quantenpunkt-Wechselwirkung und der effizienten Lichtkopplung eine Photonenabsorption von bis zu 86,47 % aufweisen können, was die Tür zum Design und zur Optimierung des nanoskaligen Infrarots öffnen kann Fotodetektor.

Designmodell des QDIP mit dem Nanohole Array

Im Allgemeinen besteht der QDIP aus dem Quantenpunktbereich und den Elektroden, und der Quantenpunktbereich besteht aus einer periodischen Quantenpunktschicht und Sperrschichten. Unter idealen Bedingungen (ohne die Einflüsse der Elektroden und des Substrats) kann angenommen werden, dass die optische Transmission des gesamten QDIP gleich der des Quantenpunktbereichs ist. Somit müssen die Elektroden und das Substrat nicht im Design des QDIP erscheinen. Konkret zeigt Abb. 1b). In der aktuellen Konfiguration werden die Quantenpunkt-Nanopartikel als Würfelform angenommen, die der Definition von Quantenpunkten entspricht, die mit vielen Atomen und Molekülen gebildet werden, und sie haben eine Länge von 40 nm, eine Breite von 40 nm und 7 bis 9 Zoll nm in der Höhe. Ein ähnliches Modell von Quantenpunkten findet sich auch in der Literatur [22]. Die Fläche des QDIP ist auf 1000 nm × 1000 nm eingestellt, und die Dicke der AlGaAs-Barriereschichten beträgt 60 nm. Das als Au gewählte Metall-Nanoloch-Array wird auf den herkömmlichen Quantenpunkt-Nanostrukturschichten des herkömmlichen QDIP platziert, das als das in Abb. 2 gezeigte verbesserte QDIP bezeichnet wird. Der Radius der Löcher kann im Bereich von 50~70 nm . eingestellt werden . Es sei darauf hingewiesen, dass das Material, aus dem der Quantenpunkt besteht, nicht einfach als Volumenmaterial mit einem bestimmten Brechungsindex angesehen werden kann. Abbildung 3 zeigt die elektrische Dispersionscharakteristik des GaAs-Materials, das verwendet wurde, um den Quantenpunkt nach der Methode von Edward D. Palik [23] zu bilden. In der Abbildung repräsentieren die blaue Kurve und die rote Kurve die Dielektrizitätskonstante von GaAs ε ^′ und ε ^″ , bzw. Abbildung 4 a und b zeigen die elektrische Dispersionscharakteristik von GaAs, Al_0.3 Ga_0,7 Als Material bzw. Goldmaterial.

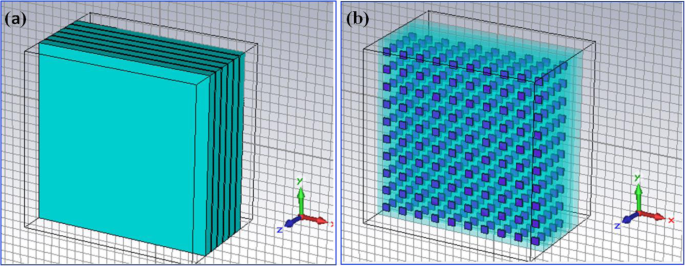
a Strukturmodelldiagramm des typischen Quantenpunkt-Infrarot-Photodetektors. b Quantenpunktverteilung in den aktiven Bereichen mit 5-Perioden-Quantenpunkt-Verbundschichten. Diese Verbundschichten bestehen aus der AlGaAs-Barriereschicht und den GaAs-Schichten

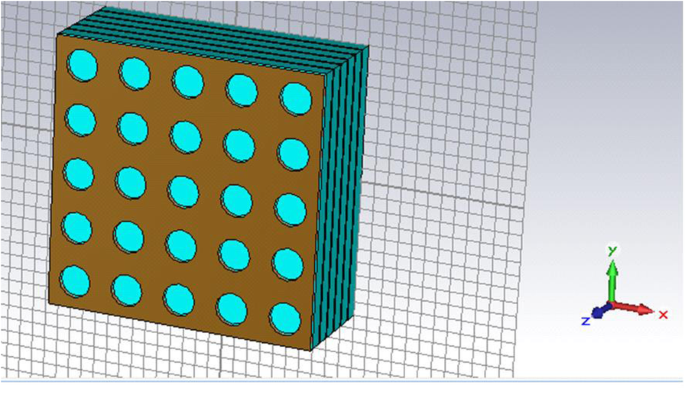
Aktive Bereiche mit Quantenpunkten mit den periodischen Metall-Nanoloch-Array-Strukturen für die verbesserte QDIP

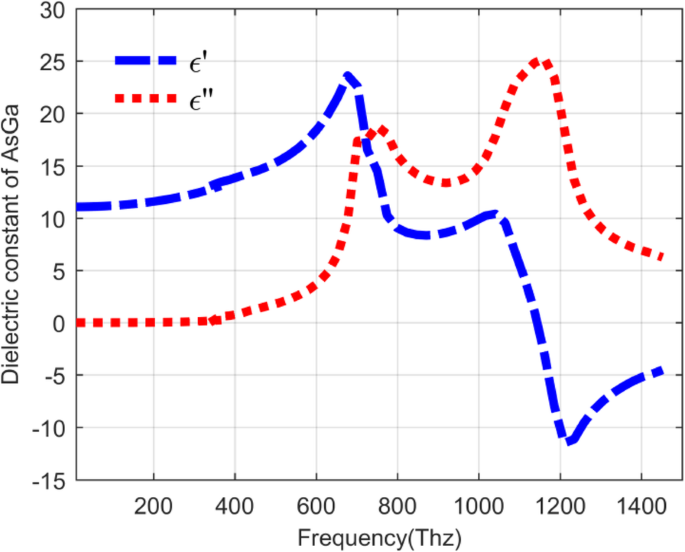
Dispersionsverhältnis von GaAs-Material

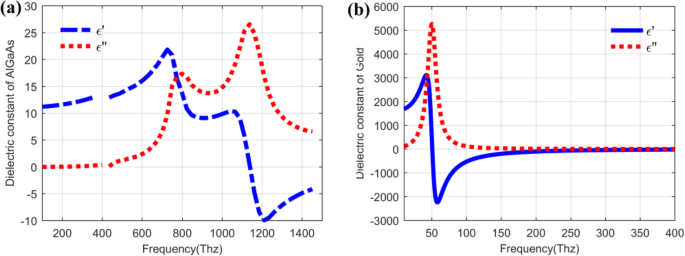
a Dispersionsverhältnis von AlGaAs-Material. b Dispersionsverhältnis von Au-Material

Berechnungsmethode basierend auf der YEE-Zelle

Basierend auf dem oben entworfenen physikalischen Modell wird das Verfahren der Finite-Elemente-Integration verwendet, um den Zustand der optischen Übertragung zu berechnen. Zunächst werden basierend auf den YEE-Zellen die Maxwell-Integralgleichungen, die das obige Modell erfüllen, wie folgt geschrieben:

In unserer Rechnung gilt Gl. 1–4 sind diskretisiert. Sowohl die Verteilung der Knoten des elektrischen Felds als auch der Knoten des magnetischen Felds werden als „Yee-Zelle“-Format gewählt. Unter Verwendung von Gl. 1 als Beispiel kann das elektromagnetische Modell des Photodetektors als die Ansammlung von "Yee-Zelle" genommen werden. Wie in Fig. 5 gezeigt, entsprechen die vier Seiten der willkürlichen Zelle Gl. 1, der den elektrischen Feldvektor e . darstellt _ich ,e _j ,e _k , und e _l . Der in Normalenrichtung liegende Vektor ist der Magnetfeldvektor b _n , und damit die vorherige Gl. 1 kann wie folgt umgeschrieben werden Gl. 5.

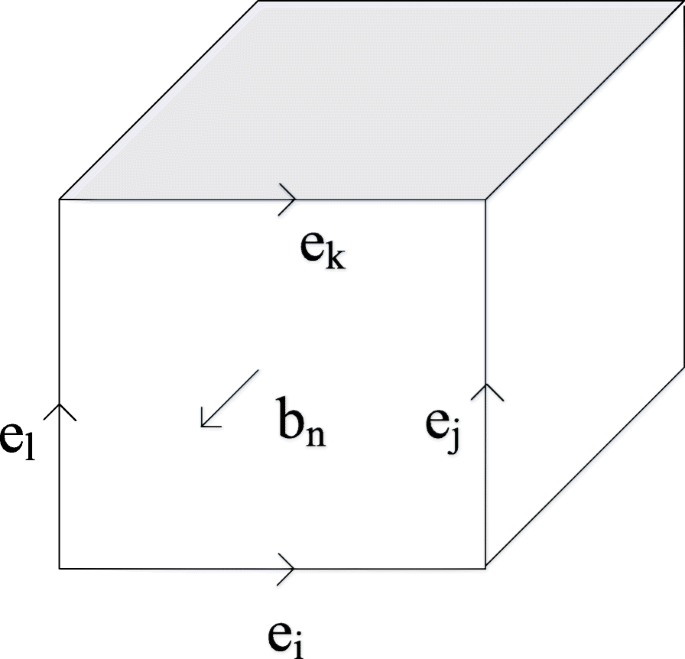
Schematische Darstellung der „YEE-Zelle“

Mit einer ähnlichen Methode kann die Gleichung des elektromagnetischen Modells des gesamten Photodetektors wie folgt geschrieben werden:

Gleichung 2 kann auch umgeschrieben werden als:

Nach der ähnlichen Methode sind die anderen Gleichungen 2 ~ 4 können diskretisiert werden als:

Kombinieren der diskretisierten Gl. 7–10 mit der Randbedingung können das elektrische Feld und das magnetische Feld iterativ gelöst werden. In dieser Studie wird die Metall-Loch-Array-Struktur oben auf dem herkömmlichen QDIP platziert, und als solche kann die Struktur die Lichtkopplung durch die Bragg-Streuung erleichtern. Die entsprechende optische Kommunikation wird weiter berechnet, die im folgenden Abschnitt diskutiert werden kann, wenn die Bedingungen der Transmission, der Reflexion und der Absorption gegeben sind. Darüber hinaus kann anhand des Zusammenhangs zwischen Absorption und Quanteneffizienz die Ansprechempfindlichkeit des QDIP angegeben werden. Konkret sei bekanntlich, dass die Ansprechempfindlichkeit des QDIP als sehr wichtiger Leistungsparameter aus dem Verhältnis von Photostrom und Leistung des einfallenden Lichts berechnet werden kann [24]. Es kann also geschrieben werden als:

wo ich _Foto ist der Photostrom des QDIP, P ist die Leistung des einfallenden Lichts, g ist die photoleitende Verstärkung, e ist die Ladung des Elektrons, h ist die Planck-Konstante, v die Frequenz des einfallenden Lichts ist und η ist die Quanteneffizienz.

Die Quanteneffizienz kann als Verhältnis der Anzahl der Elektronenlöcher und der des einfallenden Fotos definiert werden, das stark von der Absorption des Fotodetektors abhängt. Da das einfallende Licht in der Praxis den Absorptionsbereich direkt beleuchtet, kann es aufgrund der Reflexion der oberen Kontaktschicht oder der Metallschicht nicht vollständig absorbiert werden [25, 26]. Somit kann die Quanteneffizienz des QDIP geschrieben werden als:

wobei α ₀ W ist der Absorptionskoeffizient des QDIP, α ₀ d ist der Absorptionskoeffizient der einfallenden Kontaktschicht, r ist die Reflexion der einfallenden Schicht.

Beim QDIP kann die photoleitende Verstärkung als Verhältnis der Rekombinationszeit von Elektronen aus einem ausgedehnten Zustand zurück in einen Quantenpunkt definiert werden τ _Leben zur Laufzeit von Elektronen durch das Gerät τ _Gesamt , und es kann angezeigt werden als:

und unter der Bedingung, dass die Transitzeit über eine Periode der Quantenpunkt-Verbundschicht erheblich kleiner ist als die Rekombinationszeit von einem ausgedehnten Zustand zurück in einen Quantenpunkt [22, 27]_, der Gewinn kann geschrieben werden als:

wo K ist die Zahl die zusammengesetzte Quantenpunktschicht, L ist der Abstand zwischen Quantenpunktschichten, μ die Mobilität von Elektronen, E ist die elektrische Felddichte über den QDIP, v _s ist die Sättigungsgeschwindigkeit von Elektronen, h _QD ist die Höhe der Quantenpunkte, ∑_QD ist die Quantenpunktdichte in jeder Quantenpunktschicht, a _QD die laterale Größe von Quantenpunkten ist und V _t ist die Einfangrate von Elektronen.

Eingereichte Gl. (12) und Gl. (14) in Gl. (11) können wir die Ansprechempfindlichkeit des QDIP erhalten, die wie folgt dargestellt werden kann:

Ergebnisse und Diskussion

Basierend auf dem Design des obigen QDIP, wenn das einfallende Infrarotlicht auf die Oberseite dieser QDIPs im z trifft -Achsenrichtung haben die Photodetektoren die Reflexion und die Transmission des einfallenden Lichts. Das Absorptionsvermögen der Photodetektoren kann durch Untersuchung dieser optischen Transmissionsbedingungen des einfallenden Lichts bestimmt werden, die eine sehr wichtige Rolle bei der Bewertung der Leistung des Photodetektors spielen können. Abbildung 6 zeigt ihre Reflexionsbedingungen des Photodetektors ohne das Metallarray (das herkömmliche QDIP) und das mit dem Metallarray (das verbesserte QDIP). Im Vergleich zu den beiden Kurven in Abb. 6 ist zu erkennen, dass die Reflexionskoeffizientenwerte des herkömmlichen QDIP neben den Einzelwerten in den Frequenzbereichen 250~260 Thz und 279~293 Thz . geringfügig kleiner sind als die des verbesserten QDIP . Nimmt man insbesondere den Wert bei der Frequenz von 219 Thz als Beispiel, beträgt der Reflexionskoeffizientenwert des herkömmlichen QDIP –3,91 dB, während der verbesserte QDIP nur –1,31   dB beträgt. Wie oben gesagt, kann das verbesserte QDIP einen etwas höheren Wert als das herkömmliche QDIP aufweisen, aber es kann festgestellt werden, dass die minimale Absorption des verbesserten QDIP ziemlich geringer ist als die des herkömmlichen QDIP. Genauer gesagt beträgt die minimale Absorption des verbesserten QDIP –16,17 dB bei einer Frequenz von 255,10 Thz, während der Wert für den herkömmlichen QDIP gleich –13,42 dB bei 254,86 Thz ist. Der niedrige Reflexionskoeffizient des verbesserten QDIP könnte dem höheren Absorptionskoeffizienten des Metalls als dem des Halbleiters für Infrarotlicht zugeschrieben werden. Die Absorption lässt sich aus den gemeinsamen Beiträgen der Reflexion und der Transmission berechnen. Abbildung 7 a zeigt den Transmissionskoeffizienten des herkömmlichen QDIP und seine blau markierten Werte sind im Gesamtfrequenzbereich von 200~340 Thz deutlich größer als die des verbesserten QDIP. Bei der Frequenz von 298 Thz beträgt der Transmissionskoeffizient des verbesserten QDIP beispielsweise nur –10,83 dB, was 1,60-mal kleiner ist als der des herkömmlichen QDIP, der –4,15 dB beträgt. Entsprechend der Konkurrenzbeziehung zwischen Transmission, Reflexion und Absorption führt die Abnahme des Transmissionskoeffizienten zu einer Zunahme der Absorption unter der Bedingung, dass andere Verluste des einfallenden Lichts ignoriert werden.

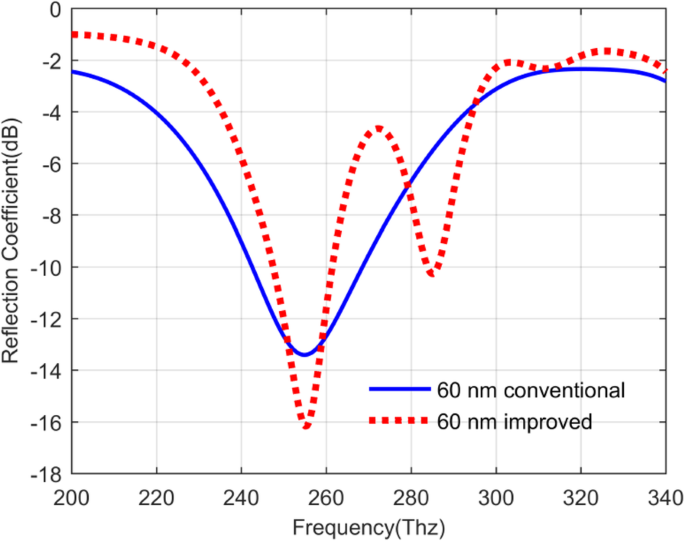
Reflexionskoeffizienten des herkömmlichen QDIP ohne Metallarray (blaue Kurve) und des verbesserten QDIP mit dem Metall-Nanoloch-Array (rote Kurve)

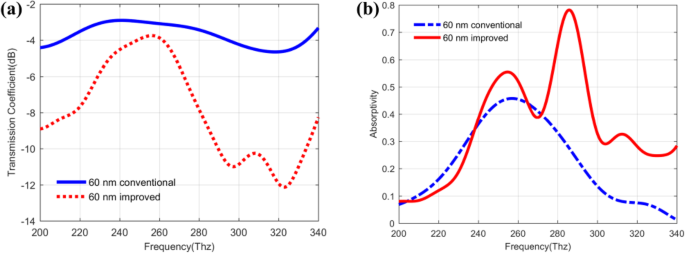
Transmissionskoeffizienten (a ) und Absorptionskoeffizienten (b ) des herkömmlichen QDIP bzw. des verbesserten QDIP

Kombiniert man die Transmissionssituation in Fig. 7a mit der Reflexionssituation in Fig. 6, kann das Absorptionsvermögen des QDIP berechnet werden, das in Fig. 7b gezeigt ist. In der Abbildung beschreibt die rote Kurve (als 60 nm verbessert markiert) das Absorptionsvermögen des verbesserten QDIP mit der Metallstruktur, und die andere blaue Kurve repräsentiert das konventionelle QDIP ohne die Metalllochstruktur (als 60 nm konventionell gekennzeichnet). Bei einem Vergleich zwischen den beiden Kurven kann festgestellt werden, dass das Absorptionsvermögen des verbesserten QDIP höher ist als das des herkömmlichen QDIP. Das Maximum des Absorptionsvermögens des verbesserten QDIP beträgt 0,782 bei der Frequenz von 286 Thz, was 1,71 mal höher ist als das des herkömmlichen QDIP, das bei der Frequenz von 257 Thz nur 0,458 beträgt. Die Gründe für die Erhöhung des Absorptionsvermögens des verbesserten QDIP können wie folgt erklärt werden. Die Metall-Nanoloch-Array-Strukturen werden auf der Oberseite des herkömmlichen QDIP eingeführt, und eine solche Konfiguration kann den Oberflächenplasmonenresonanzeffekt begünstigen, was zu einem lokalen Kopplungseffekt des einfallenden Lichts führt. Darüber hinaus kann der lokale Kopplungseffekt dazu führen, dass mehr einfallendes Licht in die darunter liegenden Halbleiter-Quantenpunktschichten eindringt, was zu einer hohen Absorption für das einfallende Licht und zu besseren photoelektrischen Eigenschaften mit größerem Photostrom und höherer Quanteneffizienz führen kann.

Um weiter zu verdeutlichen, wie der Plasmonenverstärkungseffekt in den verbesserten QDIPs realisiert werden kann, untersuchen wir auch die Einflüsse der verschiedenen Metall-Nanolochstrukturen auf das Absorptionsvermögen der verbesserten QDIPs. Wie in 8a gezeigt, entsprechen die Absorptionskurven der verbesserten QDIPs mit unterschiedlichen Metall-Nanoloch-Radius der schwarzen (50 nm), grünen (55 nm), roten (60 nm) bzw. blauen (65 nm) Kurve. Die Absorptionswerte des verbesserten QDIP zeigen den unterschiedlichen Änderungstrend unter verschiedenen Nanolöchern. Die Spitzenwerte des Absorptionsvermögens für den verbesserten QDIP betragen 0,744 (schwarze Kurve bei 289 Thz), 0,721 (grüne Kurve bei 291 Thz), 0,782 (rote Kurve bei 286 Thz) bzw. 0,707 (blaue Kurve bei 288 Thz). Offensichtlich kann unter diesen Photodetektoren der verbesserte QDIP mit einem Lochradius von 60 nm die beste Absorptionsleistung aufweisen. Gleichzeitig ist bekannt, dass auch die Dicke der Metalllochschicht Einflüsse des Absorptionsvermögens haben kann. Wie in 8b gezeigt, ändern sich die Spitzenwerte des Absorptionsvermögens entsprechend von 0,667 (263 Thz für die 10-nm-Dicke) auf 0,782 (286 ), wenn die Dicke der Metallschicht im verbesserten QDIP von 10 auf 40 nm geändert wird Thz für 20 nm), 0,662 (293 Thz für 30 nm) und 0,590 (262 Thz für 40 nm). Unter diesen Spitzenwerten kann die Metall-Nanolochschicht mit einer Dicke von 20 nm den höchsten Absorptionswert aufweisen.

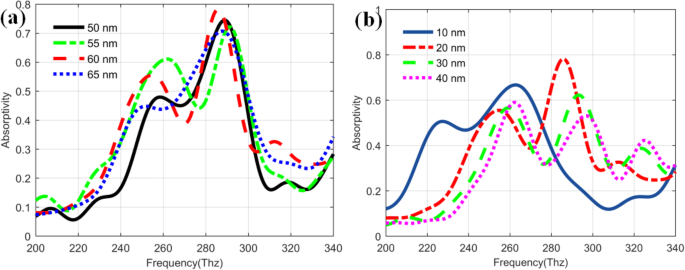
Absorptionsvermögen des verbesserten QDIP (a ) mit unterschiedlichen Radien und unterschiedlichen Metalldicken von Metall-Nanolöchern (b)

Um das obige Phänomen zu verdeutlichen, untersuchen wir weiter die Verteilungsbedingungen des elektrischen Felds an der oberen Oberfläche des verbesserten QDIP mit den unterschiedlichen Radien der Metalllöcher bei 286 Thz. Abbildung 9 zeigt die elektrische Feldverteilung bei verschiedenen Radien von Metalllöchern im Bereich von 50–65 nm. Verglichen mit den vier Bildern in Abb. 9a wird deutlich, dass die QDIPs mit den Lochradien von 50 nm (Abb. 9a) und 55 nm (Abb. 9b) aufgrund der entsprechenden elektrischen Feldverteilungen in . eine relativ schwächere Verstärkung des elektrischen Feldes aufweisen können Abb. 9 a und b auf der gesamten Fläche einschließlich der Löcher und ihrer angrenzenden Bereiche liegen, und somit ihre lokalen Kopplungseffekte des elektrischen Feldes vernachlässigt werden können, während die lokale Kopplungsfläche des elektrischen Feldes mit einem hohen elektrischen Feld in Abb 9 c und d. Die starken elektrischen Feldverteilungen um die Löcher in Fig. 9c und d mit der Form des Rings können aufgrund des Oberflächenplasmonenkopplungseffekts an der Grenzfläche zwischen den Metalllöchern und der Luft in den Metalllöchern lokalisiert werden. Verglichen mit den elektrischen Feldverteilungen in Fig. 9c und d ist der Kopplungseffekt des elektrischen Feldes in Fig. 9c stärker als der in Fig. 9d entsprechend ihrer markierten Farben, die eine Mischung aus Rot, Grün und Blau sind. In dieser Hinsicht steht die rote Farbe für das stärkste Feld und die blaue Farbe steht für das schwächste Feld. Basierend auf der obigen Analyse erzeugen die Metall-Nanolöcher mit einem Radius von 60 nm den verstärkenden elektrischen Feldeffekt durch das Oberflächenplasmon. Um den Verstärkungseffekt noch deutlicher zu machen, ist die Verteilung des elektrischen Feldes auf xz -Ebene, die der maximalen Absorption des optimierten QDIP bei der Frequenz von 286 Thz in unserer Studie entspricht, wie in Abb. 10a gezeigt, die auf dem Abschnitt y . liegt =0 (entspricht dem Feld des xz -Flugzeug). In der Abbildung aus der Richtung von z -Achse liegt die verstärkte elektrische Feldverteilung im rot markierten Bereich zwischen benachbarten Metalllöchern und das schwache Feld im blau markierten Bereich der Metalllöcher. Die elektrische Feldverteilung zeigt direkt die verbesserte Absorption des QDIP. Es ist der Verstärkungskopplungseffekt, der zur Erhöhung des Absorptionsvermögens führt und weiter zu der hohen Quanteneffizienz des verbesserten QDIP führt. Dieselben Schlüsse lassen sich natürlich auch ziehen, indem man die Magnetfeldverteilung nach den Eigenschaften der elektromagnetischen Eigenschaften des Lichts analysiert. Da die Erörterung der magnetischen Feldverteilung dieselbe wie die der elektrischen Feldverteilung ist, ist sie in dieser Studie nicht erforderlich.

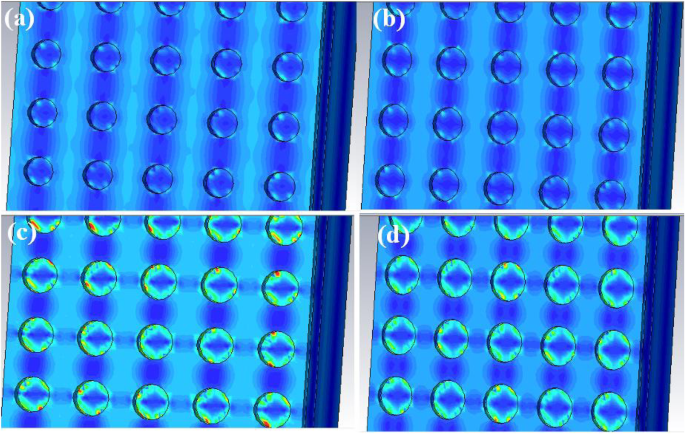
Elektrische Feldverteilung der verbesserten QDIPs mit unterschiedlichen Radien von Metall-Nanolöchern:a r =50 nm, b r =55 nm, c r =60 nm und d r =65 nm

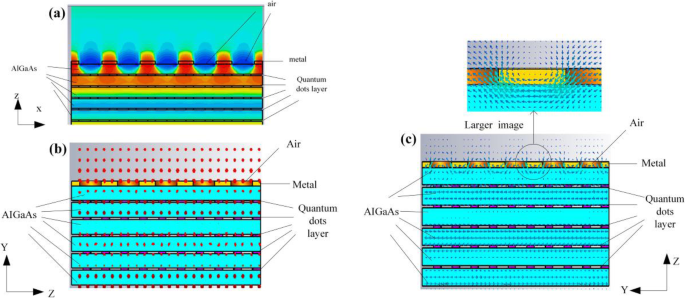
a x -direktionales elektrisches Feld des optimierten QDIP. b Polarisation des elektrischen Feldes des verbesserten QDIP. c Magnetfeldpolarisation des verbesserten QDIP

Außerdem kommt, wie oben gesagt, der Verstärkungseffekt vom Oberflächenplasmon, und die Mode der angeregten Oberflächenplasmonenwelle wird weiter bestimmt. Abbildung 10a und b zeigen die Ergebnisse des elektrischen und magnetischen Felds. In der Abbildung zeigt Abb. 10b die Polarisationsverteilung des elektrischen Feldes auf yz -Flugzeug. Es ist zu erkennen, dass das elektrische Feld normal zu yz . ist -Ebene, d.h. das elektrische Feld kann nicht das E haben _z Komponente. Abbildung 10c zeigt die Polarisationsverteilung des Magnetfelds. Es kann festgestellt werden, dass das Magnetfeld parallel zum yz . ist -ebene, d. h. es gibt die Hz-Komponente in Ausbreitungsrichtung des einfallenden Lichts, die z . ist -Richtung. Daher ist in unserer Studie die angeregte Oberflächenplasmonenwelle die TE-Mode. Um die Position zu verdeutlichen, die verwendet wird, um das Oberflächenplasmon anzuregen, ist die Verteilung des Magnetfelds in der Nähe der Metalllochgrenzfläche oben in Fig. 10c gezeigt. Es ist ersichtlich, dass das Magnetfeld an der Position zwischen benachbarten Metalllöchern stärker ist als das in den Metalllöchern. Außerdem kann gemäß dem in Fig. 10a erscheinenden elektrischen Feld auch nachgewiesen werden, dass das Verstärkungsfeld auf die Stelle zwischen benachbarten Metalllöchern konzentriert ist. Daraus kann geschlossen werden, dass der Oberflächenplasmoneneffekt von der Oberfläche zwischen Metall und Halbleiter ausgehen kann, die auf der Position zwischen benachbarten Metalllöchern liegt. Natürlich ist es erwähnenswert, dass die Verstärkung der Absorption nicht nur vom Oberflächenplasmon herrührt, sondern auch von der verstärkten Reflexion der Metallschicht, was zu einer sekundären Absorption des einfallenden Lichts führt, da das einfallende Licht entlang des QDIP beleuchtet wird Z-Achse.

Es ist bekannt, dass auch die Parameter der Metallschichten einen großen Einfluss auf die Leistung des QDIP haben können. Um die optimalen Parameter zu bestimmen, werden die Dicke der Barriereschicht und der Quantenpunktschicht weiter analysiert und unter den Bedingungen der optimierten Metallschichtdicke (20 nm) und des Metalllochradius (60 nm) diskutiert. Abbildung 11a zeigt den sich ändernden Trend des Absorptionsvermögens der Photodetektoren mit den unterschiedlichen Dicken der Barriereschicht im Bereich von 70–85 nm. Aus dem Bild zeigen diese Absorptionskurven einen ähnlichen Änderungstrend. Wenn die Dicken der Sperrschicht im Bereich von 70~85 nm variieren, betragen die entsprechenden maximalen Absorptionswerte der verbesserten QDIPs 0,7581 (70 nm, bei 322,78 Thz), 0,7763 (75 nm, bei 304,84 Thz), 0,8552 (80 nm, bei 292,75 Thz) bzw. 0,8346 (85   nm, bei 284,17). Verglichen mit diesen maximalen Absorptionswerten kann festgestellt werden, dass die Barriereschicht mit einer Dicke von 80 nm die beste Absorptionsleistung für die verbesserten QDIPs aufweisen kann. Feste andere Parameter mit den oben optimierten Werten werden die Einflüsse der Dicken der Quantenpunktschicht auf die Absorptionsleistung für das verbesserte QDIP weiter untersucht, und die entsprechenden Kurven sind in 11b gezeigt. Aus der Abbildung ist ersichtlich, dass die rote Kurve den maximalen Absorptionswert von 0,8647 bei der Frequenz von 295,48 Thz für den verbesserten QDIP mit der Schichtdicke von 7 nm aufweisen kann, was veranschaulicht, dass der Photodetektor den optimalen Übergangszustand aufweisen kann.

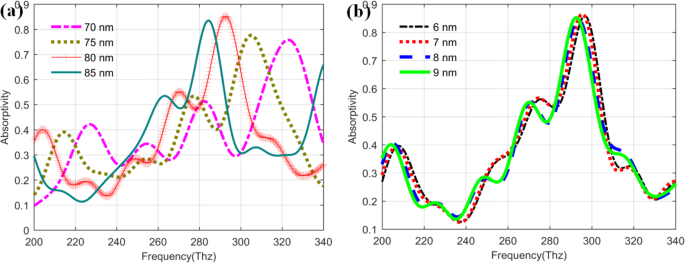
Saugfähigkeit des verbesserten QDIP mit den unterschiedlichen Dicken von a die Quantenpunktschicht und b Sperrschicht

Basierend auf der obigen Diskussion ist klar, dass nicht nur die Parameter bezüglich des QDIP den Einfluss auf die Geräteleistung haben können, sondern auch die Dicken der Quantenpunktschicht und der Sperrschicht die Geräteleistung bestimmen können. In dieser Studie können gemäß den theoretischen Berechnungsergebnissen die optimierten Parameter für die verbesserten QDIPs mit der Metallschichtdicke von 20 nm, dem Metalllochradius von 60 nm, der Quantenpunktschichtdicke von 7 nm und der Barriereschicht angegeben werden Dicke von 80 nm. Das Absorptionsvermögen des optimalen Photodetektors kann bis zu 0,8647 betragen. Darüber hinaus sind die Absorptionswerte in der roten Kurve, abgesehen von den Werten im Frequenzbereich von 222,91~262,18 Thz, beim Vergleich des herkömmlichen QDIP mit dem optimierten QDIP, wie in Fig. 12 gezeigt, ziemlich höher als die in der blauen Kurve. Das maximale Absorptionsvermögen in der roten Kurve beträgt 0,8647 bei einer Frequenz von 295,48 Thz, was 1,89-mal größer ist als in der blauen Kurve (die der vorherigen Kurve entspricht, die in Abb. 7b mit „60 nm konventionell“ gekennzeichnet ist, entsprechend das QDIP ohne Metallloch-Array) bei der Frequenz von 257 Thz. Die Frequenzverschiebung für den Peak des maximalen Absorptionsvermögens resultiert hauptsächlich aus der Änderung der Dicke des verbesserten Photodetektors. Darüber hinaus werden basierend auf den optimierten Parametern der QDIPs die Dicken der Quantenpunktschicht und der Barriereschicht, der Quanteneffizienzwert und die Empfindlichkeit des Photodetektors berechnet.

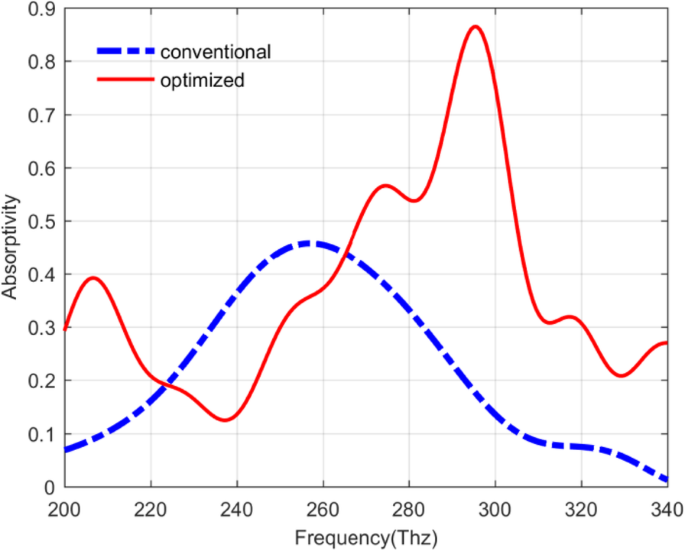
Absorptivity of the conventional QDIP in blue curve and improved QDIP in red curve with the barrier layer thickness of 80 nm

Quantum Efficiency and Responsivity of the QDIP

Based on the calculated results of the absorptivity in Fig. 12 as well as combining with the expression of the quantum efficiency and the responsivity of the QDIP above, the quantum efficiency of the QDIP and the responsivity can be calculated out, and the corresponding results are plotted in Fig. 13 a and b. Figure 13a depicts the quantum efficiency of the QDIP. In this figure, the blue dotted curve represents the quantum efficiency of the QDIP without metal array, the other red full curve is that of the optimized QDIP with metal array. Making a comparison between the two curves, it can be observed that the maximum quantum efficiency of the optimized QDIP is 0.2961 at the frequency of 295.87 Thz, and it is 1.205 times than that of the conventional QDIP, which is equal to 0.2458 at the frequency of 256.48 Thz. The increasing trend is similar to the absorptivity provided in Fig. 12 which results from the introduction of the metal hole array and the optimization of the quantum dot infrared photodetector. Based on the increasing trends for the absorptivity, we can find that the responsivity of the QDIP also reveals similar increasing trends. To be specific, Fig. 13b gives the responsivity of the optimized QDIP and the conventional QDIP, respectively. In the figure, the red curve is on behalf of the responsivity of the conventional QDIP, and the blue curve stands for that of the optimized QDIP with the metal holes layer. Similar to the analysis in Fig. 13a, the responsivity is 0.0326 mA/W at the frequency of 295.87 Thz, which is 0.0174 larger than that of the conventional QDIP at the frequency of 256.48 Thz (which is 0.0152). The increase in the responsivity can be proven in the other frequency band in the range of 229.57~254.41 Thz, which obviously demonstrates the enhancement in the performance of the photodetector due to the introduction of the metal hole array and the optimization of the quantum dot regions. Moreover, the reasons for the enhancement were detailedly discussed in detail analyzing the electric field distribution of quantum dot regions above.

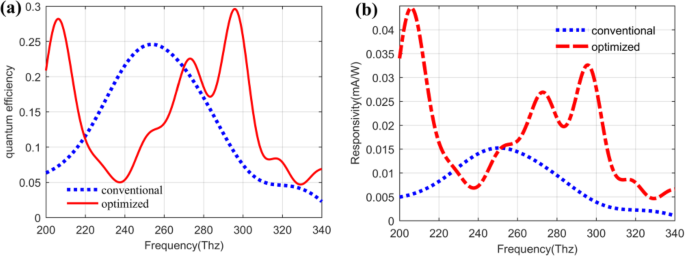
a Quantum efficiency of QDIP. b Responsivity of QDIP

Influence of the Electrodes and the Substrate

What was studied above is all under the condition of ignoring the influence of the electrodes and the substrate; in fact, the electrodes and the substrate can have certain influences on the performance, but they do not influence the description of the enhancement effects of the performance of the optimized QDIP with the metal layer. This is because the electrodes and the substrate can have almost the same influence on the absorption of the QDIP with the metal layer and without the metal layer. To illustrate the issue adequately, we recalculated the absorption of the QDIP considering the influence resulting from the substrate and the electrodes as well as the quantum efficiency, the responsivity, and so on. To be concrete, it is well known that the electrodes are generally designed at the two ends of the absorption region of the quantum dots, and thus, as shown in Fig. 14a, one is at the top of the conventional QDIP and the other is at the bottom end of the absorption region of the QDIP. That is to say, it lies at the top of the substrate, which can provide the quantum dot absorption region with the bias voltage and transmit current together with the electrodes said above. Here, it is worth mentioning that there is the metal hole array instead of the metal ring in the optimized QDIP in our study used as the electrodes. The other electrode is similar to that of conventional QDIP. Based on the above design, a concrete distribution of the electrodes is clearly calculated in Fig. 14a. Similar to Fig. 14a, in Fig. 14 b, the material of the electrodes is chosen as gold, and the substrate is chosen as AlGaAs; their thicknesses are 20 nm and 300 nm, respectively.

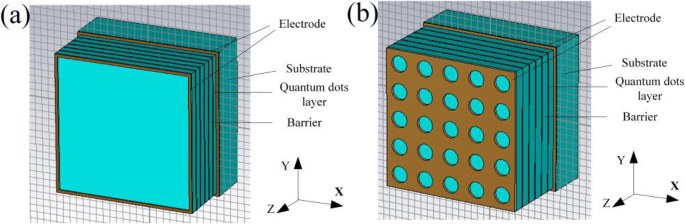
a Conventional QDIP with electrodes and substrate. b Optimized QDIP with the electrodes and substrate

Based on the introduction of electrodes and substrate in the structure of the QDIP above, we calculated the absorption of the QDIPs, and the corresponding results are compared with the QDIP without the electrodes and the substrate. Figure 15 demonstrates the influence of the electrodes and substrate on the absorptivity of the QDIP. In the figure, the blue curve and the pink curve are the absorptivity of the conventional QDIP without the electrodes and the substrate and that of the optimized QDIP without the electrodes and the substrate, respectively. The red dashed curve represents the absorptivity of the optimized QDIP with the electrodes and the substrate. Its maximum absorption is 0.7620 at the frequency of 304.35 Thz which is just 0.1027 smaller than that of the optimized QDIP without electrodes and substrate. The decrease of the absorptivity is degraded from the loss of the electrodes and the substrate, the same as the green curve with the absorptivity of the conventional QDIP with the electrodes and substrate. Compared with the absorptivity of the conventional QDIP and optimized QDIP with electrodes and substrate, the enhancement is very clear in the absorptivity of the optimized QDIP with electrodes and substrate, which is the same as the optimized QDIP in Fig. 12. In other words, though the electrodes and the substrate can result in the decrease of the absorptivity, the total absorptivity of the optimized QDIP can be enhanced compared with that of bare QDIP, and thus, the decrease can be negligible as they can have a very small influence on the description of the enhancement of the optimized QDIP when using the metal hole array.

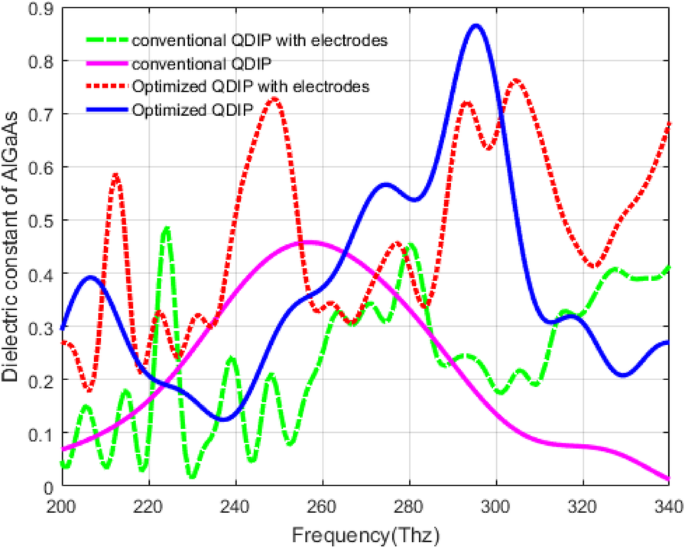
Absorption of the QDIP with electrodes and substrate

In addition, it can be observed that the change trend of the absorptivity of the QDIP with the electrodes and substrate cannot be the same as the previous curves (corresponding to the blue curve and pink curve). They are more complex with many peak values. The reasons for this phenomenon can be explained as follows. First of all, the addition of the electrodes and the substrate can produce more or less a loss and the frequency shifts due to the accumulated heating effect and the other negative influence factors. Secondly, since the material of the electrodes is chosen as the metal, in the optimized QDIP with the electrodes and the substrate, it can result in enhanced reflection and enhanced surface plasmon. The two reasons commonly favor the enhancement of the absorptivity as demonstrated in Fig. 15.

Schlussfolgerungen

In conclusion, the conventional QDIP performance can be greatly improved by adding the nanoscale metal nanohole array, and the enhanced mechanism of the performance for improved QDIPs is discussed by analyzing the reflection, the transmission, the absorption, and the distribution of the electric field. The results not only demonstrate that the improved QDIPs can have higher absorptivity than that of conventional QDIPs but also indicate that the parameters of the improved QDIPs related to the metal nanohole array together with the quantum dot composite layer can significantly influence their performance. According to theoretical calculation, the optimized parameters of the improved photodetectors are 20 nm in metal layer thickness, 60 nm in metal hole radius, 7 nm in quantum dot layer thickness, and 80 nm in barrier layer thickness. The maximum absorptivity value of the optimized photodetector can be as high as 86.47% at the frequency of ~ 300 Thz. The great enhancement of the absorptivity can be attributed to the local coupling effect caused by the enhancement of the electric field effect via the surface plasmon, and further leads to the high quantum efficiency and responsivity, which are 0.2961 and 0.0326 mA/W, respectively. It is believed that the current contribution could provide certain theoretical guidance for developing nanoscale QDIPs with high performance.

Verfügbarkeit von Daten und Materialien

Alle Daten sind uneingeschränkt verfügbar.

Abkürzungen

QDIPs:

Quantum dot infrared photodetectors

Fig

Figure

Eqs

Equations