Morphologische Evolution von Si(001)-Substraten mit Grubenmuster durch Reduktion der Oberflächenenergie

Hintergrund

Gitterfehlangepasste Heteroepitaxie mehrerer Halbleiter (wie Ge/Si oder InGaAs/GaAs) kann zur Bildung von 3D-Inseln nach dem Stranski-Krastanow (SK)-Wachstumsmodus führen. Während die Möglichkeit, solche Punkte durch reine Selbstorganisation zu erhalten [1, 2], besonders attraktiv ist und auf breites Interesse stößt, wurde bald erkannt, dass die zufällige Nukleation Anwendungen zusammen mit der Streuung in Größe und Form stark behindern könnte.

Jahrzehntelange Forschung führte zur Entwicklung einer Vielzahl von Methoden, um heteroepitaxiales Wachstum zur Bildung geordneter Strukturen voranzutreiben [3–7]. Unter diesen hat sich die Verwendung von Substraten mit Pit-Muster als eine der vielseitigsten Methoden erwiesen, um sowohl eine hohe Ordnung als auch eine Größenkontrolle von heteroepitaktischen Inseln zu erreichen [8–15].

Grübchenstrukturierte Substrate werden üblicherweise mit Methoden wie Nanoimprint-Lithographie [16–18], E-Beam-Lithographie [13, 14] kombiniert mit reaktivem Ionenätzen (RIE) [19, 20] oder nasschemischem Ätzen [21, 22] und Nanoindentation [23, 24], dh durch Top-Down-Ansätze. Mit diesen Methoden werden geordnete Muster von Pits mit hoher Präzision entworfen und führen unter geeigneten Wachstumsbedingungen [14, 25] zu einer nahezu perfekten lateralen Ordnung.

Da die tatsächliche Form von Grübchen die Energie des Systems und allgemein die Inselkeimbildung beeinflusst [26, 27], ist es entscheidend, ihre Morphologie zu kontrollieren. Das ist nicht trivial:Pits sind schließlich nur Löcher, die in den Untergrund gebohrt werden. Daher wird erwartet, dass die Kapillarität [28] bei ausreichend hohen Temperaturen eine morphologische Entwicklung hervorruft, die schließlich zu einer vollständigen Heilung führt. Tatsächlich werden häufig Glühprozesse oder eine weitere Abscheidung des Substratmaterials nach der anfänglichen Pit-Bildung verwendet, um reproduzierbare, langlebige metastabile Formen zu erreichen [8, 26]. Beachten Sie, dass selbst wenn eine Grube ihre Form stabilisiert hat, während der tatsächlichen Heteroepitaxie eine weitere Evolution vorangetrieben werden kann [29, 30].

In dieser Arbeit wollen wir die Entwicklung von Substraten mit Pit-Muster beschreiben, die durch die Reduktion der Oberflächenenergie durch Oberflächendiffusion angetrieben wird. Wir verwenden einen geeigneten Phasenfeld-Ansatz [31], der die Simulation von Längen- und Zeitskalen ermöglicht, die mit den experimentellen kompatibel sind [32]. Das Modell wurde bereits übernommen, um diffusionsbegrenzte Kinetiken während der morphologischen Evolution in heteroepitaktischen Systemen zu berücksichtigen [33–36]. Darüber hinaus wurde gezeigt, dass es die Entwicklung zum Gleichgewicht einschließlich realistischer anisotroper Oberflächenenergien richtig beschreibt [37–39].

Ohne Beschränkung der Allgemeinheit werden wir uns auf die relevanten Fälle von Si(001)-Oberflächen mit Vertiefungen konzentrieren, die in der Literatur umfassend untersucht wurden [8, 10, 14, 30, 40, 41].

Die Arbeit ist wie folgt organisiert. Im Abschnitt „Phasenfeldmodell“ veranschaulichen wir kurz das Phasenfeldmodell, mit dem die Entwicklung durch Oberflächendiffusion einschließlich anisotroper Oberflächenenergie beschrieben wird. Darüber hinaus beschreiben wir, wie die tatsächliche Si-Wulff-Form im betrachteten Ansatz berücksichtigt wird. Im Abschnitt „Glättung von Si(001)-Gruben“ wird die erwartete Glättung von Si(001)-Gruben, angetrieben durch die Reduktion der Oberflächenenergie, unter Berücksichtigung verschiedener Anfangskonfigurationen diskutiert und der kinetische Weg zum Gleichgewicht skizziert. Im Abschnitt „Nachahmung der Formänderung durch Ge-Überwachsen“ wird eine Anwendung des Verfahrens auf einen speziellen Fall von heteroepitaxialem Wachstum betrachtet, das der oberflächenenergiegetriebenen Formänderung beim Abscheiden einer dünnen Schicht von Ge auf Si-Pits entspricht. Schlussfolgerungen und Anmerkungen sind im Abschnitt „Schlussfolgerungen“ zusammengefasst.

Methoden

Phasen-Feld-Modell

Das Phasenfeldmodell berücksichtigt einen kontinuierlichen Ordnungsparameter φ , variierend zwischen φ =1 (durchgehend) und φ =0 (Vakuum) [31, 32]. Der Ansatz basiert auf einem Energiefunktional [37],

mit \(\Omega\in\mathbb{R}^{3}\) der Definitionsbereich von φ (r ) und r =(x ,y ,z ). Der erste Term entspricht der Grenzflächenenergie zwischen Phasen innerhalb der diffusen Grenzflächendomäne definiert durch φ d.h. auf die Oberflächenenergie der Festphase. \(\gamma(\hat{\mathbf{n}})\) ist die Oberflächenenergiedichte, mit \(\hat{\mathbf{n}}\) der nach außen weisenden Oberflächennormalen und ε die Dicke der Grenzfläche zwischen den Phasen. B (φ )=18φ ² (1−φ ) ² ist ein Double-Well-Potential mit einem Minima in φ =0 und φ =1 wie in Ref.-Nr. [31]. Der zweite Term in Gl. (1) ist die Willmore-Regularisierung, die im Regime der starken Anisotropie erforderlich ist, um die Bildung von scharfen Ecken zu vermeiden [37, 38, 42]. β ist ein Parameter, der der Eckenrundung entspricht.

Die Entwicklung für φ reproduziert die diffusionsbegrenzte Kinetik von Oberflächen und ist durch das entartete Cahn-Hilliard-Modell gegeben, d. h.

wobei μ =δ F /δ φ ist das chemische Potential, D der Diffusionskoeffizient ist und M (φ )=(36/ε )φ ² (1−φ ) ² ist die Mobilitätsfunktion auf die Oberfläche beschränkt. Die Gleichung für μ liest

mit κ =−ε ∇ ² φ +(1/ε )B ^′ (φ ) und g (φ )=30φ ² (1−φ ) ² [33, 37, 38]. Letzteres ist eine stabilisierende Funktion, die eine Konvergenz zweiter Ordnung in der Grenzflächendicke gewährleistet, ohne die Beschreibung des Materialtransports durch Oberflächendiffusion zu beeinträchtigen [43, 44]. Das Profil in der Richtung senkrecht zur Grenzfläche im Gleichgewicht wird gut beschrieben durch

wo d (r ) ist der vorzeichenbehaftete Abstand zum Zentrum der Grenzfläche zwischen den Phasen. Diese Gleichung wird verwendet, um die Anfangsbedingung für φ . festzulegen wie im Folgenden angegeben. Die Oberfläche der Festphase bezeichnen wir als φ ∼0.5 Isofläche. Alle geometrischen Eigenschaften der betrachteten Fläche lassen sich aus φ . ableiten , wie die nach außen weisende Flächennormale \(\hat{\mathbf{n}}=-\nabla\varphi/|\nabla\varphi |\).

Anisotrope Oberflächenenergie

Um anisotrope Oberflächenenergien zu beschreiben, haben wir die in [38, 39] eingeführte Definition der Oberflächenenergiedichte \(\gamma(\hat{\mathbf{n}})\) betrachtet:

wobei die Vorzugsorientierungen \(\hat{\mathbf{m}}_{i}\), dh die Richtungen, entlang derer die Oberflächenenergiedichte ein Minimum hat, zusammen mit ihren relativen Tiefen beliebig eingestellt werden können, α _ich , in Bezug auf γ ₀ . Die Parameter w _ich steuern die Ausdehnung der Regionen, in denen \(\gamma (\hat {\mathbf {n}})<\gamma_{0}\) um m _ich Richtungen, d.h. es sind nämlich die Breiten der Minima (siehe auch Lit. [38]).

Um die spezifische Anisotropie von Si-Kristallen zu berücksichtigen, legen wir die minimalen Energierichtungen m . fest _ich , entsprechend 001〉, 〈113〉, 〈110〉 und 〈111〉 [45]. α _ich Koeffizienten, die die Tiefe der Minima bestimmen, erhält man durch [39]

wobei α _〈001〉 =0.15 wird als Referenz gesetzt und die verschiedenen γ _ich entsprechen den Oberflächenenergiewerten der oben genannten Orientierungen, wie in Lit. berichtet. [45]. Ohne Beschränkung der Allgemeinheit setzen wir γ ₀ =1. Tatsächlich können die Verhältnisse der Minima und der Stärke der Anisotropie durch das α . gesteuert werden _ich Werte aus Gl. (6) und α _〈001〉 , während γ ₀ spielt die Rolle eines Vorfaktors in Gl. (2), beeinflusst also nur die absolute Zeitskala der Evolution.

Die Breite der Energieminima in Gl. (5) sind auf w gesetzt _ich =50 für alle Minima-Richtungen, außer w _〈113〉 =100 [39]. Nach dieser Definition der Parameter werden in der Wulff-Form scharfe Ecken vorhergesagt, d. h. die Oberflächenenergieanisotropie ist „stark“ [38, 42, 46]. Daher ist die Willmore-Regularisierung unbedingt erforderlich, um die Simulationen durchzuführen. Das β value legt die Ausdehnung des abgerundeten Bereichs an den Ecken fest, von denen bekannt ist, dass sie einen Radius proportional zu \(\sqrt {\beta}\) haben [37]. Um Simulationen durchzuführen, wird die Längenskala durch die Rundung an der Ecke um β muss größer sein als die Auflösung der räumlichen Diskretisierung des numerischen Verfahrens. Es ist jedoch erwähnenswert, dass kleine Facetten, die möglicherweise in der Wulff-Form mit einer Erweiterung in der Größenordnung von \(\sqrt {\beta}\) vorhanden sind, versteckt werden können, wenn zu große β . verwendet werden Werte sowie Facettierung im kleinen Maßstab, die Vorzugsorientierungen einschließt, die tatsächlich in der Wulff-Form vorhanden sind. In dieser Arbeit setzen wir β =0,005. Je nach Größe des Simulationsbereichs, der im Folgenden angegeben wird, ermöglicht dieser Wert eine praktikable räumliche Diskretisierung. Darüber hinaus sind alle Vorzugsorientierungen, die in die Gl. (5) und (6) sind wiedergegeben. Andererseits können mögliche Facettierungen mit kleineren Skalen als ∼0,07 aufgrund der Erweiterung der Eckenrundung nicht reproduziert werden.

Anfängliche Morphologie- und Simulationskonfiguration

Um jede morphologische Entwicklung durch das in diesem Abschnitt definierte Phasenfeldmodell zu untersuchen, ist eine geeignete Anfangsbedingung für φ muss eingestellt werden. Wir betrachten hier eine glatte Pit-Geometrie, die in eine (001)-ebene Oberfläche gehauen ist, mit einem Referenzsystem, das auf \(\hat{\mathbf{x}}=\,[\!100]\), \(\hat {\ mathbf {y}}=\,[\!010]\) und \(\hat {\mathbf {z}}=\,[\!001]\). Insbesondere betrachten wir eine kreisförmige (001) Fläche mit dem Radius L in einer Höhe h ₀ −H , glatt mit der umgebenden (001) ebenen Fläche in Höhe h . verbunden ₀ . Eine solche Geometrie wird als Anfangsbedingung für φ . gesetzt unter Ausnutzung von Gl. (4) mit d (r ) der vorzeichenbehaftete Abstand von der Oberfläche Γ (x ,y ) definiert durch

mit \(r=\sqrt {x^{2}+y^{2}}\) und

R =H /4L ist als Parameter für das Seitenverhältnis definiert, während σ ist ein Parameter, der die Ausdehnung der durchgehenden Verbindung zwischen dem Boden der Grube und dem sie umgebenden flachen Bereich steuert. Dieser Parameter wird hier auf σ . gesetzt =L /2.

In Abb. 1 gilt die Anfangsbedingung für φ ist illustriert. Abbildung 1 a zeigt Γ (x ,0) Profile mit unterschiedlichen Werten von R . Abbildung 1 b zeigt die Definition von φ mittels Gl. (4) in einer 3D-Parallelepiped-Domäne. Insbesondere zeigt diese Tafel einen Querschnitt durch die Mitte des gesamten Bereichs. Der linke Teil zeigt die der Festphase entsprechende Region, d. h. die Region, in der φ>0,5, wodurch die Oberfläche sichtbar wird, die der anfänglichen Vertiefungsmorphologie entspricht. Der rechte Teil zeigt die Werte von φ im gesamten 3D-Bereich, d. h. in den Bulk-Phasen und im kontinuierlichen Übergang zwischen ihnen.

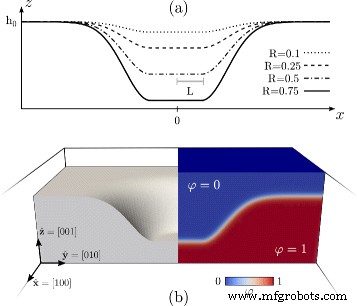
Anfangsbedingung für das Phasenfeldmodell, das einem glatten Pit an der (001)-Oberfläche eines festen Films ähnelt. a Γ (x ,0) Profile aus Gl. (7) erhalten für verschiedene R Werte. b Definition von φ im 3D-Bereich für numerische Simulationen übernommen. Sie ergibt sich aus Gl. (4) mit d (r ) die vorzeichenbehaftete Entfernung von Γ (x ,y ) mit R =0,5. Links die Festphase mit φ> 0,5 wird angezeigt. Rechts eine Farbkarte mit φ im 3D-Bereich wird gemeldet

Numerische Simulationen werden durchgeführt, um Gl. (2) und (3). Sie werden unter Verwendung der Finite-Elemente-Methode (FEM)-Toolbox AMDiS [47, 48] mit einem semi-impliziten Integrationsschema und einer Netzverfeinerung an der Schnittstelle durchgeführt [33, 38, 49]. Periodische Randbedingungen werden entlang der Richtungen \(\hat{\mathbf{x}}\) und \(\hat{\mathbf{y}}\) gesetzt. No-Flux (Neumann)-Randbedingungen werden am oberen und unteren Rand des Simulationsbereichs entlang der \(\hat{\mathbf{z}}\)-Richtung festgelegt. Die Zeitskala der Evolution wird um den Faktor 1/D skaliert , was dem Set D . entspricht =1. Im Folgenden beziehen wir uns auf den Zeitpunkt der Simulationen in willkürlichen Einheiten. Die Größe der Grube ist willkürlich auf L eingestellt =1, während die Grenzflächendicke auf ε . eingestellt ist =0,2.

Ergebnisse und Diskussion

Glättung von Si(001)-Gruben

In diesem Abschnitt veranschaulichen wir die Ergebnisse zu den morphologischen Veränderungen während der Entwicklung von grubengemusterten Si(001)-Substraten. Das oben beschriebene Modell ermöglicht die Beschreibung des Sonderfalls Silizium durch die Definition der anisotropen Oberflächenenergie wie im Abschnitt „Anisotrope Oberflächenenergie“. Wir erwarten, dass die folgenden Ergebnisse aus qualitativer Sicht für jede Größe gültig sind, vorausgesetzt, das System ist groß genug, um einen Kontinuumsansatz (\(\gtrsim 10\) nm) [32] zu verwenden und die Form kann parametrisiert werden durch das Seitenverhältnis R ähnlich Abb. 1 a. Die tatsächliche Längenskala kann durch Einstellen des L . berücksichtigt werden Parameter auf den entsprechenden in realen Einheiten, L ^r . Die Echtzeitskala kann dann beschrieben werden, indem reelle Werte von D . berücksichtigt werden und γ ₀ und Multiplizieren mit dem L ^r Länge, d. h. durch Skalierung um L ^r /L mit L einheitlich wie oben angegeben.

Konzentrieren wir uns zunächst auf die ersten Stadien der Evolution. Die durch Gl. (7) besteht aus einem Profil, das keine Vorzugsorientierung der Oberfläche aufweist. Betrachtet man die Entwicklung durch Oberflächendiffusion, die durch die Reduzierung einer anisotropen Oberflächenenergie angetrieben wird, wird eine Facettierung des anfänglichen Profils erwartet. Dies ist in Abb. 2 dargestellt, wo die Facettierung zweier Profile mit R =0,25 in Abb. 2 a und R =0.5 in Abb. 2 b berichtet. Eine Farbskala veranschaulicht die Werte \(\gamma (\hat{\mathbf{n}})\) an der Oberfläche. Dies ermöglicht es, die Facetten als die Bereiche mit einer nahezu einheitlichen Oberflächenenergiedichte zu identifizieren, die den Minima von Gl. (5), begrenzt durch lokalisierte Gebiete mit hohen Werten von \(\gamma(\hat{\mathbf{n}})\). Entsprechend dem anfänglichen Seitenverhältnis des Pits bilden sich unterschiedliche Facetten. Für das kleinere R wird die (001)-Facette am unteren Rand beibehalten und nimmt eine quadratische Form an. Die Kanten des Pits werden durch vier {113}-Facetten begrenzt, die durch kleine, dreiecksförmige {110}-Facetten verbunden sind. Entsprechend dem größeren Seitenverhältnis liegt eine größere facettierte Oberfläche vor, wenn R . berücksichtigt wird =0,5, was das Auftreten von Vorzugsorientierungen mit höherer Neigung in Bezug auf die (001)-Oberfläche ermöglicht. Insbesondere ermöglicht die Ausgangsform das Vorhandensein von {111}-Facetten, die sich zwischen zwei {113}-Facetten nahe dem Boden und dem flachen Bereich bilden. Dazwischen bilden sich breite {110} Facetten.

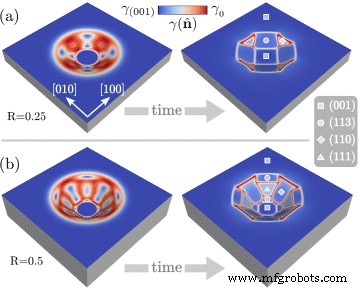
Facettierung des Anfangsprofils gemäß der Definition im Abschnitt „Initial Morphology and Simulation Setup“ gemäß Oberflächendiffusion und \(\gamma (\hat{\mathbf{n}})\) Reproduktion der Oberflächenenergie von Si. Zwei verschiedene Ausgangsmorphologien werden berücksichtigt:a R =0,25 und b R =0,5. Bei den facettierten Morphologien werden Symbole verwendet, um die Facettenfamilien zu identifizieren. Die Farbskala zeigt die Werte von \(\gamma (\hat{\mathbf{n}})\) an der Oberfläche

Die in Fig. 2 berichteten Ergebnisse zeigen die Möglichkeit, die Morphologie der facettierten Vertiefungen gemäß dem Seitenverhältnis oder allgemein gemäß der anfänglichen Morphologie vorherzusagen. Wir untersuchen nun auch die Dynamik auf langen Zeitskalen, indem wir die morphologische Entwicklung bis zum Gleichgewicht untersuchen [38]. Dies ist in Abb. 3 dargestellt, wo wir uns auf die tiefste bisher betrachtete Grube konzentrieren, d. h. mit R =0,5, und die wichtigsten morphologischen Veränderungen sind gezeigt. Insbesondere sind in Abb. 3 a bzw. b eine perspektivische Ansicht und eine Draufsicht der verschiedenen Morphologien dargestellt, die während der Evolution erhalten wurden. In der ersten Phase dieser Simulation beobachten wir das Verschwinden der steilsten {111}-Facetten und die Vergrößerung benachbarter {113}-Facetten. Dann verschmelzen die letzteren und die Schrumpfung der {110}-Facetten beginnt. Es wird festgestellt, dass diese in späteren Stadien verschwinden, nachdem sie eine dreieckige Form angenommen haben, was der Grube von oben einen quadratischen Umriss verleiht. Außerdem verschwinden {113}-Facetten schließlich und eine globale Abflachung wird erreicht. Die in dieser Simulation erhaltene Echtzeitskala kann mit Daten aus der Literatur abgeschätzt werden. Insbesondere können wir D . betrachten bestimmt durch das Arrhenius-Gesetz mit Vorfaktor und Aktivierungsenergie aus Lit. [50], wobei auch thermische Fluktuationen berücksichtigt werden. γ ₀ hat \(\gamma (\hat{\mathbf{n}})\sim 8.7\) eV/nm ² wenn \(\hat{\mathbf{n}}=(001)\) [51] aus Gl. (5), das heißt γ ₀ =10,2 eV/nm ² . Die anderen materialabhängigen Oberflächendiffusionskoeffizienten [28], d. h. das Atomvolumen und die Dichte an der Oberfläche, werden so eingestellt, dass sie den Fall von Si nachbilden. Nach diesen Werten beträgt die erwartete Dauer des gesamten Prozesses bei hoher Temperatur T ∼1100−1200 °C für L ^r von mehreren zehn Nanometern liegt in der Größenordnung von Stunden.

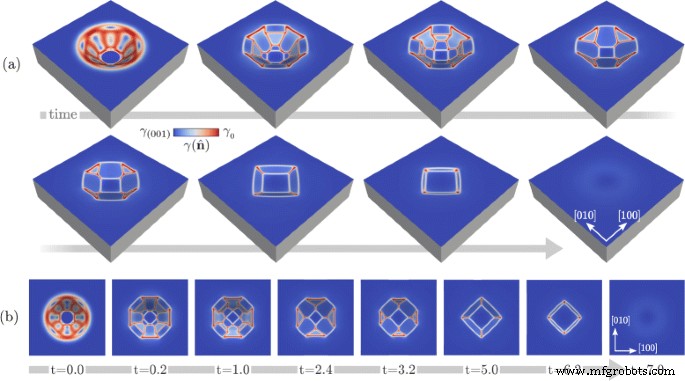
Entwicklung in Richtung des Gleichgewichts für eine Si-Grube mit einer anfänglichen Morphologie wie in Fig. 2b. a Perspektivische Ansicht mit den wichtigsten morphologischen Veränderungen. b Draufsicht der Morphologien in Tafel a . Die im Feld b gemeldete Zeit wird in willkürlichen Einheiten ausgedrückt. Die Farbskala zeigt die Werte von \(\gamma (\hat{\mathbf{n}})\) an der Oberfläche

Neben den spezifischen morphologischen Veränderungen, die während der Evolution auftreten, sind zwei Hauptmerkmale zu beachten. Erstens führt die Evolution zu der erwarteten globalen Abflachung der Oberfläche, und dies geschieht mit dem allmählichen Verschwinden steiler Facetten, die durch flachere ersetzt werden. Obwohl dieses Verhalten nur durch Argumente zur Energieminimierung und Verringerung des Seitenverhältnisses abgeleitet werden kann, ist es erwähnenswert, dass hier die vollständige Entwicklung bereitgestellt wird, die sich mit dem Vorhandensein ähnlicher Facetten, aber mit unterschiedlichen relativen Größen befasst. Dies stimmt mit der Tatsache überein, dass die während der Evolution erhaltenen Morphologien Konfigurationen außerhalb des Gleichgewichts entsprechen und einen Weg zum globalen Energieminimum definieren. Obwohl die erwarteten Facetten und ihre Energetik bekannt sind, kann die spezifische Morphologie zu einem bestimmten Zeitpunkt der Evolution nur unter Berücksichtigung der Dynamik und nicht nur unter Berücksichtigung der globalen Energieminimierung beschrieben werden [38].

Der zweite wichtige Punkt, den die Ergebnisse in Abb. 3 zeigen, betrifft die Zwischenstufen. Wenn sich die Form während der Evolution einer Geometrie mit einer Tiefe nähert, die dem mit R . erhaltenen anfänglichen Profil ähnelt =0,25, d. h. bei t ∼3.2, die durch die Energieminimierung induzierte Morphologie ähnelt sehr der in Abb. 2 b beschriebenen, selbst wenn von einer Ausgangskonfiguration mit signifikantem Tiefenunterschied (in diesem Fall doppelt) ausgegangen wird. Dies legt die Existenz eines gemeinsamen kinetischen Weges zur endgültigen Abflachung nahe, der nach der ersten schnellen Facettierung der anfänglichen Morphologie erreicht wird. Dieses Argument wird tatsächlich bestätigt und in den Diagrammen von Abb. 4 weiter veranschaulicht. Hier wird der monotone Energieabfall während der Entwicklung nach der anfänglichen Facettierung berichtet, wenn Pits mit R . betrachtet werden gleich 0,1, 0,25, 0,5 und 0,75 wie in Abb. 1 a. In Abb. 4 a wird die in willkürlichen Einheiten ausgedrückte Zeitskala betrachtet. In Abb. 4 b sind die gleichen Energieänderungen mit einer richtigen Verschiebung der Zeitskala dargestellt, was den ähnlichen Energieabfall bei Annäherung an ähnliche Seitenverhältnisse der Struktur hervorhebt. \(t^{*}_{R}\) ist definiert als der Zeitpunkt, an dem die ebene Oberfläche erhalten wird, dh der Zeitpunkt, an dem das globale Energieminimum erreicht wird, das für jede Simulation unterschiedlich ist, wie in Abb. 4a. Wie in diesem Diagramm gezeigt, überlappen sich die Energiezerfälle für R . fast 0,5. Ein sehr kleiner Unterschied wird nur beobachtet, wenn R . berücksichtigt wird =0.75, deren Energiezerfallsergebnisse noch sehr nah an den anderen Kurven liegen und die Unterschiede für \(t\gtrsim 5.0\) im Grunde verschwinden. Erwähnenswert ist, dass bei großen Abweichungen von der Ausgangskonfiguration, nämlich mit R ≫1, solche Geometrien können sich mit unterschiedlichen Auswirkungen auf Zeitskalen und Morphologien unterschiedlich entwickeln [52, 53]. Darüber hinaus ist bekannt, dass in Extremfällen topologische Veränderungen auftreten, z. B. bei sehr tiefen Gräben, die die Möglichkeit verhindern, das globale Gleichgewicht mit einer flachen (001) Oberfläche zu erreichen [34, 39, 54].

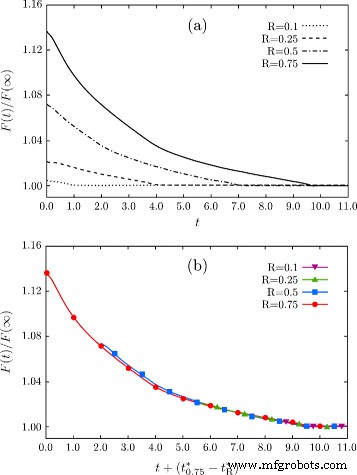
Energieabnahme während der Entwicklung von Grubengeometrien. a F (t ) normiert durch die Energie der flachen (001) Oberfläche, die als letzte Stufe der Entwicklung erhalten wird. Aus den Simulationen erhaltene Energiezerfälle mit unterschiedlichen R für das Anfangsprofil, nämlich von R =0,1 bis R =0,75, angezeigt. Die Zeit wird in willkürlichen Einheiten ausgedrückt. b Kurven wie in Panel a verschoben, um \(t_{R}^{*}\) zu entsprechen, d. h. der Zeitpunkt, zu dem die globale Abflachung der Grube in Abhängigkeit von R . erreicht wird

Es wird erwartet, dass die in den Simulationen in diesen Abschnitten erhaltenen Formen in Experimenten beobachtet werden, insbesondere wenn die Verarbeitung Bedingungen nahe der thermodynamischen Grenze umfasst. Einige der in 3 berichteten Morphologien entsprechen tatsächlich dem Umriss von Si(001)-Substraten mit Vertiefungen. Zum Beispiel eine Morphologie, die aus einer breiten (001)-Fläche besteht, die von schmalen {113}-Facetten begrenzt ist, wie in Fig. 3 bei t ∼5,0 werden beobachtet, wenn Si(001)-Substrate mit Pit-Muster mit einem Aspektverhältnis von 0,05<R . betrachtet werden <0,1 wie in Ref.-Nr. [10, 30]. Auch die relative Ausdehnung der Facetten im oben erwähnten Stadium der Simulation von Fig. 3 ist dem, was in diesen experimentellen Arbeiten berichtet wurde, sehr ähnlich. Diese Übereinstimmung zwischen Simulationen und Experimenten bewertet die hier angenommene theoretische Beschreibung der Oberflächendiffusion weiter. Wir haben uns jedoch auf die allgemeinen Merkmale des Verfahrens konzentriert und ein detaillierterer Vergleich mit spezifischen Experimenten ist nicht der Zweck dieser Arbeit.

Nachahmen der Formänderung aufgrund von Ge-Überwucherung

Wie in der Einleitung erwähnt, ist eine der Hauptanwendungen von Si-Templaten mit Vertiefungen die Kontrolle des Wachstums selbstorganisierter Inseln [55]. Dies gilt insbesondere bei Betrachtung der Positionierung von Ge oder Si_{1 − c} Ge _c Inseln auf Si(001)-Substraten [6]. Mit der im vorherigen Abschnitt angewandten Methodik können wir die morphologischen Veränderungen im Zusammenhang mit den besonderen Eigenschaften der Oberflächenenergie untersuchen. Wenn wir daher von einer geeigneten Anfangskonfiguration ausgehen, die der realen Morphologie eines Si-Pits ähnelt, und die Unterschiede in der Oberflächenenergiedichte berücksichtigen, die bei der Abscheidung eines anderen Materials zu erwarten sind, können wir den entsprechenden Beitrag zu morphologischen Veränderungen vorhersagen.

Die Fallstudie besteht hier in der Überwucherung von Ge über einem Si(001)-Pit-gemusterten Substrat mit einem Aspektverhältnis nahe 0,1. Das Profil von Abb. 3 bei t =5,0 wird als anfängliche Morphologie betrachtet. Dann wird eine Oberflächenenergie, die auch Minima entlang der 105〉-Richtungen enthält, eingestellt. Diese Definition von \(\gamma (\hat{\mathbf{n}})\) ahmt das Vorhandensein der am meisten bevorzugten Orientierung mit kleiner Steigung in Ge/Si(001)-Systemen nach [56–58]. Die hohe Stabilität von {105}-Facetten ist auf das Zusammenspiel zwischen Oberflächenrekonstruktion und Dehnungseffekten im Zusammenhang mit der Gitterfehlanpassung zwischen der Epischicht und dem Substrat zurückzuführen [59–61]. Der in Gl. (6) ist aus Lit. entnommen. [58] im Grenzbereich einer dicken Ge-Schicht. Beachten Sie, dass andere Facetten, deren Oberflächenenergie näher an (001) liegt, wie {1 1 10}, hier vernachlässigt werden. Da die Winkel zwischen den Richtungen 〈105〉 und [001] sehr klein sind, w _ich Parameter, die größer als die zuvor angenommenen sind, sind erforderlich, um die Energieminima von Gl. (5) [38]. Insbesondere setzen wir w _{105} =w _{001} =500.

In Abb. 5 ist die Entwicklung durch Oberflächendiffusion mit der neuen Definition von \(\gamma(\hat{\mathbf{n}})\) dargestellt. Abbildung 5 a zeigt die morphologische Entwicklung der Oberfläche mit einer Vergrößerung des z -Achse um den Faktor 5. In den ersten Phasen bilden sich {105}-Facetten zwischen den {113}-Facetten, die im Anfangsprofil vorhanden sind. Da 〈105〉-Orientierungen die minimale Energie haben, wie auch in Abb. 5b dargestellt, dehnen sich die entsprechenden Facetten aus, während {113}-Facetten schrumpfen. In späteren Stadien bildet sich nur noch eine von {105}-Facetten begrenzte Grube mit noch einer (001)-Fläche am Boden. Aus der Draufsicht wie in Abb. 5 b führt die Veränderung der Morphologie zu einer Drehung des Umrisses der Grube um 45°. Dies wird tatsächlich während der Abscheidung von Ge auf Si-gemusterten Substraten in Experimenten beobachtet [41] oder während des spontanen Wachstums von Grübchen aufgrund von Defekten oder Verunreinigungen [40]. Die Bildung von {105}-Facetten gilt auch als bevorzugte Keimbildungsstelle für das weitere Wachstum von Ge-Punkten [30]. Die in Fig. 5 dargestellte Entwicklung zeigt, dass eine Formänderung, die zu einer Drehung des Grubenumrisses führt, nur aufgrund der Reduzierung der Oberflächenenergie erreicht werden kann. Dies wird voraussichtlich die reale Situation unter Gleichgewichtsbedingungen sein, wenn thermodynamische Triebkräfte von Oberflächenbeiträgen dominiert werden, d. h. für kleine Ge-Volumina. Tatsächlich müssen zur vollständigen Beschreibung des Prozesses Elastizitätseffekte, Durchmischungen und das Wachstum der Festphase einbezogen werden [32]. Es ist auch erwähnenswert, dass in Experimenten noch flachere Si-Pits verwendet werden, die Facetten mit Normalen entlang {11n . zeigen } Richtungen, mit 5<n <10 [41] (d. h. {1 1 10} Facetten). Die durch diese Facetten begrenzte Pit-Geometrie würde zu einer ähnlichen Entwicklung führen, da sie der angenommenen Anfangskonfiguration von Fig. 4 mit nur einer geringeren Steigung in Bezug auf die (001)-Ebene entspricht.

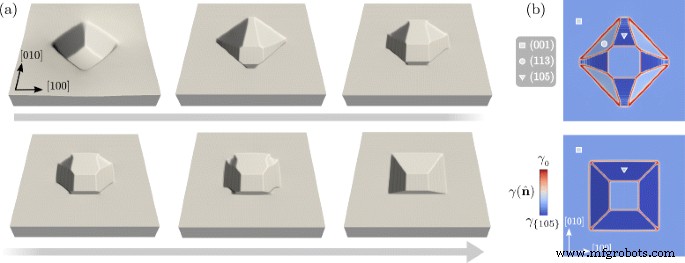
Entwicklung des Profils in Abb. 3 bei t =5.0, mit einer Definition der Oberflächenenergie einschließlich 〈105〉-Orientierungen. a Oberflächenprofile in repräsentativen Stadien der Entwicklung zur Bildung einer Grube, die nur durch {105}-Facetten begrenzt wird. z -Achse wird um den Faktor 5 vergrößert. b Draufsicht mit den \(\gamma(\hat{\mathbf{n}})\)-Werten an der Oberfläche. Die zweite und letzte Phase des Panels a werden im oberen bzw. unteren Teil berichtet. Symbole wie in Abb. 2 werden verwendet, um verschiedene Familien von Facetten zu identifizieren

Schlussfolgerungen

In dieser Arbeit haben wir ein auf Oberflächendiffusion basierendes Kontinuumsmodell verwendet, um die zeitliche Entwicklung von Gruben zu untersuchen, die in einem Si(001)-Substrat ausgehoben wurden. Durch geeignetes Angehen der (starken) Oberflächenenergie-Anisotropie mit einer Parametrisierung basierend auf der bekannten Si-Wulff-Form haben wir in Übereinstimmung mit Experimenten typische metastabile Konfigurationen vorhergesagt, einschließlich des Falles, in dem die Abscheidung eines anderen Materials neue stabile Facetten einführt. Die gesamte Entwicklung hin zur globalen Abflachung der Grube wurde veranschaulicht, und es zeigt sich, dass sie auch bei Betrachtung von Gruben mit unterschiedlichen Anfangstiefen dem gleichen kinetischen Pfad folgt. We believe that the model can be predictive also for initial configurations strongly deviating from the ones which we have analyzed as examples. As a consequence, the present approach can be useful in designing experiments based on still-unexplored pit shapes. Furthermore, the model is general and can be easily adapted to different substrates upon re-parametrizing the surface energy.