Erhöhter Einschluss von Terahertz-Oberflächenplasmonpolaritonen in Bulk-Dirac-Halbmetall-Isolator-Metall-Wellenleitern
Zusammenfassung
Es wird ein plasmonischer Subwellenlängen-Terahertz-Wellenleiter basierend auf einer Bulk-Dirac-Halbmetall-(BDS)-Isolator-Metall-(BIM)-Struktur untersucht, was darauf hindeutet, dass es einen optimierten Frequenzbereich mit besserem Einschluss sowie geringeren Verlusten gibt. Eine Breitbandmodusbeschränkung bis zu λ 0 /15 mit einem relativ geringen Verlust von 1,0 dB/λ 0 Kann erreicht werden. Wir zeigen auch, dass zwei Siliziumbänder, die in den BIM-Wellenleiter eingeführt werden, einen dynamisch abstimmbaren Filter bilden können, der Terahertz-Oberflächenplasmonenpolaritonen im tiefen Subwellenlängenbereich maßschneidert, was weiter für das Design ultrakompakter plasmonischer THz-Bauelemente mit dynamischer Abstimmbarkeit genutzt werden kann. Unsere Ergebnisse können auch potenzielle Anwendungen in der optischen Filterung bieten.
Hintergrund
Die Terahertz (THz)-Welle wurde in den letzten Jahrzehnten wegen ihrer innovativen Anwendungen wie THz-Bildgebung, biochemischer Sensorik und Kommunikation extrem beobachtet [1,2,3]. Um die Sensibilität, die Bildauflösung und das Integrationsniveau von THz-Geräten zu verbessern, ist es dringend erwünscht, die THz-Welle auf eine tiefe Subwellenlängenskala zu beschränken [4,5,6]. Oberflächenplasmonenpolaritonen (SPPs), die elektromagnetischen Oberflächenmoden, die durch die Wechselwirkung zwischen Elektron im Leitungsband des Edelmetalls und Photonen im sichtbaren Wellenlängenbereich stimuliert werden, breiten sich entlang der Metall-Isolator-Grenzfläche aus und ermöglichen die Manipulation von Licht über die klassische Beugungsgrenze hinaus [7]. Sommerfeld-Zenneck-Moden, analog zu SPPs im sichtbaren Band, können durch Metall im THz-Bereich unterstützt werden. Metamaterialien und andere künstliche Strukturen wie periodische Patches, perforierte Platten und Messingrohre wurden vorgeschlagen, um diese lose gebundenen Oberflächenwellen maßzuschneidern [8,9,10]. Leider haben schlechte Begrenzung, hoher Eigenverlust und passive Abstimmbarkeit dieses Modus seine praktischen Anwendungen stark behindert.
Graphen-Plasmonen mit relativ geringem Verlust, dynamischer Abstimmbarkeit und extremer Beschränkung auf THz-Wellen halten vielversprechende Anwendungen in hochauflösenden, ultrakompakten und dynamisch abstimmbaren Geräten. Duanet al. schlagen eine Gate-abstimmbare Breitband-Gate-Heterostruktur vor, um Terahertz-Plasmonen mit dynamischer Abstimmbarkeit und höherer Effizienz kohärent zu erzeugen und zu kontrollieren. Aufgrund der engen Begrenzung des Graphen-Plasmonenfelds kann ein robustes Differenzfrequenzsignal erzeugt werden [11]. Duanet al. untersuchen zunächst den diskreten Talbot-Effekt in dielektrischen Graphen-Plasmonenwellenleiter-Arrays bei THz-Wellenlängen, was eine neuartige Plattform für ein hochauflösendes Selbstbild von THz-Wellen im Nanomaßstab bietet [12]. Linet al. schlagen einen ultrakompakten plasmoneninduzierten transparenten Wellenleiter vor, der potenzielle Anwendungen im langsamen Licht von THz-Wellen verspricht [13, 14]. Liet al. schlagen eine Reihe funktioneller optischer Filter und Absorber auf Basis von 2D-Materialplasmonen vor, die eine hohe Integration [15], geringen Verlust und dynamische Durchstimmbarkeit aufweisen [16,17,18]. Von diesen Arbeiten können wir überzeugen, dass es die extreme Eingrenzung von Oberflächenplasmonen ist, die es möglich macht, THz-Wellen im tiefen Subwellenlängenbereich zu manipulieren.
Kürzlich rückten Bulk-Dirac-Halbmetalle (BDS), „3-D-Graphen“, aufgrund ihrer ultrahohen Trägermobilität von bis zu 9 × 10 6 . in den Fokus cm 2 V −1 s −1 , was viel höher ist als das beste Graphen von 2 × 10 5 cm 2 V −1 s −1 [19]. Im Allgemeinen ist der intrinsische Verlust von Plasmonen umso geringer, je höher die Trägermobilität ist. Darüber hinaus können die dielektrischen Funktionen von BDS durch Änderung seiner Fermi-Energie aktiv eingestellt werden. Die gute Nachricht ist, dass BDS wie Na3 Bi [19], Cd3 Als2 [20] und AlCuFe-Quasikristalle [21] sind einfacher zu verarbeiten und stabiler als Graphen, von dem erwartet wird, dass es nach Graphen eine neue Generation von plasmonischem Material darstellt. Die Modusbeschränkung von SPPs in der BDS-Isolator-Schnittstelle ist jedoch nicht optimistisch. Unsere neuere Arbeit hat die Manipulation der THz-SPPs in doppellagigen BDS-Schichtwellenleitern untersucht, was darauf hindeutet, dass der symmetrische Kopplungsmodus eine bessere Begrenzung hat als der plasmonische Wellenleitermodus in einem einschichtigen BDS-Film [22]. Der Modenindex der symmetrischen Mode beträgt 1,21 bei 1,0 THz mit der Fermi-Energie von BDS E F = 70 meV, was immer noch nicht ausreicht, um die Nachfrage nach Manipulation der THz-Welle im tiefen Subwellenlängenbereich zu decken.
In diesem Artikel schlagen wir einen BDS-Isolator-Metall (BIM)-Wellenleiter mit tiefer Subwellenlänge mit verbesserter Begrenzung, relativ geringem Verlust und wünschenswerter Abstimmbarkeit vor. Dispersionsbeziehung, Ausbreitungsverlust und Filteranwendung dieser stark eingeschränkten Mode werden untersucht. Interessanterweise gibt es einen optimierten Frequenzbereich mit einer verbesserten Begrenzung sowie einem reduzierten Verlust, der im traditionellen SPP-Modus in Metallstruktur selten berichtet wurde. Eine Breitbandmodusbeschränkung bis zu λ 0 /15 mit einem relativ geringen Verlust von 1,0 dB/λ 0 Kann erreicht werden. Anders als bei der zuvor untersuchten BDS-basierten Struktur kann die Mode dieses BIM-Wellenleiters effizient durch einen ultraschmalen Schlitz mit einer Breite kleiner als λ . übertragen werden 0 /2000. Durch die Verwendung von zwei Siliziumbändern als Reflexionsspiegel wurde ein dynamisch abstimmbarer optischer Resonator erreicht. Die Resonanzfrequenz des Resonators kann durch Variieren der Fermi-Energie von BDS dynamisch abgestimmt werden, was Anwendungen beim THz-Schalten und -Filtern finden kann.
Theorie und Simulation
Der vorgeschlagene plasmonische BIM-Wellenleiter ist schematisch in Abb. 1(a) dargestellt, wo der einschichtige BDS-Film mit einer Dicke von 0,2 μm mit einer Spaltbreite von g . platziert wird vom Silbersubstrat getrennt durch den dielektrischen Abstandshalter mit Permittivität ε r . Das Silbersubstrat im THz-Bereich kann als Grenze eines perfekten elektrischen Leiters (PEC) behandelt werden. Für das TM-polarisierte einfallende Licht kann sich die plasmonische Wellenleitermode, die in der Metall-Isolator-Grenzfläche eingeschlossen ist, entlang der x . ausbreiten Richtung mit einem Wellenvektor k SPP und exponentieller Zerfall entlang des y Richtung in den freien Raum. Durch Kombination geeigneter Randbedingungen wird der Wellenvektor k SPP des BIM-Wellenleiters kann aus der folgenden Dispersionsrelation erhalten werden:[23].
$$ -\frac{\varepsilon_r\sqrt{k_{\mathrm{SPP}}^2-{k}_0^2}}{\varepsilon_0\sqrt{k_{\mathrm{SPP}}^2-\frac{ \varepsilon_r{k}_0^2}{\varepsilon_0}}}=\left(1+\frac{i\sigma \sqrt{k_{\mathrm{SPP}}^2-{k}_0^2}}{ {\omega\varepsilon}_0}\right)\tanh\left(g\sqrt{k_{\mathrm{SPP}}^2-\frac{\varepsilon_r{k}_0^2}{\varepsilon_0}}\right ), $$ (1)wo k 0 ist der Wellenvektor des einfallenden Lichts. Durch Lösen von Gl. (1), erhalten wir den effektiven Brechungsindex n eff = k SPP /k 0 = Re(n eff ) + i Im(n eff ) des vorgeschlagenen plasmonischen Wellenleiters. Für die stark eingeschränkten plasmonischen Wellenleitermoden ist der Realteil des effektiven Brechungsindex Re(n eff ) beschreiben grob die Modenbeschränkung, während der Imaginärteil Im(n eff ) ist direkt proportional zum Modenausbreitungsverlust:Je größer Re(n eff ) ist, desto höher ist der Einschluss. Wenn g groß genug ist, sodass tanh[g (k SPP 2 − ε r k 0 2 /ε 0 )] ~ 1, Gl. (1) würde auf die Dispersionsrelation reduziert
$$ -\frac{\varepsilon_r\sqrt{k_{\mathrm{SPP}}^2-{k}_0^2}}{\varepsilon_0\sqrt{k_{\mathrm{SPP}}^2-\frac{ \varepsilon_r{k}_0^2}{\varepsilon_0}}}=\left(1+\frac{i\sigma \sqrt{k_{\mathrm{SPP}}^2-{k}_0^2}}{ {\omega\varepsilon}_0}\right), $$ (2)die den plasmonischen Wellenleitermodus darstellt, der nur von einer einzigen BDS-Schicht unterstützt wird. Die komplexe Leitfähigkeit von BDS wird in den Methoden Gl. (3)–(4) dargestellt.
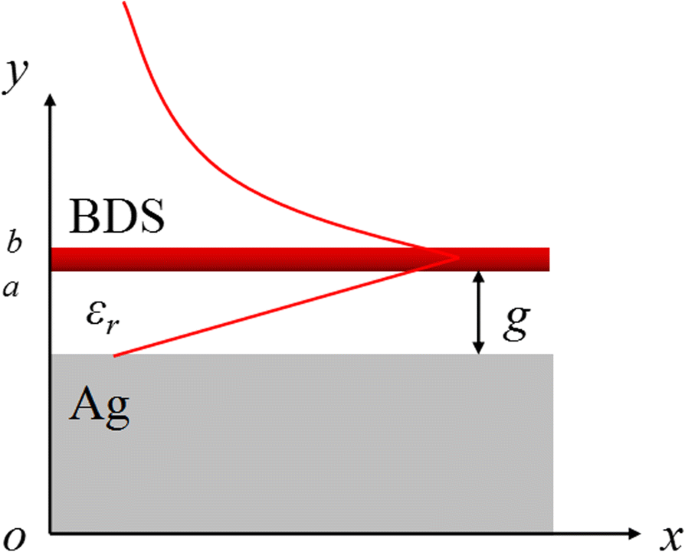
Schematische Darstellung des plasmonischen BIM-Wellenleiters:Ein einschichtiger BDS-Film wird mit einer Spaltbreite von g . platziert vom Silbersubstrat getrennt durch einen dielektrischen Abstandshalter mit Dielektrizitätskonstante ε r . Die TM-polarisierte plasmonische Wellenleitermode breitet sich entlang der x . aus Richtung und Zerfälle entlang des y Richtung. Schematische Darstellung des E x Verteilung wird durch die rote Linie dargestellt
Ergebnisse und Diskussion
Zuerst demonstrieren wir die Abhängigkeit der Modenbegrenzung und der Ausbreitungsdämpfung des BIM-Wellenleiters von der BDS-Metallspaltbreite g und Fermi-Energie E F . Durch die Einnahme von E F = 70 meV berechnen wir die effektiven Brechungsindizes des SPP-Wellenleitermodus n eff für verschiedene Werte von g , wobei seine Real- und Imaginärteile Re(n eff ) und Im(n eff ) sind in Abb. 2a bzw. b aufgetragen. Wie in Abb. 2a dargestellt, sind die Kurven für g = 10 und 100 μm verschmelzen bei Frequenzen über 0,05 THz, was darauf hindeutet, dass die plasmonischen Wellenleitermoden so eng in der BDS-Isolator-Schnittstelle begrenzt sind, dass die meisten SPP-Felder innerhalb der Skala von 10 μm verteilt sind und das Silber nicht funktionieren würde bei so großer Spaltweite. Während die Modenbeschränkung nach der Spaltbreite g . dramatisch verbessert wird allmählich von 1 μm verringert wird, je kleiner g Forschungen, und die stärkere Einschließung erreicht werden kann. Eine ähnliche Tendenz ist in der Abhängigkeit der Ausbreitungsdämpfung von der Spaltbreite g . zu beobachten , wie in Abb. 2b dargestellt. Andererseits gilt für eine feste Spaltbreite von weniger als 1 μm Re(n eff ) zeigt jeweils zunächst eine ausgeprägte Reduktion auf ein Minimum und zeigt dann ein allmählich zunehmendes Verhalten, während Im(n eff ) nimmt mit steigender Frequenz jeweils monoton ab. Somit gibt es einen optimierten Frequenzbereich, in dem die Modenbegrenzung stark erhöht wird, während der Ausbreitungsverlust allmählich verringert wird. Diese Eigenschaft wurde bei herkömmlichen plasmonischen Wellenleitermoden an der Metall-Isolator-Grenzfläche selten beobachtet. Abbildung 2c, d zeigt die Abhängigkeit des Modeneinschlusses und des Ausbreitungsverlusts von der Fermi-Energie E F der BDS-Folie, wobei die Spaltbreite g = 1 μm. Ähnlich wie bei einem einschichtigen und doppelschichtigen Wellenleiter nehmen die Modenbegrenzung und der Ausbreitungsverlust mit zunehmender Fermi-Energie kontinuierlich ab, was auf die erhöhte Metallizität und verlängerte Ladungsträgerrelaxationszeit von BDS zurückgeführt werden kann. Der Begrenzungsfaktor des plasmonischen Wellenleitermodus bei 2,5 THz kann beispielsweise bis zu λ . betragen 0 /15, wo ist λ 0 die einfallende Wellenlänge mit einem relativ geringen Verlust von 1,0 dB/λ 0 wenn die Spaltbreite des BDS-Metalls 10 nm beträgt und die Fermi-Energie 70 meV beträgt. Daher würde die Verwendung von Frameworks, die bereits oben diskutiert wurden, die Modenbegrenzung mit relativ geringem Verlust erhöhen, was für das Design von integrierten optischen Filtern, Puffern und Mach-Zehnder-Interferometern verwendet werden kann.
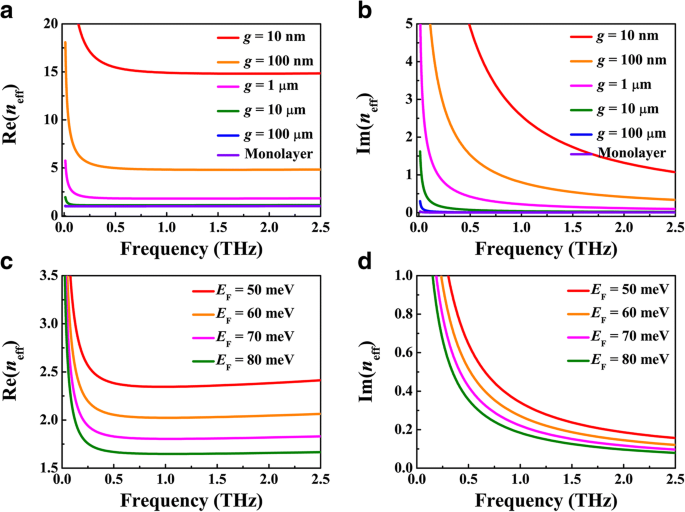
Real- und Imaginärteil des effektiven Brechungsindex n eff für a , b unterschiedliche Spaltweite g , wobei die Fermi-Energie von BDS auf E . festgelegt ist F = 70 meV und c , d verschiedene Werte der Fermi-Energie E F , wobei die Spaltbreite auf g = . festgelegt ist 1 μm
Um die oben genannte Analyse zu untersuchen, führen wir numerische Berechnungen über die Transmissionsintensität und Feldverteilung der vorgeschlagenen Wellenleiterstruktur durch. Die Simulationseinstellung ist in Methoden beschrieben. Vergleich mit dem einschichtigen BDS-Wellenleiter mit gleicher Fermi-Energie E F = 70 meV, die Übertragungsintensität des BIM-Wellenleiters bei der Frequenz von 1,56 THz beträgt 0,97, was höher ist als die des ersteren, wie in Abb. 3a gezeigt, was darauf hindeutet, dass die plasmonische Wellenleitermode in der BIM-Struktur einen geringeren Ausbreitungsverlust erleidet. Andererseits, wie in Abb. 2a angegeben, ist der Realteil des effektiven Brechungsindex von BIM bei 1,56 THz Re(n eff ) = 2.45, was viel höher ist als im Monolayer-Fall von 1.002. Um diese Aussage zu visualisieren, das Magnetfeld Hz Verteilungen dieser Modi sind in Abb. 3b, c dargestellt. Es ist klar zu erkennen, dass die stark eingeschränkte plasmonische Mode im BIM-Wellenleiter eine kürzere Schwingungsperiode aufweist als die des Monolayer-BDS-Falls. Darüber hinaus ist der größte Teil des plasmonischen Feldes in einem so engen Spalt lokalisiert ~ λ 0 /2000, das vielversprechende Anwendungen in der Nahfeldverbesserung für die nichtlineare Physik enthält.
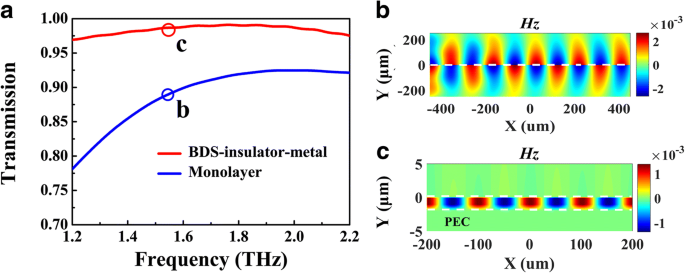
Numerische Berechnungen der Transmissionsspektren (a ) und Magnetfeld (H z ) Verteilungen (b , c ) von BIM (rote Kurve) und Monolayer (blaue Kurve) Wellenleiter, wobei E F = 70 meV, g = 50 μ m und Vorfallhäufigkeit von 1,56 THz
Unter all den oben erwähnten Anwendungen ist der optische Resonator das wesentliche Element für die Anpassung des plasmonischen THz-Wellenleitermodus. Wie in Abb. 4a dargestellt, sind zwei Silizium (n Si = 3.4) [24] Bänder werden in den dielektrischen Abstandshalter eingebettet, um die reflektierenden Spiegel zu bilden, wo die sich ausbreitende plasmonische Welle an der Silizium-Luft-Grenzfläche hin und her reflektiert werden kann, wodurch eine lokalisierte Stehwellenresonanz im BIM-Bereich zwischen den beiden Siliziumbändern entsteht . Nur die einfallende Frequenz erfüllt die Resonanzbedingung der stehenden Welle, die plasmonischen Wellen können über die Kopplung mit dem konstruierten optischen Resonator zum Ausgang des Wellenleiters übertragen werden. Abbildung 4a zeigt das Transmissionsspektrum des BIM-Wellenleiters mit zwei Siliziumbändern, wobei zwei Transmissionspeaks mit FWHM-Werten (full width at half maximum) von 0,12 und 0,09 THz offensichtlich bei den Frequenzen von 1,56 und 2,22 THz gefunden werden können, was neuartige demonstriert Bandpassfiltereffekt im Terahertz-Bereich. Die Magnetfeldverteilungen (|H z | 2 ) der Transmissionspeaks sind in Abb. 4c, e dargestellt, was impliziert, dass die von zwei Siliziumbändern eingeschlossene BIM-Region als Fabry-Perot (FP)-Kavität angesehen werden kann. Die Resonanzen erster und zweiter Ordnung sind in der FP-Kavität deutlich zu finden. Die einfallende plasmonische Welle nahe der Resonanzfrequenz kann in die FP-Kavität eingekoppelt werden und dann durch den BIM-Wellenleiter übertragen werden, der die Transmissionsspitze im Spektrum erzeugt. Während für den nicht resonanten Frequenzbereich die stehende Welle nicht gebildet werden kann und somit die einfallenden Wellen im linken Anschluss des BIM-Wellenleiters verhindert werden, wie in Fig. 4d gezeigt. Darüber hinaus kann die Transmissionsintensität in Kombination mit der Dispersionsbeziehung des BIM-Wellenleiters analytisch durch die Theorie der gekoppelten Moden (CMT) [17] berechnet werden:
$$ T\left(\omega \right)=\frac{\kappa_w^2}{{\left(\omega -{\omega}_0\right)}^2-{\left({\kappa}_w+{ \kappa}_i\right)}^2}, $$ (5)wo ω 0 die Resonanzfrequenz des FP-Resonators ist. Hier, κ w = ω 0 /(2Q w ) und κ ich = ω 0 /(2Q ich ) sind Zerfallsraten, die sich auf den Wellenleiterkopplungsverlust bzw. den intrinsischen Verlust des FP-Hohlraums beziehen. Der Qualitätsfaktor für den Gesamtverlust und den intrinsischen Verlust kann durch Q . geschätzt werden t = ω 0 /FWHM und Q oi = − Re(n eff )/(2Im(n eff )), bzw. Dann kann der Qualitätsfaktor der Wellenleiterkopplungsverluste durch Subtrahieren des Eigenverlusts vom Gesamtverlust erhalten werden, nämlich Q ei = Q oi Q ti /(Q oi − Q ti ) [17]. Die auf CMT basierenden Analyseergebnisse stimmen gut mit den numerischen Simulationen überein, wie in Abb. 4b dargestellt.
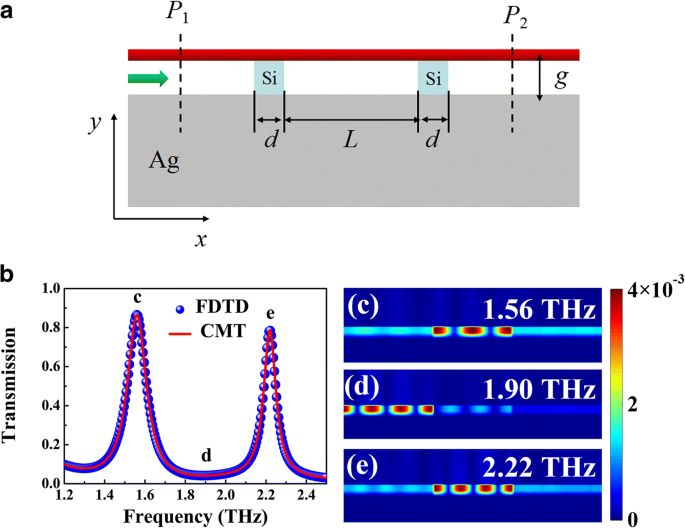
a Schema des BIM-Wellenleiters mit eingebrachten Siliziumbändern. Die Breite jedes Siliziumbandes beträgt d , und der Abstand zwischen den Bändern beträgt L . b Numerische (blaue Kugeln) und CMT-angepasste (rote Kurve) Transmissionsspektren der vorgeschlagenen Struktur wobei g = 1 μm, d = 5 μm und L = 120 μm. c –e Magnetfeldverteilungen (|H z | 2 ) von bei den Einfallsfrequenzen von 1,56 (c ), 1,90 (Tag ) und 2,22 THz (e )
Abbildung 5 zeigt die Abhängigkeit der Resonanzfrequenz von der Resonatorlänge L , wobei g = 1 μm, d = 5 μm und E F = 70 meV. Der Transmissionspeak neigt mit der Zunahme von L . zu einer Rotverschiebung , wie in Fig. 5a dargestellt, die weiter durch die Stehwellenresonanzbedingung 2k . beschrieben werden kann SPP (ω r )L + θ = 2mπ (m = 1, 2, 3, ...), wobei θ ist die reflektierende Phasenverschiebung von der Silizium-Luft-Grenzfläche und k SPP (ω r ) ist der Wellenvektor des BIM-Wellenleiters bei Resonanzfrequenz. Wie in Abb. 5b gezeigt, weisen die Resonanzfrequenzen der ersten und zweiten Moden mit der Zunahme von L . tatsächlich eine Rotverschiebung auf . Nach Gl. (1), die Modenbeschränkung wird durch die Spaltbreite g . beeinflusst die sich somit auf die Resonanzfrequenz auswirken. Abbildung 6a zeigt die Transmissionsspektren für verschiedene g , wobei L = 120 μm und E F = 70 meV. Mit der Zunahme von g , weist der Resonanzpeak in gleicher Ordnung eine Blauverschiebung auf. Dieses Phänomen kann auf die dramatische Abnahme von Re(n eff ) wie in Abb. 6c gezeigt. Die Abstimmung der Fermi-Energie von BDS kann experimentell durch alkalische Oberflächendotierung realisiert werden. Abbildung 6b zeigt die Transmissionsspektren für unterschiedliche Fermi-Energien, wobei die anderen Parameter die gleichen wie in Abbildung 4b sind. Mit steigender Fermi-Energie zeigt der Transmissionspeak eine Blauverschiebung, die auch am Resonanzbild der stehenden Welle beteiligt sein kann. Für eine feste Länge L , unterstützt die FP-Kavität die Resonanz mit definierter SPP-Wellenlänge λ SPP = λ 0 / Re(n eff ), wobei λ 0 ist die einfallende Wellenlänge. Wie in Abb. 6c gezeigt, ist Re(n eff ) wird mit der Erhöhung der Fermi-Energie reduziert. Als Ergebnis beträgt die einfallende Wellenlänge λ 0 sollte ebenfalls verringert werden, um λ . zu halten SPP als Konstante. Dies ist der Grund, warum der Transmissionspeak mit zunehmender Fermi-Energie zu einer Blauverschiebung neigt. Währenddessen wird die Bandbreite des Transmissionspeaks verengt, was auf die Abnahme von Im(n eff ), d. h. der Ausbreitungsverlust der plasmonischen Wellenleitermode im BIM-Wellenleiter.
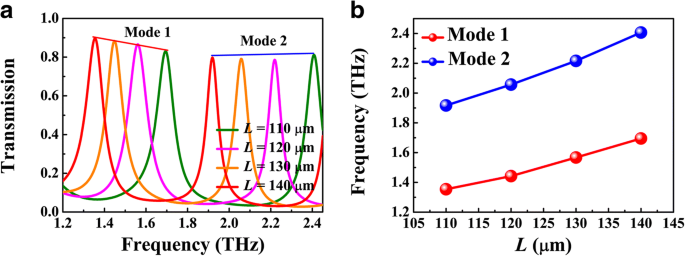
a Numerische Transmissionsspektren für verschiedene Resonatorlängen L . b Resonanzfrequenzen der Moden 1 und 2 als Funktion der Resonatorlänge L . Hier, g = 1 μm, d = 5 μm und E F = 70 meV
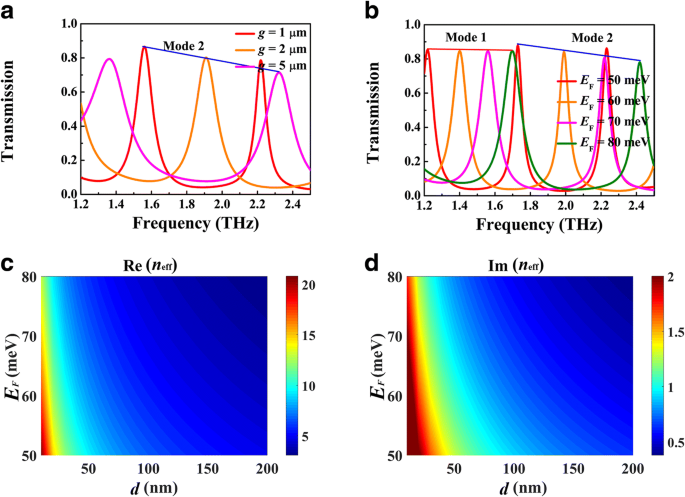
Transmissionsspektren für unterschiedliche Spaltweiten g (a ) und Fermi-Energie E F (b ), wobei die anderen Parameter dieselben wie in Abb. 4b sind. Abhängigkeit von Re(n eff ) (c ) und Im(n eff ) (d ) auf der Fermi-Energie E F und Spaltbreite g
Schlussfolgerungen
Zusammenfassend haben wir den stark begrenzten plasmonischen Terahertz-Modus demonstriert, der von einem BIM-Wellenleiter unterstützt wird. Die Modeneingrenzungs- und -verlusteigenschaften wurden mit den Variationen der BDS-Metalltrennung und der Fermi-Energie diskutiert, was darauf hindeutet, dass es einen optimierten Frequenzbereich mit verbesserter Modeneingrenzung sowie reduzierten Ausbreitungsverlusten gibt, über die im traditionellen SPP-Modus selten berichtet wurde in Metallstruktur. Anders als zuvor untersuchte BDS-basierte Strukturen kann die Mode dieses BIM-Wellenleiters in einem sehr schmalen Spalt mit einer Breite kleiner als λ . effizient unterstützt werden 0 /2000. Durch die Verwendung von zwei Siliziumbändern als reflektierende Spiegel wurde ein dynamisch abstimmbarer Bandpassfilter erreicht, bei dem die Resonanzfrequenz durch Anpassen der Fermi-Energie des BDS-Films ohne erneute Optimierung seiner Strukturparameter aktiv gesteuert werden kann.
Methoden
Numerische Ergebnisse werden mit der 2D-Finite-Difference-Time-Domain (FDTD)-Methode erhalten, bei der die perfekt aufeinander abgestimmten Schichten so eingestellt sind, dass sie das Streulicht im x . absorbieren und y Richtungen. Die Maschenweite der BDS-Folie ist auf dx . eingestellt × dy = 1 μm × 0,02 μm, um eine gute Konvergenz zu erreichen.
Die frequenzabhängige Leitfähigkeit von BDS wird durch die Kubo-Formel mit zufälliger Phasennäherung beschrieben [12, 25].
$$ \operatorname{Re}\sigma \left(\Omega \right)=\frac{e^2}{\mathrm{\hslash}}\frac{tk_F}{24\pi}\Omega G\left(\ Omega /2\right), $$ (3) $$ \operatorname{Im}\sigma \left(\Omega \right)=\frac{e^2}{\mathrm{\hslash}}\frac{tk_F} {24{\pi}^2}\left\{\frac{4}{\Omega}\left[1+\frac{\pi^2}{3}{\left(\frac{T}{E_F} \right)}^2\right]+8\Omega {\int}_0^{\varepsilon_c}\left[\frac{G\left(\varepsilon\right)-G\left(\Omega/2\right) }{\Omega^2-4{\varepsilon}^2}\right]\varepsilon d\varepsilon \right\}, $$ (4)wo G (E ) = n (−E ) − n (E ) und n (E ) ist die Fermi-Dirac-Verteilungsfunktion, E F ist die Fermi-Energie von BDS, k F = E F /ћv F ist sein Fermi-Impuls und v F = 10 6 m/s ist die Fermi-Geschwindigkeit. ε = E/E F , = ћω/E F + iћτ −1 /E F , wobei ћτ −1 = v F /(k F μ ) ist die Elektronenstreurate, die eine starke Abhängigkeit von der Ladungsträgermobilität μ zeigt. c = E c /E F (E c die Grenzenergie ist, ab der das Dirac-Spektrum nicht mehr linear ist) und t ist der Quanten-Entartungsfaktor. Am Beispiel von AlCuFe werden die Anpassungsparameter in unseren Berechnungen wie folgt festgelegt:t = 40, ε c = 3, μ = 3 × 10 4 cm 2 V −1 s −1 und E F = 70 meV.
An dieser Forschung sind keine menschlichen Teilnehmer, Daten, Gewebe oder Tiere beteiligt.
Abkürzungen
- BDS:
-
Bulk-Dirac-Halbmetalle
- BIM:
-
BDS-Isolator-Metall
- CMT:
-
Theorie der gekoppelten Mode
- FDTD:
-
Zeitbereich mit endlicher Differenz
- FWHM:
-
Volle Breite bei halbem Maximum
- SPPs:
-
Oberflächenplasmonenpolaritonen
Nanomaterialien
- Einführung in die Terahertz-Band
- Nanofasern und Filamente für eine verbesserte Wirkstoffabgabe
- Gold-Nanobiosensor basierend auf der lokalisierten Oberflächenplasmonenresonanz kann humane Brucellose diagnostizieren und stellt eine schnelle und kostengünstige Methode vor
- Lokalisierte Oberflächenplasmonenresonanz-Abhängigkeit von falsch ausgerichtetem abgeschnittenem Ag-Nanoprismen-Dimer
- Infraroteigenschaften und Terahertz-Wellenmodulation von Graphen/MnZn-Ferrit/p-Si-Heterojunctions
- Erhöhte Biokompatibilität in anodischen TaO x Nanotube-Arrays
- Defekte auf der Oberfläche von Ti-dotiertem MgAl2O4-Nanophosphor
- Die Kopplungseffekte von Oberflächenplasmonpolaritonen und magnetischen Dipolresonanzen in Metamaterialien
- Zweidimensionales Hybrid-Metallhalogenidgerät ermöglicht die Kontrolle von Terahertz-Emissionen
- Neuartige flexible Terahertz-Kamera kann Objekte mit unterschiedlichen Formen untersuchen



