Strain-abstimmbare Bandlücke und hohe Trägermobilität in SiAs- und SiAs2-Monoschichten aus First-Principles-Studien

Hintergrund

Atomar dünne zweidimensionale (2D) Kristalle haben sich zu einem der am schnellsten aufstrebenden Gebiete der modernen Materialwissenschaft entwickelt. Die vielseitigen elektronischen Eigenschaften, die ausgezeichnete Elektronenmobilität und vielversprechende Anwendungen in der Nanoelektronik und Optoelektronik treiben einen großen Prozentsatz der Physiker der kondensierten Materie dazu, nach neuen 2D-Materialien zu suchen. Nach Graphen [1–4] wurde eine Vielzahl weiterer 2D-Materialien synthetisiert, wie z. B. Silicen [5–7], Bornitrid-Nanoblätter [8, 9], Übergangsmetalldichalkogenide (TMDs) [10, 11], schwarzer Phosphor [12, 13], Borophen [14–16], Arsenen [17, 18], Telluren [19] und ihre isoelektronischen Verbindungen [20–23]. Die Liste der 2D-Materialien wird schnell erweitert, und es sind mittlerweile mehr als Tausende solcher Materialien bekannt, die das gesamte Spektrum elektronischer und anderer Eigenschaften umfassen. Und ihre neuartigen Eigenschaften, die sich von denen ihrer Massengegenstücke unterscheiden oder sogar besser sind, werden theoretisch vorhergesagt und experimentell bestätigt.

Obwohl umfangreiche und erhebliche Anstrengungen unternommen wurden, um verschiedene 2D-Materialien zu finden, darunter einige, die bereits Bandlücken oder andere wünschenswerte Eigenschaften aufweisen, wurde kein Konsens erzielt. Graphen mit hervorragender Trägermobilität, hoher mechanischer Stabilität und masselosen Dirac-Elektronen hat bisher viel Aufmerksamkeit auf sich gezogen, aber das Fehlen einer intrinsischen Bandlücke behindert seine Anwendung in der modernen Elektronikindustrie. Obwohl große Anstrengungen unternommen wurden, ist es nicht gelungen, eine beträchtliche Bandlücke ohne Nebenwirkungen zu öffnen [24, 25]. TMDs mit hoher Leistung in optoelektronischen Geräten haben zwar eine intrinsische Bandlücke, weisen jedoch eine geringe Trägermobilität auf [26–28]. Schwarzer und blauer Phosphor mit einer spannungsempfindlichen abstimmbaren Bandlücke und anisotroper hoher Ladungsträgermobilität können in Luft nicht stabil bleiben [13, 29]. Vor kurzem wurde die Synthese von geschichtetem SiAs und SiAs₂ Einkristalle wurden realisiert [30–32], was darauf hindeutet, dass nur wenige Schichtstrukturen durch mechanisches Abblättern erhalten werden können.

In der vorliegenden Arbeit haben wir auf der Grundlage von First-Principles-Dichtefunktionaltheorie-Rechnungen (DFT) zwei dynamisch und thermodynamisch stabile halbleitende Monoschichten SiAs und SiAs₂ . vorgeschlagen . Beide besitzen indirekte Bandlücken (2,39 eV bzw. 2,13 eV). Die Anwendung einer isotropen Dehnung entlang zweier Richtungen in der Ebene wandelt das SiAs praktisch um (SiAs₂ ) Monoschicht in ein Material mit direktem Spalt von 1,75 eV (1,60 eV). Darüber hinaus stellen wir fest, dass SiAs und SiAs₂ Monoschichten besitzen eine viel höhere Ladungsträgermobilität als MoS₂ und zeigen anisotropen Transport wie das schwarze Phosphoren, was sie zu einer möglichen Anwendung in der Optoelektronik macht. Unsere Arbeiten ebnen einen neuen Weg im Nanomaßstab für neuartige Funktionalitäten optischer Geräte.

Rechenmethoden

Die DFT-Berechnungen werden mit dem Vienna Ab-initio Simulation Package (VASP)-Code durchgeführt [33]. Wir verwendeten das Perdew-Burke-Ernzerhof (PBE) [34] Austauschkorrelationsfunktional unter der generalisierten Gradientenapproximation (GGA). Zur Beschreibung der Elektron-Ion-Wechselwirkung wurde die Projector Augmented Wave (PAW)-Methode [35] eingesetzt. Ein Vakuum von 20 Å senkrecht zu den Schichten (entlang der c-Achse) wurde angelegt, um die Wechselwirkung zwischen den Schichten zu vermeiden. Für den Basissatz der ebenen Welle wird eine kinetische Energiegrenze von 500 eV verwendet. Die Probenahme in der Brillouin-Zone erfolgt mit einem 15 × 5 × 1 Monkhorst-Pack [36] Raster für 2D-Platten. Konvergenzkriterien, die sowohl für die elektronische selbstkonsistente Relaxation als auch für die ionische Relaxation verwendet werden, werden auf 10 ^–4 . eingestellt und 0,01 eV/Å für Energie bzw. Kraft. Die Phononenberechnungen werden mit der Superzellenmethode durch den PHONOPY-Code [37, 38] durchgeführt, und die Realraum-Kraftkonstanten von Superzellen werden in der Dichtefunktionalstörungstheorie (DFPT) berechnet, wie sie in VASP implementiert ist. Darüber hinaus ist eine strengere Energie (10 ⁻⁸ eV/Atom) und Kraftkonvergenzkriterium (10 ⁻⁴ eV/Å) werden bei der Berechnung der Schwingungsspektren verwendet. In den Molekulardynamik(MD)-Rechnungen werden (3×3×1) Superzellen verwendet und die Temperatur im Mole-Volumen-Temperatur(NVT)-Ensemble für 6 ps mit einem Zeitschritt von 2 fs auf 300 K gehalten. Die Raman-Spektren wurden auf dem PBE-Theorieniveau unter Verwendung des CASTEP-Codes berechnet [39–41].

Ergebnisse und Diskussionen

Die geometrischen Strukturen und die Elektronendichteverteilung von entspannten freistehenden 2D-SiAs und SiAs₂ sind in Abb. 1a bzw. b dargestellt und ihre Volumenstrukturen sind in Zusatzdatei 1 dargestellt:Abbildung S1 des Zusatzmaterials. Wie in Zusatzdatei 1 gezeigt:Abbildung S1a und b, die Bulk-SiAs(SiAs₂ ) besitzt C2/m(Pbam)-Symmetrie und besteht aus gestapelten Si-As-Schichten, die schwach durch Van-der-Waals-Kräfte im Abstand von 3.06 Å (1.66 Å) gebunden sind. Die Elementarzelle von Monolayer-SiAs ist rhombisch und ihre optimierten Kristallparameter sind a ₁ =3,69Å und b ₁ =10,83Å mit φ =99,81°. SiAs enthält 6 Si-Atome und 6 As-Atome. Jedes Si-Atom hat vier nächste Nachbaratome (3 As und 1 Si), während jedes As-Atom nur drei kovalente Bindungen mit benachbarten Si-Atomen bildet. Es gibt zwei Arten von Bindungen, nämlich Si-Si- und Si-As-Bindungen. Und die Si-Si-Bindungslänge beträgt etwa 2,35 und die von Si-As liegt im Bereich von 2,39 Å und 2,43 , und die Wölbungshöhe beträgt d ₁ =4,86 ​​. In der Seitenansicht von einschichtigem SiAs wird eine brillenglasartige Struktur mit abwechselnd gebauschten Doppel- und Einzelschichten gebildet. Eine weitere Monoschichtstruktur aus Silizium und Arsenverbindungen ist SiAs₂ . Seine Primzelle enthält 4 Si-Atome und 8 As-Atome, mit einer rechteckigen Struktur und die optimierten Kristallparameter sind a ₂ =3,68Å und b ₂ =10,57 . Jedes As-Atom hat drei nächste benachbarte Si-Atome oder bildet eine kovalente Bindung mit benachbarten Si-Atomen und zwei kovalente Bindungen mit sich selbst, während jedes Si-Atom nur vier nächste benachbarte As-Atome hat. Im Gegensatz zu ersterem ist SiAs₂ besitzt eine schwächere As-As-Bindung (2.50 Å) anstelle einer Si-Si-Bindung. Und seine Si-As-Bindungen reichen von 2,41 Å bis 2,45 Å, und die Wölbungshöhe beträgt d ₂ =5,09 . Aus der Elektronendichteverteilung ziehen die As-Atome aufgrund ihrer großen Elektronegativität Elektronen von Si-Atomen an und haben eine größere Elektronendichte. Um die zukünftige experimentelle Charakterisierung zu unterstützen, haben wir die Raman-Spektren von Bulk- und Monolayer-SiAs und SiAs₂ . weiter berechnet und überprüft . Deutliche Verschiebungen zwischen der Monoschicht und den Vollkristallen sind in Zusatzdatei 1:Abbildung S2 des Ergänzungsmaterials zu sehen, dessen Ursprünge als Einfluss der Schicht-van-der-Waals-Wechselwirkung identifiziert wurden [42].

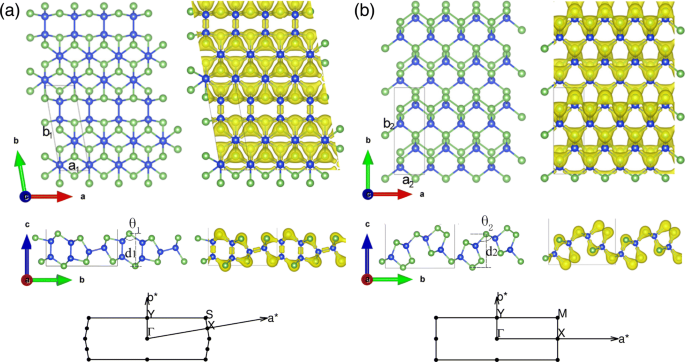
Geometrische Struktur und Elektronendichteverteilung der Monoschichten SiAs und SiAs₂ . (Farbe online) Draufsicht und Seitenansicht der Monoschichten a SiAs und b SiAs₂ geometrische Struktur und Elektronendichteverteilung und die zugehörige Brillouin-Zone. Die blaue und die grüne Kugel zeigen das Si- bzw. As-Atom an

Um die Stabilität von SiAs zu lernen (SiAs₂ ) berechneten wir zuerst die Kohäsionsenergie, definiert als E _coh =(nE _Si + mE _Als −E _Mono )/(n + m ), wobei E _Si ,E _Als , und E _Mono sind die Gesamtenergien eines einzelnen Si-Atoms, eines einzelnen As-Atoms und einer Formeleinheit von einschichtigem SiAs (SiAs₂ ) bzw. und n(m) ist die Zahl der As(Si)-Atome in der Formeleinheit. Unsere Berechnungen zeigen, dass die SiAs-Monoschicht eine Kohäsionsenergie von 5,13 eV/Atom hat, was etwas größer ist als die von SiAs₂ Monoschicht 4,98 eV/Atom. Zum Vergleich:Auf dem gleichen theoretischen Niveau betragen die Kohäsionsenergien von Arsenen und Silicen 2,99 bzw. 3,71 eV/Atom [18, 43]. Die hohen Kohäsionsenergien von SiAs und SiAs₂ zeigen, dass beide stark mit hoher Stabilität verbunden sind.

Um die strukturellen Stabilitäten von Monolayer-SiAs und SiAs₂ . weiter zu bestätigen , haben wir auch Berechnungen von Schwingungsphononenspektren durchgeführt. Wie in Abb. 2a gezeigt, machen positive Frequenzen einen Großteil der Moden aus, mit Ausnahme der transversalen akustischen Mode in der Nähe des Γ Punkt, der auf die Erweichung von Phononen zurückzuführen ist und in anderen ähnlichen Systemen beschrieben wurde [44, 45], was darauf hindeutet, dass die Strukturen beide dynamisch stabil sind. Dann führten wir 6 ps First-Principles-MD-Simulationen bei Raumtemperatur (T =300K ), wie in Abb. 2b dargestellt. Die leichte Energieschwankung und gut erhaltene Strukturen lassen vermuten, dass sie bei Raumtemperatur thermisch stabil sind. Unsere Ergebnisse implizieren, dass die Monoschichten SiAs und SiAs₂ konnte experimentell bei Raumtemperatur realisiert werden.

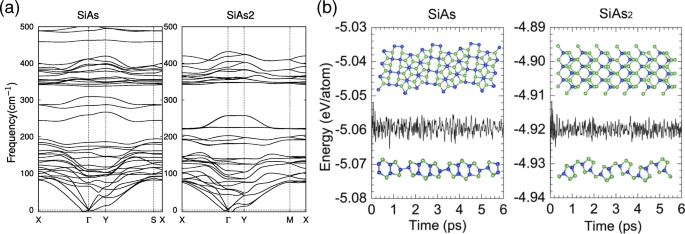
Phononendispersionskurven und MD-Simulationen der Monoschichten SiAs und SiAs₂ . a Die Phononendispersionskurven für Monolayer-SiAs und SiAs₂ . b Beziehungen von Gesamtenergie und Zeit bei Raumtemperatur-MD-Simulationen von SiAs und SiAs₂ . Ausgewählte Schnappschüsse der Monolayer-Strukturen am Ende von 6 ps werden ebenfalls bereitgestellt

Mit den optimierten Strukturen von Monolayer SiAs und SiAs₂ , jetzt achten wir auf ihre elektronischen Eigenschaften. Die berechneten Orbitalzerlegungsbandstrukturen von SiAs und SiAs₂ Monolagen sind in Abb. 3 dargestellt. Unsere Berechnungen zeigen deutlich, dass SiAs und SiAs₂ Monolagen sind beides indirekte Halbleiter mit großen Bandlücken. Bei Monolayer-SiAs liegt das Valenzbandmaximum (VBM) bei Y Punkt, während das Leitungsbandminimum (CBM) bei Γ . liegt (Abb. 3a). Die indirekte Bandlücke von Monolayer-SiAs beträgt E _g =1,72 eV innerhalb des PBE-Schemas. Man kann auch sehen, dass der VBM-Zustand bei Y Punkt umfasst das p _y Orbital, während die CBM von Γ Punkt umfasst hauptsächlich das s-Orbital, was bedeutet, dass die äußere Verformung unterschiedliche Auswirkungen auf die beiden Zustände hat und zu einem indirekten-direkten Übergang führen kann, wie im Folgenden gezeigt wird. Im Gegensatz zu SiAs ist die Monoschicht SiAs₂ ist ein nahezu direkter Halbleiter mit VBM an der Seite des Y Punkt und CBM ist von ihm etwas verschoben (Abb. 3b). Die SiAs₂ Die indirekte Bandlücke der Monoschicht beträgt E _g =1,42 eV innerhalb des PBE-Schemas. Und die VBM und CBM von SiAs₂ Monolayer bestehen aus dem p _y Orbital bzw. s-Orbital. Um einen genaueren Bandlückenwert zu erhalten, führten wir auch die Hybridfunktionalrechnungen (HSE06)[46, 47] für SiAs und SiAs₂ . durch Monoschichten. Aus den berechneten Bandstrukturen (der rechte Teil von Abb. 3a, b) sind die scharfen Kanten der Bandzustände von PBE und HSE im Wesentlichen gleich, und die indirekte Bandlücke wird immer noch innerhalb der Hybridfunktionalrechnungen vorhergesagt, aber der Lückenwert ist erhöht auf 2,39 eV und 2,07 eV für SiAs und SiAs₂ , bzw.

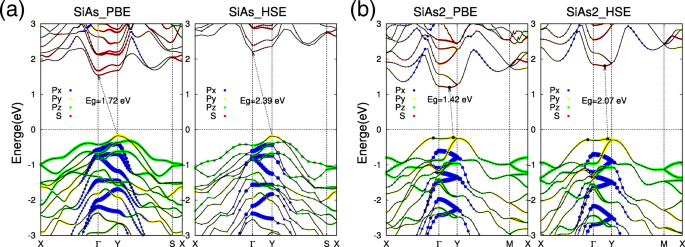
Bandstrukturen von Monolayer-SiAs und SiAs₂ berechnet von PBE und HSE06. Die elektronische Orbitalzerlegung von Bandstrukturen der Monoschichten SiAs und SiAs₂ werden als a . dargestellt und b , bzw. Die roten Punkte stehen für s Orbital, während Blau, Gelb und Grün p . sind _x ,p _y , und p _z , bzw. Das Fermi-Niveau wird auf Null gesetzt und mit einer Punktlinie angezeigt

Die Trägermobilität, die ein Schlüsselfaktor für die potenziellen Anwendungen in modernen elektronischen Geräten für die neu entdeckten 2D-Materialien ist, ist ebenso wichtig wie die Bandlücke und der Standort von CBM und VBM. Weitere Informationen zu den elektronischen Struktureigenschaften von SiAs und SiAs₂ Monoschichten berechneten wir dann ihre akustisch phononenbegrenzten Trägermobilitäten (einschließlich Elektron und Loch in x- und y-Richtung) auf der Grundlage der Deformationspotential-(DP)-Theorie [48] bei Raumtemperatur (T =300 K ). Beim Niedrigenergieregime (300 K ), dominiert die elektron-akustische-Phonon-Streuung den Trägertransport, was die akustische Phononen-begrenzte zu einem effektiven Weg macht, um die Trägermobilitäten vieler 2D-Strukturen vorherzusagen, wie z. B. des MoS₂ einschichtig [49], Telluren [19], Phosphen [50] und mehrschichtiges MoO₃ [51]. Die berechneten effektiven Massen m ^∗ und Trägermobilitäten μ von SiAs und SiAs₂ Monoschichten zeigen, dass beide hochmobil und transportanisotrop sind (siehe Zusatzdatei 1:Tabelle S1 und die Abbildungen S3 und S4) wie das schwarze Phosphoren [50]. Um die Trägermobilität von SiAs und SiAs zu schätzen₂ , führten wir zunächst eine Anpassung ihrer Bänder mit dem Modell der nahezu freien Elektronen durch, um die effektiven Trägermassen zu erhalten. Für SiAs definieren wir x und y als Richtung senkrecht zu den Gittervektoren b und a , bzw. Die \(m_{e}^{*}\) und \(m_{h}^{*}\) entlang der x-Richtung betragen ungefähr 0,15 m ₀ und 0,86 m ₀ , und entlang der y-Richtung sind 0,80 m ₀ und 0,22 m ₀ (m ₀ ist die Masse der freien Elektronen). Für SiAs₂ , die Richtung des Gittervektors a ist definiert als x , während das von b ist y . Die \(m_{e}^{*}\) und \(m_{h}^{*}\) entlang der x-Richtung betragen ungefähr 0,14 m ₀ und 0,65 m ₀ , und entlang der y-Richtung sind 2,05 m ₀ und 1,82 m ₀ , bzw. Wir haben die elastischen Konstanten (C) und die Verformungspotentiale (E1) weiter untersucht (siehe Zusatzdatei 1:Abbildung S2 und S3). Basierend auf den oben erhaltenen m ^∗ , C- und E1-Werten haben wir die Ladungsträgermobilität wie in Tabelle 1 aufgeführt geschätzt. Die Elektronenmobilitäten für SiAs(SiAs₂ ) entlang x und y Richtungen sind 0,66(0,26) und 0,54(0,11) × 10 ³ · cm ² V ⁻¹ S ⁻¹ , während die Lochbeweglichkeiten entlang x und y Richtungen sind 3,90(0,13) und 0,30(0,65) × 10 ³ · cm ² V ⁻¹ S ⁻¹ , die beide viel höher sind als die von MoS₂ [49].

Um den zugrunde liegenden Bindungsmechanismus von Si- und As-Atomen in den Monoschichten SiAs und SiAs weiter zu beleuchten₂ , die Gesamt- und Teilzustandsdichte (PDOS) von ihnen unter Verwendung des PBE-Funktionals, wobei ihre Elektronendichteverteilung VBM und CBM entspricht, sind in Fig. 4 jeweils bereitgestellt. Man sieht, dass die PDOS von As- und Si-Atomen (Abb. 4a, c) eine starke Hybridisierung von s . zeigt und p Orbitale, was auf die starke kovalente Bindung zwischen ihnen hinweist. Die Unterschiede zwischen den Monoschichten SiAs und SiAs₂ sind die Lokalisierung von p _z Orbital, die auf die unterschiedliche Bindungskoordinationsumgebung des As-Atoms zurückzuführen sind. Die einsamen Elektronenpaare, lokalisiert am As-Atom in SiAs und SiAs₂ Monoschichten, verstärken die drei nächstgelegenen Bindungsorbitale, um die Bildung von Knicken der Monoschichtstruktur zu bestimmen und das p . zu bilden _z orbitale Lokalisierungsaktion. In einschichtigem SiAs sind die freien Elektronenpaare durch eine Si-As-Bindung getrennt, die den abstoßenden Effekt abschwächt und das p . verbreitert _z orbital. Während in Monolayer-SiAs₂ , As-As-Bindung, die bei Gruppe-V-Halbleitern sehr häufig vorkommt, lokalisiert die p _z Orbital in einem tieferen Energieniveau.

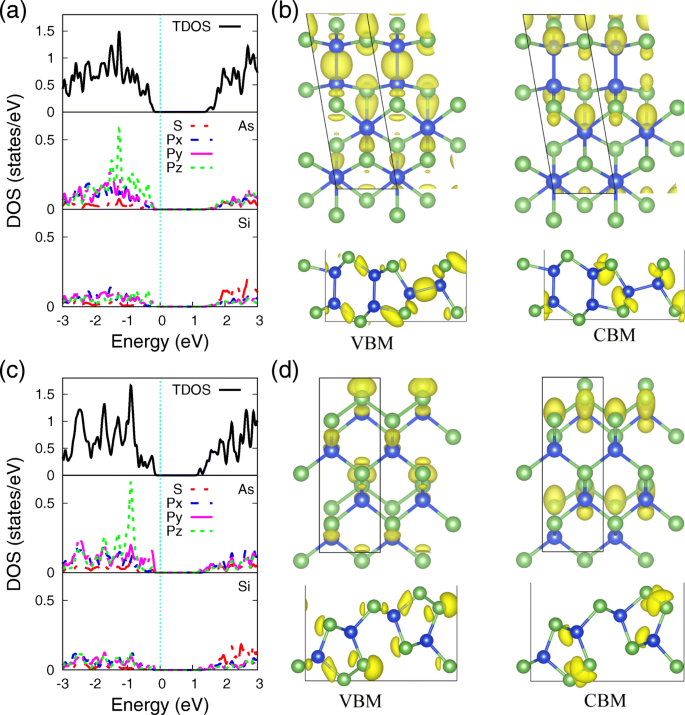
Projizierte Zustandsdichte und Elektronendichte von VBM und CBM. Die projizierte Zustandsdichte (PDOS) von As- und Si-Atomen und die Elektronendichteverteilung entsprechend VBM und CBM von (a , b ) SiAs und (c , d ) SiAs₂ Monoschichten. Der Isoflächenwert 0,034 e /Å ³

Wie wir wissen, ist der Charakter von Grenzzuständen nicht nur für ein mikroskopisches Verständnis der Leitungskanäle von Interesse, sondern auch von großer Bedeutung für das Design optimaler Kontakte.[52] Die Ladungsdichten entsprechend VBM und CBM der Monoschichten SiAs und SiAs₂ sind in Fig. 4b bzw. d dargestellt. Die VBM ist fast die Hybridisierung von 3p-Orbitalen von Si und As, während CBM hauptsächlich aus dem Beitrag von 3s-Orbitalen von Si und As besteht, die auch mit den PDOS-Ergebnissen in Abb. 4a, c und der elektronischen Orbitalzerlegung von Bandstrukturen übereinstimmen in Abb. 3.

Mechanische Belastung ist ein effektiver Weg, um die elektronischen Eigenschaften von 2D-Materialien zu modulieren, die ausgiebig verwendet werden, um die Bandstruktur von schwarzen und blauen Phosphorenen und anderen Nanoblattmaterialien zu modifizieren [53–55]. Insbesondere für das System mit geknickter Struktur sind die Energiekosten normalerweise recht gering, um eine deutliche Belastung zu bewirken. Dabei wird die mechanische Beanspruchung durch Variation der Gitterkonstanten sowie der inneren Freiheitsgrade jedes Atoms während der geometrischen Optimierung simuliert. Der Stamm ε ist definiert als ε =(l −l ₀ )/l ₀ , wo l und l ₀ sind die verspannten und Gleichgewichtsgitterkonstanten der Monoschichten SiAs und SiAs₂ . In Abb. 5a, b die detaillierten Variationen der geometrischen Struktur mit hohem Knicken von 2D-SiAs und SiAs₂ unter Dehnungen dargestellt sind. Man sieht, dass ihre Knickhöhen durch den veränderten Knickwinkel erweitert oder gestaucht werden θ ₁₍₂₎ mit biaxialen Druck- oder Zugspannungen in nahezu linearen Variationen. Und wir haben auch festgestellt, dass ihre hochbeulende geometrische Struktur auch bei recht großen Dehnungen noch gut erhalten bleibt, deren Phononenspektren, wie in Zusatzdatei 1:Abbildung S5 und S6 gezeigt, selbst im großen Dehnungsbereich keine negativen Frequenzen aufweisen. Die Lückenvariationen von Monolayer-SiAs und SiAs₂ unter biaxialen Druck- und Zugbelastungen sind in Abb. 5c bzw. d dargestellt. Man sieht, dass die elektronischen Eigenschaften von SiAs und SiAs₂ hängen empfindlich von der Dehnung ab und unterliegen einem indirekten zu einem direkten Bandübergang in einem bestimmten Dehnungsbereich und dann zu Metall in einem großen Dehnungsbereich.

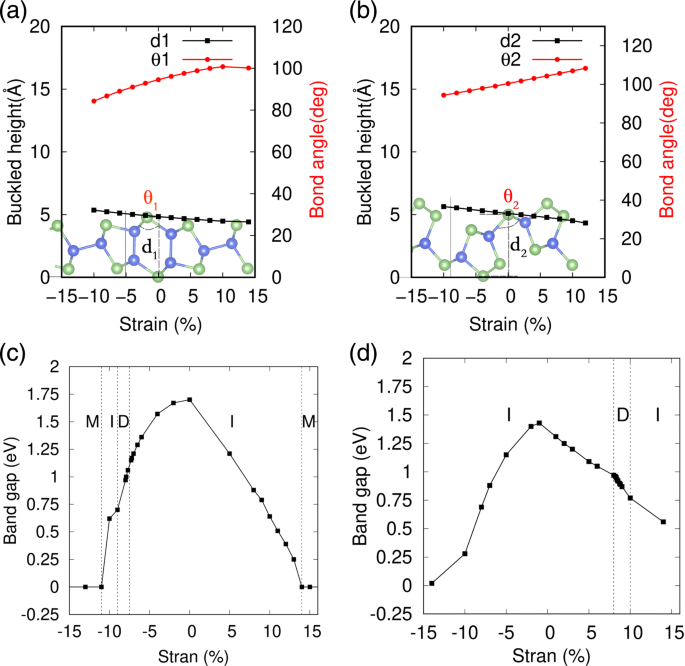
Dehnungseffekte auf die geometrischen Strukturen und Bandlücken von 2D-SiAs und SiAs₂ . a , c SiAs darstellen; und b , d bezeichnen SiAs₂; M, I und D stehen für Metall, indirekten Halbleiter bzw. direkten Halbleiter

Die detaillierten Variationen von SiAs und SiAs₂ Bandstrukturen sind in den Fign. 6 und 7 bzw. Unter biaxialen Druckspannungen nimmt die Wölbungshöhe von einschichtigem SiAs zu und die CBM verschiebt sich von Γ zu einem Punkt auf der Y-S-Linie und zurück zu Y. Während das VBM am Y-Punkt still gehalten wird, bis die Druckdehnung ε . erreicht =− 10% . Daher wechselt die Bandlücke mit zunehmender Druckspannung von indirektem Y zu Γ , über indirektes Y zu einem Punkt auf der Y–S-Linie, um Y zu Y zu leiten und zurück zu einem Punkt auf der Γ –Y-Linie zu Y, wie in Abb. 6 gezeigt. Bei Zugdehnungen bewegt sich die VBM bei Y zu einem Punkt auf der Y-S-Linie und die CBM bei Γ bewegt sich nach Y und die Bandlücke bleibt indirekt. Bei großen Dehnungen führt unabhängig von Druck oder Zug zu einem Metallübergang, wie in Abb. 5c gezeigt.

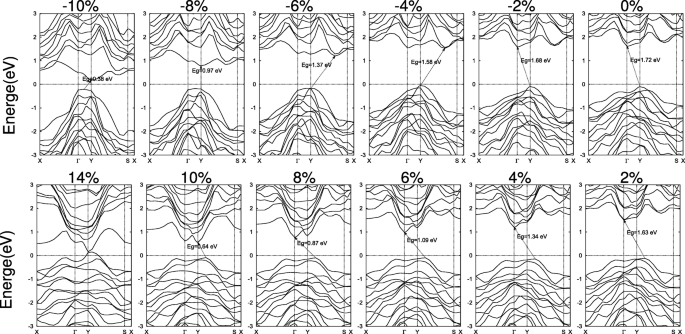
Bandstrukturen von 2D-SiAs unter den biaxialen Spannungen. Das Fermi-Niveau wird auf Null gesetzt und mit einer Punktlinie angezeigt

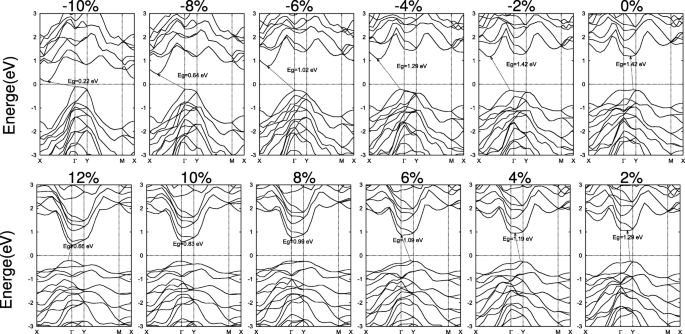
Bandstrukturen von 2D-SiAs₂ unter den zweiachsigen Spannungen. Das Fermi-Niveau wird auf Null gesetzt und mit einer Punktlinie angezeigt

In Abb. 7 wurde eine ähnliche Studie für 2D-SiAs₂ . durchgeführt . Anstelle von Kompression führen Zugdehnungen im Bereich von 8–10% zu direkten Bandlücken. wenn die Monoschicht SiAs₂ breitet sich mit abnehmender Knickhöhe unter den Zugbelastungen aus, die VBM-Verschiebung von einem Punkt auf der Γ –Y-Linie zu Γ und halte dich im Bereich von 8–10% still und verschiebe dich dann zu einem Punkt auf dem Γ –X-Linie, während sich die CBM von einem Punkt auf der Γ . bewegt –Y-Linie zu Γ und halte durch. Daher wechselt die Bandlücke mit steigender Zugdehnung von indirekt auf die Γ –Y-Linie, um Γ . zu leiten – Γ und dann zurück zu einem indirekten Punkt auf dem Γ –X-Zeile zu Γ , wie in Abb. 7 dargestellt. Druckspannungen bleiben die indirekte Bandlücke. Und große Dehnungen haben ähnliche Auswirkungen und führen zu einem Metallübergang wie bei SiAs.

Repräsentative Direktbandstrukturen von verspanntem SiAs und SiAs₂ sind auch in Zusatzdatei 1:Bild S7a und b durch die PBE- und HSE-Berechnungen dargestellt. Für SiAs eine direkte Bandlücke von E _g =1,75 eV (HSE) mit VBM und CBM lokalisiert am Y Punkte erhält man bei einer zweiachsigen Druckspannung von ε =− 7,5% . Im Gegensatz zu SiAs ist eine biaxiale Zugspannung von ε =8,5% induziert das SiAs₂ zu einem direkten Band von E _g =1,60 eV (HSE). Und die VBM und CBM sind auf der Γ Punkt.

Schlussfolgerungen

Zusammenfassend haben wir eine DFT-Berechnung nach den ersten Prinzipien durchgeführt und zwei neue Arten von 2D-Materialien aus Silizium und Arsenverbindungen vorgeschlagen, SiAs und SiAs₂ , die sowohl dynamisch als auch thermodynamisch stabil sind. Unsere Berechnungen zeigen, dass SiAs und SiAs₂ Monolagen sind indirekte Halbleiter mit Bandlücken von 2,39 eV und 2,07 eV , bzw. Die Bandlücke von SiAs und SiAs₂ Monoschichten sind empfindlich gegenüber Dehnungen, die bei einer bestimmten mechanischen Dehnung einen indirekten zu direkten Bandübergang und sogar gegenüber Metall erfahren. SiAs und SiAs₂ Monoschichten besitzen eine höhere Mobilität als MoS₂ und zeigen anisotropen Transport wie das schwarze Phosphoren. Unsere Arbeiten ebnen einen neuen Weg im Nanomaßstab für neuartige Funktionalitäten optischer Geräte.

Abkürzungen

2D:

Zweidimensional

CASTEP:

Cambridge sequenzielles Gesamtenergiepaket

CBM:

Leitungsband-Minimum

DFT:

Dichtefunktionaltheorie

DFPT:

Dichtefunktionalstörungstheorie

DP:

Verformungspotential

GGA:

Verallgemeinerte Gradienten-Approximation

MD:

Molekulardynamik

NVT:

Mol-Volumen-Temperatur

PAW:

Projektor-verstärkte Welle

PBE:

Perdew-Burke-Ernzerhof

PDOS:

Partielle Zustandsdichte

TMDs:

Übergangsmetalldichalkogenide

VASP:

Wien-Ab-initio-Simulationspaket

VBM:

Valenzband-Maximum