Elektrisch gesteuerter Valley-Pseudomagnetowiderstand in Graphen mit Y-förmiger Kekulé-Gitterverzerrung
Zusammenfassung
Wir schlagen eine neue Methode zur Regulierung des Valley-Pseudomagnetowiderstands in ballistischen Graphen-basierten Valley-Feldeffekttransistoren unter Berücksichtigung der Y-förmigen Kekulé-Gitterverzerrung und der elektrischen Barriere vor. Die Vorrichtung umfasst eine Talinjektion und eine Talerkennung durch ferromagnetische Spannungsquelle und -senke. Die Talmanipulation im Kanal wird über die Y-förmige Kekulé-Gitterverzerrung und elektrische Barriere erreicht. Der zentrale Mechanismus dieser Geräte liegt in der Y-förmigen Kekulé-Gitterverzerrung in Graphen, die eine Talpräzession induzieren kann, wodurch die Talorientierung der Kanalelektronen und damit der am Drain gesammelte Strom gesteuert wird. Wir haben festgestellt, dass die externe Vorspannung bei der Abstimmung den Pseudomagnetowiderstand des Tals zwischen positiven und negativen Werten oszillieren lässt und ein kolossaler Pseudomagnetwiderstand des Tunneltals von über 30.000% erreicht werden kann. Unsere Ergebnisse legen nahe, dass die Synergie von Valleytronics und digitaler Logik neue Paradigmen für die Valleytronic-basierte Informationsverarbeitung und das reversible Computing bieten könnte.
Einführung
Graphen ist eine zweidimensionale Schicht aus Kohlenstoffatomen, die eine ausgezeichnete Ladungsträgerbeweglichkeit aufweist und den dünnstmöglichen Kanal für die Entwicklung von Metalloxid-Halbleiter-Feldeffekttransistoren bietet [1]. Semenov hat einen Spin-Feldeffekttransistor vorgeschlagen, bei dem eine Graphenschicht als Kanal verwendet wird [2], der Spininjektion und Spindetektion durch ferromagnetische Source und Drain umfasst, und die Spinmanipulation im Kanal wird durch elektrische Steuerung des Elektronenaustauschs erreicht Wechselwirkung mit einem ferromagnetischen Gate. Darüber hinaus ist die Spin-Bahn-Wechselwirkung von Rashba ein weiteres vielversprechendes Werkzeug für die Spinkontrolle in Graphen [3]. Die Rashba-Spin-Bahn-Wechselwirkung kann eine Spinpräzession induzieren, wodurch die Spinorientierung der Kanalelektronen gesteuert wird. Die Spin-Feldeffekttransistoren inspirierten auch viele wichtige Forschungsideen, wie den Riesenmagnetwiderstand und den Tunnelmagnetwiderstand [3, 4]. Der Riesenmagnetwiderstand und der Tunnelmagnetwiderstand können in digitalen Speicher- und Magnetsensortechnologien verwendet werden.
Auf der anderen Seite besitzen Dirac-Elektronen in Graphen neben den konventionellen Ladungs- und Spin-Gegenstücken einen zusätzlichen Tal-Freiheitsgrad. Aufgrund des großen Impulsunterschieds zwischen den beiden Tälern und der Unterdrückung der intervallartigen Streuung in sauberen Graphenproben [5–7] wird angenommen, dass der Tal-Freiheitsgrad den gleichen Effekt wie der Elektronenspin beim Tragen und Manipulieren von Informationen ausübt, der führt zu einer neuen Disziplin, die als Valleytronics aufsteigt. Analog zum Spin-Feldeffekttransistor wird auch ein Valley-Feldeffekttransistor in Graphen theoretisch vorgeschlagen [8], der aus einem eindimensionalen Quantenkanal von Gap-Graphen besteht, der zwischen zwei Sessel-Graphen-Nanobändern (Source und Drain) eingebettet ist; dann wird ein elektrisches Feld des seitlichen Gates an den Kanal angelegt und moduliert die Talpolarisation der Ladungsträger aufgrund der Tal-Bahn-Wechselwirkung, wodurch die Strommenge gesteuert wird, die am Drain gesammelt wird. Aufgrund der Tatsache, dass die Valley-Kopplung in Graphen jedoch schon lange keine physikalische Realität geworden ist, gibt es nur wenige weitere Studien, die auf den Valley-Feldeffekttransistoren von Graphen und verwandten Studien basieren. Neuere Experimente von Gutierrez et al. [9] haben eine ungewöhnliche Y-förmige Kekulé(Kek-Y)-Bindungstextur im Wabengitter auf einem Graphen-Kupfer-Übergitter entdeckt, bei der eines von sechs Kohlenstoffatomen in jeder Übergitter-Elementarzelle keine Kupferatome darunter hat und eine kürzere Nächster-Nachbar-Anleihe. Darüber hinaus hat Gamayun gezeigt, dass die Kek-Y-Bindungstextur eine Möglichkeit für eine impulsgesteuerte Talpräzession bietet [10]. Beenakker et al. [11] zeigten, dass das Kek-System über die Andreev-ähnliche Reflexion einen Valley-Flip-Effekt hervorbringen kann. Vor kurzem haben Wang et al. [12] fanden heraus, dass die C-C-Bindungslängenmodulation des Kekulé-Gitters, die die Inversionssymmetrie des Systems beibehält, verwendet werden kann, um den Valley-Freiheitsgrad in ähnlicher Weise wie beim präzessierenden Austauschfeldspin zu manipulieren. Damit ist es möglich, einen neuartigen Valley-Feldeffekttransistor in Graphen zu entwickeln. Darüber hinaus gibt es keinen Bericht über die kombinierten Auswirkungen der Kek-Y-Gitterverzerrung auf den Valley-Pseudomagnetowiderstand in Graphen. Der Valley-Pseudomagnetowiderstand [13, 14] ist analog zum Magnetowiderstand im magnetischen Tunnelübergang [15], bei dem die Größe des Spinstroms von der magnetischen Ausrichtung der Elektroden abhängt [4].
Methoden
In dieser Arbeit schlagen wir einen neuen Typ von Valley-Feldeffekttransistoren (VFETs) für Graphen-basierte Elektronen vor. Das Gerätedesign geht von einer ferromagnetischen Belastung (FM-S) Source/Drain für die talpolarisierte Injektion/Detektion aus, die einem herkömmlichen Spintransistor ähnelt (siehe Fig. 1a). Die Talrotation im Graphenkanal beruht auf dem Kek-Y-Graphen-Übergitter [10–12], das durch ein epitaktisch auf Cu(111) aufgewachsenes Graphen-Übergitter erreicht werden kann, wobei die Kupferatome mit den Kohlenstoffatomen übereinstimmen [9]. Unter einigen Kohlenstoffatomen fehlen jedoch Kupferatome, was dazu führt, dass einige periodische Kupferatom-Leerstellen unter Graphen auftreten. Eine solche Substratatomleerstelle führt dazu, dass drei benachbarte Bindungen kontrahiert werden. Hier verwenden wir δ t um die diesen drei Bindungen entsprechende Energieänderung beim Hopping des Elektrons darzustellen. Wir gehen davon aus, dass das ferromagnetische Graphen aus dem gleichen FM-Metallstreifen besteht. Die beiden Magnetisierungen von Source und Drain sind entlang der Stromrichtung gerichtet (das x Achse), die mit Hilfe eines externen Magnetfelds in der Ebene entweder parallel (P) oder antiparallel (AP) ausgerichtet sein kann. Im Landau-Eichmaß hat das aus dem Streufeld entstehende magnetische Vektorpotential die Form [16, 17] \(A(r)=A_{y}(x)\overrightarrow {y}\) mit A y (x )=A y [Θ (−x )±Θ (x −L )], wobei das Plus(Minus)-Zeichen der P(AP)-Konfiguration der Magnetisierungen entspricht, Θ (x ) ist die Heaviside-Stufenfunktion. Andererseits nehmen wir an, dass auf Source und Drain der VFETs die gleiche Spannung ausgeübt wird, die durch eine Spannung auf dem Substrat des Graphens induziert werden kann [18]. Die elastische Verformung kann als Störung der Sprungamplituden behandelt werden und wirkt als Eichpotential A S (r ). Die Spannung wird entlang des x . eingestellt Richtung, in diesem Fall A S (r ) einheitlich entlang der y Achse [16]. Aus Gründen der Bestimmtheit nehmen wir ein typisches glattes Profil seines y Komponente als A Sy (x )=A S [Θ (−x )+Θ (x −L )], wobei A S ist die Amplitude. Darüber hinaus wird im Kek-Y-Gitterbereich auch eine elektrische Barriere angewendet, die durch eine externe Vorspannung abgestimmt werden kann.
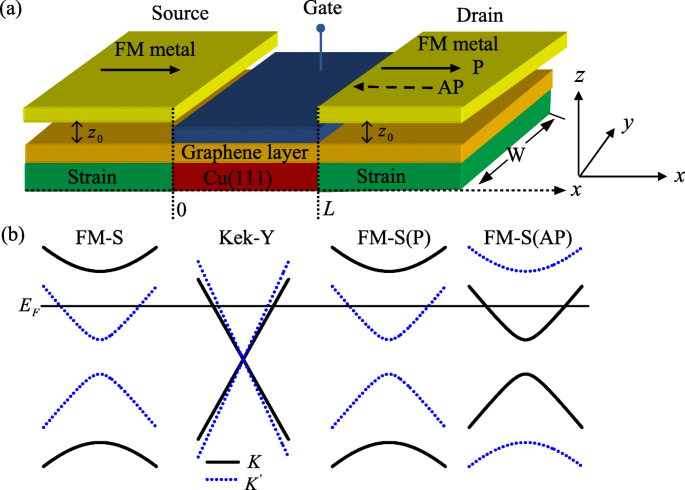
a Schematische Darstellung des VFET, der einen Graphenkanal mit Kek-Y-Gitterverzerrung und einer Gate-Vorspannung verwendet, die die Talorientierung der Kanalelektronen steuert. Source und Drain sind FM-S-Graphen, die Elektronen in einer bestimmten Polarisation injizieren und nachweisen. Wo z 0 ist der Abstand zwischen der Graphenschicht und dem FM-Streifen. L ist die Kanallänge, W ist die Breite der Graphenprobe im y Richtung und W L . b Bandstruktur in der Nähe von Dirac-Punkten. Die horizontale Linie bezeichnet die Fermi-Energie (Farbe online)
Die Fortpflanzung von Quasiteilchen mit niedriger Energieanregung in den VFETs mit Kek-Y-Graphen-Übergittern kann durch den folgenden Einzelteilchen-Hamiltonian beschrieben werden [10–12]
$$ \begin{array} [c]{ll} H=&v_{F}(\mathbf{P}\cdot\sigma)+v_{\tau}(\mathbf{P}\cdot\tau)\Theta \left(x\right) \Theta\left(Lx\right) +\\ &U\sigma_{0}\tau_{0}\Theta\left(x\right) \Theta\left(Lx\right) + A_{M}(x)\sigma_{y}+\tau_{z}A_{S}(x)\sigma_{y}. \end{array} $$ (1)Hier, σ und τ sind die Pauli-Matrizen für das Untergitter bzw. das Tal. P =(p x ,p y ) ist der Impuls masseloser Dirac-Elektronen, τ z =±1 für K und \(K^{^{\prime}}\) Täler, v F =10 6 m/s ist die Geschwindigkeit der Dirac-Elektronen im unberührten Graphen und v τ v F δ t /3t ist der Geschwindigkeitsmodifikationsterm aus dem Bindungskontraktionseffekt im Kek-Y-Gitter [12], wobei t ist die Sprungenergie zwischen den nächsten benachbarten Städten für reines Graphen. U ist die Gate-abstimmbare Potentialbarriere. A M (x )=e v F A y (x ) [19]. Die Eigenwerte des Hamiltonoperators im Graphen mit Kek-Y-Gitterverzerrung und elektrischer Barriere sind gegeben durch
$$ E_{\alpha,\beta}=U+\alpha(\hbar v_{F}+\beta\hbar v_{\tau})\sqrt{k_{x\beta} ^{2}+k_{y} ^{2}}. $$ (2)Hier, α =+1(−1) gibt das Leitungsband (Valenz) an. β =±1 bezeichnet die beiden Valley-Split-Subbänder des Leitungs- und Valenzbandes. Aufgrund der Translationsinvarianz im y Richtung, der Transversalwellenvektor k y ist konserviert. Die Eigenzustände im Graphen mit der homogenen Kek-Y-Gitterverzerrung sind charakterisiert durch \(\Psi_{\beta}^{\pm}(k_{x\beta},k_{y})=\frac {1}{ N_{\beta}}\left (1,P_{\beta}^{\pm},Q_{\beta} ^{\pm},R_{\beta}^{\pm}\right)^{T} \), wobei N β ist die Normierungskonstante \(N_{\beta}=\left (1+P_{\beta}^{2}+Q_{\beta}^{2}+R_{\beta}^{2}\right)^ {\frac {1}{2}}\) und \(P_{\beta}^{\pm}, Q_{\beta}^{\pm}\) und \(R_{\beta}^{\ pm }\) sind Funktionen, die wie folgt definiert sind:
$$ \begin{array} [c]{cc} P_{\beta}^{\pm}=&\frac{(EU)^{2}+\left(\hbar^{2}v_{F}^ {2}-\hbar^{2}v_{\tau}^{2}\right)\left(k_{x\beta}^{2}+k_{y}^{2}\right)}{2 (EU)\hbar v_{F}(\pm k_{x\beta}-{ik}_{y})},\\ Q_{\beta}^{\pm}=&\frac{(EU)^ {2}-\left(\hbar^{2}v_{F}^{2}-\hbar^{2}v_{\tau} ^{2}\right)\left(k_{x\beta}^ {2}+k_{y}^{2}\right)}{2(EU)\hbar v_{\tau}(\pm k_{x\beta}-{ik}_{y})},\\ R_{\beta}^{\pm}=&\frac{(EU)^{2}-\left(\hbar^{2}v_{F}^{2}+\hbar^{2}v_{\ tau} ^{2}\right)\left(k_{x\beta}^{2}+k_{y}^{2}\right)}{2\hbar^{2}v_{F}v_{\ tau}(\pm k_{x\beta} -{ik}_{y})^{2}}. \end{array} $$ (3)Die Übertragungswahrscheinlichkeit vom \(K^{^{\prime}}\)-Tal zum \(K(K^{^{\prime}})\)-Tal \(T_{K^{^{\prime}}), K(K^{^{\prime}})}\) kann mit der Transfermatrixtechnik [20] berechnet werden. Nach der Laudauer-Btittiker-Formel ergibt sich für den talabhängigen Leitwert [21]:
$$ G_{K^{^{\prime}},K(K^{^{\prime}})}=G_{0} {\int_{-\frac{\pi}{2}}^{\ frac{\pi}{2}}} T_{K^{^{\prime}},K(K^{^{\prime}})}\cos(\phi_{0})d\phi_{0} . $$ (4)Hier \(G_{0}=2e^{2}W/\left(v_{F}\pi^{2}\hbar^{2}\right)\left \vert E\right \vert\), W ist die Breite der Graphenprobe im y Richtung und ϕ 0 ist der Einfallswinkel bezüglich x Richtung.
Bevor wir mit den Berechnungen fortfahren, diskutieren wir die Bandstruktur mit k y =0, wie in Abb. 1b gezeigt. In der FM-S-Quellregion wird das Energieband von Graphen geschrieben als \(E=\alpha\sqrt{(\hbar v_{F}k_{x})^{2} +(A_{M}+\tau _{z}A_{S})^{2}}\). Man kann feststellen, dass das entartete Tal Lift ist und verschiedene Lücken am K . induziert werden und \(K^{^{\prime}}\) Punkte, weil das Gesamtvektorpotential A M +A S Handeln auf K Elektronen ist höher als das Gesamtvektorpotential |A M −A S | wirkend auf für \(K^{^{\prime}}\) Elektronen [19]. Dies weist darauf hin, dass nur \(K^{^{\prime}}\) Elektronen die FM-S-Quellregion passieren können, wenn sich die einfallende Energie in |A . befindet M −A S |<E <A M +A S [22, 23]. Ähnlich kann in der FM-S-Drain-Region das Energieband von Graphen geschrieben werden als \(E=\alpha \sqrt {(\hbar v_{F}k_{x})^{2}+(\pm A_{ M}+\tau_{z}A_{S})^{2}}\), wobei das Vorzeichen ± der P- und AP-Konfiguration der Magnetisierungen entspricht. Es werden also nur \(K^{^{\prime}}\) Elektronen in der P-Struktur nachgewiesen und nur K Elektronen werden in der AP-Struktur nachgewiesen, wenn sich die Fermi-Energie im Bereich von [|A . befindet M −A S |,A M +A S ]. Im Graphenkanal ist das Tal ebenfalls entartet, aber es gibt einen wichtigen Unterschied. Im Gegensatz zum Leitfall, wo die Phasen von K und \(K^{^{\prime}}\) Komponenten entwickeln sich mit dem gleichen Wellenvektor [dh \(k=E/\hbar v_{F}\)], jetzt entwickeln sie sich getrennt mit verschiedenen Wellenvektoren ( \(k_{+}=(EU)/(\hbar v_{F}+\hbar v_{\tau})\) und \(k_{-}=(EU)/(\hbar v_{F}-\ hbar v_{\tau })\)) aufgrund der Kek-Y-Graphen-Übergitter, die das Tal durchmischen (siehe Gl. 2). Dies führt zur Talpräzession der Kanalelektronen im Talraum [12]. Die Valley-Präzession in Graphen ist die Grundlage für den Valley-Feldeffekttransistor [8]. Und die Talpräzession kann auch durch einen Tal-Pseudomagnetowiderstand (VPMR) in den FM-S/Kek-Y/FM-S-Übergängen charakterisiert werden, analog zum Magnetowiderstand in Graphen-basierten Quantentunnelübergängen mit der Spin-Bahn-Wechselwirkung [4] , die definiert ist als \(VPMR=\frac {G_{P}-G_{AP}}{G_{P}}\), wobei G P und G AP die Leitfähigkeit in P- bzw. AP-Konfigurationen darstellen und \(G_{P}=G_{K^{^{\prime}},K^{^{\prime}}}, G_{AP}=G_{K ^{^{\prime}},K}\). Die Größe des Talstroms hängt von der magnetischen Ausrichtung von Source und Drain in unserem betrachteten Gerät ab.
Numerische Ergebnisse und Diskussionen
Im Folgenden präsentieren wir die numerischen Ergebnisse für den FM-S/Kek-Y/FM-S-Übergang in Graphen. In der gesamten Arbeit legen wir die Kanallänge L . fest =207nm und begrenzen die Fermi-Energie auf 20 meV<E <140meV, angenommen es erfüllt |A M −A S |<E <A M +A S . Abbildung 2a und b zeigen die berechneten Ergebnisse der Tunnelleitfähigkeit und VPMR als Funktion von v t mit Fermi-Energie E =80meV und Rechteckpotentialbarriere U =-10 meV. Wir können feststellen, dass G P und G AP haben die gleichen Schwingungsperioden, aber die inversen Phasen. Daher schwingt der VPMR mit einer Zunahme von v t und der negative Wert VPMR kann erscheinen. Diese Phänomene ähneln denen des Magnetowiderstands in ballistischen Graphen-basierten Quantentunnelübergängen mit der Spin-Bahn-Wechselwirkung [4]. Die Schwingungseigenschaften des Leitwertes von G P und G AP kann durch die Phasendifferenz zwischen den beiden Talkomponenten erklärt werden. Wenn der Einfallswinkel ϕ 0 =0, die Phasenverschiebung ist gegeben durch:\(\Updelta \theta =(k_{x+}-k_{x-})L=-\frac {2(EU)v_{\tau}}{\hbar(v_ {F}^{2}-v_{\tau}^{2})}L\). Δ θ bestimmt die Orientierung der Talpolarisation, bevor das Elektron in den Drain eintritt, relativ zu der des Drain-Zustands [8]. Für Δ θ =±2n π ,n =1,2,3⋯, die beiden Polarisationen sind ausgerichtet, was zum Leitwert G . führt P Maximum und VPMR ein hoher positiver Wert (siehe v τ =0,022, 0,033). Andererseits für Δ θ =±(2n +1)π ,n =0,1,2⋯, sie sind orthogonal zueinander, was zum Leitwert G . führt AP Minimum und VPMR negativ (wie in v . zu sehen τ =0,0167, 0,027, 0,038).
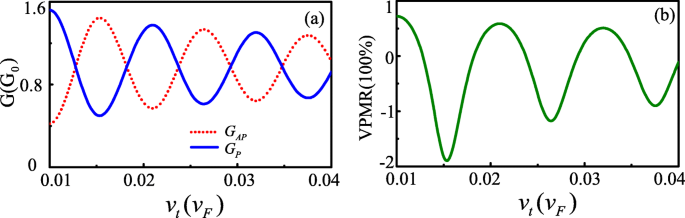
Leitfähigkeit G P ,A P und VPMR im Vergleich zu v t um L =207nm,E =80meV und U =−10meV (Farbe online)
Leitwert und VPMR sind nicht nur Schwingungsfunktionen der Hüpfenergiemodifikation, sie schwingen auch mit der Fermi-Energie und dem effektiven Barrierepotential, da Δ θ Skalen sind auch linear mit der Fermi-Energie und der Potentialbarriere U . Abbildung 3a und b zeigen die Leitfähigkeit als Funktion der Fermi-Energie bzw. des effektiven Barrierepotentials. Die entsprechenden VPMR sind in Abb. 3c und d angegeben. Sie alle zeigen Oszillationseigenschaften, die mit E . variieren und U Wert, auch wenn das effektive Barrierepotential U ist größer als die Fermi-Energie E . Der physikalische Ursprung für ein solches Phänomen hängt mit dem Klein-Tunneling zusammen [12]. Obwohl es ähnliche Oszillationsphänomene von Leitfähigkeit und VPMR für erhöhtes E . gibt, und U , können auch einige Unterschiede festgestellt werden. Als E steigt, die Differenz zwischen G P und G AP der Leitwert wird immer kleiner, was dazu führt, dass die Schwingungsamplitude von VPMR mit zunehmender Fermi-Energie abnimmt. Unter der Bedingung Δ θ =±n π erfüllt ist, die Differenz zwischen G P und G AP ist mit zunehmendem U . größer , besonders an manchen Orten, die G P und G AP Leitfähigkeit weist Schalteigenschaften auf. Die Zeichen sind für die Anwendung von VPMR wünschenswert. Bemerkenswerterweise liegt der beobachtete Maximalwert von VPMR bei über 30.000 % bei kleinem E . Dieser Wert übersteigt bei weitem den MR von ~ 175% in den ballistischen Graphen-basierten Quantentunnelübergängen mit der Spin-Bahn-Wechselwirkung [4] und dem Pseudomagnetowiderstand von ~ 100% in zweischichtigem Graphen, das durch externe Gates gesteuert wird [24], das sogar größer ist als die VPMR von ~ 10000% in einem verschmelzenden Dirac-Kegelsystem [13].
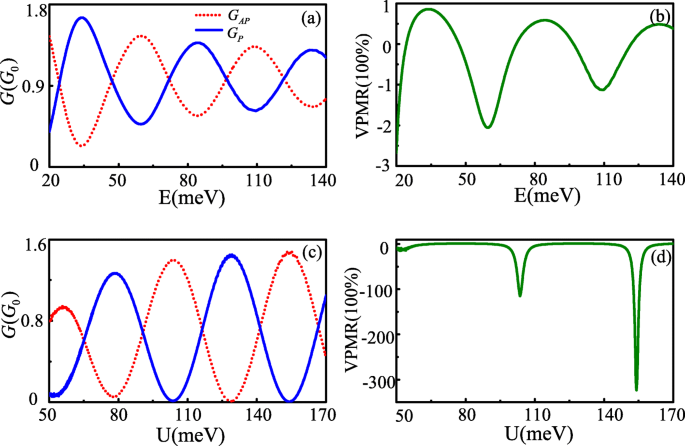
Leitfähigkeit G P ,A P (a , c ) und VPMR (b , d ) als Funktion der Fermi-Energie und der elektrischen Barriere bei L =207 nm,v t =0,02v f . die anderen Parameter sind U =−10meV für a und c , E =80meV für b und d (Farbe online)
Schlussfolgerungen
Zusammenfassend haben wir eine Art von Valley-Feldeffekttransistoren für Graphen-basierte Elektronen vorgeschlagen und den Valley-Pseudomagnetowiderstand untersucht. Wir haben gezeigt, dass die Oszillationseigenschaft des Valley-Pseudomagnetowiderstands nicht nur mit der Änderung der Sprungenergie und der Fermi-Energie zusammenhängt, sondern auch weitgehend durch das effektive Barrierepotential abgestimmt werden kann. Der durch externe Vorspannung abgestimmte Valley-Pseudomagnetowiderstand kommt dem Valley-Feldeffekttransistor-Bauelement zugute, und wir gehen davon aus, dass die hier vorgeschlagenen elektrisch gesteuerten Valley-Quantenbauelemente eine Rolle in Quanten- und quantenklassischen Hybridcomputern spielen können.
Weitere Forschung könnte die unterschiedliche Dehnung (uniaxial vs. biaxial) beinhalten, die die Valley-Streuung von Elektronen und den Transport in unseren vorgeschlagenen Graphen-basierten Valley-Feldeffekttransistoren abstimmbar ist, da die Färbung nützlich ist, um den Grad der Intervallstreuung in Kekulé-Mustern zu kontrollieren [25] . Dann werden andere zweidimensionale Materialien (MoS2 , WS2 , WSe2 , etc.) Analoga in Graphen können auch eine interessante Plattform für andere zweidimensionale materialbasierte Valley-Feldeffekttransistoren mit Y-förmiger Kekulé-Gitterverzerrung darstellen.
Verfügbarkeit von Daten und Materialien
Die Datensätze, die die Schlussfolgerungen dieses Artikels unterstützen, sind im Artikel enthalten.
Abkürzungen
- AP:
-
Antiparallel
- FM-S:
-
Ferromagnetische Dehnung
- Kek-Y:
-
Y-förmiges Kekulé
- P:
-
Parallel
- VFETs:
-
Valley-Feldeffekttransistoren
- VPMR:
-
Valley-Pseudomagnetowiderstand
Nanomaterialien
- Gitter:MachX03D FPGA verbessert die Sicherheit mit Hardware-Root-of-Trust-Funktionen
- Graphen bringt Nanomaterialien an ihren Platz
- Graphen in Lautsprechern und Ohrhörern
- Graphen-Nanoband
- RGO und dreidimensionale Graphen-Netzwerke modifizierte TIMs mit hoher Leistung gemeinsam
- Bewertung von Graphen/WO3- und Graphen/CeO x -Strukturen als Elektroden für Superkondensatoranwendungen
- Graphen/Polyanilin-Aerogel mit Superelastizität und hoher Kapazität als hochkompressionstolerante Superkondensatorelektrode
- Umweltfreundliche und einfache Synthese von Co3O4-Nanodrähten und ihre vielversprechende Anwendung mit Graphen in Lithium-Ionen-Batterien
- Graphenoxid-basierte Nanokomposite, dekoriert mit Silbernanopartikeln als antibakterielles Mittel
- Herstellung von ultrahochmolekularem Polyethylen/Graphen-Nanokomposit In-situ-Polymerisation durch sphärische und Sandwichstruktur-Graphen/Sio2-Unterstützung



