Auswirkung der Oberflächenstreuung von Elektronen auf das Verhältnis von optischer Absorption und Streuung zum Aussterben von Gold-Nanoschalen

Hintergrund

Die Gold-Nanoschale besteht aus einem dielektrischen Kern, der aus Siliziumdioxid oder Au . bestehen kann ₂ S [1, 2] und eine konzentrische Hülle aus Gold. Aufgrund der Biokompatibilität von Gold [3, 4], der leichten Konjugation von Antikörpern und Targeting-Einheiten an die Oberfläche der Goldhülle [5], der Abstimmbarkeit seiner Resonanzwellenlänge auf den nahen Infrarotbereich [2, 6] und einer Region, die als biologisches Wasserfenster bezeichnet wird, die Gewebetransmissivität ist die höchste [7], die verbesserte Lichtstreuung und -absorption der Gold-Nanoschale hat Anwendungen in der biomedizinischen Bildgebung und photothermischen Therapie gefunden [8, 9]. Die Erweiterung der Mie-Theorie für die Kern-Schale-Struktur kann verwendet werden, um die optischen Absorptions- und Streuquerschnitte einer einzelnen Gold-Nanoschale zu berechnen [10], und die Summe dieser beiden ergibt ihren Extinktionsquerschnitt. Da die Dicke der Gold-Nanoschale normalerweise kleiner oder vergleichbar ist mit der mittleren freien Weglänge der Elektronen in massivem Gold, die etwa 37,7 nm beträgt [11], durchlaufen Elektronen in der Goldschale mehr Kollisionen pro Zeiteinheit (zusätzliche Kollisionen durch Streuung von Leitungselektronen von der Schalenoberfläche) als in Bulk-Gold [12, 13]. Es wurde berichtet, dass die Oberflächenstreuung von Leitungselektronen eine Verbreiterung des Resonanzpeaks verursacht, was durch Anpassen gemessener und berechneter Spektren [6, 14,15,16] und eine Verringerung der absoluten Werte sowohl der Streuung als auch der Absorption einer einzelnen Nanoschale bestätigt wurde was durch theoretische Rechnungen nachgewiesen wurde [17,18,19]. Für streuungsbasierte biomedizinische Bildgebungsanwendungen [9, 20, 21], bei denen metallische Nanopartikel oder fluoreszierende Materialien an Zielgewebe oder -zellen angebracht werden, ist es jedoch erwünscht, das zu untersuchende Gewebe oder die untersuchten Zellen nur abzubilden und nicht thermisch zu schädigen Es ist wichtig, dass das angelagerte Nanopartikel ein hohes Streuungsverhältnis und ein niedriges Absorptionsverhältnis bei der gewünschten Wellenlänge aufweist. Der Grund, warum Streuungs- und Absorptionsverhältnisse, aber nicht ihre absoluten Werte von Bedeutung sind, besteht darin, dass eine Abnahme der absoluten Streuungs- und Absorptionswerte dadurch kompensiert werden kann, dass mehr Partikel an das Zielgewebe oder die Zielzellen angelagert werden. Die Anwendung der resonanten Lichtstreuung von metallischen Nanopartikeln in transparenten Projektionswänden [22,23,24,25] und in der Photovoltaik [26,27,28,29,30] erfordert ebenfalls gleichzeitig hohe Streuung und niedrige Absorptionsverhältnisse im gewünschten Wellenlängenbereich . Darüber hinaus erfordern Goldmetamaterialien auch Gold in Form eines dünnen Films, der als Lichtabsorber eine hohe optische Absorption [31, 32] oder als transparenter leitender Film eine hohe Transmission erreichen kann [33,34,35,36], und somit spielt auch der Oberflächenstreueffekt der Leitungselektronen eine Rolle. Daher kann es eine Anleitung zum Entwerfen einer nanoskaligen goldbezogenen Struktur geben, um den Einfluss der Oberflächenstreuung von Elektronen auf das Verhältnis von optischer Absorption und Streuung zu Extinktion für Gold-Nanoschalen zu untersuchen.

In dieser Arbeit werden zunächst Simulationen durchgeführt, um den Einfluss der Oberflächenstreuung von Elektronen auf die Verhältnisse von optischer Absorption und Streuung zu Extinktion von Gold-Nanoschalen zu untersuchen, indem die Situationen mit und ohne Oberflächenstreuung betrachtet werden. Es wird gezeigt, dass die Oberflächenstreuung der Elektronen das optische Absorptionsverhältnis erhöht und daher das Lichtstreuungsverhältnis verringert, und je dünner die Schalendicke ist, desto größer ist die Zunahme des optischen Absorptionsverhältnisses. Die erhöhte Absorption wird dann experimentell für drei Proben durch Vergleich ihrer gemessenen und simulierten Absorptions- sowie Extinktionsspektren verifiziert.

Die Simulations- und experimentellen Ergebnisse werden zuerst im Abschnitt „Ergebnisse und Diskussion“ gezeigt, und dann wird im Abschnitt „Methoden/Experiment“ eine detaillierte Methode optischer Messungen der Extinktion und Absorption bereitgestellt, um unnötige Verwirrung durch die Beschreibungen von zu vermeiden optische Messungen.

Ergebnisse und Diskussion

Goldnanoschalen mit vier unterschiedlichen Schalendicken aber gleichem Kerndurchmesser werden durch Simulation untersucht. Die Gold-Nanoschalen umfassen (80-nm-Durchmesser-Siliziumdioxidkern)@(15-nm-dicke Goldschale), (80-nm-Durchmesser-Siliziumdioxidkern)@(25-nm-dicke Goldschale), (80-nm-Durchmesser) Siliziumdioxidkern)@(35-nm-dicke Goldschale) und (80-nm-Durchmesser Siliziumdioxidkern)@(45-nm-dicke Goldschale).

Nach der Wechselwirkung parallel einfallender Lichtstrahlen mit einem einzelnen Nanopartikel wird Licht, abgesehen von den direkt transmittierten (die sich in der ursprünglichen Richtung des einfallenden Lichts ausbreiten) entweder absorbiert oder gestreut, und die Summe dieser beiden wird als Extinktion bezeichnet [37 ]. Die Streuung, Absorption und Extinktion, quantisiert in Form von Wirkungsquerschnitten, die intuitiv als die durch Streuung, Absorption bzw für Kern-Schale-Struktur [10]. Es ist jedoch natürlicher, die Querschnitte auf den geometrischen Querschnitt des Nanopartikels zu normieren, πR ² , wobei R ist der Außenradius einer Kern-Schale-Struktur zum Vergleich zwischen verschiedenen Strukturen und das Verhältnis von j Querschnitt (j =Absorption, Streuung oder Extinktion) zum geometrischen Wirkungsquerschnitt wird als j . bezeichnet Effizienz.

Die Extinktions- und Absorptionseffizienzen ohne Berücksichtigung des Oberflächenstreueffekts werden unter Verwendung der dielektrischen Funktion von Bulk-Gold [38] als Eingabe in die Mie-Theorie berechnet und in Abb. 1 als rote Linien (durchgezogen oder gestrichelt) dargestellt den Effekt der Oberflächenstreuung, wird angenommen, dass die dielektrische Funktion von Gold eine Drude-Modellkomponente hat, um das Verhalten freier Elektronen zu beschreiben [39] und einen zusätzlichen Dämpfungsterm γ _s durch Oberflächenstreuung von Leitungselektronen beigetragen wird zur Volumendämpfung hinzugefügt γ _b im Drude-Term für die korrigierte dielektrische Funktion ε _sch für Goldmuschel [19]:

wo ε _exp ist die dielektrische Bulk-Funktion von Gold aus Lit. [38], ω _p ist die Plasmafrequenz von Gold, ω ist die Frequenz des einfallenden Lichts und i ist die imaginäre Zahl. Für die berechneten Wirkungsgrade mit Oberflächenstreueffekt in Abb. 1 (blaue Linien, durchgezogen oder gestrichelte) ω _p und γ_b werden mit 8,55 eV bzw. 18,4 meV angenommen [19]. Und γ _s ist gegeben durch [19]:

wo v _F ist die Fermi-Geschwindigkeit von Elektronen in Gold und beträgt 1,40 × 10 ⁶ m/s [19] und L _B ist die effektive mittlere freie Weglänge der Elektronen in der Schale, abgeleitet unter Annahme des Billardstreuungsmodells [13], bei dem die Reflexionen der Elektronen an den beiden Oberflächen der Schale spiegelnd sind, und ist gegeben durch

wo r _o und r _ich sind der äußere bzw. der innere Radius der Nanoschale. Die Brechungsindizes des umgebenden Mediums und des Siliziumdioxidkerns werden mit 1,5 bzw. 1,45 angenommen.

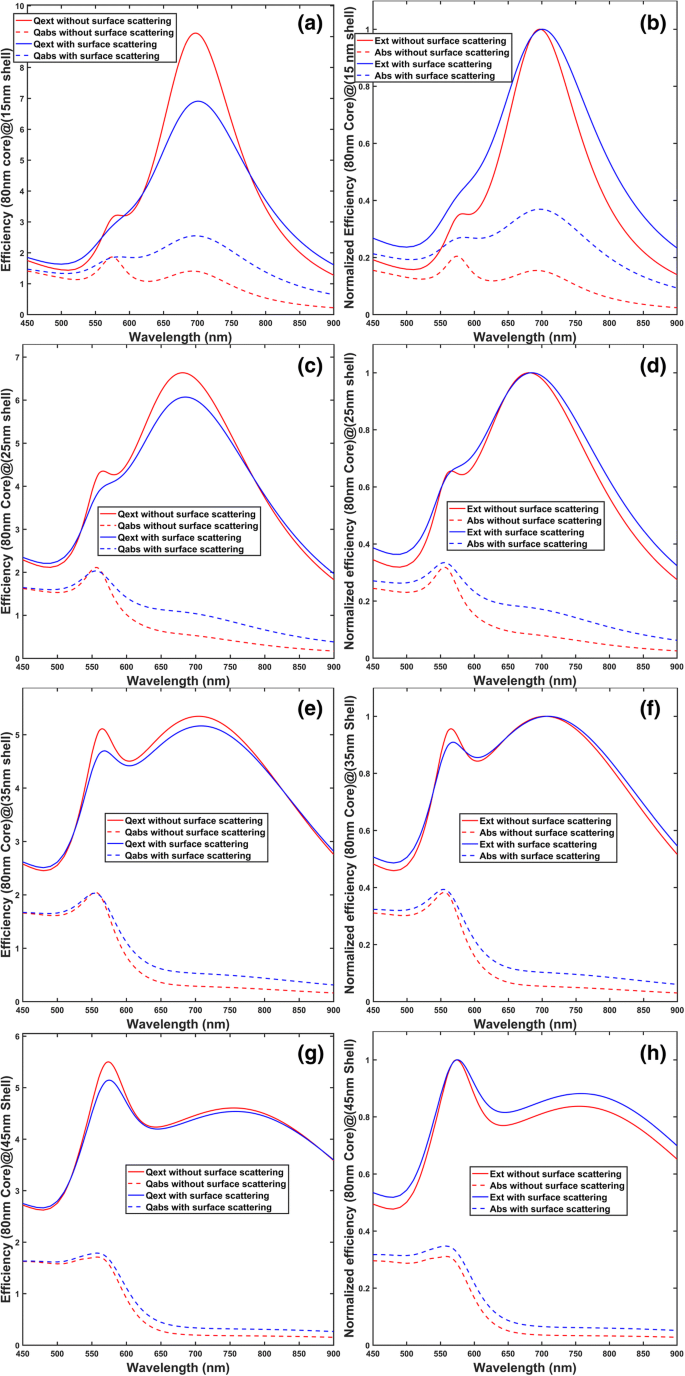
Berechnete Extinktions- und Absorptionseffizienzen mit und ohne Berücksichtigung der Oberflächenstreuung von Leitungselektronen, wobei Q _ext (Ext) steht für Extinktionseffizienz (normalisierte Extinktion) und Q _Bauchmuskeln (Abs) steht für Absorptionseffizienz (normalisierte Absorption). Die Streueffizienz (normalisierte Streuung) ist die Differenz zwischen dem Q _ext (Ext) und Q _Bauchmuskeln (Abs). Alle Berechnungen werden nach der Mie-Theorie durchgeführt, wobei die Indizes des Siliciumdioxids und des umgebenden Mediums mit 1,45 bzw. 1,5 angenommen werden. Die Dielektrizitätskonstanten von Gold ohne Oberflächenstreuung stammen aus Lit. [38], während diejenigen mit Oberflächenstreuung durch Gl. (1)~(3). a und b sind für (80-nm-Durchmesser-Silica-Kern)@(15-nm-dicke Goldhülle). c und d sind für (80-nm-Durchmesser-Silica-Kern)@(25-nm-dicke Goldhülle). e und f sind für (80-nm-Durchmesser-Silica-Kern)@(35-nm-dicke Goldhülle). g und h sind für (80-nm-Durchmesser-Silica-Kern)@(45-nm-dicke Goldhülle). Die linke Spalte, d. h. a , c , e , und g , sind die entsprechenden Wirkungsgrade, wie sie nach der Mie-Theorie berechnet wurden. Die rechte Spalte, d. h. b , d , und f , ist der Wirkungsgrad normalisiert auf den dipolaren Resonanzpeak (der Resonanzpeak zwischen 700 und 800 nm) und h die Wirkungsgrade normalisiert auf die quadrupolare Resonanzspitze (die Spitze zwischen 550 und 600 nm)

Aus der linken Spalte von Fig. 1 ist für die vier Schalendicken nach Einbeziehung des Oberflächenstreueffekts zu erkennen, dass sowohl das Extinktions- als auch das Absorptionsspektrum eine Verbreiterung erfahren und dass, während die Extinktionsspektren in der Größenordnung abnehmen, die Absorptionsspektren a . zunehmen bei der dipolaren Resonanzspitze (die Spitze zwischen 700 und 800 nm) und scheinen sich bei der quadrupolaren Resonanzspitze (die Spitze zwischen 550 und 600 nm) nicht zu ändern. Die Abnahme der Extinktionseffizienzgröße und die Zunahme der Absorptionseffizienzgröße führen zu einer Erhöhung des Verhältnisses von Absorption zu Extinktion nach Einbeziehung des Oberflächenstreueffekts. Dies wird durch die rechte Spalte von Fig. 1 bestätigt, in der beobachtet wird, dass die Absorption sowohl an den dipolaren als auch an den quadrupolaren Peakpositionen zunimmt (d. h. die blauen gestrichelten Linien befinden sich über den roten gestrichelten Linien). Intuitiv wird die Zunahme des Absorptionsverhältnisses nach Berücksichtigung des Oberflächenstreueffekts mit zunehmender Schalendicke weniger signifikant, wie in (b), (d), (f) und (h) in Abb. 1 beobachtet werden kann. Dies liegt daran, dass je dicker die Schale ist, desto geringer ist die Häufigkeit der Kollisionen der Elektronen mit den Schalenoberflächen, dh der Oberflächenstreueffekt wird verringert. Das Phänomen wird auch durch Tabelle 1 bestätigt. Für jede Schalendicke das Absorptionsverhältnis mit (ohne) Oberflächenstreuung, berechnet aus dem Verhältnis der Region unter der blauen (rot) gestrichelten Kurve zu der Region unter der blauen (rot) durchgezogenen Kurve , ist in Tabelle 1 tabellarisch dargestellt. Um den Mechanismus hinter dem Anstieg des Absorptionsverhältnisses weiter zu untersuchen, wird die räumliche Verteilung des Quadrats der Amplitude des nahen elektrischen Felds |E | ² sind in Abb. 2 aufgetragen. In Abb. 2 ist zu erkennen, dass |E | ² s ohne Oberflächenstreuung berechnete sind größer als solche mit Oberflächenstreuung, was folgendermaßen erklärt werden kann:Unter der Annahme, dass die Oberflächenstreuung wirksam wird, erfahren Leitungselektronen mehr Stöße von Schalenoberflächen als diejenigen in massivem Gold, daher ist die durchschnittliche Schwingungsamplitude der Leitungselektronen verringert, was zu verringertem |E . führt | ² s . Und da Kollisionen von Leitungselektronen mit Schalenoberflächen zum Energieverlust in Form von Wärme beitragen, wird das Absorptionsverhältnis nach Einbeziehung des Oberflächenstreueffekts erhöht.

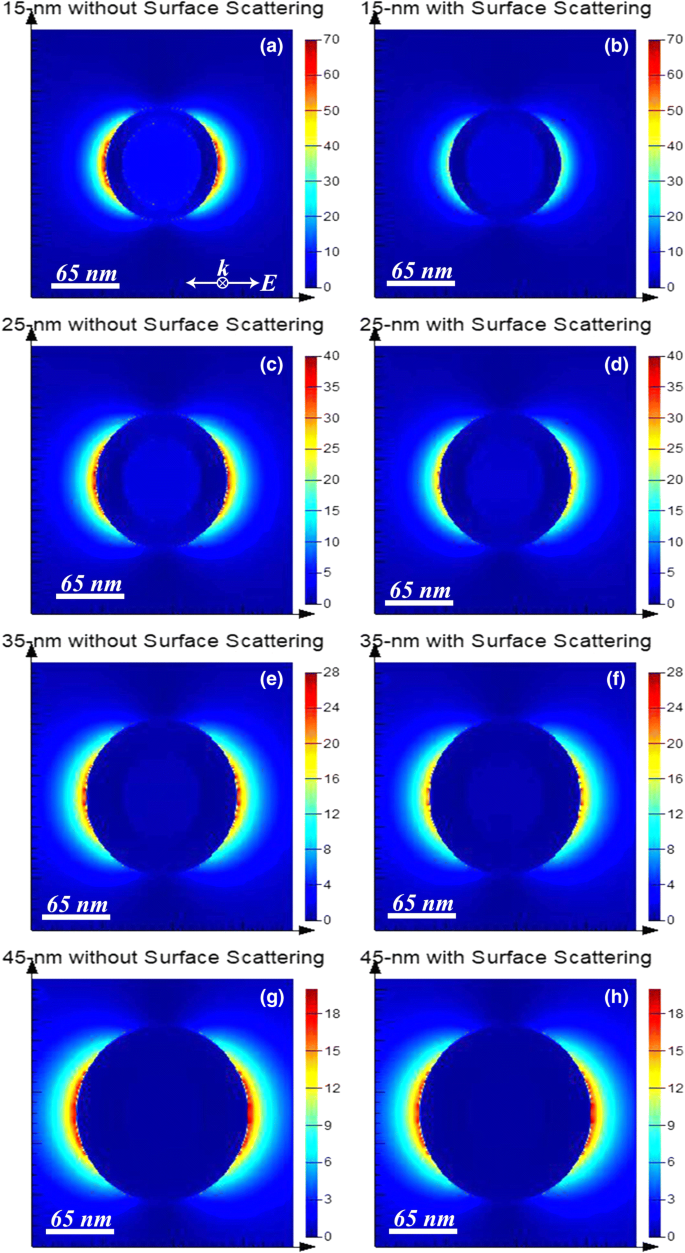
Quadrat der Amplitude des nahen elektrischen Felds |E | ² Auftragungen der vier in Fig. 1 gezeigten Strukturen bei ihren entsprechenden dipolaren Resonanzpeakwellenlängen. a und b sind für (80-nm-Durchmesser-Silica-Kern)@(15-nm-dicke Goldhülle) bei 700 nm aufgetragen. c und d sind für (80-nm-Durchmesser-Silica-Kern)@(25-nm-dicke Goldhülle) bei 684 nm aufgetragen. e und f sind für (80-nm-Durchmesser-Silica-Kern)@(35-nm-dicke Goldhülle) bei 706 nm aufgetragen. g und h sind für (80-nm-Durchmesser-Silica-Kern)@(45-nm-dicke Goldhülle) bei 756 nm aufgetragen. Die linke Spalte, d. h. a , c , e , und g , zeigt |E | ² berechnet mit Dielektrizitätskonstanten von Bulk-Gold aus Lit. [38]. Die rechte Spalte, d. h. b , d , f , und h , zeigt |E | ² berechnet mit Dielektrizitätskonstanten von Gold modifiziert mit Oberflächenstreuung über Gl. (1)~(3). Die Polarisation und die Ausbreitungsrichtung des einfallenden Lichts sind für alle Figuren gleich und werden in a . dargestellt . Die Simulation wird von der Software „FDTD Solutions“ durchgeführt, wobei die Gittergröße des dreidimensionalen Mesh-Override-Bereichs 1 nm beträgt

Abhängig von der Materialverfügbarkeit werden Absorption und Extinktion experimentell für drei Nanoschalen unterschiedlicher Schalendicke, aber ähnlicher Kerndurchmesser gemessen:(80 nm-Durchmesser Siliziumdioxidkern)@(16-nm-dicke Goldschale), (79-nm-Durchmesser Siliziumdioxidkern)@(29-nm-dicke Goldschale) und (88-nm-Durchmesser Siliziumdioxidkern)@(36-nm-dicke Goldschale), deren TEM-Bilder in Abb. 3 gezeigt sind. Abbildung 4 zeigt den Vergleich zwischen den experimentell gemessenen und theoretisch simulierten Ergebnissen für die drei Nanoschalen. In Abb. 4 ist zu erkennen, dass die berechneten Absorptionsquerschnitte unter Berücksichtigung des Oberflächenstreueffekts gut mit den Messergebnissen für alle drei Nanoschalen übereinstimmen, während die gemessenen und simulierten Absorptionen stark abweichen, wenn die Oberfläche Streueffekt wird nicht berücksichtigt.

TEM-Bilder der drei Gold-Nanoschalen, die in experimentellen Messungen verwendet wurden. a Quarzkern mit 80 nm Durchmesser, 16 nm dicker Goldmantel. b Quarzkern mit 79 nm Durchmesser, 29 nm dicker Goldmantel. c Quarzkern mit 88 nm Durchmesser, 36 nm dicker Goldmantel. Die detaillierten Charakterisierungsinformationen finden Sie in den unterstützenden Informationen

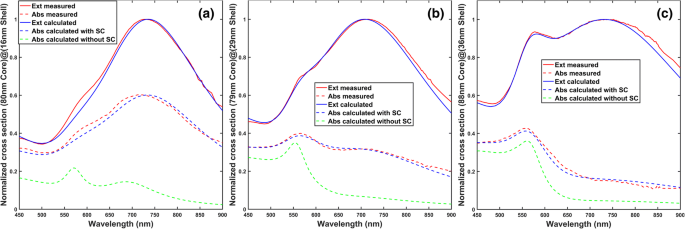
Vergleiche zwischen gemessenen und berechneten Absorptionsspektren mit und ohne Berücksichtigung der Oberflächenstreuung von Leitungselektronen. Alle Berechnungen werden nach der Mie-Theorie durchgeführt. Das umgebende Medium ist PVA (Polyvinylalkohol) mit einem Brechungsindex von 1,5. Beachten Sie, dass das umgebende Medium der Nanoschalen in unserem Experiment (PVA, n = 1,5) unterscheidet sich von dem in den Begleitinformationen bereitgestellten Charakterisierungsblatt, das Wasser ist. Die Tenside, die die Nanoschalen beschichten, können vernachlässigt werden, da die Tenside dünne Polymere sind und einen ähnlichen Brechungsindex wie das umgebende Medium von PVA haben. Der Brechungsindex von Siliziumdioxid wird in den Berechnungen mit 1,45 angenommen. Die Dielektrizitätskonstanten von Gold ohne Oberflächenstreuung stammen aus Lit. [38], während diejenigen mit Oberflächenstreuung durch Gl. (1) und (4). In allen Abbildungslegenden steht „Ext“ für Extinktion, „Abs“ für Absorption und „SC“ für Oberflächenstreuung. In jeder Abbildung sind "Ext berechnet" und "Abs berechnet mit SC" die Extinktions- und Absorptionsspektren, die mit den in Tabelle 2 gezeigten Anpassungsparametern berechnet wurden, während "Abs berechnet ohne SC" der Absorptionsquerschnitt ist, der ohne Berücksichtigung von Größenverteilung und Oberfläche berechnet wurde Streuung. a (80-nm-Durchmesser-Siliziumdioxid-Kern)@(16-nm-dicke Goldhülle). b (79-nm-Durchmesser-Siliziumdioxid-Kern)@(29-nm-dicke Goldhülle). c (Kern aus Siliciumdioxid mit 88 nm Durchmesser)@(36-nm-dicke Goldhülle)

Um die berechneten Extinktionen (die durchgezogenen blauen Linien) an die experimentell gemessenen Extinktionen (die durchgezogenen roten Linien) anzupassen, die in Abb. 4 gezeigt sind, wird der Ausdruck der zusätzlichen Dämpfung γ _s in Gl. (1) aufgrund von Oberflächenstreuung ist gegeben durch Gl. (4) unten gezeigt [15], anstelle von Gl. (2).

wo A ist ein dimensionsloser Anpassungsparameter und ein größeres A zeigt eine größere Dämpfung an und d _s ist die Schalendicke. Der Anpassungsparameter A wird von vielen Faktoren beeinflusst:Elektronendichte an der Oberfläche, Wirkung der Grenzfläche, Anisotropie der Teilchen und quantenmechanischer Berechnung, und ihr Wert liegt nachweislich zwischen 0,1 und über 2 [40, 41]. Beachten Sie, dass wir Gl. (2) in die Form von Gl. (4) um den theoretischen Wert von A . zu vergleichen vorhergesagt durch ein Billard-Streuungsmodell an diejenigen, die aus dem Experiment angepasst wurden, indem zuerst der Wert von L . berechnet wird _B in Gl. (2) unter Verwendung von Gl. (3) und schreibe dann L _B in Gl. (2) in die Form d _s /A , wie in Gl. (5a) bis (5d) unten:

schreiben

dann

wo

Beachten Sie, dass Gl. (5d) gibt ein A Wert von etwa 0,5 [13]. Die Werte der Anpassungsparameter für die berechneten Spektren der drei in Abb. 4 gezeigten Nanoschalen sind in Tabelle 2 tabellarisch aufgeführt.

Die berechneten Extinktions- und Absorptionsspektren in Abb. 4, die auf den dipolaren Peak normiert sind, haben die Oberflächenstreuung und die Größenverteilung berücksichtigt. Für jede Nanoschale werden die Standardabweichungen des Kerndurchmessers und der Schalendicke jeweils berechnet, indem die in Tabelle 2 angegebenen Werte für Kerndurchmesser und Schalendicke mit dem Variationskoeffizienten aus den in den Begleitinformationen bereitgestellten Charakterisierungsblättern multipliziert werden. Die im Fitting verwendeten Kerndurchmesser sind größer als die in den Charakterisierungsblättern angegebenen Werte. Dies liegt daran, dass die Größe der Silikatkugeln bei der TEM-Untersuchung schrumpft [42, 43] und die Schalendicken durch Subtrahieren der Kerndurchmesser in Tabelle 2 von den in den Charakterisierungsblättern angegebenen Gesamtdurchmessern erhalten werden. Die Peakbreiten der berechneten Extinktionsspektren werden so abgestimmt, dass sie mit den gemessenen übereinstimmen, und dann werden die entsprechenden Absorptionsspektren mit den abgestimmten Parametern berechnet. Die Werte von A vom Billard-Streumodell vorhergesagt würde 0,60, 0,52 bzw. 0,53 für die drei Nanoschalen betragen, wenn Gl. (5d) angewendet, die offensichtlich kleiner sind als die angepassten A die in Tabelle 2 aufgeführten Werte, nämlich 1,33, 1,67 bzw. 1,33 für die drei Nanoschalen. Da ein größerer Wert von A in Gl. (4) bedeutet eine größere Dämpfung freier Elektronen, es wurde beobachtet, dass die tatsächliche Dämpfung von Leitungselektronen größer ist als die vom Billardstreuungsmodell vorhergesagte, wobei die zusätzliche Dämpfung auf die chemische Grenzfläche zwischen der Schale und dem umgebenden Medium zurückzuführen sein könnte sowie der Siliziumdioxidkern [44, 45], Elektronendichte an der Oberfläche, Anisotropie der Teilchen und quantenmechanische Berechnungen, wie bereits erwähnt. Die Möglichkeit einer diskontinuierlichen Schale kann ausgeschlossen werden, indem das TEM-Bild im Charakterisierungsblatt in den unterstützenden Informationen betrachtet wird. Beachten Sie, dass die Peakverbreiterung aufgrund der Größenverteilung der Nanoschalen bereits bei der Anpassung berücksichtigt wurde, d. h. die angepassten Werte von A berücksichtigt nicht die Größenverteilung. Details zur Messung der Extinktion und Absorption sind im Abschnitt „Methoden/Experiment“ beschrieben.

Methoden/Experimental

In diesem Abschnitt wird für die in Abbildung 4 untersuchten Nanoschalen beschrieben, wie sie in dünnen PVA-(Polyvinylalkohol-)Filmen dispergiert werden und wie die Extinktion und Absorption dieser Nanoschalen aus optischen Messungen der mit Nanopartikeln dispergierten PVA-Dünnschichten abgeleitet werden.

Die drei in Abb. 4 untersuchten Nanoschalen, dh (80-nm-Durchmesser-Siliciumdioxid-Kern)@(16-nm-dicke Goldhülle), (79-nm-Durchmesser-Siliciumdioxid-Kern)@(29-nm-dicke Goldhülle) , und (88-nm-Durchmesser Siliziumdioxidkern)@(36-nm-dicke Goldschale), die der Einfachheit halber in der folgenden Diskussion als 16-nm-, 29-nm- bzw. 36-nm-Gold-Nanoschalen abgekürzt werden direkt von einem spezialisierten Unternehmen, nanoComposix, erworben und deren Charakterisierungsblätter sind in den unterstützenden Informationen aufgeführt (zusätzliche Datei 1).

Die Nanoschalen wurden bei der Aufnahme in Wasser dispergiert, wobei die 16-nm-Gold-Nanoschale eine Konzentration von 0,02 mg/ml und die anderen beiden eine Konzentration von 0,05 mg/ml aufwiesen. Für die 16-nm-, 29-nm- und 36-nm-Gold-Nanoschalen wurden 34, 25 und 34 ml ihrer Lösungen verwendet, um den in Nanopartikeln dispergierten PVA-Film herzustellen. Vor dem Mischen der erhaltenen Nanoschalenlösungen mit PVA-Pulver (80 % hydrolysiert, Sigma-Aldrich) wurde jede Nanoschalenlösung durch Zentrifugieren und Redispergieren auf 9 ml konzentriert. Dann wurden 0,9 g PVA-Pulver zu jeder konzentrierten Nanoschalenlösung zugegeben und die Mischungen wurden 2 h gerührt. Danach wurde jede gerührte Lösung in einer Vakuumkammer entblasen und dann in ein 5 × 5 cm ² . gegossen Glasform, und die Form wurde in einen Abzug gestellt, um die Lösung natürlich trocknen zu lassen. Nachdem die Lösungen getrocknet waren, wurden die PVA-Filme aus den Glasformen gerissen und sind in Abb. 5 dargestellt. Ein reiner PVA-Film ohne dispergierte Nanopartikel wurde ebenfalls hergestellt, außer dass 9 ml Wasser anstelle der Nanoschalenlösung mit . vermischt wurden PVA-Pulver.

a Mit der 16-nm-Gold-Nanoschale dispergierter Film. b Mit der 29-nm-Gold-Nanoschale dispergierter Film. c Mit der 36-nm-Gold-Nanoschale dispergierter Film. d Reine PVA-Folie

Der Extinktionsquerschnitt σ _ext einer Nanoschale hängt mit der direkten Transmission T . zusammen eines dünnen Films von Nanoschalen durch das Lambert-Beer-Gesetz [44]:

wo N ist die Flächendichte von Nanopartikeln, d. h. die Anzahl der Nanoschalen pro Flächeneinheit (beachten Sie, dass diese Fläche senkrecht zur Ausbreitungsrichtung des einfallenden Lichts liegt). Die direkte Transmission T wird erhalten, indem die gemessene direkte Durchlässigkeit eines mit Nanohülle dispergierten PVA-Films auf die des reinen PVA-Films ohne dispergierte Nanopartikel normiert wird. Also N σ _ext ist durch die folgende Gleichung gegeben:

Beachten Sie, dass anstelle von σ _ext , nur N σ _ext wird aus experimentellen Messungen abgeleitet, da es auf die Gesamtform des Spektrums ankommt. In Abb. 4, N σ _ext wird so normalisiert, dass der Maximalwert von N σ _ext des Spektrums ist 1.

Der Absorptionsquerschnitt σ _Bauchmuskeln einer einzelnen Nanoschale hängt mit dem Intensitätsverlust eines parallel einfallenden Lichtstrahls aufgrund von Absorption zusammen ∆I _Bauchmuskeln nachdem es einen dünnen Film aus Nanopartikeln passiert hat, basierend auf dem Beer-Lambert-Gesetz [44]:

wo ich ₀ ist die Intensität des einfallenden Lichts.

Der nächste Schritt besteht also darin, experimentell eine Abschwächung des einfallenden Lichts nur aufgrund der Absorption der Nanopartikel zu finden. Gleichung (8) geht davon aus, dass das Partikel rein absorbierend ist [44]. Für Nanopartikel, die Licht gleichzeitig absorbieren und streuen, gilt Gl. (8) ist wegen Mehrfachabsorptionen nicht gültig. Bei einem Ensemble solcher Nanopartikel werden, wenn das einfallende Licht zum ersten Mal auf ein Nanopartikel trifft, einige Lichtstrahlen absorbiert und andere gestreut. Aber wenn diese Streulichtstrahlen auf ihrem Weg aus dem Ensemble der Nanopartikel auf weitere Nanopartikel treffen, wird ein Teil von ihnen wieder absorbiert, was zu Mehrfachabsorptionen führt. Mehrfache Absorptionen des Streulichts deuten darauf hin, dass durch Messung der Gesamtlichtmenge, die nicht von dem mit Nanoschalen dispergierten PVA-Film absorbiert wird, die N σ _Bauchmuskeln abgeleitet nach Gl. (8) neigt dazu, die Absorption zu überschätzen. Da der PVA-Film in unseren Experimenten jedoch dünn ist (ca. 0,3 mm) und die Konzentration der Nanoschalen nicht hoch ist, wird angenommen, dass der größte Teil des Lichts einer Einfachstreuung (und damit einer Einzelabsorption) unterliegt [25]. Unter dieser Annahme ist der experimentelle Aufbau mit einer Ulbrichtkugel zur Messung der Gesamtlichtmenge, die nicht von dem mit Nanoschalen dispergierten PVA-Film absorbiert wird, in Abb. 6 dargestellt. In Abb. 6 T ₁ , T ₂ , oder R ist proportional zur Lichtmenge, die in der Ulbrichtkugel eingeschlossen ist, d. h. der Lichtmenge, die nicht aus der offenen Öffnung auf der rechten Seite austritt. In der folgenden Diskussion wird davon ausgegangen, dass T ₁ , T ₂ , und R sind proportional zur von der Ulbrichtkugel gesammelten Lichtintensität mit dem gleichen Koeffizienten α .

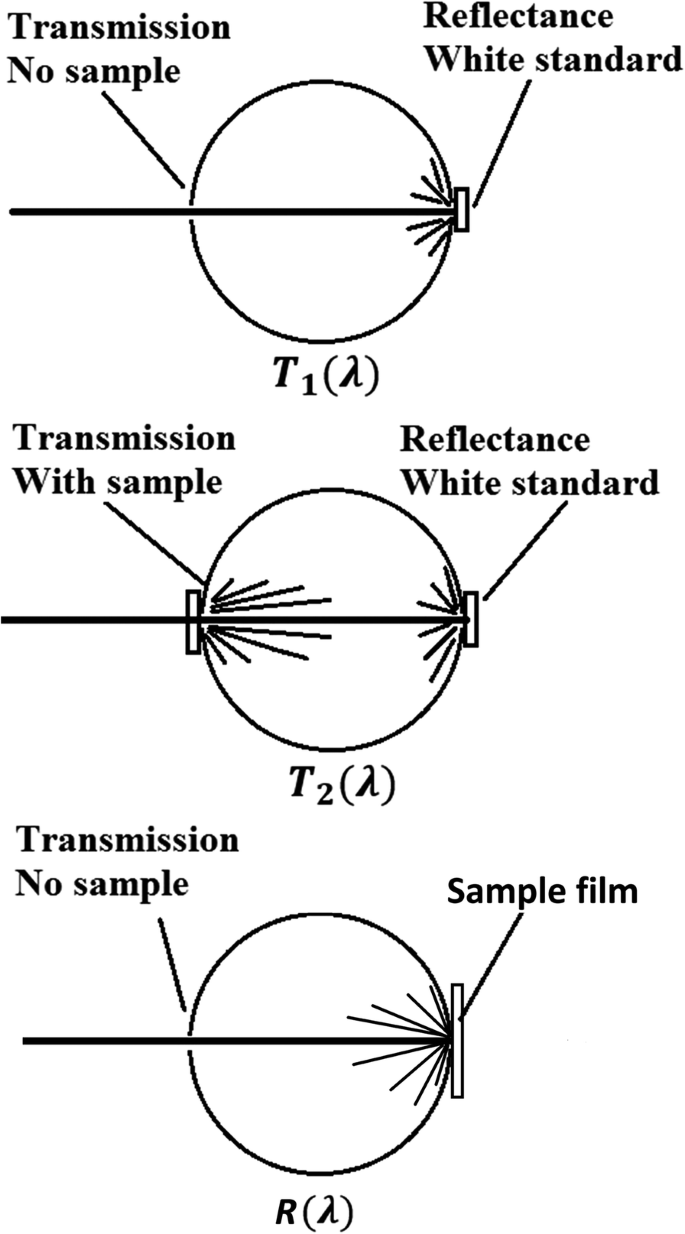
Versuchsaufbau zur Messung der Absorption. Die direkt gemessenen Werte sind T ₁ (λ ), T ₂ (λ ) und R (λ ) wobei T _ich (ich = 1, 2) oder R (λ ) ist proportional zur Lichtmenge, die in der Ulbrichtschen Kugel eingeschlossen ist. Aus diesen Messwerten wird die Absorption abgeleitet. Dieses Setup ist eine vereinfachte Version des in Referenz [22]

Gleichung (8) kann umgeordnet werden in \( \left({I}_0-\Delta {I}_{\mathrm{abs}}\right)={I}_0{e}^{-N\bullet {\ sigma}_{\mathrm{abs}}}\), und seine linke Seite stellt die Gesamtlichtmenge dar, die nicht absorbiert wird, nachdem das einfallende Licht durch den Probenfilm hindurchgegangen ist. Aus den Messungen in Abb. 6 können wir die folgenden Gleichungen schreiben:

Ersetzen von Gl. (9) und Gl. (10) in \(\left({I}_0-\Delta{I}_{\mathrm{abs}}\right)={I}_0{e}^{-N\bullet {\sigma}_{ \mathrm{abs}}} \), und mit einem Rauschterm zusätzlich zu N σ _Bauchmuskeln , kann die folgende Gleichung erhalten werden:

wo Lärm stammt aus der PVA-Matrix. Aufgrund der ersten Reflexion des einfallenden Lichts an der Grenzfläche Luft/PVA treten etwa 4% des einfallenden Lichts nie in den Dünnfilm ein (nach den Fresnel-Gleichungen bei senkrechtem Einfall an einer Grenzfläche zweier unterschiedlicher Medien mit den Indizes n ₁ (= 1 für Luft) und n ₂ (= 1,5 für PVA), die Lichtreflexion R ist gegeben durch \( R={\left|\frac{n_1-{n}_2}{n_1+{n}_2}\right|}^2 \)) und somit Gl. (11) wird modifiziert als

Unter der Annahme des Rauschens in der reinen PVA-Folie ohne dispergierte Nanopartikel ist derselbe wie in den Nanoschalen-dispergierten Filmen, ein ähnlicher Ausdruck kann für die reine PVA-Folie abgeleitet werden:

wobei \({T}_2^{\prime}\left(\lambda\right)\) und R ^′ (λ ) werden für die reine PVA-Folie auf die gleiche Weise wie T . gemessen ₂ (λ ) und R (λ ) jeweils für den Nanoschalen-dispergierten Film.

Aus Gl. (12) und (13), N σ _Bauchmuskeln ist durch den folgenden Ausdruck gegeben:

Während der Anpassung an die experimentellen Ergebnisse, bei denen der Wert von A in Gleichung (4) so ​​eingestellt wird, dass die Peakbreite des berechneten Extinktionsspektrums zu der gemessenen passt, stellt sich heraus, dass das normalisierte N σ _Bauchmuskeln ist immer noch etwas größer als die berechnete Absorption, die den Oberflächenstreueffekt beinhaltet. Dies legt nahe, dass mehrere Absorptionen von Streulicht immer noch zu einer zusätzlichen Absorption beitragen können, wie zuvor erörtert. Es wird hier also geschätzt, dass ein Teil p (0 < p < 1) des Streulichts, wenn keine Mehrfachabsorptionen auftreten, wird in der tatsächlichen Situation absorbiert, wobei p wird für die 16-nm-Nanoschale auf 10 % und für die 29 nm und 36 nm auf 5 % geschätzt. The following two equations are set to account for the multiple scattering effect:

wo N  ∙ σ _Bauchmuskeln ^′ and N  ∙ σ _sca ^′ are the light absorption and scattering, respectively, when no multiple absorptions happen, and N  ∙ σ _Bauchmuskeln and N  ∙ σ _ext are the experimentally measured absorption and extinction given by Eq. (14) and Eq. (7) respectively. The extinction in Eqs. (15) and (16) is the same because multiple scattering does not induce error in the measurement of N  ∙ σ _ext . From Eqs. (15) and (16), the corrected expression for the measured absorption is given below:

In Fig. 4, the corrected absorption N  ∙ σ _Bauchmuskeln ^′ is also normalized to the maximum value of the N  ∙ σ _ext spectrum calculated with Eq. (7).

Schlussfolgerungen

In this work, surface scattering of conduction electrons in gold nanoshell is shown to not only broaden the extinction peak width, but also increase the ratio of light absorption to extinction and thus decrease the ratio of light scattering to extinction. It is also found that the thinner the shell thickness, the more increase of the absorption ratio. And the increase of light absorption ratio is verified by fitting of calculated absorption spectra to measured ones.