Plasmonenresonanz bei der Photoabsorption kolloidaler hochdotierter ZnO-Nanokristalle

Hintergrund

Optische Eigenschaften von Nanopartikeln werden zu einem großen Teil durch das Vorhandensein lokalisierter Oberflächenplasmonenresonanzen (LSPR) in ihren Anregungsspektren bestimmt [1–8]. Kriegel et al. [2] veröffentlichte einen recht detaillierten Überblick über aufkommende kolloidale Nanokristalle (NCs), darunter fremdstoffdotierte Metalloxid-NCs, Kupferchalkogenid-NCs und degenerativ dotierte Halbleiter-NCs, und diskutierten ausführlich ihre optischen Eigenschaften sowie Anwendungen für die Sensorik im Nahfeld Verbesserung der Spektroskopie, durchstimmbare optoelektronische Geräte oder biomedizinische Anwendungen. Alle diese neuen Materialien sind eine Alternative zu Edelmetall-NCs, die in den letzten Jahrzehnten intensiv untersucht wurden; für eine umfassende Übersicht siehe auch Lit. [9]. Es wurde gezeigt, dass es möglich ist, die optische Reaktion von stark dotierten Halbleiter-Nanokristallen (NCs) bis in den IR-Bereich [10–15] abzustimmen, indem verschiedene Kontrollparameter beeinflusst werden [11, 13, 16–20] neue Perspektiven für die Nanophotonik. Der Hauptvorteil von Halbleiter-NCs besteht darin, dass die Trägerdichte über ein breites Intervall abgestimmt werden kann. Während ein metallischer Leiter eine feste Elektronendichte hat, kann ein Halbleiter dotiert werden, um beliebige Ladungsträgerdichten in einem Bereich von 10 ¹⁶ . zu erreichen ÷10 ²² cm ⁻³ [10, 13, 21, 22]. Die Trägerdotierung ermöglicht den Zugang zu abstimmbarem LSPR in einem weiten Frequenzbereich vom THz bis zum IR und dem sichtbaren Bereich [13]. Eine solche Einstellbarkeit der Ladungsträgerdichte ist eine einzigartige Eigenschaft von Halbleiter-Nanopartikeln und kann nicht mit Metalltröpfchen erreicht werden [23–25]. Die Dotierung kann durch den Einbau verschiedener Arten von Verunreinigungen in das Kristallgitter erfolgen [7, 10, 18], und die Plasmonenresonanzfrequenz kann durch aktive Steuerung der Ladungsträger eingestellt oder umgeschaltet werden [13, 16–18, 21, 22]. Darüber hinaus hängt die Plasmonenfrequenz und ihre Linienform nicht nur von der Ladungsträgerdichte des NC ab, sondern auch von der Art der Dotierung, die „bulk-like“ oder „surface-like“ sein kann [15, 22]. Im ersteren Fall wird die Ladung der freien Ladungsträger durch die Ladung der Dotierungsverunreinigungen im gesamten NC-Volumen neutralisiert, während im letzteren Fall die freien Ladungsträger durch Donatoren/Akzeptoren aus den umgebenden Medien, die sich an der NC-Schnittstelle.

Theoretische Studien der optischen Reaktion von Halbleiter-Nanopartikeln haben signifikante Unterschiede zwischen quantenmechanischen und klassischen Beschreibungen ergeben [5, 22, 24, 26]. Mit abnehmender Nanopartikelgröße verschiebt sich die Plasmonenresonanz zu höheren Energien mit sichtbarer Abweichung von klassischen Vorhersagen [5, 21, 22]. Darüber hinaus unterliegen die dynamischen Eigenschaften hochdotierter NCs einem Übergang vom Größenquantisierungsregime zum klassischen Regime der Plasmonenoszillationen [22]. Sie kann beobachtet werden, indem entweder die Anzahl der Träger oder die NC-Größe variiert wird.

In dieser Arbeit präsentieren wir eine theoretische Analyse der optischen Reaktion von photodotierten ZnO-NCs, wie sie experimentell in Lit. untersucht wurde. [21, 27]. In diesen experimentellen Studien wurden die Photoabsorptionsquerschnitte von kolloidalem ZnO-NC fester Größe und Trägerdichte gemessen. Die Photoelektronen des Leitungsbandes wurden in ZnO NC durch einen Photodotierungsprozess erzeugt, während die Löcher von den Löchern einfangenden Zentren im umgebenden Toluol eingefangen wurden. Die mittlere Konzentration der leitenden Elektronen n _e in fast kugelförmigen photodotierten Nanokristallen mit unterschiedlichen Radien (von 1,75 bis 6 nm) wurde eine Obergrenze von (1,4±0,4)×10 ²⁰ . erreicht cm ⁻³ [21, 27]. Die Intraband-Extinktion wurde im Bereich von 0,2 bis 1,0 eV gemessen, und es wurden signifikante Unterschiede zur klassischen Vorhersage des Drude-Modells beobachtet. Die Autoren zeigten, dass ein quantenmechanischer Ansatz basierend auf Einteilchenübergängen die experimentelle Größenabhängigkeit der Resonanzfrequenz nur qualitativ liefert [21].

Das Ziel dieses Artikels ist es, den theoretischen Ansatz der Plasmonenresonanzen in photodotierten ZnO-NCs zu überdenken, indem er über die wechselwirkungsfreie Einzelpartikel-Näherung hinausgeht [21, 27]. Es basiert auf der selbstkonsistenten quantenmechanischen Vielteilchenbehandlung von Leitungselektronen innerhalb der Random Phase Approximation (RPA) mit lokalem Austausch [28]. Es wurde gezeigt, dass freie Ladungsträger in Halbleiter-Nanopartikeln atomähnliche Schalen bilden [29, 30]. Wir lösen die Kohn-Sham-Gleichungen der lokalen Dichteapproximation (LDA), um die Elektronenschalenstruktur zu beschreiben. Die für die kollektiven Plasmonenanregungen verantwortlichen Elektronenkorrelationen werden innerhalb der RPA berücksichtigt. Wir zeigen, dass sich die Plasmonenresonanz in ZnO NC wesentlich von der bekannten Mie-Resonanz in metallischen Tröpfchen unterscheidet. Im Gegensatz zu masseartig dotierten NCs gibt es in oberflächenartig dotierten ZnO-NCs keine wiederherstellende positive Ladung. Folglich drückt die Coulomb-Abstoßung zwischen freien Elektronen diese nahe an die NC-Oberfläche. Diese spezielle elektronische Konfiguration führt wiederum zu einem Dipolmodus, bei dem nur die Winkelfreiheitsgrade angeregt werden, während die elektronische Radialbewegung nicht beteiligt ist. Im Gegensatz zum gewöhnlichen Mie-Oberflächendipolplasmon, bei dem Elektronen reinen Translationsoszillationen unterliegen, unterliegen Elektronen in hochdotierten ZnO-NCs tangentialen Schwingungen innerhalb der eher dünnen elektronischen Hülle, ähnlich den Plasmonenschwingungen in Fullerenmolekülen [31]. Wir zeigen auch, dass der Übergang dieser Plasmonenmode vom klassischen zum Quanten-Confinement-Regime durch das Verhältnis der NC-Größe zum effektiven Bohr-Radius bestimmt wird und nicht von der Anzahl der freien Elektronen abhängt. Die Quanteneffekte bei Plasmonenoszillationen führen zu einer Blauverschiebung der Dipolresonanzfrequenz, die gut mit der experimentell beobachteten LSPR-Größenabhängigkeit übereinstimmt [21].

Methoden

Ziel der Studie ist die theoretische Analyse der optischen Eigenschaften von photodotierten ZnO-Nanokristallen. Die Grundzustandskonfigurationen der Systeme mit unterschiedlichen Teilchenzahlen wurden innerhalb der lokalen Dichteapproximation berechnet. Die Grundzustandswellenfunktionen sind Einteilchenenergien, die durch selbstkonsistentes numerisches Lösen des Satzes von Kohn-Sham-Gleichungen [32] erhalten wurden. Die vollständige Basis der Einteilchenzustände wurde mit der B-Spline-Methode [33] erzeugt, indem die Basisfunktionen in einer Kavität mit großem Radius über endlich viele B-Splines erweitert wurden. Der Kavitätenradius wurde gleich dem NC-Radius gewählt. Die gewünschte Genauigkeit der Berechnungen unter Verwendung der diskreten B-Spline-Basis wurde durch die geeignete Wahl der Anzahl und der Reihenfolge der bei der Berechnung verwendeten B-Splines erreicht. Wir haben 50 B-Splines der Ordnung 7 verwendet, um eine ausreichende Genauigkeit zu erreichen (10 ⁻⁵ ) der Ergebnisse. Zur Ermittlung der Eigenwerte und Eigenvektoren der RPA-Matrixgleichung [28] wurde das Standard-Unterprogramm RG aus dem Eigensystem-Unterprogrammpaket (EISPACK) verwendet, dessen Lösung uns die Menge der Dipol-Anregungsenergien und die entsprechenden Oszillatorstärken liefert. Das Photoabsorptionsspektrum wurde durch die Verbreiterung der berechneten Schwingungsstärkeverteilung durch Lorentz-Profile mit fester Faltungsbreite erhalten.

Ergebnisse und Diskussion

Grundzustandsstruktur

Wir betrachten das System von N Leitungsbandelektronen lokalisiert innerhalb des ZnO NC mit Radius R . Gemäß [21] nehmen wir an, dass die Anzahl der Elektronen mit der NC-Größe variiert als N =4π n _e R ³ /3, wobei die feste mittlere Elektronenkonzentration n _e =1,4×10 ²⁰ cm ⁻³ , wird durch das höchste erreichbare Niveau im Photodotierungsverfahren bestimmt. Der Radius der betrachteten NCs reicht von 2,4 bis 6 nm; dementsprechend die Anzahl der Leitungselektronen, N , variieren von 8 bis 128.

Wir verwenden die Näherung der Hüllkurvenfunktion, um die Elektronenbewegung zu beschreiben, unter der Annahme, dass R ist viel größer als die Gitterkonstante. Es ist bekannt, dass die elektronische Bandstruktur von massivem ZnO durch ein nicht isotropes und nicht parabolisches Energiespektrum gekennzeichnet ist [34]. Für das aktuelle Problem der kollektiven Dynamik von N delokalisierten Elektronen werden wir diese kleinen Energiespektrumeffekte vernachlässigen und eine isotrope parabolische Energiedispersion mit effektiver Masse \(m_{e}^{*}=0.3~m_{e}\) betrachten [34]. Aus dem gleichen Grund betrachten wir die ZnO-NCs als sphärische Systeme.

Da die Elektronen aufgrund des hohen Leitungsband-Offsets an der NC-Grenzfläche stark innerhalb des ZnO-NC-Volumens lokalisiert sind [6], erzwingen wir, dass alle Elektronenwellenfunktionen an der NC-Grenze verschwinden r =R . Daher betrachten wir N wechselwirkende Elektronen, die in einer unendlichen kugelförmigen Vertiefung lokalisiert sind, deren Gesamtladungsneutralität durch eine positive Ladungsflächenverteilung sichergestellt wird, die kein Feld innerhalb des NC erzeugt. Der effektive Hamiltonoperator des betrachteten Systems ist einfach:

wo V (r _a ,r _b ) steht für die Paarelektronen-Coulomb-Wechselwirkung. Sein expliziter Ausdruck, der die Polarisation des ZnO-Materials und des umgebenden Mediums berücksichtigt, wird als Multipolentwicklung geschrieben [3],

wo r _< und r _> sind die kleinste bzw. größte der beiden radialen Positionen. Den Dielektrizitätskonstanten von ZnO und Toluol werden ihre Volumenwerte ε . zugewiesen _ich =3,7 und ε _m =2,25 [21] bzw.. Mit diesen Parametern ist der effektive Bohr-Radius \(a_{0}=\hbar^{2} \varepsilon_{i}/m_{e}^{*} e^{2} =0.65\) nm kleiner als der NC-Radius.

Die Einteilchen-Elektronenenergien ε _ich , und Hüllkurvenfunktionen ψ _ich den Satz von LDA Kohn-Sham-Gleichungen erfüllen,

wobei das mittlere Feldpotential V _mf ist gegeben durch die Summe von direkt, V _D (r ) und tauschen, V _x (r ), Teile,

wobei \(\rho =\sum_{i}|\psi_{i}|^{2}\) die Elektronendichte ist. Beachten Sie, dass wir den lokalen dichteabhängigen Austauschterm in seiner Dirac-Form wie üblich durch einen realistischeren lokaldichteabhängigen Austauschkorrelationsterm ersetzen könnten. Wir tun dies nicht, da die theoretische Konstruktion angeregter Zustände, die automatisch folgt, einen großen Teil der Grundzustandskorrelationen der RPA-Natur ausmacht.

Der Einfachheit halber betrachten wir kugelsymmetrische Elektronenkonfigurationen mit geschlossenen elektronischen Schalen. In diesem Fall werden die Einteilchen-Wellenfunktionen als Produkte von Radial-, Winkel- und Spinkomponenten angegeben [35]. Folglich ist der Index i =(n ,l ), wobei n ist die radiale Quantenzahl und l der Drehimpuls. Die numerische Lösung von Gl. (3) für Elektronenzahl N <130 zeigte, dass die Elektronenkonfiguration im Grundzustand aus besetzten elektronischen Zuständen mit den niedrigsten radialen Quantenzahlen n . besteht =1. Diese elektronischen Zustände haben knotenlose radiale Wellenfunktionen und unterscheiden sich durch die Werte der Drehimpulse l . Unter Berücksichtigung der Spin-Entartung sind die „magischen“ Elektronenzahlen für solche symmetrischen Konfigurationen also N =2(l _max +1) ² , wo l _max ist der maximale Drehimpuls des höchsten besetzten elektronischen Zustands. In Abb. 1 zeigen wir die Dichteverteilungen ρ (r ) für den NC mit N =18, 50, 128 Elektronen. Man sieht, dass die radiale Dichteverteilung immer schmaler wird und sich mit zunehmender Größe zur NC-Schnittstelle hin verschiebt. Der Einsatz von Abb. 1 zeigt die Größenabhängigkeit des mittleren elektronischen Wertes der elektronischen Radialverteilung 〈r 〉 auf dem NC-Radius R und das Verhältnis δ r /R , seiner Dispersion \(\delta r =\sqrt {\langle r^{2} \rangle - {\langle r\rangle}^{2}}\) (die als effektive elektronische Schalenbreite angesehen werden kann) zu der NC-Radius. Dieses Verhältnis, das für den kleinsten NC mit N . nur ∼ 0,15 beträgt =8 Elektronen nimmt für die größeren Systeme schnell ab. Numerisch ist die Breite der elektronischen Hülle δ r beträgt etwa zwei Drittel des effektiven Bohr-Radius a ₀ wohingegen der Peak der elektronischen Hülle aufgrund der Quantenreflexion um ungefähr R . von der NC-Grenzfläche verschoben ist −〈r 〉≃2a ₀ . Diese Eigenschaft des elektronischen Systems folgt aus der starken Coulomb-Abstoßung, die die Elektronen an die NC-Grenze drückt und eine hohlkugelförmige Ladungsverteilung bildet. Wenn der NC-Radius groß genug ist, ist die Coulomb-Abstoßungskraft an der NC-Grenze e ² N /ε _ich R ² wird viel stärker als die Fliehkraft \(\hbar^{2}l(l+1)/m_{e}^{*}{\langle r\rangle}^{3}\) selbst für den höchsten besetzten Zustand mit \(l=l_{max}=\sqrt {N/2}-1\). Man kann sehen, dass ihr Verhältnis a . beträgt ₀ /2R . Deshalb trennen sich die radiale und die winklige Elektronenbewegung, wenn R ≫a ₀ . In diesem Fall ähnelt das elektronische System einem Quantenrotator, z. B. das Energiespektrum besetzter Einzelteilchenzustände ε _ich von Gl. (3) wird durch die Formel gut angenähert,

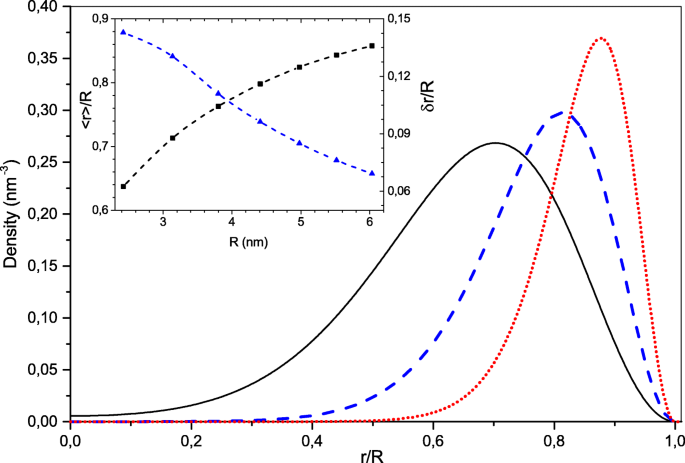
Radiale Dichteverteilungen für NCs mit unterschiedlicher Anzahl delokalisierter Elektronen, N =18 (durchgezogen schwarz wie), 50 (gestrichelte blaue Linie), 128 (gestrichelte rote Linie). Im Einschub ist der reduzierte mittlere Radius (schwarz) und seine Streuung (blau) als Funktion des NC-Radius dargestellt

Optische Reaktion

Bei der linearen Antwort-Approximation induziert ein externes harmonisches elektrisches Feld zeitabhängige selbstkonsistente Felder gleicher Frequenz. Die Kenntnis der entsprechenden Schwingungen kleiner Amplitude liefert Informationen über die angeregten Dipolzustände sowie über die Übergangswahrscheinlichkeiten zwischen Grundzustand und angeregten Zuständen. Für ein System, dessen Grundzustand eine Slater-Determinante ist |Φ ₀> werden die korrelierten angeregten Vielteilchendipolzustände innerhalb des RPA-Ansatzes als lineare Überlagerung einer Teilchen-Loch-Anregung konstruiert [36]:

. $$ (6)

Die Indizes i ,m , (j ,n ) beziehen sich auf die Einteilchenzustände über (unter) dem Fermi-Niveau F; \(\hat{a}^{+}\) und \(\hat{a}\) sind die Erzeugungs- bzw. Zerstörungs-Einzelteilchen-Operatoren.

Die vorwärts gerichteten \(X_{ij}^{\nu}\) und die rückwärts gerichteten \(Y_{ij}^{\nu}\) Amplituden können durch Lösen der Matrix-RPA-Gleichung erhalten werden [ 28]:

$$ \left(\begin{array}{ll} \mathbf{A} &\mathbf{B} \\ \mathbf{B}^{\star} &\mathbf{A}^{\star} \end{ array} \right) \left(\begin{array}{l} \mathbf{X}^{\nu} \\ \mathbf{Y}^{\nu} \end{array} \right) =\omega_{ \nu} \left(\begin{array}{l} \mathbf{X}^{\nu} \\ -\mathbf{Y}^{\nu} \end{array} \right), $$ (7 )

wobei die Eigenwerte ω _ν sind die Anregungsenergien. Die Matrizen A und B sind wie folgt definiert

$$ {\begin{ausgerichtet} A_{ij,mn}&\,=\,\delta_{im}\delta_{jn}\left(\varepsilon_{i}-\varepsilon_{j}\right) \,+ \, \left\langle in\left| \hat{v}\right| jm\right\rangle,\quad B_{ij,mn}&\,=\,\left\langle im\left| \hat{v}\right| jn\right\rangle \\\hat{v}(\mathbf{r},\mathbf{r}^{\prime}) &=V(\mathbf{r},\mathbf{r}^{\prime} )+\delta\left(\mathbf{r}-\mathbf{r}^{\prime}\right)\delta V_{x}/\delta\rho. \end{aligned}} $$ (8)

Beachten Sie nebenbei, dass die Rückwärtsamplituden \(Y_{ij}^{\nu}\) den Beitrag der Elektron-Loch-Grundzustandskorrelationen \(\hat{a}_{j}^{+}\hat{ a}_{i}|\Phi _{0}>\), bzw. zur Anregung des angeregten Zustands |Φ _ν > der Häufigkeit ω _ν .

Die entsprechenden Dipoloszillatorstärken f _ν werden in Form der RPA-Amplituden X . ausgedrückt ^ν und J ^ν ,

$$ f_{\nu} =\frac{2 m_{e}^{*} D^{2}_{\nu}\omega_{\nu}}{\hbar^{2}}, \quad D_{ \nu} =\sum_{ij} \left(X^{(\nu)}_{ij} d_{ij} + Y^{(\nu)}_{ij} d_{ji} \right), $ $ (9)

wo d _ij =〈ich |z |j 〉 sind die Einzelteilchen-Dipol-Matrix-Elemente.

Die Photoabsorptionsquerschnitte wurden durch Verbreiterung der berechneten Oszillatorstärkeverteilung durch Lorentz-Profile mit der Faltungsbreite von 0,2 ω . erhalten . Photoabsorptionsspektren zusammen mit Oszillatorstärkeverteilungen für NCs mit N =8 (a), 32 (b), 50 (c) und 128 (d) Elektronen sind in Abb. 2 gezeigt. In Abb. 2d vergleichen wir den berechneten Photoabsorptionsquerschnitt mit den experimentellen Daten von Lit. [21] für ZnO NC mit R 6 nm. Man sieht, dass in allen betrachteten NCs die Spektren von einer einzigen Resonanzlinie dominiert werden, deren Position tatsächlich das Maximum des Photoabsorptionsquerschnitts bestimmt. Tatsächlich wird dies erwartet, da das elektronische Einteilchen-Spektrum einem Quantenrotator ähnelt. Die stärksten Übergänge treten für eine maximale Wellenfunktion überlappend auf, d. h. bei gleicher radialer Quantenzahl n . In unserem Fall gibt es nur einen solchen optischen Übergang vom höchsten besetzten Zustand j =(1,l _max ) zum niedrigsten freien Zustand i =(1,l _max +1). Die entsprechende Dipolanregung unterscheidet sich jedoch stark vom wechselwirkungsfreien Einteilchenübergang, wenn eine starke Coulomb-Abstoßung Elektronenkorrelationen wichtig und überwältigend macht. Dies ist der Fall, wenn R ≫a ₀ . Nämlich die Energie der kollektiven Erregung, ω _ν , übersteigt die Energie des Einteilchenübergangs

$$ \Delta =\left(\epsilon_{1, l_{max}+1} -\epsilon_{1, l_{max}}\right)=\frac{\hbar^{2} (l_{max}+ 1)}{m_{e}^{*}{\langle r\rangle}^{2}}. $$ (10)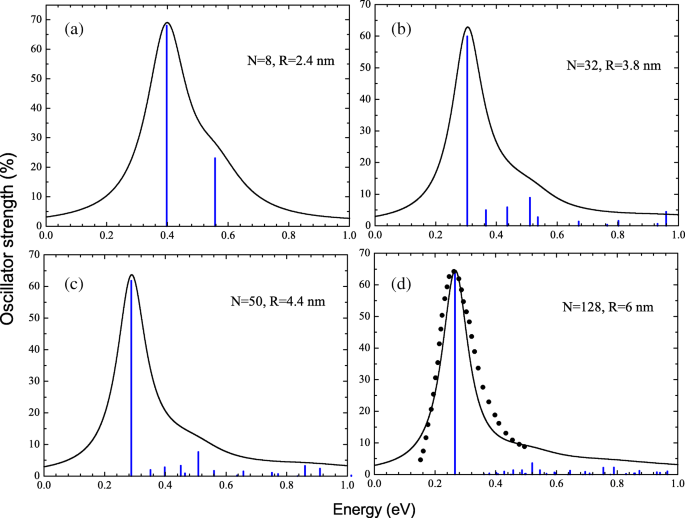

Oszillator-Stärkeverteilungen und entsprechende Photoabsorptions-Peakprofile, berechnet innerhalb des RPAE-Ansatzes für NCs mit N =8 (a ), 32 (b ), 50 (c ) und 128 (d ) Leitungsbandelektronen. Vergleich experimenteller [21] (schwarze Quadrate) und berechneter (durchgezogene Linie) Resonanzpeakprofile für NC mit R ≈6 nm (d )

In Abb. 3 vergleichen wir die Positionen der Photoabsorptionsmaxima, ω _res , hier berechnet (blaue Kreise) mit experimentellen Ergebnissen von [21] (rote Sterne). Man beobachtet eine bemerkenswerte Übereinstimmung zwischen experimentellen Daten und unseren theoretischen Ergebnissen. Zum Vergleich tragen wir hier auch die Energien Δ des Einteilchenübergangs (grüne Quadrate). Elektronenkorrelationen erhöhen die kollektive Anregungsenergie im Vergleich zu Δ . erheblich . Eine einfache Analyse von RPA Gl. (7) erklärt diese Beobachtung. Betrachten wir nur den optischen Hauptübergang von j =(1,l _max ) bis j =(1,l _max +1) besagt, dass die RPA-Gl. (7) reduziert sich auf eine 2×2-Matrixgleichung, deren Eigenwert ω ist einfach:

$$ \omega^{2}=\Delta^{2} +2V\Delta, $$ (11)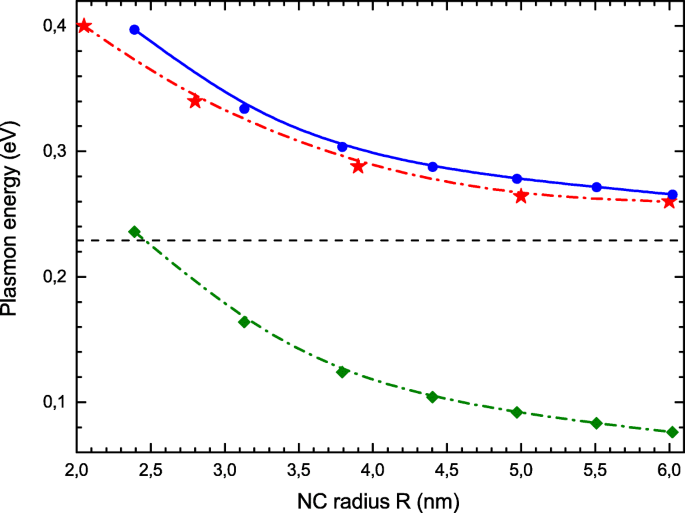

Größenabhängigkeit der LSPR-Energie. Experimentelle Werte [21] (rote Sterne), RPA mit lokalem Austausch (blaue Kreise), Energien des Einzelteilchenübergangs (grüne Rauten in der unteren Kurve). Der klassische Wert (13) wird durch die horizontale gestrichelte Linie angezeigt

wobei \(V=\left\langle ij\left|\hat{v}\right|ij\right\rangle\) das RPA-Coulomb-Matrixelement bezeichnet. Der erste Begriff in der r.h.s. von Gl. (11) gibt den Einzelteilchenbeitrag an, während der zweite Term aus Teilchen-Loch-Wechselwirkungen resultiert. Ihr Verhältnis kann abgeschätzt werden, indem man die radiale Elektronenkoordinate an der Oberfläche nimmt, r =R im RPA-Matrixelement V , und vernachlässigt den Austauschterm. Diese Schätzung ergibt

$$ \frac{2V}{\Delta} \simeq \frac{4R\varepsilon_{i}}{a_{0}(\varepsilon_{i}+2\varepsilon_{m})} \simeq \frac{2R} {a_{0}}. $$ (12)

Somit dominiert der Beitrag der Elektronenkorrelationen, wenn R ≫a ₀ . Im Grenzfall großer NCs konzentriert sich die Elektronendichteverteilung auf die NC-Oberfläche; daher ist nach Gl. (12), die Resonanzenergie in Gl. (11) neigt zu

$$ \omega =\sqrt{\frac{2\hbar^{2}e^{2}N}{m_{e}^{*}(\varepsilon_{i}+2\varepsilon_{m})R^ {3}}}, $$ (13)

was genau mit der klassischen Dipol-Plasmonenfrequenz in einer dünnen Kugelschale übereinstimmt [37]. Diese Plasmonenmode entspricht einer tangentialen Elektronenschwingung. Auf diese Weise ähnelt sie der Oberflächenplasmonenresonanz in C ₆₀ Moleküle, wobei die Resonanzfrequenz durch die Gleichung analog zu Gl. (13) [38]. Beachten Sie, dass diese Plasmonenmode wie der Fulleren-Fall [39] zwei Drittel der Gesamtschwingungsstärke einnimmt (siehe Abb. 2). Dies geschieht, weil diese Schwingung nur die Winkelfreiheitsgrade umfasst, wodurch die radiale Bewegung ungestört bleibt.

Im Gegensatz zur bekannten rein translatorischen Dipol-Oberflächen-Plasmonenmode in homogenen Kugeln handelt es sich bei der hier betrachteten Mode um eine Kompressionsmode. Die induzierte Dichte erzeugt ein elektrisches Feld parallel zur Oberfläche, das die Rolle der Rückstellkraft für diesen Plasmonenmodus spielt. Darüber hinaus trägt die rein Quantenvariation des lokalen Fermi-Niveaus aufgrund induzierter Dichteoszillationen zur Rückstellkraft bei. Der entsprechende Quantendruckbeitrag zur Resonanzfrequenz ist gegeben durch Δ Term in Gl. (11). Er ist kleiner als der Coulomb-Beitrag in allen betrachteten NCs wegen der Kleinheit des effektiven Bohr-Radius a ₀ in ZnO. In NCs mit einem größeren Wert von a ₀ , konnte man den Übergang von der klassischen Dipol-Plasmonenresonanz zum Quanten-Confinement-Regime bei R . beobachten ∼a ₀ . Es ist erwähnenswert, dass bei dotierten NCs der Parameter a ₀ /R welche die klassische/quantenartige Natur der Dipolresonanz kontrolliert, hängt nur von der NC-Größe und nicht von der Anzahl der freien Träger ab N .

In Abb. 3 bezieht sich die horizontale Linie auf die klassische Plasmonenresonanzenergie (13). Die Blauverschiebung der Resonanzfrequenz gegenüber ihrem klassischen Wert wird durch zwei Quanteneffekte verursacht, den oben diskutierten Quantendruckbeitrag und die Abnahme des mittleren Elektronenradius. Letzteres geschieht, weil Elektronen aufgrund der Quantenreflexion von der Grenze in das NC-Volumen gedrückt werden, sodass 〈r 〉≃R −2a ₀ . Dieser Effekt erhöht das Matrixelement V was wiederum die Resonanzfrequenz erhöht. Grob lässt sich dieser Effekt durch Ersetzen des NC-Radius R . reproduzieren im Nenner von Gl. (13) von 〈r . Nach Gl. (11)–(13), beide Effekte liefern die blaue Frequenzverschiebung proportional zum inversen NC-Radius ∝1/R . Zahlenmäßig ist der Beitrag des letzten jedoch der größte.

Schlussfolgerungen

Um diesen Brief abzuschließen, haben wir eine Theorie ausgearbeitet, die die starke Dipolresonanz, die in hoch n-dotierten kolloidalen ZnO-NCs beobachtet wird, gut vorhersagt. Der neue Typ von Oberflächendipolplasmonenanregungen wurde theoretisch mit dem Vielteilchenquantenansatz untersucht. Wir haben gezeigt, dass die starke Coulomb-Abstoßung in photodotierten ZnO-Nanokristallen zu einer spezifischen Elektronenverteilung im Grundzustand führt, die in einer dünnen Oberflächenschicht nahe der Innenoberfläche lokalisiert ist. Wenn der Dipol angeregt wird, hält diese elektronische Verteilung eine kollektive Plasmonenschwingung aufrecht, die im Wesentlichen aus einer Winkelbewegung besteht. Der Übergang dieser Oberflächenplasmonenmode vom klassischen zum Quanten-Confinement-Regime wird durch einen einzigen Parameter bestimmt, der dem Verhältnis der Nanokristallgröße zum effektiven Bohr-Radius entspricht. Elektronenreflexion von der NC-Schnittstelle verringert den Radius der elektronischen Hülle. Außerdem liefert die Variation des lokalen Fermi-Niveaus einen zusätzlichen Beitrag zur Rückstellkraft des Plasmonoszillators. Diese Quanteneffekte führen zu einer Größenabhängigkeit der Resonanzplasmonenfrequenz, die eine bemerkenswerte Übereinstimmung mit experimentellen Beobachtungen ist. Im Grenzbereich des großen NC-Radius tendiert die Resonanzlinie glatt zur klassischen Plasmonenfrequenz einer geladenen Schale infinitesimaler Breite.

Abkürzungen

LDA:

Näherung der lokalen Dichte

LSPR:

Lokalisierte Oberflächenplasmonenresonanz

NC:

Nanokristall

RPA:

Zufällige Phasenannäherung