Formstabilität metallischer Nanoplatten:Eine Studie zur Molekulardynamik

Einführung

Als eine wichtige Klasse funktioneller Nanomaterialien wurden metallische Nanoplättchen aufgrund ihrer hervorragenden katalytischen Aktivitäten [1,2,3,4], einstellbaren optischen Eigenschaften [1,5,6,7] und ihrer potentiellen Verwendung in Mikroschaltkreisen umfassend synthetisiert und untersucht , unter anderem [8, 9]. Die Anwendungsleistung von Nanomaterialien hängt bekanntlich stark von deren Strukturen und Morphologien ab. Daher sollte ein tiefgreifendes Verständnis der Formstabilität dieser metallischen Nanoplättchen von entscheidender Bedeutung für ihre Synthese und Verwendung sein. Aus thermodynamischer Sicht weicht die Struktur einer einzelnen Nanoplatte vom energetischen Minimum ab und soll sich aufgrund der Tendenz zur Minimierung der Oberflächenenergie zu einem kugelförmigen Nanopartikel entwickeln. Als metastabile Konfigurationen werden Nanoplättchen jedoch aufgrund der Beteiligung komplexer kinetischer Faktoren in Experimenten nicht selten beobachtet [10]. Eine relativ höhere Temperatur erhöht die Möglichkeit für das System, dem kinetischen Einfangen zu entkommen und den Zustand mit niedrigerer Energie zu realisieren. Insbesondere bei Nanoplättchen mit einer Dicke von mehreren Atomlagen implizieren die signifikant hohen Oberflächen-Volumen-Verhältnisse einen großen Anteil an Atomen mit schwacher Bindung (dh hoher Mobilität), die gegenüber der Umgebung empfindlich und daher vermutlich einfach sind um die Formänderung herbeizuführen. Induziert durch die angepassten äußeren Bedingungen wurden die Veränderungen von Form und Struktur im festen Bereich beobachtet [11,12,13,14,15]. Beachten Sie, dass diese Art von Umwandlungen nicht eindeutig durch die Thermodynamik bestimmt ist, um sich zu den energetisch günstigeren Kugeln zu entwickeln, während der umgekehrte Weg von kugelförmigen Partikeln zu den anisotropen Platten, ähnlich der Ostwald-Reifung, auch durch die Thermik ausgelöst wurde Behandlung [11].

Experimentelle Untersuchungen wurden durchgeführt, um die thermischen Eigenschaften von metallischen Nanoplättchen zu untersuchen. In-situ-Ergebnisse des Transmissionselektronenmikroskops (TEM) in Kombination mit anderen Strukturanalysen zeigen beispielsweise, dass Au-Nanoplättchen (110) Facetten um die Kanten herum aufweisen, die aus den instabilsten Atomen bestehen, und dass beim Erhitzen eine Fragmentierung auftritt [15]. Dennoch ist es für das mikroskopische Experiment äußerst schwierig, quantitative Charakterisierungen des Formentwicklungsmechanismus bereitzustellen. Alternativ kann die Molekulardynamik (MD)-Simulation als ideales Werkzeug direkte Bilder der Formtransformationen mit atomarer Auflösung darstellen. Dementsprechend führten wir die MD-Rechnungen an metallischen Nanoplatten durch, um ihre Mechanismen der Morphologieänderung durch Beschreibung des Krümmungs- und Knickprozesses aufzuzeigen. Metalle mit kubisch-körperzentrierten (bcc) Gittern werden angesprochen, da es trotz ihrer gemeinsamen Existenz in Experimenten noch immer an relevanten Erkenntnissen über ihre Formstabilität mangelt [16]. Diese Studie dient als Referenz sowohl zur Synthese als auch zur Anwendung dieser metallischen Nanoplättchen.

Methoden

Eisen(Fe)-Nanoplättchen mit bcc-Gitter (Gitterkonstante a =2,8665 Å), die aus drei Atomschichten bestehen (der Durchmesser d =32a in den meisten Fällen) wurden zuerst modelliert. Anfänglich werden ihre Oberflächen jeweils auf unterschiedliche Ebenen mit niedrigem Index eingestellt, einschließlich (111), (001) und (110). Darüber hinaus wurden auch andere bcc-metallische Nanoplättchen wie W, Nb, Mo und Cr entsprechend konstruiert. Diese Modelle wurden über Befehle im MD-Paket LAMMPS [17] erstellt.

Die interatomaren Wechselwirkungen wurden durch die entsprechenden Potentiale der Embedded-Atom-Methode (EAM) beschrieben [18,19,20,21,22]. Die anfänglichen Modelle wurden zunächst durch die konjugierte Gradientenmethode (CGM) quasi-statisch auf einen lokalen minimalen Energiezustand entspannt. Nach vollständiger Relaxation wurde eine kontinuierliche Erwärmung in einem kanonischen (NVT) Ensemble mit LAMMPS simuliert und die Zustandsgrößen (Energie und Spannungstensor) entsprechend exportiert. Die Temperatur wurde so eingestellt, dass sie von 1 auf 300 °K (oder höher) mit einer Schrittweite von 1 °K ansteigt. Bei einem Zeitschritt von 2 °fs wird die Relaxationszeit von 200 °sek bei jeder Temperatur verwendet, und die statistisch gemittelten Mengen werden aus den letzten 8 ps. Die Unsicherheit der Simulationen beruht hauptsächlich auf zwei Aspekten:der Genauigkeit der Potentiale und der Konvergenz der Energie bei jeder Temperatur. Beachten Sie, dass die von uns verwendeten Potentiale in molekularen Simulationen weit verbreitet und wiederholt verifiziert wurden [23,24,25,26,27], während 200 ps als ausreichend untersucht werden, damit das System sein thermisches Gleichgewicht erreichen kann, glauben wir daher, dass unsere Simulationen sind zuverlässig.

Außerdem ist der lokale Spannungstensor des i_ten Atom wurde berechnet durch

wobei α und β könnte x . sein , y , und z; F _ij und R _ij sind die Kraft und der Abstand zwischen den Atomen i und j , bzw. [28]. Ω_i ist das lokale Volumen, das mit dem Volumen der Voronoi-Polyeder identifiziert werden kann, das durch die senkrechten Ebenen gebildet wird, die die Linien zwischen Atom i . halbieren und alle seine Nachbaratome, die mit der Methode des gleichen Volumens berechnet wurde [29].

Ergebnisse und Diskussion

Mit steigender Temperatur entwickeln sich die Morphologien der drei Fe-Nanoplättchen mit unterschiedlichen Mustern. Die oberen Diagramme im linken Feld von Abb. 1 zeigen ihre temperaturabhängigen potentiellen Energien (E _p ). Für die drei Nanoplättchen führen Kristallebenen mit unterschiedlichen Miller-Indizes zu einer klaren Hierarchie der strukturellen Stabilität. Den Berechnungen zufolge betragen die gemittelten potentiellen Energien pro Atom (in Abb. 1 nicht gezeigt) − 2,833, − 3,457 bzw. − 3,668 eV/Atom für die Anfangskonfigurationen mit (111), (001) und (110) Oberflächen. Wenn man bedenkt, dass die Nanoplättchen so dünn wie drei Atomschichten sind, liegt es nahe, dass ihre Energiewerte in der gleichen Größenordnung wie die Oberflächenenergien der drei entsprechenden Kristallebenen (2,58, 2,47 und 2,37 J/m ^{2 .) liegen} für (111)-, (001)- bzw. (110)-Flächen [30]). Bei deutlich höheren potentiellen Energien sind die Nanoplättchen mit flachen (111)- und (001)-Kristallebenen nicht in der Lage, ihre ursprüngliche Struktur wie konstruiert beizubehalten. Sie verwandeln sich sofort in metastabile Zustände mit gekrümmten Oberflächen (vgl. Schnappschüsse (a) und (b) im rechten Teil von Abb. 1). Im Gegensatz dazu weist die (110)-Nanoplatte die beste strukturelle Stabilität auf. Seine Morphologie (siehe Abb. 1c) bleibt über den gesamten untersuchten Temperaturbereich invariant, was durch die mit einem linearen Trend stetig ansteigende Energie bestätigt werden kann. Wie bei den anderen beiden Nanoplättchen weisen ihre Formverformungen unterschiedliche Merkmale auf. Die am wenigsten stabile (111)-Nanoplatte nimmt unmittelbar nach der Relaxation eine unregelmäßige Form an (siehe Abb. 1a), und diese unregelmäßige Geometrie erleichtert das Fortschreiten der Schrumpfung zu einem kompakten Partikel. Daher nimmt seine potentielle Energie periodisch ab und erreicht schließlich das viel niedrigere Niveau als die (001)-Nanoplatte. Die Satteloberfläche der in Abb. 1b gezeigten (001)-Nanoplatte bleibt jedoch erhalten, bis sie bei etwa 200  K zu unregelmäßigen Partikeln wird. Die Entwicklung dieser Struktur mit mittlerer struktureller Stabilität wird von einer relativ milden Energieänderung begleitet, die in vier . unterteilt werden kann Stufen, die durch Punktlinien in den Diagrammen der potentiellen Energie abgegrenzt sind.

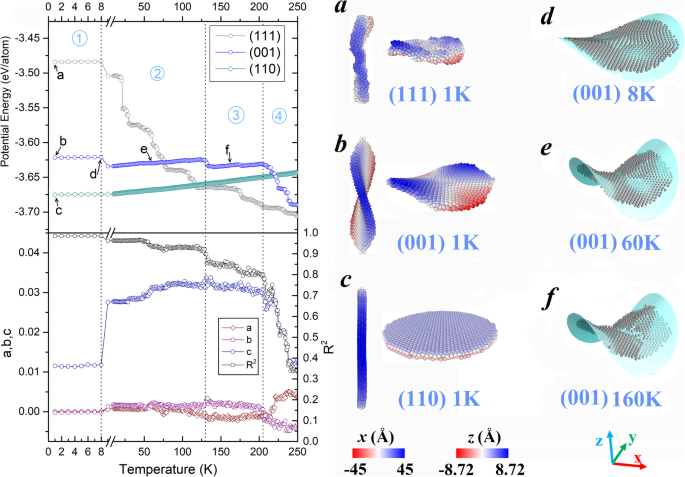
Linkes Feld:Temperaturentwicklung der potentiellen Energie von drei Nanoplatten (obere Plots) und die geometrischen Parameter, die durch Anpassen der mittleren Schicht der (001)-Nanoplatte (untere Plots) erhalten wurden; Rechtes Feld:a , b , c Schnappschüsse von drei Nanoplättchen nach Entspannung. d , e , f Schnappschüsse der mittleren Schicht in der (001)-Nanoplatte, aufgenommen bei repräsentativen Temperaturen. Cyan-Flächen bezeichnen die entsprechenden Anpassungsergebnisse

Um die Morphologievariation quantitativ zu untersuchen, haben wir die mittlere Schicht der (001)-Nanoplatte mit der quadratischen Oberflächengleichung z . angepasst = ax ² + by ² + cxy + d. Die Anpassungsergebnisse sind unter den Energiediagrammen in Abb. 1 angegeben, in denen a, b und c die geometrischen Parameter in der Gleichung sind und R ² bezieht sich auf das Bestimmtheitsmaß. R ² gibt den Anpassungsgrad an, und sein Idealwert ist gleich 1. Entsprechend den Energievariationen werden auch die entsprechenden Übergänge dieser Anpassungsparameter an den kritischen Punkten zwischen verschiedenen Stufen beobachtet. Die kritischen Temperaturen werden mit 8, 129 und 205 °K identifiziert. Während der ersten drei Stufen wird der Wert von R ² bleibt höher als 0,8, was bedeutet, dass die (001)-Nanoplatte ungefähr ihre Sattelform beibehält. Da der Parameter c offensichtlich größer ist als a und b, sind die beiden erhabenen Abschnitte der Nanoplatte entlang der [110]-Richtung ausgerichtet. Währenddessen steigt der Wert von c nach der ersten Stufe deutlich an, was auf die bemerkenswert nach oben gebogene Oberfläche hindeutet. Diese Tendenz ist deutlich an den repräsentativen Momentaufnahmen in Abb. 1d–f zu erkennen, die jeweils bei 8, 60 und 160 K aufgenommen wurden potenzielle Energie. Diese geringfügigen Anpassungen von Form und Energie enden bei 205 K, wo die vierte Stufe beginnt und die ursprüngliche Satteloberfläche allmählich zu einem unregelmäßigen Partikel mit weiter minimierter Energie zusammenfällt.

Um den Deformationsmechanismus der (001)-Nanoplatte im Detail zu untersuchen, untersuchten wir die Atomanordnungen und die Spannungsverteilung. Nach der Relaxation bei 1 K wird die potentielle Energie der Nanoplatte zu einem großen Teil durch Strukturbiegen entlang der [110]-Richtung freigesetzt, wie oben diskutiert. Während der Bildung dieses metastabilen Zustands wird keine Diffusion von Atomen zwischen den Schichten beobachtet. 2a zeigt die vertikale Ansicht seiner oberen Oberfläche. Beachten Sie, dass die Situation in den anderen beiden Atomschichten im Wesentlichen der im Folgenden beschriebenen ähnelt. Aus der Analyse der Gitterstruktur werden die meisten Atome (außer den weiß gefärbten) identifiziert, um (110)-Facetten zu bilden, dh das anfängliche (001)-Gitter wandelt sich in die am dichtesten gepackte Struktur im bcc-Kristall um und die Rekonstruktion findet statt . In Abb. 2a sind Atome in den benachbarten Facetten unterschiedlichen Farben zugeordnet. Die Elementarzelle jeder Facette ist durch ein grünes Rechteck gekennzeichnet, in dem die kurze gelbe Linie ihre jeweilige [110]-Richtung anzeigt. Wie zu sehen ist, sind diese (110)-Facetten, die in der unteren rechten Ecke von Fig. 2a schematisch dargestellt sind, in unterschiedlichen Orientierungen angeordnet. Die Verteilung ist ungefähr symmetrisch. Nehmen wir als Beispiel ein Viertel der Gesamtoberfläche, die Facetten 1 und 2 sind im Wesentlichen parallel ausgerichtet, und sie sind ungefähr senkrecht zu den Facetten 4 und 5. Die Atome in Facette 3 sind leicht verzerrt, um die Gitter der beiden Facetten 1 und aufzunehmen 2.

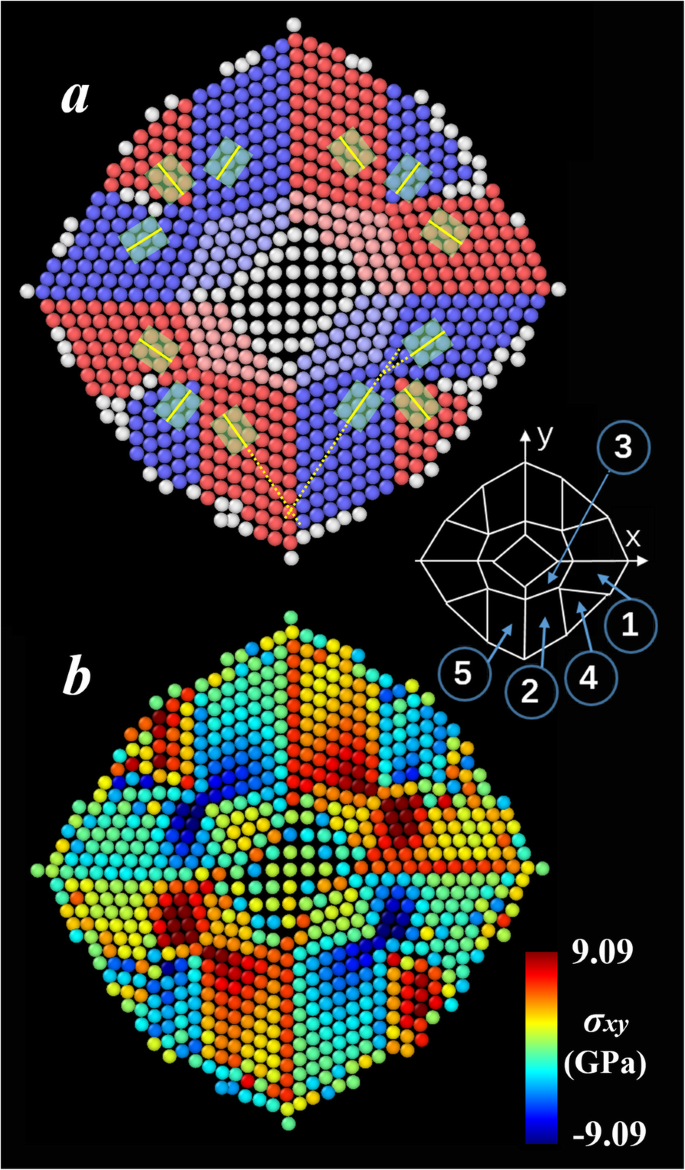
a Schnappschuss der oberen Oberfläche der (001)-Nanoplatte nach Relaxation bei 1 K und b die entsprechende Schubspannungsverteilung

Aus der Analyse der berechneten Spannung in der Nanoplatte ergibt sich, dass die Schubspannung eine offensichtliche Korrelation zur Verformung zeigt, die sie von anderen Komponenten des Spannungstensors unterscheidet. Daher betrachten wir die Schubspannung als primäre Antriebskraft der Biegeverformung und stellen ihre Verteilung in Abb. 2b dar. Offensichtlich ist die Spannung aufgrund der durch die Entstehung dieser (110)-Facetten induzierten Nahordnung nicht mehr gleichmäßig verteilt. Aus dem Vergleich von Abb. 2 a und b ergibt sich, dass die Spannungsverteilung stark mit der Orientierungsanordnung der Facetten korreliert. Die Spannungen in den roten Facetten in Abb. 2a sind im Allgemeinen positiv, während sie in den blauen negativ sind. Diese Beobachtung legt nahe, dass sich die roten und blauen Facetten grob in die entgegengesetzte Richtung bewegen. In der Nähe der Korngrenzen werden signifikante Spannungslücken beobachtet. Diese akkumulierten Spannungen gehen mit der Bildung von (110)-Facetten einher und würden durch weitere Verformung der Nanoplatte freigesetzt.

Abbildung 3 zeigt zwei kritische Transformationen während der anschließenden Verformung der (001)-Nanoplatte. Um mit Abb. 2 konsistent zu sein, haben wir nur die Atome in der oberen Schicht dargestellt. Es werden Verteilungen sowohl der Spannung als auch der Z-Koordinaten dargestellt. Wie aus Abb. 3a ersichtlich ist, ähnelt die Spannungsverteilung bei 8 K der Situation bei 1 K (vgl. Abb. 2b) und die Biegung existiert (vgl. Abb. 3c und Abb. 1d). Wenn die Temperatur auf 9 K ansteigt, entwickelt sich die Biegung deutlich, wie in Abb. 3d zu sehen ist. Inzwischen kann man feststellen, dass die ursprünglich aufgebauten Spannungslücken verschwinden (vgl. Abb. 3 a und b). Aus dieser weiteren Biegeverformung resultiert die Freisetzung von Schubspannungen. Dementsprechend sinkt die potentielle Energie (vgl. Abb. 1) und die Nanoplatte geht in einen stabileren Zustand über. Der zweite in Abb. 3 gezeigte Übergang beginnt bei 129 K und endet bei 134 K und erfährt einen breiteren Temperaturbereich. Beachten Sie, dass nach dem Übergang bei 9 K noch beträchtlich große positive Spannungen im mittleren Bereich der Oberfläche vorhanden sind (vgl. Abb. 3b). Tatsächlich bleibt dieser Spannungszustand während der gesamten zweiten Stufe des Formänderungsprozesses (9–129 K) bestehen (vgl. Abb. 3e). In ähnlicher Weise ist es auch die treibende Kraft des folgenden Übergangs. Danach werden, wie in Fig. 3f zu sehen ist, diese roten Atome in Fig. 3e grün (oder blau), was darauf hinweist, dass die vorhandene positive Spannung abgebaut wird. Um die zwischen 129 und 134 K stattfindende Formumwandlung hervorzuheben, ist in Abb. 3 g und h nur die Hälfte der Atome in der oberen Fläche dargestellt, wobei der grüne Kasten den veränderten Bereich hervorhebt. Der Bereich im grünen Kasten knickt in Richtung −Z . ein Richtung, was zur Abweichung von der früheren Sattelform führt. Diese Abweichung könnte auch durch den offensichtlichen Abfall von R . bestätigt werden ² Wert in Abb. 1.

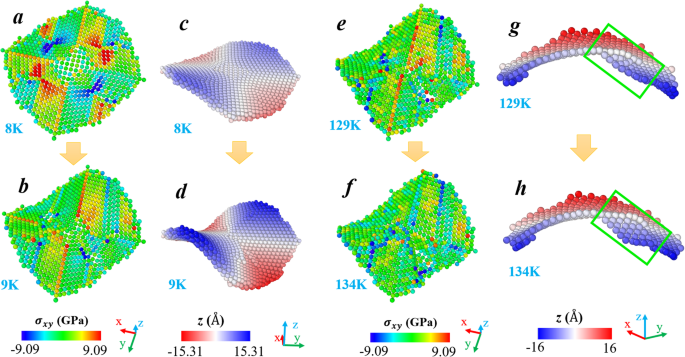
Zwei kritische Umwandlungen während der Temperaturentwicklung der (001)-Nanoplatte. Für jeden Zustand sind die Atome jeweils nach a . gefärbt , b , e , f ihre Werte der Schubspannung und c , d , g , h Z Koordinaten

Wie oben diskutiert, wird die Formtransformation der (001)-Nanoplatte durch die Scherspannung getrieben, deren Verteilung stark von der Gitteranordnung abhängt. Um die Möglichkeit der Anpassung der Morphologie durch kristallines Orientierungsdesign weiter zu veranschaulichen, haben wir eine Nanoplatte aus dreischichtigen (110)-Atomen modelliert, in der jede Schicht in vier unterschiedlich orientierte Facetten aufgeteilt ist, wie in Abb. 4a (bezeichnet als „modulierte (110) Nanoplatte“ im Folgenden). Orangefarbene Linien in der schematischen Darstellung zeigen ihre jeweiligen [110] Richtungen an. Um einen Vergleich zu erleichtern, haben wir die reguläre (110)-Nanoplatte in Abb. 4d gezeigt. Für die Anfangskonfiguration beträgt die berechnete potentielle Energie der modulierten (110)-Nanoplatte – 3.617 eV/Atom, höher als der entsprechende Wert der regulären (110)-Nanoplatte (−3.668 eV/Atom) aufgrund der Grenzflächenenergie. Im Gegensatz zum gleichmäßigen Muster der Schubspannungsverteilung der regulären (110)-Nanoplatte (vgl. Abb. 4e) treten in Abb. 4b bemerkenswerte Spannungslücken zwischen benachbarten Facetten auf. Diese Lücken sind bei den Atomen, die sich in der Nähe der Korngrenzen befinden, besonders bedeutsam. Nach der Relaxation bei 1 K erweitert sich der Bereich mit dem Spannungsgradienten, um mehr Atome um die Grenzen herum einzubeziehen, wie in Abb. 4c zu sehen ist. Währenddessen sinkt die gemittelte potentielle Energie auf −3.653 eV/Atom, und die Verbiegung der Konfiguration führt zu einer Sattelplatte, ähnlich der (001)-Nanoplatte. Da die Temperatur während der Formentwicklung der modulierten (110)-Nanoplatte kontinuierlich erhöht wird, können drei Stufen mit 179 und 277 K als kritische Punkte identifiziert werden. In der ersten Stufe bleibt die Sattelform trotz geringfügiger Schwankungen im Wesentlichen erhalten, wie in der eingefügten Momentaufnahme von 100 K veranschaulicht. Nach dem Übergang bei 179 K wandelt sich die Konfiguration jedoch wieder in eine scheibenartige Form um und behält diese Form ohne offensichtliche Veränderung bei. während der zweiten Phase (siehe zum Beispiel den eingefügten Schnappschuss von 200 K). Beachten Sie, dass um den kritischen Punkt (179 K) der erhabene Teil in der Mitte kombiniert mit der fragmentierten Oberflächenebene immer noch der Konfiguration mit niedrigerer Energie entspricht. Wenn die Temperatur schließlich 277 K erreicht, beginnt das System zu unregelmäßigen Partikeln zu schrumpfen (siehe nebenstehende Momentaufnahme von 300 K), was zu einer radikalen Reduzierung der potentiellen Energie führt, ähnlich der vierten Stufe der beschriebenen (001)-Nanoplatte vorhin. Beachten Sie, dass die potentielle Energie der regulären (110)-Nanoplatte bei 552 K drastisch abzunehmen beginnt (die entsprechenden Datenpunkte sind in Abb. 1 nicht vollständig dargestellt), die modulierte (001)-Nanoplatte zeigt eine deutlich verringerte Formstabilität. Diese Ergebnisse zeigen, dass die Gestaltung kristalliner Orientierungen ein effizienter Ansatz ist, um die Formstabilität zu modulieren.

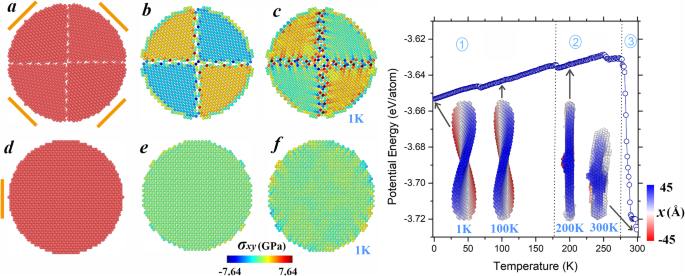
Linkes Feld:Schematische Darstellung von a die modulierte (110) Nanoplatte und d der reguläre. b , c , e , f Stellen Sie jeweils ihre Schubspannungsverteilungen in den Anfangskonfigurationen und bei 1  K dar. Rechtes Feld:Temperaturabhängige potentielle Energien der modulierten (110)-Nanoplatte. Schnappschüsse in den Einsätzen werden bei repräsentativen Temperaturen aufgenommen

Um ein umfassendes Verständnis der Formentwicklungsmuster zu erhalten, haben wir bcc Fe(001)-Nanoplättchen mit unterschiedlichen Durchmessern (einschließlich d =12a , 40a , und 50a ). Ihre potentiellen Energien und typischen Konfigurationen während des Erwärmungsprozesses sind in Abb. 5 gezeigt. Beachten Sie, dass die oben erwähnte Nanoplatte mit d =32a wird auch zum Vergleich gezeigt. Bei relativ hoher potentieller Energie durchläuft die kleinste Nanoplatte im Vergleich zu den anderen mehr Stadien. Wie in der Momentaufnahme von Abb. 5a zu sehen ist, ist die Nanoplatte mit dem Durchmesser von 12a behält seine flachen Oberflächen (a) bei, bis die Biegung bei 52 K beginnt (b) und sich schließlich die Sattelform bei 62 K bildet (c). Diese Sattelstruktur hält jedoch nicht in einem breiten Temperaturbereich, und die folgende Diffusion zwischen den Schichten findet bei 84 K statt, was zu einem starken Abfall der potentiellen Energie führt. Die verdickte Nanoplatte, die in Fig. 5(d) beispielhaft dargestellt ist, behält ihre Eigenschaften bei, bis eine weitere Konzentration bei etwa 200 K auftritt. Wie bei der Nanoplatte mit d =40a , wird die Sattelform stabil bei Temperaturen im Bereich von 1 bis 190 °K gehalten, bevor sie zu einem kompakten Partikel zusammenfällt. Im Fall der Nanoplatte mit d =50a , die Sattelform bleibt bis 134 K (angezeigt durch den Pfeil am „g“-Punkt) und verformt sich dann zu einer unregelmäßigen Struktur, wie in Abb. 5f dargestellt. Wie zu sehen ist, bei 190 K, wo die Nanoplatte mit d =40a fängt gerade an zu kollabieren, der mit d =50a hat seine Formtransformation vom Sattel zum Unregelmäßigen bereits abgeschlossen. Diese Beobachtungen legen nahe, dass mit zunehmendem Durchmesser von 12a bis 40a , wird der Temperaturbereich, in dem die Sattelform stabil sein könnte, allmählich breiter; wenn der Durchmesser jedoch weiter wächst (auf 50a B.) nimmt die Stabilität der Sattelform bis zu einem gewissen Grad ab. Das heißt, obwohl ein größerer Durchmesser zu einer besseren strukturellen Stabilität führt (niedrigere potentielle Energie im Grundzustand), ist dies nicht der einzige bestimmende Faktor, der die Stabilität beeinflusst, sondern auch der Einfluss anderer Aspekte (wie kinetische und Entropieeffekte) spielt eine wichtige Rolle. besonders wenn die Nanoplatte groß genug ist.

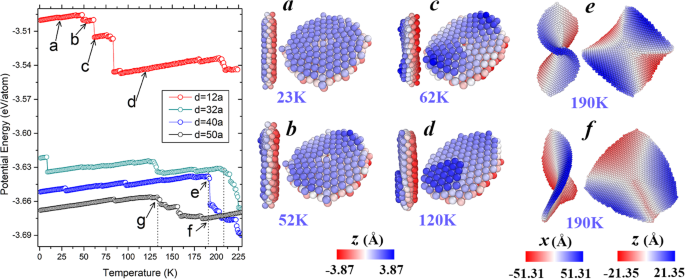
Linkes Bild:Temperaturentwicklung potentieller Energien von bcc Fe (001) Nanoplättchen mit unterschiedlichen Durchmessern. Rechtes Panel:Schnappschüsse der Nanoplatte mit d =12a um a 23 K, b 52 K, c 62 K und d 120 K; Schnappschüsse der Nanoplatte mit e d =40a bei 190 K und (f) d =50a bei 190 K

Neben dem Einfluss des Durchmessers werden auch Nanoplättchen unterschiedlicher Dicke berücksichtigt. Die potentielle Energie der Nanoplatte (d =32a ) mit unterschiedlichen Schichten sind in Fig. 6 gezeigt. Beachten Sie, dass die oben erwähnte 3-Atomschicht-Nanoplatte auch zum Vergleich gezeigt ist. Wie aus der Entwicklung der potentiellen Energien hervorgeht, zeigt sich, dass die Nanoplättchen mit 1 oder 2 Atomschichten im Vergleich zu denen mit 3 Schichten offensichtlich mehr Stadien durchlaufen. Tatsächlich kollabieren sie bei viel niedrigeren Temperaturen zu unregelmäßigen Formen. Im Gegensatz dazu ist die ursprüngliche Struktur der Nanoplatte mit 4 Schichten bis 97 K gut erhalten (vgl. Abb. 6a). Allerdings wandeln sich seine scheibenförmigen (001)-Ebenen bei 98 K in elliptische (110)-Ebenen mit höherer Stabilität (vgl. Abb. 1), was mit einer abrupten Abnahme der potentiellen Energie einhergeht. Diese erzeugte 4-Schicht-(110)-Nanoplatte behält ihre Konfiguration bei, bis das Schmelzen eintritt. Diese Ergebnisse zeigen, dass dickere Nanoplättchen im Allgemeinen eine bessere Stabilität aufweisen und die Sattelform nur bei relativ geringen Dicken existiert. Für weitere Einblicke in die Allgemeingültigkeit der Evolutionsmuster haben wir auch mehrere andere metallische bcc-Nanoplättchen (einschließlich W, Nb, Mo und Cr) mit Durchmessern von 32a . modelliert , die zunächst aus drei Schichten (001)-orientierter Atome bestehen. Abbildung 7 veranschaulicht die temperaturabhängigen potentiellen Energien dieser Nanoplättchen und die dazugehörigen atomistischen Schnappschüsse bei repräsentativen Temperaturen. Nach der Relaxation bei 1 K rekonstruieren alle ursprünglich gleichförmigen (001)-Ebenen und bilden (110)-Facetten mit unterschiedlichen Orientierungen. Bei niedrigeren Temperaturen tritt die Sattelform als universeller metastabiler Zustand in jeder Nanoplatte auf, ähnlich wie bei der Fe-Nanoplatte. Mit fortschreitender Erwärmung erfolgt die Umwandlung in ein unregelmäßiges Teilchen bei unterschiedlichen Temperaturen, bei denen die potentiellen Energien stark abnehmen. Im Vergleich dazu hält die sattelförmige Stufe für W-Nanoplatten im breitesten Temperaturbereich (bis 582 K), was auf ihre außerordentliche strukturelle Stabilität (anfänglich E _p =− 7,94 eV/Atom). Im Gegensatz dazu behält die am wenigsten stabile Cr-Nanoplatte ihre Sattelform nur bis 62 K bei, danach treten nacheinander Bumping und Buckling auf (vgl. die Schnappschüsse bei 61 und 250 K in Abb. 7). Bei den anderen beiden Nanoplättchen neigt Nb dazu, die ursprüngliche ebene Oberfläche wiederherzustellen (vgl. die Momentaufnahme von 135 K in Abb. 7), und Mo zeigt eine erhebliche Biegung (vgl. die Momentaufnahme von 150 K) vor ihrem endgültigen Kollaps. Diese beiden Situationen ähneln grob den modulierten (110) und (001) Fe-Nanoplättchen. Die obigen Ergebnisse zeigen, dass die in den Fe-Nanoplättchen beobachteten metastabilen Zustände auch in anderen bcc-metallischen Nanoplättchen existieren. Konfigurationen mit unterschiedlicher struktureller Stabilität folgen unterschiedlichen Evolutionsmustern. Darüber hinaus ist anzumerken, dass sich Nanoplättchen in den meisten unserer Simulationen bereits unterhalb der Raumtemperatur in kompakte Partikel umwandeln, was auf ihre geringe Größe zurückzuführen ist. Dennoch sind die identifizierten Evolutionsmechanismen von allgemeiner Bedeutung. Die Ergebnisse der relativen Stabilität dieser Nanoplättchen zwischen verschiedenen Ebenenorientierungen, Größen und Elementen konnten auf größere Systeme übertragen werden. Die Beschreibung von Formtransformationsmechanismen kann als Referenz dienen, um die gewünschten Morphologien durch Kontrolle der Kristallorientierung oder Legierung zu erhalten [31, 32].

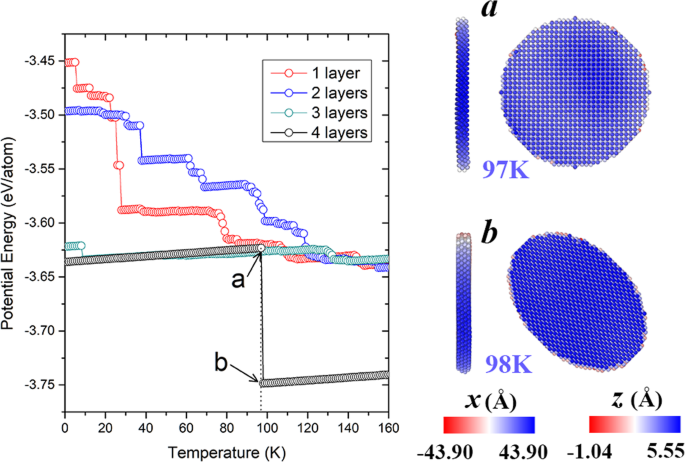
Linkes Bild:Temperaturentwicklung potentieller Energien von Fe(001)-Nanoplättchen mit unterschiedlicher Schichtzahl. Rechtes Panel:Schnappschüsse der Nanoplatte mit jeweils 4 Schichten bei a 97 K und b 98 K

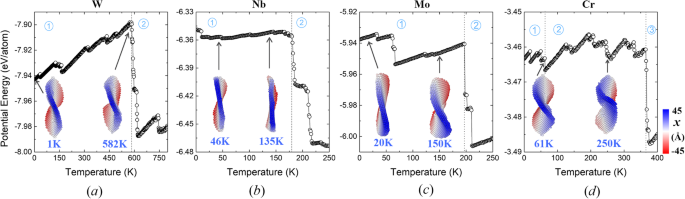
Temperaturentwicklung potentieller Energien von a W, b Nb, c Mo und d Cr-Nanoplättchen bzw. Momentaufnahmen der repräsentativen Staaten werden als Einschübe angezeigt

Schlussfolgerungen

Zusammenfassend wurde die Formentwicklung von bcc Fe-Nanoplatten mit Oberflächen mit niedrigem Index durch MD-Simulationen untersucht. Die Diskrepanz in der strukturellen Stabilität führt zu unterschiedlichen Mustern bei der Morphologietransformation. (110) Nanoplatte ist die stabilste und behält ihre ursprüngliche Konfiguration bis zur höchsten Temperatur. Im Gegensatz dazu sind (111)- und (001)-Nanoplättchen nicht in der Lage, fest zu existieren, beide neigen dazu, selbst unterhalb der Raumtemperatur in unregelmäßige Partikel zu zerfallen. Vor diesem endgültigen Kollaps wandelt sich die Oberfläche der (001)-Nanoplatte jedoch in (110)-Facetten mit unterschiedlichen Orientierungen um und bildet zwischenzeitlich eine Sattelform, die in einem relativ breiten Temperaturbereich hält. Dieser Transformationsprozess wird durch die Schubspannung getrieben, deren Verteilung eng mit der Facettenanordnung zusammenhängt. Weiteres Biegen und Knicken beim anschließenden Erhitzen entspricht der Spannungsfreisetzung. Darüber hinaus wurden Simulationen an der modulierten (110)-Nanoplatte, (001)-Nanoplatten mit unterschiedlichen Durchmessern und Dicken und anderen bcc-metallischen (001)-Nanoplatten durchgeführt. Die Ergebnisse zeigen, dass die Formentwicklung durch Facettenorientierungen, Plattengrößen und Komponenten abgestimmt werden kann. Diese Studie offenbart den Mechanismus der Formentwicklung von bcc-metallischen Nanoplättchen auf atomarer Ebene und bietet somit eine theoretische Grundlage für die Morphologiekontrolle bei der Synthese metallischer Nanomaterialien.

Verfügbarkeit von Daten und Materialien

Alle während dieser Studie generierten oder analysierten Daten sind in diesem veröffentlichten Artikel enthalten.

Abkürzungen

a:

Gitterkonstante

bcc:

Körperzentriert-kubisch

d:

Durchmesser

EAM:

Eingebettete Atommethode

E _p :

Potentielle Energie

MD:

Molekulardynamik

R ² :

Bestimmtheitsmaß

TEM:

Transmissionselektronenmikroskop