Starke Valenzelektronen-abhängige und logische Beziehungen elementarer Verunreinigungen in 2D-Binärhalbleitern:ein Fall einer GeP3-Monoschicht aus Ab-Initio-Studien

Einführung

Seit der Entdeckung von Graphen [1, 2], der Familie der zweidimensionalen (2D) Kristalle wie Übergangsmetalldichalkogenide (TMDs) [3], Silicen [4], Germanen [5], Phosphoren [6], Telluren [ 7] und so weiter haben aufgrund ihrer einzigartigen elektrischen, optischen und magnetischen Eigenschaften große Aufmerksamkeit auf sich gezogen [8,9,10]. Graphen verhält sich beispielsweise wie masselose Dirac-Fermionen, was zu einer ultimativen Hochladungsträgermobilität führt [11, 12]. Daher ist es vielversprechend, den 2D-Quantenspin-Hall-Effekt, die verbesserte Thermoelektrizität, die Supraleitung [13] und sogar den quantenanomalen Hall-Effekt [14,15,16] zu unterstützen. In Kombination mit der wachsenden Zahl verfügbarer Kristallstrukturdatenbanken wurden moderne Computerwerkzeuge verwendet, um neu unentdeckte 2D-Materialien zu erforschen. Bis jetzt werden mehr als 1000 2D-Materialien vorhergesagt und einige von ihnen werden experimentell hergestellt [17,18,19], was zu einem interessanten Gebiet der physikalischen, chemischen und Materialwissenschaften wird. Solche grundlegenden Studien und Erforschungen von 2D-Materialien fördern auch ihre großen potentiellen Anwendungen im Sensorfeld [20,21,22,23,24,25].

Jing et al. Neues 2D-Material gemeldet - GeP₃ Monolayer, der eine höhere chemische Stabilität als BP-Monolayer aufweist und ausgezeichnete elektronische und optische Eigenschaften besitzt. Darüber hinaus ist die 2D-GeP₃ Monoschicht scheint aufgrund des starken Quanteneinschlusses zwischen den Schichten eine halbleitende Eigenschaft zu haben. Sie fanden heraus, dass die GeP₃ Monoschicht weist eine moderate und einstellbare Bandlücke von etwa 0,55 eV auf [26]. Aufgrund der hohen Kapazität und guten Zyklenstabilität ist GeP₃ Dünnschicht wird für Lithium-Ionen-Batterien als vielversprechende Anode vorgeschlagen [27]. Liet al. untersuchte auch die GeP₃ Nanoband und entdeckten, dass die Bandlücken mit zunehmender Breite gerade-ungerade Oszillationen aufweisen können [28].

Die Dotierung ist eine praktische Strategie, um die elektronischen und magnetischen Eigenschaften der 2D-Schichtmaterialien des Wirts grundlegend abzustimmen [29]. Außerdem durchbricht es die Beschränkung eines einzelnen Materials in den Anwendungen vieler Bereiche und Geräte. Wie wir wissen, kann der 2D-Monoschicht-Halbleiter zu bemerkenswert verstärkten Elektron-Elektron-Wechselwirkungen führen, von denen sowohl aus theoretischen Vielteilchenrechnungen als auch aus Experimenten gezeigt wurde, dass sie eine Renormierung der großen Bandlücke und ein Exziton erzeugen [30, 31]. Verglichen mit der Dotierung in Volumenhalbleitern wird erwartet, dass die Dotierung in 2D-Halbleitern aufgrund des starken Elektroneneinschlusseffekts auch einige abnormale Verhaltensweisen zeigt, dh mit Bor oder Stickstoff dotiertes Graphen kann eine kleine Bandlücke am Dirac-Punkt öffnen, und die Die Bandlücke von Graphen kann auch um K (oder K')-Punkte herum effektiv geöffnet werden, indem kleine BN-Domänen eingeführt werden [32]. Bandlücken von schwarzem Phosphoren zeigen ein oszillierendes Verhalten, indem sie verschiedene Elemente mit geraden oder ungeraden Valenzelektronenzahlen dotieren [33, 34]. In dieser Arbeit versuchen wir, die Untersuchung von Dotierungselementen der Gruppe IV–V in 2D binärem GeP₃ . zu erweitern einschichtiger Halbleiter.

Hier haben wir die systematischen Studien des substitutiv dotierten GeP₃ . durchgeführt Monolayer mit den Dotierstoffen der Gruppe III bis VI. Die elektronischen Eigenschaften dotierter Systeme werden sowohl durch die Anzahl der Valenzelektronen der Dotierstoffe als auch durch die Dotierstellen dramatisch beeinflusst. Die zentralen Körner sind (1) für einen einzelnen Dotierstoff, die Ergebnisse hängen empfindlich von den Substitutionsstellen ab und die Substitution an zwei Arten von Dotierungsstellen führt zu völlig inversen Ergebnissen. (2) Die leitenden Eigenschaften der Co-Dotierung können durch einen logischen Operator durch die des einzelnen Dotierungsmittels abgeleitet werden. Darüber hinaus legt die berechnete Bildungsenergie verschiedener Dotierungsarten nahe, dass einige von ihnen energetisch sehr günstig gegenüber thermischen Fluktuationen sind.

Rechenmethoden

Alle unsere dichtefunktionaltheoretischen Berechnungen innerhalb der allgemeinen Gradienten-Approximation werden mit dem Vienna ab initio Simulation Package [35] durchgeführt. Die Austausch- und Korrelationsterme wurden mit dem Perdew-Burke-Ernzerhof (PBE)-Funktional beschrieben, und das projektorverstärkte Wellenpotential wurde verwendet, um die Elektron-Ion-Wechselwirkung zu beschreiben [36,37,38]. Das dotierte GeP₃ Monolayer wurde in einer periodischen 2 × 2 Superzelle mit 32 Atomen modelliert, und eine größere Superzelle von 3 × 3 wurde auch verwendet, um unsere Ergebnisse zu überprüfen. Ein Vakuumraum von etwa 20 Å entlang der z Richtung wurde gewählt, um die Wechselwirkung zwischen benachbarten Schichten zu eliminieren. Für die Einzeldotierung wurde ein Ge- oder P-Atom durch einen Dotierstoff der Gruppe III (IV, V und VI) ersetzt. Die geometrischen Strukturen werden durch Vergleich mit den berichteten Ergebnissen bestimmt, einschließlich der Gitterkonstante und der elektronischen Eigenschaften des Wirts GeP₃ Monoschicht. In den Dotierungssystemen dürfen sich alle Atome in den Superzellen entspannen, bis die Hellmann-Feynman-Kraft kleiner als 0,02 eVÅ ⁻¹ . ist , aber die Gitterkonstanten der Oberflächenzellen werden während der Atomrelaxation fixiert. Eine kinetische Energiegrenze von etwa 600 eV und 6 × 6 × 1 k -Netze wurden jeweils verwendet [39].

Um die Verfügbarkeit der Dotierstoffe im GeP₃ zu überprüfen Monoschicht, die Bildungsenergie (E _f ) von Dotierstoffen X (X =Gruppe III–VI) wird nach den beiden folgenden Formeln berechnet. Für einzelne Dotierstoffe haben wir Folgendes:

und für das Co-Dotierungssystem wird eine ähnliche Formel verwendet:

wo E _f (GeP₃ : X ) und E (GeP₃ ) sind die Gesamtenergien des X-dotierten und intrinsischen GeP₃ Monolayer mit der gleichen Superzelle. E (GeP₃ : XY ) ist die Gesamtenergie des kodotierten XY-Systems, E _X und E _J sind die Atomenergien der Dotierstoffe X oder Y bezogen auf ihre entsprechenden Volumenstrukturen und E _ich , E _j sind die Energien der substituierten Atome, wobei i und j das Ge- bzw. P-Atom bezeichnen [40, 41].

Ergebnisse und Diskussionen

Gerade-ungerade Schwingungen für Einzelelement-Dotierungssysteme

Abbildung 1a zeigt die Ober- und Seitenansicht der Struktur des GeP₃ 2 × 2 Superzelle, und Abb. 1b ist die entsprechende 2D-Brillouin-Zone von GeP₃ Monoschicht. Die optimierten Gitterkonstanten von GeP₃ Monolayer sind \(\mathrm{a}=\mathrm{b}=6.96\ {\AA}\), und die berechnete Bandlücke beträgt etwa 0.26 eV, was gut mit anderen theoretischen Berechnungen übereinstimmt.

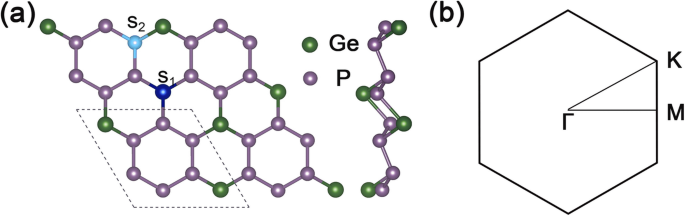
Geometrische Struktur und Brillouin-Zone von GeP₃ . a Draufsicht und Seitenansicht der optimierten Geometrie von GeP₃ mit einer 2 × 2 Superzelle. Die gestrichelte Linie zeigt die Elementarzelle von GeP₃ Monoschicht, S₁ die Stelle der Substitutionsposition der Ge-Stelle darstellt und S₂ stellt die Stelle dar, an der das Atom der Position P substituiert wird. b die 2D-Brillouin-Zone von GeP₃ Monoschicht

Zuerst haben wir die Bandstrukturen von Einzelelement-dotiertem GeP₃ . aufgetragen Monoschicht mit einem substituierten Ge-Atom (hier wählen wir B, C, N, O, Al, Si, P, S, Ga, As und Se als Dotierstoffe). Die Ergebnisse sind jeweils in Abb. 2a–l dargestellt. Wir können deutlich sehen, dass sich das Fermi-Niveau nach oben verschiebt und die Leitungsbänder für Gruppe V (N, P, As) aufgrund eines weiteren Elektron-Dotierungsmittels kreuzt, während für Gruppe III (B, Al, Ga)-Dotierungsmittel aufgrund eines Elektrons weniger, das man verschiebt sich nach unten und kreuzt die Valenzbänder. Zum Beispiel entspricht in Fig. 2f und j ihr Valenzbandmaximum gerade den teilweise besetzten Bändern, die in Fig. 2e und i gezeigt sind. Für Dotierstoffe der Gruppe IV (C, Si und Ge) und VI (O, S und Se) weisen die Systeme jedoch aufgrund der gleichen oder zweier weiterer Elektronen als das Ge-Atom ein Halbleitermerkmal auf. Eine solche Abstimmung des Übergangs von Halbleiter zu Metall ergibt sich aus der Besetzung der Anzahl von Valenzelektronen, nämlich der Besetzung ungerader (gerade) Valenzelektronen führt zu metallischen (halbleitenden) Eigenschaften.

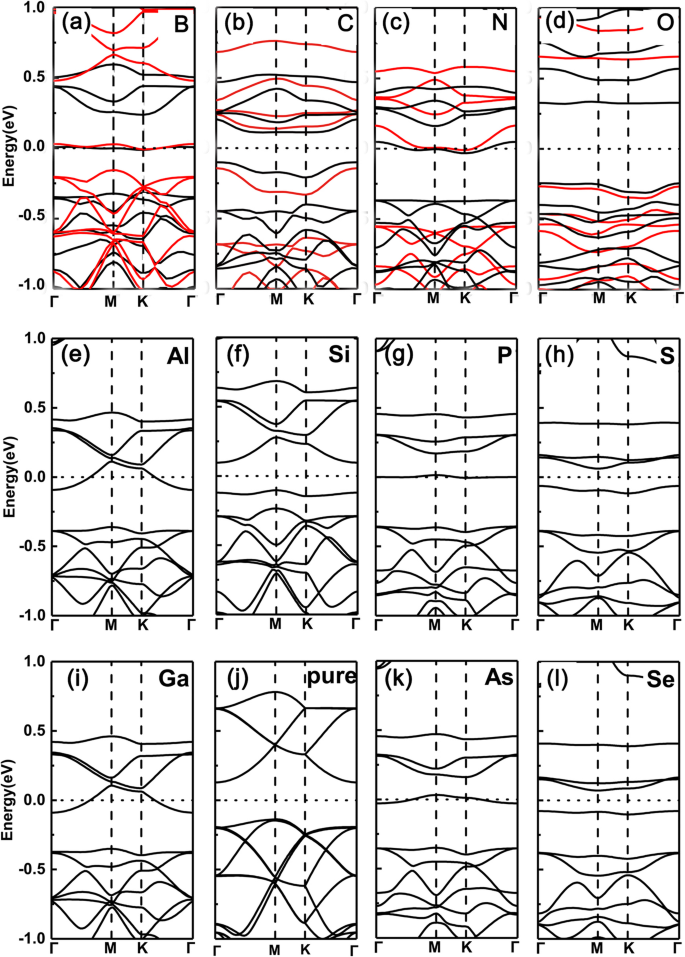
Bandstrukturen der verschiedenen Dotierstoffe in GeP₃ Monoschicht mit substituiertem Ge-Atom. a B, b C, c N, t Oh, e Al, f Si, g P, h S, i Ga, j Reines GeP₃ , k Wie, l Se. Berechnete Bandstrukturen für eine \( \mathsf{2}\times \mathsf{2} \) Superzelle mit verschiedenen Dotierstoffen in GeP₃ Monoschicht der Gruppe III bis VI, jeweils mit substituiertem Ge-Atom, zusammen mit dem von reinem GeP₃ Monoschicht. Sowohl die PBE- als auch die HSE06-Funktionalität werden in der obersten Reihe verwendet

Um die Gültigkeit der obigen Ergebnisse, die von PBE-Funktionalen abgeleitet wurden, zu bestätigen, verwenden wir auch die Funktionale der Hybriddichte (HSE06), um die dotierten Systeme der obersten Reihe zu überprüfen. Es ist klar, dass PBE-Funktionale tatsächlich die Fehler von Bandlücken aufgrund der Unterschätzung angeben. In unseren untersuchten Systemen haben jedoch alle beträchtliche Lücken, was bedeutet, dass die durch die PBE-Funktionale verursachten Fehler zwischen metallischen oder halbleitenden Eigenschaften normalerweise nicht auftreten (Dies liegt daran, dass in einigen kleinen Bandlücken von Halbleitern PBE-Funktionale normalerweise auftreten auf den Fehler zwischen leitenden und metallischen Eigenschaften). Darüber hinaus beschäftigen wir uns in unserer Studie mit den metallischen oder halbleitenden Eigenschaften und nicht mit den spezifischen Werten der Bandlücken. Im Vergleich zu den von PBE-Funktionalen abgeleiteten Lücken vergrößern sich die Lücken von HSE06-Funktionalen deutlich. Auch bei diesen bleiben die Metall-Halbleiter-Schwingungen intakt. Daher sind die auf der Grundlage von PBE-Funktionalen gezogenen zentralen Inhaltsstoffe zuverlässig.

Im krassen Gegensatz dazu sind die Fälle, in denen P-Atome durch dieselben Dotierstoffe substituiert werden, jedoch vollständig umgekehrt, wie in den Abbildungen 3a–l gezeigt. Das heißt, für Dotierstoffe der Gruppe V (N, As) und Gruppe III (B, Al, Ga) bleiben die dotierten Systeme halbleitende Eigenschaften, während für Gruppe IV (C, Si, Ge) und VI (O, S, Se) Dotierstoffe, die zu metallischen Eigenschaften übergehen (hier findet sich der gleiche Trend auch zwischen PBE- und HSE06-Funktionalitäten). Dies liegt daran, dass die Valenzelektronen gleich (zwei weniger) wie (als) das intrinsische GeP₃ . bleiben für Dotierstoffe der Gruppe V (Gruppe III), aber ein Elektron weniger (mehr) für Dotierstoffe der Gruppe IV (VI).

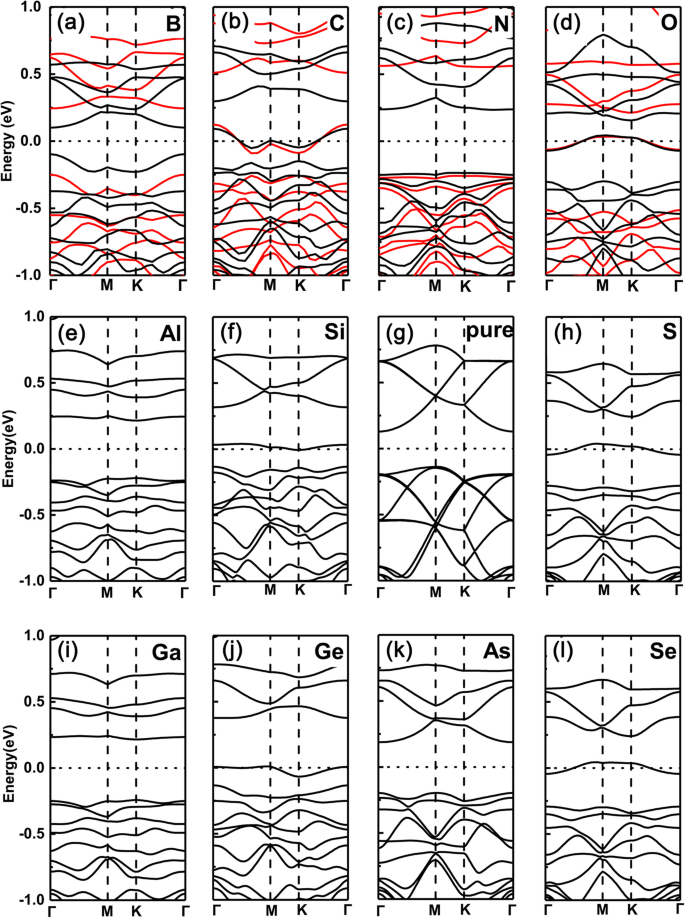
Bandstrukturen der verschiedenen Dotierstoffe in GeP₃ Monoschicht mit substituiertem P-Atom. a B, b C, c N, t Oh, e Al, f Si, g P, h S, i Ga, j Reines GeP₃ , k Wie, l Se. Berechnete Bandstrukturen für eine \( \mathsf{2}\times \mathsf{2} \) Superzelle mit verschiedenen Dotierstoffen in GeP₃ Monoschicht der Gruppe III bis VI, jeweils mit substituierten P-Atomen, zusammen mit der von reinem GeP₃ Monoschicht. Sowohl die PBE- als auch die HSE06-Funktionalität werden in der obersten Reihe verwendet

Um die Oszillationen des Übergangs von Halbleiter- zu Metalleigenschaften besser darzustellen, haben wir den sich ändernden Trend der Bandlücke als die verschiedenen Dotierstoffe aufgetragen, wie in Fig. 4a bzw. b gezeigt. Wir können deutlich sehen, dass sich der Übergang von halbleitenden zu metallischen Eigenschaften drastisch umkehrt. Insbesondere treten metallische (halbleitende)-halbleitende (metallische) Oszillationen auf, wenn die Ge(P)-Stelle als Dotierstoffe im Bereich von Gruppe III bis VI ersetzt werden. Außerdem haben wir ein interessantes Phänomen gefunden, das zeigt, dass die Größe der Bandlücke fast gleich der intrinsischen GeP₃ . bleibt Monoschicht, wenn die Dotierstoffe die gleichen Valenzelektronen wie das Ge-Atom haben. Wenn die Dotierstoffe jedoch zwei Elektronen mehr haben als das Ge-Atom, ändert sich die Größe der Bandlücken relativ stärker. Nichtsdestotrotz ändert sich für die Dotierstoffe an P-Zentren unabhängig von der Anzahl der Valenzelektronen die Größe der Bandlücken immer relativ stark. Dies kann durch den gemeinsamen Effekt des Radius des Atoms und der verfügbaren Valenzelektronen verstanden werden, nämlich Dotierstoffe mit fast gleichem (kleinerem oder größerem) Radius und Valenzelektronen wie (als) Ge-Atom verursachen einen relativ kleineren (größeren) Effekt auf das elektronische Eigenschaften wie die Bandlücke. Dies bedeutet, dass man nicht nur die Schwingungen von halbleitenden-metallischen Übergängen abstimmen kann, sondern auch die Größe der Bandlücke durch Auswahl geeigneter Dotierstoffe und der verschiedenen Dotierungsstellen.

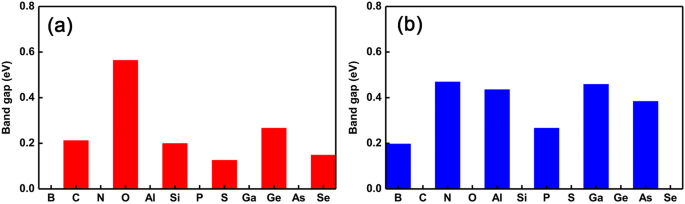
Bandlücken aller einfach dotierten Systeme. Bandlücken von dotiertem GeP₃ Monoschichten mit den verschiedenen Dotierstoffen im Bereich von Gruppe V bis VI. a die Substitution von Ge-Atomen und b jeweils die Substitutions-P-Atome

Um die Veränderung der elektronischen Strukturen verschiedener Dotierstoffe im GeP₃ . zu verstehen Monolayer haben wir die partielle Zustandsdichte (PDOS) der intrinsischen und Dotierungsgruppe IV–V in GeP₃ . aufgetragen Monolayer, wie in Abb. 5a–d gezeigt. Es ist deutlich zu erkennen, dass das Valenzbandmaximum (VBM) und das Leitungsbandminimum (CBM) des GeP₃ Monoschicht stammt hauptsächlich aus beiden p-Orbitalen von Ge- und P-Atomen. Wenn Dotierstoffe mit der gleichen Anzahl an Valenzelektronen wie das Ge-Atom, wie C und Si, verfügbar sind, gibt es Verunreinigungszustände, die sich gerade über der VBM des intrinsischen GeP₃ . befinden Monoschicht, weil das p-Orbitalenergieniveau von C und Si höher ist als das des P-Atoms (siehe Abb. 5a). Daher ist die Leitfähigkeitseigenschaft intakt und die Größe der Bandlückenänderung ist relativ klein. Wenn die Dotierstoffe jedoch ein Elektron mehr als das Ge-Atom haben, wie beispielsweise N, P und As, gibt es auch Störstellenzustände in der Bandlücke und die Störstellenzustände stammen aus der Hybridisierung der Aufspaltung von CBM (dominant) und den Zuständen von Dotierstoffen (siehe Abb. 5b).

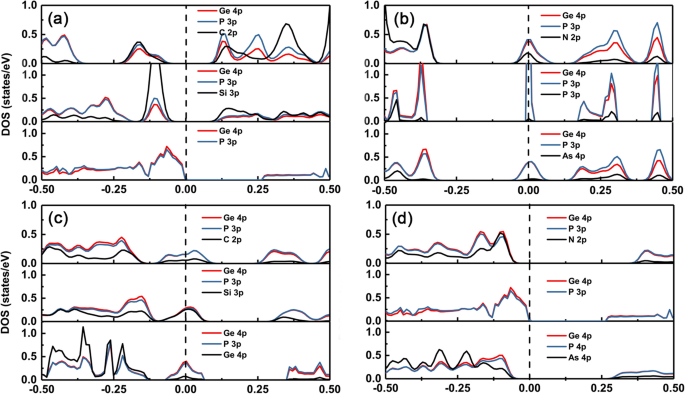
DOS für die dotierten Systeme. Die partielle Zustandsdichte (rechts) für Atome der Gruppe IV (C, Si und Ge) und der Gruppe V (N, P und As), dotiert mit GeP₃ . Die vertikale geschwärzte gestrichelte Linie ist das Fermi-Niveau. (a) und (b) substituiertes Ge-Atom, (c) und (d) substituiertes P-Atom

Bei der Dotierung an der P-Stelle hingegen, wenn die Dotierstoffe ein Valenzelektron weniger als das P-Atom haben, wie z ) und die Zustände der Dotierstoffe. Wenn die Dotierstoffe hingegen die gleiche Anzahl an Valenzelektronen wie das P-Atom haben, wie zum Beispiel Gruppe V, behalten die dotierten Systeme immer noch eine halbleitende Eigenschaft (siehe Abb. 5c). Die Bandlücken werden relativ größer als die von intrinsischem GeP₃ Monoschicht aufgrund der größeren Fehlanpassung der Gitterkonstanten. Darüber hinaus haben wir auch beobachtet, dass die Bandlücke des N-Dotanden größer ist als die des As-Dotanden, wenn P-Atome substituiert werden. Dies liegt daran, dass das p-Orbital-Energieniveau des As-Atoms höher ist als das des N-Atoms. Je höher das p-Orbital-Energieniveau ist, desto stärker ist die Aufwärtsverschiebung der Verunreinigungszustände weg von VBM (siehe Abb. 5d).

Logische Beziehungen für Co-Doping-Systeme

Auf der Grundlage der oben genannten Erkenntnisse zu einzelnen unterschiedlichen Dotierstoffen können wir daher Co-Dotierungssysteme entwerfen, die die von uns gewünschten elektronischen Eigenschaften erfüllen. Hier zeigen wir nur die Ergebnisse von B, C, N und O als Beispiele, um den Co-Dotierungseffekt zu veranschaulichen, aber die Schlussfolgerung ist robust gegenüber den verschiedenen ausgewählten Dotierstoffen. Zum Beispiel können bei der Co-Dotierung des Ge-Platzes beide Dotierstoffe mit einem Valenzelektron weniger natürlich zu halbleitenden Eigenschaften führen, während für die beiden Dotierstoffe mit einer Anzahl von Valenzelektronen weniger und mehr die Co-Dotierungssysteme somit auch haben eine halbleitende Eigenschaft.

Für die beiden Dotierstoffe mit einem weniger (mehr) und demselben Valenzelektron behalten die Co-Dotierungssysteme jedoch immer noch die metallische Eigenschaft als eine Eigenschaft weniger (mehr) von Valenzelektronen-Dotierstoffen bei. Vereinfacht gesagt wird diese Idee durch unsere weiteren Dichtefunktionaltheorie(DFT)-Berechnungen von codotierten Systemen genau bestätigt, siehe die Ergebnisse in Abb. 6a–l für die Bandstrukturen von B, C, N und O codotiertem GeP₃ einschichtig.

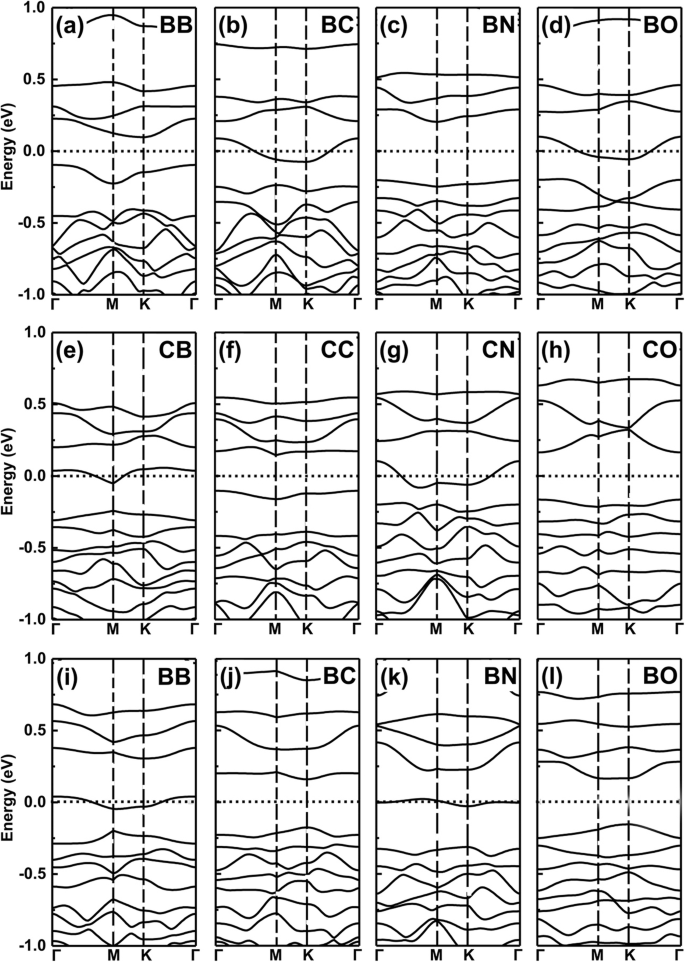
Bandstrukturen kodotierter Systeme. Die Bandstrukturen von B, C, N und O co-dotiertem GeP₃ Monoschicht. a –d Die beiden Dotierstoffe ersetzen zwei Ge-Atome in GeP₃ Monoschicht, e –h die beiden Dotierstoffe ersetzen zwei P-Atome, i –l die beiden Dotierstoffe ersetzen jeweils ein Ge-Atom und ein P-Atom

Jetzt können wir als Beispiel eine logische Operation „UND“ geben, wobei die metallische Eigenschaft auf „M“ und die Halbleitercharakteristik auf „S“ gesetzt wird. Wir definieren die logischen Beziehungen:M AND M = S, S AND S = S bzw. M AND S = M. Hierin gehorchen diese Ergebnisse, die wir oben erhalten haben, solchen logisch ähnlichen Beziehungen, zum Beispiel führen die Dotierstoffe mit einem Valenzelektronen mehr und einem weniger zu einer metallischen Eigenschaft, aber wenn wir die beiden Dotierstoffe als Co-Dotierung verwenden, wie B und N auf Ge-Plätzen, wie in Fig. 7a und b gezeigt, werden die codotierten Systeme erwartungsgemäß halbleitende Eigenschaften, siehe Fig. 6c. Wenn wir B-C co-dotiertes GeP₃ wählen Monoschichtsystem, weist es ein metallisches Merkmal auf, wie es bei M UND S der Fall ist (siehe Abb. 4a, b). Das gleiche gilt für die Co-Dotierung von C-N-, N-O- und B-O-Atomen in GeP_3, Ersetzen zweier Ge-Atome, zweier P-Atome oder eines Ge- und P-Atomes, wie in Abb. 7c–f gezeigt.

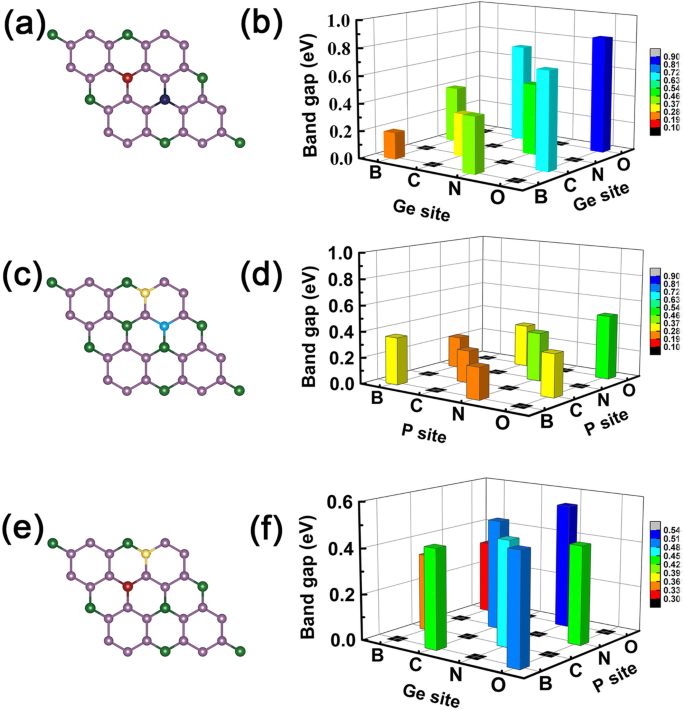
Bandlücken aller codotierten Systeme. Die Größe der Bandlücken von kodotiertem GeP₃ Monolayer, links die Skizze der co-dotierten Stellen und rechts die Größe der Bandlücken entsprechend den Dotierungselementen. a , b Die Dotierungselemente besetzen die beiden Ge-Atome. c , d Die Dotierungselemente besetzen die beiden P-Atome. e , f Der Fall für Dotierungselemente besetzen die Ge- bzw. P-Atome

Abschließend überprüften wir die Stabilität sowohl der einfach dotierten als auch der co-dotierten Systeme, um sicherzustellen, dass sie weiter im Experiment realisiert werden können. Die Bildungsenergie wird mit den Gl. (1) und (2) für Einzel- bzw. Co-Dotierungsfälle. Die Ergebnisse sind in Abb. 8a–e dargestellt. Aus Abb. 8a und b können wir deutlich erkennen, dass das E _f der einzelnen Dotierstoffe in Ge-Standorten sind alle ähnlich denen von GeP₃ Monoschicht (als Referenzpunkt auf Null gesetzt), ausgenommen C-, N- und S-Atome. Wir haben auch festgestellt, dass die Bildungsenergien für Dotierstoffe von B-, O-, P-, Ge- und Se-Atomen viel kleiner sind als bei anderen Dotierstoffen, was darauf hindeutet, dass sie in einem Experiment sehr leicht zu dotieren sind. Für Dotierstoffe in den P-Zentren haben Dotierstoffe von B-, O-, P- und Ge-Atomen eine relativ kleinere Bildungsenergie und sind auch leicht zu dotieren. C, N, Al und Ga sind nicht leicht zu dotieren.

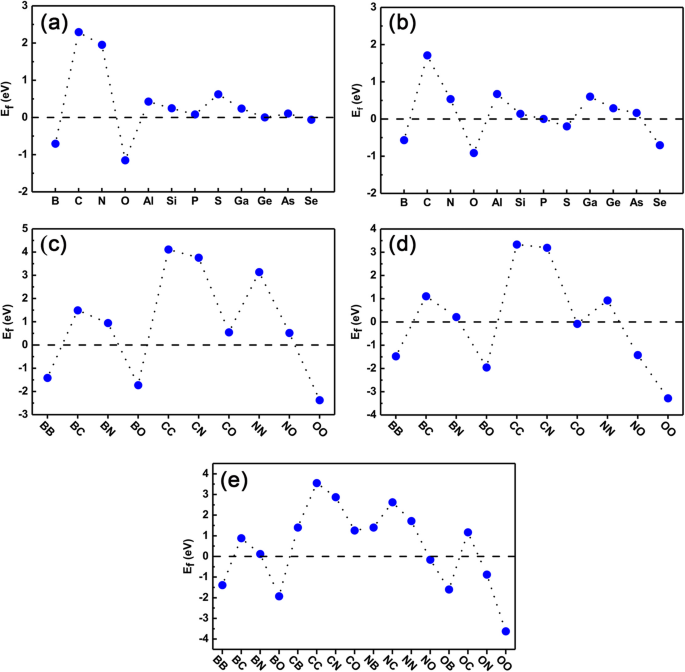
Bildungsenergie aller dotierten Systeme. Die berechnete Bildungsenergie von Einzelelement-Dotierungs- und Co-Dotierungssystemen. a , b das Dotierstoff-substituierte Ge-Atom bzw. das P-Atom sind; c –e Die durch zwei Ge-Atome, zwei P-Atome und ein Ge-Atom bzw. ein P-Atom substituierten Co-Dotanden

Was die Bildungsenergie der Co-Dotierung betrifft, sind Abb. 8c–e die Bildungsenergie der Co-Dotierung mit, wobei zwei Dotierstoffe die Positionen von zwei Ge-Atomen (bezeichnet als Ge-Ge-Zentren), zwei P-Atomen (bezeichnet als PP Zentren), ein Ge- und ein P-Atom (bezeichnet als Ge-P-Zentren). Hier zeigen wir nur die Ergebnisse der Dotierstoffe von B, C, N und O als Beispiel. Für Ge-Ge-Plätze und P-P-Plätze kann die Bildungsenergie der Co-Dotierung grob abgeschätzt werden, indem die Bildungsenergien der Einzelelement-Dotierung separat gemittelt werden. Offensichtlich sind die Bildungsenergien für BB-, BO- und OO-Codotierungen in Ge-Ge-Zentren und BB-, BO-, NO- und OO-Codotierungen in P-P-Zentren relativ klein und können im Experiment leicht realisiert werden. Für CC-, CN- und NN-Co-Dotierung in Ge-Ge-Zentren und CC- und CN-Co-Dotierung in P-P-Zentren sind die Bildungsenergien jedoch relativ höher, was darauf hindeutet, dass sie im Experiment schwer zu dotieren sind. Bei der Co-Dotierung mit Ge-P-Plätzen, wie in Fig. 8e gezeigt, wird die Bildungsenergie komplexer als bei der Co-Dotierung mit Ge-Ge- oder P-P-Plätzen, da es einen Ladungstransfer zwischen den Dotierstoffen gibt. In jedem Fall haben die BB-, BO- und OO-Codotierungen die kleineren Bildungsenergien, während die CC-, CN- und NN-Codotierungen größere Bildungsenergien aufweisen. Im Allgemeinen hängt die Bildungsenergie stark von der Anzahl der Valenzelektronen des Dotierungsmittels ab. Insbesondere wenn die beiden Dotierstoffe ein Elektron weniger (mehr) als die substituierten Atome aufweisen, ist die Bildungsenergie des kodotierten Systems niedriger (höher) als die der entsprechenden Einzeldotierstoffe wie BB (NN) kodotierten Ge-Zentren. Dies liegt daran, dass eine Konkurrenz zwischen der verringerten (erhöhten) Energie von reduzierten (erhöhten) Elektronen dotierter Systeme und der Coulomb-Abstoßung besteht. Bei der Loch-Loch-Co-Dotierung ist die Energie im ersteren Fall viel größer als im letzteren Fall, was zu einer ziemlich verringerten Bildungsenergie in Co-Dotierungssystemen wie BB führt, während bei der Elektron-Elektron-Co-Dotierung beide erstere und spätere Fälle führen zu einer höheren Bildungsenergie wie NN. Für Löcher- und Elektronen-co-dotierte Systeme wie BN-co-dotierte Ge-Zentren ist die Bildungsenergie jedoch dramatisch niedriger als in den entsprechenden einfach dotierten Fällen. Dies liegt daran, dass es in einem solchen codotierten System keinen Energiegewinn durch hinzugefügte oder reduzierte Elektronen in den Systemen gibt und die Coulomb-Wechselwirkung eine entscheidende Rolle bei der Bildung von codotierten Dotierstoffen spielt. Zusammenfassend lässt sich sagen, dass unsere bisherigen Studien zur Elementdotierung in schwarzem Phosphoren einen gewissen Grad an Universalität aufweisen und für die Anwendung anderer 2D-Halbleitermonoschichten, wie BN, MoS_{2 ., erwartet werden ,} und so weiter.

Um schließlich die Stabilität der obigen dotierten Systeme im Vergleich zum undotierten Fall zu überprüfen, führten wir die AIMD (ab-initio-Molekulardynamik) durch, um die Energie gegen die Zeit zu zeigen, wie in Abb. 9a–f gezeigt. Wir können deutlich sehen, dass die Schwingungsamplitude konvergent ist, solange die Zeit ausreichend ist (~ 4 ps), was bedeutet, dass die dotierten Systeme bei thermischen Fluktuationen bis zu 300 K für C-dotiertes GeP_{3<. nicht kollabieren /sub> in Abb. 9a. Selbst für das aktivste C-Atom-dotierte GeP3 , kann die extreme Temperatur bis zu 300 K betragen, wie in Abb. 9c gezeigt. Außerdem nehmen wir als Beispiel auch die Metall-Al-Substitution am Ge-Platz, das berechnete Ergebnis ist in den Abb. 9e und f dargestellt, aus denen wir deutlich erkennen können, dass die Energie-Schwingamplitude mit der Zeit allmählich abnimmt, d.h. die Energie könnte konvergent sein, solange die Zeit ausreichend ist und die Struktur des dotierten Systems thermisch stabil gegenüber Temperaturschwankungen ist. Daher ist zu erwarten, dass solche dotierten Systeme in weiteren Experimenten mit dem hochwertigen GeP3 . realisiert werden können Monolayer wird vorbereitet.}

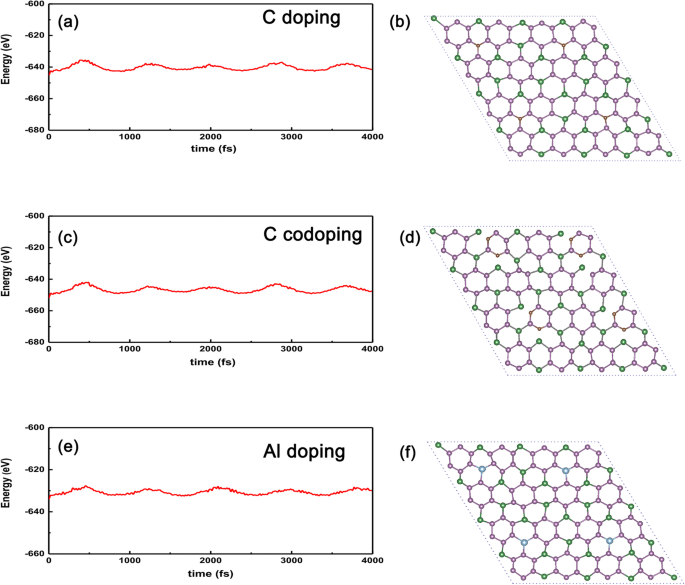
AIMD für die C-, Zwei-C- und Al-Atom-dotierten Systeme. AIMD bestätigt die thermische Stabilität von a C-Atom-dotiertes GeP₃ mit ersetzendem Ge-Atom, c zwei C-Atome dotiert mit GeP₃ mit Substitution von zwei P-Atomen und e Al-Atom-dotiertes GeP₃ mit Substitution bei 300 K. Die Strukturen in b C, d zwei C-Atom und f Al entsprechen ihren endgültigen Strukturen nach 4000 fs

Abschließend wollen wir die Reliabilität unserer hier vorgestellten Studie diskutieren. Unsere hier präsentierten Schlussfolgerungen sind theoretisch vorhergesagte Ergebnisse, aber sehr zuverlässig. Dies liegt daran, dass über unser hier verwendete Wirtsmaterial und seine Bulk-Phase aus geschichtetem GeP₃ . berichtet wurde existiert bereits [26]. Daher müssen unsere untersuchten, durch Dotierung induzierten verwandten Phänomene im Experiment weiter bestätigt werden, sobald die Monoschicht GeP₃ wird weiter realisiert. Dann könnte eine Dotierung der entsprechenden Atome durchgeführt werden. Der Einfachheit halber Dotieren eines Elektrons oder Lochs in einer Monoschicht GeP₃ könnte durch die Adsorption einiger Moleküle realisiert werden.

Schlussfolgerung

Zusammenfassend haben wir die elektronischen Eigenschaften von Dotierstoffen der Gruppe III bis VI in 2D-GeP₃ . untersucht Monoschicht und finden Sie, dass das dotierte GeP₃ mit Substitution am Ge-Platz zeigt Metall-Halbleiter-Oszillationen als Funktion der Anzahl der Valenzelektronen der Dotierstoffe, während solche Oszillationen bei Substitution am P-Platz umgekehrt werden. Basierend auf den Ergebnissen einzelner Dotierstoffe konnten wir die Leitungseigenschaften der Co-Dotierung in GeP₃ . vorschlagen , die durch eine einfache logische Operation erhalten werden kann. Schließlich berechnen wir die Bildungsenergien verschiedener Dotierstoffe und stellen fest, dass einige der codotierten Systeme, insbesondere für die Elektron-Loch- und Loch-Loch-Co-Dotierung, wegen der Coulomb-Anziehung energetisch günstiger sind. Unsere Ergebnisse stellen nicht nur ein neues Phänomen dar, sondern schlagen auch einen faszinierenden Weg zur Abstimmung der elektronischen Eigenschaften in 2D-Binärhalbleitern vor.

Verfügbarkeit von Daten und Materialien

Die während der laufenden Studie generierten und/oder analysierten Datensätze sind auf Anfrage beim entsprechenden Autor erhältlich.

Abkürzungen

1D:

Eindimensional

2D:

Zweidimensional

AIMD:

Ab-initio-Moleküldynamik

BP:

Schwarzes Phosphoren

CBM:

Leitungsband-Minimum

DFT:

Dichtefunktionaltheorie

HSE06:

Hybriddichtefunktional

PBE:

Perdew-Burke-Ernzerhof

PDOS:

Partielle Zustandsdichte

VBM:

Valenzband-Maximum