







Industrietechnik
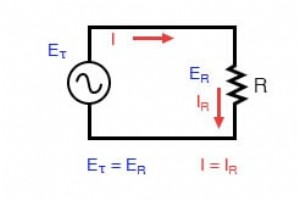
Momentanwerte in Wechselstromkreisen Reiner ohmscher Wechselstromkreis:Widerstandsspannung und -strom sind in Phase. Wenn wir Strom und Spannung für einen sehr einfachen Wechselstromkreis, bestehend aus einer Quelle und einem Widerstand (Abbildung oben), grafisch darstellen würden, würde dies
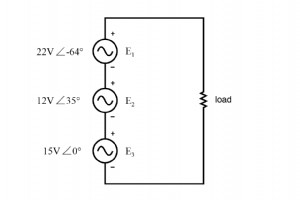
Lassen Sie uns drei Wechselspannungsquellen in Reihe schalten und komplexe Zahlen verwenden, um additive Spannungen zu bestimmen. Alle Regeln und Gesetze, die man im Studium von Gleichstromkreisen gelernt hat, gelten auch für Wechselstromkreise (Ohmsches Gesetz, Kirchhoffsche Gesetze, Netzanalyseve
Komplexe Zahlen sind für die Analyse von Wechselstromkreisen nützlich, da sie eine bequeme Methode bieten, die Phasenverschiebung zwischen Wechselstromgrößen wie Spannung und Strom symbolisch anzugeben. Für die meisten Menschen ist die Äquivalenz zwischen abstrakten Vektoren und realen Schaltungsgr
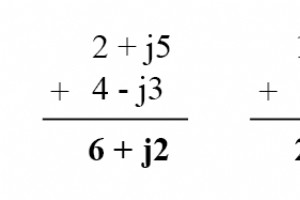
Da komplexe Zahlen, genau wie Skalarzahlen, legitime mathematische Einheiten sind, können sie wie jede andere Art von Zahlen addiert, subtrahiert, multipliziert, dividiert, quadriert, invertiert usw. werden. Einige wissenschaftliche Taschenrechner sind so programmiert, dass sie diese Operationen di
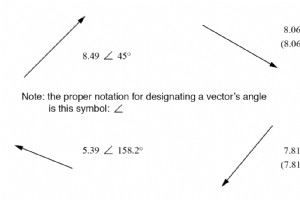
Um mit komplexen Zahlen zu arbeiten, ohne Vektoren zu zeichnen, benötigen wir zunächst eine Art mathematische Standardnotation. Es gibt zwei Grundformen der Notation komplexer Zahlen:polar und rechteckig . Polarform einer komplexen Zahl In der Polarform wird eine komplexe Zahl durch die Länge . bez
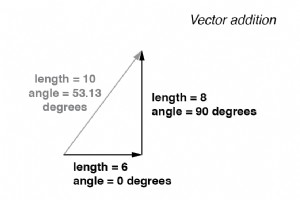
Wenn Vektoren mit ungewöhnlichen Winkeln addiert werden, addieren sich ihre Größen (Längen) ganz anders als die skalarer Größen:(Abbildung unten) Vektorgrößen werden bei ungleichen Winkeln nicht direkt addiert. Wenn zwei Wechselspannungen – 90 ° phasenverschoben – durch Reihenschaltung addie
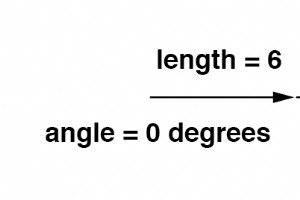
Denken Sie daran, dass Vektoren mathematische Objekte sind, genau wie Zahlen auf einem Zahlenstrahl:Sie können addiert, subtrahiert, multipliziert und geteilt werden. Addition ist vielleicht die am einfachsten zu visualisierende Vektoroperation, also beginnen wir damit. Wenn Vektoren mit gemeinsamen
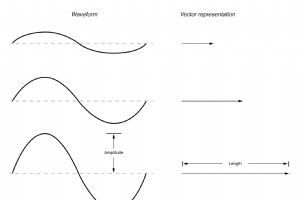
OK, wie genau können wir also Wechselspannungs- oder Stromgrößen in Form eines Vektors darstellen? Die Länge des Vektors stellt die Größe (oder Amplitude) der Wellenform dar, wie folgt:(Abbildung unten) Je größer die Amplitude der Wellenform ist, desto länger ist der entsprechende Vektor. Der
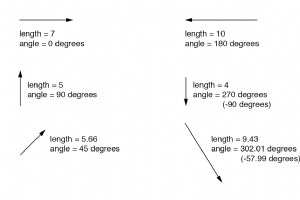
Wenn ich die Entfernung zwischen zwei Städten beschreiben müsste, könnte ich eine Antwort geben, die aus einer einzelnen Zahl in Meilen, Kilometern oder einer anderen linearen Maßeinheit besteht. Wenn ich jedoch beschreiben sollte, wie man von einer Stadt in eine andere reist, müsste ich mehr Infor
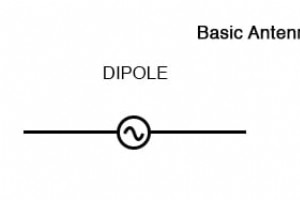
Eine der faszinierendsten Anwendungen von Elektrizität ist die Erzeugung unsichtbarer Energiewellen, die als Radiowellen bezeichnet werden . Der begrenzte Umfang dieser Lektion zum Thema Wechselstrom erlaubt keine vollständige Erforschung des Konzepts, einige der Grundprinzipien werden behandelt. M
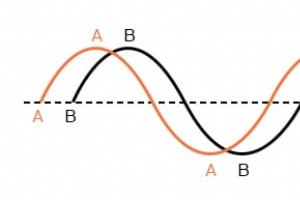
Die Dinge werden kompliziert, wenn wir zwei oder mehr Wechselspannungen oder -ströme in Beziehung setzen müssen, die nicht zueinander passen. Mit „außerhalb des Taktes“ meine ich, dass die beiden Wellenformen nicht synchronisiert sind:dass ihre Spitzen und Nullpunkte nicht zu den gleichen Zeitpunkte
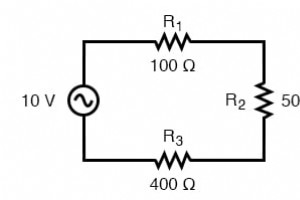
Im Laufe der nächsten Kapitel werden Sie lernen, dass Messungen und Berechnungen von Wechselstromkreisen aufgrund der komplexen Natur des Wechselstroms in Stromkreisen mit Induktivität und Kapazität sehr kompliziert werden können. Bei einfachen Schaltungen (Abbildung unten), die nur eine Wechselstr
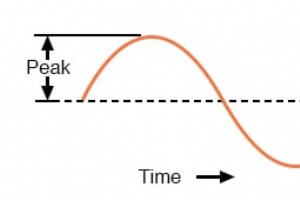
Bisher wissen wir, dass Wechselspannung in der Polarität und Wechselstrom in Richtung wechselt. Wir wissen auch, dass Wechselstrom auf verschiedene Weise wechseln kann, und indem wir den Wechsel über die Zeit verfolgen, können wir ihn als „Wellenform“ darstellen. Wir können die Wechselrate messen,
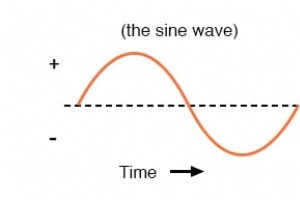
Wenn eine Lichtmaschine Wechselspannung erzeugt, ändert sich die Polarität der Spannung im Laufe der Zeit, jedoch auf ganz besondere Weise. Im zeitlichen Verlauf nimmt die „Welle“, die von dieser Spannung mit wechselnder Polarität von einer Lichtmaschine verfolgt wird, eine unterschiedliche Form an,
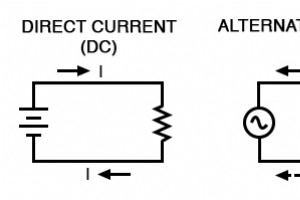
Die meisten Elektrostudenten beginnen ihr Studium mit dem sogenannten Gleichstrom (DC), d. h. Elektrizität, die in eine konstante Richtung fließt und/oder eine Spannung mit konstanter Polarität besitzt. Gleichstrom ist die Art von Elektrizität, die von einer Batterie erzeugt wird (mit eindeutigen P
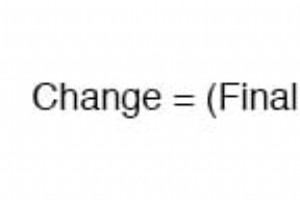
Manchmal ist es notwendig, die Zeitdauer zu bestimmen, die eine Blindschaltung braucht, um einen vorbestimmten Wert zu erreichen. Dies gilt insbesondere in Fällen, in denen wir eine RC- oder L/R-Schaltung entwerfen, um eine präzise Timing-Funktion auszuführen. Um dies zu berechnen, müssen wir unsere
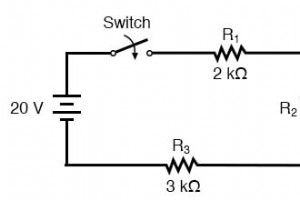
Was tun wir, wenn wir auf eine Schaltung stoßen, die komplexer ist als die bisherigen einfachen Reihenkonfigurationen? Nehmen Sie diese Schaltung als Beispiel: Die einfache Zeitkonstantenformel (τ=RC) basiert auf einem einfachen Serienwiderstand, der mit dem Kondensator verbunden ist. Auch di
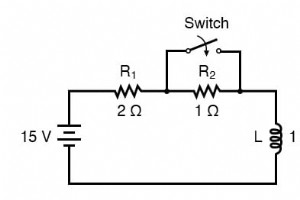
Unter Umständen müssen Sie einen DC-Blindstromkreis analysieren, wenn die Anfangswerte von Spannung und Strom nicht einem vollständig „entladenen“ Zustand entsprechen. Mit anderen Worten, der Kondensator könnte in einem teilweise geladenen Zustand starten, anstatt bei Null Volt zu starten, und eine
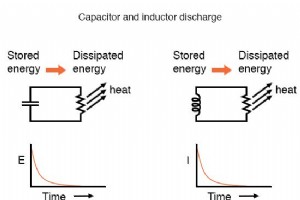
Informationen zu L/R-Zeitkonstanten Für neue Elektronikstudenten ist es oft verwunderlich, warum sich die Zeitkonstantenberechnung für eine induktive Schaltung von der einer kapazitiven Schaltung unterscheidet. Für eine Widerstands-Kondensator-Schaltung berechnet sich die Zeitkonstante (in Sekunden

Es gibt einen sicheren Weg, jeden der Werte in einem reaktiven Gleichstromkreis im Laufe der Zeit zu berechnen. Berechnung von Werten in einem reaktiven Gleichstromkreis Der erste Schritt besteht darin, die Anfangs- und Endwerte für jede Menge zu identifizieren, die der Kondensator oder die Indukti
Industrietechnik